Физика плазмы, 2021, T. 47, № 1, стр. 40-60
Особенности возбуждения электромагнитного поля в емкостном ВЧ-разряде. II. Симметричный разряд, полностью заполняющий вакуумную камеру при симметричном и несимметричном возбуждении
С. А. Двинин a, *, О. А. Синкевич b, **, З. А. Кодирзода c, Д. К. Солихов c, ***
a МГУ им. М.В. Ломоносова, физический факультет
Москва, Россия
b Национальный исследовательский университет Московский энергетический институт
Москва, Россия
c Таджикский национальный университет, физический факультет
Душанбе, Таджикистан
* E-mail: dvinin@phys.msu.ru
** E-mail: oleg.sinkevich@itf.mpei.ac.ru
*** E-mail: davlat56@mail.ru
Поступила в редакцию 10.02.2020
После доработки 12.05.2020
Принята к публикации 20.05.2020
Аннотация
Аналитически и численно исследуются электродинамические характеристики емкостного ВЧ-разряда низкого давления (частота столкновений электронов много меньше частоты поля) при возбуждении его электромагнитным полем частотой от 10 до 1000 МГц. Разряд полностью заполняет металлическую цилиндрическую разрядную камеру, содержит активный электрод большой площади и подложкодержатель, к которым подведен сигнал от ВЧ-генераторов. Разряд поддерживается поверхностными волнами, распространяющимися вдоль границы плазма–слой пространственного заряда–металл. Получены общие аналитические выражения для импеданса разряда, как четырехполюсника, и показано, что положение резонансов токов и напряжений, связанных с распространением поверхностных волн вдоль трехслойной структуры, как функции плотности электронов существенно модифицируется за счет возбуждения высших мод поля. В рамках матричной модели слоя пространственного заряда, рассмотрены режимы возбуждения поля симметричным и антисимметричным полями. При возбуждении антисимметричным полем необходим учет вклада в импеданс от слоя пространственного заряда, формирующегося у боковой стенки вакуумной камеры. Полученные результаты качественно согласуются с численным расчетом импеданса и распространения поля в разряде с помощью программы COMSOL Multiphysics®.
Статья посвящена теоретическому исследованию емкостного высокочастотного разряда с высокой плотностью электронов с электродами большой площади. Данная задача в последние 20 лет активно изучается в связи с разработкой плазменных реакторов, используемых технологических процессах [1–7]. Первые теоретические анализы таких разрядов использовали модель длинных линий, и предполагали поддержание разряда поверхностными волнами, распространяющимися вдоль границ электродов, металлической разрядной камеры и плазмы [8, 9]. Эти модели не объясняли ряда наблюдаемых в экспериментах эффектов: появления геометрического резонанса плазма–слой пространственного заряда (СПЗ), хотя он прекрасно объясняется в квазистатической модели для разряда малого размера, асимметрией разряда. В работе [10] исследовалась возможность подавления стоячих поверхностных волн за счет нарушения синхронизма волн у различных торцов плазмы, в [11, 12] – эффекты, связанные с асимметрией электродов, в [13–15] – влияние структуры электромагнитного поля на пространственную однородность плазмы. В [16–19] предложено использовать изменение фазы между ВЧ-напряжениями, подаваемыми на верхний и нижний электроды, для управления распределением поля и повышения степени однородности плазмы. Поскольку при этом изменении фазы происходит возбуждение не только симметричных поверхностных волн, но и антисимметричных, начались исследования разрядов при антисимметричном возбуждении [20, 21]. Появились работы, учитывающие как электродинамические свойства разряда, так и интегральный баланс частиц и энергий (глобальные модели разряда) [22, 23], мультичастотное возбуждение плазмы [24, 25], вклад гармоник, возбуждающихся за счет нелинейности слоев пространственного заряда [26–28]. Было показано, что соизмеримость размеров вакуумной камеры и длины поверхностных волн обусловливает появление резонансов тока и резонансов напряжения на вольтамперных характеристиках разряда [8–12], а нелинейность слоев пространственного заряда существенно сказывается на значениях плотности электронов, при которых наблюдается резонанс [29–32]. В работе [33] обнаружен эффект спонтанного нарушения симметрии разряда в высокочастотном емкостном разряде. Численные моделирования [34–40] и экспериментальные исследования [41–45] разрядов вышеназванного типа показывают, что характеристики поверхностных волн, соотношение их амплитуд и амплитуд, высших нераспространяющихся волн, зависят от плотности плазмы, толщины слоя пространственного заряда, геометрии области возбуждения, генерации гармоник, что обусловливает непрерывное появление новых работ, посвященных исследованию этих процессов и вызывает сложности с интерпретацией получаемых результатов.
Данное исследование является продолжением работы [46] в которой рассчитаны характеристики поверхностных волн и получены простейшие выражения для импеданса разряда, частично заполняющего разрядную камеру. Здесь сравниваются результаты аналитического и численного расчетов импеданса разряда, полностью заполняющего цилиндрическую разрядную камеру, выполненную из металла, содержащую активный электрод и подложкодержатель, к которым подведен сигнал от ВЧ-генераторов. Для упрощения интерпретации и логического анализа результатов рассматривается линейная задача, в которой толщина слоев разряда считается не зависящей от плотности электронов, хотя это предположение зачастую не выполняются в эксперименте. В соответствии с этими предположениями глобально разряд можно описывать как линейный четырехполюсник, параметры которого зависят от размеров вакуумной камеры и электродов, средней плотности электронов в камере, характеристик слоев пространственного заряда, свойств цепи, подводящей ВЧ-сигнал от генераторов к электродам. Оригинальной частью данной статьи является учет совместного влияния как поверхностных волн и так высших нераспространяющихся мод в рамках трехслойной структуры из плазмы с двумя слоями пространственного заряда на границах, окруженной металлом. При аналитическом расчете амплитуд волн необходимо корректно записать условия ортогональности различных собственных волн и провести разложение поля источника по этим волнам. До настоящего времени такие исследования для структур с неоднородным заполнением и разными знаками диэлектрической проницаемости в разных пространственных областях волноведущей структуры не проводились. В данной работе показано: учет возбуждения высших мод приводит к существенному сдвигу плотностей электронов, при которых наблюдается резонанс по сравнению с работами, в которых эти моды не учитываются, а при антисимметричном возбуждении разряда существенную роль играет падение напряжения на слое пространственного заряда у боковой стенки. Изменение пространственной структуры электромагнитного поля может быть использовано для управления пространственным распределением плотности электронов в плазме. Аналитические формулы, полученные в данной работе, справедливы в широкой области частот ВЧ-генератора, превышающих ионную ленгмюровскую частоту. Более подробно границы применимости вычислений, проведенных в данной работе, обсуждены в ее первой части [46]. Расчеты по аналитическим формулам и результаты численного моделирования приведены для частоты 137 МГц, где рассматриваемые эффекты проявляются наиболее ярко, хотя играют существенную роль и при более низких, и тем более при более высоких частотах.
1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИМПЕДАНСА РАЗРЯДА
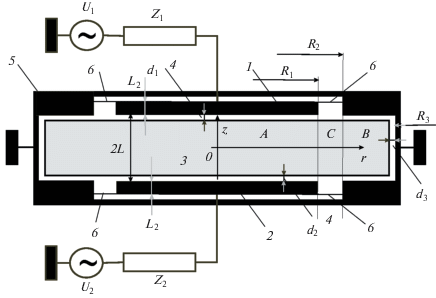
В продолжение работы [46], рассмотрим разряд в цилиндрической металлической камере радиуса R3 (рис. 1). Камера содержит два пластинчатых электрода 1 и 2 радиуса R1 с межэлектродным расстоянием 2L, подключенных к источникам ВЧ-мощности U1 и U2 на частоте ω с внутренними сопротивлениями Z1 и Z2 через отверстия в стенках вакуумной камеры (на рисунке не показаны). Эти электроды расположены на том же уровне, что и боковые торцы разрядной камеры, по существу являясь их продолжением, но отделенным от торцов диэлектрической свободной от плазмы щелью размером R2–R1. Образующаяся в разряде плазма 3 отделена от электродов и боковой части рабочей камеры 5 слоями пространственного заряда 4. Толщины слоев у электродов, торцов рабочей камеры и ее боковой стенки равны d1, d2 и d3 (в данной работе мы предполагаем d1 = d2).
Рис. 1.
Типичная схема экспериментальной установки:1, 2 – электроды, 3 – плазма, 4 – слои пространственного заряда между плазмой и стенкой (электродами), 5 – вакуумная камера, 6 – сечения, в которых рассчитывался импеданс разряда. 2L – межэлектродное расстояние, d1, d2, d3 – толщины слоев пространственного заряда.
Распределение плотности электронов ne в разрядной камере предполагается однородным. Относительная диэлектрическая проницаемость плазмы рассчитывалась в модели холодной плазмы [47, 48] $\varepsilon = {{\varepsilon }_{P}} = 1 - {{{{n}_{e}}} \mathord{\left/ {\vphantom {{{{n}_{e}}} {{{n}_{C}}\left( {1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)}}} \right. \kern-0em} {{{n}_{C}}\left( {1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)}}$; ν – эффективная частота столкновений электронов, e, m – заряд и масса электронов соответственно. В реальном разряде толщина слоев пространственного заряда определяется плотностью плазмы, напряженностью электрического поля в слое, его частотой, формой напряжения (наличием гармоник) и т.п. Слои рассматривались в рамках матричной модели [1], толщина слоя предполагалась постоянной, не зависящей от других параметров. Данное упрощение позволяет исключить из многопараметрического расчета импеданса разряда изменения толщины слоя пространственного заряда, которая может зависеть от плотности электронов и напряженности поля сложным образом. Частичным оправданием использования данного приближения может быть также тот факт, что очень часто разряд поддерживается одновременно полем нескольких частот, причем толщина слоя пространственного заряда определяется сигналом более низкой частоты.
Система уравнений Максвелла для описанной выше геометрии разрядной камеры (рис. 1) решалась с помощью пакета COMSOL Multiphysics® (лицензия принадлежит физическому факультету МГУ им. М.В. Ломоносова). Расчет проводился в области пространства, включающей центральную часть камеры (0 < r < R3, –L < z < L) и межэлектродное пространство, (R1 < r < R2, –L < |z| < < L + L2). На электродах ставились нулевые граничные условия для тангенциальной компоненты электрического поля. На внешней границе 6 (R1 < < r < R2, |z| = L + L2) азимутальное магнитное поле считалось заданным ${{H}_{\varphi }}\left( {r, \pm \left( {L + {{L}_{2}}} \right)} \right) = {{{{I}_{ \pm }}} \mathord{\left/ {\vphantom {{{{I}_{ \pm }}} {2\pi r}}} \right. \kern-0em} {2\pi r}}$. Отдельно рассматривались синфазный режим (токи электродов равны и ток, втекающий через верхний электрод I+, равен току, вытекающему через нижний I–, а ток на корпус вакуумной камеры равен нулю) и противофазный (равные токи втекают через электроды и замыкаются на корпус вакуумной камеры, ${{I}_{ + }} = - {{I}_{ - }}$). Разность потенциалов между электродом и камерой и импеданс разряда рассчитывались на границе 6 по формулам ${{U}_{ \pm }} = \int_{{{R}_{1}}}^{{{R}_{2}}} {{{E}_{r}}\left( {r, \pm (L + {{L}_{2}})} \right)dr} $, ${{Z}_{ \pm }} = \pm {{{{U}_{ \pm }}} \mathord{\left/ {\vphantom {{{{U}_{ \pm }}} {{{I}_{ \pm }}}}} \right. \kern-0em} {{{I}_{ \pm }}}}$. При синфазном возбуждении напряжение между электродами U12 будет равно 2U+. При этом цепь подвода энергии (область расчета L < |z| < L + L2) вносит дополнительный емкостной импеданс. Распределение плотности электронов в плазме при расчетах было однородно, а диэлектрическая проницаемость рассчитывалась в модели холодной плазмы.
Примеры расчетов импеданса разряда Z приведены на рис. 2 (синфазное возбуждение) и на рис. 3 (противофазное возбуждение), далее мы везде опускаем индексы ±. Частота поля 135.6 МГц, межэлектродное расстояние 2L = 8 см. Радиус разрядной камеры R3 10 (a), 20 (b) и 30 (с) см. Радиусы R1 и R2 при расчетах были равны 4, 14 и 24 см, и 5, 15 и 25 см, отношение ν/ω = 0.1. Толщины всех слоев пространственного заряда считались равными 0.3 см. Размер L2 был равен 1 см.
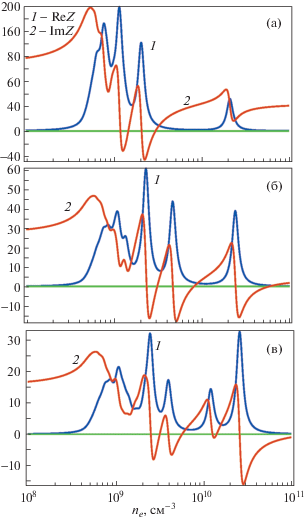
Рис. 2.
Импеданс разряда в Омах для полностью заполненной плазмой камеры (1 – Re Z, 2 – Im Z) толщина слоев d1 = d2 = d3 = 3 мм. Частота поля 135.6 МГц, межэлектродное расстояние 2L = 8 см. Радиус разрядной камеры 10 (a), 20 (б) и 30 (в) см. Отношение ν/ω здесь и ниже на всех рисунках равно 0.1. Синфазное возбуждение.
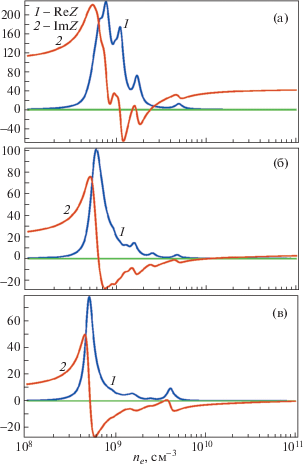
Рассчитанные зависимости импеданса от плотности электронов имеют очень сложный характер, который нуждается в физической интерпретации. При высоких плотностях электронов длина поверхностной волны близка к длине волны в вакууме и ее поле плохо проникает в плазму, поэтому импеданс выходит на постоянное значение. Укорочение поверхностной волны, которое происходит при уменьшении плотности электронов, приводит к появлению резонансов, если размеры системы кратны некоторому числу полуволн (мнимая часть импеданса проходит через ноль или бесконечность). На зависимостях импеданса Z от плотности можно выделить резонансы тока (в резонансной точке ${{d\operatorname{Im} Z} \mathord{\left/ {\vphantom {{d\operatorname{Im} Z} {d{{n}_{e}} < 0}}} \right. \kern-0em} {d{{n}_{e}} < 0}}$) и резонансы напряжения (${{d\operatorname{Im} Z} \mathord{\left/ {\vphantom {{d\operatorname{Im} Z} {d{{n}_{e}} > 0}}} \right. \kern-0em} {d{{n}_{e}} > 0}}$). На зависимостях Y(ne) = 1/Z(ne) знаки производных в резонансной точке ${{d\operatorname{Im} Y} \mathord{\left/ {\vphantom {{d\operatorname{Im} Y} {d{{n}_{e}}}}} \right. \kern-0em} {d{{n}_{e}}}}$ будут обратными. Резонансы для антисимметричного поля (поверхностная волна короче) наблюдается при более высоких плотностях электронов, чем для симметричного. Рассчитанные численно зависимости импеданса от плотности электронов имеют сложный изрезанный характер, который не может быть объяснен при учете возбуждения только одной поверхностной волны, без учета высших мод, поэтому при аналитическом исследовании этой задачи необходим одновременный учет высших мод, отсутствующий в упомянутых во введении работах.
2. АНАЛИТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ ИМПЕДАНСА, ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ СОБСТВЕННЫХ ФУНКЦИЙ ТРЕХСЛОЙНОЙ ВОЛНОВЕДУЩЕЙ СТРУКТУРЫ
Для аналитического расчета импеданса разряда, по аналогии с работой [46], представим поле внутри разрядной камеры в виде суммы собственных волн трехслойной структуры (ТС) металл–слой пространственного заряда–плазма–слой пространственного заряда–металл [8, 9, 12, 14]. Используя выражения, приведенные в [46] для электромагнитного поля при r < R1 для осевой компоненты электрического поля Ez и азимутальной компоненты магнитного поля Hφ, получим следующие представления:
(1)
$\begin{gathered} \, + {{A}_{{0 - }}}\left( {\begin{array}{*{20}{c}} {i{{{\mathbf{e}}}_{{0 - z}}}\left( z \right){{J}_{0}}\left( {{{h}_{{0 - }}}r} \right)} \\ {{{{\mathbf{h}}}_{{0 - \varphi }}}\left( z \right){{J}_{1}}\left( {{{h}_{{0 - }}}r} \right)} \end{array}} \right) + \\ \, + \sum\limits_{n = 1}^\infty {{{{\tilde {A}}}_{{n + }}}} \left( {\begin{array}{*{20}{c}} {i{{{\mathbf{e}}}_{{n + z}}}\left( z \right){{I}_{0}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \\ {{{{\mathbf{h}}}_{{n + \varphi }}}\left( z \right){{I}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \end{array}} \right) + \\ \end{gathered} $Здесь два первых слагаемых соответствуют возбуждению симметричной и антисимметричной поверхностных волн с радиальными постоянными распространения ${{h}_{{0 + }}}$ и ${{h}_{{0 - }}}$, а сумма содержит затухающие моды (постоянные затухания ${{\tilde {h}}_{{n \pm }}} = i{{h}_{{n \pm }}}$). Для поля волны при r > R1 можно записать аналогичные выражения
(2)
$\begin{gathered} \, + {{B}_{{0 - }}}\left( {\begin{array}{*{20}{c}} {i{{{\mathbf{e}}}_{{0 - z}}}\left( z \right){{Q}_{0}}\left( {{{h}_{{0 - }}}r} \right)} \\ {{{{\mathbf{h}}}_{{0 - \varphi }}}\left( z \right){{Q}_{1}}\left( {{{h}_{{0 - }}}r} \right)} \end{array}} \right) + \\ \, + \sum\limits_{n = 1}^\infty {{{B}_{{n + }}}} \left( {\begin{array}{*{20}{c}} {i{{{\mathbf{e}}}_{{n + z}}}\left( z \right){{K}_{0}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \\ {{{{\mathbf{h}}}_{{n + \varphi }}}\left( z \right){{K}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \end{array}} \right) + \\ \end{gathered} $В выражении (2)
– решения уравнения Бесселя, удовлетворяющие условию ${{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{3}}} \right) = 0$ на боковой стенке, откуда следует
(3)
$\, - \left( {{{B}_{0}}\left( {\begin{array}{*{20}{c}} {i{{{\mathbf{e}}}_{{0 \pm z}}}\left( z \right){{Q}_{0}}\left( {{{h}_{{0 \pm }}}r} \right)} \\ {{{{\mathbf{h}}}_{{0 \pm \varphi }}}\left( z \right){{Q}_{1}}\left( {{{h}_{{0 \pm }}}r} \right)} \end{array}} \right) + } \right.$В силу симметрии при расчетах рассматривается только одна из половин (z > 0) разрядной камеры, для нее же рассчитывается падение напряжение и импеданс. Для определения коэффициентов разложения в рядах (1) и (2) необходимо умножить скалярно выражения (3) на соответствующие собственные функции сопряженного оператора ${\mathbf{e}}_{{m \pm z}}^{ + }\left( z \right)$ и ${\mathbf{h}}_{{m{\mathbf{\varphi }} \pm }}^{ + }\left( z \right)$ [49, 50] и проинтегрировать по оси 0Z c учетом веса и условий ортогональности. Магнитные поля (Hφ) E-волн удовлетворяют уравнению (h – постоянная распространения, индекс ± опускаем)
(4)
$\begin{gathered} {{\nabla }_{ \bot }} \times {{{\mathbf{E}}}_{ \bot }} - ih\left( {{{{\mathbf{e}}}_{r}} \times {{{\mathbf{E}}}_{ \bot }}} \right) = ik\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} {{{\mathbf{H}}}_{ \bot }}, \\ {{\nabla }_{ \bot }} \times {{{\mathbf{H}}}_{ \bot }} + ih\left( {{{{\mathbf{H}}}_{ \bot }} \times {{{\mathbf{e}}}_{z}}} \right) = - ik\sqrt {\frac{{{{\varepsilon }_{0}}}}{{{{\mu }_{0}}}}} \varepsilon {{{\mathbf{E}}}_{ \bot }}. \\ \end{gathered} $В этом случае условия ортогональности имеют вид $\left( {{{{\mathbf{e}}}_{{n \pm }}},{\mathbf{h}}_{{m \pm }}^{ + }} \right) = {{\delta }_{{nm}}}N_{{m \pm }}^{2}$, $\left( {{{{\mathbf{h}}}_{n}},{\mathbf{e}}_{{m \pm }}^{ + }} \right) = {{\delta }_{{nm}}}\tilde {N}_{{m \pm }}^{2}$, где $\left\{ {{\mathbf{e}}_{{m \pm }}^{ + },{\mathbf{h}}_{{m \pm }}^{ + }} \right\}$ – полная система собственных функций сопряженного к (4) оператора, а ${{N}_{{m \pm }}}$, ${{\tilde {N}}_{{m \pm }}}$– соответствующие нормы. Аналогичные условия нормировки следуют из [50]. Выражения для норм совпадают с приведенными в Приложении 1 с точностью до постоянного множителя. При этом из системы уравнений (3) следуют выражения для коэффициентов ${{U}_{ \pm }} = \left( {{{U}_{1}} \pm {{U}_{2}}} \right)$
(5)
$\begin{gathered} {{A}_{{0 \pm }}}{{J}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right) - {{B}_{{0 \pm }}}{{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right) = - i{{U}_{ \pm }}\frac{{{\mathbf{e}}_{{0 \pm z}}^{ + }\left( L \right)}}{{N_{{0 \pm }}^{{E2}}}}, \\ {{A}_{{n \pm }}}{{I}_{1}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right) = - {{B}_{{n \pm }}}{{K}_{1}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right), \\ \end{gathered} $Отсюда получаем выражения для коэффициентов разложения
(6)
$\begin{gathered} \, \times {{\left( {{{J}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right) - \frac{{{{J}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}{{{{Q}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}{{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)} \right)}^{{ - 1}}}, \\ {{A}_{{n \pm }}} = - i{{U}_{ \pm }}\frac{{{{{\mathbf{e}}}_{{n \pm z}}}\left( L \right)}}{{N_{{n \pm }}^{{E2}}}} \times \\ \end{gathered} $Используя связь собственных функций для электрического и магнитного полей, получим
(7)
$\begin{gathered} {{I}_{ \pm }} = - 2\pi i{{R}_{1}}{{U}_{ \pm }}\sqrt {\frac{{{{\varepsilon }_{0}}}}{{{{\mu }_{0}}}}} \left( {{{{\left( {\frac{{{{J}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}{{{{J}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}} - \frac{{{{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}{{{{Q}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}} \times } \right. \\ \, \times \frac{k}{{{{h}_{{0 \pm }}}}}\frac{{{{{\mathbf{h}}}_{{0 \pm \varphi }}}\left( L \right){\mathbf{h}}_{{0 \pm \varphi }}^{ + }\left( L \right)}}{{N_{{0 \pm }}^{{H2}}}} + \sum\limits_{n = 1}^\infty {\left( {\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}} + } \right.} \\ \, + \left. {{{{\left. {\frac{{{{K}_{0}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}}{{{{K}_{1}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}}\frac{k}{{{{{\tilde {h}}}_{{n \pm }}}}}\frac{{{{{\mathbf{h}}}_{{n \pm \varphi }}}\left( L \right){\mathbf{h}}_{{n \pm \varphi }}^{ + }\left( L \right)}}{{N_{{n \pm }}^{{H2}}}}} \right). \\ \end{gathered} $Импеданс разряда при симметричном Z+ или антисимметричном Z– возбуждении может быть рассчитан по формуле
(8)
$\begin{gathered} {{Z}_{ \pm }} = \frac{{iL}}{{2\pi {{R}_{1}}}}\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \left\{ {{{{\left( {\frac{{{{J}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}{{{{J}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}} - \frac{{{{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}{{{{Q}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}}} \right. \times \\ \, \times \frac{k}{{{{h}_{{0 \pm }}}}}\frac{{{{{\mathbf{h}}}_{{0 \pm \varphi }}}\left( L \right){\mathbf{h}}_{{0 \pm \varphi }}^{ + }\left( L \right)L}}{{N_{{0 \pm }}^{{H2}}}} + \sum\limits_{n = 1}^\infty {\left( {\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}}} \right.} + \\ {{\left. {\, + {{{\left. {\frac{{{{K}_{0}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}}{{{{K}_{1}}\left( {{{{\tilde {h}}}_{{n \pm }}}{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}}\frac{k}{{{{{\tilde {h}}}_{{n \pm }}}}}\frac{{{{{\mathbf{h}}}_{{n \pm \varphi }}}\left( L \right){\mathbf{h}}_{{n \pm \varphi }}^{ + }\left( L \right)L}}{{N_{{n \pm }}^{{H2}}}}} \right\}}^{{ - 1}}}. \\ \end{gathered} $Более простой вид последней формулы по сравнению с общей, приведенной в [46], связан с тем, что согласно (5) коэффициенты разложения зависят только от приложенного к разряду напряжения и не зависят от протекающего по разряду тока. В общем случае напряжение на электродах U1, U2 и их токи I1, I2 связаны соотношением
Из полученного результата следует, что разомкнутая линия передачи между электродами (r < R1) и замкнутая линия передачи между точкой возбуждения и стенкой (r > R1) подключены к источникам питания последовательно. Линии, соответствующие поверхностным волнам и высшим модам поля, соединены параллельно. В данном приближении классический геометрический резонанс напряжений плазма–слой пространственного заряда невозможен. В одномодовом режиме резонанс напряжений происходит, если напряжение на внутренней разомкнутой линии (0 < r < R1) равно напряжению на внешней замкнутой линии (R1 < r < R3). Данное условие соответствует выполнению соотношения ${{Q}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right){{J}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right) - {{J}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right){{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right) = 0$.
Обращение тока в ноль означает равенство бесконечности импеданса одной из упомянутых выше соединенных последовательно линий ${{Q}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right) = 0$ или ${{J}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right) = 0$. При этом точка подвода мощности совпадает с узлом тока одной из волн. Согласно формуле (8) импеданс обращается в бесконечность (в отсутствие потерь), если диэлектрическая проницаемость плазмы равна нулю, так как в этом случае магнитное поле не возбуждается и отсутствует протекание тока по электроду и стенке трубки. Этот резонанс аналогичен резонансу трубки, ограниченной диэлектриком, и при учете емкости подводящей линии он сдвигается в область более высоких плотностей электронов [46]. Резонанс напряжений наблюдается в том случае, если емкостной импеданс разомкнутой центральной линии передачи компенсируется индуктивным импедансом замкнутой периферийной линии.
Согласно формулам Приложения I при плотностях электронов выше удвоенной критической $N_{{0 \pm }}^{2} > 0$ и $N_{{n \pm }}^{2} < 0$, и, следовательно, поверхностная волна вносит емкостной импеданс, а высшие моды – индуктивный. Однако в отличие от разряда, ограниченного диэлектрическими стенками [46], в данном случае амплитуды высших мод оказываются достаточно малыми, поскольку источники возбуждения находятся не в центральной области (здесь амплитуды полей высших мод велики), а в области слоя, где поля высших волн малы. Поэтому амплитуды высших мод и их вклады в импеданс должны быть существенно ниже, чем в предыдущем случае.
Результаты расчета импеданса разряда по формулам для синфазного и противофазного возбуждения (рис. 4) показывают, что в обоих случаях в области возбуждения поверхностных волн импеданс в среднем имеет индуктивный характер, который приносят нераспространяющиеся моды, но при учете импеданса, вносимого поверхностными волнами, он может быть и емкостным, и индуктивным в зависимости от радиуса и плотности плазмы. В случае симметричного возбуждения индуктивная составляющая импеданса выше из-за большей глубины проникновения волны в плазму (меньших значений постоянной затухания ${{\tilde {h}}_{{n \pm }}}$).
Рис. 4.
Импеданс разряда в Омах для полностью заполненной плазмой камеры (1 – Re Z, 2 – Im Z) толщина слоев d1 = d2 = d4 = 3 мм при симметричном (a–в) и антисимметричном (г–е) возбуждении. Частота 135.6 Мгц. Радиус разрядной камеры 10 (a, г), 20 (б, д) и 30 (в, е) см. Расчет по аналитическим формулам.
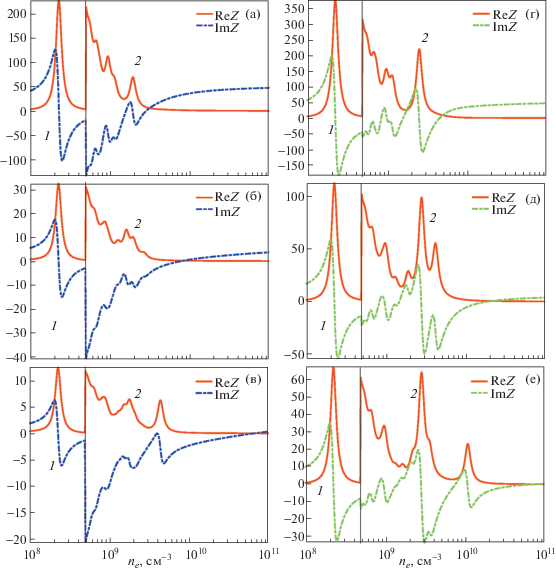
Резонансный характер зависимости импеданса от плотности электронов в условиях расчета сильнее проявляется в разряде меньшего размера, что связано с большим затуханием поверхностной волны при распространении к центру разряда. Поскольку импеданс разряда очень сильно зависит от плотности электронов, в области 1 (ne < 2nC) масштаб кривых на рисунке уменьшен в 20 раз.
Прямое сравнение аналитических расчетов (рис. 4) с численными (рис. 2, 3) невозможно, так как в первом случае рассчитывается импеданс в точке возбуждения (r = (R1 + R2)/2), а во втором – в сечениях 6 (рис. 1), поэтому к току, протекающему через разряд, добавляется ток, протекающий по отрезку линии передачи, подводящей ВЧ- сигнал к разряду. Поскольку длина этой линии много меньше длины волны, то, согласно [46], общий импеданс разряда будет
Результаты расчета по этой формуле показаны на рис. 5. Дополнительная емкость, вносимая внешней цепью, считалась равной 10, 30 и 50 пФ для радиусов разрядной камеры 10, 20 и 30 см, что примерно соответствует емкости цилиндрического конденсатора с радиусами электродов R1 и R2 и высотой цилиндра 1 см. Сопоставление с расчетом в COMSOL Multiphysics® (рис. 2, 3) дают качественное, а иногда и количественное, совпадение для симметричного разряда, несмотря на пренебрежение слоями пространственного заряда у боковой стенки, учете только трех электродинамических мод и пренебрежение конечным размером области возбуждения. Аналитические формулы правильно описывают в среднем индуктивный характер разряда в области концентраций электронов 5 × 108–5 × 109 см–3, положение резонансов и значение импеданса в нерезонансной области. Существенная погрешность наблюдается при описании формы резонанса токов, лежащего в области границы существования поверхностных волн (ne ~ 2nC), что связано с неприменимостью в этой области использованной для их описания теории возмущений.
Рис. 5.
То же, что и на рис. 4. Расчет по аналитическим формулам при учете дополнительной емкости, вносимой подводящей линией передачи.
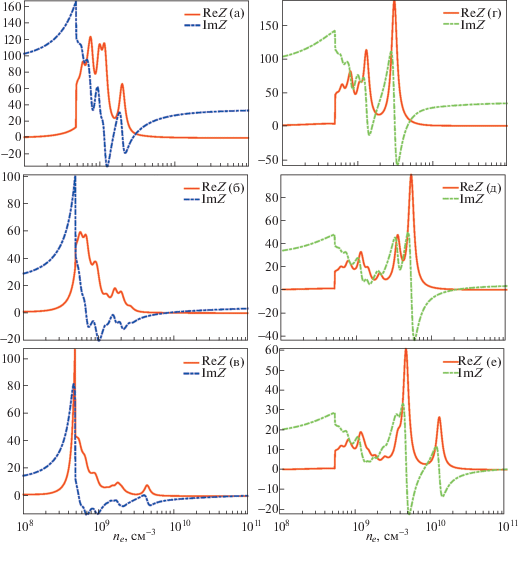
Для антисимметричного возбуждения, несмотря на общее качественное согласие аналитических и численных расчетов, наблюдается большее число резонансов и другое их расположение на оси плотностей электронов. Скорее всего, это отличие обусловлено отсутствием учета слоев пространственного заряда у боковой стенки в рассматриваемой модели. При симметричном возбуждении, когда ток течет по боковой стенке, параллельно границе плазмы, токи через СПЗ малы и их влияние несущественно. В антисимметричном случае ток через СПЗ течет, поэтому его вкладом в импеданс пренебречь нельзя и можно ожидать появления резонанса, аналогичного резонансу плазма–слой пространственного заряда, между индуктивным импедансом плазмы (или длинной линии между областью возбуждения и слоем), и импедансом слоя у боковой границы плазмы. Поскольку осевое распределение поля неоднородно, то возможно резонансное возбуждение поверхностных волн, распространяющихся вдоль боковой поверхности вакуумной камеры. Эти процессы в данной работе в силу их несущественности при симметричном возбуждении плазмы и математической громоздкости не рассматриваются.
3. ЧИСЛЕННЫЙ РАСЧЕТ ПРОСТРАНСТВЕННОЙ СТРУКТУРЫ ПОЛЯ В РАЗРЯДЕ И АНАЛИЗ ПРИРОДЫ РЕЗОНАНСОВ
Проведем сравнение результатов аналитического анализа с данными численного моделирования структуры электромагнитного поля с помощью пакета COMSOL Multiphysics® в широком диапазоне плотностей электронов для вакуумной камеры, размеры которой указаны в разд. 1. Ниже приведены результаты для плотностей электронов, для которых наблюдался резонанс токов и напряжений (см. рис. 2, 3) или резкое изменение реактивной части импеданса при увеличении мнимой.
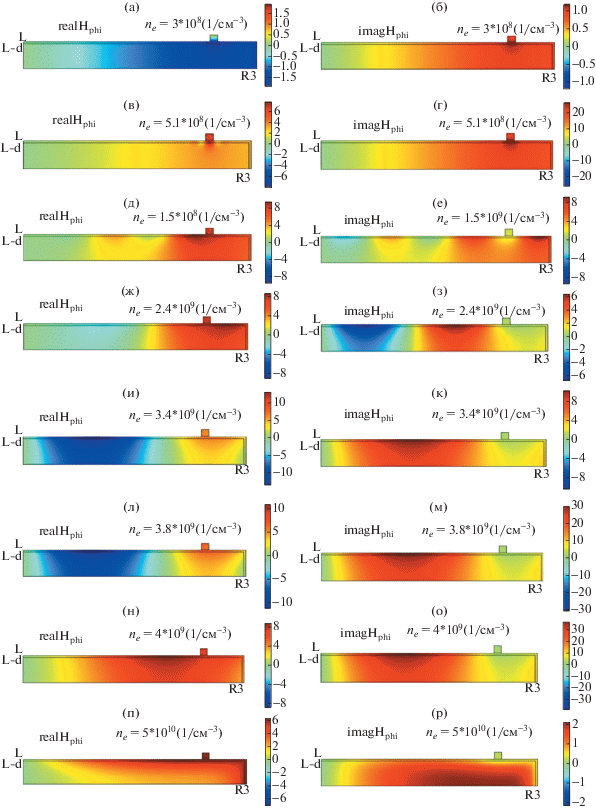
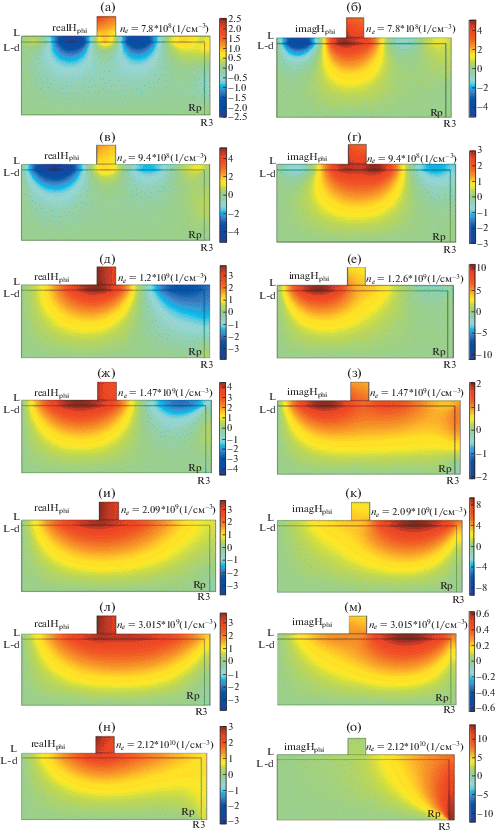
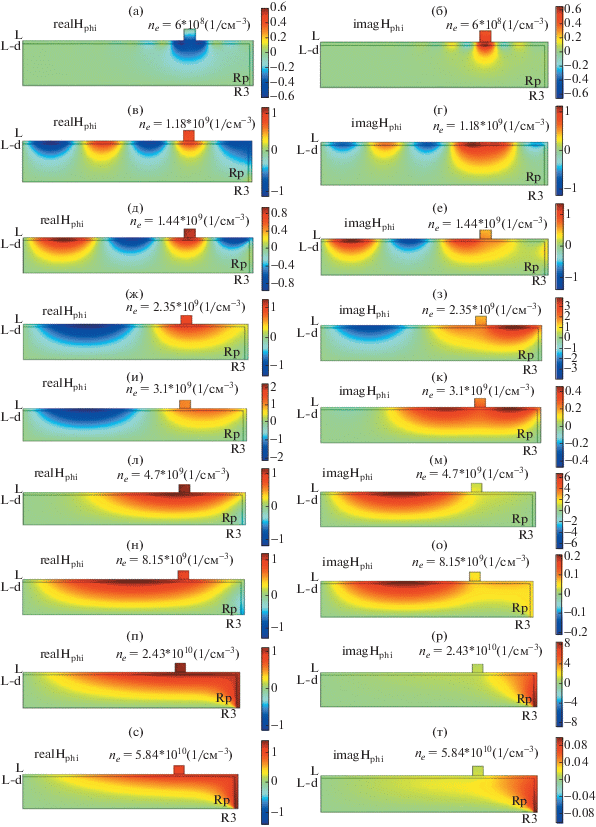
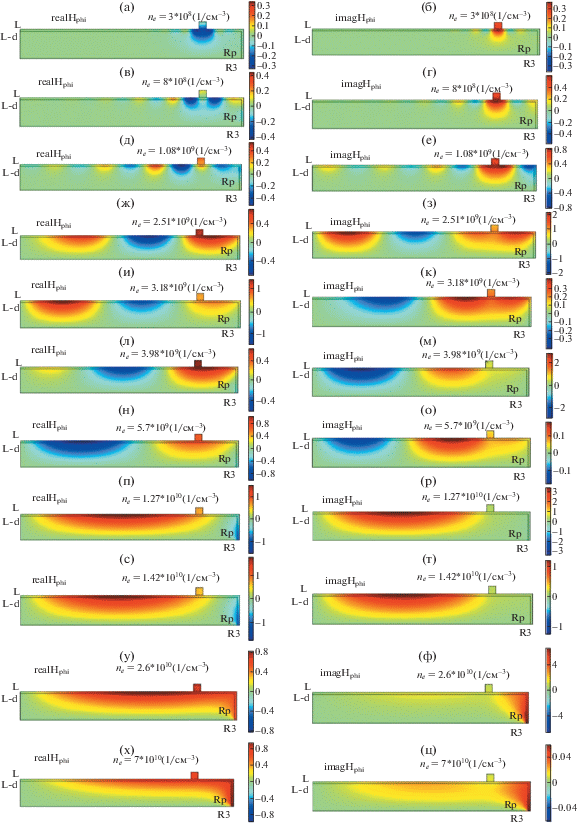
Здесь обсуждаются результаты расчетов азимутального магнитного поля для условий, при которых различные типы распределений проявляют себя наиболее ярко, приведенные на рис. 6–8 (для синфазного возбуждения плазмы) и рис. 9–11 (для противофазного) в разрядных камерах с внешним радиусом 10 см (рис. 6, 9), 20 см (рис. 7, 10), 30 см (рис. 8, 11).
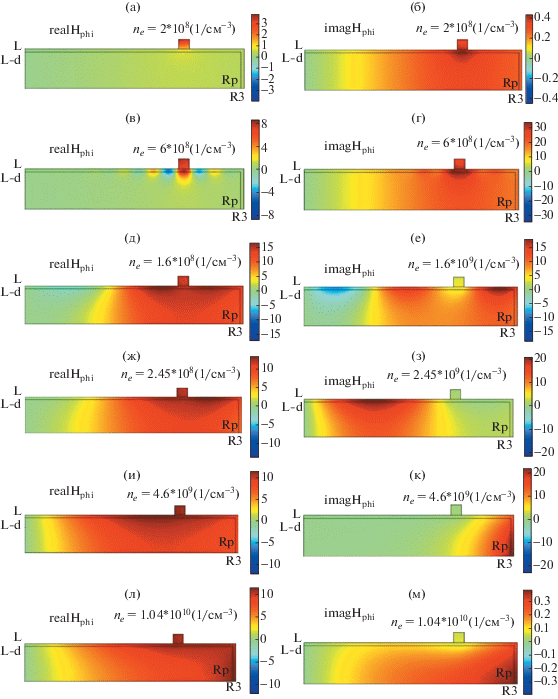
Рис. 6.
Изменение пространственной структуры магнитого поля с ростом плотности электронов для полностью заполненной плазмой камеры (слева – Re H, справа – Im H, A/м) толщина слоев d1 = d2 = d3 =d = 3 мм. Поле возбуждается током I = 1 А частотой 135.6 Мгц. Радиус разрядной камеры R3 – 10 см. Симметричное возбуждение. Плотность электронов приведена на рисунке. Rp = R3 – d – радиус плазмы..
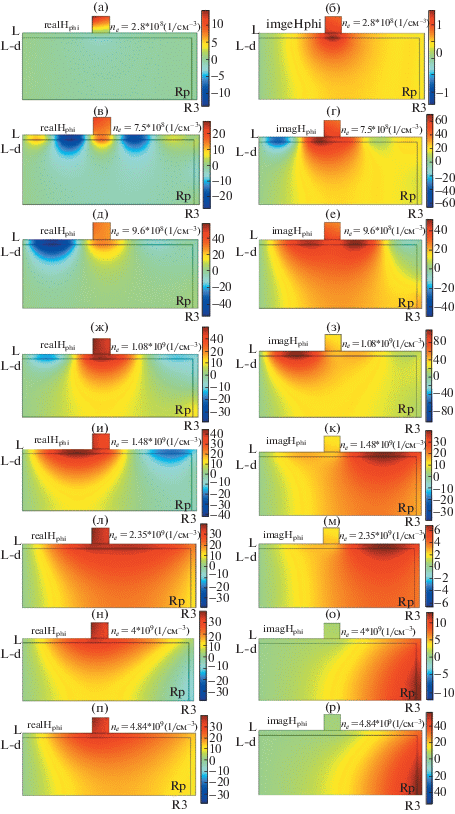
В области плотностей электронов 3 × 108 < ne < < 5 × 108 см–3(nС < ne < 2nС) поверхностные волны не распространяются, и поле в области возбуждения затухает на глубине скин-слоя (рис. 6a, б, 7a, б, 8a–г, 9a, б, 10a, б).
При плотности электронов, слегка выше удвоенной критической, во всех случаях в плазме возбуждается поверхностная волна, распространяющаяся в обе стороны от области возбуждения. Коэффициент поглощения коротких поверхностных волн велик, поэтому волна затухает быстрее, чем дойдет до центра рабочей камеры или до боковой стенки (рис. 6–11).
Увеличение плотности электронов сопровождается увеличением длины поверхностной волны и уменьшением ее коэффициента затухания (см. [46, 50, 51]. Поэтому в окрестности источника формируется стоячая поверхностная волна, а при определенных плотностях наблюдаются резонансы токов и напряжений.
Поскольку длина поверхностных волн при противофазном возбуждении меньше, чем при синфазном, для противофазного возбуждения резонанс с целым числом полуволн наблюдается при более высоких плотностях электронов, чем при синфазном. Согласно расчетам дисперсионной кривой (рис. 6 статьи [46]) резонанс напряжений, соответствующий наибольшей плотности (h0±R = 2.405), должен наблюдаться: при плотностях 5 × 109 см–3 и 3 × 109 см–3 для радиуса 10 см, при 7.3 × 109 см–3 и 1.8 × 109 см–3 для радиуса 20 см (первое число соответствует синфазному, а второе – противофазному возбуждению) и ~7 × × 1010 см–3 для 30 см. При радиусе 30 см резонансные плотности и в первом, и во втором случае близки, так как волны у различных границ плазмы плохо проникают в нее и взаимодействуют слабо. Для синфазного возбуждения эти цифры близки к полученным в численных расчетах. При более высоких плотностях разряд имеет емкостной импеданс. На ряде рисунков максимум магнитного поля у бокового слоя достигается в центральной (по координате z) части трубки, это свидетельствует о возбуждении в окрестности боковой стенки стоячей поверхностной волны (рис. 6н–p, рис. 7и–к). На рисунках 8н, о магнитное поле поверхностной волны сдвинуто примерно на π/2 относительно поля основной моды, что говорит о резонансном характере возбуждения. Вносимые этой волной потери подавляют возможность резонанса.
Для противофазного возбуждения (рис. 9–11) рост плотности электронов также приводит к появлению ярко выраженной стоячей поверхностной волны в радиальном направлении, число полуволн которой уменьшается с ростом плотности электронов. Резонанс напряжений в этих режимах наблюдается при более высоких плотностях электронов, чем это следует из простой оценки, следующей из расчета дисперсионной зависимости. Для разряда в камере радиусом 30 см эта плотность, соответствующая резонансу напряжений, лежит при плотностях выше 1011 см–3 поэтому этот резонанс на рис. 3 отсутствует. Анализ пространственных распределений магнитного поля показывает, что максимальные поля сосредоточены в периферийной области (рис. 10п–т и 11у–ц), поэтому разряд при этих плотностях должен существовать в режиме резонанса плазма–слой в периферийной области. При меньшем радиусе электрода (10 см) разряд и без учета слоя пространственного заряда имеет емкостной импеданс, поэтому дополнительная емкость, вносимая периферийным слоем пространственного заряда, не меняет емкостной характер импеданса. Однако максимум распределения поля при высоких плотностях электронов также наблюдается в периферийной области (рис. 9н, о). Данные, представленные на рисунках, показывают, что амплитуда этого поля может существенно меняться от величины, превышающей амплитуду поля радиальной волны (рис. 9н, о, рис. 10п, p, рис. 11у, ф), до пренебрежимо малой, по сравнению с ней (рис. 10с, т, рис. 11х, ц).
Сложный характер изменения импеданса в области плотностей электронов 4 × 108– 4 × 109 см–3 также демонстрирует возможность возбуждения поверхностных волн у торца плазмы, которая не рассматривалась в аналитических исследованиях в данной работе.
Суммируем более кратко основные физические выводы из приведенных выше аналитических и численных расчетов.
1. Импеданс разряда, который важен для согласования технологических процессов, определяется как высшими нераспространяющимися модами поля, возбуждаемыми в окрестности области возбуждения, так и поверхностными волнами, распространяющимися вдоль интерфейса плазма–слой пространственного заряда–металл. В рассматриваемом приближении (${{R}_{2}}--{{R}_{1}} \ll L$ различные моды волн возбуждаются независимо друг от друга (параллельное включение импедансов), что отражено появлением соответствующих слагаемых только в фигурных скобках в знаменателе (8). При этом линии передачи, соответствующие возбуждению волн в центральной и периферийной области, оказываются соединенными последовательно (слагаемые в круглых скобках). Таким образом, изменяя точку подвода энергии можно изменять соотношение между амплитудами полей в центральной и периферийной областях. Соотношение амплитуд поверхностных волн и высших мод определяется близостью слагаемого для поверхностных волн $\left( {{{{{J}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{J}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)} {{{J}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}} \right. \kern-0em} {{{J}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}} - {{{{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{Q}_{0}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)} {{{Q}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}} \right. \kern-0em} {{{Q}_{1}}\left( {{{h}_{{0 \pm }}}{{R}_{1}}} \right)}}} \right)$ к резонансу. Коэффициент связи соответствующей линии передачи с источником поля зависит от множителей $k{{{{{\mathbf{h}}}_{{n \pm \varphi }}}\left( L \right){\mathbf{h}}_{{n \pm \varphi }}^{ + }\left( L \right)L} \mathord{\left/ {\vphantom {{{{{\mathbf{h}}}_{{n \pm \varphi }}}\left( L \right){\mathbf{h}}_{{n \pm \varphi }}^{ + }\left( L \right)L} {\left( {{{{\tilde {h}}}_{{n \pm }}}N_{{n \pm }}^{{H2}}} \right)}}} \right. \kern-0em} {\left( {{{{\tilde {h}}}_{{n \pm }}}N_{{n \pm }}^{{H2}}} \right)}}$, т.е. от осевого распределения поля для возбуждаемой волны.
2. Для синфазного возбуждения разряда в рабочем диапазоне плотностей электронов вследствие отсутствия тока на боковую стенку можно пренебречь влиянием СПЗ у боковой стенки, за исключением, возможно, области очень близкой к удвоенной критической плотности, когда поверхностная волна у боковой стенки будет находиться в условиях резонанса. При достаточно большом расстоянии между областью возбуждения и боковой стенкой эта волна не должна возбуждаться вследствие затухания радиальной поверхностной волны на отрезке (R3 – R2).
3. Для противофазного возбуждения разряда возможно появление дополнительного резонанса плазма–слой пространственного заряда у боковой стенки. В рамках используемой в данной задачи модели этот резонанс может быть включен в рассмотрение изменением функций ${{Q}_{0}}\left( {{{h}_{{0 \pm }}}r} \right)$ и ${{Q}_{1}}\left( {{{h}_{{0 \pm }}}r} \right)$, с учетом того факта, что длинная линия, описывающая распространение поверхностной волны в периферийной области, уже не будет замкнутой, а будет соединена с землей через некоторую “эффективную” емкость СПЗ. Авторы не проводили детальные расчеты по такой усложненной модели, чтобы не увеличивать объем данной работы.
Обсудим теперь кратко влияние изменения частоты поля, поддерживающего плазму, на вид рассматриваемых кривых, при неизменности остальных параметров плазмы. Расчеты показали, что качественно картина зависимости импеданса от плотности электронов не меняется. Однако импеданс разрядной камеры в целом при малых и высоких (когда глубина скин-слоя много меньше характерных размеров плазмы) увеличивается обратно пропорционально частоте, так как в этом случае импеданс камеры определяется ее полной емкостью (ne → 0), либо емкостью слоев пространственного заряда (ne → ∞). Положение резонанса токов, либо области, где существенным становится возбуждение поверхностных волн, а также резонанса плазма–слой пространственного заряда на оси плотностей электронов изменяется пропорционально изменению критической концентрации ${{n}_{C}} = {{{{\varepsilon }_{0}}m{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}m{{\omega }^{2}}} {{{e}^{2}}}}} \right. \kern-0em} {{{e}^{2}}}}$, пропорционально квадрату частоты. Изменение положения резонансов, связанных с возбуждением поверхностных волн, также примерно пропорционально изменению критической концентрации, однако для них возможен сдвиг по плотности, связанной с тем, что указанные законы подобия не работают для дисперсионной кривой поверхностной волны, хотя качественно ее поведение и асимптотики при ne → 2nС и ne → ∞ не изменяются.
Уменьшение частоты поля в два раза (до 67.8 МГц) приведет к уменьшению области плотностей электронов, где существенны резонансы. Верхняя граница области плотностей электронов, где лежат рассматриваемые резонансы уменьшится с 1010 см–3 до 2 × 109 см–3, для симметричных волн и с 8 × 1010 см–3 до 2 × 1010 см–3 для несимметричных. Уменьшение частоты поля до 27.12 МГц приводит к дальнейшему снижению этих плотностей до 2 × 108 см–3 и 2 × 109 см–3.
Приведенные оценки касаются проявления резонансов, связанных пространственным распределением поля поверхностных волн. Ограничение глубины проникновения поля в плазму, которое обычно не принимается во внимание в кинетических моделях плазмы, в соответствии с результатами [8] должно учитываться при плотностях электронов выше 1010 см–3.
5. ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ
1. При возбуждении емкостного высокочастотного разряда в камере с большой площадью электродов пространственное распределение электромагнитного поля и импеданс разряда существенно модифицируются при изменении плотности электронов.
2. Аналитические расчеты поля в емкостном высокочастотном разряде низкого давления показали, что представление поля в виде суммы поверхностных и нераспространяющихся собственных мод Е-волн в трехслойной структуре слой пространственного заряда–плазма–слой пространственного заряда, окруженной металлическими электродами, позволяет правильно объяснить поведение импеданса. Плотности электронов в плазме, при которых наблюдается резонанс, в большинстве случаев рассчитываются с точностью до ±10%.
3. При больших размерах электродов и малых частотах столкновений (${\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega } < {\lambda \mathord{\left/ {\vphantom {\lambda L}} \right. \kern-0em} L}$) возможно проявление резонансов тока и резонансов напряжения, связанных с кратностью радиуса разряда определенному числу полуволн поверхностной волны. Хотя механизм возбуждения высших мод в разряде в полностью заполненной камере отличается от возбуждения в разряде с диэлектрической боковой стенкой, и их амплитуда должна быть меньше, они приводят к изменению плотностей электронов, при которых наблюдается резонанс, а в широкой области плотностей электронов емкостный разряд имеет в среднем индуктивный импеданс.
4. Стоячие поверхностные волн, возбуждение которых возможно у торцевого слоя пространственного заряда, существенны в области плотностей электронов, в несколько раз превышающих критическую. Эти волны в разряде малого радиуса, когда радиус сравним или меньше высоты разряда, оказывают существенное влияние на импеданс разряда в целом.
5. При высоких плотностях электронов и противофазном возбуждении существенную роль играет слой пространственного заряда у боковой стенки плазмы. Для разряда высокой плотности его наличие приводит к появлению нового резонанса, который можно также рассматривать как геометрический резонанс плазма-слой пространственного заряда, где индуктивный импеданс периферийной плазмы компенсируется емкостным импедансом периферийного слоя пространственного заряда. Поле внешнего источника при этом сосредотачивается в периферийной области.
6. Сопоставление результатов аналитических расчетов и численного моделирования свойств разряда с помощью пакета COMSOL Multiphysics® показало их удовлетворительное качественное, а в некоторых режимах и количественное, согласие.
Список литературы
Lieberman M.A., Lichtenberg A.J. Principles of Plasma Discharges and Material Processing. N.-Y.: Wiley, 2005.
Samukawa S., Hori M., Raul S., Tachibana K., Bruggeman P., Kroesen G., Whitehead J.C., Murphy A.B., Gut-sol A.F., Starikovskaia S., Kortshagen U., Boeuf J.-P., Sommerer T.J., Kushner M.J., Czarnetzki U., Mason N. // J. Phys. D.: Appl. Phys. 2012. V. 45. P. 253001.
Adamovich I., Baalrud S.D., Bogaerts A., Bruggeman P.J., Cappelli M., Colombo V., Czarnetzki U., Ebert U., Eden J.G., Favia P., Graves D.B., Hamaguchi S., Hie-ftje G., Hori M., Kaganovich I.D., Kortshagen U., Kushner M.J., Mason N.J., Mazouffre S., Mededovic Thagard S., Metelmann H.-R., Mizuno A., Moreau E., Murphy A.B., Niemira B.A., Oehrlein G.S., Petrovic Z.Lj., Pitch-ford L.C., Pu Y.-K., Rauf S., Sakai O., Samukawa S., Starikovskaia S., Tennyson J., Terashima K., Tur-ner M.M., van de Sanden M.C.M., Vardelle A. // J. Phys. D: Appl. Phys. 2017. V. 50. P. 323001.
Perrin J., Schmitt J., Hollenstein C., Howling A., Sansonnes L. // Plasma Phys. Contr. Fusion. 2000. V. 42. P. B353.
Liu Y.X., Zhang Yu-Ru, Bogaerts A., Wang Y.-N. // J. Vac. Sci. Technol. A. 2015.V. 33. P. 020801. https://doi.org/10.1116/1.4907926
Schmitt J., Elyaakoubu M., Sansonnes L. // Plasma Sources Sci. Technol. 2002. V. 11. P. A206.
Park A.E., Cho B.U., Lee J.K. // IEEE Trans. Plasma Sci. 2003. V. 31. P. 628.
Liberman M.A., Booth J.P., Chabert P., Rax J.M., Turner M.M. // Plasma Sources Sci. Technol. 2002.V. 11. P. 283.
Chabert P., Ramimbault J.-L., Rax J.-M., Lieber-man M.A. // Phys. Plasmas. 2004. V.11. P. 1175.
Chabert P., Ramimbault J-L., Rax J-M, Pepper A. // Phys. Plasmas. 2004. V. 11. P. 4081.
Proschek N., Yin Y., Charles S., Aanesland A., McKen-zie D.R., Bilek M.M., Boswell R.W. // Plasma Sources Sci. Technol. 2005. V. 14. P. 407.
Sansonnens L., Howling A.A., Hollenstein Ch. // Plasma Sources Sci. Technol. 2006. V. 15. P. 302.
Chabert P. // J. Phys. D.: Appl. phys. 2007. V. 40. P. R63.
Howling A.A., Sansonnens L., Hollenstein C. // Thin Solid Films. 2007. V. 515. P. 5059.
Mussenbrock T., Hemke T., Ziegler D., Brinkman R.P., Klick M. // Plasma Sources Sci. Technol. 2008. V. 17. P. 025018.
Sung D., Woo J., Lim K., Kim K., Volynets V., Kim G.-H. // J. Appl. Phys. 2009. V. 106. P. 023303.
Xu X., Zhao S-X., Zhang Yu-Ru, Wang Y.-N. // J. Appl. Phys. 2010. V.108. P. 043308.
Zhang Yu-Ru, Xu X., Bogaerts A., Wang Y.-N. // J. Phys. D: Appl. Phys. 2012. V. 45. P. 015202.
Zhang Yu-Ru, Xu X., Bogaerts A., Wang Y.-N. // J. Phys. D: Appl. Phys. 2012. V. 45. P. 015203.
Lieberman M.A., Lichtenberg A.J., Kawamura E., Chabert P. // Phys. Plasmas. 2016. V. 23. P. 013501. https://doi.org/10.1063/1.4938204
Wen De-Qi, Kawamura E., Lieberman M.A., Lichten-berg A.J., Wang Y.-N. // Phys. Plasmas. 2017. V. 24. P. 083517.
Saikia P., Bhuyan H., Escalona M., Favre M., Rawat R.S., Wyndham E. // AIP Advances. 2018. V. 8. P. 045113.https://doi.org/10.1063/1.5022654
Saikia P., Bhuyan H., Escalona M., Favre M., Bora B., Kakati M., Wyndham E., Rawat R.S., Schulze J. // J. Appl. Phys. 2018. V. 123. P. 183303. https://doi.org/10.1063/1.5023884
Kawamura E., Lieberman M.A., Graves D.B. // Plasma Sources Sci. Technol. V. 23. P. 064003.
Schmidt F., Schulze J., Johnson E., Booth J.-P., Keil D., French D.M., Trieschmann J., Mussenbrock T. // Plasma Sources Sci. Technol. 2018. V. 27. P. 095012.
Gekelman W., Barnes M., Vincena S., Pribyl P. // Phys. Rev. Lett. 2009. V. 103. P. 045003.
Lieberman M.A., Lichtenberg A.J., Kawamura E., Marakhtanov A.M. // Plasma Sources Sci. Technol. V. 24. P. 055011.
Zhao K., Wen De-Qi, Liu Y.-X., Lieberman M.A., Economou D.J., Wang Y.-N. // Phys. Rev. Lett. 2019. V. 122. P. 185002.
Mussenbrock T., Brinkman R.P. // Plasma Sources Sci. Technol. 2007. V. 16. P. 377.
Mussenbrock T., Brinkman R.P., Lieberman M.A., Lichtenberg A.J., Kawamura E. // Phys. Rev. Lett. 2008. V. 101. P. 085004.
Wen De-Qi, Kawamura E., Lieberman M.A., Lichtenberg A.J., Wang Y.-N. // Plasma Sources Sci. Technol. 2017. V. 26. P. 015007.
Wilczek S., Trieschmann J., Schulze J., Donkó Z., Brinkmann R.P., Mussenbrock T. // Plasma Sources Sci. Technol. 2018. V. 27. P. 125010.
Kawamura E., Lieberman M.A., Lichtenberg A.J. // Phys. Plasmas. 2018. V. 25. P. 093517.
Lee I., Graves D.B., Lieberman M.A. // Plasma Sources Sci. Technol. 2008. V. 17. P. 015018.
Eremin D., Hemke T., Brinkmann R.P., Mussenbrock T. // J. Phys. D: Appl. Phys. 2013. V. 46. P. 084017.
Kawamura E., Lieberman M.A., Lichtenberg A.J. // Phys. Plasmas. 2014. V. 21. P. 123505.
Wen De-Qi, Kawamura E., Lieberman M.A., Lichtenberg A.J., Wang Y.-N. // J. Phys. D: Appl. Phys. 2017. V. 50. P. 495201.
Sharma S., Mishra S.K., Kaw P.K., Turner M.M. // Phys. Plasmas. 2017. V. 24. P. 013509. https://doi.org/10.1063/1.4973889
Eremin D. // IEEE Trans. Plasma Sci. 2017. V. 45. P. 527.
Schmidt F., Mussenbrock T., Trieschmann J. // Plasma Sources Sci. Technol. 2018. V. 27. P. 105017.
Hebner G.A., Barnat E.V., Miller P.A., Paterson A.M., Holland J.P. // Plasma Source Sci. Technol. 2006. V. 15. P. 889.
Ding K., Lieberman M.A., Lichtenberg A.J., Shi J.J., Zhang J. // Plasma Sources Sci. Technol. 2014. V. 23. P. 065048.
Saikia P., Bhuyan H., Favre M., Wyndham E., Veloso F. // Phys. Plasmas. 2017. V. 24. P. 013503. https://doi.org/10.1063/1.4973233
Zhao K., Liu Y.-X., Kawamura E., Wen De-Qi, Lieberman M.A., Wang Y.-N. // Plasma Sources Sci. Technol. 2018. V. 27. P. 055017.
Saikia P., Bora B., Schulze J., Bhuyan H. // Phys. Plasmas. 2018. V. 25. P. 083501. https://doi.org/10.1063/1.5032296
Двинин С.А., Синкевич О.А., Кодирзода З.А., Соли-хов Д.К. // Физика плазмы. 2020. Т. 46. № 12, С. 1094–1118.
Гинзбург В.Л. Распространение электромагнитных волн в плазме. М.: Наука, ГРФМЛ, 1961.
Александров А.Ф., Богданкевич Л.С., Рухадзе А.А. Основы электродинамики плазмы. М.: Энергоатомиздат, 1976.
Никольский В.В. Вариационные методы для внутренних задач электродинамики. М.: Наука. 1967. С. 169.
Фелсен Л., Маркувитц Н. Излучение и рассеяние волн. Т. 1. М.: Мир. 1978. 547 с.
Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970. 512 с.
Двинин С.А., Вологиров А.Г., Михеев В B., Свиридкина В.С. // Физика плазмы. 2008. Т. 34. С. 746.
Пономарев В.Н., Солнцев Г.С. // ЖТФ. 1966. Т. 36. С. 1376.
Никольский В.В., Никольская Т.А. Электродинамика и распространение радиоволн. М.: Наука, 1989. 543 с.
Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1990. 442 с.
Стреттон Дж.А. Теория электромагнетизма. М.: Гостехиздат. 1948. 540 с.
Дополнительные материалы отсутствуют.