Физика плазмы, 2021, T. 47, № 2, стр. 99-108
О возможности аномального рассеяния необыкновенной СВЧ-волны колебаниями промежуточного частотного диапазона, локализованными в периферийном транспортном барьере термоядерной установки
Е. З. Гусаков a, А. Ю. Попов a, *
a Физико-технический институт им. А.Ф. Иоффе РАН
С.-Петербург, Россия
* E-mail: a.popov@mail.ioffe.ru
Поступила в редакцию 26.06.2020
После доработки 18.08.2020
Принята к публикации 08.09.2020
Аннотация
Анализируется параметрическая распадная неустойчивость, приводящая к аномальному рассеянию СВЧ-волн необыкновенной поляризации на колебаниях промежуточного частотного диапазона, локализованных в периферийном транспортном барьере термоядерной установки. Эффект может иметь место при электронном циклотронном нагреве плазмы на второй гармонике резонанса мульти-мегаваттными СВЧ-пучками.
1. ВВЕДЕНИЕ
Электронный циклотронный резонансный нагрев (ЭЦРН) широко применяется в современных тороидальных устройствах магнитного удержания высокотемпературной плазмы. В настоящее время ЭЦРН рассматривается как наиболее надежный метод локального нагрева электронов во вращающемся магнитном острове. Согласно современным представлениям считается, что этот локальный нагрев позволит осуществлять контроль неоклассической тиринг-моды в токамаке-реакторе ИТЭР. Полная мощность СВЧ‑излучения, генерируемая мегаваттными гиротронами и планируемая к применению в ИТЭР, составляет 20 МВт. В настоящее время обсуждается использование ЭЦР-нагрева плазмы и в термоядерной установке следующего поколения Д-ЕМО. С этой целью уже сейчас начата разработка стационарных СВЧ-генераторов – гиротронов с выходной мощностью излучения 2–5 МВт [1, 2]. Поскольку приближается время физического пуска ИТЭР, актуальной задачей является исследование до момента начала ее функционирования всех аспектов поведения СВЧ-волн в высокотемпературной плазме и анализ возможности возбуждения паразитных физических эффектов, которые могут сопровождать их распространение и значительно ухудшать эффективность и локальность дополнительного нагрева электронов. Важность этой задачи подчеркивается как результатами последних экспериментов по ЭЦРН-плазмы, так и теоретическими предсказаниями. В частности, недавние экспериментальные наблюдения свидетельствуют о возможности возбуждения аномальных явлений при распространении мощных пучков СВЧ-волн в плазме тороидальных ловушек. Среди этих явлений можно выделить аномальное рассеяние греющего излучения [3–5] и генерацию групп высокоэнергичных ионов [6, 7] при дополнительном нагреве электронов в условиях, когда не существует линейных механизмов передачи энергии между этими заряженными частицами. Теоретическая модель [8–11], расширяющая традиционную схему описания трехволнового взаимодействия [12, 13] и учитывающая наличие немонотонных профилей плотности и магнитного поля и возможность запирания вблизи их максимумов дочерних волн, позволяет детально описать аномальное рассеяние [14], наблюдавшееся в экспериментах. Она интерпретирует аномальное рассеяние как результат нелинейного слияния различных дочерних волн, возбуждающихся при первичных и вторичных распадах СВЧ-волны накачки. Кроме того, эта теоретическая модель может объяснить появление “хвостов” на ионной функции распределения как результат резонансного взаимодействия ионов с низкочастотными ионными бернштейновскими волнами, генерируемыми при параметрической неустойчивости [9, 15]. Возможность значительного аномального поглощения волны накачки, предсказанная аналитически в работах [16–19], нашла подтверждение в модельных экспериментах на линейной установке [20], а предсказание излучения на частоте, равной половине частоты волны накачки [21], – в экспериментах по ЭЦРН в токамаке ASDEX-Upgrade [22].
Одним из “узких” мест при распространении СВЧ-волны в плазме токамака является область периферии, где могут наблюдаться как когерентные плазменные образования (блобы, филаменты), плотность в которых существенно выше фоновой, так и области с большим градиентом плазменных параметров. В частности, на границе плазмы может располагаться периферийный транспортный барьер. С одной стороны, характерный пространственный масштаб профиля плотности в барьере, как правило, много больше вакуумной длины волны СВЧ-колебаний, а дрейфовая турбулентность в нем подавлена, что не позволяет ожидать в этой области значительного линейного и нелинейного отражения или рассеяния греющего излучения. С другой стороны, наличие большого градиента плотности может оказывать существенное влияние на свойства волн промежуточного диапазона частот и приводить к появлению новых окон прозрачности для них [23, 24]. Как мы покажем ниже, в периферийном транспортном барьере термоядерной установки возможны, во-первых, существование потенциальных волн, отсутствующих в однородной среде, и, во-вторых, локализация этих волн, родственных косым ленгмюровским волнам (КЛВ), вдоль направления неоднородности из-за градиентных эффектов и в тороидальном направлении из-за гофрировки магнитного поля. Порог возбуждения таких двумерно локализованных волн, как было показано ранее в [8–10], во многих случаях оказывается существенно ниже значений, предсказанных для генерации нелокализованных дочерних волн [25], и может быть превзойден в экспериментах с мульти-мега-ваттными пучками СВЧ-волн.
В настоящей статье мы исследуем аномальное рассеяние СВЧ-волн накачки необыкновенной поляризации на колебаниях промежуточного частотного диапазона, локализованных в периферийном транспортном барьере термоядерной установки.
2. ПУЧОК ВОЛН НАКАЧКИ В ОБЛАСТИ НЕЛИНЕЙНОГО ВЗАИМОДЕЙСТВИЯ
Учитывая, что параметрический распад возможен в узкой окрестности вокруг точки, где выполнены распадные условия для частот и волновых векторов нелинейно связанных волн, введем локальную декартову систему координат $(x,y,z)$ и будем пренебрегать эффектами кривизны и шира магнитного поля, свойственными тороидальным установкам. Координата x совпадает с направлением неоднородности, координата y направлена вертикально и координата z – вдоль магнитного поля, модуль напряженности которого в этом узком вдоль направления неоднородности слое имеет вид
(1)
$H = \bar {H}\left( {1 - \delta \left( {x,y} \right)\cos \left( {N\frac{z}{R}} \right)} \right),$Будем считать, что гауссов пучок волн накачки необыкновенной поляризации распространяется вдоль направления неоднородности поперек магнитного поля. В выбранной системе координат при падении на слой плазмы, в котором возможен параметрический распад этих волн, он может быть представлен в виде
(2)
$\, \times \exp \left( { - \frac{{\omega _{0}^{2}}}{{{{c}^{2}}}}\frac{{n_{y}^{2} + n_{z}^{2}}}{2}\left( {{{w}^{2}} - iw_{f}^{2}} \right) + } \right.$(3)
$\begin{gathered} \varepsilon n_{ \bot }^{4} - \left( {\left( {\varepsilon + \eta } \right)\left( {\varepsilon - n_{z}^{2}} \right) - {{g}^{2}}} \right)n_{ \bot }^{2} + \\ \, + \eta \left( {{{{\left( {\varepsilon - n_{z}^{2}} \right)}}^{2}} - {{g}^{2}}} \right) = 0, \\ \end{gathered} $(4)
$\omega _{{ce}}^{2}{\text{/}}\omega _{0}^{2} \ll 1,\quad \omega _{{pe}}^{2}{\text{/}}\omega _{0}^{2} \ll 1.$C учетом неравенств (4) компоненты тензора “холодной” плазмы имеют вид $\eta = 1 - \frac{{\omega _{{pe}}^{2}}}{{{{\omega }^{2}}}},$ $\varepsilon \cong \eta - $ $ - \;\frac{{\omega _{{pe}}^{2}}}{{{{\omega }^{2}}}}\frac{{\omega _{{ce}}^{2}}}{{{{\omega }^{2}}}},$ $g \cong \frac{{\omega _{{ce}}^{{}}}}{\omega }\frac{{\omega _{{pe}}^{2}}}{{{{\omega }^{2}}}} \ll 1$, ${{\omega }_{{pe}}}$, ${{\omega }_{{ce}}}$ – электронная плазменная и электронная циклотронная частоты. Кроме того, поперечный коэффициент преломления равен
и вектор поляризации имеет вид(6)
${{{\mathbf{e}}}_{0}} = {\mathbf{e}}\left( {{{\omega }_{0}}} \right) \simeq - \frac{{ig + {{n}_{y}}{{n}_{x}}}}{{n_{x}^{2}}}{{{\mathbf{\bar {e}}}}_{x}} + {{{\mathbf{\bar {e}}}}_{y}} + i\frac{{{{\omega }_{0}}}}{{{{\omega }_{{сe}}}}}\frac{{{{n}_{z}}}}{{{{n}_{x}}}}{{{\mathbf{\bar {e}}}}_{z}},$(7)
$\begin{gathered} {{{\mathbf{E}}}_{0}} \cong \sqrt {\frac{{8{{P}_{0}}}}{{с{{w}^{2}}}}} \frac{{{\mathbf{A}}\left( {{{\omega }_{0}},{\mathbf{r}}} \right)}}{{2\sqrt {{{n}_{x}}\left( {{{\omega }_{0}},x} \right)} }}\frac{1}{{\sqrt {1 - i\frac{{w_{f}^{2}}}{{{{w}^{2}}}}} }} \times \\ \, \times \exp \left( { - \frac{{{{y}^{2}}}}{{2\left( {{{w}^{2}} - iw_{f}^{2}} \right)}} - \frac{{{{z}^{2}}}}{{2\left( {{{w}^{2}} - iw_{f}^{2}} \right)}} + } \right. \\ \, + \left. {i\frac{{{{\omega }_{0}}}}{c}\int\limits_{ - \infty }^x {dx{\kern 1pt} '{{n}_{x}}\left( {{{\omega }_{0}},x{\kern 1pt} '} \right)} - i{{\omega }_{0}}t} \right) + c.c., \\ \end{gathered} $Отметим, что в электрическом поле пучка необыкновенной волны накачки, как и в случае плоской волны, доминирует полоидальная компонента. Тем не менее, мы удерживаем здесь и малую компоненту, направленную вдоль магнитного поля и приводящую к существенному росту нелинейной связи параметрически возбуждаемых волн.
Далее проанализируем распад пучка волн накачки (2), в результате которого возбуждаются рассеянная необыкновенная волна на частоте ${{\omega }_{s}}$ и косые ленгмюровские волны (КЛВ) на частоте ${{\omega }_{L}}$. Частоты дочерних волн удовлетворяют неравенствам ${{\omega }_{{pi}}} \leqslant {{\omega }_{L}} = {{\omega }_{0}} - {{\omega }_{s}} \ll {{\omega }_{{pe}}}$. В последующих разделах рассмотрим поведение дочерних волн в области периферийного транспортного барьера.
3. НИЗКОЧАСТОТНАЯ ДОЧЕРНЯЯ КЛ-ВОЛНА В ОКРЕСТНОСТИ ТРАНСПОРТНОГО БАРЬЕРА
Потенциал КЛВ в неоднородной плазме в отсутствие нелинейной накачки описывается уравнением Пуассона
где дифференциальный оператор имеет вид(9)
$\begin{gathered} \hat {D}\left( {{{\omega }_{L}}} \right) = \varepsilon \left( {{{\omega }_{L}}} \right)\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right) - \\ \, - i\frac{{\partial g\left( {{{\omega }_{L}}} \right)}}{{\partial x}}\frac{\partial }{{\partial y}} + \eta \left( {{{\omega }_{L}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}. \\ \end{gathered} $Компоненты тензора “холодной” плазмы в выражении (9) равны
(10)
$\begin{gathered} \varepsilon \left( {{{\omega }_{L}}} \right) \simeq 1 + \frac{{\omega _{{pe}}^{2}}}{{\omega _{{ce}}^{2}}} - \frac{{\omega _{{pi}}^{2}}}{{\omega _{L}^{2}}}, \\ g\left( {{{\omega }_{L}}} \right) \simeq \frac{{\omega _{{pe}}^{2}}}{{{{\omega }_{L}}{{\omega }_{{ce}}}}} \gg 1,\quad \eta \left( {{{\omega }_{L}}} \right) \cong - \frac{{\omega _{{pe}}^{2}}}{{\omega _{L}^{2}}}, \\ \end{gathered} $Далее будем искать решение, которое описывает волну, которая бежит в направлении y, т.е. $\phi \propto \exp \left( {i{{q}_{y}}y} \right)$. В этом случае уравнение (8) сводится к
(11)
$\begin{gathered} \left( {\varepsilon \left( {{{\omega }_{L}},x,z} \right)\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} - q_{y}^{2}} \right) + } \right. \\ \, + \left. {{{q}_{y}}\frac{{\partial g\left( {{{\omega }_{L}},x,z} \right)}}{{\partial x}} - \left| {\eta \left( {{{\omega }_{{LH}}}} \right)} \right|\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)\phi = 0. \\ \end{gathered} $Функция $\left| {\partial g\left( {{{\omega }_{L}}} \right){\text{/}}\partial x} \right|$ имеет локальный максимум в области периферийного транспортного барьера. Чтобы проиллюстрировать этот факт, возьмем профиль плотности, который является близким к тем, что измерялись в области транспортного барьера на токамаке ASDEX-Upgrade [27], см. рис. 1. На этом же рисунке показана пространственная производная профиля плотности, которая имеет локальный максимум в области барьера. В окрестности этого максимума мы можем аппроксимировать функцию параболой
(12)
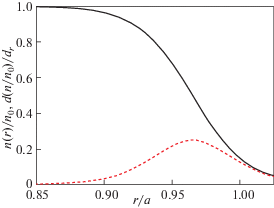
$\frac{1}{{\varepsilon \left( {{{\omega }_{L}}} \right)}}\left| {\frac{{\partial g\left( {{{\omega }_{L}},x} \right)}}{{\partial x}}} \right| \approx Q\left( {1 - \frac{{{{x}^{2}}}}{{l_{g}^{2}}}} \right).$Рис. 1.
Профиль плотности, нормированной на значение плотности в центре ${{n}_{0}} = 4.5 \times {{10}^{{19}}}$ м–3, близкий к тем, что наблюдались в ASDEX-Upgrade [25] (сплошная линия), и профиль производной плотности (пунктир).
Наибольшее время в потенциальной яме вдоль направления неоднородности КЛВ проводит в окрестностях точек поворота, где выполняется неравенство ${{q}_{y}} \gg \left| {\partial {\text{/}}\partial x} \right|$. Учитывая параболическую аппроксимацию (12) и раскладывая коэффициенты уравнения также по степеням координаты z, получим
(13)
$\begin{gathered} \left( {\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} - K_{x}^{4}{{x}^{2}}} \right) - \frac{{\left| {\eta \left( {{{\omega }_{L}}} \right)} \right|}}{{\varepsilon \left( {{{\omega }_{L}}} \right)}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}} - K_{z}^{4}{{z}^{2}}} \right) + } \right. \\ \left. {\, + \mathop {\left( {{{q}_{y}}Q - q_{y}^{2}} \right)}\limits_{} } \right){{\phi }_{0}} = 0, \\ \end{gathered} $Решение этого уравнения выражается через полиномы Эрмита
(14)
$\begin{gathered} \phi \left( {t,{\mathbf{r}}} \right) = \frac{{{{\phi }_{0}}\left( {x,z} \right)}}{2}\exp \left( {i{{q}_{y}}y - i{{\omega }_{s}}t} \right) + c.c., \\ {{\phi }_{0}}\left( {x,z} \right) = {{B}_{{pr}}}{{{\tilde {\phi }}}_{p}}\left( {{{K}_{x}}x} \right){{{\tilde {\phi }}}_{r}}\left( {{{K}_{z}}z} \right), \\ \end{gathered} $(15)
${{q}_{y}}Q - q_{y}^{2} = \left( {2p + 1} \right)K_{x}^{2} - \left( {2r + 1} \right)\frac{{\left| {\eta \left( {{{\omega }_{L}}} \right)} \right|}}{{\varepsilon \left( {{{\omega }_{L}}} \right)}}K_{z}^{2}.$В отсутствие градиента плотности ($Q = 0$) такая КЛ-волна, распространяющаяся практически перпендикулярно внешнему магнитному полю, существовать не может. Появление новых областей прозрачности для КЛВ в неоднородной плазме было впервые обнаружено в работе [23]. В дальнейшем в [24] была показана возможность существования быстрых квазипотенциальных волн промежуточного диапазона частот, распространяющихся строго поперек магнитного поля. Кроме того, в [24] продемонстрировано, что при большом значении градиента плотности такие колебания могут быть локализованы в направлении неоднородности. Эта волна обладает примечательным свойством. В некотором диапазоне волновых векторов в пределах области локализации вдоль направления неоднородности она меняет знак групповой скорости в поперечном внешнему магнитному полю и градиенту плотности $y$-направлении
(16)
${{\upsilon }_{{gy}}} \sim \frac{{\partial D\left( {{{\omega }_{L}}} \right)}}{{\partial {{q}_{y}}}} = Q\left( {1 - \frac{{{{x}^{2}}}}{{l_{g}^{2}}}} \right) - 2{{q}_{y}}.$При усреднении по области локализации КЛ-волна, обладающая y-компонентой волнового вектора, примерно равной
(17)
$q_{y}^{{opt}} \approx \frac{Q}{2} - \frac{{\sqrt 2 }}{{{{l}_{g}}}}\left( {p + \frac{1}{2}} \right),$Для этой волны единственным источником потерь из области распада в направлении поперечной координаты y является дифракция – более медленный процесс, нежели конвективный вынос. Этот факт делает возможным предполагать, что именно такие КЛ-волны, имеющие поперечное значение волнового вектора, близкое к значению (17), являются наиболее неустойчивыми и возбуждаются при распаде волны накачки прежде всего.
4. ВЫСОКОЧАСТОТНАЯ ДОЧЕРНЯЯ НЕОБЫКНОВЕННАЯ ВОЛНА В ОБЛАСТИ РАСПАДА
Обсудим поведение дочерней высокочастотной волны необыкновенной поляризации. В отсутствие нелинейного взаимодействия частное решение, которое описывает электрическое поле дочерней необыкновенной волны, распространяющейся в обратном волне накачки направлении, в приближении Вентцеля–Крамерса–Бриллюэна (ВКБ) имеет вид (см. (2))
(18)
$\begin{gathered} {{{\mathbf{E}}}_{s}} = {{{\mathbf{e}}}_{s}}\left( x \right)\frac{{{{A}_{s}}\left( {{{n}_{{sy}}},{{n}_{{sz}}}} \right)}}{{2\sqrt {{{\upsilon }_{{gx}}}\left( {{{\omega }_{s}},x} \right){\text{/}}c} }} \times \\ \, \times \exp \left( {i\frac{{{{\omega }_{s}}}}{c}\int\limits_\infty ^x {dx{\kern 1pt} '{{n}_{x}}\left( {{{\omega }_{s}},x{\kern 1pt} ',{{n}_{{sy}}},{{n}_{{sz}}}} \right) + } } \right. \\ \left. {\, + i\frac{{{{\omega }_{s}}}}{c}{{n}_{{sy}}}y + \mathop {i\frac{{{{\omega }_{s}}}}{c}{{n}_{{sz}}}z + i{{\omega }_{s}}t}\limits_{} } \right) + c.c., \\ \end{gathered} $(19)
${{n}_{{sy}}} = c{{q}_{y}}{\text{/}}{{\omega }_{s}} > {{n}_{x}}\left( {{{\omega }_{s}},{{n}_{{sy}}},{{n}_{{sz}}}} \right) \gg {{n}_{{sz}}}.$В этом случае пучок волн необыкновенной поляризации распространяется квазипоперечно по отношению к пучку волн накачки c основной компонентой вектора поляризации, направленной вдоль направления неоднородности,
(20)
${{{\mathbf{e}}}_{s}} \cong {{{\mathbf{\bar {e}}}}_{x}} - \frac{{{{n}_{{sx}}}}}{{{{n}_{{sy}}}}}{{{\mathbf{\bar {e}}}}_{y}} - i\frac{{{{\omega }_{s}}}}{{{{\omega }_{{сe}}}}}\frac{{{{n}_{{sz}}}}}{{{{n}_{{sy}}}}}{{{\mathbf{\bar {e}}}}_{z}}.$В следующем разделе будет получена система уравнений, которая описывает нелинейную связь дочерних волн в присутствии пучка волн накачки.
5. УРАВНЕНИЯ, ОПИСЫВАЮЩИЕ ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ ДОЧЕРНИХ ВОЛН В ОКРЕСТНОСТИ ТРАНСПОРТНОГО БАРЬЕРА
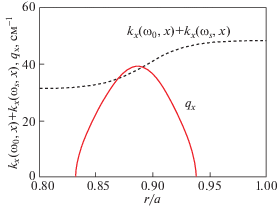
На рис. 2 демонстрируется возможность нелинейного возбуждения КЛВ в условиях, типичных для токамака ASDEX-Upgrade. Пунктирной линией показана сумма волновых чисел ${{k}_{x}}({{\omega }_{0}},x)\, + $ $ + \;{{k}_{x}}({{\omega }_{s}},x)$, где ${{k}_{x}}\left( {{{\omega }_{{0,s}}}} \right) = {{\omega }_{{0,s}}}{{n}_{x}}\left( {{{\omega }_{{0,s}}}} \right){\text{/}}c$, волны накачки ${{f}_{0}}$ и дочерней волны ${{f}_{s}}$. Волновое число низкочастотной КЛ дочерней волны ${{q}_{x}} = $ ${{q}_{x}}({{q}_{y}})$, которое определяется при решении уравнения (8) методом ВКБ и соответствует локализованной в плазме радиальной моде с номером $p = 142$, изображено на рисунке сплошной линией. Отметим, что разница между ближайшими собственными частотами порядка $\Delta \omega = 2\pi ({{f}_{p}} - {{f}_{{p - 1}}}) \approx $ ${{10}^{7}}$ рад/с. Как будет показано ниже, инкремент неустойчивости много меньше этого значения, что позволяет говорить о существовании дискретного спектра собственных мод. Дисперсионные кривые приведены для профиля плотности, изображенного на рис. 1, магнитного поля в центре ${{H}_{0}} = 2.25$ Тл и электронной температуры в области взаимодействия ${{T}_{e}} = 0.3$ кэВ. Отметим, что в точках, где кривые пересекаются, выполнены распадные резонансные условия. Таким образом, вблизи этих точек ${{x}_{d}}$, положение которых определяется решением уравнения $\Delta K = {{k}_{x}}\left( {{{\omega }_{0}},{{x}_{d}}} \right) + $ $ + \;{{k}_{x}}\left( {{{\omega }_{s}},{{x}_{d}}} \right) - {{q}_{x}} = 0$, возможно развитие параметрической распадной неустойчивости.
Рис. 2.
Разность волновых чисел ${{k}_{x}}\left( {{{\omega }_{0}},x} \right) + {{k}_{x}}\left( {{{\omega }_{s}},x} \right)$, ${{k}_{x}}\left( {{{\omega }_{{0,s}}}} \right) = {{\omega }_{{0,s}}}{{n}_{x}}\left( {{{\omega }_{{0,s}}}} \right){\text{/}}c$, необыкновенных волн (пунктир) и волновое число ${{q}_{x}} = {{q}_{x}}({{q}_{y}})$ (сплошная линия), являющееся ВКБ-решением уравнения (9). В точках пересечения кривых выполнено распадное резонансное условие $\Delta K\, = \,{{k}_{x}}({{\omega }_{0}},x)\, + \,{{k}_{x}}({{\omega }_{s}},x)\, - {{q}_{x}}\, = 0$. ${{f}_{0}} = 140$ ГГц, ${{f}_{s}} = 139.23$ ГГц, ${{q}_{y}} = 24$ см–1.
Для описания параметрической неустойчивости пучка волн накачки (2) учтем в уравнениях Пуассона и Максвелла нелинейные плотности заряда и тока, описывающие трехволновое взаимодействие. Уравнение Пуассона для потенциала КЛВ в присутствии волны накачки имеет вид
где нелинейная плотность заряда ρ равна (см. Приложение, где соответствующее выражение приведено в фурье-представлении)Уравнение (21) описывает потенциал волны промежуточного диапазона частот, источником являются биения между волной накачки и рассеянной волной (правая часть уравнения). В присутствии нелинейной плотности заряда амплитуда ${{B}_{{pr}}}$ в выражении (14) перестает быть постоянной величиной. Подставим (14) в уравнение (21). Умножим обе части этого уравнения на ${{\tilde {\phi }}_{p}}\left( {{{K}_{x}}x} \right){\kern 1pt} *{{\tilde {\phi }}_{r}}\left( {{{K}_{z}}z} \right){\kern 1pt} *$ и проинтегрируем по координатам x и z. В интеграле по координате z дважды проведем интегрирование по частям и выразим вторую производную функции ${{\tilde {\phi }}_{r}}\left( {{{K}_{z}}z} \right){\text{*}}$ через ее саму, используя свойства полиномов Эрмита. В результате получим
(22)
$\begin{gathered} \left( {\frac{\partial }{{\partial t}} + i\Lambda \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right){{B}_{{pr}}} = i\frac{{\omega _{{pe}}^{2}cK_{z}^{2}}}{{{{\omega }_{0}}\omega _{L}^{2}\left\langle {\partial D{\text{/}}\partial {{\omega }_{L}}} \right\rangle }} \times \\ \, \times \int\limits_{ - \infty }^\infty {dxdz\left( {2r + 1 - K_{z}^{2}{{z}^{2}}} \right){{{\tilde {\phi }}}_{p}}\left( {{{K}_{x}}x} \right){\kern 1pt} *{{{\tilde {\phi }}}_{r}}\left( {{{K}_{z}}z} \right){\kern 1pt} * \times } \\ \, \times \frac{{\left( {{{{\mathbf{E}}}_{0}} \cdot {{{\mathbf{e}}}_{y}}} \right){\kern 1pt} *\left( {{{{\mathbf{E}}}_{s}} \cdot {{{\mathbf{e}}}_{x}}} \right)}}{{\bar {H}}}. \\ \end{gathered} $Здесь введено обозначение $\Lambda = {{\left. {{{\left\langle {\frac{{{{\partial }^{2}}D}}{{2\partial q_{y}^{2}}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\frac{{{{\partial }^{2}}D}}{{2\partial q_{y}^{2}}}} \right\rangle } {\left\langle {\frac{{\partial D}}{{\partial {{\omega }_{L}}}}} \right\rangle }}} \right. \kern-0em} {\left\langle {\frac{{\partial D}}{{\partial {{\omega }_{L}}}}} \right\rangle }}} \right|}_{{q_{y}^{{(0)}}}}}$, коэффициенты дифракции КЛВ усреднены по области ее локализации. Процедура усреднения определяется следующим образом: $\left\langle F \right\rangle = $ $ = \int_{ - \infty }^\infty {dx} \int_{ - \infty }^\infty {dz} F\left( {x,z} \right){{\left| {{{{\tilde {\phi }}}_{p}}\left( {{{K}_{x}}x} \right)} \right|}^{2}}{{\left| {{{{\tilde {\phi }}}_{r}}\left( {{{K}_{z}}z} \right)} \right|}^{2}}$. В левой части уравнения (22) мы опустили член, описывающий конвективные потери КЛВ в направлении координаты y. Для случая, показанного на рис. 2, ${{q}_{y}} = 24$ см–1 близко к оптимальному значению (17) и значения усредненных по области локализации групповой скорости и коэффициента дифракции равны ${{u}_{{Ly}}} \approx 2 \times {{10}^{3}}$ см/с, $\Lambda \approx 3 \times $ × 106 см2/с, соответственно.
Далее получим уравнение для высокочастотной дочерней волны. С этой целью подставим в неоднородные уравнения Максвелла, содержащие в правой части нелинейную плотность тока, выражение (18). Свернем эти три уравнения с вектором поляризации ${\mathbf{e}}_{s}^{*}$, определение которого дано ранее в выражении (20). В присутствии нелинейного взаимодействия волны накачки и низкочастотных колебаний, описываемых нелинейной плотностью тока, амплитуда ${{A}_{s}}$ перестает быть постоянным множителем и становится функцией координат. Координатная зависимость описывается следующим неоднородным уравнением, содержащим нелинейную вынуждающую силу:
(23)
$\begin{gathered} \sqrt {\frac{{{{n}_{x}}\left( {{{\omega }_{s}},0} \right)}}{{{{n}_{x}}\left( {{{\omega }_{s}},x} \right)}}} \left( {{{n}_{x}}\left( {{{\omega }_{s}},x} \right)\frac{\partial }{{\partial x}} + n_{{sy}}^{{(0)}}\frac{\partial }{{\partial y}}} \right){{A}_{s}}\left( {t,{\mathbf{r}}} \right) = \\ \, = \frac{{4\pi i}}{c}J\left( {{{\omega }_{0}} - {{\omega }_{L}},n_{{sy}}^{{(0)}},{\mathbf{r}}} \right) \times \\ \, \times \exp \left( { - i{{\omega }_{s}}t + i\frac{{{{\omega }_{s}}}}{c}\int\limits_x^\infty {dx{\kern 1pt} '{{n}_{x}}\left( {{{\omega }_{s}},x{\kern 1pt} '} \right)} } \right), \\ \end{gathered} $(24)
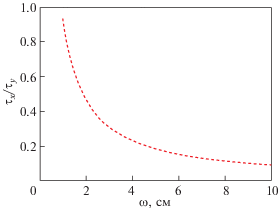
$\begin{gathered} {{A}_{s}}\left( {t,{\mathbf{r}}} \right) = - i\frac{{4\pi }}{c}\int\limits_x^\infty {\frac{{dx{\kern 1pt} '}}{{\sqrt {{{n}_{x}}\left( {{{\omega }_{s}},0} \right){{n}_{x}}\left( {{{\omega }_{s}},x} \right)} }}} \times \\ \, \times J\left( {{{\omega }_{0}} - {{\omega }_{L}},n_{{sy}}^{{(0)}},x{\kern 1pt} ',y,z} \right) \times \\ \, \times \exp \left( { - i{{\omega }_{s}}t + i\frac{{{{\omega }_{s}}}}{c}\int\limits_{x'}^\infty {dx{\kern 1pt} '{\kern 1pt} '{{n}_{x}}\left( {{{\omega }_{s}},x{\kern 1pt} '{\kern 1pt} ',n_{{sy}}^{{(0)}}} \right)} } \right). \\ \end{gathered} $Рис. 3.
Зависимость отношения характерных времен пребывания дочерней волны в области параметрического взаимодействия от размера пучка.
Подставим (24) в правую часть уравнения (22). После несложных преобразований и интегрирования по частям получим
(25)
$\left( {\frac{\partial }{{\partial t}} + i\Lambda \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right){{B}_{{pr}}} = {{\gamma }_{0}}\exp \left( { - \frac{{{{y}^{2}}}}{{{{{\tilde {w}}}^{2}}}}} \right){{B}_{{pr}}},$(26)
${{\gamma }_{0}} = \frac{{\omega _{{pe}}^{4}\omega _{{ce}}^{2}{{\kappa }^{3}}}}{{\omega _{0}^{3}\omega _{L}^{4}\left\langle {\partial D{\text{/}}\partial {{\omega }_{L}}} \right\rangle }}\frac{{{{P}_{0}}}}{{{{{\tilde {w}}}^{2}}{{{\bar {H}}}^{2}}}}.$В (26) введено обозначение
(27)
$\, \times \exp \left( {i\frac{{{{\omega }_{s}}}}{c}\int\limits_x^{x'} {dx{\kern 1pt} '{\kern 1pt} '{{n}_{x}}\left( {{{\omega }_{s}},x{\kern 1pt} '{\kern 1pt} ',{{n}_{{sy}}}} \right)} - } \right.$Аппроксимируя невязку распадного резонансного условия (см. рис. 2) в пределах слоя нелинейного взаимодействия как
(28)
$\Delta K\left( x \right) \cong 3\frac{{{{{\left( {x - {{x}_{d}}} \right)}}^{2}}}}{{l_{d}^{3}}} - \Delta K\left( {{{x}_{d}}} \right),$(29)
$\begin{gathered} {{\kappa }^{3}} \cong \frac{{{{2}^{{5/6}}}\sqrt {2{\text{/}}3} }}{{{{2}^{p}}p!}}\frac{{l_{d}^{2}{{K}_{x}}K_{z}^{4}}}{{{{n}_{x}}\left( {{{\omega }_{0}},{{x}_{d}}} \right){{n}_{x}}\left( {{{\omega }_{s}},{{x}_{d}}} \right)}} \times \\ \, \times \exp \left( { - i\frac{\pi }{6}} \right)\int\limits_0^\infty {ds\exp \left( {i\frac{{\Delta K\left( {{{x}_{d}}} \right){{l}_{d}}}}{{{{2}^{{1/3}}}}}{{s}^{2}} - i{{s}^{6}}} \right)} \times \\ \, \times \int\limits_{ - \infty }^\infty {d\eta {{{\left( {2r + 1 - {{\eta }^{2}}} \right)}}^{2}}\exp \left( { - \frac{{{{\eta }^{2}}}}{{{{{\tilde {w}}}^{2}}K_{z}^{2}}}} \right){{{\left| {{{{\tilde {\phi }}}_{r}}\left( \eta \right)} \right|}}^{2}}} , \\ \end{gathered} $Уравнение (25) описывает абсолютную неустойчивость волны, испытывающей дифракционные потери и локализованное усиление [10, 28]. Для того чтобы показать это аналитически, предположим, что мощность волны накачки существенно превышает порог возбуждения неустойчивости. В этом случае функция $\exp \left( { - \frac{{{{y}^{2}}}}{{{{w}^{2}}}}} \right)$ может быть разложена в ряд Тейлора, $\exp \left( { - {{y}^{2}}{\text{/}}{{w}^{2}}} \right) \simeq 1 - {{y}^{2}}{\text{/}}{{w}^{2}}$, а решение уравнения выражается через функцию параболического цилиндра, амплитуда которой экспоненциально растет во времени с инкрементом [10, 28]
(30)
$\begin{gathered} \gamma = \left| {{{\gamma }_{0}}} \right|\cos \left( \psi \right) - \left( {2l + 1} \right) \times \\ \times \;\sqrt {\frac{\Lambda }{{{{{\tilde {w}}}^{2}}}}\left| {{{\gamma }_{0}}} \right|} \cos \left( {\psi {\text{/}}2 - \pi {\text{/}}4} \right). \\ \end{gathered} $В свою очередь, поправка к частоте КЛВ равна
(31)
$\begin{gathered} \delta \omega = \left| {{{\gamma }_{0}}} \right|\sin \left( \psi \right) - \left( {2l + 1} \right) \times \\ \times \;\sqrt {\frac{\Lambda }{{{{{\tilde {w}}}^{2}}}}\left| {{{\gamma }_{0}}} \right|} \sin \left( {\psi {\text{/}}2 - \pi {\text{/}}4} \right). \\ \end{gathered} $В выражениях (30) и (31) $\tan \left( \psi \right) = \frac{{\operatorname{Im} \left( {{{\gamma }_{0}}} \right)}}{{\operatorname{Re} \left( {{{\gamma }_{0}}} \right)}}$ и $l \in \mathbb{Z}$.
Грубую оценку порога возбуждения неустойчивости можно получить, положив $\gamma = 0$ в выражении (30),
(32)
$\left| {{{\gamma }_{0}}\left( {P_{0}^{{th}}} \right)} \right| = \frac{\Lambda }{{{{{\tilde {w}}}^{2}}}}\frac{{\cos {{{\left( {\psi {\text{/}}2 - \pi {\text{/}}4} \right)}}^{2}}}}{{\cos {{{\left( \psi \right)}}^{2}}}}.$Отметим, что согласно (31) и (27) порог абсолютной неустойчивости по мощности, определяемый из условия равенства нулю инкремента, зависит от ширины пучка волны накачки только за счет зависимости от этого параметра фактора ${{\kappa }^{3}}$. Согласно соотношению (30) эта зависимость насыщается при ${{w}^{2}}K_{z}^{2} > 1$, когда ширина пучка накачки превосходит размер области локализации КЛВ вдоль по магнитному полю. Для примера рассмотрим случай, когда область параметрического распада (${{x}_{d}}$) расположена в окрестности фокуса пучка $x = R$. При этом, если выполнены условия ${{w}^{2}}\;\; \gg \;\;\frac{c}{{{{\omega }_{0}}}}\int_{{{x}_{d}}}^R {\frac{{dx{\kern 1pt} '}}{{{{{\left( {\varepsilon \left( {{{\omega }_{0}},x{\kern 1pt} '} \right)\;\; - \;\;g{{{\left( {{{\omega }_{0}},x{\kern 1pt} '} \right)}}^{2}}{\text{/}}\varepsilon \left( {{{\omega }_{0}},x{\kern 1pt} '} \right)} \right)}}^{{1/2}}}}}} $ и ${{w}^{2}}\;\; \gg \;\;\frac{c}{{{{\omega }_{0}}}}\int_x^R {dx{\kern 1pt} '\frac{{1 + g{{{\left( {{{\omega }_{0}},x{\kern 1pt} '} \right)}}^{2}}{\text{/}}\varepsilon {{{\left( {{{\omega }_{0}},x{\kern 1pt} '} \right)}}^{2}}}}{{{{{\left( {\varepsilon \left( {{{\omega }_{0}},x{\kern 1pt} '} \right){\kern 1pt} \; - {\kern 1pt} \;g{{{\left( {{{\omega }_{0}},x{\kern 1pt} '} \right)}}^{2}}{\text{/}}\varepsilon \left( {{{\omega }_{0}},x{\kern 1pt} '} \right)} \right)}}^{{1/2}}}}}} $, дифракцией пучка поперек и вдоль магнитного поля в резонансном слое можно пренебречь, что позволяет считать его фронт плоским, пренебрегая малой кривизной и полагая ${{w}_{f}} = 0$. Для типичных параметров экспериментов выполняется строгое неравенство ${{\left( {{{\omega }_{{сe}}}\omega _{{pe}}^{2}{\text{/}}\omega _{0}^{3}} \right)}^{2}} \ll 1$. В этом случае приведенные выше критерии значительно упрощаются и сводятся к одному ${{w}^{2}} \gg $ $ \gg \frac{c}{{{{\omega }_{0}}}}\int_{{{x}_{d}}}^R {\frac{{dx{\kern 1pt} '}}{{\varepsilon {{{\left( {{{\omega }_{0}},x{\kern 1pt} '} \right)}}^{{1/2}}}}}} $.
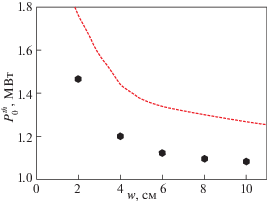
На рис. 4 проиллюстрирована аналитическая зависимость инкремента неустойчивости (30) от мощности пучка накачки для двух значений радиуса пучка (номера мод КЛВ $p = 142$, $r = 0$) в случае плоского фронта волны. На этом же рисунке символами указаны значения инкремента, полученные численно в результате решения уравнения (25). Как видно, аналитическое решение хорошо описывает значения инкремента в надпороговой области, однако сильно занижает его около порога. В результате оказывается существенно завышенным и значение порога неустойчивости. На рис. 5 приведены зависимости порога возбуждения неустойчивости от размера пучка для случая плоского фронта волны, которые определены в результате численного решения уравнения (25) для типичных параметров экспериментов на токамаке ASDEX-Upgrade (см. подписи к рис. 1 и 2), а также из аналитического соотношения (32). Как видно из рисунка, численно определенная зависимость порога от ширины пучка находится в качественном соответствии с предсказаниями аналитического рассмотрения, а именно, зависимость выходит на насыщение, когда размер пучка порядка размера области локализации КЛВ вдоль магнитного поля ($1{\text{/}}{{K}_{z}} = 9$ см). Тем не менее, численное значение порога оказывается существенно ниже грубой аналитической оценки.
Рис. 4.
Зависимость инкремента неустойчивости (30) от мощности пучка накачки для двух значений радиуса пучка. Для небольших мощностей зависимость показана в окне. Номера мод КЛВ $p = 142$, $r = 0$. Плоский фронт волны ${{w}_{f}} = 0$ см.

Рис. 5.
Зависимость порога возбуждения неустойчивости от размера пучка. Символы – результат численного решения уравнения (25), пунктирная линия – аналитическая оценка (32). Номера мод КЛВ $p = 142$, $r = 0$. Плоский фронт волны ${{w}_{f}} = 0$ см.
Отметим, что рассеяние волны накачки возможно и в результате параметрического возбуждения собственных, распространяющихся по малому обходу токамака, полоидальных мод нижнегибридной волны. Грубая оценка инкремента этого нелинейного процесса дает значение, которое меньше в квадрат отношения малого радиуса токамака и диаметра пучка накачки раз, чем то, что определено в настоящей статье (см. выражение (30)). Тем не менее, порог возбуждения собственных полоидальных мод, определяемый затуханием нижнегибридной волны при распространении по малому обходу в токамаке, может быть ниже, чем в рассмотренном в статье случае. Это позволяет говорить о возможности нелинейного возбуждения таких полоидальных собственных мод в современных экспериментах с уровнем мощности в микроволновом пучке меньшем мегаватта. Кроме того, следует сказать, что возбуждение собственных полоидальных мод можно ожидать на стадии насыщения неустойчивости, рассмотренной в настоящей работе. Этот процесс будет проанализирован в отдельной статье.
6. ЗАКЛЮЧЕНИЕ
В статье продемонстрирована возможность возбуждения абсолютной параметрической распадной неустойчивости рассеяния необыкновенной волны накачки на угол порядка 90 градусов при ее прохождении через периферийный транспортный барьер в магнитной ловушке. Как следствие неустойчивости также раскачивается косая ленгмюровская волна, локализованная в зоне барьера и между локальными пробками магнитного поля. Порог неустойчивости может быть превзойден при использовании для электронного циклотронного нагрева плазмы на второй гармонике резонанса мульти-мега ваттных греющих пучков. В результате развития этой неустойчивости может снижаться эффективность ЭЦР-нагрева плазмы и меняться профиль вкладываемой мощности.
Работа выполнена при поддержке проекта РНФ 16-12-10043; расчет коэффициентов нелинейной связи проведен в рамках государственного контракта ФТИ им. А.Ф. Иоффе 0040-2014-0023.
Список литературы
Литвак А.Г., Денисов Г.Г., Запевалов В.Е., Куф-тин А.Н., Малыгин В.И., Чирков А.В., Соколов Е.В., Тай Е.М., Солуянова Е.А., Мясников В.Е., Агапо-ва М.В., Ильин В.К., Ничипоренко В.О., Попов Л.Г., Усачев С.В., Ильин В.И., Новиков В.Н. // Электронная техника. Сер. 1: СВЧ-техника. 2013. Т. 518. С. 142.
Schmid M., Franck J., Kalaria P., Avramidis K.A., Gantenbein G., Illy S., Jelonnek J., Pagonakis I.Gr., Rzesnicki T., Thumm M. // Fusion Engineering and Design. 2015. V. 96–97. P. 589.
Westerhof E., Nielsen S.K., Oosterbeek J.W., Salew-ski M., de Baar M.R., Bongers W.A., Bürger A., Hen-nen B.A., Korsholm S.B., Leipold F., Moseev D., Stej-ner M., Thoen D.J. and the TEXTOR Team // Phys. Rev. Lett. 2009. V. 103. 125001.
Nielsen S.K., Salewski M., Westerhof E., Bongers W., Korsholm S.B., Leipold F., Oosterbeek J.W., Moseev D., Stejner M. and the TEXTOR Team // Plasma Phys. Control. Fusion. 2013. V. 55. 115003.
Hansen S.K., Nielsen S.K., Stober J., Rasmussen J., Salewski M., Stejner M., Hoelzl M. and the ASDEX Upgrade Team // Proc. 46th EPS Conf. on Plasma Physics. 2019. ECA. V. 43C. P1.1075.
Coda S. for the TCV Team // Nucl. Fusion. 2015. V. 55. 104004.
Martínez M., Zurro B., Baciero A., Jiménez-Rey D., Tribaldos V. // Plasma Phys. Control. Fusion. 2018. V. 60. 025024.
Gusakov E.Z., Popov A.Yu. // Phys. Rev. Lett. 2010. V. 105. 115003.
Gusakov E.Z., Popov A.Yu. // Europhys. Lett. 2012. V. 99. P.15001.
Popov A.Yu., Gusakov E.Z. // Europhys. Lett. 2016. V. 116. P. 45002.
Popov A.Yu., Gusakov E.Z., Irzak M. A. // Plasma Phys. Control. Fusion. 2020. V. 62. 025015.
Piliya A.D. // Proc. 10th Conf. Phenomena in Ionized Gases, Oxford, 1971. P. 320.
Rosenbluth M.N. // Phys. Rev. Lett. 1972. V. 29. P. 564.
Gusakov E.Z., Popov A.Yu. // Phys. Plasmas. 2016. V. 23. 082503.
Gusakov E.Z., Popov A.Yu. // Nucl. Fusion. 2018. V. 58. 096033.
Gusakov E.Z., Popov A.Yu., Saveliev A.N. // Phys. Plasmas. 2018. V. 25. 062106.
Гусаков Е.З., Попов А.Ю. // Письма в ЖЭТФ. 2019. Т. 109. С. 723.
Gusakov E.Z., Popov A.Yu. // Nucl. Fusion. 2019. V. 59. 104003.
Gusakov E.Z., Popov A.Yu. // Plasma Phys. Control. Fusion. 2020. V. 62. 025028.
Altukhov A.B., Arkhipenko V.I., Gurchenko A.D., Gusa-kov E.Z., Popov A.Yu., Simonchik L.V., Usachonak M.S. // Europhys. Lett. 2019. V. 126. 15002.
Gusakov E.Z., Popov A.Yu., Tretinnikov P.V. // Nucl. Fusion. 2019. V. 59. 106040.
Hansen S.K. // PhD thesis. Technical University of Denmark & Max-Planck-Institut für Plasmaphysik, 2019.
Гусаков Е.З., Ирзак М.А., Пилия А.Д. // Письма в ЖЭТФ. 1997. Т. 65. С. 26.
Gusakov E.Z., Dyachenko V.V., Irzak M.A., Shcherbi-nin O.N., Khitrov S.A. // Plasma Phys. Control. Fusion. 2010. V. 52 . 075018.
Cohen B.I., Cohen R.H., Nevins W.M., Rognlien T.D. // Rev. Mod. Phys. 1991. V. 63. P. 949.
Miettunen J., Airila M.I., Groth M., Lindholm V., Makkonen T., Äkäslompolo S. and the ASDEX Upgrade Team // J. Nucl. Mater. 2015. V. 463. P. 459.
Ryter F., Rathgeber S.K., Barrera Orte L., Bernert M., Conway G.D., Fischer R., Happel T., Kurzan B., McDermott R.M., Scarabosio A., Suttrop W., Viezzer E., Willensdorfer M., Wolfrum E. and the ASDEX Upgrade Team // Nucl. Fusion. 2013. V. 53. 113003.
Гусаков Е.З., Попов А.Ю. // Письма в ЖЭТФ. 2017. Т. 105. С. 64.
Дополнительные материалы отсутствуют.
Инструменты
Физика плазмы


