Физика плазмы, 2022, T. 48, № 10, стр. 944-950

1. ВВЕДЕНИЕ

Плоские нелинейные бегущие волны в сплошной среде – это решения уравнений динамики сплошной среды, зависящие от радиуса-вектора r и времени t в комбинации $\theta = \left\langle {{\mathbf{r}},{\mathbf{k}}} \right\rangle - at$, где $a = {\text{const}}$ называется фазовой скоростью, величина θ – фазой волны, а k – фиксированный единичный вектор, определяющий направление распространения волны. Таким образом, в бегущей волне профили всех параметров сплошной среды перемещаются в пространстве (т.е. “бегут”) как единое целое без искажений со скоростью a вдоль вектора k.

Особый интерес представляют специальные типы бегущих волн – уединенные волны (солитоны), для которых все параметры сплошной среды при $\theta \to \pm \infty $ имеют конечные и равные пределы. Эти предельные значения при нахождении солитона рассматриваются как граничные условия.

При исследовании солитонов в сплошной среде используются два подхода. В первом – солитоны получаются как решения модельных уравнений, линейка которых в настоящее время довольно внушительная, начиная с уравнений Кортевега-де-Фриза (КдФ), нелинейное уравнение Шредингера (НУШ) [1–3] и кончая уравнениями для плазмы типа Кадомцева–Петвиашвили (КП) [4], Захарова [5] и др. [6–8]. Во втором подходе уравнения для бегущих волн (в частности, солитонов) выводятся из первых принципов, а солитоны ищутся как специальные решения полученных уравнений. В качестве первых принципов при гидродинамическом описании сплошной среды рассматриваются законы сохранения массы, энергии, импульса с добавлением к ним в случае плазмы законов электродинамики. Ниже мы руководствуемся вторым подходом, поскольку достоверность решений модельных уравнений для плазмы требует дополнительной верификации, а при выводе модельных уравнений используются неформальные, порой нестандартные приемы. В то же время уравнения бегущих волн, получаемые из первых принципов, как правило, намного сложнее модельных, но их достоверность такая же, как и породивших их первых принципов. Учитывая сказанное, исследование солитонов из первых принципов сопряжено с серьезными проблемами, и число решенных задач невелико.

Выделим в качестве достижений ионно-звуковые солитоны [9] и солитоны в холодной двухжидкостной квазинейтральной плазме [10–13], полученные на базе уравнений электромагнитной гидродинамики [14] (в западной литературе именуемых “extended MHD” и “inertial MHD”). Последние применялись в [15] для исследования структуры фронта ударной волны в бесстолкновительной плазме. В [16] численно исследовалось взаимодействие указанных солитонов, и было установлено, что они взаимодействуют подобно материальным частицам (см. также [14]). К солитонам, изученным в [10], в монографии [14] добавлен еще один допускающий полное аналитическое описание класс уединенных волн, представляющих собой волновые пакеты поперечных колебаний, бегущих вдоль магнитного поля.

Уравнения бегущих волн в холодной квазинейтральной двухжидкостной плазме [14, 16] достаточно сложны и до сих пор полностью не проинтегрированы. Они существенно упрощаются в приближении холловской магнитной гидродинамике (ХМГД), и, как показано в настоящей работе, граничная задача о нахождении уединенной волны в указанном приближении получисленно-полуаналитически может быть полностью решена. При этом возможен в полном объеме учет температур электронов и ионов.

Холловская МГД активно использовалась многими авторами, в частности, для описания мелкомасштабных явлений в плазме, например, баллонных мод и эффектов турбулентности [17, 18], при изучении быстрого перезамыкания магнитных силовых линий в слаборезистивной плазме [19, 20], при исследовании плазменных переключателей [21], а также ионно-звуковых ударных волн [22].

Численно существование плоских уединенных волн в холловской МГД, часто используемой в плазменных исследованиях, было установлено в [23, 24]. В этой работе решается граничная задача для уединенных волн в холловской МГД. В частности, найдены границы изменения фазовой скорости, для которой существует уединенная волна, бегущая справа налево или слева направо. Работа является законченным необходимым этапом для последующего исследования взаимодействия полученных уединенных волн в приближении холловской МГД. Исследование взаимодействия найденных солитонов сопряжено с рядом вычислительных проблем, и полученные авторами результаты требуют дополнительной верификации, что не позволило включить их в настоящую работу. Требуют прояснения ряд вопросов: будут ли солитоны взаимодействовать подобно материальным частицам, сохраняя свои характеристики (амплитуду, фазовую скорость и пр.) после взаимодействия?; каково время взаимодействия?; возникает ли при взаимодействии излучение?; порождаются ли солитоны одиночным импульсом? и т.д. Аналогичные исследования обычно проводятся на базе модельных уравнений и требуют применения достаточно рафинированной техники – метод обратной задачи рассеяния, преобразования Бэклунда, уравнения Лакса, цепочки Тода и пр. [2, 3]. Наши исследования основаны на первых принципах.

Наличие уединенных волн в холловской МГД указывает на появлении дисперсии. Как следует из работы, возникновение дисперсии в холловской МГД обусловлено холловскими слагаемыми в законе Ома и значит именно эти слагаемые ответственны за возникновение солитонов в холловской МГД.

Предложенная теория полезна при анализе явлений, наблюдаемых в космической и лабораторной плазме. Например, нелинейные колебания, в частности, уединенные и ударные волны в межзвездной среде, возникают при образовании солнечного ветра, когда солнечная корона выбрасывает с большой скоростью огромную массу горячей водородной плазмы [25]. В работе [26] отмечены примеры наблюдаемых уединенных волн в магнитосфере и магнитопаузе Земли. В лабораторной плазме под действием сильного импульсного магнитного поля, толкающего плазму, также могут возникать нелинейные колебания, в том числе ударные и уединенные волны [27].

2. ОСНОВНЫЕ УРАВНЕНИЯ

Уравнения холловской МГД для бездиссипативной плазмы в гауссовской системе единиц имеют вид [28]:

где ${{\lambda }_{i}} = {{m}_{i}}{\text{/}}(Ze)$, ${{m}_{i}}$ – масса ионов плазмы, e – заряд электрона, Z – кратность заряда ионов, полное давление плазмы ${{p}_{\Sigma }} = {{p}_{i}} + {{p}_{e}}$, ${{p}_{i}}$ и ${{p}_{e}}$ парциальные давления ионов и электронов, и предполагается, что электронная и ионная компоненты плазмы суть идеальные политропные газы с общим показателем адиабаты $\gamma \geqslant 1$. Уравнения идеальной классической МГД получатся, если в правой части закона Ома отбросить два последних слагаемых – так называемые холловские члены, это $\sim {\kern 1pt} [{\mathbf{j}},{\mathbf{H}}]$ и $\sim {\kern 1pt} \nabla {{p}_{e}}$, а в уравнении для электронного давления отбросить слагаемое $\sim {\kern 1pt} {\mathbf{j}} \cdot \nabla ({{p}_{e}}{\text{/}}{{\rho }^{\gamma }})$, и после этого сложить уравнения для давлений. Возникновение плоских бегущих волн в холловской МГД обусловлено, как будет показано ниже, именно холловским членом $\sim {\kern 1pt} [{\mathbf{j}},{\mathbf{H}}]$ в правой части закона Ома.

Бегущие волны, распространяющиеся в плазме, подчиненной системе (1), вдоль оси $Ox$ с фазовой скоростью a, являются непрерывно дифференцируемыми решениями системы (1) вида

заданными на вещественной прямой. Подставляя функции (2) в систему (1) с учетом равенств $\partial {\text{/}}\partial y = \partial {\text{/}}\partial z = 0$, получим систему обыкновенных дифференциальных уравнений (ОДУ) на функции (2), которая имеет несколько первых интегралов, позволяющих частично проинтегрировать ее, и, тем самым, понизить размерность задачи. В итоге получается следующая система уравнений на поперечное магнитное поле ${{{\mathbf{H}}}_{ \bot }} = ({{H}_{y}},{{H}_{z}})$ и продольную скорость $u = {{U}_{x}} - a$ в системе отсчета бегущей волны: где J ≠ 0, H_x ≠ 0, $D > 0$, $K \geqslant 0$, ${{H}_{x}} \ne 0$, $({{q}_{y}},{{q}_{z}}) \ne 0$ – произвольные константы. Система (3), (4) называется уравнениями плоских бегущих волн в холловской МГД (см. также [22]). По решению $({{H}_{y}},{{H}_{z}},u)$ системы (3), (4) остальные параметры бегущей с фазовой скоростью $a$ волны восстанавливаются по формулам: где S, R, $q_{y}^{0}$, $q_{z}^{0}$ – произвольные константы, связанные с константами ${{q}_{y}}$, ${{q}_{z}}$ соотношениями:

В силу (5), (6) каждое решение системы (3), (4) порождает двухпараметрическое семейство бегущих волн. Формулы (5), (6) проясняют физический смысл констант интегрирования: ${{H}_{x}}$ – продольное магнитное поле, J – объемная плотность продольного потока массы, D – объемная плотность продольного потока импульса в системе отсчета бегущей волны. Из (6) следует $({{q}_{y}},{{q}_{z}}) = {\mathbf{E}}_{ \bot }^{'}$, где ${\mathbf{E}}{\kern 1pt} ' = {\mathbf{E}} + {{c}^{{ - 1}}}[{{{\mathbf{U}}}_{0}},{\mathbf{H}}]$ – электрическое поле в системе отсчета, двигающейся относительно лабораторной системы со скоростью U₀ = = $\left( {a,q_{y}^{0}{\text{/}}J,q_{z}^{0}{\text{/}}J} \right)$.

Уравнения бегущих волн (3), (4) состоят из дифференциальных уравнений (3) относительно ${{H}_{y}}$, ${{H}_{z}}$, куда входит и функция $u(\theta )$, и алгебраического уравнения (4), из которого в принципе можно выразить $u(\theta )$ через ${{H}_{y}}(\theta )$ и ${{H}_{z}}(\theta )$. Основная проблема в том, что $u(\theta )$, в силу уравнения (4), при $K > 0$ – двузначная функция $({{H}_{y}},{{H}_{z}})$. Уравнение (4) задает в пространстве $({{H}_{y}},{{H}_{z}},u)$ сфероид вращения – двумерную поверхность, являющуюся объединением двух замкнутых кусков, называемых ниже северным и южным полушариями (рис. 1), которые определяются при $\gamma = 1$ (изотермическая плазма) уравнениями:

причем знак “+” отвечает северному полушарию, а знак “–” – южному, и для определенности, здесь и ниже считается $J > 0$ (и тогда $u > 0$). Северное и южное полушария пересекаются по окружности Γ радиуса ${{H}_{m}}$, называемой ниже экватором. Двумерная поверхность, определяемая уравнением (4), является результатом вращения овала $Ju + K{\text{/}}{{\left| u \right|}^{\gamma }} + H_{z}^{2}{\text{/}}(8\pi ) = D$ в плоскости (H_z,  u) вокруг оси u (рис. 1). При $\gamma = 1$ характерные точки овала имеют вид ${{u}_{*}} = {{(K{\text{/}}J)}^{{1{\text{/}}2}}}$, u_± = $ = \left\{ {D{\text{/}}J \pm {{{[{{D}^{2}}{\text{/}}{{J}^{2}} - 4K{\text{/}}J]}}^{{1{\text{/}}2}}}} \right\}{\text{/}}2$. Северное полушарие получается вращением дуги WNE, а южное – дуги WSE вокруг оси u. Заметим, что условие $\gamma = 1$ служит лишь для упрощения получаемых формул, а основные результаты с соответствующими изменениями будут справедливы и для случая $\gamma > 1$. В частности, уравнение (4) для любого $\gamma > 1$ имеет ровно два положительных вещественных корня при фиксированных ${{H}_{y}}$, ${{H}_{z}}$.

Обосновывается это следующим образом. Так как из физических соображений всегда $Ju > 0$, то либо $J > 0$, $u > 0$, либо $J < 0$, $u < 0$. Если рассмотреть функцию $F(u) = Ju + K{\text{|}}u{{{\text{|}}}^{{ - \gamma }}}$, где $J > 0$, $K > 0$, $u > 0$, то эта функция будет иметь параболовидный профиль с минимумом в точке ${{u}_{ * }} = \sqrt[{\gamma + 1}]{{K\gamma {\text{/}}J}}$. Соответственно при пересечении его прямой $F(u) = {\text{const}}$ будем иметь либо ноль точек, либо одну точку, либо две точки пересечения. При сделанном допущении $H_{y}^{2} + H_{z}^{2} < H_{m}^{2} = $ $ = 8\pi \left( {D - F({{u}_{*}})} \right)$ уравнение (4) имеет ровно два положительных корня при любом $\gamma > 1$.

Бегущая волна, лежащая только в северном или только в южном полушарии ищется из системы ОДУ (3), где положено $u = {{u}_{ + }}({{H}_{y}},{{H}_{z}})$ для северного и $u = {{u}_{ - }}({{H}_{y}},{{H}_{z}})$ для южного полушарий, в замкнутом круге $H_{y}^{2} + H_{z}^{2} \leqslant H_{m}^{2}$ на плоскости $\{ ({{H}_{y}},{{H}_{z}})\} $. Самый сложный случай, когда бегущая волна расположена одновременно и в северном, и в южном полушариях, и в силу этого пересекает экватор Γ. Можно показать, что бегущие волны, являющиеся уединенными, всегда расположены либо в северном, либо в южном полушариях, что существенно упрощает их исследование.

3. ГРАНИЧНАЯ ЗАДАЧА ДЛЯ УЕДИНЕННОЙ ВОЛНЫ

С геометрической точки зрения уединенная волна реализуется как интегральная кривая системы (3), лежащая на сфероиде (4), которая за бесконечное время выходит из некоторой точки на сфероиде и за бесконечное время входит в эту же точку (рис. 1). При этом роль времени играет фаза волны θ. Указанная точка является с необходимостью особой точкой системы (3), и определяется граничными условиями на $ \pm \infty $. Как уже отмечалось, геометрическая петля, реализующая уединенную волну, всегда лежит либо в северном, либо в южном полушарии, и не пересекает экватор.

Заметим, что за счет поворота системы координат в поперечной плоскости всегда можно считать ${{q}_{z}} = 0$, что ниже предполагается.

Пусть на бесконечности заданы величины (граничные условия)

и задана фазовая скорость волны a. Поставим задачу нахождения уединенной волны, имеющей на $ \pm \infty $ заданные значения параметров (8) и бегущей вдоль оси $Ox$ с фазовой скоростью a. Для этой волны значение $u( \pm \infty )$ и величины J, D, K, $q_{y}^{0}$, $q_{z}^{0}$ однозначно определяются по граничным значениям формулами (5), (6)

Значения констант ${{q}_{z}} = 0$, ${{q}_{y}} = - {{c}^{{ - 1}}}(a - $ $ - \;H_{x}^{2}{\text{/}}(4\pi {{\rho }_{\infty }}a))$ определяются требованием, чтобы точка (${{H}_{y}} = 0$, ${{H}_{z}} = {{H}_{\infty }}$, $u = - a$) на сфероиде являлась особой для системы (3). Тогда из (6) вычисляются константы R и S.

Безразмерные значения параметров уединенной волны относительно характерных масштабов ${{H}_{0}} = {{H}_{\infty }}$, ${{\rho }_{0}} = {{\rho }_{\infty }}$, ${{v}_{0}} = {{H}_{\infty }}{\text{/}}{{(4\pi {{\rho }_{\infty }})}^{{1{\text{/}}2}}}$, ${{L}_{0}} = c{\text{/}}{{\omega }_{{pi}}}$, где ${{\omega }_{{pi}}} = {{(4\pi {{\rho }_{0}})}^{{1{\text{/}}2}}}{\text{/}}{{\lambda }_{i}}$, подчиняются в случае $\gamma = 1$ системе уравнений

где a – безразмерное значение фазовой скорости, p – безразмерное значение константы ${{q}_{y}}$, а $\beta = {{H}_{x}}{\text{/}}{{H}_{0}}$, $K = {{p}_{\infty }}{\text{/}}\left( {{{\rho }_{\infty }}v_{0}^{2}} \right)$, – безразмерные константы. В системе (9), (10) есть два неопределенных параметра, a и p. Имеет место правило знаков: при $a > 0$ (волна бежит слева направо) имеем $u < 0$, $J < 0$, при $a < 0$ (волна бежит справа налево) имеем $u > 0$, $J > 0$.

Рассмотрим случай $a < 0$. Тогда $u > 0$, в безразмерном виде ${{H}_{z}}( \pm \infty ) = 1$, ${{H}_{y}}( \pm \infty ) = 0$, $u( \pm \infty ) = \;{\text{|}}a{\text{|}}$ и точка ${{H}_{y}} = 0$, ${{H}_{z}} = 1$, $u = {\text{|}}a{\text{|}}$ является особой для системы (9), (10), что позволяет найти параметр $p = {\text{|}}a{\text{|}} - {{\beta }^{2}}{\text{/|}}a{\text{|}}$. Параметр a ищется более сложным образом.

Из классификации особых точек для системы ОДУ на плоскости [29] следует, что при $\left| a \right| \ne \sqrt K $ для существования интегральной кривой, исходящей и входящей в особую точку за бесконечное время, необходимо (но не достаточно) чтобы эта особая точка была седловой. Помимо особой точки (0.1) в зависимости от фазовой скорости существуют от одной до трех особых точек, но все они имеют тип “центр” – собственные числа матрицы Якоби чисто мнимые и сопряженные. Характер решения определяется типом особой точки (0.1) и не зависит от других особых точек. Матрица Якоби ${{M}_{J}}$ системы (9) в особой точке (0.1) имеет вид:

где для $\left| a \right| > \sqrt K $ особая точка лежит на северном полушарии, и в (9) надо поставить $u = {{u}_{ + }}({{H}_{y}},{{H}_{z}})$, а для $\left| a \right| < \sqrt K $ особая точка лежит на южном полушарии, и в (9) надо поставить $u = {{u}_{ - }}({{H}_{y}},{{H}_{z}})$. Функции ${{u}_{ \pm }}({{H}_{y}},{{H}_{z}})$ имеют вид: причем при $\left| a \right| \ne \sqrt K $ особая точка (0.1, $\left| a \right|$) не попадает на экватор, а точка (0.1) лежит внутри круга $H_{y}^{2} + H_{z}^{2} \leqslant H_{m}^{2}$, ${{H}_{m}} = {{\left[ {2{{{(\left| a \right| - \sqrt K )}}^{2}} + 1} \right]}^{{1/2}}}$. Особая точка (0.1) седловая тогда и только тогда, когда собственные числа матрицы ${{M}_{J}}$ являются вещественными и имеют разные знаки, что равносильно неравенству $p\left( {p + (\partial u{\text{/}}\partial {{H}_{z}})(0.1)} \right) < 0$. Отсюда вытекает следующий результат.

Пусть ${{\lambda }_{ \pm }}\;\, = \;\,\{ K\;\, + \;\,{{\beta }^{2}}\;\, + \,\;1\;\, \pm \;\,[{{(K\;\, + \;\,{{\beta }^{2}}\;\, + \;\,1)}^{2}}\;\, - $ $ - \;4K{{\beta }^{2}}{{]}^{{1/2}}}\} {\text{/}}2$. Тогда:

1) Особая точка (0.1, |a|) лежит на северном полушарии и является седловой для системы (9) тогда и только тогда, когда $\max {{\{ K,{{\beta }^{2}}\} }^{{1{\text{/}}2}}} < \left| a \right| < \lambda _{ + }^{{1{\text{/}}2}}$.

2) Особая точка (0.1, |a|) лежит на южном полушарии и является седловой для системы (9) тогда и только тогда, когда $\lambda _{ - }^{{1{\text{/}}2}} < \left| a \right| < \min {{\left\{ {K,{{\beta }^{2}}} \right\}}^{{1{\text{/}}2}}}$.

3) Для седловой точки (0.1, |a|) сепаратрисса, исходящая из особой точки (0.1) касается вектора $\left( {\sqrt {A{\text{/}}p} ,1} \right)$, где $A = - \left( {p + (\partial u{\text{/}}\partial {{H}_{z}})(0.1)} \right)$.

В размерном виде K и ${{\beta }^{2}}$ равны квадратам звуковой и продольной компоненте альфвеновской скорости, соответственно, а $\lambda _{ \pm }^{{1{\text{/}}2}}$ – быстрой (знак “+”) и медленной (знак “–”) магнитозвуковым скоростям, и ограничения на фазовую скорость, полученные выше, приобретают понятный физический смысл.

Сформулированные условия существования решения граничной задачи для уединенной волны являются необходимыми. При их выполнении для существования решения граничной задачи достаточно, чтобы сепаратриса, исходящая из особой точки (0.1), снова возвращалась в эту особую точку. Последнее проверяется численно.

4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

С учетом результата 3) рассмотрим численное решение задачи Коши для системы (9) при $a < 0$ с начальным условием ${{H}_{y}}(0) = - \varepsilon {{(A{\text{/}}p)}^{{1{\text{/}}2}}}$, ${{H}_{z}}(0) = 1 - \varepsilon $, где $\varepsilon > 0$ достаточно малая величина. При этом для $\max {{\{ K,{{\beta }^{2}}\} }^{{1{\text{/}}2}}} < \left| a \right| < \lambda _{ + }^{{1{\text{/}}2}}$ в (9) $u = {{u}_{ + }}({{H}_{y}},{{H}_{z}})$, а для $\lambda _{ - }^{{1{\text{/}}2}} < \left| a \right| < \min {{\{ K,{{\beta }^{2}}\} }^{{1{\text{/}}2}}}$ в (9) $u = {{u}_{ - }}({{H}_{y}},{{H}_{z}})$. Для численного решения системы (9) использован метод Рунге–Кутта 4-го порядка и считалось $\varepsilon = {{10}^{{ - 6}}}$. Результаты расчетов доказывают существование уединенной волны для всех $\left| a \right|$ из указанных в 1) и 2) диапазонов, профили параметров которой вычисляются по безразмерным соотношениям (5), (6):

Таким образом, проведенный теоретический и численный анализ доказывает существование двух семейств решений граничной задачи для уединенных волн, каждое из которых параметризуется величиной фазовой скорости из указанных выше диапазонов. Уединенные волны первого семейства лежат на северном полушарии и для них $\left| a \right| > \sqrt K $ (быстрые волны), а второго семейства – на южном полушарии, и для них $\left| a \right| < \sqrt K $ (медленные волны).

В случае $a > 0$ получается аналогичный результат. Если $a = \sqrt K $, то ${{H}_{m}} = 1$ и особая точка (0.1) попадает на границу круга $H_{y}^{2} + H_{z}^{2} = H_{m}^{2}$. Этот случай требует дополнительного исследования.

Верификация полученных результатов проводится подстановкой их в уравнения холловской МГД (1). Параметры полученного численно солитона с учетом (11) берутся в качестве начального условия для решения системы (1), которая в случае плоской симметрии и обезразмеривания указанным выше способом значений всех величин для изотермической плазмы ($\gamma = 1$) имеет вид

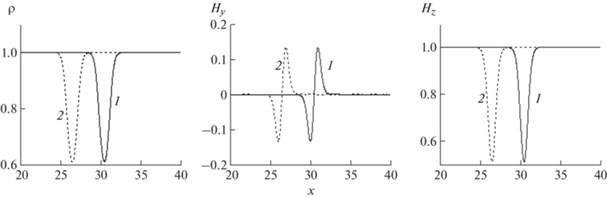
Результаты расчета системы (12) модифицированным методом Лакса–Вендроффа [14, 16] показывают, что полученная численно уединенная волна действительно со скоростью $a$ двигается как единое целое справа налево (рис. 2), пока β не превосходит некоторое критическое значение. Для больших β волна с течением времени разрушается, что, вероятно, свидетельствует о ее неустойчивости. Исследование неустойчивости уединенной волны требует дополнительного исследования и выходит за рамки настоящей работы.

5. ЗАКЛЮЧЕНИЕ

Выше из первых принципов была выведена система уравнений бегущих вдоль оси Ox волн для холловской МГД, состоящая из трех уравнений – двух обыкновенных дифференциальных уравнений первого порядка относительно компонент поперечного магнитного поля в волне и алгебраического уравнения, связывающего поперечное магнитное поле и продольную скорость плазмы в волне в системе отсчета волны. Получены явные формулы, позволяющие вычислить параметры плазмы в бегущей волне через поперечное магнитное поле и продольную скорость. Поставлена и решена граничная задача для уединенной волны. Показано, что эта волна имеет неединственное решение. Аналитически найдены диапазоны изменения фазовой скорости, для которых граничная задача разрешима. Установлено, что существует два семейства уединенных волн, доставляющих решение граничной задачи и параметризованных фазовой скоростью. Для волн первого семейства (быстрые холодные волны) фазовая скорость больше звуковой, а для волн второго семейства (медленные горячие волны) – меньше. В пределе холодной плазмы медленные горячие уединенные волны исчезают. Проведена верификация найденных уединенных волн подстановкой их в уравнения холловской МГД.

Наличие уединенных волн в холловской МГД указывает на появление дисперсии. Как следует из работы, возникновение дисперсии в холловской МГД обусловлено холловскими слагаемыми в законе Ома, и именно эти слагаемые ответственны за возникновение уединенных волн в холловской МГД.

С помощью предложенной теории можно проводить исследования уединенных волн, наблюдаемых в лабораторной и космической плазме. В частности, уединенные волны возникают в межзвездной среде при образовании солнечного ветра, а также в магнитосфере и магнитопаузе Земли. В лабораторной плазме уединенные волны возникают под действием сильного импульсного магнитного поля, толкающего плазму.