Физика плазмы, 2022, T. 48, № 10, стр. 967-974
Влияние ионно-звуковых солитонов на функции распределения фоновой плазмы
Ф. М. Трухачев a, b, c, *, М. М. Васильев a, b, О. Ф. Петров a, b
a Объединенный институт высоких температур РАН
Москва, Россия
b Московский физико-технический институт
Долгопрудный, Россия
c Белорусско-Российский университет
Могилев, Беларусь
* E-mail: ftru@mail.ru
Поступила в редакцию 17.06.2022
После доработки 07.07.2022
Принята к публикации 07.07.2022
- EDN: DMXGHU
- DOI: 10.31857/S0367292122600704
Аннотация
В рамках МГД-модели проведен анализ динамики ансамблей ионов фоновой плазмы в присутствии ионно-звуковых солитонов. Найдена функция распределения по скоростям для ионов, возмущенная солитонами. Показано, что солитоны трансформируют исходное равновесное распределение ионов к виду, который сходен с распределением плазмы, содержащей пучок ионов. Определены характерные особенности возмущенной ионной функции распределения, соответствующей солитонам различной амплитуды. Рассмотрен случай движения каскада солитонов, часто наблюдаемый на практике.
1. ВВЕДЕНИЕ
Волны и неустойчивости играют важную роль в динамике плазмы. Анализ влияния волновых процессов на функции распределения фоновой плазмы является актуальной физической проблемой. Действительно, с одной стороны, подобные исследования развивают кинетическую теорию плазмы [1], теорию неравновесных систем [2], а с другой – могут использоваться для диагностики ее свойств и создания новых методов нагрева [3–6].
В нашей работе, представлено решение проблемы возмущения функции распределения фоновой плазмы при движении ионно-звуковых (ИЗ) солитонов. Эта задача впервые была обозначена в работе [7], в которой исследовались электрические токи, индуцируемые в бесстолкновительной плазме солитонами акустического типа. В частности, с использованием МГД-моделей и одночастичного приближений было показано, что ИЗ-солитоны осуществляют односторонний перенос ионов на расстояние в несколько радиусов Дебая. Для солитонов с положительной полярностью потенциала (солитонов сжатия), направление переноса ионов совпадает с направлением движения волны. При этом скорость, а следовательно, и кинетическая энергия ионов в модели “холодной” плазмы до и после взаимодействия с солитонами оказываются равными нулю (меняется только положение ионов в пространстве). Внутри солитона скорость ионов оказывается положительной (см. также [8]). Такой перенос приводит к возникновению ионных токов импульсного характера с постоянной составляющей. Такие токи получили название “солитонных токов” [7] (см. также [9–11]). Временное разрешение токоизмерительных приборов необходимых для регистрации солитонных токов должно быть на уровне периода ионной плазменной частоты [9], что не всегда выполняется на практике [12, 13]. Солитонные токи могут оказывать существенное влияние на свойства плазмы в том случае, если в ней распространяется большой ансамбль солитонов. Такая ситуация часто наблюдается в космической плазме [13–15]. Ненулевая постоянная составляющая солитонных токов указывает на то, что возмущенная солитонами ионная функция распределения должна отличаться от максвеловской. Актуальность наших исследований подчеркивается тем, что солитоны и нелинейные волны играют важную роль в современной физике плазмы, и это подтверждается большим количеством исследований в таких областях как астрофизика [13–22], космология [23–25], термоядерный синтез [26, 27], общая физика плазмы [28], и др.
2. ОСНОВНЫЕ УРАВНЕНИЯ
Определим профиль потенциала и другие параметры ИЗ-солитона. Воспользуемся одномерной бесстолкновительной МГД-моделью плазмы с холодными ионами и горячими электронами [7]. Модель включает нормированные уравнения движения и непрерывности для ионов, уравнение Больцмана для электронов и уравнение Пуассона, связывающее обе популяции заряженных частиц
(1)
$\frac{{\partial {{v}_{i}}}}{{\partial t}} + {{v}_{i}}\frac{{\partial {{v}_{i}}}}{{\partial x}} = - \frac{{\partial {{\Phi }}}}{{\partial x}},$(2)
$\frac{{\partial {{n}_{i}}}}{{\partial t}} + \frac{{\partial {{n}_{i}}{{v}_{i}}}}{{\partial x}} = 0,$Здесь ne, ni – соответственно электронная и ионая концентрации, нормированные на невозмущенную концентрацию n0, ${{v}_{i}}$ – ионная скорость, нормированная на скорость ионного звука Cs = = (Te/mi)1/2, Te – температура электронной популяции, mi – масса иона; ${{\Phi }} = e\varphi {\text{/}}{{T}_{e}}$ – нормированный потенциал электростатического поля волны, e – элементарный заряд. Время t нормировано на величину$~\omega _{i}^{{ - 1}}$, где ${{\omega }_{i}} = \sqrt {4\pi {{n}_{0}}{{e}^{2}}{\text{/}}{{m}_{i}}} $ – ионная плазменная частота, пространственная координата нормирована на радиус Дебая ${{\lambda }_{D}} = \sqrt {{{T}_{e}}{\text{/}}4\pi {{e}^{2}}{{n}_{0}}} $. В нашей модели Ti = 0, таким образом, необходимое условие для существования ионно-звуковых волн ${{T}_{e}} \gg {{T}_{i}}$ выполняется автоматически. Будем искать решения для волн, прошедших все стадии эволюции, движущихся с постоянной амплитудой, формой и скоростью V, которая после нормировки выражается числом Маха M = V/Сs. Переходя в движущуюся вместе с волной систему координат, вводя новую переменную $S = х - Mt$, нормированную ионную концентрацию можно выразить в виде [7]
Далее систему (1)–(4) можно преобразовать к единственному уравнению Пуассона [7]
(5)
$\frac{{{{\partial }^{2}}{{\Phi }}}}{{\partial {{S}^{2}}}} = \exp \left( {{\Phi }} \right) - \frac{M}{{\sqrt {{{M}^{2}} - 2{{\Phi }}} }}.$Однократное интегрирование (5) по Φ с учетом граничных условий dΦ/dS = 0 при Φ = 0 дает выражение для псевдопотенциала Сагдеева [7]
(6)
$U\left( {{\Phi }} \right) = \left( {1 - {{e}^{{{\Phi }}}}} \right) - \left( {M\sqrt {{{M}^{2}} - 2{{\Phi }}} - {{M}^{2}}} \right).$На рис. 1a представлена зависимость U(Φ) для разных значений M, корни Φ0 соответствуют амплитуде солитонов. Как видно, амплитуда солитонов растет с ростом их скорости M (см. рис. 4a из [7]). Профиль солитона Φ(S) является решением дифференциального уравнения (6), которое можно найти либо численно, либо в приближении малых амплитуд ($\left| {{{\Phi }_{0}}} \right| \ll 1$). Во втором случае, используют разложение $U\left( {{\Phi }} \right) \approx {{A}_{2}}{{{{\Phi }}}^{2}} + {{A}_{3}}{{{{\Phi }}}^{3}}$, где ${{A}_{2}} = \frac{1}{{2{{M}^{2}}}} - \frac{1}{2}$, ${{A}_{3}} = \frac{1}{{2{{M}^{4}}}} - \frac{1}{6}$, аналитическое выражение для профиля ИЗ-солитона можно записать в виде [7]
(7)
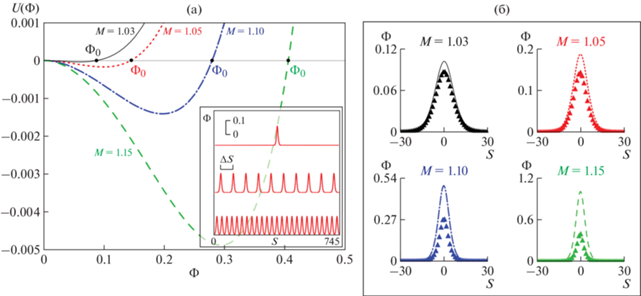
${{\Phi }}\left( S \right) \approx {{\Phi }}_{0}^{*}{\text{sec}}{{{\text{h}}}^{2}}\left( {\sqrt { - \frac{{{{A}_{2}}}}{2}} S} \right),$Рис. 1.
Псевдопотенциал Сагдеева $U\left( {{\Phi }} \right)$ при разных значениях параметра M (a). На вставке к рисунку отображены возможные волновые решения уравнения (5) в виде одного солитона, последовательности солитонов с интервалом следования ΔS, и кноидальных волн соответственно. Различным типам решений соответствуют различные начальные условия. Для одного солитона и последовательности солитонов отличия в начальных условиях невелики, а профили солитонов в обоих случаях практически совпадают; профили потенциала ИЗ-солитона при M = 1.03; M = 1.05; M = 1.1; M = 1.15 (б). Аналитические решения отображены сплошной, пунктирной, штрихпунктирной и штриховой кривыми соответственно. Символами “▲” отображены соответствующие численные решения.
Зная профиль солитона и параметры плазмы, перейдем к анализу функции распределения частиц.
3. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ИОНОВ ПО СКОРОСТЯМ. УСРЕДНЕНИЕ ПО АНСАМБЛЮ
Функцию распределения легких, горячих электронов можно с большой точностью считать Максвеловской. Поэтому ограничимся поиском функции распределения для ионов. Будем искать функцию распределения в форме распределения по проекции скорости. Выражение для одномерной функции распределения по скоростям можно записать в виде
где ${{v}_{i}}$ – проекция скорости иона вдоль оси x; ${{\Delta }}N$ – количество частиц со скоростями, лежащими в интервале от ${{v}_{i}}$ до ${{v}_{i}} + {{\Delta }}{{v}_{i}}$; $N$ – полное количество ионов в рассматриваемой области. Сделаем ряд важных замечаний.Замечание 1. В нашей модели холодной плазмы все ионы равномерно распределены в пространстве и имеют нулевую начальную скорость. Таким образом, начальное положение ионов в фазовом пространстве отличается только положением в пространстве.
Замечание 2. В отсутствие солитонов, распределение ионов по скоростям можно описать дельта-функцией, которая является предельным случаем распределения Максвелла при нулевой температуре.
Замечание 3. Как упоминалось выше, докритические ИЗ солитоны возмущают скорость ионов только в своей окрестности, при этом скорость ионов принимает только положительные значения [7]. Ионы при этом перемещаются на несколько радиусов Дебая в направлении движения волны. Движение ионов приводит к генерации ионных токов импульсного характера с постоянной составляющей. Следовательно, возмущенная функция распределения ионов по скоростям должна быть ассиметричной относительно нуля. В противном случае средняя скорость ионов, а также постоянная составляющая ионного тока были бы равны нулю.
Выберем ансамбль, содержащий N ионов фоновой плазмы, которые равномерно расположены на прямой линии вдоль оси x, как показано на рис. 2. Пусть в начальный момент времени солитон находится слева от ансамбля ионов, так, чтобы он не возмущал динамические параметры выбранных ионов. Скорость солитона направлена слева направо, т.е. в сторону ансамбля ионов. Найдем распределение скоростей для ионов ансамбля в момент, когда солитон окажется примерно в центре ансамбля. Параметры движения однозарядных ионов в неподвижной системе координат можно найти из второго закона Ньютона [9, 29]
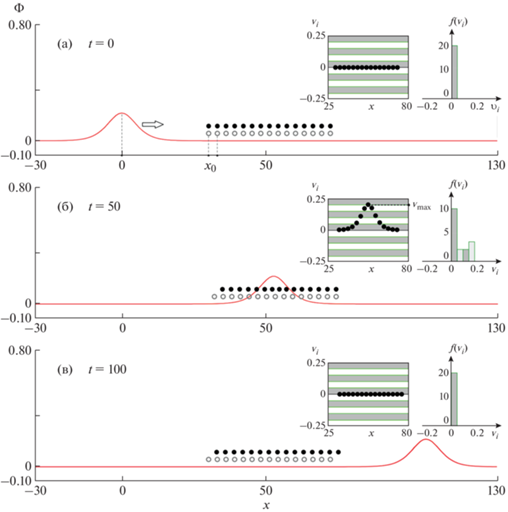
где ${\mathbf{E}} = - \nabla \varphi $ – самосогласованное электрическое поле солитона. Важно отметить, что рассматриваемый ансамбль ионов является частью всей ионной популяции, участвующей в самосогласованном волновом процессе. Поэтому движение отдельных ионов описывает движение всей ионной популяции. В одномерном случае, с учетом принятых ранее нормировок уравнение (9) можно преобразовать к видуРис. 2.
Фазы процесса взаимодействия ИЗ-солитона с ансамблем ионов. Символами “○” и “⚫” обозначены начальные и текущие положения ионов ансамбля. Символы “○” и “⚫” разнесены по вертикали для наглядности. Фаза 1, состояние до взаимодействия, начальная скорость ионов ансамбля равна нулю (a); фаза 2, ИЗ-солитон достигает середины ансамбля, скорость ионов отлична от нуля (б); фаза 3, солитон покидает ансамбль, скорость ионов снова равна нулю, при этом все ионы переместились вперед на несколько λD (в). На вкладках к рисункам представлено положение частиц в пространстве скоростей (фазовом пространстве), а также распределения ионов ансамбля по проекциям скоростей.
Функцию Ф(x,t) можно получить в явном виде подставив S = x – Mt в (7) или численно (в виде таблицы). Уравнение (10) справедливо для всех ионов рассматриваемого ансамбля, отличия заключаются лишь в начальных условиях, которые описывают положение отдельных ионов в начальный момент времени. Более того, как показано на рис. 12 а из работы [7], траектории всех ионов одинаковы (отличия состоят в пространственно-временном сдвиге). Начальные условия следующие:
1) количество ионов в ансамбле N = 15;
2) начальная скорость всех ионов ансамбля ${{v}_{i}}\left( 0 \right) = dx{\text{/}}dt = 0$;
3) начальное положение ионов: ${{x}_{1}}\left( 0 \right) = {{x}_{0}}$, ${{x}_{2}}\left( 0 \right) = ~{{x}_{0}} + \Delta x, \ldots ,{{x}_{N}}\left( 0 \right) = {{x}_{0}} + \Delta x\left( {N - 1} \right)$, где ${{x}_{0}} = 30$ – начальное положение первой частицы ансамбля, $\Delta x = 3$ – расстояние между соседними частицами ансамбля;
4) начальное положение солитона xS(0) = 0, скорость M = 1.05 (соответствующий профиль отображен на рис. 1).
Для решения уравнения (10) применялся метод Рунге–Кутты 4-го порядка. На рис. 2 показаны основные фазы процесса взаимодействия ИЗ-солитона с ансамблем ионов, а именно: начальное состояние системы (а); состояние когда солитон находится в центре ансамбля ионов (b); состояние релаксации, когда солитон удаляется от ансамбля (c).
Положение ионов ансамбля отображено символами “⚫”, в то время как начальное положение частиц отображено символами “○”. Для наглядности символы “⚫” и “○” разнесены по вертикали. Положение частиц в пространстве скоростей (фазовые графики), а также гистограммы распределения по скоростям f(${{v}_{i}}$) отображены на вкладках на рис. 2. Шкала скоростей на фазовых графиках разбита на интервалы с шагом $\Delta {{v}_{i}}$ = 0.05. Эти интервалы использовались для определения дискретной функции распределения f(${{v}_{i}}$), рассчитываемой по формуле (8).
Как видно из рис. 2a, в начальном состоянии (фаза 1), все ионы ансамбля покоятся, их скорость равна нулю. Как указывалось выше (замечание 2), в таком случае их распределение по скоростям стремится к дельта-функции. Такое же распределение наблюдается после того, как ИЗ‑солитон покидает ансамбль ионов (фаза 3). Фаза 3 отличается от фазы только положением ионов, которые были перемещены солитоном на расстояние $\ell $ ~ 3λD, межчастичное расстояние и скорость ионов принимают исходные значения $\Delta x = 3$, ${{v}_{i}} = 0$ соответственно. Процесс взаимодействия уединенного иона с ИЗ-солитоном подробно описан в [7, 9].
Интерес для нас представляет фаза 2, которую можно считать активной фазой взаимодействия солитон–частица. В этой фазе солитон находится примерно в центре ансамбля ионов. Как видно из вкладки к рис. 2б, скорость ионов ансамбля в этом случае принимает неотрицательные значения (т.е. ${{v}_{i}} \geqslant 0$). В данном случае распределение по скоростям для ионов можно легко определить по формуле (8). Для этого достаточно подсчитать количество частиц в каждом интервале скоростей [${{v}_{i}}$, ${{v}_{i}}$ + $\Delta {{v}_{i}}$) (для удобства соседние интервалы залиты разным цветом). Из вкладки к рис. 2б видно, что распределение частиц по скоростям имеет несимметричную форму, что согласуется с замечанием 3. В частности, f(${{v}_{i}}$) = 0 при ${{v}_{i}}$ < 0, однако f(${{v}_{i}}$) > 0 в интервале положительных скоростей 0 ≤ ${{v}_{i}}$ < 0.2. Именно в этом интервале лежит скорость ионов, взаимодействующих с солитоном.
Понятно, что точность получения функции $f({{v}_{i}})$ будет возрастать при увеличении количества частиц в ансамбле N, а также при уменьшении приращений Δx, $\Delta {{v}_{i}}$. На рис. 3 представлены возмущенные ионные функции распределения для фазы 2 при относительно большом ансамбле частиц N = 1000 и разных значений числа Маха (и, соответственно, разных амплитудах солитона Φ0). При расчете были выбраны следующие параметры: Δx = 0.04; $\Delta {{v}_{i}}$ = 0.01. Методика расчета полностью совпадала с методикой получения данных, представленных на рис. 2. А именно, уравнение (10) решалось N раз для разных начальных положений иона. В результате получался массив из N дискретных зависимостей ${{v}_{i}}(t)$. Далее фиксировалось время t при котором солитон находился примерно в центре ансамбля ионов (например, t = 50 в случае, представленном на рис. 2б). Получался одномерный массив (строка) размерностью N, который содержал скорости всех ионов ансамбля в заданный момент времени. Полученный массив обрабатывался простым алгоритмом, который проводил подсчет частиц в каждом из интервалов скоростей [${{v}_{i}}$; ${{v}_{i}}$ + $\Delta {{v}_{i}}$). Отметим, что теперь в уравнении (10) использовался численный профиль электрического поля солитона, поскольку формула (7) давала большую погрешность при больших Φ0. Численные профили Φ(S), отображенные на рис. 1б, определялись в результате интегрирования уравнения (6) (или (5)) методом Рунге–Кутты, при этом начальным условием Φ(0) = Φ0 для численного решения уравнения (6) являлся ненулевой корень уравнения U(Φ) = 0 (как показано на рис. 1a).
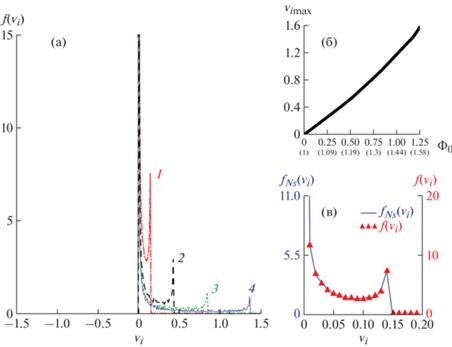
Рис. 3.
Возмущенные функции распределения ионов по скоростям $f({{v}_{i}})$ (в фазе 2) для больших ионных ансамблей N = 1000 при разных значениях числа Маха: кривая 1 – M = 1.05; 2 – M = 1.15; 3 – M = 1.3; 4 – M = 1.5; другие параметры моделирования: $\Delta x = 0.04$, $\Delta {{v}_{i}} = 0.01$ (a); максимальная скорость ионов внутри солитона, как функция его амплитуды ${{v}_{{i{\text{max}}}}}\left( {{{{{\Phi }}}_{0}}} \right)$ (б); возмущенная функция распределения, рассчитанная для ансамбля солитонов, который показан на вставке к рис. 1а при следующих параметрах: M = 1.05, N = 1000, $\Delta x = 0.745$, $\Delta v = 0.01$ (в).
Проанализируем полученные результаты. Для всех значений параметра M, форма ионной функции распределения по скоростям имеет два локальных максимума, обозначим их как ${{v}_{1}}$ и ${{v}_{2}}$ соответственно. Первый максимум находится в окрестности нуля (т.е. $~{{v}_{1}} = 0$) при любых M. В это же время, второй максимум находится в области положительных скоростей. Первый максимум является фундаментальным, он определяется невозмущенными ионами фона. Для рассматриваемой модели первый максимум формируется: во-первых, ионами, которые еще не вступали во взаимодействие с солитоном; во-вторых, ионами, которые уже релаксировали после взаимодействия. В отсутствии солитонов, этот максимум вырождается в дельта-функцию, которая описывает функцию распределения ионов в невозмущенном состоянии. Положение второго максимума функции распределения сдвигается вправо с увеличением скорости солитона M (а также его амплитуды ${{{{\Phi }}}_{0}}$). Из графиков, представленных на рис. 3 можно сделать вывод о том, что второй максимум соответствует максимальной скорости, которую ионы приобретают при взаимодействии с солитоном, ${{v}_{2}} = {{v}_{{i{\text{max}}}}}$. Величина ${{v}_{{i{\text{max}}}}}$ наглядно отображена на вставке на рис. 2б. Зависимость ${{v}_{{i{\text{max}}}}}\left( {{{{{\Phi }}}_{0}}} \right)$ отображена на рис. 3б. Как видно, величина ${{v}_{{i{\text{max}}}}}$ возрастает с увеличением амплитуды солитона (и его скорости). Для солитонов большой амплитуды ${{v}_{{i{\text{max}}}}} \to M$.
Важным аспектом является нормировка функции распределения, которая заключается в традиционном условии $\mathop \smallint \nolimits_{ - \infty }^\infty f\left( {{{v}_{i}}} \right)d{{v}_{i}} = 1$. В рассматриваемом случае, нормировка функции $f\left( {{{v}_{i}}} \right)$ возникает естественным образом, в соответствии с фор-мулой (8), а именно $\sum f\left( {{{v}_{i}}} \right){{\Delta }}{{v}_{i}} = \left( {\sum {{\Delta }}N} \right){\text{/}}N = 1$. Другими словами, нормировка производится делением на число частиц в ансамбле N. С величиной N связан размер области, которую занимает ансамбль ионов в пространстве. Размер области можно найти по формуле $X = N{{\Delta }}x$. Мы имеем X = 40λD для результатов, представленных на рис. 3a. В нашем моделировании солитон полностью помещается внутрь области X, т.е. D < X, где D – ширина солитона. Если выполняется условие D < X (желательно чтобы с некоторым запасом), то форма функции $f({{v}_{i}})$ соответствует представленной на рис. 3a. При увеличении области моделирования X наблюдается рост первого максимума функции распределения $f({{v}_{1}})$, вместе с уменьшением второго максимума $f({{v}_{2}})$. Это объясняется тем, что с увеличением ширины области моделирования X увеличивается число невозмущенных ионов. Легко показать, что дискретная функция распределения вырождается в дельта-функцию при $X \to \infty $.
С практической точки зрения, величина X связана с пространственно-временным разрешением при измерении функции распределения заряженных частиц в плазме. Конкретный вид такой связи зависит от многих экспериментальных факторов и здесь обсуждаться не будет.
Из рис. 3a видно, что форма функции распределения, возмущенная солитоном, сходна с функцией распределения плазмы, которая содержит пучок (см., например, рис. 1.17 из [30]).
4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Из полученных результатов можно сделать вывод, что влияние солитона на функцию распределения фоновой плазмы ограничено той областью, где расположен солитон. Это значит, что описанный нами феномен требует высокого пространственно-временного разрешения при экспериментальном исследовании. По порядку величины требуемое разрешение оценивалось в работах [7, 9] на уровне единиц радиусов Дебая и единиц периодов ионной плазменной частоты. Ситуация существенно упрощается если исследовать группу последовательно движущихся солитонов. В таком случае, требования к разрешению значительно снижаются, достаточно измерить функции распределения с большим временем накопления информации. Как упоминалось выше, в экспериментах часто наблюдался случай движения групп солитонов [13–15]. Феномен больших солитонных ансамблей (солитонного газа) также исследовался теоретически (см., например, [31] и ссылки внутри). Сравним полученные результаты с уже известными результатами. В работах [7, 9, 10], в рамках МГД-моделей, был рассмотрен случай движения большой группы солитонов. В такой ситуации средний солитонный ток оказывался довольно большим. Рассмотрим случай движения группы из NS одинаковых солитонов. Такую ситуацию можно смоделировать либо суммируя сдвинутые в пространстве солитонные решения [32], либо из численного интегрирования уравне-ния (5), выбрав нужные начальные условия [7, 9]. Мы воспользуемся второй методикой. Все характеристики солитонов соответствуют числу Маха M = 1.05. При интегрировании уравнения (5), начальные условия выбраны следующим образом: Φ|S= 0 = 1.2 × 10–5; dΦ/dS|S= 0 = 0, так чтобы период следования солитонов составил T = 71. Тогда расстояние между центрами солитонов может быть определено по простой формуле ΔS = TM ≈ 74.5. Соответствующее численное решение представлено на вставке к рис. 1а (в середине). При NS = 10, ситуация соответствует, той что представлена в [7] на рис. 8 . Распределение ионов по скоростям на всем интервале ΔSNS = 745 можно найти, действуя согласно алгоритму, описанному в разд. 3. Обозначим соответствующую функцию распределения как fNs(${{v}_{i}}$). Функция fNs(${{v}_{i}}$) отображена на рис. 3в. Параметры расчетов следующие: $\Delta x = 0.745$, $\Delta {{v}_{i}} = 0.~01$. Как видно, функция fNs(${{v}_{i}}$) соответствует с точностью до постоянного множителя (нормировки) функции $f({{{v}}_{i}})$, представленной на рис. 3a для M = 1.05. Зная функцию распределения по скоростям, можно найти среднюю плотность тока по формуле [33, 34]
где q – заряд частиц. В одномерном случае, с учетом нормировок формулу (11) для средней плотности ионного тока можно переписать в виде ${{J}_{i}} = \mathop \smallint \nolimits_{ - \infty }^\infty {{v}_{i}}{{f}_{{Ns}}}\left( {{{v}_{i}}} \right)d{{v}_{i}}$ или для дискретного случая(12)
${{J}_{i}} = \mathop \sum \limits_k \left( {{{\Delta }}{{v}_{i}}k} \right){{f}_{{Ns}}}\left( {{{\Delta }}{{v}_{i}}k} \right){{\Delta }}{{v}_{i}}.$Для параметров, соответствующих рис. 3в имеем ${{J}_{i}} \approx 0.023$. При увеличении точности дискретных расчетов (в частности, при N = 4000, Δx = 0.18625, $\Delta v$ = 2.5 × 10–4), получаем ${{J}_{i}} \approx 0.026$. Рассчитанное значение хорошо согласуется с результатами [7], которые были получены независимо с использованием МГД-моделей, а также в рамках одночастичного приближения.
Стоит ожидать, что если солитоны в группе не идентичны [31], то второй максимум функции распределения будет “размываться”. Логическим продолжением нашей работы является получение формул, описывающих возмущенные функции распределения заряженных частиц.
5. ЗАКЛЮЧЕНИЕ
На основе одномерной МГД-модели двухкомпонентной бесстолкновительной плазмы и одночастичного (Лагранжева) приближения проведен анализ ионной функции распределения, возмущенной ионно-звуковым солитоном или группой солитонов. Расчеты проведены путем анализа скоростей большого ансамбля ионов, участвующих во взаимодействии с солитоном. Показано, что возмущенная функция распределения имеет вид, подобный функции распределения плазмы с ионным пучком, т.е. имеет два максимума. Первый максимум является фундаментальным, он расположен в точке ${{v}_{i}} = 0$. Этот максимум определяется ионами, которые находятся вдали от солитона в рассматриваемый момент времени. Второй максимум находится в области ${{v}_{i}} > 0$, причем он лежит в дозвуковой области для солитонов малой амплитуды, и в сверхзвуковой области для солитонов большой амплитуды. Величина среднее плотности ионного тока ${{J}_{i}}$, индуцированного группой солитонов, рассчитанная с использованием функции распределения, отлично согласуются с результатами [7, 9], полученными в рамках МГД-моделей.
Работа выполнена при поддержке гранта РНФ 19-12-00354 П.
Список литературы
Климонтович Ю.Л. Кинетическая теория неидеального газа и неидеальной плазмы. М.: Наука, 1975.
Пригожин И. Введение в термодинамику необратимых процессов. М.-Ижевск: Регулярная и хаотическая динамика, 2001.
Stasiewicz K., Lundin R., Marklund G. // Physica. Scripta. 2000. V. 84. P. 60.
Jaemin Seo, Na Y.-S., Hahm T.S. // Nuclear Fusion. 2021 V. 61. P. 096022.
Bernstein I., Green J.M., Kruskal M.D. // Phys. Rev. 1957. V. 108. P. 546.
Gurevich A.B. // Sov. Phys. JETP. 1967. V. 26. P. 575.
Trukhachev F.M., Vasiliev M.M., Petrov O.F.// High. Temp. 2020. V. 58. P. 520.
Johnston C.R., Epstein M. // Phys. Plasmas. 2000. V. 7. P. 906.
Trukhachev F.M., Tomov A.V. // Cosmic Res. 2016. V. 54. P. 351.
Trukhachev F.M., Tomov A.V., Mogilevsky M.M., Chugunin D.V. // Tech. Phys. Lett. 2018. V. 44. P. 494.
Trukhachev F.M., Vasiliev M.M., Petrov O.F. // Proc. 18th Int. Workshop “Complex Systems of Charged Particles and Their Interactions with Electromagnetic Radiation”, Moscow, 2022. P. 59.
Дюбулоз М., Бертелье Ж.Ж., Малингр М., Жирар Л., Ковин Ж., Гальперин Ю.И., Чугунин Д.В., Годефруа М., Гогли Ж., Герен К., Илиано Ж.М., Косса П., Лебланк Ф., Легофф Ф., Мулярчик Т.М., Пари Ж., Сцепуржинский В., Виват Ф., Зинин Л.В. // Косм. исслед. 1998. Т. 36. С. 4.
Pickett J.S., Kahler S.W., Chen L.-J., Huff R.L., Santolík O., Khotyaintsev Y., Décréau P.M.E., Winning-ham D., Frahm R., Goldstein M.L., Lakhina G.S., Tsurutani B.T., Lavraud B., Gurnett D.A., André M., Fazakerley A., Balogh A., Rème H. // Nonlin. Processes Geophys. 2004. V. 11. P. 183.
Matsumoto H., Kojima H., Miyatake T., Omura Y., Okada M., Nagano I., Tsutsui M. // Geophys. Res. Lett. 1994. V. 21. P. 2915.
Bounds S., Pfaff R., Knowlton S., Mozer F., Temerin M., Kletzing C. // J. Geophys. Res. 1999. V. 104. P. 28 709.
Williams J.D., Chen L.-J., Kurth W.S., Gurnett D.A., Dougherty M.K. // Geophys. Res. Lett. 2006. V. 33. P. L06103.
Haas F., Mahmood S.// Phys. Rev E. 2015. V. 92. P. 053112.
Lakhina G.S., Singh S., Rubia R., Devanandhan S. // Plasma. 2021. V. 4. P. 681.
Mukherjee A., Acharya S.P., Janaki M.S. // Astrophys. Space Sci. 2021. V. 366. P. 7.
Mozer F.S., Bonnell J.W., Hanson E.L.M., Gasque L.C., Vasko I.Y. // Astroph. J. 2021. V. 911. P. 89.
Jahangir R., Ali S. // Frontiers Phys. 2021. V. 9. P. 622820.
Acharya S.P., Mukherjee A., Janaki M.S. // Nonlin. Dynamics. 2021. V. 105. P. 671.
Dubinov A.E., Saikov S.K., Tsatskin A.P. // J. Exp. Theor. Phys. 2011. V. 112. P. 1051.
Khattak M.N., Mushtaq A., Ehsan Z. // Chinese J. Phys. 2016. V. 54 (4). P. 503.
Dubinov A.E., Lebedeva X.I. // Chaos, Solitons & Fractals. 2021. V. 152. P. 111391.
Dashtban N., Motevalli S.M., Mohsenpour T. // Plasma Phys. Rep. 2018. V. 44. P. 854.
Lu F.F., Liu S.Q. // AIP Advances. 2021. V. 11. P. 055112.
Ghosh U.N., Saha A., Pal N., Chatterjee P. // J. Theor. Appl. Phys. 2015. V. 9. P. 321.
Trukhachev F.M., Vasiliev M.M., Petrov O.F., Vasilie-va E.V. // Phys. Rev. E. 2019. V. 100. P. 063202.
Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков. М.: Атомиздат, 1979.
Carbone F., Dutykh D., El G.A. // Europ. Phys. Lett. 2016. V. 113. P. 30003.
Trukhachev F.M., Vasiliev M.M., Petrov O.F., Vasilie-va E.V. // J. Phys. A: Math. Theor. 2021. V. 54. P. 095702.
Куликова И.В. // Прикладная физика. 2020. № 2. P. 27.
Власов А.А. Теория многих частиц. М.: Государственное издательство технико-теоретической литературы, 1950.
Дополнительные материалы отсутствуют.


