Физика Земли, 2020, № 1, стр. 5-29

Морфоструктурное районирование

В качестве объектов распознавания [Гельфанд и др., 1972; 1973а] было предложено использовать морфоструктурные узлы или пересечения осей морфоструктурных линеаментов. Последние выделяются в рамках морфоструктурного районирования (МСР) территории. Авторство этого метода принадлежит видному геоморфологу Елизавете Яковлевне Ранцман [Ранцман, 1979; Ранцман, Гласко, 2004]. В сотрудничестве с математиками удалось превратить МСР в метод системного анализа, формализовав его приложение к конкретному региону и обеспечив воспроизводимость результатов [Алексеевская и др., 1977; Габриэлов и др., 1977; 1982; Alekseevskaya et al., 1977].

Суть МСР состоит в разделении рассматриваемой территории на систему иерархически упорядоченных районов, обладающих определенной степенью однородности морфоструктур. МСР, как и любое районирование, подразумевает объединение объектов, обладающих схожими признаками и их численными показателями, и их отделение от объектов, характеризуемых иными признаками или их показателями [Алексеевская и др., 1977; Alekseevskaya et al., 1977]. Под понятием “морфоструктура”, введенным в геоморфологию академиком АН СССР И.П. Герасимовым [Герасимов, 1946; Ранцман, 1979], понимается совокупность проявлений в рельефе тектонических движений земной коры (в том числе хребты, котловины и др.) [Алексеевская и др., 1977; Alekseevskaya et al., 1977].

В ходе проведения МСР выделяются морфоструктуры трех рангов [Гвишиани и др., 1988а; Ранцман, 1979; Ранцман, Гласко, 2004]:

• горная страна (I-ый ранг) – территория с единым типом процесса горообразования и определенным обликом рельефа; соседние территории обладают или другим типом горообразования, или другим обликом рельефа (при том же типе горообразования);

• горные страны подразделяются на мегаблоки (II-ой ранг) – области, в пределах которых все численные показатели изменяются закономерно, а при переходе через границу закономерность нарушается;

• мегаблоки подразделяются на блоки (III‑ий ранг) – области, в пределах которых все численные показатели изменяются без резких скачков, а при переходе за границы области происходит резкое значительное изменение хотя бы одного из численных показателей.

Морфоструктурными линеаментами объявляются линейные зоны, разграничивающие горные страны, мегаблоки и блоки. Линеаментам присваивается ранг, равный наивысшему рангу разделяемых им морфоструктур [Алексеевская и др., 1977; Alekseevskaya et al., 1977]:

• линеаменты I-ого ранга – границы горных стран;

• линеаменты II-ого ранга – границы мегаблоков;

• линеаменты III-ого ранга – границы блоков.

Линеаменты подразделяются на продольные, поперечные и главные сдвиги [Алексеевская и др., 1977; Alekseevskaya et al., 1977]:

• продольный линеамент – параллелен основному простиранию крупных элементов рельефа, в его зоне выражены вертикальные движения, все продольные линеаменты следуют вдоль границ крупных элементов рельефа;

• поперечный линеамент – ориентирован косо или вкрест основному простиранию крупных элементов рельефа, характер тектонических движений в его зоне трудно устанавливаем, все поперечные линеаменты выражены прерывистыми формами;

• главный сдвиг – ориентирован косо относительно крупных элементов рельефа, но представляет собой зоны крупных разломов, в которых происходят крупномасштабные горизонтальные перемещения (выделяется только в случае, когда горизонтальные тектонические движения создают самостоятельные крупные элементы рельефа).

Морфоструктурным узлом называется область, возникшая вследствие пересечения или причленения двух или более линеаментов (как правило, продольных и поперечных). В узлах формируется мелкоблоковая структура, отраженная на дневной поверхности мозаичным сочетанием различных ландшафтов, почвенного покрова, горных пород и др. [Ранцман, Гласко, 2004]. Установление точных границ узлов является трудоемкой процедурой, реализуемой исключительно с использованием данных, являющихся результатом специальных полевых исследований.

В случае отсутствия таких данных в качестве узлов берутся некоторые окрестности пересечений линеаментов. Как правило, в качестве таких окрестностей рассматриваются круги с центрами в точке пересечения осей морфоструктурных линеаментов [Алексеевская и др., 1977; Alekseevskaya et al., 1977]. При решении задачи распознавания мест возможного возникновения землетрясений выбор радиуса таких кругов (окрестностей пересечений линеаментов) зависит от пороговой магнитуды M₀ сильных землетрясений.

Развитие метода морфоструктурного районирования проходило в несколько этапов. Первоначально (70-е годы) работы по МСР проводились исключительно в интересах метода EPA. Аргументом в пользу использования данных о рельефе при распознавании мест возможного возникновения сильных землетрясений является предположение о непосредственной связи расположения крупных элементов рельефа с горообразовательными тектоническими движениями, захватывающими глубины, на которых формируются очаги коровых землетрясений [Гвишиани и др., 1988а].

На втором этапе (80-е годы) схемы МСР также использовались для распознавания мест крупных залеганий углеводородов. На третьем этапе (90-е годы) было установлено, что районы пересечений линеаментов характеризуются повышенным числом аварийных событий [Ранцман, Гласко, 2004].

Для построения схем МСР используются данные о рельефе, геологии, структуре и глубинном строении изучаемого региона, а также результаты дешифрирования космоснимков Земли. Принципы и методика морфоструктурного районирования подробно изложены в работах [Герасимов, Ранцман, 1973; Алексеевская и др., 1977; Габриэлов и др., 1977; Ранцман, 1979; Гвишиани и др., 1988а; Ранцман, Гласко, 2004; Alekseevskaya et al., 1977].

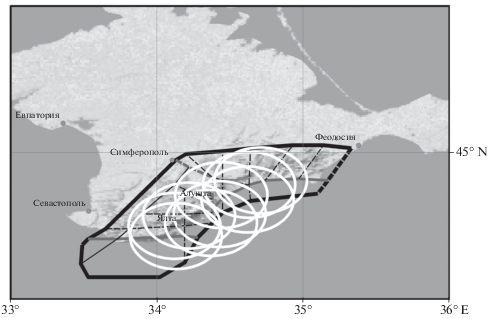
На рис. 1 показана схема МСР полуострова Крым [Соловьев и др., 2017]. Многочисленные другие примеры МСР сейсмоопасных регионов будут показаны в следующем разделе статьи.

Рис. 1.

Схема морфоструктурного районирования полуострова Крым (толстые черные линии – линеаменты I-го ранга; средние серые – II-го ранга, тонкие черные – III-го ранга; сплошными линиями показаны продольные линеаменты, пунктирными – поперечные) и места возможного возникновения землетрясений с М ≥ 6.0 (белые круги).

Приуроченность эпицентров сильных землетрясений к пересечениям морфоструктурных линеаментов

Подход EPA базируется на гипотезе о приуроченности эпицентров сильных землетрясений к пересечениям морфоструктурных линеаментов [Гельфанд и др., 1973а; Кособоков, Соловьев, 2018]. При этом под приуроченностью здесь понимаются достаточно малые расстояния между пересечениями и эпицентрами. Такая приуроченность выглядит вполне очевидной, когда эпицентры всех сильных землетрясений в регионе расположены внутри кругов некоторого радиуса с центрами в точках пересечений линеаментов, а площадь, покрытая этими кругами, является достаточно малой по сравнению с площадью всего изучаемого региона [Гвишиани и др., 1988а]. Так, например, приуроченность визуально очевидна в регионе Алтай–Саяны–Прибайкалье [Горшков и др., 2018; Дзебоев и др., 2019]. В то же время морфоструктурная сеть может быть настолько густой (например, Кавказ [Соловьев и др., 2016]), что объединение кругов, содержащих эпицентры сильных землетрясений, покрывает почти весь регион. Для проверки статистической значимости гипотезы о приуроченности эпицентров сильных землетрясений к пересечениям был разработан специальный алгоритм [Гвишиани, Соловьев, 1980], впервые примененный для сравнительного анализа положений эпицентров сильных землетрясений и пересечений линеаментов на территории Южной Америки.

Векторные объекты распознавания в пространстве геолого-геофизических данных

Алгоритм распознавания образов, используемый в подходе EPA [Гвишиани и др., 1988а; Горшков, 2010; Gorshkov et al., 2003a], представляет собой дихотомию с обучением [Бонгард, 1967]. Распознавание мест возможного возникновения сильных землетрясений выполняется на базе векторного представления объектов распознавания в пространстве геолого-геофизических и геоморфологических характеристик.

Выделенные в рамках МСР объекты распознавания описываются единым набором характеристик. Эти характеристики должны быть априорно связаны с принципиальной возможностью отражать специфику мест высокой сейсмичности. Для каждого региона подбираются и измеряются соответствующие наборы характеристик, которые также будем называть параметрами [Гвишиани и др., 2013а; Gvishiani et al., 2013]. Как правило, используемые характеристики отражают степень тектонической активности в окрестностях объектов распознавания. За годы развития EPA сформировался достаточно устойчивый список характеристик, используемых для распознавания в различных сейсмоактивных регионах [Дзебоев и др., 2019]. Все характеристики можно условно разбить на три группы [Гвишиани и др., 1988а]:

• характеристики, описывающие контрастность и интенсивность тектонических движений, – параметры, связанные с высотами рельефа, сочетаниями типов рельефа, площадью рыхлых толщ;

• характеристики, описывающие степень тектонической раздробленности, – параметры, описывающие линеаментную структуру в окрестности объектов;

• характеристики, описывающие глубинную неоднородность, – гравитационные и геомагнитные параметры. Отметим, что идея использовать геомагнитные параметры в подходе EPA принадлежит А.Д. Гвишиани, а эффективность использования литосферных магнитных аномалий впервые была показана в работе [Соловьев и др., 2016].

В окрестностях объектов распознавания измеряются значения используемых характеристик. Необходимо отметить, что в случае морфоструктурных узлов под окрестностью понимается область, ограниченная его границами, а в случае пересечений осей морфоструктурных линеаментов – область, ограниченная кругом заданного радиуса с центром в точке пересечения линеаментов. Очевидно, что узлы могут иметь различные размеры окрестностей и площадь окрестности может использоваться в качестве одной из характеристик. После вычисления значений характеристик каждому объекту распознавания ставится в соответствие вектор с действительными компонентами, элементами которого являются значения геолого-геофизических и геоморфологических характеристик, описывающих объект.

Алгоритмы дихотомии, реализующие блок распознавания в методе EPA, оперируют объектами, представленными векторами с двоичными компонентами. Преобразование исходных векторов, описывающих объекты, в бинарные векторы выполняется с помощью процедур дискретизации и кодировки [Гвишиани и др., 1988а; Горшков, 2010; Gorshkov et al., 2003a].

Основополагающей частью распознавания в классическом методе EPA является формирование и выполнение обучения. Обучаясь на векторах сформированного материала обучения, алгоритм дихотомии находит их характерные признаки (В- и Н-признаки). Затем все множество объектов W экзаменуется на основе этих признаков. Задается значение порога голосования Δ, и объекты, у которых разность между числом В-признаков и числом Н-признаков, которыми они обладают, не меньше, чем порог Δ, относятся к классу В [Гвишиани и др., 1988а; Горшков, 2010; Gorshkov et al., 2003a].

Подчеркнем, что в подходе EPA ставится не только задача распознать дизъюнктивные морфоструктурные узлы или пересечения осей морфоструктурных линеаментов, в окрестностях которых возможно возникновение сильных землетрясений, но и задача получения геолого-геоморфологического описания таких мест, т.е. выявление критериев высокой сейсмичности для рассматриваемого региона. Как это делается – описано ниже.

Семейство алгоритмов “Голосование по Набору Признаков”

В начале 1980-х возможности блока распознавания метода EPA были существенно расширены благодаря исследованиям А.Д. Гвишиани, В.А. Гурвича, в которых было введено понятие алгоритма ГНП (Голосование по Набору Признаков) [Гвишиани, Гурвич, 1983а; 1983б; 1992; и др.], определенного как строгая математическая конструкция. Класс алгоритмов ГНП включает в себя достаточно широкое семейство алгоритмов классификации с обучением. Для алгоритмов класса ГНП является возможным вывести условия, позволяющие аналитически контролировать достоверность результата в предельной задаче распознавания.

При этом для некоторого подкласса (ГНП с нормальными весами) выполнение этих условий допускает конструктивную проверку. Таким образом, алгоритмы класса ГНП естественно использовать как блок распознавания образов при решении предельных задач распознавания. В частности, для определения мест возможного возникновения сильных землетрясений [Гвишиани, Гурвич, 1992], т. к. последняя является именно такой предельной задачей [Гвишиани, Гурвич, 1983а].

Для определения класса алгоритмов ГНП введем следующие обозначения:

• $w \in W$ – множество объектов распознавания;

• ${{B}_{0}}$ и ${{H}_{0}}$ – материалы обучения классов $B$ и $H$ соответственно;

• ${{\Omega }_{n}}$ – множество бинарных векторов длины $n;$

• $\Phi :W \to {{\Omega }_{n}}$ – заданное отображение (кодировка объектов).

Пусть некоторый признак r, характерный для класса В, есть подмножество в ${{\Omega }_{n}}.$ Рассмотрим набор признаков $U = \left\{ {{{r}_{1}},...,{{r}_{N}}} \right\}$ и будем считать, что объект $w$ обладает признаком r, если $\Phi \left( w \right) \in r.$ Пусть ${{\Phi }^{{ - 1}}}\left( r \right) \subseteq W$ – множество объектов, обладающих признаком r, а $\sigma = \left( {{{\sigma }_{1}},...,{{\sigma }_{N}}} \right)$ = = $\left( {\sigma \left( {{{r}_{1}},{{W}_{0}}} \right),...,\sigma \left( {{{r}_{N}},{{W}_{0}}} \right)} \right)$ – числовой вектор весов признаков зависящих от материала обучения ${{W}_{0}} = {{B}_{0}}\coprod {{H}_{0}}.$

Алгоритмы класса ГНП решают вопрос отнесения объекта $w \in W$ к классу $B$ или $H$ путем голосования по набору признаков U. Результат голосования $F\left( w \right)$ определяется как сумма весов всех признаков, которыми обладает объект $w$ и зависит от $\Phi \left( w \right){\text{:}}$ $F\left( w \right)$ = $\sum\nolimits_{r \in U:\Phi \left( w \right) \in r} {\sigma \left( {r,{{W}_{0}}} \right)} .$ Пусть $\Delta $ некоторый порог голосования. Объект $w$ относится к классу B, если $F\left( w \right) \geqslant \Delta $ и к классу H, если $F\left( w \right) < \Delta .$ Тем самым, для задания конкретного алгоритма класса ГНП необходимо задать набор признаков $U$ и вектор весов $\sigma = \sigma \left( {{{W}_{0}}} \right).$ В таком случае $\Delta $ будет единственным свободным параметром алгоритма [Гвишиани, Гурвич, 1992].

Алгоритмы распознавания образов, используемые в подходе EPA

Как правило, в классическом подходе EPA для распознавания мест возможного возникновения землетрясений используются алгоритмы “Кора-3” [Вайнцвайг, 1973; Гвишиани и др., 1988а; Gorshkov et al., 2003a], “Подклассы” [Гельфанд и др., 1976; Кособоков, Ротвайн, 1977; Gelfand et al., 1976; и др.] и “Правило Хемминга” [Гвишиани, Кособоков, 1981; Кособоков, 1982; Гвишиани, Гурвич, 1992; и др.]. Как показано в работе [Гвишиани, Гурвич, 1992], все эти алгоритмы входят в класс алгоритмов ГНП, описанных в предыдущем пункте.

Наиболее простым из перечисленных трех алгоритмов является “Правило Хемминга”. Его применение состоит из двух этапов. На первом этапе строится ядро класса В. Оно представляет собой двоичный вектор, компоненты которого более “типичны” соответствующим компонентам двоичных векторов из обучающей выборки В₀, чем из обучающей выборки Н₀. На этом завершается обучение алгоритма. На втором этапе вычисляется расстояние Хемминга ρ от каждого двоичного вектора, соответствующего объекту распознавания, до ядра класса В. В итоге к классу В относят объекты, для которых ρ ≤ ∆ (∆ – заданный порог). Все остальные объекты относят к классу Н [Гвишиани и др., 1980а; 1988а; Кособоков, 1982]. По сути, порог ∆ является единственным свободным параметром алгоритма.

Наиболее часто используемым в EPA алгоритмом по-прежнему является алгоритм “Кора-3" [Бонгард, 1967], созданный М.М. Бонгардом и соавторами для решения задач медицинской диагностики еще в 60-х гг. прошлого века. Этот алгоритм нашел применение также и в других прикладных задачах (классификация водоносных и нефтеносных пластов, поиск нефтяных и урановых месторождений) [Бонгард и др., 1966; Бонгард, 1967; Вайнцвайг, 1973; Гвишиани, Гурвич, 1992; Ранцман, Гласко, 2004].

Алгоритм “Кора-3”, так же как и алгоритм “Правило Хемминга”, состоит из двух этапов. На первом из них выполняется обучение. На базе объектов, входящих в обучающие выборки В₀ и Н₀, формируются наборы признаков, характерных для этих выборок. Признак A определяется с помощью 6-ти чисел: три целых числа j, k, l (1 ≤ j ≤ k ≤ l ≤ L, где L – длина бинарных векторов, описывающих объекты распознавания) и три бинарных числа δ₁, δ₂, δ₃, принимающих значения 0 или 1. По определению, объект (бинарный вектор) ω = (ω₁, ω₂, …, ω_L) обладает признаком A, если значение булевой функции f(A, ωⁱ) = (δ₁ ≡ $\omega _{j}^{i}$) & (δ₂ ≡ $\omega _{k}^{i}$) & (δ₃ ≡ $\omega _{l}^{i}$) равно 1.

Для определения характерных признаков задаются четыре порога S₁, C₁, S₂ и C₂, которые являются параметрами алгоритма. Признак называется характерным признаком класса В, если число объектов из обучающей выборки В₀, которые им обладают, не меньше чем порог S₁, а число объектов из обучающей выборки Н₀, которые им обладают, не больше чем порог C₁. Соответственно, признак называется характерным признаком класса Н, если число объектов из обучающей выборки Н₀, которые им обладают, не меньше чем порог S₂, а число объектов из обучающей выборки В₀, которые им обладают, не больше чем порог C₂.

Для характерных признаков вводятся отношения подчиненности и эквивалентности. Характерный признак A является подчиненным по отношению к другому характерному признаку B того же класса, если все объекты из множества обучения этого класса, которые обладают признаком A, обладают также признаком B и есть хотя бы один объект из множества обучения, который обладает признаком B, но не обладает признаком A. Два характерных признака эквивалентны, если ими обладают одни и те же объекты соответствующего множества обучения. При формировании окончательных наборов характерных признаков классов В и Н, (В-признаков и Н-признаков) алгоритм исключает подчиненные признаки, а из группы эквивалентных оставляет только один признак.

На втором этапе выполняется классификация всех объектов из множества W на основе В- и Н-признаков с помощью еще одного параметра алгоритма – порога голосования Δ. Объект распознавания относится к классу В, если разность между числами В-признаков и Н-признаков, которыми он обладает, не меньше порога Δ. В результате множество W разделяется на два класса В и Н.

Алгоритм “Подклассы” является предложенной Ш.А. Губерманом модификацией алгоритма “Кора-3” и позволяет проводить распознавание в случае, когда материал обучения В₀ разбит на подмножества (“подклассы”). Впервые этот алгоритм применялся в исследованиях [Гельфанд и др., 1976; Gelfand et al., 1976] при распознавании высокосейсмичных зон в Калифорнии, где в качестве объектов распознавания использовались точки на разломах, а подклассы, на которые было разбито В₀, состояли из объектов, расположенных в окрестностях эпицентров уже известных сильных землетрясений. Другими словами, для каждого из таких эпицентров формируется подкласс, состоящий из объектов, находящихся в окрестности этого эпицентра, а затем объединение этих подклассов образует множество В₀. Если какой-то объект попадает в несколько подклассов, то он входит во множество В₀ несколько раз в составе тех подклассов, в которые он попал. По сравнению с алгоритмом “Кора-3” меняется определение характерного признака класса В: с порогом S₁ сравнивается не число объектов из В₀, обладающих признаком, а число подклассов, обладающих им (по определению, подкласс обладает признаком, если хотя бы один входящий в него объект обладает этим признаком).

На разных этапах развития подхода EPA для распознавания использовались и другие алгоритмы: “Expert Communication (EC)” [Sallantin, 1983], “Правило Байеса” [Гвишиани, Кособоков, 1981], различные версии алгоритма “Кора-3” [Гельфанд и др., 1976; и др.] и другие.

Особое место в блоке распознавания образов метода EPA занимает созданный в 1983 г. известным французским математиком Жаном Саллантеном (Jean Sallantin) алгоритм “EC” [Sallantin, 1983]. В рамках советско-французского проекта “Распознавание сильных и значительных землетрясений в регионах умеренной сейсмичности – Альпы, Большой Кавказ, Пиренеи” [Вебер и др., 1985; 1986а; 1986б; Гвишиани и др., 1987а; Cisternas et al., 1985; Gvishiani et al., 1987] французские участники предложили выполнить независимое изучение этих регионов методами распознавания образов. При этом использовались как различные принципы определения объектов распознавания (на основе МСР и отрезки разломов неотектонической схемы региона), так и принципиально отличные алгоритмические блоки EPA (“Кора-3” и “EC”). Независимое распознавание (dual recognition) подтвердило достоверность обоих подходов, т.к. результаты оказались достаточно близки. По результатам советско-французского проекта в 1988 г. в издательстве “Наука” была опубликована монография [Гвишиани и др., 1988а].

Отличием алгоритма “Правило Байеса” от описанных алгоритмов является то, что он не нуждается в двоичном представлении объектов распознавания, но остается необходимой процедура дискретизации, т.е. компоненты векторов, соответствующих объектам, должны принимать конечное число значений. Для построения решающего правила алгоритма необходимо задать априорную вероятность принадлежности объекта классу В и порог ∆ [Гвишиани и др., 1980а]. Для векторов, представляющих объекты, на основе обучающих выборок вычисляются оценки вероятностей их принадлежности классам В и Н. Объекты, у которых разность этих оценок не меньше ∆, относятся к классу В, а остальные объекты относятся к классу Н.

Распознавание мест возможного возникновения сильных землетрясений

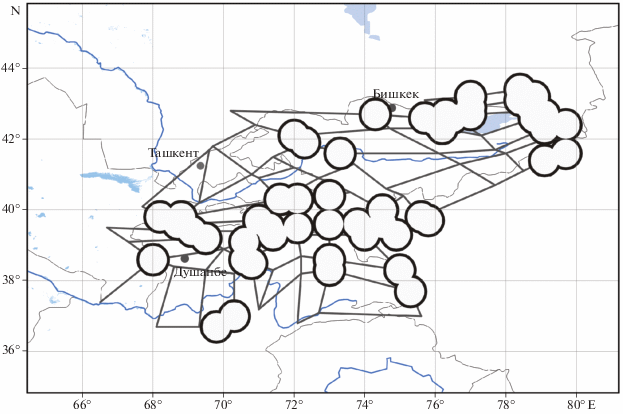
Алгоритмические основы подхода EPA были разработаны в 1972 г. в процессе решения задачи распознавания алгоритмом “Кора-3” дизъюнктивных узлов Востока Средней Азии (Тянь-Шань и Памир), в пределах которых возможно возникновение землетрясений с М ≥ 6.5 [Гельфанд и др., 1972; 1973а; Gelfand et al., 1972]. В результате удалось определить ряд новых узлов, в которых землетрясения с М ≥ 6.5 еще не происходили, но могут произойти в будущем.

Позже распознавание в этом же регионе было выполнено вновь алгоритмом “Кора-3” с использованием в качестве объектов распознавания пересечений линеаментов [Жидков, Кособоков, 1978; Жидков и др., 1980]. Результаты распознавания по узлам [Гельфанд и др., 1972; 1973а] и по пересечениям [Жидков, Кособоков, 1978] оказались хорошо согласованными. В последующем в этом регионе произошло 9 землетрясений с М ≥ 6.5. Эпицентры восьми из них расположены в узлах, отнесенных к классу В в 1972–1978 гг. Более того, два эпицентра расположены в узлах, в которых землетрясения с М ≥ 6.5 ранее не были известны [Горшков и др., 2001; Соловьев и др., 2014; Gorshkov, Novikova, 2018]. Отметим, что в работах [Гельфанд и др., 1972; 1973б; Gelfand et al., 1972] для региона впервые были определены критерии высокой сейсмичности на языке использовавшихся в исследовании геолого-геофизических характеристик. На рис. 2 показаны места возможного возникновения землетрясений с М ≥ 6.5 из работы [Жидков, Кособоков, 1978].

Рис. 2.

Схема линеаментов Тянь-Шаня и Памира и места возможного возникновения землетрясений с М ≥ 6.5 (оконтурены жирными линиями) [Жидков, Кособоков, 1978; Соловьев и др., 2014].

Работы [Гельфанд и др., 1972; 1973а; Gelfand et al., 1972] положили начало уже почти 50-летнему циклу публикаций, посвященных решению методом EPA задач распознавания мест возможного возникновения сильных землетрясений в различных горных странах мира. Результаты этих исследований опубликованы, в основном, в сборнике “Вычислительная сейсмология”, советских и российских журналах “Физика Земли” (“Известия АН СССР. Сер. Физика Земли”), “Доклады Академии наук” (“ДАН СССР”) и “Вулканология и сейсмология”, а также ведущих иностранных журн. “Tectonophysics”, “Physics of the Earth and Planetary Interiors”, “Pure and Applied Geophysics”, “Geophysics”, “Annales Geophysicae”, “International J. Geophysics”, “J. Seismology and Earthquake Engineering” и др. Распознаванию методом EPA посвящен ряд монографий [Ранцман, 1979; Гвишиани и др., 1988а; Гвишиани, Гурвич, 1992; Ранцман, Гласко, 2004; Горшков, 2010; Dubois, Gvishiani, 1998; Gvishiani, Dubois, 2002; и др.]. Результаты распознавания мест будущих сильных землетрясений опубликованы в виде глав в монографиях [Gorshkov et al., 2003a; Gvishiani et al., 2019; и др.], вышедших в издательстве Springer. В разные годы исследователями задачи EPA защищены три докторские и восемь кандидатских диссертаций.

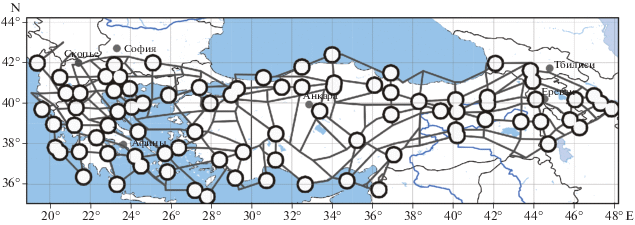
В 1973 г. с помощью алгоритма “Кора-3” было выполнено распознавание мест возможного возникновения землетрясений с М ≥ 6.5 в объединенном регионе Балкан, Эгейского моря, Анатолии и Армянского нагорья. В качестве объектов распознавания рассматривались морфоструктурные узлы [Гельфанд и др., 1974а]. В 1974 г. распознавание для этого региона было проведено с использованием других объектов распознавания – пересечений осей морфоструктурных линеаментов [Гельфанд и др., 1974б]. На рис. 3 показаны места возможного возникновения землетрясений с М ≥ 6.5 из работы [Гельфанд и др., 1974б].

Рис. 3.

Схема линеаментов и места возможного возникновения землетрясений с М ≥ 6.5 [Гельфанд и др., 1974б; Соловьев и др., 2014] (оконтурены жирными линиями) в объединенном регионе Балкан, Эгейского моря, Анатолии и Армянского нагорья.

В 1975 г. в работе [Жидков и др., 1975] результаты [Гельфанд и др., 1974а] и [Гельфанд и др., 1974б] были сопоставлены друг с другом. В результате были получены независимые классификации пересечений линеаментов в подрегионах объединенного региона. Отметим, что результаты [Жидков и др., 1975; Гельфанд и др., 1974а] хорошо согласуются. В работе [Жидков и др., 1975] наряду с алгоритмом “Кора-3” использовался и алгоритм “Подклассы”.

В 1977 г. для рассматриваемого объединенного региона было выбрано новое значение порога M₀ = 7.0 [Кособоков, Ротвайн, 1977]. В качестве объектов алгоритм “Подклассы” [Кособоков, Ротвайн, 1977] использовал пересечения линеаментов, отнесенные в работе [Гельфанд и др., 1974б] к классу В при пороге М₀ = 6.5.

Анализ, выполненный в работах [Соловьев и др., 2014; Gorshkov, Novikova, 2018], показывает высокий уровень достоверности результата, полученного в работе [Гельфанд и др., 1974б]. После публикации [Гельфанд и др., 1974б] в рассматриваемом регионе произошло 31 землетрясение с М ≥ 6.5. Эпицентры 28 из них расположены в узлах, распознанных как высокосейсмичные. При этом 8 эпицентров расположены в узлах, в которых ранее землетрясения с М ≥ 6.5 не происходили.

Во второй половине 70-х гг. в рамках советско-американской геолого-геофизической программы, выполнявшейся АН СССР и Геологической службой США (USGS), к развитию подхода EPA подключились известные американские геофизики Ф. Пресс (F. Press, в последующем президент Национальной академии наук США в 1981–1993 гг.) и Л. Кнопоф (L. Knopoff). Распознавание мест возможного возникновения землетрясений с М ≥ 6.5 в Калифорнии и на прилегающих территориях было выполнено советско-американской группой ученых в 1976 г. с использованием алгоритмов “Кора-3” и “Подклассы” [Гельфанд и др., 1976; Gelfand et al., 1976]. Со стороны АН СССР в проекте участвовал Институт физики Земли им. О.Ю. Шмидта, а с американской – UCLA Университет Калифорнии в Лос-Анджелесе.

В этом исследовании независимо рассматривались два типа объектов распознавания: точки на крупных геологических разломах, взятые с равномерным шагом, и пересечения морфоструктурных линеаментов. В работах [Гельфанд и др., 1976; Gelfand et al., 1976] были подтверждены два важных факта: приуроченность эпицентров землетрясений с М ≥ 6.5 к пересечениям морфоструктурных линеаменов и существование в Калифорнии поперечных линеаментов. Это удалось показать путем сопоставления результатов распознавания, полученных в работах [Гельфанд и др., 1976; Gelfand et al., 1976], с использованием объектов разного типа. В 1977 г. для рассматриваемого региона было выполнено распознавание алгоритмом “Кора-3” с использованием гравитационных аномалий [Артемьев и др., 1977]. Результаты [Гельфанд и др., 1976; Артемьев и др., 1977; Gelfand et al., 1976] хорошо согласуются.

В работе [Кособоков, Ротвайн, 1977] критерии мест возможного возникновения землетрясений с М ≥ 7.0, полученные алгоритмом “Подклассы” для объединенного региона Балкан, Эгейского моря, Анатолии и Армянского нагорья, были успешно применены к определению высокосейсмичных зон на территории Калифорнии. Все известные на тот момент землетрясения с М ≥ 7.0 были расположены в выявленных таким новым распознаванием окрестностях объектов. После опубликования в 1976 г. результатов [Гельфанд и др., 1976; Gelfand et al., 1976] в регионе произошло 14 землетрясений с М ≥ 6.5. Эпицентры 13 расположены в окрестностях объектов отнесенных к классу В. При этом 4 землетрясения произошли в районе, где сильные землетрясения ранее не происходили [Соловьев и др., 2014; Gorshkov, Novikova, 2018].

В 1979 г. советско-итальянской группой ученых проведено распознавание мест возможного возникновения землетрясений c М ≥ 6.0 на территории Апеннинского полуострова [Горшков и др., 1979; Caputo et al., 1980]. Для распознавания использовался алгоритм “Подклассы” и пересечения линеаментов в качестве объектов распознавания. Результаты распознавания в Италии не столь хорошо подтвердились последующей сейсмичностью, как в других регионах. После опубликования результатов [Горшков и др., 1979; Caputo et al., 1980] на территории изучаемого региона Италии произошло 11 землетрясений с М ≥ 6.0. Эпицентры 7 из них расположены в окрестностях пересечений линеаментов, отнесенных к классу В. При этом в окрестности одного пересечения землетрясения с М ≥ 6.0 ранее не происходили [Соловьев и др., 2014; Gorshkov, Novikova, 2018]. Эпицентры 4 землетрясений оказались вне окрестностей высокосейсмичных пересечений. Это может быть объяснено [Соловьев и др., 2014] недостатками схемы МСР Апеннинского полуострова, построенной совместно с итальянскими коллегами.

В 1980–1982 гг. было проведено формализованное морфоструктурное районирование горного пояса Анд [Габриэлов и др., 1982]. При этом, приуроченность эпицентров землетрясений с М ≥ 7.0 к пересечениям морфоструктурных линеаментов на территории Южной Америки оказалась неочевидной, и ее наличие было обосновано с использованием специально разработанного алгоритма [Гвишиани, Соловьев, 1980]. На основе этого было выполнено распознавание мест возможного возникновения землетрясений с M ≥ 7.75 на Тихоокеанском побережье Южной Америки [Гвишиани, Соловьев, 1981; Гвишиани и др., 1982; Гвишиани, Соловьев, 1982]. Для распознавания использовался алгоритм “Кора-3” и пересечения линеаментов, полученные методом МСР, примененным с некоторыми дополнениями по сравнению с предыдущими работами. А именно, в дополнение к трем рангам линеаментов введены линеаменты высшего ранга – океанический желоб и материковый склон. В схему линеаментов включены линейные зоны, подходящие к горному поясу Анд со стороны океана и платформы, введен новый тип горообразования – современная геосинклиналь [Габриэлов и др., 1982]. В работе [Жидков и др., 1990] было выполнено независимое распознавание для меньшего магнитудного порога M₀ = 7.0.

После опубликования результатов [Гвишиани и др., 1982] в регионе произошло 7 землетрясений с M ≥ 7.75. Положения их эпицентров дают аргументы в пользу достоверности полученного результата. Эпицентры пяти из них расположены в окрестностях пересечений линеаментов, распознанных как опасные, при этом два из них – в районах, где сильные землетрясения ранее не происходили [Соловьев и др., 2014; Gorshkov, Novikova, 2018].

В 1978–1980 гг. было выполнено распознавание мест возможного возникновения сильнейших (M ≥ 8.2) землетрясений Тихоокеанского сейсмического пояса [Гвишиани и др., 1978; 1980а]. Аргументом в пользу выбора этого региона для исследований явились его масштаб и высочайший уровень сейсмической активности. Так, до выполнения распознавания за первые три четверти XX века в пределах Тихоокеанского сейсмического кольца произошло 80% от общего количества землетрясений мира с M ≥ 8.2 [Гвишиани и др., 1980а]. Тихоокеанский сейсмический пояс включает несколько зон субдукции океанических плит под обрамляющие континенты.

Целью исследований [Гвишиани и др., 1978; 1980а] являлось выявление в Тихоокеанском поясе сегментов, где могут возникать землетрясения с M ≥ 8.2, и определение общих критериев таких сегментов. Следует заметить, что Тихоокеанский пояс неоднороден по характеру и истории основных разломов, а, следовательно, и по условиям возникновения землетрясений [Гвишиани и др., 1980а]. По этой причине у исследователей не было уверенности в существовании общих критериев мест сильнейших землетрясений всего региона. Однако аргументом в пользу их существования стала высказанная В.И. Кейлис-Бороком гипотеза о том, что распознанные в различных регионах критерии высокой сейсмичности могут обладать универсальными инвариантами. Гипотеза базировалась на опыте переноса критериев сейсмичности между регионами [Гельфанд и др., 1973в; Кособоков, Ротвайн, 1977].

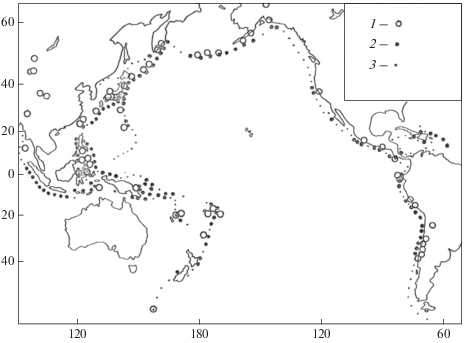
В качестве объектов распознавания в Тихоокеанском сейсмическом поясе брались точки на кривой, трассирующей оси глубоководных желобов и подножия континентальных склонов, образующих пояс. Распознавание проводилось алгоритмом “Кора-3” в работе [Гвишиани и др., 1978], алгоритмами “Правило Хемминга”, “Кора-3” и “Правило Байеса” в работе [Гвишиани и др., 1980а]. Достоверность результатов распознавания была подтверждена, в том числе, успешным переносом выявленных критериев высокой сейсмичности Тихоокеанского пояса на территорию Альпийского пояса и Южно-Антильского региона [Кособоков, 1980]. В работе [Гвишиани, Кособоков, 1983] с помощью специально разработанного математического аппарата обосновано, что для Тихоокеанского пояса наибольшей статистической значимостью обладает результат EPA для пороговой магнитуды M₀ = 8.0, полученный с помощью алгоритма распознавания “Правило Хемминга”. На рис. 4 показан основной результат распознавания из работы [Гвишиани и др., 1978].

Рис. 4.

Тихоокеанский сейсмический пояс. Основной вариант распознавания мест возникновения сильнейших (M ≥ 8.2) землетрясений из работы [Гвишиани и др., 1978]: 1 – эпицентры землетрясений с M ≥ 8.2; 2 – объекты распознавания, отнесенные к классу В; 3 – отнесенные к классу Н.

В работе [Гвишиани и др., 1984б] построена схема МСР Тихоокеанского побережья полуострова Камчатка и выполнен перенос на этот регион критериев высокой сейсмичности (M₀ = 7.75), полученных для горного пояса Анд Южной Америки [Гвишиани и др., 1982]. Объекты распознавания Камчатки, отнесенные к классу В на основе переноса критериев, содержат в своих окрестностях эпицентры всех ранее произошедших коровых инструментальных землетрясений с M ≥ 7.75. После [Гвишиани и др., 1984б] на Камчатке произошло одно землетрясение с M ≥ 7.75, и его эпицентр расположен в окрестности объекта из класса В.

В начале 80-х годов прошлого века в рамках соглашения о сотрудничестве между АН СССР и Национальным центром исследований Франции (CNRS) успешно развивалось советско-французское сотрудничество по исследованиям в области сейсмогенезиса [Гвишиани и др., 1984а], научное руководство которым осуществляли директора Московского и Парижского институтов физики Земли М.А. Садовский и Ж. Жобер. Ядром этого сотрудничества стал проект распознавания мест возможного возникновения сильных и значительных землетрясений в трех областях Альпийского орогенного пояса Евразии, обладающих умеренным уровнем сейсмичности: на Большом Кавказе, в Западных Альпах и Пиренеях. По результатам этих исследований в 1988 г. опубликована монография [Гвишиани и др., 1988а].

Целью проекта был поиск общих признаков мест возможного возникновения значительных (с M ≥ 5.0) землетрясений в трех рассматриваемых регионах. В проекте участвовали Институт физики Земли им. О.Ю. Шмидта АН СССР, Институт географии АН СССР, Институты физики Земли Парижа и Страсбурга, Бюро по геологии и минералогии Франции, Университет Монпелье. Французские ученые А. Систернас, К. Вебер, Э. Филип, Ж. Саллантен, П. Годфруа, работая в едином коллективе с возглавляемыми А.Д. Гвишиани советскими геофизиками, геоморфологами и математиками, сыграли важную роль в успешном выполнении проекта.

В 1981–1986 гг. внимание исследователей было нацелено на распознавание мест возможного возникновения землетрясений с M ≥ 5.0 в Западных Альпах. В работе [Вебер и др., 1981] по комплексу геолого-геофизических и геоморфологических данных была построена схема МСР, обоснована приуроченность эпицентров сильных землетрясений к окрестностям пересечений морфоструктурных линеаментов. В работе [Горшков и др., 1982] методом EPA было выполнено распознавание с помощью алгоритма “Кора-3” для пересечений осей линеаментов в качестве объектов распознавания. Результат согласовывался с расположением эпицентров исторических землетрясений.

В работах [Вебер и др., 1985; Cisternas et al., 1985] результат работы [Горшков и др., 1982] был существенно уточнен. В этих работах был применен дуальный подход. Задача в Западных Альпах независимо решалась коллективами из СССР и Франции. Первые проводили EPA-распознавание, используя те же объекты и алгоритм, что и в работе [Горшков и др., 1982]. Набор характеристик, описывающих объекты, был несколько расширен.

Французская группа заменила МСР неотектонической схемой (НТС). Объекты распознавания определялись как равновеликие участки разломов НТС. Их векторное представление представлялось в основном значениями тектонических характеристик.

Несмотря на принципиальные различия в подходах результаты, полученные советской и французской группами, достаточно хорошо согласовывались. На рис. 5 показаны места возможного возникновения землетрясений с М ≥ 5.0 из работ [Вебер и др., 1985; Cisternas et al., 1985], распознанные советскими учеными.

Рис. 5.

Схема линеаментов Западных Альп и места возможного возникновения землетрясений с М ≥ 5.0 [Вебер и др., 1985; Соловьев и др., 2014; Cisternas et al., 1985] (оконтурены жирными линиями).

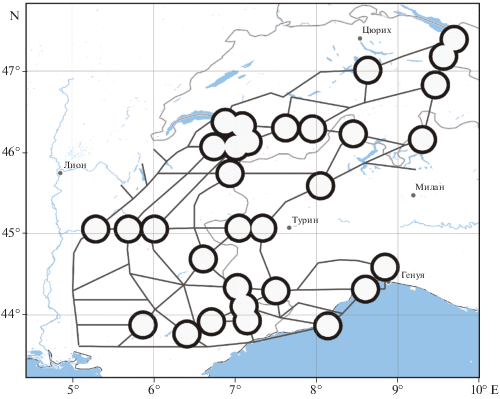
В работе [Вебер и др., 1986а] было продолжено развитие дуального подхода: выполнено распознавание алгоритмом “Кора-3" для определенных на основе НТС объектов, векторное описание которых состояло из характеристик, использованных ранее французскими учеными в работе [Вебер и др., 1985]. Результат оказался близким к результату, ранее полученному советской группой [Вебер и др., 1985; Cisternas et al., 1985].

Результат распознавания в Альпах [Вебер и др., 1985; Cisternas et al., 1985] характеризуется высокой степенью достоверности. После его опубликования в Западных Альпах произошло 6 землетрясений с M ≥ 5.0. Эпицентры 5 из них расположены в областях В. В одной из них сильные землетрясения ранее не происходили [Соловьев и др., 2014; Gorshkov, Novikova, 2018].

В 1987 г. в работах [Гвишиани и др., 1987а; 1987в; Gvishiani et al., 1987] с помощью алгоритма “Кора-3” на базе пересечений линеаментов было выполнено распознавание мест возможного возникновения землетрясений с M ≥ 5.0 в Пиренеях. Достоверность распознавания подтверждается путем переноса критериев высокой сейсмичности с Пиренеев на Западные Альпы и наоборот, а также результатами распознавания в объединенном регионе – Пиренеи–Западные Альпы [Гвишиани и др., 1987а]. Согласно работам [Соловьев и др., 2014; Gorshkov, Novikova, 2018] после 1987 г. на Пиренеях произошло 6 сильных землетрясений. Эпицентры 5 расположены в окрестностях пересечений, отнесенных к классу В. Одно землетрясение произошло в районе, где землетрясения такой магнитуды ранее не наблюдались [Соловьев и др., 2014].

В 1986–1988 гг. было проведено распознавание для территории Большого Кавказа. В этом регионе задача решалась алгоритмом “Кора-3” для трех магнитудных порогов и двух типов объектов распознавания. В 1986 г. подход EPA применен к морфоструктурным узлам для пороговой магнитуды M₀ = 6.5 [Гвишиани и др., 1986]. В 1987 г. классификация морфоструктурных узлов выполнена для M₀ = 5.5 [Гвишиани и др., 1987б]. Наконец, в 1988 г. выполнена классификация пересечений осей морфоструктурных линеаментов для еще более низкой пороговой магнитуды M₀ = 5.0 [Гвишиани и др., 1988а]. В 2001, 2014 и 2018 гг. в работах [Горшков и др., 2001; Соловьев и др., 2014; Gorshkov, Novikova, 2018] был проведен детальный анализ результата распознавания из работы [Гвишиани и др., 1988а]. Оказалось, что эпицентры всех 13 землетрясений с M ≥ 5.0, произошедших на Большом Кавказе после 1988 г., располагаются вблизи пересечений линеаментов, распознанных как опасные. При этом 9 землетрясений произошли в окрестности пересечений, в районе которых ранее такие землетрясения не были известны [Соловьев и др., 2014]. Таким образом, качество распознавания на Кавказе можно считать одним из самых высоких в истории применения EPA.

В целом, результаты советского-французского проекта оказались впечатляющими. Удачным переносом сформированных в каждом из трех регионов критериев сейсмичности на два других [Гвишиани и др., 1988а] и результатами распознавания в объединении четырех регионов Средиземноморской области [Гвишиани и др., 1988б] было показано, что в критериях сейсмичности, помимо региональной составляющей, содержатся и признаки, общие для всех рассмотренных регионов. В связи с этим в развитии EPA появилась надежда на возможность существования универсальных критериев повышенной сейсмичности.

Начиная с 1990 г. в блоке распознавания EPA стал применяться только алгоритм “Кора-3”, а в случае малого материала обучения выполнялся перенос критериев, полученных в сходном регионе. В качестве объектов распознавания в основном использовались пересечения осей морфоструктурных линеаментов.

В 1991 г. в работе [Горшков и др., 1991] построена МСР схема для Малого Кавказа и выполнено распознавание мест возможного возникновения землетрясений с M ≥ 5.5.

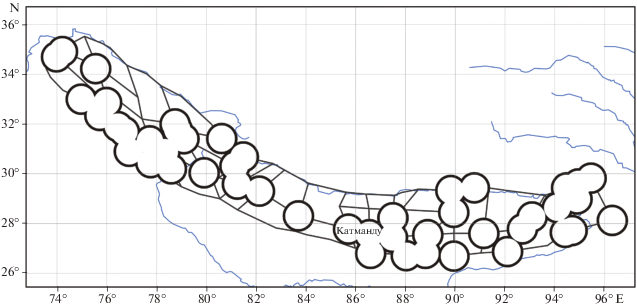
Начиная с 1992 г. исследования EPA продолжились силами Международного института теории прогноза землетрясений и математической геофизики РАН. Ключевую роль в этих исследованиях играют А.И. Горшков и А.А. Соловьев. В 1992–1994 гг. амбициозной целью применения EPA стал регион Гималаев, который изучался российско-индийской группой ученых [Бхатия и др., 1992]. Была построена схема МСР и распознаны места возможного возникновения землетрясений с M ≥ 6.5. Достоверность полученного результата изучалась в работе [Gorshkov et al., 2012], где был сделан вывод о целесообразности использования результатов распознавания при оценке сейсмической опасности. Согласно работам [Соловьев и др., 2014; Gorshkov, Novikova, 2018] в Гималаях после публикации [Бхатия и др., 1992] до 2018 г. произошло 5 землетрясений с M ≥ 6.5. Эпицентры трех из них расположены в окрестностях пересечений, распознанных как высокосейсмичные. При этом один эпицентр находится в окрестности пересечения, где ранее не было землетрясений с M ≥ 6.5 [Соловьев и др., 2014; Gorshkov, Novikova, 2018]. На рис. 6 показаны места возможного возникновения землетрясений с М ≥ 6.5 из работы [Бхатия и др., 1992].

Рис. 6.

Схема линеаментов Гималаев и места возможного возникновения землетрясений с М ≥ 6.5 [Бхатия и др., 1992; Соловьев и др., 2014] (оконтурены жирными линиями).

В работе [Бхатия и др., 1994] метод EPA применен в Гималаях для пороговой магнитуды M₀ = 7.0. Из-за невозможности проведения обучения в силу малого количества землетрясений с M ≥ 7.0 в Гималаях классификация объектов на высоко- и низкосейсмичные была выполнена путем переноса критериев высокой сейсмичности горного пояса Анд Южной Америки, полученных для такой же пороговой магнитуды в 1990 г. [Жидков и др., 1990]. Результаты распознавания [Бхатия и др., 1992; 1994] достаточно хорошо согласуются.

В 2000 г. российско-итальянская группа ученых применила метод EPA в Карпато-Балканском горном поясе для пороговой магнитуды M₀ = 6.5 [Gorshkov et al., 2000]. Как и в Гималаях [Бхатия и др., 1992], из-за малого количества землетрясений с M ≥ 6.5 и, соответственно, невозможности проведения обучения классификация объектов осуществлялась путем переноса критериев высокой сейсмичности региона Памир–Тянь-Шань, определенных для M ≥ 6.5 алгоритмом “Правило Хемминга” [Кособоков, 1982]. Эти же критерии были использованы для классификации объектов распознавания (пересечений линеаментов) в Туркмено-Хоранских горах (Копетдаг, Кучано-Мешхедская межгорная впадина, Эльбурс, Аладаг и Биналуд) для пороговой магнитуды M₀ = 6.5 [Горшков и др., 2002]. Позже в этом регионе (Копетдаг–Аладаг-Биналуд) методом EPA было выполнено полномасштабное распознавание для M₀ = 6.0 [Горшков, Новикова, 2012].

В 2002–2003 гг. в результате российско-итальянского сотрудничества метод EPA был применен для M₀ = 6.0 в регионах: Альпы, полуостровная Италия, Балканы, Карпаты и Динариды [Gorshkov et al., 2002; 2003b], а затем в 2004 г. в Альпах и Динаридах [Gorshkov et al., 2004]. В работе [Gorshkov et al., 2004] также выполнено распознавание в Динаридах для M₀ = 6.5 путем переноса критериев высокой сейсмичности из региона Памир–Тянь-Шань [Кособоков, 1982].

В истории EPA несомненный интерес представляет работа [Горшков, Соловьев, 2009], в которой были распознаны места возможного возникновения землетрясений с M ≥ 6.0 в огромном регионе, включающем в себя четыре горных пояса Средиземноморья: Альпы, Динариды и северная часть Сербо-Македонского массива, Апенины и Сицилия (распознавание здесь было выполнено ранее [Gorshkov et al., 2002]), Карпаты и Балканиды. Распознавание проводилось отдельно для каждой горной страны. При этом в Карпатах и Балканидах по отмеченным выше причинам классификация объектов осуществлялась переносом критериев сейсмичности из Динарид [Горшков, Соловьев, 2009].

В 2010 г. в работе [Горшков, 2010] обобщены результаты многолетних исследований по распознаванию мест возможного возникновения сильных землетрясений в Альпийско-Гималайском подвижном поясе от Пиренеев и Бетской Кордильеры на западе до Гималаев на востоке, а именно: Альпы и Динариды, Карпато-Балканский горный пояс, Апенины и Сицилия, Иберийская плита [Gorshkov et al., 2010], Туркмено-Хоранские горы, Эльбурс, Малый Кавказ, Гималаи.

На примере центральной части Русской платформы показана принципиальная возможность применения подхода EPA для распознавания сейсмоопасных районов на платформенных территориях и намечены возможности использования метода EPA для распознавания рудоносных узлов [Горшков, 2010].

Метод EPA был применен для пороговой магнитуды M₀ = 7.0 в Черноморско-Каспийском регионе, включающем в себя Кавказ, Эльбурс и Копетдаг, межгорные Рионскую и Куринскую впадины, глубоководную Южно-Каспийскую котловину [Новикова, Горшков, 2018]. Важным для сейсморайонирования результатом стал тот факт, что в пределах Южно-Каспийской глубоководной котловины, характеризующейся более тонкой океанической корой, не было распознано мест, способных генерировать землетрясения с M ≥ 7.0.

В 2015–2017 гг. дальнейшее развитие подхода EPA было стимулировано проектом Российского научного фонда (РНФ) № 15-17-30020 “Применение системного анализа для оценки сейсмической опасности в регионах России, включая Кавказ–Крым и Алтай–Саяны–Прибайкалье”, выполненного Геофизическим центром РАН. На примере Кавказа было впервые показано, что данные по литосферным магнитным аномалиям обладают высокой информативностью для определения мест возможного возникновения сильнейших, сильных и значительных землетрясений [Соловьев и др., 2016].

В работе [Горшков и др., 2017] построена схема МСР горной части полуострова Крым и определены места возможного возникновения сильных землетрясений с M ≥ 6.0 путем переноса критериев этого уровня сейсмичности с Кавказа [Соловьев и др., 2013; 2016]. В регионе Алтай–Саяны–Прибайкалье построена схема МСР и проведено полноценное применение метода EPA для M₀ = 6.0 [Горшков и др., 2018].

До 2015 г. значения используемых характеристик объектов распознавания измерялись вручную с бумажных карт. В 2015 г. в рамках реализации проекта РНФ создана автоматизированная система для измерения геолого-геофизических и геоморфологических характеристик объектов. Для этого был разработан инструмент геообработки для ГИС-системы компании Esri – ArcGIS. Основными достоинствами инструмента являются: автоматизация процесса, который раньше выполнялся вручную, большая точность измерений характеристик, удобство работы с цифровыми картами формата ГИС [Соловьев и др., 2018].

С точки зрения анализа успехов и неуспехов метода EPA представляет интерес работа [Gorshkov, Novikova, 2018], в которой для всех регионов, где применялся метод EPA, выполнен полный анализ расположения эпицентров землетрясений с M ≥ M₀, где M₀ – пороговая магнитуда в соответствующем регионе, произошедших после опубликования результатов распознавания. Оказывается, что 86% таких сильнейших, сильных и значительных землетрясений произошло в достаточно малых окрестностях пересечений осей морфоструктурных линеаментов (или в морфоструктурных узлах), распознанных как высокосейсмичные. Это является одним из аргументов в пользу приводимых в работе [Peresan et al., 2015] положений о существенности вклада EPA в оценку сейсмической опасности территории.

В течение почти 50 лет истории развития метода EPA была создана и развита эффективная методика распознавания мест возможного возникновения землетрясений для различных пороговых магнитуд M₀ в горных странах и на платформенных территориях. Полученные путем применения метода ЕРА результаты сегодня вносят существенный вклад в проведение сейсмического районирования, которое, в свою очередь, является одним из основных этапов оценки сейсмической опасности.

Обучение по одному классу

Стартовым этапом в алгоритмах дихотомии, входящих в блок распознавания метода EPA, является формирование материала обучения. При этом множество обучения состоит из двух непересекающихся подмножеств: B₀ – объекты обучения высокосейсмичного класса B и H₀ – объекты обучения низкосейсмичного класса H [Гвишиани и др., 1988а; Соловьев и др., 2014]. Алгоритмы выявляют геолого-геофизические признаки, характерные для высоко- и низкосейсмичного классов. Затем, все множество объектов распознавания экзаменуется на обладание этими признаками. При их наличии объекты экзамена объявляются соответственно высоко- или низкосейсмичными [Гвишиани и др., 1988а].

Обучающая выборка B₀ формируется из объектов распознавания, к которым приурочены достоверно определенные эпицентры ранее произошедших сильных (с М ≥ М₀) землетрясений. В случае использования в качестве объектов распознавания морфоструктурных узлов – это объекты, содержащие эпицентры сильных землетрясений, а в случае пересечений линеаментов – объекты, в некоторых окрестностях которых находятся эпицентры сильных землетрясений [Гвишиани и др., 1988а; Соловьев и др., 2014]. Очевидно, что обучающая выборка B₀ с большой вероятностью не содержит априорных ошибок.

Формирование аналогичного “чистого” материала обучения класса H затруднительно. В обучающую выборку H₀ включаются либо все объекты, не вошедшие в B₀, либо объекты, в окрестностях которых известны лишь землетрясения с магнитудой М < М₀ – δ, где δ > 0 и, как правило, имеет значение 0.5 или 1 [Гвишиани и др., 1988а; Соловьев и др., 2014]. Очевидно, что такое определение выборки H₀ не гарантирует невозможности возникновения сильных землетрясений в окрестностях входящих в него объектов, и часть объектов из H₀ в результате классификации может быть отнесена к классу В. Заметим, что выделение таких объектов наряду с отнесенными к классу В объектами, не входившими в обучающую выборку, и является целью применения метода EPA. Использование H₀ в качестве обучающей выборки класса H основано на предположении, что процент объектов из H₀, которые на самом деле принадлежат классу В сравнительно мал. Это предположение подтверждалось во всех случаях применения метода EPA, но невозможность получения “чистой” обучающей выборки класса H остается его недостатком.

В ходе работ над проектом РНФ № 15-17-30020 метод EPA получил развитие в виде создание нового алгоритма, примененного в блоке распознавания. Алгоритм получил название “Барьер” [Гвишиани и др., 2017а]. Принципиальным отличием “Барьера” от классических алгоритмов распознавания EPA является то, что обучение в нем ведется только по одной обучающей выборке B₀. Задача алгоритма “Барьер” – определить характерные черты объектов из этой обучающей выборки и на их базе выявить объекты “похожие” на объекты из B₀. Говоря языком теории множеств, “Барьер” решает задачу построения в конечном множестве объектов его подмножества B, расширяющего единственный и достоверный класс обучения B₀ [Гвишиани и др., 2017а].

Первоначальный вариант алгоритма “Барьер”, обладая несомненным преимуществом, состоящим в отсутствии необходимости обучающей выборки класса H, тем не менее, уступает классическим алгоритмам метода EPA, так как не выявляет геолого-геофизические характеристики высокосейсмичных объектов изучаемого региона [Гвишиани и др., 1988а; Соловьев и др., 2014; Дзебоев и др., 2019]. Для количественной оценки вклада используемых геолого-геофизических характеристик в формирование класса B алгоритм “Барьер” был модифицирован. А именно были созданы вычислительные блоки алгоритма, позволяющие оценить, как средний вклад геолого-геофизических характеристик, так и их вклад через попадание в тройки “сильнейших” характеристик [Дзебоев и др., 2019]. Новая версия алгоритма получила название “Барьер-3”. Конструкция алгоритмов “Барьер” и “Барьер-3” устроена таким образом, что объекты обучения из B₀ в конечной классификации всегда попадают в класс B. Подробное описание математической конструкции алгоритмов дано в работах [Гвишиани и др., 2017а; Дзебоев и др., 2019].

Алгоритм “Барьер-3” хорошо зарекомендовал себя при распознавании мест возможного возникновения землетрясений с М ≥ 6.0 в регионе Алтай–Саяны–Прибайкалье [Дзебоев и др., 2019] и на Кавказе. В обеих задачах в качестве объектов распознавания использовались пересечения морфоструктурных линеаментов. Ранее распознавание в этих регионах было выполнено алгоритмом “Кора-3” [Соловьев и др., 2016; Горшков и др., 2018]. Результаты, полученные с помощью двух разных алгоритмов, оказались достаточно близкими как в классификации пересечений линеаментов, так и в выявлении критериев высокой сейсмичности рассмотренных регионов [Дзебоев и др., 2019]. Согласованность результатов применения алгоритмов “Барьер-3” и “Кора-3” является аргументом в пользу их достоверности.

Результаты распознавания алгоритмом “Барьер-3” в регионе Алтай–Саяны–Прибайкалье использованы для оценки влияния Алтае-Саянской орогенной области на устойчивость структурно-тектонических блоков земной коры и сейсмическую опасность в зоне контакта Западно-Сибирской платформы и Сибирской плиты. Это дало возможность сделать выводы в отношении устойчивости структурно-тектонических блоков в этом районе, существенные для оценки возможности захоронения в них радиоактивных отходов [Дзебоев и др., 2019].

В работе [Дзебоев и др., 2019] выдвинута идея интерпретации объединения результатов распознавания, полученных алгоритмами “Барьер-3” и “Кора-3”, как нечеткого множества объектов, в окрестности которых возможно возникновение сильных землетрясений.

Динамические и предельные задачи распознавания

Динамичность задачи распознавания мест возможного возникновения сильных землетрясений заключается в том, что в ней классификация объектов распознавания w ∈ W на классы В и Н – есть процесс, разворачивающийся во времени, т.е. В = В(t) и Н = Н(t).

Дадим определение динамической задачи. Пусть t ∈ [T₀, T₁] – время (T₁ ≤ ∞), и в каждый момент времени t имеется разбиение $W\left( t \right) = B\left( t \right)\coprod {H\left( t \right)} ,$ т.е. существует отображение $F\left( {w,\;t} \right):\;W \times \left[ {{{T}_{0}},\;{{T}_{1}}} \right]$ → → $\left\{ {B\left( t \right),\;H\left( t \right)} \right\}.$ С течением времени объекты могут переходить из Н(t) в В(t). Если момент времени t фиксирован, то исходные данные динамической задачи составляет информация о поведении системы на отрезке времени [T₀, t]. Эта информация определяет материал обучения на момент времени t.

Пусть теперь фиксирован другой момент времени t ^/, причем t < t ^/ < T₁. Тогда под решением динамической задачи для момента t^/ понимается распознавание классификации W(t  ^/) $ = B\left( {{{t}^{/}}} \right)\coprod {H\left( {{{t}^{/}}} \right)} ,$ которая должна соответствовать функции F на множествах $W \times \left[ {{{t}^{/}}} \right]$ и $W \times \left[ {{{T}_{0}},\;t} \right]$ [Гвишиани, Гурвич, 1983а; 1992].

Для переноса сделанного определения на случай t^/ → ∞ необходимо существование предела $\mathop {\lim }\limits_{t \to \infty } F\left( {w,\;t} \right) = F\left( {w,\;\infty } \right)$ (или $\mathop {\lim }\limits_{t \to \infty } \left( {B\left( t \right)\coprod {H\left( t \right)} } \right)$). В этом случае $W\left( t \right) = B\left( t \right)\coprod {H\left( t \right)} $ является прогнозом предельного состояния рассматриваемой системы при t → ∞. Это приводит к классификации объектов распознавания, не зависящей от времени, что и является решением задачи прогноза мест возможного возникновения сильных землетрясений. Такая динамическая задача распознавания называется предельной [Гвишиани, Гурвич, 1983а; 1992]. В работе [Гвишиани, Гурвич, 1992] построены строгие достаточные условия корректности постановки предельной задачи распознавания.

В работах [Гвишиани, 1982; Гвишиани, Гурвич, 1982] введено условие стабильности классификации объектов (устойчивости во времени). Пусть, как и прежде, $W$ и ${{W}_{0}} = {{B}_{0}}\coprod {{{H}_{0}}} $ – множество объектов распознавания и материал обучения, а $W = B\coprod H $ – результат классификации объектов на высоко- и низкосейсмичные, полученный некоторым алгоритмом. Эта классификация называется стабильной, если для каждого множества ${{B}^{/}}:{{B}_{0}} \subseteq {{B}^{/}} \subseteq B$ существуют свободные параметры алгоритма такие, что новая классификация $W\left( {{{B}^{/}},{{H}^{/}}} \right) = {{B}_{1}}\coprod {{{H}_{1}}} $ совпадает с $W = B\coprod H .$

Сформулированное условие стабильности использовано для обоснования независимости от времени классификации пересечений линеаментов в регионах Малой Азии и Эгейского бассейна (M₀ = 7.0) [Гвишиани, 1982], полученных в работах [Кособоков, Ротвайн, 1977; Гвишиани, Кособоков, 1981], а также востока Средней Азии (M₀ = 6.5) [Гвишиани, Гурвич, 1982], полученного в работе [Гвишиани, Кособоков, 1981]. В работе [Гвишиани, Гурвич, 1983а] сформулированы необходимые и достаточные условия для стабильности классификации, полученной алгоритмом класса ГНП [Гвишиани и др., 1985].

Выполнение условия стабильности, очевидно, говорит в пользу достоверности классификации. В работе [Гвишиани, Гурвич, 1984] показано, что классификация, неустойчивая в момент получения, может стать устойчивой в будущем. Такая ситуация имеет место в случае, когда достаточно мало объектов, распознанных как высокосейсмичные, уже проявили себя таковыми [Гвишиани и др., 1985]. В работе [Гвишиани, Гурвич, 1984] вводятся понятия локальной стабильности классификации и системы стабилизирующих множеств. С их помощью на примере Востока Средней Азии [Гельфанд и др., 1972; Гвишиани, Кособоков, 1981] построены условия стабилизации классификации со временем.

В работе [Гвишиани и др., 1985] с помощью алгоритма “Кора-3” получена корректная (т.е. ${{B}_{0}} \subseteq B$) классификация объектов восточной части Тихоокеанского подвижного пояса [Гвишиани и др., 1978; 1980а] для M₀ = 8.2 и сформулированы строгие условия стабилизации этой классификации.

Контрольные эксперименты

Наилучшим обоснованием достоверности результатов распознавания мест возможного возникновения сильных землетрясений является апостериорная проверка на основе данных о сильных землетрясениях рассматриваемого региона, то есть сравнение результата с расположением эпицентров таких землетрясений, произошедших после его получения. Но такая проверка может быть выполнена лишь по прошествии достаточно длительного времени после получения результата. Оценка достоверности классификации объектов на высоко- и низкосейсмичные непосредственно после ее получения осуществляется с помощью контрольных вычислительных экспериментов [Гельфанд и др., 1974а; 1976; Горшков и др., 1979; Гвишиани и др., 1988а; 2018; Горшков, 2010; Gelfand et al., 1976; Caputo et al., 1980]. В классическом методе EPA применяются следующие основные контрольные эксперименты.

• Эксперимент “Сейсмическое будущее” (СБ) [Гельфанд и др., 1976; Гвишиани и др., 1988а; Gelfand et al., 1976] состоит в повторении полученной классификации объектов $W = B\coprod H ,$ используя в качестве обучающих выборок В₀ и Н₀ множества В и Н. Эксперимент считается удачным, если не более 5% от общего количества объектов распознавания меняют свою принадлежность по сравнению с исходной классификацией. Эксперимент проверяет стабильность классификации по отношению к сильным землетрясениям, которые могут произойти в будущем. В соответствии с работой [Гвишиани, Гурвич, 1984] эксперимент СБ выполняет проверку классификации на локальную стабильность, и, следовательно, его удачный исход есть необходимое условие для принятия полученного результата классификации в качестве решения задачи EPA [Гвишиани и др., 1988а; Горшков, 2010].

• Эксперимент “Сейсмическая история” (СИ) [Гельфанд и др., 1976; Гвишиани и др., 1988а; Gelfand et al., 1976] выполняется путем отбрасывания эпицентров сильных землетрясений за последние t лет и исключения из В₀ объектов, связанных с отброшенными землетрясениями. Эксперимент считается успешным, если в новой классификации исключенные объекты будут отнесены к классу В.

• Эксперимент “Проверка устойчивости” [Гвишиани и др., 1988а; Горшков, 2010] есть обобщение эксперимента СБ. В нем делается попытка повторить классификацию $W = B\coprod H ,$ используя в качестве обучающих выборок В₀ и Н₀ подмножества $B_{0}^{/} \subseteq B$ и $H_{0}^{/} \subseteq H.$ Эксперимент считается удачным, если не более 10% от общего количества объектов меняют свою первоначальную классификацию.

• Эксперимент “Скользящий контроль” [Гвишиани и др., 1988а; Горшков, 2010] состоит в получении классификаций объектов распознавания обучаясь на материалах обучения В₀ и Н₀, в которых поочередно исключается по одному объекту. В получаемых в эксперименте классификациях все объекты из В₀ (кроме, возможно, объекта исключенного в данном варианте распознавания) должны быть отнесены к классу В. Эксперимент считается удачным, если не более 20% объектов из обучающей выборки W₀ изменили свою классификацию при их исключении из обучения.

• Эксперимент “Голосование по совокупности эквивалентных признаков” выполняется только в случае использования алгоритмов “Кора-3” или “Подклассы” [Гвишиани и др., 1988а; Горшков, 2010]. При их использовании результат классификации может зависеть от того, какие признаки из групп эквивалентных будут отобраны в наборы характерных признаков В и Н. Эксперимент выполняется с целью выявления такой зависимости и считается успешным, если не более 5% объектов меняют классификацию при отборе других представителей групп эквивалентных признаков.

• Эксперименты на рандомизированных данных [Гвишиани, Кособоков, 1981; Гвишиани и др., 1988а] предназначены для оценки вероятности ошибки классификации и проверки ее неслучайности. В экспериментах выполняется последовательность классификаций, в которых материалы обучения В₀ и Н₀ формируются случайным образом из всего множества объектов распознавания. Результат эксперимента считается тем лучше, чем в большем количестве классификаций со случайным материалом обучения имеет место отнесение к классу Н объектов из В₀.

• Эксперименты повторения результата [Гвишиани и др., 1988а; Горшков, 2010] состоят в повторении результата классификации после изменения хода решения задачи, начиная с какого-либо этапа. Например, использование другого алгоритма классификации, других объектов распознавания, дополнительных характеристик объектов, информации об исторических сильных землетрясениях и т.д. Эксперимент считается удачным, если не более 20% объектов меняют свою классификацию.