Физика Земли, 2020, № 1, стр. 150-162

ВВЕДЕНИЕ

Объем сейсмических данных увеличивается экспоненциально, создавая потребность в эффективных алгоритмах автоматической обработки. Под обработкой понимается детектирование сигналов землетрясений, идентификация их основных фаз с определением их времен вступления, амплитуд и частотного состава, направления прихода волны. Далее оцениваются эпицентральное расстояние, магнитуда, глубина очага и т.д. В зависимости от целей анализа интерес могут представлять те или иные параметры сейсмического сигнала или шума. В воздухе витает идея создания универсального инструмента анализа сейсмических данных. Мы имеем в виду многозадачную глубокую нейронную сеть (ГНС) [Kislov, Gravirov, 2018; Ross et al., 2018; Yuan et al., 2018; Meyer et al., 2019]. Ее возможно легко настроить на решение любой задачи. Современные архитектуры сетей включают ячейки долговременной памяти (LSTM), что снимает ограничения на длину сигнала. Однако, в связи со спецификой сейсмических данных и из-за неопределимого заранее круга задач, потребуется очень глубокая сеть. Кроме того, для первоначального обучения сети мало использовать какой-либо прототип. Надо обучать сеть именно на сейсмических данных, на больших данных, в идеале, на всех доступных данных! Сейсмические данные значительно отличаются от других временных рядов. Временные окна, которые обычно используются для анализа, часто содержат много шума, имеют высокую размерность, данные избыточны, в любом месте окна могут быть расположены импульсные сигналы. Данные могут быть представлены как одним, так и несколькими каналами. Помимо параметров источника сигнала и среды распространения на вид полезного сигнала влияют характеристики сейсмических приборов и средств регистрации. Кроме того, записи сейсмических явлений часто занимают значительный временной интервал, и на записи одновременно могут присутствовать сигналы из разных источников.

Чтобы упростить архитектуру сети и облегчить обучение, естественно проводить предподготовку данных. Обычно она проходит в два этапа. Первый – станционное детектирование сигнала, фильтрация шума и исключение случайных выбросов. Для детектирования успешно применяют метод STA/LTA [Allen, 1982]. Известны также другие технологии [Madureira, Ruano, 2009; Кислов, Гравиров, 2010; Sheng et al., 2015; Yoon et al., 2015], в том числе нейросетевые [Wang, Teng, 1995; Dai, MacBeth, 1997; Zhao, Takano, 1999; Gentili, Michelini, 2006; Kislov, Gravirov, 2010; Гравиров и др., 2012]. Второй этап зависит от целей анализа. Вычисляется спектрограмма или скалограмма, огибающая сигнала, поляризационная трасса и т.д. [Kislov, Gravirov, 2017; Ганнибал, 2018]. Каждый раз заново разрабатывается новый метод предварительной обработки данных. Удачная предобработка может на порядки повысить эффективность дальнейшего анализа.

ГНС обладает замечательным свойством многозадачности, т.е. обученная сеть может быть легко перестроена на решение другой задачи. Если предполагается возможность адаптации модели к нескольким задачам (multi-task learning) и решение других, пока не определенных задач, следует посмотреть на подготовку данных с другой стороны. Предобработка данных чаще всего препятствует возможности использовать многозадачность ГНС. В результате предобработки может быть потеряна потенциально полезная информация, необходимая для решения других задач, в том числе еще не сформулированных. Необходимо учитывать, что потенциально полезная информация не должна быть потеряна. Естественный вывод, что самой надежной предобработкой является ее отсутствие. Нужно лишь масштабировать амплитуду сигнала в приемлемый для ГНС диапазон, а все проблемы переложить на нейронную сеть. Например, в работе [Perol et al., 2018] на вход сверточной сети подается окно трехкомпонентных данных в виде изображения 1000 × 3 (1000 отсчетов на три компоненты) без всякой предобработки этих данных. Однако таким методом можно решить лишь ограниченный круг задач. Предварительная обработка данных обязательна для достижения лучшей производительности ГНС [Zheng et al., 2018; Zhang et al., 2016].

Чтобы охарактеризовать десятисекундную сейсмическую запись, вполне достаточно тридцати числовых параметров. Если бы мы могли корректно их измерить, мы бы действительно далее изучали тайны Земли, а не тайны сигналов. Пока это не представляется возможным. Если предобработка выделит особенности сигнала, устранит его избыточность и позволит рассматривать в меньшем пространстве – это, несомненно, упростит алгоритмы последующей обработки и облегчит их обучение [Gravirov, Kislov, 2014]. Предобработка должна снижать аппаратурные шумы, импульсные сигналы, ассоциирующиеся с антропогенным воздействием и давать заключение о пригодности сигнала для дальнейшего анализа.

Современные алгоритмы детектирования работают вполне надежно и могут за счет ложных срабатываний быть подстроены на 100-процентный захват цели. Будем считать, что большинство поступивших в предобработку окон временных рядов содержат полезный сейсмический сигнал. Этим мы устраним проблему дисбаланса данных при обучении нейронных сетей. Дисбаланс есть результат того, что один класс (например, землетрясения, предположим, что они образуют один класс) представлен в данных обучения редко по сравнению с другим классом (шумом). Алгоритм обучения нейронной сети создаст гипотезу, соответствующую небольшому количеству примеров, но слишком конкретно (т.е. произойдет переобучение для конкретной задачи или класса).

Надо создать алгоритм предобработки, при котором не будут потеряны информативные особенности сигнала. Его можно будет использовать при любом последующем анализе, хотя в первую очередь имеется в виду многозадачное применение ГНС. Наметим ряд методик, которые, как мы надеемся, будут представлять практический интерес. Подходы, обсуждаемые в этой статье, не предназначены для простого сжатия данных с целью хранения или передачи. Предподготовка должна облегчить дальнейший анализ, упростить архитектуру нейронной сети и ее обучение.

МЕТОДЫ ПРЕДОБРАБОТКИ ДАННЫХ

Предподготовка данных включает [Kong et al., 2018; Kotsiantis et al., 2006] форматирование данных, удаление и/или восстановление данных, извлечение информативных характеристик, масштабирование полученного вектора признаков.

При форматировании сигнал надо привести к единой частоте дискретизации и разрезать поток данных на окна определенной длины (например, по 1000 отсчетов). Возможно и другое форматирование данных. Вектор данных можно, например, формировать из амплитуд сигнала, соответствующих одному моменту времени, полученных по разным каналам регистрации и/или с разных компонент. Вместо амплитуд могут быть использованы отнесенные к одному моменту времени какие-либо представления сигнала. Такой вариант не очень удобен. Сейсмическое событие может занимать очень длинный участок временного ряда данных. Выявление его особенностей потребует особо сложной рекуррентной цепочки. Такое представление данных не приведет к упрощению ГНС, и мы ее рассматривать не будем.

Под удалением понимается исключение явно негодных данных, например, из-за превышения сигналом его динамического диапазона (clip). Можно попытаться восстановить или заменить поврежденные данные по тому или иному алгоритму. Возможен и несколько другой подход. Если применять ГНС с несколькими входами, каждый из которых обрабатывает свой канал или компоненту, можно при работе не только игнорировать один из входов, но и, используя ГНС в качестве генеративной модели, восстановить данные пропущенного входа с помощью прохода “сверху вниз”.

Извлечение характеристик – это процесс удаления как можно большего количества нерелевантной и избыточной информации. Наш подход использует шаблоны в самом наборе данных. Мы стараемся выделить отличия одной сейсмограммы от другой, а не отличия сейсмограмм от других наборов данных. Эти отличия затем будут предметом дальнейших вычислений или анализа [Guyon, Elisseeff, 2003]. В качестве метода извлечения характеристик может быть использовано преобразование сигнала или фильтрация шума без снижения размерности [Gravirov et al., 2013]. Способ извлечения характеристик может иметь физическую интерпретацию. Этим повышается наглядность метода, улучшается возможность контроля. С другой стороны, признаки, не имеющие четкого физического значения, могут обеспечить лучшую способность распознавания.

Масштабирование – перевод тем или иным способом амплитуд в приемлемый для ГНС диапазон. При этом и абсолютное значение, и соотношения этих величин в разных окнах могут иметь значение, т.е. данные масштабирования тоже должны поступать в сеть.

Для корректной работы ГНС необходимы сведения о частотных характеристиках сейсмостанций, представленные, например, нолями и полюсами, а также географические координаты сейсмических датчиков и привязка регистрируемых сейсмограмм к точному времени. Эти метаданные данные подаются уже на один из последних слоев сети.

ПРИНЦИПЫ ИЗВЛЕЧЕНИЯ ИНФОРМАТИВНЫХ ХАРАКТЕРИСТИК ДАННЫХ

Пусть сигнал – это окно сейсмической записи длиной N отсчетов. Каждое окно w_i принадлежит множеству W*^N, в котором представлены только записи сейсмометров (для обозначения размерности используем надстрочные символы). Временные ряды, не имеющие сейсмического происхождения, не представлены в этом пространстве. В результате некоторого преобразования v_i = f(w_i) мы превращаем w_i в другое представление v_i длиной M отсчетов, в котором видны особенности сейсмического сигнала. А все множество возможных окон W*^N отображается на множество представлений V^M.

При этом существует и обратное преобразование 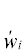= g(v_i); W*^N = G(V^M).

Ошибки преобразований приводят к тому, что 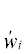несколько отличаются от w_i. Это отличие не должно превышать некоторого значения Е. Главное, чтобы при допустимой ошибке Е восстановленный сигнал отображал то же самое сейсмическое событие, со значениями параметров в соответствующем допуске. Здесь плохо подходит формальная процедура определения ошибки E, например, применение метода наименьших квадратов.

Напомним, что в исходном сигнале содержится шум. Таким образом, реальное множество W^N значительно превосходит идеальное W*. Плюс к этому, в погоне за компактностью представления v_i мы соглашаемся с некоторой потерей информации при прямом преобразовании. Таким образом, близкие входные сигналы будут иметь одно и то же компактное представление. Различие входных сигналов также не должно превышать Е. Это приводит к дополнительному сужению V^M. Прямое и обратное преобразования должны быть стабильны относительно небольших возмущений на входах. “Эквидистантные” во временной области сейсмограммы должны быть “близки” после преобразования. Тогда анализ, проводимый во временной области, может быть в равной степени возможен в области преобразования. Если же вместо сейсмического сигнала w_i на вход преобразования f(w_i) попадет сигнал, не принадлежащий W^N, он тоже отразится в V^M, но при обратном преобразовании восстановленный сигнал будет отличаться от входного с большой ошибкой. Если преобразование сигнала реализуется с помощью машинного обучения, есть смысл вносить в обучающую выборку шум.

Обычно данные искусственно зашумляются гауссовским шумом. Мы считаем этот подход порочным, хотя и наиболее простым. Гауссовский шум довольно легко поддается снижению, так как не является редким сигналом. Трудности возникают с нестационарными колеблющимися, прерывистыми и импульсными шумами. При этом техногенные шумы, которые чаще всего приводят к ошибкам в анализе сигналов, обычно нестационарны и далеки от распределения Гаусса. Искусственное зашумление правильнее производить смешением полезного сигнала с реальными шумовыми трассами [Гравиров, Кислов, 2015], хотя это требует большой дополнительной работы с обучающими данными. Заметим, что при искусственном зашумлении обучающих примеров (и их последующим масштабировании), надо ориентироваться на уровень сигнала. В противном случае, при его низком уровне мы будем обучать алгоритм на чистом шуме.

Мы не пользуемся понятием “отношение сигнал/шум” (signal to noise ratio – SNR). В работе [Кислов, Гравиров, 2013] обоснована неоднозначность этой характеристики и предложен альтернативный подход к оценке шума. Мы будем просто говорить о том, какой вид помех мы имеем в виду.

Методы и способы решения поставленной задачи могут существенно различаться. Определим, что мы хотим от предварительной подготовки данных:

− выделение информативных особенностей сейсмического сигнала,

− подавление помех разнообразной природы,

− сжатие данных,

− возможность восстановления очищенного от шума сигнала,

− возможность работы алгоритма в реальном времени.

Главной, конечно, является первая процедура. Заметим, что указанные процедуры взаимосвязаны, и, выполнение одних часто приводит, хотя бы частично, к выполнению других. Восстановление сигнала не является обязательным, однако его возможность очень полезна для контроля преобразования данных и может быть необходима при использовании в качестве последующей обработки методов, отличных от нейросетевых.

CS-МЕТОД

Широко известно следствие теоремы В.А. Котельникова (которую теперь почему-то называют теоремой Найквиста–Шеннона) о том, что если максимальная частота в сигнале равна или превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует. Но наша цель сжать не сигнал, а информацию, которую он содержит [Candes et al., 2006; Donoho, 2006]. И в этом отношении теорема Котельникова не накладывает никаких ограничений.

Предположим, что сжатие сигнала подразумевает выделение, а не запутывание его информативных особенностей (что в общем случае неверно). Все методы сжатия данных разными способами стараются прийти к одному результату – найти такое F-преобразование (1), чтобы M $ \ll $ N. Тогда для нашего случая (см. ВВЕДЕНИЕ) идеальным вариантом было бы снижение размерности входного вектора с 1000 до 30.

Рассмотрим метод, который в русскоязычной литературе именуется опознанием, а в английской Compressed Sensing, Sparse Sampling или Compressive Sampling и традиционно обозначается буквами CS. В геофизике этот метод применяется уже около 40 лет [Taylor et al., 1979; Oldenburg et al., 1983; Santosa, Symes, 1986, Vera Rodriguez et al., 2012; Gan et al., 2016].

Пусть w^N – сигнал (исходные данные высокой размерности), который мы хотим проецировать в пространство более низкой размерности. Линейные отображения определяются матрицами Ф^{M × N}, которые действуют как кодер:

Представим сигнал через некоторый базис w = = Ψx, где столбцы матрицы Ψ^N×N являются координатами базиса Ψ, а вектор-столбец x^N содержит коэффициенты, которые представляют сигнал w^N в базисе Ψ. Это эквивалентные представления одного и того же сигнала, w во временной области, а x в Ψ-области. Представление x^N будет называться s‑разреженным, если x является линейной комбинацией только s базисных векторов, т.е. выполняется условие ${{\left\| x \right\|}_{{\ell 0}}} \leqslant s$ ($\ell $0-норма определяется как количество ненулевых элементов вектора). Это означает, что все компоненты этого вектора равны нулю кроме s штук. Вектор x называется сжимаемым, если s компонент вектора достаточно велики, а остальные (большинство) малы. На самом деле, CS использует правило, что все естественные сигналы редки, когда они выражены надлежащим образом Ψ [Candès, Wakin, 2008]. После преобразования целевой сигнал должен хорошо аппроксимироваться разреженным вектором [Foucart, Rauhut, 2013]. Можно точно восстановить любой w, если M ≥ N и матрица Ф имеет полный ранг. Напротив, при M < N, уравнение y – Φz = 0 имеет бесконечное число решений $z{\text{,}}$ что делает невозможным однозначное восстановление w^N по y^M, если они связаны соотношением (2). Для восстановления исходного сигнала CS использует информацию о том, что x – сжимаемый.

В соответствии с теорией CS, кодирование данного сигнала представляет собой простую линейную процедуру y = Ax, где матрица A = ΦΨ часто называется матрицей измерений, сенсорной или чувствительной матрицей.

Матрица измерений должна удовлетворять RIP-условию (Restricted Isometry Property). Его выполнение с высокой вероятностью может быть достигнуто просто за счет выбора матрицы A со случайными элементами, распределенными, например, по нормальному закону или закону Бернулли (рандомизация процесса). Случайные матрицы в значительной степени некогерентны с любым фиксированным базисом Ψ [Bourgain et al., 2011]. Чем меньше когерентность, тем меньше может быть M. Случайные матрицы не бывают оптимальными или стабильными и зачастую применяются другие варианты [Ji et al., 2008; Gurbuz et al., 2009; Robucci et al., 2010].

Сжатие в некоторой степени снижает шум, который в большинстве случаев не имеет разреженного представления. Под шумом понимается то, что соответствует обнуляемым компонентам вектора. Процедура CS весьма эффективна при небольшом уровне шума [Ben-Haim et al., 2010; Haupt, Nowak, 2006]. Такое шумоподавление зиждется на гипотезе о сигнале малой размерности и большой амплитуды и о шуме большой размерности и маленькой амплитуды. CS может понизить не только гауссовский шум, но и любой симметрично распределенный шум с нулевым средним, не зависящий от элементов вектора проекции.

Следующий этап – выбор алгоритма восстановления. Можно ли корректно восстановить сигнал из сжатого вектора y, зависит от матрицы измерений, самого сжатого вектора y и алгоритма, используемого для восстановления. В CS восстановление сигнала возможно только с помощью нелинейных алгоритмов. В терминах линейной алгебры при M < N имеются меньше уравнений, чем неизвестных, что делает решение в целом некорректным. Обычно в качестве меры соответствия восстановленного сигнала исходному или размера ошибки используется $\ell $1-оптимизация. Восстановленный сжимаемый сигнал $\hat {x} = \arg \min {{\left\| {x{\kern 1pt} '} \right\|}_{\ell }}_{1}$ будет с высокой вероятностью соответствовать исходному при M ≥ С₁s log(N/s), где C₁ – постоянная, зависящая от способа создания матрицы измерений. Это задача выпуклой оптимизации, которую можно свести к задаче линейного программирования, известной как выбор базиса (basis pursuit) [Foucart, Rauhut, 2013]. Для восстановления применяют и другие алгоритмы [Blumensath, Davies, 2009].

Чтобы учесть шум преобразований и шум, изначально присутствующий в данных используют $\ell $1-оптимизацию с ослабленными ограничениями: $\min {{\left\| {\hat {x}} \right\|}_{{\ell 1}}}$ : ${{\left\| {A\hat {x} - y} \right\|}_{{\ell 2}}} \leqslant \varepsilon ,$ где ε характеризует шум. Это выпуклая задача (конусная программа второго порядка), и она может быть эффективно решена.

Ошибка восстановления состоит из двух слагаемых: первое пропорционально величине сейсмического шума и шума регистрации, а второе - ошибка аппроксимации, которую можно получить в бесшумном случае. Таким образом, качество реконструкции изрядно ухудшается с увеличением шума в данных. Ни один метод восстановления не может быть принципиально лучше при произвольных возмущениях ε.

Мы уже отмечали трудности определения “величины ошибки” E для извлеченных из сейсмических данных характеристик, тем более, не зная заранее, какие характеристики могут понадобиться. Среди них можно упомянуть времена вступлений отдельных фаз землетрясения, направления прихода волн этих фаз на сейсмические датчики, частотные полосы фаз, их амплитуды и величины затуханий в среде. Оценить ошибку по этим параметрам возможно лишь, сравнив исходную и восстановленную сейсмограммы (рис. 1).

Очевидно, что сжатые данные имеют меньшую “приведенную погрешность”, чем восстановленные. При этом многие виды анализа возможны без восстановления сигнала [Davenport et al., 2010], например, если CS-процедура встроена непосредственно в ГНС [Li et al., 2018]. Поскольку CS – это матричные вычисления, алгоритм может быть легко встроен в нейронную сеть как дополнительный слой. Параметры этого слоя фиксированы и не обновляются во время обучения [Shen et al., 2018].

CS все чаще применяется в сейсморазведке и обработке данных сейсмических сетей, где использование многих датчиков и сжатие их данных практически не ухудшает картину анализа [Yao et al., 2011]. Про сейсморазведку см. также [Herrmann, 2019].

Наибольшими препятствиями применения CS как средства предподготовки данных для дальнейшего анализа, являются требование малости шума и необходимость высокой разреженности. Когда измерения искажаются случайным шумом, каждое уменьшение числа отсчетов m в два раза также снижает качество цифрового восстановления в два раза [Davenport et al., 2012]. Уровень s-разреженности сейсмических сигналов может быть недостаточен для существенного сжатия. При этом алгоритмы CS с восстановлением требует больших вычислительных затрат и их применение затруднительно в системах реального времени.

СЖИМАЮЩЕЕ КОДИРОВАНИЕ С ТРАНСФОРМАЦИЕЙ

Для сжатия звука и видео, например, в форматах JPEG, MP3, используется трансформирующее кодирование, в котором также используются s-разреженные представления. Сигнал w^N преобразуется в вектор y = Φw, в котором s-компонент обладают большими значениями, а остальные (N – s) малыми значениями, и поэтому они могут игнорироваться. В итоге кодируются сами s-значений и номера их позиций в векторе w.

В качестве трансформирующих преобразований обычно используются дискретные вейвлет-преобразование, Фурье или косинусное преобразования.

При анализе сейсмических данных сжимающее кодирование с трансформацией имеет ряд недостатков по сравнению с CS-методом. Даже при малом s, использование этих алгоритмов требует больших вычислительных затрат. Все N коэффициентов преобразования надо вычислять, хотя от большинства из них (кроме s штук) никакого толка. Дополнительно должны быть закодированы местоположения больших коэффициентов s [Граничин, Павленко, 2010]. Сжимающее кодирование явно проигрывает по сравнению с CS.

АВТОЭНКОДЕР

Еще в 2006 г. было известно [Hinton, Salakhutdinov, 2006], что автоэнкодеры (AE) могут использоваться для поиска низкоразмерных особенностей сложных наборов данных. В последние годы вновь возрос интерес к этим нейронным сетям [Creswell, Bharath, 2019; Shi et al., 2019]. В работе [Bao et al., 2017], например, представлена сложная структура, состоящая из вейвлет-преобразования сигнала, его сжатия и выделения особенностей с помощью AE и последующей обработки рекуррентной нейронной сетью. Были проведены работы по использованию AE для сжатия сейсмических сигналов длинной 512 отсчетов в 32-мерный вектор [Valentine, Trampert, 2012].

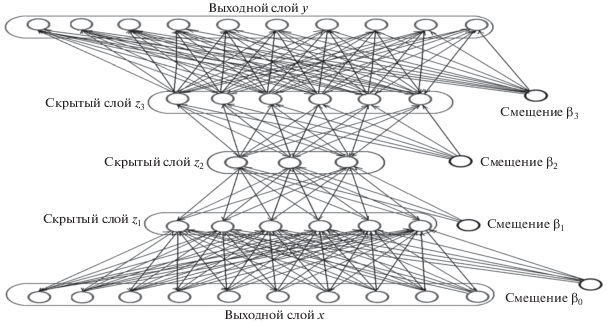
Самый простой AE – это обычная нейронная сеть с одним скрытым слоем, обучаемая по методу обратного распространения ошибки реконструировать свои собственные входы (y = x). Входной и выходной слои имеют равное число нейронов. Вход x отображается на скрытый слой z (слой латентных переменных) z = h₁(Wx + β₀). Затем z отображается на выходной слой y = h₂(W 'z + β₁). Здесь h обозначает поэлементную функцию активации (например, сигмоидальную функцию, ReLU или другую); регулируемые параметры: β – смещения (bias weights, offsets), W – весовая матрица. Тем самым, AE также обучается сведению к минимуму ошибки восстановления (например, среднеквадратичной ошибки) $E(x,y) = {{\left| {\left| {x - y} \right|} \right|}^{2}}$ = = $\left| {\left| {x - {{h}_{2}}({\text{W}}{\kern 1pt} {\text{'}}({{h}_{1}}({\text{W}}x + {{\beta }_{0}})) + {{\beta }_{1}})} \right|} \right|.$ Скрытый слой должен содержать меньше нейронов, чем входной (сокращение размерности). Применяют также разреженную активацию, тогда скрытый слой больше входного, причем количество активных нейронов значительно меньше неактивных, выдающих низкий сигнал. И сокращение размерности, и разреженная активация помогают в процессе обучения выявлять закономерности во входных данных [Кислов, Гравиров, 2017]. AE преобразует данные высокой размерности в данные низкой размерности, как и метод главных компонент (principal component analysis, PCA), но при этом преобразование является нелинейным. С соответствующими ограничениями AE более перспективны, чем PCA или другие известные методы.

Глубокий AE, содержащий много скрытых слоев, может более качественно сжимать данные, выявляя в них особенности. Обозначим выход i-го слоя z_i, i ∈ {1, …, q + 1}. При этом z₀ ≡ x; y ≡ z_{q + 1}, где q – количество скрытых слоев. Тогда z_i = h_i(z_{i – 1}W_i + β_i). Обычно глубокий AE содержит 5–7 слоев, иногда до 11-ти (рис. 2). В нашем случае размеры слоев 1000, 500, 250, 60, 250, 500, 1000 нейронов. Средний слой – 60-мерный вектор – и есть сжатое представление сигнала.

При обучении необходимо настроить матрицы W и смещения β так, чтобы минимизировать некоторую функцию потерь L(x, y). Ее можно задавать по-разному, лишь бы сохранялись расстояния между ответами. Обычно используется алгоритм обратного распространения ошибки, хотя он не очень подходит для нескольких скрытых слоев с миллионами параметров. При правильном выборе шага градиентного спуска, он сходится к локальному минимуму. Процесс упрощается, если используются связанные веса W_i = ${\text{W}}_{{q - i + {\text{2}}}}^{{\text{T}}},$ то есть весовые матрицы кодирования и декодирования транспонированы друг для друга, что приводит к меньшему числу параметров, а, следовательно, к более быстрому обучению сети. С другой стороны, если отказаться от этого принципа, можно снизить ошибку восстановления сигнала [Majumdar, Tripathi, 2017].

Среди автоэнкодеров нас интересуют AE с возможностью сжатия данных с шумоподавлением (Stacked Denoising Autoencoders, SDAE), хотя частично эти функции поддерживаются и другими видами AE. SDAE – стохастический автоэнкодер. При его обучении на вход подается искусственно зашумленный сигнал. Зашумление обычно оформляется как добавление гауссовского шума или случайный процесс обнуления части входов. Это заставляет AE выявлять наиболее сильные взаимосвязи, при этом не строя тождественных отображений. SDAE должен удалить шум, чтобы генерировать выходные данные, близкие к входным. Зашумление проводится только при обучении первого скрытого слоя. Для следующих слоев мы просто используем выход из предыдущих слоев.

Обучение глубоких AE может быть проведено с жадной послойной подготовкой, проводимой без учителя. Последнее время бытовало мнение, что это излишество и что случайная инициализация весов, использование функции активации ReLU и некоторые ухищрения дают возможность обучить сеть с помощью только точной настройки (fine-tuning). Однако для того, чтобы получить от AE максимальный эффект этого мало [Erhan et al., 2010]. Помимо подготовки без учителя, могут быть и более сложные алгоритмы. Например, после каждого этапа подготовки, можно настраивать нижележащие слои.

Чем больше слоев в AE, тем лучше выделяются признаки. Однако помимо того, что у глубокого AE снижается пропускная способность, значительно увеличивается трудность его обучения. Чрезмерное сжатие данных также ведет к потере информации [Gehring et al., 2013]. В пределе в центральном слое остается один нейрон. Тогда AE пронумеровывает все учебные примеры и восстанавливает их по номеру.

Ситуация с полнотой передачи информации и возможностью адаптации метода AE к реальному шуму во многом сходна с проблемами алгоритма CS. С другой стороны, поскольку AE обучается на большом количестве реальных данных, взаимосвязи отдельных особенностей сигнала сохраняются полнее. Как и у CS сжатые данные имеют меньшую “приведенную погрешность”, чем восстановленные и их выгоднее использовать при дальнейшем анализе сигнала. Обученный AE работает на порядки быстрее CS.

ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ

В качестве возможных способов предподготовки сейсмических записей рассмотрим технику вейвлет-анализа и фильтрации [Стадник, 2004; Saad et al., 2019]. Вейвлет-преобразование позволяет перевести исследуемый сейсмический сигнал из временного представления в частотно-временное [Chen et al., 2019]. Выбор конкретного вида вейвлета зависит от класса решаемых задач. Для получения оптимальных алгоритмов преобразования разработаны определенные критерии, но они, как правило, неполно учитывают все разнообразие сейсмических сигналов [Комаров, 2010].

Вейвлет-преобразование представляет собой свертку анализируемого сигнала x(t), t∈(–∞, ∞) с вейвлет-функциями $\psi \left( {\frac{{t - b}}{a}} \right),$ a, b∈(–∞, ∞), a ≠ 0. В основе большинства применяемых компьютерных алгоритмов лежит непрерывное вейвлет-преобразование, комплексной функции x(t) в комплексную функцию w(a, b):

где: a, b ∈ R; a ≠ 0; x(t)-сигнал; ψ(t) – оконная функция, называемая вейлетом. Параметр а – масштаб (scale) – определяет размер вейвлет-функции $\psi \left( {\frac{{t - b}}{a}} \right).$ Его аналогом в Фурье-анализе является период гармонического колебания. Величина b – сдвиг по оси времени функции ψ(t) – позволяет соотносить результат преобразования со шкалой времени t∈(–∞, ∞). Поскольку сейсмические данные x(t) представляют собой временной ряд следующих друг за другом с постоянным шагом Δt значений: x_k = x(t_k), t_k = Δt k, k = 0, 1, … N – 1, их дискретное вейвлет-преобразование задается следующим выражением: где

При переходе от функции (3) к (5) из знаменателя формулы (3) убирается множитель |a|^1/2 с его заменой $\int_{ - \infty }^\infty {{{e}^{{ - {\text{ }}\frac{{{{{(t - b)}}^{2}}}}{{{{a}^{2}}B}}}}}dt} = a\sqrt {B\pi } .$ Это устраняет зависимость амплитуд гармонических компонент от параметра а, что обычно мешает правильно оценить их относительные интенсивности по представлению вейвлет-спектров.

В качестве входа ГНС удобно использовать элементы локального спектра энергии или скалограммы, способной описывать распределение энергии по масштабам.

Так как это распределение локализовано во времени с помощью параметра сдвига b, то (6) можно назвать локальной скалограммой (рис. 3). В нижней части скалограммы расположены коэффициенты с малыми номерами, дающие детальную картину сигнала, а сверху – с большими номерами, дающие огрубленную картину сигнала.

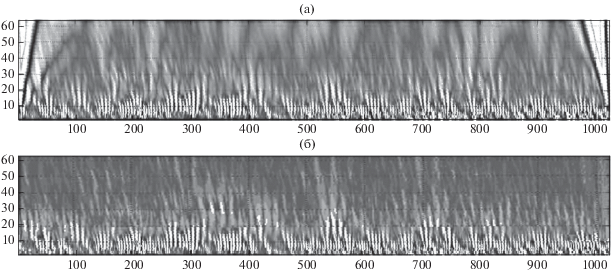
На рис. 3а хорошо видно усложнение спектра по краям, так называемые краевые разрывы. Нами разработан алгоритм, который реализует адаптивный выбор полос пропускания фильтра, позволяющий проводить обработку и фильтрацию входных цифровых сейсмических данных [Gravirov et al., 2014]. Можно выделить мешающую низкочастотную составляющую и всплески, ассоциируемые с техногенными помехами и удалить их из исходного процесса (см. рис. 3б) [Lin et al., 2013]. В ходе экспериментов были опробованы различные типы вейвлетов: Хаара, Симлета различных порядков, Мейера и другие. Мы остановились на вейвлетах Добеши четвертого порядка “db4”. При их использовании форма восстановленного сигнала наименее отличалась от оригинала.

Легко увидеть, что полученная информация избыточна. Обычно для дальнейшей обработки выбирают 5–8 наиболее характерных уровней разложения (которые имеют максимальную амплитуду, и про которые известно, что они не насквозь шумовые).

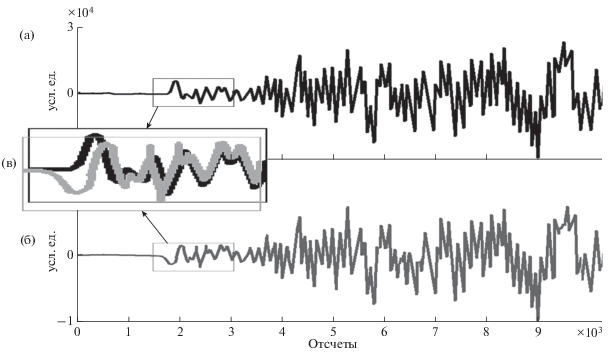
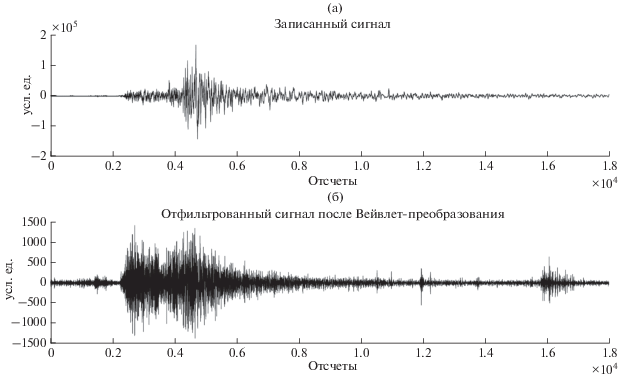
Спектральные полосы могут быть выбраны на основе спектра мощности [Altunkaynak, 2014]. Разложение по каждой полосе – своеобразная карта признаков сигнала [Hu, Wang, 2018]. Восстановление сигнала по характерным картам дает очищенный от шума сигнал. Восстановление по одному из порядков вейвлет-разложения дает возможность рассмотреть выделяемые этой картой признаки. На рис. 4 представлены исходная запись горизонтальной составляющей землетрясения, происшедшего 12.02.2005 г. у побережья Мексики на глубине 20 км и восстановленный по порядку № 64 этот же сигнал. Запись сейсмической станции ACAP Калифорнийского университета в Лос-Анджелесе, расстояние от эпицентра 2850 км.

В нашем примере при использовании восьми коэффициентов для трехкомпонентного сейсмометра, на вход ГНС мы будем подавать такой массив: (1024 отсчетов) × (8 коэффициентов) × (3 компоненты сейсмометра) = 24 576 числовых значений. При использовании сверточного слоя в качестве входа ГНС это вполне реально. Учитывая, что признаки заранее разложены по коэффициентам (и, естественно, по компонентам), это должно привести к выигрышу в сложности архитектуры сети и времени обучения. Использование вейвлетов также позволит отследить и подчеркнуть характерные места изменения спектральной структуры сигнала [Gravirov et al., 2013].

ОБСУЖДЕНИЕ

В этой работе рассматривались различные методы предварительной обработки сейсмических данных для моделей глубокого обучения. Эти методы преобразуют сегменты сейсмических записей в различные типы представлений, из которых ГНС могут извлекать необходимые для анализа характеристики сигнала. Мы исследовали наиболее перспективные методы, хотя возможны и другие подходы [Lv et al., 2017]. Сделать корректные заключения о преимуществе того или иного метода не представляется возможным в силу разнообразия сейсмологических задач, тем более что могут появиться и новые задачи. Разные методы предподготовки преследуют несколько разные цели. Общие для них – выделение особенностей сигнала, снижение шума и сжатие данных – очень взаимосвязаны. Кодирующая часть АЕ хорошо сжимает данные, но проигрывает в шумоподавлении. Вейвлет-предподготовка увеличивает входные данные ГНС, но хорошо выделяет особенности сигнала, CS хорошо устраняет “симметричный” шум и хорошо сжимает данные, но требует дополнительного контроля сохранения информации.

Каждый метод подразумевает и возможность восстановления сейсмических записей, очищенных от шумов. Однако при этом добавляется ошибка восстановления, и увеличиваются вычислительные затраты. Восстановление лучше использовать только для визуализации и контроля, а дальнейшую работу проводить только с преобразованными данными. Вычисления могут производиться в низкоразмерном пространстве, дающем преимущества по времени вычислений. Преобразование должно выделять информацию, подсвечивать особенности данных, а не запутывать их, иначе только после распаковки данные будут пригодны для обработки. Удалению подлежат только шумовые составляющие записей: аппаратурные шумы и техногенные помехи. Алгоритмы предобработки должны допускать возможность дальнейшей специализированной обработки полезного сигнала, нацеленной на решение разных сейсмологических задач.

ВЫВОДЫ

Проблемы сейсмологии обуславливают необходимость разработки новых гибких инструментов анализа, легко перестраиваемые на решение новых задач. Внедрение нейросетевых технологий в практику сейсмических наблюдений может значимо увеличить их достоверность и информативность, автоматизировать процесс выделения и обработки сигналов сейсмических событий. Многое зависит от качества данных. Если данные содержат постороннюю и нерелевантную информацию, ГНС могут давать менее точные и менее понятные результаты. Поэтому предварительная обработка сейсмических записей является важным шагом в процессе машинного обучения.

Этап предварительной обработки необходим для устранения избыточности данных, определение их пригодности, решения проблем шума. Предобработка необходима не только для анализа сейсмических записей с помощью ГНС, но и для других методов анализа. Она не приводит к потере информации, а способствует увеличению количества полезной информации на единицу данных.

Какой же из рассмотренных методов предобработки наиболее перспективен?

CS – очень эффективный метод. Но его основные преимущества скажутся, когда сейсмические приемники будут осуществлять рандомные наблюдения. Это дело будущего. Тогда, проводя анализ сжатых данных (без восстановления) можно получить значительный эффект в снижении вычислительных затрат и упрощении алгоритмов.

Качественно обученный АЕ с расширенной версией шумоподавления может решать многие важные задачи сейсмологии. Однако он не обеспечивает эффективного подавления многообразных техногенных помех.

Нам кажется, что при современном уровне развития ГНС, предпочтительным методом предобработки сейсмических записей является вейвлет-преобразование. Помимо отличной способности этого метода фильтровать шумы разнообразной природы, это очень наглядный метод, позволяющий четко локализовать изменения сигнала во времени.

Целью данной работы было сравнение различных подходов к предварительной обработке данных для задач анализа сейсмических записей и предоставление справочных материалов для будущих исследований.