Физика Земли, 2020, № 1, стр. 43-52
Времена повышенной вероятности возникновения сильнейших землетрясений мира: 30 лет проверки гипотезы в реальном времени
В. Г. Кособоков 1, 2, 3, *, П. Д. Щепалина 1, **
1 Институт теории прогноза землетрясений и математической геофизики РАН
г. Москва, Россия
2 Парижский институт физики Земли
г. Париж, Франция
3 Международная организация сейсмической безопасности
г. Арсита, Италия
* E-mail: volodya@mitp.ru
** E-mail: polllina95@mail.ru
Поступила в редакцию 25.04.2019
После доработки 17.06.2019
Принята к публикации 24.06.2019
Аннотация
Вот уже 30 лет каждое полугодие в режиме реального времени алгоритм среднесрочного прогоза землетрясений М8 применяется глобально, определяя области, в которых сильнейшие землетрясения мира актуально наиболее вероятны. На сегодняшний день статистика результатов, полученных в Глобальном тесте, с достоверностью выше 99% свидетельствует о достаточно высокой эффективности прогнозов по алгоритму M8, а также в его комбинации с алгоритмом MSc, уточняющим локализацию очаговой зоны ожидаемого землетрясения. Тем самым нулевая гипотеза случайного возникновения в сейсмоактивных районах отвергнута с сейсмологической определенностью, по крайней мере, для сильнейших землетрясений мира из магнитудных диапазонов 8.0+ и 7.5+. Результаты этого экспериментального тестирования являются косвенным подтверждением предсказуемости сильных землетрясений, а также как существования общих динамических характеристик, так и разнообразного поведения при фазовых переходах в сложной иерархической нелинейной системе разломов-и-блоков литосферы Земли.
1. ВВЕДЕНИЕ
Катастрофическая природа землетрясений хорошо известна из-за разрушительных последствий многих из них. Очевидная внезапность, а также отсутствие регулярности и редкость экстремальных сейсмических событий способствовали формированию общего представления о том, что землетрясения являются непредсказуемыми явлениями.
Общеизвестно, что обычно прогнозирование экстремальных явлений является непростой задачей: по определению экстремальное событие является редким в ряду родственных явлений. Вообще говоря, это сразу подразумевает исследование весьма малой выборки случаев с помощью деликатных статистических методов, применяемых к данным разного качества, собранным в различных условиях. Многие экстремальные события коррелированы и/или сгруппированы, по-видимому, далеки от независимости и следуют некоторому “странному” распределению, такому как, например, моно- или мультифрактальное, которое вряд ли является однородным. Очевидно, что такая “необычная” ситуация усложняет поиск и определение предшествующего поведения, которое будет использоваться для целей прогноза.
Прогнозирование землетрясений, в целом, – неточная профессия. Было предложено много методов для прогнозирования землетрясений, и, возможно, некоторые из этих методов могут оказаться надежными. Некоторые из них могут быть даже полезны для снижения сейсмических рисков и потерь в результате катастрофических землетрясений и связанных с ними явлений. Однако, к сожалению, большинство известных в настоящее время методов прогнозирования землетрясений не могут быть адекватно протестированы и оценены из-за отсутствия точного определения и/или нехватки данных для их надежной проверки [Wyss, 1997; Schorlemmer et al., 2018; Kato, 2019]. Редким исключением является алгоритм распознавания образов M8, прототип которого был разработан в 1984 г. [Кейлис-Борок, Кособоков, 1984] для предсказания великих землетрясений с магнитудой от 8.0 и выше, отсюда и его название. Этот компьютерный алгоритм изначально был задуман для использования, нацеленного и на другие диапазоны магнитуд, и к 1986 г. его оригинальная версия уже была испытана на примерах ретроспективных прогнозов менее сильных землетрясений, вплоть до магнитуды 5.0 [Kossobokov, 1986]. С тех пор алгоритм М8 используется для систематического мониторинга сейсмической активности в ряде сейсмических регионов мира. После первых успешных прогнозов землетрясений 1988 г. в Спитаке (Армения) и 1989 г. в Лома Приета (Калифорния) [Keilis-Borok, Kossobokov, 1990; Keilis-Borok et al., 1990] совместно с учеными Геологической службы и Национального центра информации о землетрясениях США был разработан строгий Глобальный тест для оценки эффективности воспроизводимых среднесрочных прогнозов землетрясений со средней неопределенностью локализации их эпицентров [Healy et al., 1992]. Уже на этапе разработки, предшествующем публикации официального отчета о принципах планируемого тестирования, в реальном времени были предсказаны землетрясения 05.04.1990 г. (МS = 7.5) в районе Марианских островов и 22.04.1991 г. (МS = 7.6) в Коста-Рике [Healy et al., 1992, с. 17], информация о возможности которого обсуждалась с представителями региональных сейсмологических центров Латинской Америки во время Школы по прогнозу землетрясений и уменьшению сейсмического риска (Каракас, Венесуэла, февраль–март 1991 г.). 08.03.1991 г. руководитель Школы академик РАН В.И. Кейлис-Борок проинформировал об этом Президента Венесуэлы К.А. Переса во время предоставленной аудиенции.
2. ГЛОБАЛЬНЫЙ ТЕСТ АЛГОРИТМА ПРОГНОЗА ЗЕМЛЕТРЯСЕНИЙ
Важнейшим условием, необходимым для принятия новой идеи научным сообществом, является точная формулировка в виде допускающей проверку гипотезы и распространение ее среди ученых, которые находят гипотезу интересной и полезной. Как уже отмечалось, прогноз землетрясений дает яркий пример проблемы, над которой работает значительная часть геофизиков, чьи достижения остаются непризнанными до настоящего времени.
Несмотря на ряд реализовавшихся предсказаний магнитудного диапазона, места и времени сильных землетрясений по алгоритму М8, оценка эффективности методологии в начале 1990-х гг. основывалась в основном на опыте ретроспективных симуляций прогноза [Keilis-Borok, Kossobokov, 1990]. Для экспериментального прогноза в реальном времени была разработана и реализована схема систематического применения алгоритма М8, а при возможности, определяющейся локальной полнотой глобального каталога, и его комбинации с алгоритмом MSc.
2.1. Дизайн Глобального теста алгоритма М8
Национальный Совет по оценке предсказаний землетрясений (National Earthquake Prediction Evaluation Council, NEPEC) в июне 1988 г. рекомендовал Геологической службе США провести систематическую проверку метода прогноза землетрясений по алгоритму М8 [Updike, 1989]. В разработке теста и его реализации приняли непосредственное участие сотрудник Международного института теории прогноза землетрясений и математической геофизики РАН В.Г. Кособоков и сотрудники двух центров Геологической службы США – Дж. Х. Хили (Менло-Парк, Калифорния) и Дж. У. Дьюи (Голден, Колорадо).
Алгоритмы. В ходе теста каждый из алгоритмов прогноза рассматривается как “черный ящик” с полностью зафиксированными параметрами. Значения параметров и тексты программ опубликованы в работах [Healy et al., 1992; Kossobokov, 1997]. Каждые полгода прогнозы обновляются по доступным к этому моменту данным глобальных сейсмологических наблюдений.
Данные. В ходе теста используются глобальный каталог Национального центра информации о землетрясениях и Геологической службы США [Global Hypocenters Data Base, 1989] и его пополнения к текущему моменту времени. При этом используются наиболее полные из доступных данных и алгоритмическая классификация землетрясений на основные толчки и афтершоки. (Отметим, что 25.09.2013 г. Геологическая Служба США прервала поддержку сайта с данными, которые предполагалось использовать в 1992 г.: регулярные пополнения с использованием актуальных каталогов PDE monthly, PDE weekly, и QED пришлось заменить пополнением из онлайн поиска в глобальной базе ANSS (Advanced National Seismic System; https://earthquake.usgs.gov/earthquakes/search/).
Аналогично алгоритмам прогноза пополнение и предобработка каталога полностью автоматизированы, детально описаны, программно реализованы (в варианте “черного ящика” с полностью зафиксированными параметрами) и опубликованы до начала тестирования в 1992 г. [Healy et al., 1992; Kossobokov, 1997].
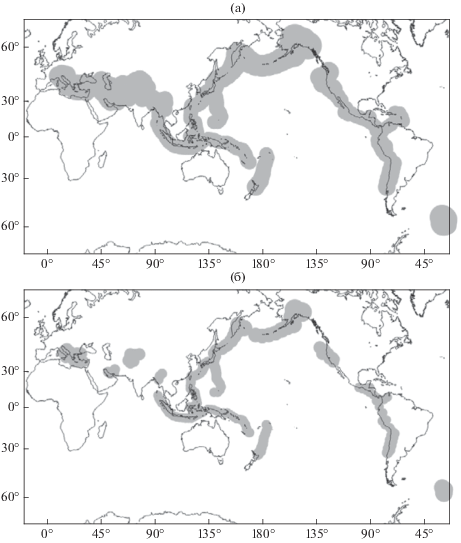
Регионы. Для каждого магнитудного диапазона M0+ = {M|M0 ≤ M < M0+ ΔM} прогноз ведется в кругах одинакового радиуса, центры которых расположены вдоль основных сейсмотектонических поясов Земли (рис. 1). Радиус кругов зафиксирован и соответствует магнитудному диапазону M0+: R(M0) = 1/2 × (exp(M0 − 5.6) + 1) в градусах земного меридиана. Рассматриваются два значения M0 = 7.5 и 8.0, при едином ΔM = 0.75. В каждом из 262 кругов радиуса 667 км (рис. 1а) и 180 кругов радиуса 427 км (рис. 1б) долговременная средняя интенсивность сейсмичности превышает годовой уровень 16 основных толчков с магнитудой от 4.0. Следует специально отметить, что прогнозы безусловно относятся лишь к тем областям в пределах кругов, где возникновение землетрясения возможно, что необходимо учитывать при оценке объема тревоги (см. ниже Оценка результатов).
Рис. 1.
Регионы Глобального теста алгоритмов M8 и MSc, ориентированных на прогноз землетрясений в диапазоне M0+: (а) – 262 круга радиуса 667 км для M0 = 8.0 и (б) – 180 кругов радиуса 427 км для M0 = 7.5.
Информирование о результатах. С 1991 г. результаты, полученные при очередном полугодовом пополнении каталога, в частности, информация о кругах, где согласно алгоритму M8 объявлены периоды повышенной вероятности возникновения землетрясений из диапазонов М8.0+ и М7.5+, об областях, уточняющих область тревоги по алгоритму MSc, а также обо всех землетрясениях с магнитудой от 7.5 и выше за последние полгода, рассылаются заинтересованным адресатам.
В настоящее время результаты мониторинга публикуются в портале ограниченного доступа Института теории прогноза землетрясений и математической геофизики РАН (http://www.mitp.ru/ en/restricted_global/predlist1.html). Рассылка сообщений о прогнозах регулярно осуществляется в январе и июле каждого года по электронной почте в более чем 150 адресов.
Оценка результатов. В ходе Глобального теста результаты прогноза аккумулируются. Конкретнее, для каждого из двух диапазонов прогнозирования начиная с 1985 г. для каждого полугодия фиксируется число предсказанных и пропущенных землетрясений–целей и мера объединения всех регионов, которые по диагностике алгоритма М8 находятся в состоянии повышенной вероятности возникновения этих землетрясений. При этом используемая мера учитывает эмпирическую плотность распределения сейсмичности на поверхности Земли за продолжительный период (1964–1984 гг.) и адекватно определяет вероятность p случайно удачной диагностики в нулевой гипотезе, получившей название “Сейсмическая рулетка” [Kossobokov et al., 1999]. Рецепт определение p крайне прост: (1) выберите носитель меры сейсмичности территории – эталонный каталог реальных землетрясений, каждому из которых соответствует единичный элемент эмпирической меры сейсмогенного пространства; (2) подсчитайте количество таких элементов внутри рассмотренной территории и используйте его как знаменатель дроби; (3) для каждого фиксированного момента времени подсчитайте количество элементов внутри совокупности текущих областей тревоги рассмотренной территории и используйте его как числитель дроби; (4) усредните полученную дробь по всему периоду прогноза. Результат равен p.
Статистическая значимость результатов определяется по значению статистического уровня значимости α = 1 − B(n − 1, N, p) или двойственного ему уровня доверия 1 − α = B(n − 1, N, p), где B – функция кумулятивного биномиального распределения. Чем ниже уровень статистической значимости и, наоборот, чем выше уровень доверия, тем значительнее отличия достигнутых результатов прогноза от результатов случайного угадывания в условиях нулевой гипотезы. В практических приложениях для определения значимых результатов обычно используются значения уровня доверия в 95 и 99%.
2.2. Результаты Глобального теста
Предполагалось проведение эксперимента в течение периода времени, достаточного для окончательного заключения об эффективности метода. В этом смысле эксперимент в настоящее время можно считать завершенным, поскольку в результате глобальной сейсмической активизации уже пятилетней статистики оказалось достаточно для утверждения высокой значимости прогнозов с помощью алгоритмов M8 и M8-MSc, целью которых являются сильнейшие землетрясения мира с магнитудой 8.0 и выше [Kossobokov et al., 1999].
Статистические выводы о достоверности и надежности прогноза по алгоритмам М8 и M8-MSc могут быть сделаны на основании табл. 1, которые суммируют результаты прогноза с 1985 г. по настоящее время (30.04.2019 г.), указывая на то, что регулярные прогнозы по М8 и M8-МSc статистически значимо отличаются от случайного. При этом об эфективности прогнозов можно судить по величине некоторой функции потерь [Molchan, 2010]. Так, например, по значению суммы процентов пропусков цели (n°) и объема тревоги (p), которая по статистике прогнозов по алгоритму М8 в диапазонах М7.5+ и М8.0+ за 1992–2019 гг. равна 80 и 68% соответственно (93 и 77% – для комбинации M8-MSc), что отличается от 100% нулевой гипотезы и позволяет утверждать возможность использования прогнозов Глобального теста для заметного сокращения потерь от сильнейших землетрясений мира [Davis et al., 2012]. Заметим, что значения широко распространенного “выигрыша в вероятности” (1 − n°)/p как меры эффективности прогнозов в диапазонах М7.5+ и М8.0+ равны 1.8 и 2.1 для алгоритма M8 и 1.8 и 2.8 для комбинации M8-MSc.
Таблица 1.
Оценка эффективности алгоритмов M8 и M8-MSc
| Период теста | Землетрясения-цели | Объем тревоги p | Уровень доверия 1 – α | ||||
|---|---|---|---|---|---|---|---|
| всего | предсказано | M8 | M8-MSc | M8 | M8-MSc | ||
| M8 | M8-MSc | ||||||
| Магнитудный диапазон M7.5+ | |||||||
| 1985–2019 | 85 | 43 | 17 | 29.22% | 9.12% | >99.99% | 99.84% |
| 1992–2019 | 73 | 33 | 11 | 25.33% | 8.34% | 99.98% | 96.10% |
| Магнитудный диапазон M8.0+ | |||||||
| 1985–2019 | 27 | 17 | 11 | 30.92% | 14.59% | 99.94% | 99.91% |
| 1992–2019 | 25 | 15 | 9 | 28.13% | 12.66% | 99.91% | 99.75% |
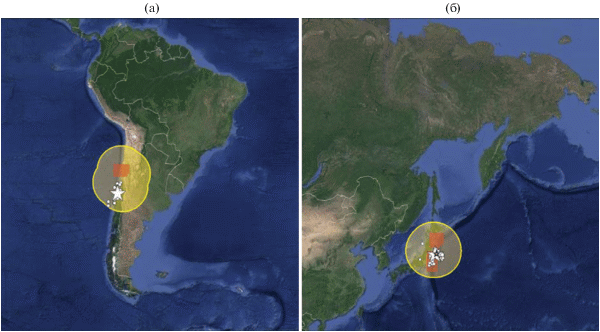
В качестве примера на рис. 2 приведен прогноз на первую половину 2010 г. ожидаемых землетрясений из диапазона М8.0+, а на рис. 3 увеличенные области, где 27.02.2010 и 11.03.2011 гг. произошли ожидаемые великие землетрясения. При этом, поскольку оба события имеют магнитуду за пределом диапазона М8.0+, очевидный упех предсказаний этих мегаземлетрясений не учитывался в таблице. Однако в совокупности с ретроспективным анализом ситуации перед первым из серии мегаземлетрясений XXI столетия 26.12.2004 г. в Индийском океане эти свидетельства дают основание для предположения о том, что алгоритмы, эффективность которых доказана для событий из магнитудных диапазонов М7.5+ и М8.0+, могут быть использованы также и для прогноза еще более сильных землетрясений [Kossobokov, 2011].
Рис. 2.
Глобальный тест алгоритмов M8 и MSc в диапазоне М8.0+: январь–июнь 2010 г. (от 06.01.2010 г.). Круги, в которых период повышенной вероятности возникновения землетрясения не диагностирован (бледно-желтый), диагностирован по алгоритму М8 (темно-желтый), и области уточнения по алгоритму MSc (красный), даны под 1 × 1° маской глобальной сейсмичности.
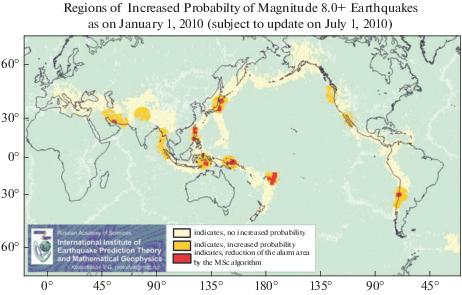
Рис. 3.
Глобальный тест алгоритмов M8 и MSc в диапазоне М8.0+: области прогноза перед землетрясениями 27.02.2010 г. MW 8.8 у берегов Мауле, Чили (а) и 11.03.2011 г. MW 9.1 у Тихоокеанских берегов острова Хонсю, Япония (б). Эпицентры основных толчков (звезда) и их первых афтершоков (ромбы) заполняют 600- и 500-км сегменты Южно-Американской и Японской зон субдукции. Землетрясение Санрику-Оки 09.03.2011 г. MW 7.3 (голубая звездочка) оказалось форшоком мегаземлетрясения Тохоку 11 марта.
3. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ И ВЫВОДЫ
Все модели неверны, однако, некоторые их них в состоянии достаточно адекватно осветить проблему и/или могут быть полезны [Box, 1979]. Отрицание непредсказуемости землетрясений, полученное в результате строгого тестирования алгоритма М8, обнадеживает поиски его модификаций, а также других алгоритмов и подходов к решению задач прогноза катастрофических землетрясений. Не исключено, что некоторые из них не пройдут проверку тестированием фактических предсказаний в реальном времени. Более того, некоторые окажутся вводящими в заблуждение и даже заведомо не полезными, как это случилось с вероятностным анализом сейсмической опасности [Кособоков, Некрасова, 2011; Wyss et al., 2012; Panza et al., 2014].
Очевидно, что для снижения потерь от катастрофических событий, любая достоверная информация об их подготовке может использоваться для проведения мер предупреждения и оказаться полезной на практике. В работе [Davis et al., 2012] приводятся конкретные оценки как экономических потерь от землетрясения и цунами 11.03.2011 г. в Японии, так и того, что могло быть сделано заранее, если бы среднесрочный прогноз великого землетрясения по алгоритму М8 для восточного побережья острова Хонсю использовался как основание к принятию превентивных мер предотвращения потенциально возможного ущерба от события такого масштаба. В частности, показано, что для АЭС Фукусима наращивание высоты дамбы противостоящей цунами было заведомо экономически оправданным, а вот ремонт тоннелей и уклонов шоссе в районах сильных сотрясений и возможного подтопления не был необходим как реакция на достоверный среднесрочный прогноз с эффективностью алгоритма М8. Основными причинами неиспользования прогноза для предотвращения ущерба перед землетрясением в Тохоку были (1) неадекватные связи между менеджерами по чрезвычайным ситуациям и японскими геофизиками, владевшими информацией о прогнозе землетрясения, и (2) отсутствие практического применения существующих методологий для руководства подготовкой к чрезвычайным ситуациям и разработки политики в отношении того, как принимать решения на основе информации, предоставленной среднесрочным прогнозом, имеющим ограниченную, но известную точность в определении силы, места и времени ожидаемого землетрясения.
Следует помнить о том, что точность определения величины землетрясения имеет естественную эпистемическую ошибку до 1/4 магнитуды [Gutenberg, Richter, 1954]. Заметим, что упоминавшийся выше переход Геологической службы США к использованию глобального каталога ANSS изменил обе выборки землетрясений из диапазонов M7.5+ и M8.0+. В частности, в январе 1985 г. по 25.09.2013 г. общее число землетрясений в мире из диапазона M7.5+ почти не изменилось (со 136 до 137), однако, совпадающих землетрясений в выборках из ANSS и GHDB оказалось лишь 110. Расхождение в совокупности составило 53 события: 27 землетрясений из выборки ANSS отнесены к более слабым событиям в GHDB и 26 землетрясений из выборки GHDB отнесены к более слабым событиям в ANSS. В диапазоне M8.0+ ситуация аналогична: 5 из 29 землетрясений из выборки ANSS отнесены к более слабым событиям в GHDB и 11 из 26 землетрясений из GHDB отнесены к более слабым событиям в ANSS. Тем не менее, с 1985 г. диагностика по алгоритму М8 периодов повышенной вероятности сильнейших землетрясений по версии ANSS остается статистически значимой с уровнем доверия 99.2 и 98.2% для диапазонов M7.5+ и M8.0+ соответственно.
На рис. 4 точность географической локализации прогнозов по алгоритму М8 сравнивается со спортивной стрельбой из пневматического пистолета с расстояния 10 метров: все 17 землетрясений из диапазона М8.0+, оправдавших прогнозы Глобального теста, три “пропуска цели” и два из трех мегаземлетрясений попали в “бычий глаз” (черный круг мишени), из которых 12 – в “яблочко” (10 баллов) и лишь три ушли в “молоко”. В результате 27 “выстрелов” выбито 203 очка, что, наверное, не так уж и плохо для первой пристрелки начинающего спортсмена.
Рис. 4.
Положение эпицентров землетрясений из диапазона М8.0+, 1985–2018 гг. (красные кружки) по отношению к центру ближайшего круга, где в этот момент диагностироваан период повышенной вероятности по алгоритму М8. Внешний круг использованной мишени для стрельбы из пневматического пистолета с расстояния 10 м соответствует кругу радиуса 2754 км, где согласно работе [Dobrovolsky et al., 1979] может готовиться землетрясение магнитуды 8.0, а желтая окружность в центре мишени соответствует радиусу 667 км, используемому в алгоритме М8 для прогноза таких землетрясений. Положение эпицентров двух мегаземлетрясений 2010 и 2011 гг. отмечено звездочками. (В центре использованной мишени видны следы от 5 выстрелов спортсмена).
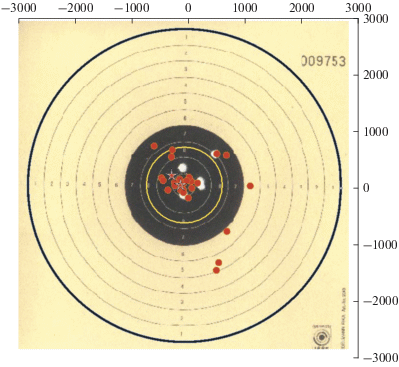
Среднесрочная точность диагностики по алгоритму М8 (месяцы–годы) хотя и не слишком велика, но адекватна характеру используемых сейсмологических данных и, как уже показано выше, вполне достаточна для принятия решений о проведении не только инспекций и учений служб спасения и гражданской обороны, но и других своевременных профилактических мер, позволяющих предотвратить заметную часть социального и экономического ущерба от ожидаемого, потенциально разрушительного землетрясения [Davis et al., 2012].
С физической точки зрения “черный ящик” алгоритма М8, принятый в Глобальном тесте, использует достаточно традиционное описание динамической системы, дополняя стандартное фазовое пространство скоростей (измеряемых числом толчков N) и ускорений (измеряемых дифференциалом L числа толчков N) в потоке сейсмичности величинами безразмерной концентрации (измеряемых величиной Z, обратной критерию образования хрупкого разрыва [Александров, Журков, 1933]) и группируемости (измеряемых максимальным числом афтершоков основных толчков B). Алгоритм распознает область экстремально больших значений координат фазового пространства как окрестность сингулярности сейсмогенной системы разломов и блоков. Попадание вектора измеряемых величин (N, L, Z, B) в эту область свидетельствует о повышении вероятности катастрофы до уровня достаточного для ее эффективного предсказания и служит критерием объявления тревоги [Keilis-Borok, Kossobokov, 1990a]. Выбор критерия в алгоритме М8 определяет специфическую среднесрочную активизацию, своеобразный обратный каскад сейсмичности [Gabrielov et al., 1999], вблизи эпицентра готовящегося события.
В заключение отметим, что оригинальная версия алгоритма M8 допускает модификации, основанные на моделировании сейсмической активности и вероятностном подходе к прогнозированию и/или обнадеживающих результатов использования в региональном масштабе, предназначенного для прогноза более слабых, однако, потенциально разрушительных землетрясений [Bhatia et al., 1989; Kossobokov et al., 1989; 1992; 1999b; 2002; Latoussakis, Kossobokov, 1990; Gahalaut et al., 1992; Kossobokov, Mazhkenov, 1994; Kossobokov, Carlson, 1995; Romashkova et al., 1998; Harte et al., 2003; Romashkova et al., 2004; Peresan et al., 2005; Kossobokov, 2011; Mojarab et al., 2015; Mojarab et al., 2017], а территория Глобального теста алгоритмов M8 и MSc в версии 1992 г. в настоящее время может быть расширена [Kossobokov, 2017].
Результаты глобального экспериментального тестирования алгоритма М8 являются косвенными подтверждениями предсказуемости значительной части землетрясениий, существования динамических моделей сейсмичности, которые характерны для различных тектонических сред, и разного поведения в течение фазовых переходов сложной иерархической, нелинейной системы разломов-и-блоков естественно-фрактальной литосферы Земли. Статистические данные, достигнутые за годы глобального экспериментального тестирования, свидетельствуют не только в пользу нетривиальности алгоритма М8 [Kossobokov et al., 1999a; Kossobokov, 2004; Molchan, Romashkova, 2010; Jordan, 2011; Kossobokov, Soloviev, 2015], но и предоставляют объективные данные для оперативной оценки сейсмической опасности и моделирования ожидаемой последовательности землетрясений [Kossobokov et al., 2000; Ghil et al., 2011]. Показано [Davis et al., 2012], что разумные экономически эффективные действия могут быть предприняты для сокращения ожидаемого ущерба, если достоверность прогноза известна, но не обязательно высока. Информация о прогнозе может быть использована для повышения готовности к стихийным бедствиям и уменьшения последствий крупных катастрофических землетрясений. Вопросы, связанные с определением, валидацией и возможным использованием методологий прогнозирования, рассматриваются более подробно в работах [Peresan et al., 2012; Kossobokov et al., 2015]. Специалисты-практики уверены, что любая надежная прогнозная информация о возможных землетрясениях может быть полезной при проектировании и строительстве сейсмостойкой инфраструктуры, и, как правило, хорошо воспринимается населением в качестве напоминания и своевременного предупреждения о надвигающейся опасности.
Список литературы
Александров А.П., Журков С.Н. Явление хрупкого разрыва. М.: Гостехиздат. 1933. V. 51 с.
Кейлис-Борок В.И., Кособоков В.Г. Комплекс долгосрочных предвестников для сильнейших землетрясений мира. Землетрясения и предупреждение стихийных бедствий. 27-й Международный геологический конгресс, 4–14 августа 1984 г., М. Коллоквиум С6. М.: Наука. 1984. Т. 61. С. 56–66.
Кособоков В.Г., Некрасова А.К. Карты Глобальной программы оценки сейсмической опасности (GSHAP) ошибочны // Вопросы инженерной сейсмологии. 2011. (ISSN 0132-2826). Т. 38(1). С. 65–76.
Кособоков В.Г., Соловьев А.А. Об оценке результатов тестирования алгоритмов прогноза землетрясений // Докл. РАН. 2015. Т. 460. № 6. С. 710–712. https://doi.org/10.7868/S0869565215060213
Advanced National Seismic System; https://earthquake. usgs.gov/earthquakes/search/
Bhatia S.C., Chalam S.V., Gaur V.K., Keilis Borok V.I., Kossobokov V.G. On intermediate term prediction of strong earthquakes in the Himalayan arc region using pattern recognition algorithm M8. Proc. Indian Ac. Sci. // Earth Planet. Sci. 1989. V. 98. № 1. P. 111–123.
Box G.E.P. Robustness in the strategy of scientific model building / Launer R.L., Wilkinson G.N. (Eds.). Robustness in Statistics, Academic Press. 1979. P. 201–236.
Davis C., Keilis-Borok V., Kossobokov V., Soloviev A. Advance Prediction of the March 11, 2011 Great East Japan Earthquake: A Missed Opportunity for Disaster Preparedness. Int. // J. Disaster Risk Reduction. 2012. № 1. P. 17–32. https://doi.org/10.1016/j.ijdrr.2012.03.001
Dobrovolsky I.P., Zubkov S.I., Miachkin V.I. Estimation of the size of earthquake preparation zones // Pure and Applied Geophysics. 1979. V. 117. № 5. P. 1025–1044. https://doi.org/10.1007/BF00876083
Gabrielov A., Newman W.I., Turcotte D.L. An exactly soluble hierarchical clustering model: inverse cascades, self-similarity, and scaling // Phys. Rev. 1999. E 60. P. 5293–5300.
Gahalaut V.K., Kuznetsov I.V., Kossobokov V.G., Gabrielov A.M., Keilis-Borok V.I. Application of pattern recognition algorithm in the seismic belts of the Indian convergent plate margins – M8 algorithm. Proc. Indian Acad. Sci. // Earth Planet. Sci. 1992. V. 101. № 3. P. 239–254.
Gelfand I., Guberman Sh., Keilis-Borok V., Knopoff L., Press F., Ransman E., Rotwain I., Sadovsky A. Pattern recognition applied to earthquakes epicenters in California // Phys. Earth Planet Inter. 1976. № 11. P. 227–283.
Ghil M., Yiou P., Hallegatte S., Malamud B.D., Naveau P., Soloviev A., Friederichs P., Keilis-Borok V., Kondrashov D., Kossobokov V., Mestre O., Nicolis C., Rust H.W., Shebalin P., Vrac M., Witt A., Zaliapin I. Extreme events: dynamics, statistics and prediction. Nonlin. Processes Geophys. 2011. V. 18. P. 295–350. http://dx.doi.org/ Global Hypocenters Data Base CD-ROM NEIC/USGS, Denver, CO. 1989. https://doi.org/10.3133/75https://doi.org/10.5194/npg-18-295-201
Gorshkov A., Kossobokov V., Soloviev A. 6. Recognition of Earthquake-Prone Areas. / Keilis-Borok V.I., Soloviev A.A. (Eds). Nonlinear Dynamics of the Lithosphere and Earthquake Prediction. Springer, Heidelberg. 2003. P. 141–207.
Gutenberg B., Richter C.F. Seismicity of the Earth, 2nd ed., Princeton University Press, Princeton. N.J. 1954. 310 p.
Harte D., Li D.-F., Vreede M., Vere-Jones D. Quantifying the M8 prediction algorithm: reduction to a single critical variable and stability results. New Zealand // J. Geol. Geophys. 2003. V. 46. P. 141–152.
Healy J.H., Kossobokov V.G., Dewey J.W. A test to evaluate the earthquake prediction algorithm, M8, U.S. Geol. Surv. Open-File Report 92-401. 1992. 23 p. with 6 Appendices.
Jordan T.H. (Chair). Operational earthquake forecasting: state of knowledge and guidelines for utilization. Report by the International Commission on Earthquake Forecasting for Civil Protection // Annals of Geophys. 2011. V. 54. № 4. 391 p. https://doi.org/10.4401/ag-5350
Kato M. (2019) On the Apparently Inappropriate Use of Multiple Hypothesis Testing in Earthquake Prediction Studies // Seismological Research Letters. 2019. https://doi.org/10.1785/0220180378
Keilis-Borok V.I., Kossobokov V.G. Periods of high probability of occurrence of the world’s strongest earthquakes, Computational Seismology 19, Allerton Press Inc. 1987. P. 45–53.
Keilis-Borok V.I., Kossobokov V.G. Times of Increased Probability of Strong Earthquakes (M ≥ 7.5) Diagnosed by Algorithm M8 in Japan and Adjacent Territories // J. Geophys. Res. 1990b. V. 95(B8). P. 12 413–12 422.
Keilis-Borok V.I., Kossobokov V.G. Premonitory activation of seismic flow: algorithm M8 // Phys. Earth Planet. Inter. 1990a. V. 61. P. 73–83.
Keilis-Borok V.I., Kossobokov V.G., Smith S.W. Reduction of territorial uncertainty of earthquake forecasting // Phys. Earth Planet. Inter. 1990b. V. 61. R1-R4.
Keilis-Borok V.I., Knopoff L., Kossobokov V.G., Rotvain I.M. Intermediate term prediction in advance of the Loma Prieta earthquake // Geophys. Res. Letters. 1990a. V. 17. № 9. P. 1461–1464.
Keilis-Borok V.I. The lithosphere of the Earth as a nonlinear system with implications for earthquake prediction // Rev. Geophys. 1990. V. 28(1). P. 19–34.
Kosobokov V.G., Mazhkenov S.A. Times of increased probability of large earthquakes in the Eastern Tien Shan diagnosed by the M8 algorithm / D.K. Chowdhury (Ed). Computational Seismology and Geodynamics. Am. Geophys. Un. 1. Washington D.C. The Union. 1994. P. 16–19.
Kossobokov V. Peresan A. Panza G.F. On operational earthquake forecast and prediction problems // Seismol. Res. Lett. 2015. V. 86(2). P. 287–290. https://doi.org/10.1785/0220140202
Kossobokov V.G., Rastogi B.K., Gaur V.K. On self similarity of premonitory patterns in the regions of natural and induced seismicity. Proc. Indian Ac. Sci. 1989. (Earth Planet. Sci.). V. 98. № 4. P. 309–318.
Kossobokov V.G., Soloviev A.A. Evaluating the results of testing algorithms for prediction of earthquakes // Doklady Earth Sci. 2015. V. 460(2). P. 192–194.
Kossobokov V. Are Mega Earthquakes Predictable? Izvestiya, Atmos. Oceanic Phys. 2011. V. 46(8). P. 951–961. https://doi.org/10.1134/S0001433811080032
Kossobokov V. Chapter 18. Times of Increased probabilities for occurrence of catastrophic earthquakes: 25 years of hypothesis testing in real time / Wyss M., Shroder J. (Eds). Earthquake Hazard, Risk, and Disasters. Elsevier, London. 2014. P. 477–504.
Kossobokov V., Shebalin P. 4. Earthquake Prediction / Keilis-Borok V.I., Soloviev A.A. (Eds). Nonlinear Dynamics of the Lithosphere and Earthquake Prediction. Springer, Heidelberg. 2003. P. 141–207.
Kossobokov V.G. Testing an Earthquake Prediction Algorithm: The 2016 New Zealand and Chile Earthquakes // Pure Appl. Geophys. 2017. V. 174. № 5. P. 1845–1854. https://doi.org/10.1007/s00024-017-1543-9
Kossobokov V.G. Chapter 4. User Manual for M8 / Healy J.H., Keilis-Borok V.I., Lee W.H.K. (Eds). Algorithms for earthquake statistics and prediction. IASPEI Software Library. 1997. V. 6. Seismol. Soc. Am., El Cerrito. CA. P. 167–221. with Disk #4: M8 Programs and Test Data Files.
Kossobokov V.G. Earthquake prediction: Basics, achievements, perspectives // Acta Geod. Geoph. Hung. 2004. V. 39(2–3). P. 205–221.
Kossobokov V.G. Earthquake prediction: 20 years of global experiment // Nat. Hazards. 2013. V. 69(2). P. 1155–1177. https://doi.org/10.1007/s11069-012-0198-1
Kossobokov V.G., Carlson J.M. Active zone size vs. activity: A study of different seismicity patterns in the context of the prediction algorithm M8 // J. Geophys. Res. 1995. V. 100(B4). P. 6431–6441.
Kossobokov V.G., Healy J.H., Dewey J.W. Testing an earthquake prediction algorithm // Pure Appl. Geophys. 1997. V. 149. P. 219–232.
Kossobokov V.G., Healy J.H., Keilis-Borok V.I., Dewey J.W., Khokhlov A.V. The test of an intermediate-term earthquake prediction algorithm: the design of real-time monitoring and retroactive application // Dokl. Academii Nauk. 1992. V. 325. № 1. P. 46–48 (in Russian).
Kossobokov V.G., Keilis-Borok V.I., Smith S.W. Localization of intermediate term earthquake prediction // J. Geophys. Res. 1990. V. 95(B12). P. 19763–19772.
Kossobokov V.G., Keilis-Borok V.I., Turcotte D.L., Malamud B.D. Implications of a statistical physics approach for earthquake hazard assessment and forecasting // Pure Appl. Geophys. 2000. V. 157. P. 2323–2349.
Kossobokov V.G., Romashkova L.L., Keilis-Borok V.I., Healy J.H. Testing earthquake prediction algorithms: Statistically significant real-time prediction of the largest earthquakes in the Circum-Pacific, 1992–1997. Phys. Earth Planet. Inter. 1999a. V. 111(3–4). P. 187–196. https://doi.org/10.1016/S0031-9201(98)00159-9
Kossobokov V.G., Romashkova L.L., Panza G.F., Peresan A. Stabilizing intermediate-term medium-range earthquake predictions // J. Seismology Earthquake Engineering. 2002. V. 4(2–3). P. 11–19.
Kossobokov V.G., Shebalin P.N., Healy J.H., Dewey J.W., Tikhonov I.N. A real-time intermediate-term prediction of the October 4, 1994, and December 3, 1995, southern Kuril Islands earthquakes / D.K. Chowdhury (Ed), Computational Seismology and Geodynamics / Am. Geophys. Un., 4, Washington, D.C.: The Union. 1999. P. 57–63.
Kossobokov V.G., Soloviev A.A. Prediction of extreme events: Fundamentals and prerequisites of verification // Russ. J. Earth Sci. 2008. V. 10. ES2005. https://doi.org/10.2205/2007ES000251
Kossobokov. V.G. The test of algorithm M8, In: M. A. Sadovsky (Ed.). Algorithms of long-term earthquake prediction. CERESIS. Lima, Peru. 1986. P. 42–52.
Kossobokov V.G., Maeda K., Uyeda S. Precursory activation of seismicity in advance of the Kobe, 1995 earthquake // Pure Appl. Geophys. 1999c. V. 155. P. 409–423.
Latoussakis J., Kossobokov V.G. Intermediate Term Earthquake Prediction in the Area of Greece: Application of the Algorithm M8, Pure Appl. Geophys. 1990. V. 134(2). P. 261–282.
Mojarab M., Kossobokov V., Memarian H., Zare M. An application of earthquake prediction algorithm M8 in eastern Anatolia at the approach of the 2011 Van earthquake // J. Earth Syst. Sci. 2015. V. 124. P. 1047–1062. https://doi.org/10.1007/s12040-015-0584-7
Mojarab M., Memarian H., Zare M., Kossobokov V. Adjusting the earthquake prediction algorithm M8 for application in Iranian Plateau with special reference to the 16 April 2013, M7.7 Saravan and the 24 September 2013, M7.7Awaran earthquakes // J. Seismol. (accepted). 2017.
Molchan G.M. Space-time earthquake prediction: the error diagrams // Pure appl. Geophys. 2010. V. 167(8–9). P. 907–917. https://doi.org/10.1007/s00024-010-0087-z
Molchan G., Romashkova L. Earthquake prediction analysis based on empirical seismic rate: the M8 algorithm // Geophys. J. Int. 2010. V. 183. № 3. P. 1525–1537. https://doi.org/10.1111/j.1365-246X.2010.04810.x
Panza G.F., Kossobokov V., Peresan A., Nekrasova A. Chapter 12. Why are the standard probabilistic methods of estimating seismic hazard and risks too often wrong? / Wyss M., Shroder J. (eds) Earthquake Hazard, Risk, and Disasters. Elsevier, London. 2014. P. 309–357.
Peresan A., Kossobokov V., Romashkova L., Panza G.F. Intermediate-term middle-range earthquake predictions in Italy: a review // Earth Sci. Rev. 2005. V. 69(1–2). P. 97–132.
Peresan A., Kossobokov V.G., Panza G.F. Operational earthquake forecast/prediction // Rend. Fis. Acc. Lincei. 2012. V. 23. P. 131–138. https://doi.org/10.1007/s12210-012-0171-7
Romachkova L.L., Kossobokov V.G., Panza G.F., Costa G. Intermediate-term prediction of earthquakes in Italy: Algorithm M8 // Pure Appl. Geophys. 1998. V. 152. P. 37–55.
Romashkova L.L., Kossobokov V.G. Intermediate-term earthquake prediction based on spatially stable clusters of alarms // Dokl. Earth Sci. 2004. V. 398(7). P. 947–949.
Schorlemmer D., Werner M.J., Marzocchi W., Jordan T.H., Ogata Y., Jackson D.D., Mak S., Rhoades D.A., Gerstenberger M.C., Hirata N. et al. The Collaboratory for the Study of Earthquake Predictability: Achievements and priorities // Seismol. Res. Lett. 2018. V. 89. P. 1305–1313. https://doi.org/10.1785/0220180053
Updike R.G. (Ed.). Proceedings of the National Earthquake Prediction Evaluation Council, June 6–7, 1988. Reston, Virginia, U.S. Geol. Surv. Open-File Rep. 1989. P. 89–144. https://doi.org/10.3133/ofr89144
Wyss M. Second round of evaluation of proposed earthquake precursors // Pure Appl. Geophys. 1997. V. 149. P. 3–16.
Wyss M., Nekrasova A., Kossobokov V. Errors in expected human losses due to incorrect seismic hazard estimates // Natural Hazards. 2012. V. 62(3). P. 927–935. https://doi.org/10.1007/s11069-012-0125-5
Дополнительные материалы отсутствуют.


