Физика Земли, 2020, № 1, стр. 30-42
Увеличение радиуса корреляции и цепочки землетрясений перед сильнейшими сейсмическими событиями
П. Н. Шебалин *
Институт теории прогноза землетрясений и математической геофизики РАН
г. Москва, Россия
* E-mail: shebalin@mitp.ru
Поступила в редакцию 25.04.2019
После доработки 17.06.2019
Принята к публикации 24.06.2019
Аннотация
В работе обобщается опыт эксперимента по заблаговременному прогнозу землетрясений по алгоритму Reverse Tracing of Precursors (RTP), в основе которого лежит явление увеличения радиуса корреляции сейсмичности перед землетрясениями. За период теста 2003–2019 гг. в пяти регионах мира произошло 28 сильных землетрясений, из них 23 в области и в период тревог, диагностированных по алгоритму. При этом вероятность случайного успеха в регионах не превышала 30% и в среднем составляла около 15%. Эти результаты подтверждают эффективность алгоритма RTP. Тесты показали также высокую степень неслучайности совпадения сильных землетрясений и предшествующих им индикаторов увеличения радиуса корреляции – цепочек землетрясений.
1. ВВЕДЕНИЕ
Прогноз землетрясений, как недавно заявил Билл Гейтс11, является одной из 10 наиболее важных глобальных проблем современности. Вместе с тем, прогресс развития науки в этом направлении заметно отстает от решения других глобальных проблем, таких как секвестрация углерода (удаление углекислого газа из атмосферы и его безопасное хранение) или создание безопасного беспилотного автотранспорта. Главной причиной сложности задачи общепринято считать неустойчивый характер среды в областях разломов в литосфере, в которых происходят землетрясения. Большое количество разнородных факторов, влияющих на возникновение землетрясений (геометрия разломов, поле напряжений, реология, содержание флюидов и химические взаимодействия, тепловой поток и распределение температур, вязкость среды, пластические деформации и др.), а также фрактальные свойства среды привели в конце 1980-х гг. к концепции литосферы как сложной иерархической самоорганизующейся системы [Bak et al., 1988]. Возрастание радиуса корреляции перед критическими переходами является одним из известных свойств таких систем [Bak, Tang, 1989; Sammis, Smith, 1999]. Пространственная корреляция предвестников, проявляющихся на разных этапах процесса подготовки землетрясений, является проявлением другого известного свойства таких систем, известного как признак чередования (intermittence [Gabrielov et al., 2000]. На каждом этапе система частично сохраняет память о предыдущих состояниях, и поэтому предвестники реализуются примерно в том же пространственном объеме. Следует отметить, что в рамках классической теории упругих взаимодействий корреляция сейсмичности на расстояниях в сотни километров и тем более ее вариации во времени необъяснимы. Но после землетрясения Ландерс в Калифорнии в 1992 г. магнитудой M = 7.6 наблюдалась ярко выраженная активизация сейсмичности на расстояниях до 1000 км от эпицентра землетрясения [Hill et al., 1993], подтвердившая возможность такого явления. Другой пример дальнего взаимодействия – явление удаленных афтершоков [Prozorov, Shreider, 1990]. Все это послужило толчком к поиску эффекта предвестникового возрастания радиуса корреляции в сейсмичности. Примерно одновременно были опубликованы работы [Shebalin et al., 2000; Zoller et al., 2001], в которых исследовалось это явление на реальной сейсмичности. Впоследствии это привело к совместной публикации двух групп исследователей [Заляпин и др., 2002].
Следующий шаг состоял в поиске алгоритма прогноза землетрясений на основе этого явления. По предложению В.И. Кейлиса-Борока были рассмотрены два варианта, ROC и ACCORD, которые ретроспективно тестировались в Южной Калифорнии [Keilis-Borok et al., 2002]. Алгоритм ROC состоит в выявлении небольшого числа (3 или 4) землетрясений умеренной силы, близких по времени, но удаленных по расстоянию. Алгоритм ACCORD отражает почти одновременный рост сейсмической активности в нескольких частях рассматриваемой области. Область исследований на основе карты активных разломов разделена на K-зон линейным размером около 50 км. В каждой зоне в скользящем временном окне подсчитывается число событий заданной магнитуды, и предвестник идентифицируется в момент t, если, как минимум, в K1-зонах это число превышает заданный порог. Ретроспективные тесты обоих алгоритмов показали высокую эффективность.
Дальнейшее развитие подхода состояло в попытке комбинации алгоритмов ROC и ACCORD, которая не требовала бы предварительного разделения рассматриваемого региона на зоны. Автор данной статьи предложил использовать для этого специальный вид кластеров небольших землетрясений, формирующихся из попарно близких между собой по времени и по расстоянию событий, но простирающихся суммарно на большие расстояния. Такие кластеры получили название “цепочки землетрясений” [Shebalin, 2006]. Цепочки землетрясений ретроспективно наблюдались перед сильными землетрясениями в ряде регионов мира за несколько недель или месяцев перед ними. Этот относительно краткосрочный предвестник сам по себе в ретроспективных тестах оказался существенно неслучайным, хотя значительная доля цепочек не сопровождалась сильными землетрясениями (ложные тревоги). Чтобы сократить долю ложных тревог, возникла идея исследовать наличие среднесрочных предвестников землетрясений в пределах цепочек. Были использованы восемь функционалов, отражающих уровень сейсмичности, суммарную площадь очагов, возрастание средней магнитуды, возрастание сейсмической активности, группирование событий в виде роев, “микровзрывы” афтершоков, синхронную активизацию на большой территории и преобразование распределения магнитуд. С помощью этих функционалов исключались цепочки, для которых в ретроспективных тестах в данном регионе их значения чаще соответствовали ложным тревогам. Таким образом, была реализована схема, в которой более краткосрочный предвестник (цепочка землетрясений) указывал пространственную область, в которой затем оценивалась вероятность ложной тревоги по более долгосрочным предвестникам. Соответственно, алгоритм в целом получил название RTP (Reverse Tracing of Precursors – Обратное отслеживание предвестников) [Шебалин, 2006; Shebalin et al., 2003; 2004; 2006; Keilis-Borok et al., 2004a; 2004b]. Эффективность алгоритма в ретроспективных тестах оказалась существенно выше по сравнению с использованием только цепочек землетрясений.
Алгоритм RTP был разработан в начале 2003 г. и впервые представлен на Генеральной ассамблее IUGG в июле 2003 г. в Саппоро, Япония. В докладе был продемонстрирован текущий прогноз для территории Японии; этот же прогноз был снова представлен в брифинге для журналистов. Значительный интерес к докладу был вызван, в частности, тем, что соавтором доклада был выдающийся японский геофизик проф. С. Уеда. Данный прогноз подтвердился: 25.09.2003 г. в области тревоги, вблизи о-ва Хоккайдо произошло землетрясение Токачи-оки магнитудой 8.3.
Незадолго до Генеральной Ассамблеи IUGG в Саппоро совместной группой российских и американских ученых был подготовлен и разослан документ, содержавший прогноз землетрясения магнитуды 6.4 или выше на период с 27.05.2003 г. по 28.02.2004 г. в Центральной Калифорнии. Российскую группу возглавлял В.И. Кейлис-Борок, американскую – К. Аки, выдающийся сейсмолог, незадолго до этого возглавлявший Южнокалифорнийский центр землетрясений (SCEC). Документ содержал два прогноза, полученных по независимым методикам, один из них по алгоритму RTP. 22.12.2003 г. в области прогноза произошло землетрясение Сан-Симеон магнитудой 6.5.
Два успешных прогноза с интервалом менее трех месяцев между сильными землетрясениями, подтвердившими эти прогнозы, вызвали значительный резонанс. В Калифорнии была возобновлена работа комиссии по оценке прогнозов землетрясений (CEPEC – California Earthquake Prediction Evaluation Council) для принятия решения по новому прогнозу по методике RTP, данному для небольшой области в районе пустыни Мохаве в Южной Калифорнии на период 05.12.2003–05.09.2004 гг. Этот прогноз был распространен только среди узкого круга коллег, но каким-то образом данные о нем просочились в прессу. По инициативе директора SCEC Т. Жордана 20.02.2004 г. совместно с Геологической службой США была организована конференция, на которой состоялось всестороннее обсуждение методики RTP. На конференцию были приглашены ведущие специалисты по прогнозу землетрясений из МИТПАН (такую аббревиатуру имел ИТПЗ РАН в тот период) В.И. Кейлис-Борок, Г.М. Молчан, В.Г. Кособоков, И.А. Заляпин, П.Н. Шебалин. В тот же день состоялось заседание CEPEC, посвященное текущему прогнозу. Решение было принято позднее, в апреле 2004 г. – CEPEC признала методику законным подходом, что в условиях преобладающего мнения о невозможности прогноза землетрясений стало почти сенсацией. Однако тревога оказалось ложной. Ложными оказались еще несколько тревог в Калифорнии. Тем не менее, с 2004 г. был начат эксперимент по проверке эффективности алгоритма RTP во времени, близком к реальному, в четырех регионах мира: Японии (M ≥ 7.2), Калифорнии (M ≥ 6.4), Италии (M ≥ 5.5), Восточном Средиземноморье (M ≥ 6.0).
В конце 2004 г. был начат аналогичный эксперимент по прогнозу землетрясений магнитудой 7.2 и более в регионах Курилы–Камчатка–Командоры, Алеуты–Аляска и на Тихоокеанское побережье Канады, США и северной Мексики. В двух последних регионах эксперимент продолжался в течение 2005–2011 гг. За этот период там было диагностировано 4 тревоги, две из них подтвердились землетрясением 15.06.2005 г. в море вблизи Калифорнии магнитудой 7.2 и землетрясением 19.12.2007 г. вблизи Андреановых островов, Алеуты, США, магнитудой 7.2. С 2012 г. эксперимент в этих двух регионах не ведется.
В регионе Курилы–Камчатка–Командоры в конце 2004 г. было диагностировано две предвестниковые цепочки на севере Курильских островов и на Камчатке. Оценка вероятности ложной тревоги по среднесрочным предвестникам составила соответственно 48% и 29%. Аналогично прогнозу в Южной Калифорнии, информация о прогнозе была передана лишь специалистам и через Президиум РАН в МЧС с конкретными рекомендациями в Российский экспертный совет по прогнозу землетрясений, оценке сейсмической опасности и риска. Через МЧС информация о прогнозе, к сожалению, попала в прессу и вызвала значительный резонанс. Автору данной работы даже пришлось объяснять в прямом эфире “Вестей” канала Россия, что вероятность реализации прогноза составляет около 50% и что ситуация находится под контролем МЧС. Обе тревоги оказались ложными. 20.04.2006 г. на севере Камчатки произошло Олюторское землетрясение магнитудой 7.6. Из-за недостатка данных этот район не входит в тест алгоритма. По стечению обстоятельств мобилизация сил МЧС на Камчатке по рекомендации Экспертного совета по прогнозу землетрясений в 2005 г. оказалась эффективной для быстрого предотвращения последствий Олюторского землетрясения. Позднее, новый прогноз землетрясения магнитудой 7.2 и выше в районе Курильских островов оказался успешным и подтвердился землетрясением 15.11.2006 г. магнитудой 8.3 вблизи о-ва Симушир.
Тест алгоритма RTP продолжается по настоящее время в 5 регионах мира путем фиксации заблаговременных прогнозов и сопоставлением с фактически произошедшими землетрясениями. В данной работе подводится итог 15 лет теста алгоритма RTP в этих регионах. Анализ итогов и дополнительные результаты позволяют наметить пути совершенствования метода.
2. РАССМАТРИВАЕМЫЕ РЕГИОНЫ И ИСХОДНЫЕ ДАННЫЕ
Тест алгоритма RTP проводится в пяти регионах мира, для которых в 2003–2004 гг. были фиксированы границы и параметры алгоритма. Отметим, что выбор границ в ряде случаев был не вполне удачен. В разделе 4 приводится пример сильного землетрясения, перед которым была идентифицирована тревога RTP, но эпицентр землетрясения оказался за пределами рассматриваемого региона. Главной задачей выбора было установление формальных границ регионов для возможности точной фиксации успехов и неудач прогнозов.
Регион Хонсю–Хоккайдо–Южные Курилы. Для этого региона используется региональный каталог Японского метеорологического агентства22. Северная часть рассматриваемого региона (рис. 1а) ограничена зоной, по которой в каталоге JMA предоставляются данные с представительной магнитудой, достаточной для алгоритма RTP. Эта зона, благодаря сотрудничеству японских и российских сейсмологов, включает часть Курильских островов и о-ва Сахалин, а также часть Хабаровского края и север КНДР. Южная часть региона из-за смены характера сейсмичности ограничена переходом от Японского желоба к желобу Изу-Бонин, поэтому южная часть о-ва Хонсю и о-в Кюсю не входят в рассматриваемый регион.
Рис. 1.
Регионы теста алгоритма RTP: (a) – Хонсю–Хоккайдо–Южные Курилы; (б) – Калифорния–Орегон–Невада; (в) – Центральные Аппенины, Альпы, Северные Динариды и долина По; (г) – Курилы–Камчатка. Сплошной линией показаны границы регионов. Штриховая линия обозначает оси проекции эпицентров и областей тревоги для пространственно-временных диаграмм (рис. 2–рис. 5). Звездочками обозначены эпицентры землетрясений – целей прогноза.
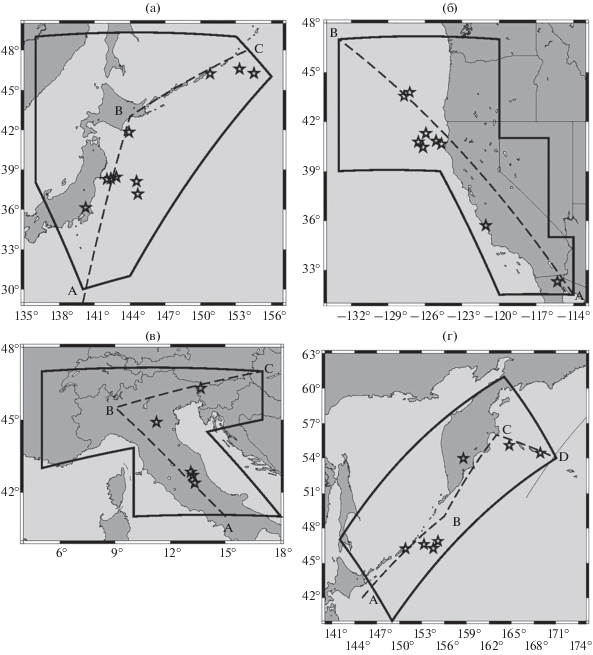
Регион Калифорния–Орегон–Невада. Границы этого региона (рис. 1б) помимо штата Калифрния, США, включают запад штата Невада, юго-запад штата Орегон, значительную часть океанической территории и небольшая северная часть Мексики. В качестве исходных данных в тесте используется каталог ANSS33. В этом каталоге в значительной степени решена проблема стыковки данных по Южной и по Центральной и Северной Калифорнии, в которых действуют независимые сети сейсмических станций.
Регион Центральные Аппенины, Альпы, Северные Динариды и долина По. Этот регион (рис. 1в) фактически охватывает территории севера Италии, а также прилегающие территории Франции, Швейцарии, Австрии, Хорватии, Словении. Первоначально в этом регионе также использовался каталог ANSS. Однако с середины 2004 г. в этом каталоге был повышен уровень минимальной магнитуды землетрясений, включаемых в каталог, для территорий за пределами США, в том числе, и в Европе, до 4.0. Поэтому в период 2004–2007 гг. для данного региона каталог пополнялся данными Европейско-Средиземноморского сейсмологического центра44, а c 2008 г. – данными бюллетеня Национального центра землетрясений Национального института геофизики и вулканологии Италии55.
Регион Восточное Средиземноморье. Для теста алгоритма в этом регионе использовался сейсмологический бюллетень Геофизического института Израиля66. Данные бюллетеня с представительной магнитудой, достаточной для теста алгоритма, охватывают достаточно большую территорию в пределах 28–36° с.ш., 32–38° в.д., включающую помимо Израиля прилегающие территории Египта, Иордании, Сирии, Ливана, а также о-в Кипр.
Регион Курилы–Камчатка. Тест в этом регионе был начат в конце 2004 г. Границы региона (рис. 1г) охватывают территории Камчатки, Командорских и Курильских островов. Наиболее полным для региона в целом является каталог ANSS, который и был использован для теста.
В каждом из рассматриваемых регионов, в тех случаях, когда не оговорено специально, используется каталог основных толчков (афтершоки исключены) с магнитудой M ≥ Mmin. Для выделения афтершоков используется хорошо известный “оконный” метод с параметрами Гарднера–Кнопова [Gardner, Knopoff, 1974].
3. МЕТОД RTP
3.1. Цепочки землетрясений
Цепочка землетрясений отражает возрастание радиуса корреляции землетрясений; качественно – это плотная, протяженная и быстро формируемая последовательность слабых и умеренных землетрясений. Определение цепочки является обобщением предвестников ROC и Accord [Заляпин и др., 2002; Keilis-Borok еt al., 2002; Shebalin et al., 2000; Zaliapin et al., 2002]. Назовем два землетрясения соседями, если их эпицентры находятся на расстоянии r или менее и если они произошли в пределах τ0по времени друг от друга. Цепочка – это последовательность землетрясений, в которой каждое землетрясение имеет хотя бы одного соседа, принадлежащего к этой последовательности, и не имеет соседей вне этой последовательности. Средняя плотность эпицентров убывает с увеличением магнитуды землетрясений. Соответственно, величина r масштабирована следующим правилом:
где $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} $ – минимальная магнитуда в паре. Отметим, что это определение может напоминать определение пары основной толчок – афтершок или форшок – основной толчок. Отличие состоит в том, что предельное пространственное расстояние определяется магнитудой не сильнейшего события, а, наоборот, слабейшего, а временной параметр не зависит от магнитуды. Условие минимальной магнитуды в паре является важным для того, чтобы цепочки отражали возросший радиус корреляции в широком диапазоне энергий. В таком определении более редкие сильные события могут образовывать пары даже на больших расстояниях, тогда как частые слабые события могут являться соседями лишь на малых расстояниях. Цепочка действительно отражает увеличение радиуса корреляции землетрясений, если она имеет достаточно большое протяжение и включает достаточно большое число эпицентров. Соответственно, рассматриваются только цепочки с достаточно большим числом элементов k ≥ k0 и диаметром (наибольшим расстоянием между элементами) l ≥ l0.При использовании полного каталога, без исключения афтершоков, описанным условиям в некоторых случаях могут удовлетворять афтершоки сильных землетрясений. Задача прогноза сильных афтершоков является отдельной независимой задачей [Воробьева, 2006; Баранов, Шебалин, 2017; 2019; Баранов и др., 2019; Шебалин, Баранов, 2019], поэтому построение цепочек землетрясений производится по каталогу с удаленными афтершоками; для каталога установлен нижний порог по магнитуде Mmin (табл. 1). Для каждого региона величина Mmin выбрана эмпирически, ее значение не ниже представительной магнитуды. Простейший метод [Gardner, Knopoff, 1974] для этих целей вполне достаточен. Для пяти регионов, в которых ведется тест алгоритма RTP, параметры цепочек приведены в табл. 1.
Таблица 1.
Значения параметров цепочек землетрясений
| Регион | M0 | Mmin | τ, сут | r0, км | с | k0 | l0, км |
|---|---|---|---|---|---|---|---|
| Хонсю–Хоккайдо–Ю. Курилы | 7.2 | 3.5 | 20 | 7.5 | 0.33 | 25 | 800 |
| Калифорния–Орегон–Невада | 6.2 | 2.9 | 20 | 6.7 | 0.35 | 6 | 185 |
| Долина По, Альпы, С. Динариды | 5.5 | 2.9 | 45 | 6.7 | 0.35 | 6 | 130 |
| Восточное Средиземноморье | 6.0 | 3.0 | 40 | 6.7 | 0.35 | 8 | 175 |
| Курилы–Камчатка | 7.2 | 4.0 | 12 | 6.7 | 0.35 | 6 | 400 |
3.2. R-окрестность цепочки землетрясений
Цепочка землетрясений – это лишь множество точек, представленных эпицентрами элементов цепочки. Чтобы определить пространственную область, связанную с цепочкой, и в которой может ожидаться сильное землетрясение, было введено определение R-окрестности цепочки [Keilis-Borok et al., 2004]. Рассмотрим все эпицентры, входящие в цепочку, не обращая внимания на их последовательность во времени, кроме первого. Найдем эпицентр, ближайший к первому, и соединим их прямым отрезком. Затем найдем эпицентр, находящийся на минимальном расстоянии к эпицентрам, уже соединенным отрезком, и соединим соответствующие точки. Процедура повторяется до тех пор, пока не будут исчерпаны все элементы цепочки. R-окрестностью цепочки назовем область, образованную объединением кругов радиуса R c центрами вдоль всех проведенных отрезков.
R-окрестность цепочки используется в алгоритме RTP как область тревоги, в которой в течение периода T после возникновения последнего элемента цепочки ожидается возникновение землетрясения магнитуды М ≥ М0. Выбранные авторами метода RTP значения М0 для пяти рассматриваемых регионов приведены в табл. 1. Величина T во всех случаях установлена равной 270 сут.
3.3. Среднесрочные предвестники
Оригинальный подход, используемый в алгоритме RTP, состоит в обратном отслеживании предвестников землетрясений. Сначала в некоторой пространственной области диагностируется более краткосрочная тревога, которая определяет границы этой области (R-окрестность цепочки), а затем в этой области анализируются среднесрочные предвестники и, если оказывается, что эти предвестники не указывают на повышенную вероятность землетрясения, то тревога не объявляется. В качестве среднесрочных предвестников используется 8 функционалов, отражающих возрастание сейсмической активности (“Сейсмическая активность”, “Сигма”, “Ускорение”, табл. 2), группирования землетрясений в пространстве и времени (“Рои”, “В-микро”), радиуса корреляции землетрясений (“Аккорд”), а также преобразование распределения магнитуд (“Возрастание магнитуды”, “Гамма”) [Keilis-Borok, 2002]. Каждый из функционалов нормирован с учетом разных размеров цепочек. Для этого вводится условие, определяющее порог по магнитуде для расчета функционалов [Keilis-Borok et al., 2002]:
где: n(M*) – среднегодовое число основных толчков с магнитудой M ≥ M*, определяемое в R-окрестности цепочки в интервале времени (t0 – 5 лет, t0 – 1 год); t0 – время начала цепочки. Для каждого из предвестников рассматривались функционалы во временной и событийных шкалах. Во временной шкале интервал накопления данных задается в виде временного интервала фиксированной длины s, а в событийной шкале в виде последовательности из заданного числа событий N. В табл. 2 приведены оба варианта.Здесь: NA – число событий в R-окрестности цепочки, удовлетворяющих условию A; Ar(t) –площадь объединения кругов радиуса r с центрами в эпицентрах с магнитудой M ≥ M* в R-окрестности цепочки во временном или событийном окне; Mkl – магнитуда l-го афтершока от k-го основного толчка. Восемь функционалов, помимо параметров цепочки, имеют в общей сложности 4 параметра. Для каждого из 8 функционалов во временной и в событийной шкалах использовалось 8 наборов параметров, приведенных в табл. 3.Таблица 2.
Формальные определения среднесрочных предвестников
| Среднесрочный предвестник | Во временной шкале | В событийной шкале |
|---|---|---|
| “Сейсмическая активность” | ${{F}_{U}}\left( {t,s} \right) = \frac{{{{N}_{{t - s \leqslant {{t}_{k}} < t}}}}}{s}$ | $\widetilde {{{F}_{u}}}\left( {{{t}_{j}},N} \right) = \frac{N}{{{{t}_{j}} - {{t}_{{j - N + 1}}}}}$ |
| “Сигма” | ${{F}_{{\Sigma }}}\left( {t,s} \right) = \mathop \sum \limits_{t - s \leqslant {{t}_{k}} < t} {{10}^{{{{M}_{k}} - M{\text{*}}}}}$ | $\widetilde {{{F}_{{\Sigma }}}}\left( {{{t}_{j}},N} \right) = \mathop \sum \limits_{k = j - N + 1}^j {{10}^{{{{M}_{k}} - M{\text{*}}}}}$ |
| “Возрастание магнитуды” | ${{F}_{M}}\left( {t,s} \right) = \frac{{\sum\limits_{t - \frac{s}{2} \leqslant {{t}_{k}} < t} {{{M}_{k}}} }}{{{{N}_{{t - \frac{s}{2} \leqslant {{t}_{k}} < t}}}}}{\text{\;}}$ – $\frac{{\sum\limits_{t - s \leqslant {{t}_{k}} < t - s/2} {{{M}_{k}}} }}{{{{N}_{{t - s \leqslant {{t}_{k}} < t - s/2}}}}}$ | $\widetilde {{{F}_{{\text{M}}}}}\left( {{{t}_{j}},N} \right) = \frac{1}{{\left[ {\frac{N}{2}} \right]}}\left( {\mathop \sum \limits_{k = j - N + 1}^{j - N + \left[ {\frac{N}{2}} \right]} {{M}_{k}} - \mathop \sum \limits_{k = j - \left[ {\frac{N}{2}} \right] + 1}^j {{M}_{k}}} \right)$ |
| “Ускорение” | ${{F}_{{\text{С}}}}\left( {t,s} \right) = \frac{{\sum\limits_{t - \frac{s}{2} \leqslant {{t}_{k}} < t} {\frac{1}{{{{t}_{k}} - {{t}_{{k - 1}}}}}} }}{{{{N}_{{t - \frac{s}{2} \leqslant {{t}_{k}} < t}}}}}{\text{\;}}--{\text{\;}}\frac{{\sum\limits_{t - s \leqslant {{t}_{k}} < t - s/2} {\frac{1}{{{{t}_{k}} - {{t}_{{k - 1}}}}}} }}{{{{N}_{{t - s \leqslant {{t}_{k}} < t - s/2}}}}}$ | $\widetilde {{{F}_{{\text{C}}}}}\left( {{{t}_{j}},N} \right) = \mathop \sum \limits_{k = j - N + 1}^{j - N + \left[ {\frac{N}{2}} \right]} \frac{1}{{{{t}_{k}}\, - \,{{t}_{{k - 1}}}}}\, - \,\mathop \sum \limits_{k = j - \left[ {\frac{N}{2}} \right] + 1}^j \frac{1}{{{{t}_{k}}\, - \,{{t}_{{k - 1}}}}}$ |
| “Рои” | ${{F}_{W}}\left( {t,s} \right) = 1 - \frac{{{{A}_{r}}\left( t \right)}}{{\pi {{r}^{2}}{{N}_{{t - s \leqslant {{t}_{k}} < t}}}}}$ | $\widetilde {{{F}_{{\text{W}}}}}\left( {{{t}_{j}},N} \right) = 1 - \frac{{{{A}_{r}}\left( {{{t}_{j}}} \right)}}{{\pi {{r}^{2}}N}}$ |
| “B-микро” | ${{F}_{{{{B}_{\mu }}}}}\left( {t,s} \right) = \mathop \sum \limits_{t - s \leqslant {{t}_{k}} < t} \mathop \sum \limits_l {{10}^{{{{M}_{{kl}}}}}}$ | $\widetilde {{{F}_{{{{B}_{\mu }}}}}}\left( {{{t}_{j}},N} \right) = \mathop \sum \limits_{k = j - N + 1}^j \mathop \sum \limits_l {{10}^{{{{M}_{{kl}}}}}}$ |
| “Аккорд” | ${{F}_{A}}\left( {t,s} \right) = \frac{{{{A}_{r}}\left( t \right)}}{{\pi {{r}^{2}}}}$ | $\widetilde {{{F}_{{\text{A}}}}}\left( {t,N} \right) = \frac{{{{A}_{r}}\left( t \right)}}{{\pi {{r}^{2}}}}$ |
| “Гамма” | ${{F}_{G}}\left( {t,s} \right) = \frac{1}{{{{N}_{{{{M}_{k}} \geqslant {{M}_{{1/2}}}}}}}}\mathop \sum \limits_{{{M}_{k}} \geqslant {{M}_{{1/2}}}} \left( {{{M}_{k}} - M{\text{*}}} \right)$ | $\widetilde {{{F}_{{\text{G}}}}}\left( {{{t}_{j}},N} \right) = \frac{1}{{{{N}_{{{{M}_{k}} \geqslant {{M}_{{1/2}}}}}}}}\mathop \sum \limits_{{{M}_{k}} \geqslant {{M}_{{1/2}}}} \left( {{{M}_{k}} - M{\text{*}}} \right)$ |
Таблица 3.
Значения параметров для предвестников
| Временная шкала | Событийная шкала | |||||||
|---|---|---|---|---|---|---|---|---|
| № | R, км | s, сут | T, годы | n* | R, км | N | T, годы | n* |
| 1 | 50 | 730 | 0.5 | 20 | 50 | 20 | 0.5 | 10 |
| 2 | 50 | 730 | 2 | 20 | 50 | 20 | 2 | 10 |
| 3 | 100 | 730 | 0.5 | 20 | 100 | 20 | 0.5 | 20 |
| 4 | 100 | 730 | 2 | 20 | 100 | 20 | 2 | 20 |
| 5 | 50 | 1800 | 0.5 | 20 | 50 | 50 | 0.5 | 10 |
| 6 | 50 | 1800 | 2 | 20 | 50 | 50 | 2 | 10 |
| 7 | 100 | 1800 | 0.5 | 20 | 100 | 50 | 0.5 | 20 |
| 8 | 100 | 1800 | 2 | 20 | 100 | 50 | 2 | 20 |
3.4. Распознавание предвестниковой цепочки
Для каждого функционала при фиксированных значениях параметра устанавливается пороговое значение на основе материала обучения – цепочек, для которых известно, происходили ли в их R-окрестности сильные землетрясения. Пусть neq – число сильных землетрясений в обучении, nN – число цепочек, в R-окрестности которых в период T сильные землетрясения не происходили. Обозначим $n_{P}^{{{{f}_{P}}}}({{C}_{P}})$ – число пропусков цели, то есть сильных землетрясений вне R-окрестностей цепочек в периоды T при значении предвестника FP ниже порога CP, а $n_{P}^{{{{f}_{a}}}}({{C}_{P}})$ – число ложных тревог, то есть цепочек со значением предвестника FP выше порога CP, но в R-окрестности которых в период T не происходили сильные землетрясения. Минимум суммарной относительной ошибки, равной $\frac{{n_{P}^{{{{f}_{P}}}}({{C}_{P}})}}{{{{n}^{{eq}}}}}$ + $\frac{{n_{P}^{{{{f}_{a}}}}({{C}_{P}})}}{{{{n}_{N}}}},$ достигается обычно на некотором интервале значений порога CP. В качестве окончательного значения порога CP принимается середина этого интервала. Для разных значений параметров пороги CP разные.
В тесте алгоритма RTP в реальном времени каждая цепочка после завершения периода T добавляется в материал обучения, и пороги пересчитываются. Таким образом, для распознавания предвестниковой цепочки используется вся информация, накопившаяся к текущему моменту времени. Для принятия решения используется простая мера распознавания образов, получившая название расстояние Хемминга [Гвишиан и др., 1980]. Информация о предвестниках представляется бинарным вектором PU размерности 128 (8 функционал в двух вариантах, во временной и в событийной шкалах, 8 наборов параметров). Каждая компонента имеет значение 1, если соответствующий функционал при соответствующих значениях параметров превышает соответствующий порог CP, и 0 в противоположном случае. Чем больше длина |PU| вектора PU (число компонент, имеющих значение 1, расстояние Хемминга), тем больше рассматриваемая цепочка “похожа” на идеальную предвестниковую цепочку. Решающее правило для отбора предвестниковых цепочек определяется условием |PU| ≥ C. Величина С в тесте алгоритма в реальном времени определяется, аналогично порогам CP, для каждой новой цепочки по материалу обучения. Для порога С используется условие: при данном пороге число ложных тревог в материале обучения равно 1/2 или, при нечетном числе цепочек в материале обучения, наибольшему значению, меньшему 1/2. Таким образом обеспечивается предполагаемая вероятность ложных тревог в тесте около 1/2 от общего числа тревог.
4. РЕЗУЛЬТАТЫ ТЕСТА АЛГОРИТМА RTP В 2004–2019 гг.
Параметры алгоритма RTP фиксированы до начала эксперимента (табл. 1 и табл. 3), за исключением пороговых значений CP для функционалов и параметра C, автоматически переопределяемых по мере увеличения материала обучения. Параллельно тестировался алгоритм полностью и отдельно его составляющая – цепочки землетрясений. Результаты теста удобно представить в виде координат (τ, η) (табл. 4) точек на диаграмме ошибок [Molchan, 1991; 2010], а также в виде пространственно-временных диаграмм (рис. 2–рис. 6). Величина τ характеризует долю пространства–времени, занятого тревогами, но учитывает, что пространственное распределение эпицентров землетрясений неравномерно [Kossobokov, Shebalin, 2003]. Эту величину можно считать также вероятностью случайного успеха прогноза [Shebalin et al., 2014] при данной модели распределения вероятности землетрясений. В качестве такой модели используется обычно сглаженное фактическое распределение эпицентров магнитудой выше заданного порога [Kossobokov, Shebalin, 2003]. В данной задаче в сглаживании нет необходимости из-за достаточно больших размеров областей тревоги (R-окрестности цепочек землетрясений); в качестве порогов по магнитуде в разных регионах используются значения из табл. 1 (колонка Mmin). Величина η – это доля пропусков цели, то есть доля землетрясений магнитудой Mm и выше (табл. 1), не попавших в пространственно-временную область тревоги относительно общего числа таких землетрясений в регионе за период теста. Для случайных прогнозов сумма τ + η близка к 1. Чем меньше эта сумма, тем ближе результаты прогнозов к идеальному. Еще одна характеристика качества прогнозов – величина max(τ, η) [Molchan, 1991].
Таблица 4.
Результаты теста алгоритма RTP и его первого этапа (цепочки землетрясений) в пяти регионах в 2003–2019 гг.
| Регион | Число целей прогноза | Алгоритм RTP | Цепочки землетрясений | ||
|---|---|---|---|---|---|
| τ | η | τ | η | ||
| Хонсю–Хоккайдо–Ю. Курилы | 8 | 0.30 | 0 | 0.43 | 0 |
| Калифорния–Орегон–Невада | 8 | 0.15 | 0.25 | 0.29 | 0.13 |
| Долина По, Альпы, С. Динариды | 5 | 0.13 | 0.2 | 0.27 | 0.2 |
| Восточное Средиземноморье | 0 | 0 | 0 | 0.004 | 0 |
| Курилы–Камчатка | 7 | 0.08 | 0.29 | 0.21 | 0.29 |
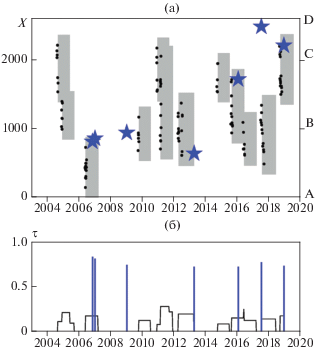
Рис. 2.
Результаты теста алгоритма RTP в регионе Хонсю–Хоккайдо–Южные Курилы, 2003–2019 гг.: (а) – пространственно-временная диаграмма тревог и землетрясений–целей прогноза. Координата х – расстояние вдоль оси проекции от точки A (рис. 1); положение точек B и C (рис. 1) отмечено справа. Серые области обозначают пространство и время тревог. Черные точки – эпицентры, сформировавшие предвестниковую цепочку. Звездочки обозначают землетрясения–цели прогноза; (б) – зависимость вероятности случайного прогноза (параметра τ) от времени, расчеты параметра τ проведены с шагом 10 дней. Вертикальными линиями показаны моменты землетрясений – целей прогноза, их высота зависит от магнитуды.
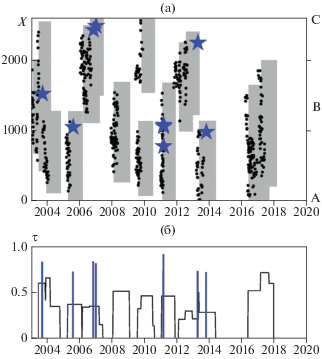
В регионе Хонсю–Хоккайдо–Южные Курилы за период теста произошло 10 землетрясений магнитудой M ≥ 7.2, 2 из которых были очевидными афтершоками землетрясения 11.03.2011 г., M = 9.1 (их время и положение эпицентров близко совпадают). Таким образом, целями прогноза мы считаем 8 землетрясений. В этот же период было диагностировано 25 цепочек землетрясений, 10 из которых были распознаны как предвестниковые. Все землетрясения произошли в области и в период тревоги. На рис. 2а показана пространственно-временная диаграмма тревог, диагностированных по алгоритму RTP, а на рис. 2б зависимость величины τ от времени; график этой величины показывает “мгновенную” вероятность случайного успеха прогнозов, то есть условную вероятность попадания эпицентра произвольного землетрясения в область текущей тревоги.
Следует отметить, что землетрясению Тохоку 11.03.2011 г., М = 9.1 менее чем за 3 дня до него предшествовал форшок магнитудой 7.4. Предвестниковая цепочка сформировалась всего за 3 дня до форшока [Шебалин, 2011; Shebalin, 2011]. Отмечу также, что цепочка, сформировавшаяся в конце 2003 г. на юге Японии, существенно заходила за формальные границы региона, и два землетрясения в сентябре 2004 г. (MW = 7.2 и 7.4), имеющие эпицентры внутри этой цепочки, оказались за формальными границами региона на расстоянии около 100 км. Границы региона были сформированы до начала эксперимента в марте 2003 г. и не менялись в течение теста.
Как было описано во Введении, тест алгоритма в регионе Калифорния–Орегон–Невада после успешного начала привел к значительному числу ложных тревог в Южной Калифорнии до 2010 г. В дальнейшем число ложных тревог сократилось, и землетрясение 4.04.2010 г. вблизи границы между Мексикой и США магнитудой 7.2, произошло в области тревоги. Уменьшение числа ложных тревог, как можно надеяться, связано с перенастройкой алгоритма по мере увеличения материала обучения. Всего за период теста в регионе произошло 9 землетрясений магнитуды 6.2 и выше, одно из которых является очевидным афтершоком, диагностировано 42 цепочки, из которых 15 распознаны на втором этапе алгоритма как предвестниковые (рис. 3). Два землетрясения произошли вне тревоги (эпицентры обоих находятся в океане).
Рис. 3.
Результаты теста алгоритма RTP в регионе Калифорния–Орегон–Невада, 2003–2019 гг. Обозначения как на рис. 2.
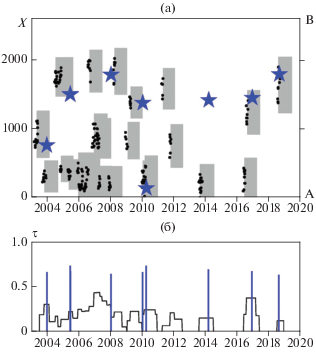
Результаты теста алгоритма в регионе Центральные Аппенины, Альпы, Северные Динариды и долина По представлены на рис. 4. За период теста с 2004 г. произошло 5 землетрясений магнитудой 5.5, диагностировано 23 цепочки, из которых 10 были распознаны как предвестниковые. Землетрясение в Аквиле 06.04.2009 г. магнитудой 6.3 не предварялось цепочкой землетрясений. Это единственный пропуск цели в тесте алгоритма в регионе.
Рис. 4.
Результаты теста алгоритма RTP в регионе Центральные Аппенины, Альпы, Северные Динариды и долина По, 2004–2019 гг. Обозначения как на рис. 2.
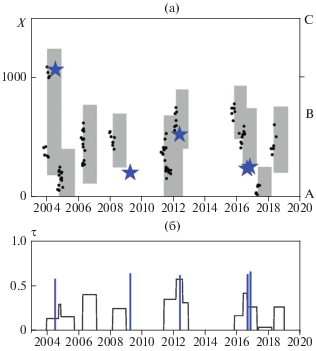
В регионе Восточное Средиземноморье за период теста была диагностирована лишь одна цепочка землетрясений, но она не была распознана как предвестниковая. Землетрясений магнитуды 6 и выше в регионе в этот период не произошло. В июне–июле 2018 г. в районе Мертвого моря в Израиле произошла серия сейсмических событий, на которую обратили внимание коллеги из Института наук о Земле, в Иерусалиме, знакомые с методикой RTP. По их запросу был произведен детальный анализ сейсмичности в тестируемом районе восточного Средиземноморья, включающего территорию Израиля с вариацией параметров алгоритма. Тесты показали, что сильное землетрясение в регионе маловероятно, несмотря на видимую активизацию сейсмичности.
Тест в регионе Курилы–Камчатка был начат в конце 2004 г. За этот период в регионе произошло 7 землетрясений магнитудой 7.2 и выше. Всего было диагностировано 38 цепочек землетрясений, на втором этапе было оставлено 12 из них. 2 землетрясения оказались вне областей тревоги (рис. 5). Одно из них, Ближне-Алеутское землетрясение 17.07.2017 г. магнитудой 7.7 произошло вблизи границы региона, и его пропуск может быть связан именно с этим фактором. Еще один пропуск – землетрясение 15.01.2009 г. магнитудой 7.4 вблизи Курильских островов. Эпицентр этого землетрясения располагался к северо-востоку от эпицентров Симуширских землетрясений 15.11.2006 г., М = 8.3 и 13.01.2007 г., М = 8.1, успешно предсказанных по алгоритму RTP.
Рис. 5.
Результаты теста алгоритма RTP в регионе Курилы–Камчатка, 2004–2019 гг. Обозначения как на рис. 2.
5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ И ВЫВОДЫ
Всего за период теста в пяти регионах произошло 28 землетрясений – целей прогноза, то есть землетрясений магнитудой не менее M0 (табл. 1). Лишь 5 из этих землетрясений оказались вне областей и периодов тревоги по алгоритму RTP. Вероятность случайного успеха в пяти регионах не превышает 0.3 (табл. 4) и в среднем составляет около 0.15. Вероятность не менее 23 верных угадываний из 28 при вероятности успеха 0.3 в схеме Бернулли очень мала. В каждом регионе сумма η + τ не превышает 0.4. Таким образом, полученные результаты теста подтверждают эффективность алгоритма RTP. Главный недостаток метода состоит в большой пространственной протяженности областей тревоги.
Первый этап алгоритма RTP – цепочки землетрясений – являются его главной компонентой. Важно убедиться, что это не просто способ каким-то определенным образом выделить пространственную область для дальнейшего анализа на втором этапе применения алгоритма, но что цепочки землетрясений могут использоваться в качестве самостоятельного прогнозного алгоритма, пусть даже менее эффективного, но дающего неслучайный результат. Результаты теста позволяют это сделать. Если в качестве областей тревоги использовать R-окрестности всех диагностированных цепочек, а периодом тревоги, как и в полном алгоритме RTP, считать 270 сут, то вне областей и периодов тревоги окажется лишь 4 землетрясения из 28. Вероятность случайного успеха τ в пяти регионах не превышает 0.43. В схеме Бернулли вероятность минимум 24 успехов в 28 испытаниях с вероятностью успеха 0.43 составляет 0.001. Сумма η + τ в пяти регионах не превышает 0.5. Это позволяет сделать вывод о неслучайности совпадения сильных землетрясений и предшествующих им индикаторов увеличения радиуса корреляции – цепочек землетрясений.
Сделанный вывод приводит к необходимости более детального исследования изменчивости радиуса корреляции сейсмичности в пространстве и времени. Необходимо также понять физическую природу таких вариаций. Наблюдения последних лет свидетельствуют о возможной значительной роли в сейсмогенезисе неупругих деформаций, “медленных” и “тихих” землетрясений, которые не фиксируются стандартными сейсмическими сетями. Сопоставление вариаций радиуса корреляции сейсмичности с полем деформаций по данным GPS/GLONASS поможет прояснить их природу.
Результаты тестов свидетельствуют о существенном, но не радикальном улучшении прогнозов по алгоритму RTP на втором этапе алгоритма – распознавании предвестниковых цепочек. В реализованной в алгоритме RTP схеме распознавание делается на основе 8 функционалов в двух формах (временная и событийная шкалы) (табл. 2) с восемью наборами параметров, определяющих пространственные и временные масштабы (табл. 3), представляемых в виде бинарного вектора размерности 128. Очевидно, что лишь небольшая доля из 128 компонент являются независимыми. Модификация алгоритма распознавания, в которой использовался бы вектор меньшей размерности с независимыми компонентами, могла бы улучшить результаты прогнозов. Один из возможных путей модификации исследовался автором в работе [Shebalin, 2018]. Идея подхода состоит в представлении прогнозов в виде зависящей от времени вероятностной модели сейсмичности, в которой разные предвестники землетрясений учитываются в виде множителей, локально увеличивающих или уменьшающих вероятность землетрясений. Множители рассчитываются по методу Differential Probability Gain [Shebalin et al., 2012; 2014]. В такой схеме взаимозависимость предвестников учитывается автоматически.
Список литературы
Баранов С.В., Шебалин П.Н. О прогнозировании афтершоковой активности. 2. Оценка области распространения сильных афтершоков // Физика Земли. 2017. № 3. С. 43–61. https://doi.org/10.7868/S0002333717020028
Баранов С.В., Шебалин П.Н. О прогнозировании афтершоковой активности. 3. Динамический закон Бота // Физика Земли. 2018. № 6. С. 129–136.
Баранов С.В., Павленко В.А., Шебалин П.Н. О прогнозировании афтершоковой активности. 4. Оценка максимальной магнитуды последующих афтершоков // Физика Земли. 2019. № 4. С. 15–32.
Воробьева И.А. Прогноз повторного сильного землетрясения. Алгоритмы прогноза землетрясений // Вычислительная сейсмология. Вып. 37. 2006. С. 181–285.
Гвишиани А.Д., Зелевинский А.В., Кейлис-Борок В.И., Кособоков В.Г. Распознавание участков Тихоокеанского пояса, где возможны землетрясения с M ≥ 8.2. Методы и алгоритмы интерпретации сейсмологических данных // Вычислительная сейсмология. Вып. 13. 1980. С. 30–43.
Заляпин И., Лиу Ж., Золлер Г., Кейлис-Борок В., Туркотт Д. К вопросу о увеличении радиуса сейсмической корреляции перед сильными землетрясениями в Калифорнии. Проблемы теоретической сейсмологии и сейсмичности // Вычислительная сейсмология. Вып. 33. (на английском языке). 2002. С. 141–161.
Молчан Г.М., Дмитриева О.Е. Идентификация афтершоков: обзор и новые подходы // Вычислительная сейсмология. 1991. Вып. 24. С. 19–50.
Смирнов В.Б. Прогностические аномалии сейсмического режима. I. Методические основы подготовки исходных данных // Геофизические исследования. 2009. Т. 10. № 2. С. 7–22.
Шебалин П.Н. Цепочки эпицентров как индикатор возрастания радиуса корреляции сейсмичности перед сильными землетрясениями // Вулканология и сейсмология. 2005. № 1. С. 3–15.
Шебалин П.Н. Методология прогноза землетрясений с периодом ожидания менее года. Алгоритмы прогноза землетрясений // Вычислительная сейсмология. Вып. 37. 2006. С. 6–180.
Шебалин П.Н. Широкомасштабная краткосрочная активизация сейсмичности перед сильнейшими землетрясениями Японии и Курил // Геофизические процессы и биосфера. 2011. Т. 10. № 1. С. 36–46.
Шебалин П.Н., Баранов С.В. О прогнозировании афтершоковой активности. 5. Оценка длительности опасного периода // Физика Земли. 2019. № 5. С. 22–37.
Baiesi M., Paczuski M. Scale–free networks of earthquakes and aftershocks // Phys. Rev. E. 2004. V. 69. № 6. https://doi.org/10.1103/PhysRevE.69.066106
Bak P., Tang C., Wiesenfeld K. Self-organized criticality // Phys. Rev. A. 1988. V. 38. P 364–374.
Bak P., Tang C. Earthquakes as a self-organized critical phenomenon // J. Geophys. Res. 1989. V. 94. P. 15635–15637.
Dieterich J.H. A constitutive law for rate of earthquake production and its application to earthquake clustering // J. Geophys. Res. 1994. V. 99. № B2. P. 2601–2618. https://doi.org/10.1029/93JB02581
Gabrielov A.M., Zaliapin I.V., Newman W.I., Keilis-Borok V.I. Colliding cascades model for earthquake prediction // Geophys. J. Int. 2000. V. 143. P. 427–437.
Gardner J.K., Knopoff L. Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian? // Bulletin of the Seismological Society of America. 1974. V. 64. № 5. P. 1363–1367.
Gutenberg B., Richter C.F. Seismicity of the Earth and Associated Phenomena, 2nd ed. Princeton, N.J.: Princeton University Press. 1954. 273 p.
Hill D.P., Reasenberg P.A, Michael A. et al. Seismicity remotely triggered by the magnitude 7.3 Landers, California, earthquake // Science. 1993. V. 260. P. 1617–1623.
Keilis-Borok V.I., Shebalin P.N. (Eds.). Dynamics of lithosphere and earthquake prediction. PEPI 111 (Special Issue). 1999. P. 179–330.
Keilis-Borok V., Ismail-Zadeh A., Kossobokov V., Shebalin P. Non-linear dynamics of the lithosphere and intermediate-term earthquake prediction // Tectonophysics. 2001. V. 338. P. 247–280.
Keilis-Borok V.I., Malinovskaya L.N. One regularity in the occurrence of strong earthquakes // J. Geophys. Res. 1964. V. 69. P. 3019–3024.
Keilis-Borok V.I. Earthquake prediction: state-of-the-art and emerging possibilities // Ann. Rev. Earth Planet. Sci. 2002. V. 30. P. 1–33.
Keilis-Borok V.I., Shebalin, P.N., Zaliapin I.V. Premonitory patterns of seismicity months before a large earthquake: Five case histories in Southern California // Proc. Natl. Ac. Sci. 2002. V. 99. P. 16562–16567.
Keilis-Borok V., Shebalin P., Gabrielov A., Turcotte D. Reverse tracing of short-term earthquake precursors // Phys. Earth Planet. Inter. 2004a. V. 145/1-4. P. 75–85.
Keilis-Borok V., Shebalin P., Aki K., Jin A., Gabrielov A., Turcotte D., Liu Z., Zaliapin I. Documented Prediction of the San Simeon Earthquake 6 Months in Advance: Premonitory Change of Seismicity, Tectonic Setting, Physical Mechanism. Seismological Society of America, Annual Meeting, Palms Spring, California, April 2004. Abstracts. 2004b. Abstract 04-291.
Kossobokov V., Shebalin P. Earthquake prediction. Nonlinear Dynamics of the Lithosphere and Earthquake Prediction / ed. V.I. Keilis-Borok and A.A. Soloviev. Springer-Verlag, Berlin-Heidelberg. 2003. P. 141–207.
Molchan G. Structure of optimal strategies in earthquake prediction // Tectonophysics. 1991. V. 193. P. 267–276.
Molchan G. Space-time earthquake prediction: the error diagrams // Pure Appl. Geophys. 2010. V. 167. № 8–9. P. 907–917. https://doi.org/10.1007/s00024-010-0087-z
Molchan G.M., Dmitrieva O.E. Aftershock identification: methods and new approaches // Geophys. J. Int. 1992. V. 109. P. 501–516. https://doi.org/10.1111/j.1365-246X.1992.tb00113.x
Narteau C., Shebalin P., Holschneider M., Le Mouël J.-L., Allègre C. Direct simulations of the stress redistribution in the scaling organization of fracture tectonics (SOFT) model // Geophys. J. Int. 2000. V. 141. P. 115–135.
Prozorov A.G., Schreider S.Yu. Real time test of the long-range aftershock algorithm as a tool for mid-term earthquake prediction in Southern California // Pure Appl. Geophys. 1990. V. 133. P. 329–347.
Sammis C.G., Smith S.W. Seismic cycles and evolution of stress correlation in cellular automaton models of finite fault networks // Pure Appl. Geophys.1999. V. 155. P. 307–334.
Shebalin P., Keilis-Borok V., Zaliapin I., Uyeda S., Nagao T., Tsybin N. Advance Short-Term Prediction of the Large Tokachi-oki Earthquake, September 25, 2003, M = 8.1 – A Case History. Earth, Planets and Space, Terrapub, Tokyo, Japan. 2004. V. 56. P. 715–724.
Shebalin P., Keilis-Borok V.I., Zaliapin I., Uyeda S., Nagao T., Tsybin N. Short-term Premonitory Rise of the Earthquake Correlation Range. IUGG2003, June 30–July 11. 2003. Sapporo, Japan. Abstracts. 2003. P. A184.
Shebalin P., Zaliapin I., Keilis-Borok V.I. Premonitory rise of the earthquakes’ correlation range: Lesser Antilles // Phys. Earth Planet. Int. 2000. V. 122. P. 241–249.
Shebalin P.N. Large-scale short-term seismicity activation prior to the strongest earthquakes of Japan and the Kurile islands // Izvestiya. Atmospheric and Oceanic Physics. 2011. T. 47. № 8. C. 922–928.
Shebalin P., Narteau C. Holschneider M. From alarm-based to rate-based earthquake forecast models // Bull. Seimol. Soc. of Am. 2012. V.1 02(1). P. 64–72.
Shebalin P., Narteau C. Depth dependent stress revealed by aftershocks // Nature Communications. 2017. V. 8. № 1317. https://doi.org/10.1038/s41467-017-01446-y
Shebalin P., Narteau C., Holschneider M., Zechar J. Combining earthquake forecast models using differential probability gains // Earth, Planets and Space. 2014. V. 66:37. P. 1–14.
Shebalin P., Baranov S. Long-Delayed Aftershocks in New Zealand and the 2016 M7.8 Kaikoura Earthquake // Pure and applied Geophysics. 2017. V. 174(10). P. 3751–3764. https://doi.org/10.1007/s00024-017-1608-9
Shebalin P. Combining Probabilistic Seismicity Models with Precursory Information. Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies, Geophysical Monograph 234, First Edition. Ouzounov D., Pulinets S., Hattori K., and Taylor P. (eds.). American Geophysical Union. John Wiley & Sons, Inc. 2018. P. 173–195.
Schorlemmer D., Gerstenberger M., Wiemer S., Jackson D.D., Rhoades D.A. Earthquake likelihood model testing // Seismol. Res. Lett. 2007. V. 78. P. 17–29.
Vorobieva I., Narteau C., Shebalin P., Beauducel F., Nercessian F., Clouard V., Bouin M. P. Multiscale Mapping of Completeness Magnitude of Earthquake Catalogs // Bulletin of the Seismological Society of America. 2013. V. 103. P. 2188–2202.
Zaliapin I., Keilis-Borok V.I., Axen G. Premonitory spreading of seismicity over the fault’s network in southern California: precursor Accord // J. Geophys. Res. 2002. V. 107(B10). P. 2221–2232.
Zoller G., Hainzl S., Kurths J. Observation of growing correlation length as an indicator for critical point behavior prior to large earthquakes // J. Geophys. Res. 2001. V. 106. P. 2167–2176.
Дополнительные материалы отсутствуют.


