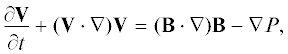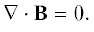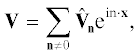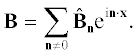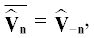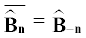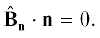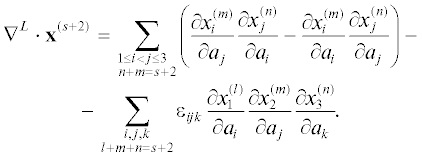Физика Земли, 2020, № 2, стр. 148-160
Численный алгоритм интегрирования по времени задач идеальной магнитогидродинамики, опирающийся на аналитичность их решений
В. А. Желиговский 1, *, О. М. Подвигина 1, **
1 Институт теории прогноза землетрясений и математической геофизики РАН
г. Москва, Россия
* E-mail: vlad@mitp.ru
** E-mail: olgap@mitp.ru
Поступила в редакцию 25.04.2019
После доработки 17.06.2019
Принята к публикации 24.06.2019
Аннотация
Доказано, что если в начальный момент скорость течения жидкости и магнитное поле – аналитические функции пространственных переменных, то решение системы трехмерных уравнений идеальной магнитогидродинамики аналитично по пространственным переменным и времени на некотором временном интервале строго положительной длины. С использованием свойства вмороженности магнитного поля построены разложения решения в эйлеровых и лагранжевых координатах в ряды Тейлора по времени. Для коэффициентов этих рядов выведены рекуррентные соотношения. Эти результаты положены в основу эйлерова и лагранжева алгоритмов численного интегрирования уравнений идеальной магнитогидродинамики по времени. Лагранжев алгоритм опробован в расчетах; в решении наблюдается образование структур меньших размерностей.
1. ВВЕДЕНИЕ
Физические условия на поверхности Земли существенно зависят от поведения вещества в пространстве, окружающем планету. Солнечный ветер – поток ионизированных частиц, выброшенных из Солнечной короны, – способен оказывать негативное воздействие как на технические устройства (спутники и средства связи), так и непосредственно на самочувствие людей. Поэтому изучение течения плазмы и электромагнитных процессов в космическом пространстве – одна из практически важных задач физики Земли. Эти процессы удовлетворяют системе уравнений идеальной магнитогидродинамики, состоящей из уравнения Эйлера, описывающего динамику течения жидкости и включающего в себя силу Лоренца, характеризующую воздействие магнитного поля на жидкость, и уравнения магнитной индукции, описывающего эволюцию во времени магнитного поля. До настоящего времени важнейшими алгоритмами для численного решения задач идеальной гидро- и магнитогидродинамики остаются численные схемы фиксированного относительно малого порядка (такие, например, как схемы Рунге–Кутта).
Разработка более эффективных алгоритмов требует лучшего понимания математических свойств и структуры решений соответствующих уравнений. Так, течения идеальной (невязкой) жидкости описываются уравнением Эйлера. С течением времени в его решениях, как правило, развиваются мелкомасштабные структуры, что приводит к неограниченному росту градиентов поля скорости, а это, в свою очередь, создает пока еще не преодоленные сложности для теоретического исследования математических свойств решений. С другой стороны, из анализа численных решений известно, что имеет место и, в некотором смысле, обратное явление: в зонах больших градиентов у изначально существенно трехмерных потоков развиваются доминирующие структуры меньших размерностей, что, в принципе, способно упростить задачу.
До сих пор неизвестно, имеет ли уравнение Эйлера (и даже уравнение Навье–Стокса, описывающее течение вязкой жидкости) глобальное (т.е. существующее при сколь угодно больших временах) решение, и единственны ли решения при данных начальных данных. Сложность этих фундаментальных вопросов связана с тем, что неизвестно, не теряют ли они с течением времени свою гладкость, или у решений возможно развитие коллапса (т.е. возникновение сингулярности) за конечное время. Для простоты далее будем рассматривать только решения периодические в пространстве. Из известного к настоящему времени, значительного массива результатов о решениях бессиловых уравнений Эйлера (см., например, [Majda, Bertozzi, 2002]) отметим следующие: если в начальный момент течение – аналитическое (по пространству) векторное поле, то оно остается аналитическим по пространственным переменным и времени, как минимум на конечном промежутке времени строго положительной длины [Benachour, 1976], а если начальное течение двумерно, то эта аналитичность гарантирована в любой момент времени [Bardos et al., 1976]. Гладкость решения влечет его единственность.
Если на идеальную жидкость не действуют никакие силы, то аналитичность по времени траекторий жидких частиц можно гарантировать на конечном интервале, даже когда начальное течение ${{{\mathbf{V}}}^{{({\text{in}})}}}$ имеет только минимальную гладкость, например, если ряд Фурье завихренности $\nabla \times {{{\mathbf{V}}}^{{({\text{in}})}}}$ сходится абсолютно [Zheligovsky, Frisch, 2014]. Уравнение Эйлера в лагранжевых переменных можно тогда один раз проинтегрировать по времени; так устанавливается факт независимости от времени т.н. инвариантов Коши [Cauchy, 1827]. Используя этот результат, в лагранжевых переменных можно построить разложение поля смещений частиц в ряд Тейлора по времени, имеющий заведомо ненулевой радиус сходимости. Это дало возможность разработать новый метод [Podvigina et al., 2016] для численного интегрирования бессилового уравнения Эйлера, в котором шаг по времени выполняется посредством суммирования ряда Тейлора.
Принадлежность решений уравнений идеальной магнитогидродинамики различным классам Жевре по пространственным эйлеровым переменным рассмотрена в работе [Cheng, Xu, 2019]; из принадлежности функции классу Жевре индекса $\alpha = 1$ следует его пространственная аналитичность. В следующем разделе мы даем простое оригинальное доказательство пространственной аналитичности решений уравнений идеальной магнитогидродинамики при условии аналитичности начальных данных. Оно основано на применении метода, предложенного в статье [Zheligovsky, 2011] и использующего идеи работ [Foias, Temam, 1989; Levermore, Oliver, 1997].
Из этого результата следует аналитичность траекторий жидких частиц и магнитного поля по времени. Как и при отсутствии магнитного поля в рассматриваемой физической системе, используя пространственные лагранжевые переменные, траектории жидких частиц можно разложить в ряд Тейлора по времени (магнитное поле оказывается подчиненным неизвестным полем, т.к. оно обладает свойством вмороженности [Моффат, 1980]). Из аналитичности решения по времени следует сходимость этого ряда. Таким образом, оказывается возможным сформулировать алгоритм для решения магнитогидродинамической задачи, аналогичный алгоритму для чисто гидродинамического случая. Отметим, что пространственная аналитичность начальных данных теперь оказывается существенным условием, т.к. в отличие от случая решений бессилового уравнения Эйлера, из-за наличия в уравнении, описывающем динамику течения жидкости, силы Лоренца, каждый последующий коэффициент в разложении решения в ряд Тейлора по времени зависит теперь от вторых пространственных производных предыдущих коэффициентов. Это явление “потери производных” оказывается существенным усложнением задачи – в чисто гидродинамическом случае его не было.
В третьем разделе статьи указанный алгоритм использован для решения трехмерной задачи идеальной магнитогидродинамики. Выводы сформулированы в последнем разделе.
2. АНАЛИТИЧНОСТЬ РЕШЕНИЙ УРАВНЕНИЙ ИДЕАЛЬНОЙ МАГНИТОГИДРОДИНАМИКИ
В этом разделе мы выводим оценки для норм Жевре–Соболева решений уравнений идеальной магнитогидродинамики в эйлеровых переменных на некотором конечном интервале времени $[0,t*)$ в предположении, что начальные данные – аналитические функции пространственных переменных.
Течение жидкости, скорость которой ${\mathbf{V}}({\mathbf{x}},t),$ в присутствии магнитного поля ${\mathbf{B}}({\mathbf{x}},t)$ описывается в эйлеровых пространственных координатах уравнениями:
(считаем, что на жидкость действует только магнитная сила Лоренца), где $P$ – давление. Жидкость предполагается несжимаемой, а магнитное поле соленоидально:В начальный момент (при $t = 0$) скорость жидкости ${{{\mathbf{V}}}^{{({\text{in}})}}}$ и магнитное поле ${{{\mathbf{B}}}^{{({\text{in}})}}}$ заданы. Считаем, что поля периодичны в пространстве с кубом периодичности ${{\mathbb{T}}^{3}} = {{[0,2\pi ]}^{3}}$ (наши результаты легко распространить на случай различных периодов по разным декартовым переменным) и имеют нулевые средние. Будет использовано их разложение в ряды Фурье:
Поскольку поля действительны, (черта сверху означает комплексное сопряжение). Условия соленоидальности (1.3)–(1.4) принимают вид Норма Жевре–Соболева пространственно-периодического векторного или скалярного поля ${\mathbf{f}}$ с коэффициентами Фурье $\mathop {\widehat {\mathbf{f}}}\nolimits_n $ определяется для $\sigma > 0$ равенством(5)
$\left| {\mathbf{f}} \right|_{{{\sigma },q}}^{2} = \sum\limits_{{\mathbf{n}} \ne 0} {{{{\left| {\mathop {\widehat {\mathbf{f}}}\nolimits_{\mathbf{n}} } \right|}}^{2}}{{{\text{e}}}^{{2{\sigma }|{\mathbf{n}}|}}}{{{\left| {\mathbf{n}} \right|}}^{{2q}}}} ,$При $\sigma = 0,$ (5) определяет норму в пространстве Соболева ${{H}_{q}}({{\mathbb{T}}^{3}}),$ которую обозначим ${{\left\| \cdot \right\|}_{q}}.$ Пусть ${{\left| \cdot \right|}_{q}}$ обозначает норму в пространстве Лебега ${{L}_{q}}({{\mathbb{T}}^{3}}).$ По теореме вложения для соболевских пространств [Берг, Oliver, 1980; Трибель, 1980], для любого положительного $q < 3{\text{/}}2$ существует константа ${{C}_{q}}$ такая, что для любой функции $f \in {{H}_{q}}({{\mathbb{T}}^{3}})$ выполнено неравенство
(6)
${{\left| f \right|}_{{{6 \mathord{\left/ {\vphantom {6 {(3 - 2q)}}} \right. \kern-0em} {(3 - 2q)}}}}} \leqslant {{C}_{q}}{{\left\| f \right\|}_{q}}.$Обозначим ${{\mathcal{P}}_{{\mathbf{n}}}}$ линейный оператор проекции трехмерного вектора на плоскость, нормальную к ${\mathbf{n}} \ne 0{\text{:}}$
Эволюция коэффициентов Фурье скорости жидкости и магнитного поля описывается уравнениями
(7.1)
$\frac{{{\text{d}}{{{{\mathbf{\hat {V}}}}}_{{\mathbf{n}}}}}}{{{\text{d}}t}} + i\sum\limits_{\mathbf{k}} {\left( {({{{{\mathbf{\hat {V}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \cdot {\mathbf{k}}){{\mathcal{P}}_{{\mathbf{n}}}}{{{{\mathbf{\hat {V}}}}}_{{\mathbf{k}}}} - ({{{{\mathbf{\hat {B}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \cdot {\mathbf{k}}){{\mathcal{P}}_{{\mathbf{n}}}}{{{{\mathbf{\hat {B}}}}}_{{\mathbf{k}}}}} \right)} = 0,$(7.2)
$\frac{{{\text{d}}{{{{\mathbf{\hat {B}}}}}_{{\mathbf{n}}}}}}{{{\text{d}}t}} - {\text{i}}{\mathbf{n}} \times \sum\limits_{\mathbf{k}} {({{{{\mathbf{\hat {V}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \times {{{{\mathbf{\hat {B}}}}}_{{\mathbf{k}}}})} = 0,$Будем считать, что при некотором $\sigma > 0$ и $s > 3{\text{/}}2$ начальные данные имеют конечные нормы ${{\left| {{{{\mathbf{V}}}^{{({\text{in}})}}}} \right|}_{{{\sigma },s}}}$ и ${{\left| {{{{\mathbf{B}}}^{{({\text{in}})}}}} \right|}_{{{\sigma },s}}}.$ Следуя [Zheligovsky, 2011], рассмотрим замену переменных
(8.1)
${{{\mathbf{\hat {V}}}}_{{\mathbf{n}}}}(t) = {{{\mathbf{\hat {v}}}}_{{\mathbf{n}}}}(t){{{\text{e}}}^{{ - {\sigma }|{\mathbf{n}}|g(p(t))}}},$(8.2)
${{{\mathbf{\hat {B}}}}_{{\mathbf{n}}}}(t) = {{{\mathbf{\hat {b}}}}_{{\mathbf{n}}}}(t){{{\text{e}}}^{{ - {\sigma }|{\mathbf{n}}|g(p(t))}}},$(8.3)
$\begin{gathered} p(t) = \left\| {{\mathbf{v}}({\mathbf{x}},t)} \right\|_{s}^{2} + \left\| {{\mathbf{b}}({\mathbf{x}},t)} \right\|_{s}^{2}, \\ {\mathbf{v}}({\mathbf{x}},t) = \sum\limits_{\mathbf{n}} {{\mathbf{\hat {v}}}(t){{{\text{e}}}^{{{\text{i}}n \cdot {\mathbf{x}}}}}} ,\,\,\,\,b({\mathbf{x}},t) = \sum\limits_{\mathbf{n}} {{{{{\mathbf{\hat {b}}}}}_{{\mathbf{n}}}}(t){\kern 1pt} {{{\text{e}}}^{{{\text{i}}n \cdot {\mathbf{x}}}}}} , \\ \end{gathered} $Легко показать, используя монотонность $g,$ что
Наша цель – доказать, что ${\mathbf{v}}$ и ${\mathbf{b}}$ ограничены в ${{H}_{s}}({{\mathbb{T}}^{3}})$ на некотором временном отрезке $[0,t*),$ где $t* > 0.$ Подстановка (8) приводит систему (7) к виду:
(9.1)
$\begin{gathered} \frac{{{\text{d}}{{{{\mathbf{\hat {v}}}}}_{{\mathbf{n}}}}}}{{{\text{d}}t}} - \sigma \left| {\mathbf{n}} \right|{{{{\mathbf{\hat {v}}}}}_{{\mathbf{n}}}}g{\kern 1pt} '(p)\frac{{{\text{d}}p}}{{{\text{d}}t}} + \\ + \,\,i\sum\limits_{\mathbf{k}} {\left( {({{{{\mathbf{\hat {v}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \cdot {\mathbf{k}}){{\mathcal{P}}_{{\mathbf{n}}}}{{{{\mathbf{\hat {v}}}}}_{{\mathbf{k}}}} - ({{{{\mathbf{\hat {b}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \cdot {\mathbf{k}}){{\mathcal{P}}_{{\mathbf{n}}}}{{{{\mathbf{\hat {b}}}}}_{{\mathbf{k}}}}} \right)} \times \\ \times \,\,{{{\text{e}}}^{{{\sigma }(|{\mathbf{n}}| - |{\mathbf{n}} - {\mathbf{k}}| - |{\mathbf{k}}|)g(p)}}} = 0, \\ \end{gathered} $(9.2)
$\begin{gathered} \frac{{{\text{d}}{{{{\mathbf{\hat {b}}}}}_{n}}}}{{{\text{d}}t}} - \sigma \left| {\mathbf{n}} \right|{{{{\mathbf{\hat {b}}}}}_{n}}g{\kern 1pt} '(p)\frac{{{\text{d}}p}}{{{\text{d}}t}} - {\text{i}}n \times \\ \times \,\,\sum\limits_k {({{{{\mathbf{\hat {v}}}}}_{{n - k}}} \times {{{{\mathbf{\hat {b}}}}}_{k}}){{{\text{e}}}^{{{\sigma }(|n| - |n - k| - |k|)g(p)}}}} = 0. \\ \end{gathered} $Скалярно умножая (9.1) и (9.2) на ${{\left| {\mathbf{n}} \right|}^{{2s}}}{{{\mathbf{\hat {v}}}}_{{ - {\mathbf{n}}}}}$ и ${{\left| {\mathbf{n}} \right|}^{{2s}}}{{{\mathbf{\hat {b}}}}_{{ - {\mathbf{n}}}}}$ соответственно и суммируя оба полученные равенства по всем ${\mathbf{n}} \ne 0,$ находим:
(10)
$\begin{gathered} \frac{{{\text{d}}p}}{{{\text{d}}t}}\left( {\frac{1}{2} - \sigma g{\kern 1pt} '(p)\left( {\left\| {{\mathbf{v}}(x,t)} \right\|_{{s + 1{\text{/}}2}}^{2} + \left\| {{\mathbf{b}}(x,t)} \right\|_{{s + 1{\text{/}}2}}^{2}} \right)} \right) - \\ - \,\,{\text{Im}}\sum\limits_{{\mathbf{n}}{\text{,}}{\mathbf{k}}} {\left( {({{{{\mathbf{\hat {v}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \cdot {\mathbf{k}})({{{{\mathbf{\hat {v}}}}}_{{\mathbf{k}}}} \cdot {{{{\mathbf{\hat {v}}}}}_{{ - {\mathbf{n}}}}}) - ({{{{\mathbf{\hat {b}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \cdot {\mathbf{k}})({{{{\mathbf{\hat {b}}}}}_{{\mathbf{k}}}} \cdot {{{{\mathbf{\hat {v}}}}}_{{ - {\mathbf{n}}}}}) - } \right.} \\ \left. { - \,\,({{{{\mathbf{\hat {b}}}}}_{{ - {\mathbf{n}}}}} \times {\mathbf{n}}) \cdot ({{{{\mathbf{\hat {v}}}}}_{{{\mathbf{n}} - {\mathbf{k}}}}} \times {{{{\mathbf{\hat {b}}}}}_{{\mathbf{k}}}})} \right){{\left| {\mathbf{n}} \right|}^{{2s}}}{{{\text{e}}}^{{{\sigma }(|{\mathbf{n}}| - |{\mathbf{n}} - {\mathbf{k}}| - |{\mathbf{k}}|)g(p)}}} = 0. \\ \end{gathered} $Если преобразовать последнее слагаемое, используя свойства векторного произведения и ортогональность (4) и делая замену индексов суммирования ${\mathbf{n}} \to - {\mathbf{k}},$ ${\mathbf{k}} \to {\mathbf{n}} - {\mathbf{k}}{\text{:}}$
По неравенству треугольника, показатель экспоненты в сумме по n и k в (10) неположителен, и она не превосходит 1. Оценим эту сумму:
(11)
$\begin{gathered} \frac{{{\text{d}}p}}{{{\text{d}}t}}\left( {\frac{1}{2} - \sigma g{\kern 1pt} '(p)\left( {\left\| {{\mathbf{v}}(x,t)} \right\|_{{s + 1{\text{/}}2}}^{2} + \left\| {\mathbf{b}} \right\|_{{s + 1{\text{/}}2}}^{2}} \right)} \right) \leqslant \\ \leqslant {{2}^{{max(s - 3{\text{/}}2,0)}}}\sum\limits_{n,k} {{{{\left| {\mathbf{n}} \right|}}^{{s + 1{\text{/}}2}}}\left( {{{{\left| {{\mathbf{n}} - {\mathbf{k}}} \right|}}^{{s - 1{\text{/}}2}}} + {{{\left| {\mathbf{k}} \right|}}^{{s - 1{\text{/}}2}}}} \right) \times } \\ \times \,\,\left( {\left| {{{{\hat {v}}}_{{n - k}}}} \right|\left| {\mathbf{k}} \right|\left| {{{{\hat {v}}}_{k}}} \right|\left| {{{{\hat {v}}}_{{ - n}}}} \right| + \left| {{{{{\mathbf{\hat {b}}}}}_{{n - k}}}} \right|\left| {\mathbf{k}} \right|\left| {{{{{\mathbf{\hat {b}}}}}_{k}}} \right|\left| {{{{\hat {v}}}_{{ - n}}}} \right| + } \right. \\ + \,\,\left. {\left| {\mathop {{\mathbf{\hat {b}}}}\nolimits_k } \right|\left| {{\mathbf{n}} - {\mathbf{k}}} \right|\left| {{{{\hat {v}}}_{{n - k}}}} \right|\left| {\mathop {{\mathbf{\hat {b}}}}\nolimits_{ - n} } \right| + \left| {\mathop {\hat {v}}\nolimits_{n - k} } \right|\left| {\mathbf{k}} \right|\left| {\mathop {{\mathbf{\hat {b}}}}\nolimits_k } \right|\left| {\mathop {{\mathbf{\hat {b}}}}\nolimits_{ - n} } \right|} \right). \\ \end{gathered} $Каждое из четырех слагаемых оценим аналогично первому из них. Очевидно,
(12)
$\begin{gathered} \sum\limits_{{\mathbf{n}},{\mathbf{k}}} {{{{\left| {\mathbf{n}} \right|}}^{{s + 1{\text{/}}2}}}\left( {{{{\left| {{\mathbf{n}} - {\mathbf{k}}} \right|}}^{{s - 1{\text{/}}2}}} + {{{\left| {\mathbf{k}} \right|}}^{{s - 1{\text{/}}2}}}} \right)} \left| {\mathop {\widehat {\mathbf{v}}}\nolimits_{{\mathbf{n}} - {\mathbf{k}}} } \right|\left| {\mathbf{k}} \right|\left| {{{{{\mathbf{\hat {v}}}}}_{{\mathbf{k}}}}} \right|\left| {{{{{\mathbf{\hat {v}}}}}_{{ - {\mathbf{n}}}}}} \right| = \\ = \,{{(2\pi )}^{{ - 3}}}\int\limits_{{{\mathbb{T}}^{3}}} {\left( {{{f}_{{s - 1{\text{/}}2}}}({\mathbf{x}}){{f}_{1}}({\mathbf{x}})\, + \,{{f}_{{s + 1{\text{/}}2}}}({\mathbf{x}}){{f}_{0}}({\mathbf{x}})} \right)} {{f}_{{s + 1{\text{/}}2}}}({\mathbf{x}}){\text{d}}{\mathbf{x}}, \\ \end{gathered} $(13)
${{f}_{q}}({\mathbf{x}},t) = \sum\limits_{\mathbf{n}} {\left| {{{{{\mathbf{\hat {v}}}}}_{{\mathbf{n}}}}(t)} \right|{{{\left| {\mathbf{n}} \right|}}^{q}}{{{\text{e}}}^{{{\text{i}}n \cdot {\mathbf{x}}}}}} $Используя неравенство Гельдера, теорему вложения Соболева (6) и равенство Парсеваля, продолжим при $s > 3{\text{/}}2$ оценку (12):
Таким образом, получаем из (10):
(14)
$\frac{{{\text{d}}p}}{{{\text{d}}t}} \leqslant {{C}_{s}}\frac{{\sqrt p }}{{ - g{\kern 1pt} '(p)}},\,\,\,\,{\text{где}}\,\,\,\,{{C}_{s}} = {{({{c}_{s}} + {{C}_{1}}{{C}_{{1{\text{/}}2}}})} \mathord{\left/ {\vphantom {{({{c}_{s}} + {{C}_{1}}{{C}_{{1{\text{/}}2}}})} {(\sigma \sqrt 8 {{\pi }^{3}})}}} \right. \kern-0em} {(\sigma \sqrt 8 {{\pi }^{3}})}}.$(Строго говоря, это неравенство выведено в предположении конечности норм ${{\left\| {{\mathbf{v}}({\mathbf{x}},t)} \right\|}_{{s + 1{\text{/}}2}}}$ и ${{\left\| {{\mathbf{b}}({\mathbf{x}},t)} \right\|}_{{s + 1{\text{/}}2}}}.$ Точное доказательство состоит в установлении неравенства (14) для приближений Фурье–Галеркина к решению – для них, очевидно, указанные нормы конечны, – а затем применении методов компактности.) Решая дифференциальное неравенство (14), находим
(15)
$\int\limits_{p(0)}^{p(t)} {\frac{{ - g{\kern 1pt} '(p)}}{{\sqrt p }}{\text{d}}p \leqslant {{C}_{s}}t} .$Это неравенство устанавливает контроль над нормами решения $p(t)$ на конечных временах $t < t{\text{*}}.$ Для оценки $t*,$ рассмотрим (15) для функций ${{g}_{{\gamma }}}(p) = {{({{p(0)} \mathord{\left/ {\vphantom {{p(0)} p}} \right. \kern-0em} p})}^{{\gamma }}}.$ В силу (8.3), функция $p(t)$ при $t > 0$ также зависит от $\gamma ,$ что будем обозначать нижним индексом $\gamma .$ Интегрируя (15) по времени от 0 до $t,$ получаем
(16)
$t < \frac{{2\gamma }}{{2\gamma + 1}}\mathop {\left( {{{C}_{s}}\sqrt {p(0)} } \right)}\nolimits^{ - 1} .$Отсюда следует
Таким образом, решение ${\mathbf{V}}(x,t),$ ${\mathbf{B}}(x,t)$ аналитично в слое ширины
при условии (16). Поскольку эти оценки выполнены при любом $\gamma > 0$ и правые части (16) и (17) растут при увеличении $\gamma ,$ получаем в пределе $\gamma \to \infty ,$ что имеет местоТеорема. Пусть поля ${{{\mathbf{V}}}^{{({\text{in}})}}}$ и ${{{\mathbf{B}}}^{{({\text{in}})}}}$ аналитичны в слое ширины $\sigma > 0$ и нормы ${{\left| {{{{\mathbf{V}}}^{{({\text{in}})}}}} \right|}_{{{\sigma },s}}}$ и ${{\left| {{{{\mathbf{B}}}^{{({\text{in}})}}}} \right|}_{{{\sigma },s}}}$ конечны при некотором $s > 3{\text{/}}2.$ Тогда решение системы (1) с такими начальными данными аналитично в слое ширины $\sigma (t) = ({{1 - t} \mathord{\left/ {\vphantom {{1 - t} {t{\text{*}}}}} \right. \kern-0em} {t{\text{*}}}})\sigma $ при любом $t < t*,$ где
Решения допускают оценку
Отметим, что построенные оценки времени и размера области аналитичности грубы, т.к. в них не учтено существенное сокращение, имеющее место, например, при вычислении векторного произведения в (1.2).
Коэффициенты разложения в конечный ряд Фурье приближения Фурье–Галеркина к решениям исходной системы (1) удовлетворяют автономной системе обыкновенных дифференциальных уравнений конечной размерности, правые части которых аналитически зависят от неизвестных коэффициентов Фурье. По теореме Коши [Петровский, 1970] эти коэффициенты являются аналитическими функциями времени. Гармоники Фурье аналитичны по пространственной переменной, поэтому каждое приближение аналитично по паре переменных $({\mathbf{x}},t)$. Поскольку (как уже указано выше) для этих приближений верны равномерные по номеру приближения оценки, аналогичные выведенным, их можно аналитически продолжить во всю область
Опираясь на выведенные априорные оценки, легко показать, что приближения Фурье–Галеркина сходятся к решению исходной системы (1) равномерно в любой компактной подобласти области аналитичности $\mathfrak{W},$ поэтому по теореме Вейерштрасса [Шабат, 1976] и их предельные поля ${\mathbf{V}}({\mathbf{x}},t)$ и ${\mathbf{B}}({\mathbf{x}},t)$ – аналитические функции пары переменных в $\mathfrak{W}.$
Лагранжевы координаты ${\mathbf{a}}$ частицы жидкости – это ее декартовы координаты в начальный момент времени. Траектории частиц ${\mathbf{x}}({\mathbf{a}},t)$ удовлетворяют обыкновенному дифференциальному уравнению:
(18)
${\mathbf{\dot {x}}} = {\mathbf{V}}({\mathbf{x}},t),\,\,\,\,{\mathbf{x}}({\mathbf{a}},0) = {\mathbf{a}},$3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ДЛЯ КОЭФФИЦИЕНТОВ РЯДОВ ТЕЙЛОРА ПО ВРЕМЕНИ
Аналитичность по времени решений уравнений идеальной магнитогидродинамики в эйлеровых или лагранжевых переменных позволяет разложить их в ряды Тейлора по времени, для коэффициентов которых можно построить рекуррентные соотношения.
Наиболее просто они выглядят для решений в эйлеровых координатах. Именно, для коэффициентов рядов Тейлора по времени
(19)
$\begin{gathered} {\mathbf{V}}({\mathbf{x}},t) = \sum\limits_{{\mathbf{n}} = 0} {{{{\mathbf{V}}}_{n}}({\mathbf{x}}){{t}^{n}}} ,\,\,\,\,P({\mathbf{x}},t) = \sum\limits_{{\mathbf{n}} = 0} {{{P}_{n}}({\mathbf{x}}){{t}^{n}}} , \\ {\mathbf{B}}({\mathbf{x}},t) = \sum\limits_{{\mathbf{n}} = 0} {{{{\mathbf{B}}}_{n}}({\mathbf{x}})\,{{t}^{n}}} \\ \end{gathered} $(20.1)
$n{{{\mathbf{V}}}_{n}}\, = \,\sum\limits_{k = 0}^{n - 1} {\left( { - ({{{\mathbf{V}}}_{k}} \cdot \nabla ){{{\mathbf{V}}}_{{n - 1 - k}}}\, + \,({{{\mathbf{B}}}_{k}} \cdot \nabla ){{{\mathbf{B}}}_{{n - 1 - k}}}\, - \,\nabla {{P}_{n}}} \right)} ,$(20.2)
$n{{{\mathbf{B}}}_{n}} = \nabla \times \sum\limits_{k = 0}^{n - 1} {{{{\mathbf{V}}}_{k}} \times {{{\mathbf{B}}}_{{n - 1 - k}}}} ,$В лагранжевых координатах уравнения (1.1) и (1.2) принимают соответственно вид:
Точка обозначает т.н. материальную производную, т.е. производную по времени при фиксированной лагранжевой координате:Уравнение (21.2) имеет следующее решение в лагранжевых переменных (см. [Моффат, 1980]):
(22)
${\mathbf{B}}({\mathbf{a}},t) = \sum\limits_{j = 1}^3 {B_{j}^{{({\text{in}})}}({\mathbf{a}})\frac{{\partial {\mathbf{x}}({\mathbf{a}},t)}}{{\partial {{a}_{j}}}}} ,$После взятия ротора по лагранжевым переменным от обеих сторон этого уравнения градиент справа исчезает, и уравнение принимает вид:
(23)
$\begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\sum\limits_{j = 1}^3 {\left( {{{\nabla }^{L}}\mathop {\dot {x}}\nolimits_j \times {{\nabla }^{L}}{{x}_{j}}} \right)} = \\ = \,\,\left. {\sum\limits_{j = 1}^3 {{{\nabla }^{L}}(({{{\mathbf{B}}}^{{({\text{in}})}}} \cdot {{\nabla }^{L}})} \left( {({{{\mathbf{B}}}^{{({\text{in}})}}} \cdot {{\nabla }^{L}}){{x}_{j}}} \right)} \right) \times {{\nabla }^{L}}{{x}_{j}} \\ \end{gathered} $Рассмотрим ряд Тейлора по времени для траекторий частиц жидкости:
(24)
${\mathbf{x}}({\mathbf{a}},t) = \sum\limits_{s = 0}^\infty {{{{\mathbf{x}}}^{{(s)}}}({\mathbf{a}}){{t}^{s}}} .$Подстановка ряда (24) в (23) дает для $s \geqslant 0$ равенство при степени ${{t}^{s}}{\text{:}}$
(25)
$\begin{gathered} (s + 1)(s + 2){{\nabla }^{L}} \times {{{\mathbf{x}}}^{{(s + 2)}}} + (s + 1) \times \\ \times \,\,\sum\limits_{n = 1}^{s + 1} {\sum\limits_{j = 1}^3 {n\left( {{{\nabla }^{L}}x_{j}^{{(n)}} \times {{\nabla }^{L}}x_{j}^{{(s + 2 - n)}}} \right)} } = \\ = \sum\limits_{n = 0}^s {\sum\limits_{j = 1}^3 {{{\nabla }^{L}}\left( {\left( {{{{\mathbf{B}}}^{{({\text{in}})}}}\, \cdot \,{{\nabla }^{L}}} \right)\left( {\left( {{{{\mathbf{B}}}^{{({\text{in}})}}}\, \cdot \,{{\nabla }^{L}}} \right)x_{j}^{{(n)}}} \right)} \right)} } \, \times \,{{\nabla }^{L}}x_{j}^{{(s - n)}}, \\ \end{gathered} $Условие несжимаемости (1.3) эквивалентно равенству $det\left\| {{{\partial {{x}_{i}}} \mathord{\left/ {\vphantom {{\partial {{x}_{i}}} {\partial {{a}_{j}}}}} \right. \kern-0em} {\partial {{a}_{j}}}}} \right\| = 1,$ из которого было получено (см. [Zheligovsky, Frisch, 2014]) соотношение:
Здесь индексы суммирования положительны: $n \geqslant 1,$ $m \geqslant 1,$ $l \geqslant 1,$ а ${{\varepsilon }_{{ijk}}}$ – единичный антисимметричный тензор.Итак, для любого индекса $s \geqslant 2$ можно вычислить ротор (25) и градиент (26) коэффициента Тейлора с этим индексом, если известны все коэффициенты с меньшими индексами. Соответственно, можно вычислить
Таким образом, можно сформулировать два метода интегрирования системы уравнений (1) по времени, использующие аналитичность решений по времени. Первый из них (который естественно назвать эйлеровым) предполагает построение рядов Тейлора (19) для решений в эйлеровых переменных, используя соотношения (20) и суммируя на каждом шагу по времени эти ряды Тейлора. Второй (который назовем лагранжевым) отличается тем, что опирается на аналитичность решений в лагранжевых переменных. В этом алгоритме приведенные выше рекуррентные соотношения позволяют последовательно вычислять коэффициенты ряда Тейлора по времени (24) для перемещения частиц жидкости ${\mathbf{x}}({\mathbf{a}},t),$ и далее следовать плану [Podvigina et al., 2016] решения бессилового уравнения Эйлера: суммируя ряд Тейлора (24), определяем перемещение частиц, в начальный момент времени находящихся в узлах регулярной пространственной сетки; в конечных точках перемещения находим скорости частиц (суммируя ряд Тейлора (24), продифференцированный по времени) и магнитное поле (22), и, используя каскадную интерполяцию ([Purser, Leslie, 1991; Podvigina et al., 2016]), находим решение ${\mathbf{V}}({\mathbf{x}},t)$ и ${\mathbf{B}}({\mathbf{x}},t)$ в новый момент времени на регулярной сетке. Эти шаги можно повторять, пока не будет достигнуто время, на которое желательно проинтегрировать систему (1), и пока решение не продемонстрирует сингулярное поведение, утеряв пространственную аналитичность (сохраняя или не сохраняя при этом пространственную гладкость).
4. ПРИМЕР РАСЧЕТА ЗАДАЧИ ИДЕАЛЬНОЙ МАГНИТОГИДРОДИНАМИКИ ЛАГРАНЖЕВЫМ АЛГОРИТМОМ
Мы провели вычисления для случайным образом выбранных начальных гладких трехмерных полей:
Из двух рассмотренных алгоритмов был выбран лагранжев, поскольку тестовые расчеты, выполненные в работе [Podvigina et al., 2016], показали, что в применении для чисто гидродинамической задачи этот алгоритм более эффективен (позволяя провести расчет решения на заданном интервале времени за меньшее время процессора). Вычисление коэффициентов временного ряда Тейлора с использованием рекуррентных соотношений (25) и (26) проводили стандартным псевдоспектральным методом с разрешением ${{256}^{3}}$ гармоник Фурье. На каждом шагу по времени суммировали 6 или 12 членов ряда Тейлора. Временной шаг выбирался автоматически из условия, что среднеквадратичная величина последнего суммируемого слагаемого (векторного поля, зависящего от лагранжевых переменных) в обрезанном ряду Тейлора равна заданной погрешности ${{10}^{{ - 12}}}.$
Расчеты проводили до времени $t = 2.$ На рис. 1 и рис. 2 показаны изоповерхности кинетической и магнитной энергий, соответственно, с шагом $ \sim 0.5$ единиц времени. (Рисунки построены для моментов окончания шагов интегрирования, в которых были превышены целевые временные пороги, кратные 0.5, поэтому эти времена не кратны 0.5 точно.) На рис. 1 видно, что с течением времени в поле скорости образуются двумерные структуры и концентрированные сгустки высокой кинетической энергии течения. В магнитном поле (рис. 2) в процессе эволюции возникают одномерные структуры (жгуты). Это согласуется с существующими представлениями о развитии в гидродинамических и магнитогидродинамических системах структур меньшей размерности.
Рис. 1.
Изоповерхности плотности кинетической энергии течения на уровне 1/3 (левый столбец) и 1/2 (правый столбец) максимума с шагом по времени ∼0.5 (точные времена указаны на рисунке).
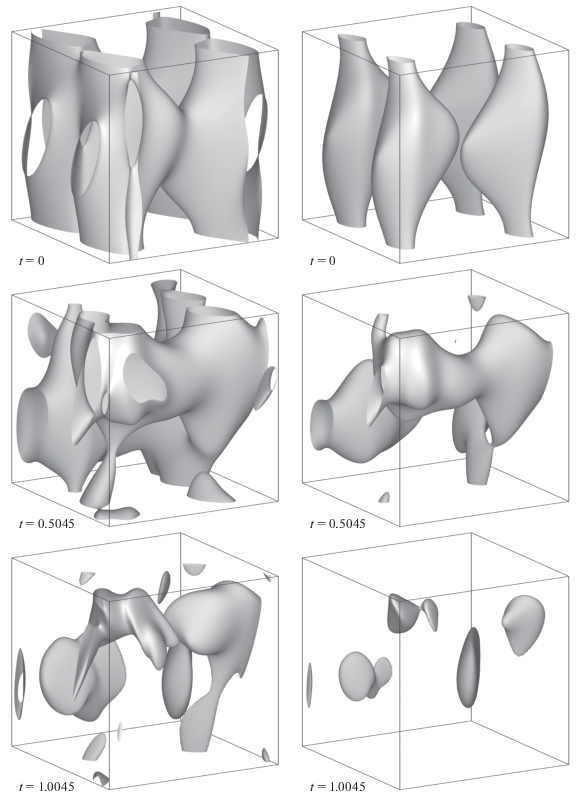
Рис. 1.
Окончание.
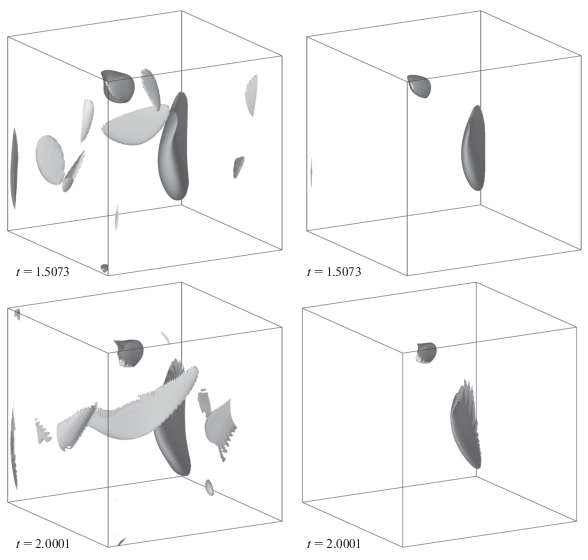
Рис. 2.
Изоповерхности плотности магнитной энергии на уровне 1/3 (левый столбец) и 1/2 (правый столбец) максимума с шагом по времени ∼0.5 (точные времена указаны на рисунке).
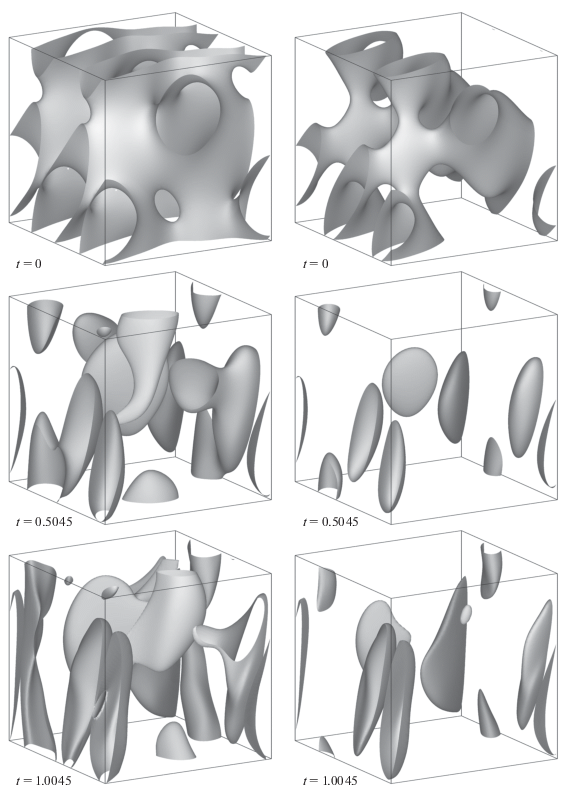
Рис. 2.
Окончание.

В табл. 1 приведены данные об изменении с течением времени максимальной плотности кинетической, $E_{{max}}^{{\text{K}}},$ и магнитной, $E_{{max}}^{{\text{M}}},$ энергий и пространственные средние этих плотностей, ${{\bar {E}}^{{\text{K}}}}$ и ${{\bar {E}}^{{\text{M}}}}$ соответственно. Максимальная плотность магнитной энергии ко времени $t = 2$ увеличивается в 1.9 раз, а кинетической энергии – в 5.4 раза (этим объясняется относительная малость объема, ограниченного приведенными на рис. 1 изоповерхностями при $t \geqslant 1.5$). Рост максимумов энергий на фоне мало меняющихся их пространственных средних также свидетельствует о формировании контрастных пространственных структур. Проверено выполнение сохранения полной энергии ${{({{{\left| {\mathbf{V}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}})} \mathord{\left/ {\vphantom {{({{{\left| {\mathbf{V}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}})} 2}} \right. \kern-0em} 2}{\text{:}}$ с течением времени эта величина несколько уменьшается (в связи с тем, что использованное в расчете пространственное разрешение ограничено и поэтому не может правильно описать развитые процессы прямого каскада энергии), однако это уменьшение не превышает 0.006 при $t = 2.$
Таблица 1.
Максимальные плотности кинетической и магнитной энергий и их пространственные средние
| Время | $E_{{max}}^{{\text{K}}}$ | $E_{{max}}^{{\text{M}}}$ | ${{\bar {E}}^{{\text{K}}}}$ | ${{\bar {E}}^{{\text{M}}}}$ |
|---|---|---|---|---|
| 0 | 3.77 | 6.48 | 0.724 | 1.160 |
| 0.5045 | 4.80 | 10.88 | 0.689 | 1.194 |
| 1.0045 | 9.25 | 10.22 | 0.697 | 1.186 |
| 1.5073 | 15.81 | 10.02 | 0.700 | 1.183 |
| 2.0001 | 20.48 | 12.58 | 0.668 | 1.215 |
Из рекуррентных соотношений (20) и (25) следует, что (в отличие от (26) и случая лагранжевых рекуррентных соотношений (25) для бессилового уравнения Эйлера) каждый коэффициент зависит от пространственных производных коэффициентов меньших индексов первого (20) или второго (25) порядка, и, таким образом, при вычислении последовательности коэффициентов неявно используются производные коэффициентов меньших индексов все более высоких порядков. Поскольку вычисление производных – численно неустойчивая процедура (неустойчивость которой может усугубляться ошибками, возникающими при интерполировании полей после завершения шага по времени с равномерной сетки лагранжевых переменных на равномерную сетку эйлеровых переменных), естественно предположить, что уже при вычислении коэффициентов с достаточно малыми индексами возможна катастрофическая потеря точности. Чтобы проверить, насколько этот эффект существенен, расчеты проведены 4 раза: была использована стандартная так называемая “двойная” точность представления чисел с плавающей запятой (данные типа real*8 Фортрана) и “четверная” (данные типа real*16), а также суммировались 6 или 12 членов ряда Тейлора по времени. При этом существенного различия в результатах расчетов не обнаружено (несмотря на то, что векторные поля – коэффициенты ряда Тейлора – оказываются велики по норме, что качественно соответствует ожидаемому проявлению влияния многократного повторного дифференцирования, возникающего в рекуррентных соотношениях при наличии магнитного поля).
На рис. 1 и рис. 2 видно, что при $t = 1.5073$ в зонах большой кривизны изоповерхностей энергии магнитного поля на них возникает “бахрома”; в меньшей степени этим поражены изоповерхности кинетической энергии. При $t = 2.0001$ это явление имеет уже весьма развитый характер – “мелкой рябью” покрыты многие изоповерхности и вдалеке от их “кромок”. Это характерное проявление недостаточности пространственного разрешения, использованного в вычислениях. Именно недостаточное разрешение, а не ограниченная точность вычислений оказывается главным препятствием для продолжения численного интегрирования уравнений идеальной магнитогидродинамики. Вместе с тем, эти два явления взаимосвязаны: численное дифференцирование рядов Фурье сводится к умножению коэффициентов на соответствующие волновые числа, а при использовании в вычислениях большего числа гармоник Фурье для увеличения пространственного разрешения растет величина этих сомножителей, что предъявляет повышенные требования к точности.
5. ЗАКЛЮЧЕНИЕ
Рассмотрена система уравнений идеальной (бездиффузионной) магнитогидродинамики, состоящей из уравнения Эйлера, включающего силу Лоренца, и уравнения магнитной индукции, описывающих эволюцию во времени соответственно течения несжимаемой жидкости и магнитного поля в трехмерном пространстве. Показано, что, если в начальный момент поле скорости жидкости и магнитное поле – аналитические функции пространственных переменных, то существует интервал времени, на котором решение этой системы уравнений аналитично по пространству и времени в эйлеровых и, как следствие, в лагранжевых переменных. Поведение магнитного поля в лагранжевых переменных описывается известным соотношением (22), характеризующим явление вмороженности магнитного поля, которое сводит систему к единственному уравнению для скорости течения.
Используя это соотношение и основываясь на аналитичности решения, мы построили разложение поля скорости течения в лагранжевых переменных в ряд Тейлора по времени. Для коэффициентов этого ряда для скорости, представленной в лагранжевых координатах, выведены рекуррентные соотношения (25), обобщающие рекуррентные соотношения для решений бессилового уравнения Эйлера [Zheligovsky, Frisch, 2014; Podvigina et al., 2016]. Для решений, представленных в эйлеровых переменных, коэффициенты ряда Тейлора удовлетворяют равенствам (20). Сформулированы лагранжев и эйлеров алгоритмы для численного интегрирования уравнений идеальной магнитогидродинамики, основанные на использовании этих рекуррентных соотношений. В принципе, они точнее стандартных алгоритмов, т.к. имеют произвольный порядок точности; какие порядки реально достижимы в вычислениях, зависит от имеющихся в наличии компьютерных ресурсов (прежде всего, оперативной памяти).
Лагранжев алгоритм опробован в расчетах. Результаты показывают, что, в согласии с существующими представлениями, в процессе временной эволюции в течении и магнитном поле образуются структуры меньших размерностей, например, жгуты магнитного поля. С течением времени энергия передается в структуры малого пространственного масштаба (прямой каскад), в решении растут величины пространственных градиентов. Для корректного описания этих процессов необходимо проводить расчеты с достаточно большим пространственным разрешением. Ограниченность используемого разрешения не позволила нам продвинуться далее $t = 2.$ В связи с этим представляется целесообразным в последующей работе исследовать вопрос, какой из двух описанных алгоритмов менее чувствителен к ограниченному пространственному разрешению на больших временных интервалах.
Успех применения лагранжева алгоритма для численного решения бессилового уравнения Эйлера основан на том, что при переходе к лагранжевым координатам в уравнении исчезает нелинейное адвекционное слагаемое $({\mathbf{V}} \cdot \nabla ){\mathbf{V}}.$ Сила Лоренца $({\mathbf{B}} \cdot \nabla ){\mathbf{B}},$ имеющая аналогичную структуру, в уравнении остается, что имеет ряд негативных с вычислительной точки зрения последствий, главное из которых – эффект потери производных. Как известно, в переменных Эльзаcсера [Elsasser, 1950] ${{{\mathbf{S}}}^{ \pm }} = {\mathbf{V}} \pm {\mathbf{B}}$ уравнения идеальной магнитогидродинамики (1) принимают вид
(27)
$\frac{{\partial {{{\mathbf{S}}}^{ + }}}}{{\partial t}}\, + \,({{{\mathbf{S}}}^{ + }} \cdot \nabla ){{{\mathbf{S}}}^{ - }} = - \nabla p,\,\,\,\frac{{\partial {{{\mathbf{S}}}^{ - }}}}{{\partial t}}\, + \,({{{\mathbf{S}}}^{ + }} \cdot \nabla ){{{\mathbf{S}}}^{ - }}\, = - \nabla p,$Список литературы
Берг Й., Лефстрем Й. Интерполяционные пространства: введение. М.: Мир. 1980. 264 с. (Пер. с англ.: Bergh J., Löfström J. Interpolation spaces. An introduction. Berlin: Springer. 1976. 207 p.)
Моффат Г.К. Возбуждение магнитного поля в проводящей среде. М.: Мир. 1980. 342 с. (Пер. с англ.: Moffatt H.K. Magnetic field generation in electrically conducting fluids. Cambridge Univ. Press. 1978. 320 p.)
Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: ИЛ, Наука. 1970. 280 с.
Трибель Х. Теория интерполяции, функциональные пространства, дифференциальные операторы. М.: Мир. 1980. 664 с. (Пер. с англ.: Triebel H. Interpolation theory. Function spaces. Differential operators. Berlin: VEB Deutscher Verlag der Wissenschaften. 1978. 528 p.)
Шабат Б.В. Введение в комплексный анализ. Часть I. Функции одного переменного. М.: Наука. 1976. 320 с. Часть II. Функции нескольких переменных. М.: Наука. 1976. 400 с.
Bardos C., Benachour S., Zerner M. Analycité des solutions périodiques de l’équation d’Euler en deux dimensions // C.R. Acad. Sci. Paris. 1976. V. 282. P. 995–998.
Benachour S. Analyticité des solutions périodiques de l’équation d’Euler en trois dimensions // C.R. Acad. Sci. Paris A. 1976. V. 283. P. 107–110.
Cauchy A.L. Sur l’état du fluide à une époque quelconque du mouvement. Mémoires extraits des recueils de l’Académie des sciences de l’Institut de France, Théorie de la propagation des ondes à la surface d’un fluide pesant d’une profondeur indéfinie (1815). Extraits des Mémoires présentés par divers savants à l’Académie royale des Sciences de l’Institut de France et imprimés par son ordre. Sciences mathématiques et physiques. Tome I. 1827. Seconde Partie. P. 33–73. [http://gallica.bnf.fr/ark:/12148/bpt6k90181x.r=Oeuvres+ completes+%27Augustin+Cauchy.langFR.]
Cheng F., Xu C.-J. On the Gevrey regularity of solutions to the 3d ideal MHD equations // Discrete and continuous dynamical systems. 2019. V. 39. P. 6485–6506. [arxiv.org/abs/1702.06840]. 2017.
Elsasser W.M. The hydromagnetic equations // Phys. Rev. 1950. V. 79. P. 183.
Foias C., Temam R. Gevrey class regularity for the solutions of the Navier–Stokes equations // J. Funct. Anal. 1989. V. 87. P. 359–369.
Levermore C.D., Oliver M. Analyticity of solutions for a generalized Euler equation // J. Differential Equations. 1997. V. 133. P. 321–339.
Majda A.J., Bertozzi A.L. Vorticity and incompressible flow. Cambridge Univ. Press. 2002. 558 p.
Podvigina O., Zheligovsky V., Frisch U. The Cauchy–Lagrangian method for numerical analysis of Euler flow // J. Computational Physics. 2016. V. 306. P. 320–342. [arxiv.org/abs/1504.05030].
Purser R.J., Leslie L.M. An efficient interpolation procedure for high order three-dimensional semi-Lagrangian models // Mon. Weather Rev. 1991. V. 119. P. 2492–2498.
Zheligovsky V. A priori bounds for Gevrey–Sobolev norms of space-periodic three-dimensional solutions to equations of hydrodynamic type // Advances in differential equations. 2011. V. 16. P. 955–976. [arxiv.org/abs/1001.4237].
Zheligovsky V., Frisch U. Time-analyticity of Lagrangian particle trajectories in ideal fluid flow // J. Fluid Mech. 2014. V. 749. P. 404–430. [arxiv.org/abs/1312.6320].
Дополнительные материалы отсутствуют.
Инструменты
Физика Земли