Физика Земли, 2020, № 2, стр. 21-28
Определение станционных аномалий времен пробега телесейсмических волн по обменным волнам
1 Институт физики Земли РАН им. О.Ю. Шмидта
г. Москва, Россия
2 Федеральный исследовательский центр комплексных исследований Арктики РАН
г. Архангельск, Россия
* E-mail: ima@ifz.ru
Поступила в редакцию 18.02.2019
После доработки 11.07.2019
Принята к публикации 07.10.2019
Аннотация
В статье рассмотрены два метода оценки станционных аномалий времен пробега телесейсмических первичных и вторичных волн. В обоих методах используются времена пробега обменных фаз, образованных на верхней границе переходной зоны мантии. В первом методе используются непосредственно времена пробега обменных волн, во втором оценка искомых параметров выполняется на основе простой двухслойной модели. Оба подхода дают сравнимые значения для коэффициента корреляции между станционными аномалиями поперечных и продольных волн. Использование модели усложняет вычисления, однако позволяет непосредственно получить оценки средних значений сейсмических параметров мантии. Для иллюстрации были использованы данные наблюдений для северной части Финляндии.
ВВЕДЕНИЕ
Станционные аномалии (иногда используется термин станционная поправка) времен прихода телесейсмических волн S и P определяются как разница времени прихода соответствующей фазы на станцию и средним временем прихода этой фазы, типичным для исследуемого региона. Практическое измерение поправок $\delta {{t}_{S}}$, $\delta {{t}_{P}}$ позволяет определить параметры a и b регрессионного соотношения между ними:
Эти параметры привлекаются для анализа свойств верхней мантии. Идея использования отношений станционных поправок первичных и вторичных волн коротко можно изложить так [Hales, Doyle, 1967]: сравним два соседних региона, в первом из которых мантийные скорости продольных и поперечных волн имеют значения ${{v}_{{P,0}}}$ и ${{v}_{{S,0}}}.$ Пусть во втором регионе эти скорости отличаются на небольшие величины $\delta {{v}_{P}}$ и $\delta {{v}_{S}}$ и равны соответственно ${{v}_{{P,0}}} - \delta {{v}_{P}}$ и ${{v}_{{S,0}}} - \delta {{v}_{S}}$. Обозначим буквой L путь, который проходит волна в каждом из регионов, будем считать его одинаковым в обоих случаях. В линейном приближении разница времен пробега волны во втором регионе по сравнению с первым составит $\delta {{t}_{P}} = {{L\delta {{v}_{P}}} \mathord{\left/ {\vphantom {{L\delta {{v}_{P}}} {v_{{P,0}}^{2}}}} \right. \kern-0em} {v_{{P,0}}^{2}}}$ для P-волн, и $\delta {{t}_{S}} = {{L\delta {{v}_{S}}} \mathord{\left/ {\vphantom {{L\delta {{v}_{S}}} {v_{{S,0}}^{2}}}} \right. \kern-0em} {v_{{S,0}}^{2}}}$ для волн S (в этих оценках мы пренебрегли вкладом геометрии распространения лучей, что не всегда правомерно [Hales, Herrin, 1972]). Таким образом, имеем:
Первоначально для определения значений коэффициентов линейной регрессии a использовались прямые измерения времен прихода телесейсмических волн (см., напр., [Hales, Doyle, 1967]). Однако измерения времен прихода S-волн связаны со значительными техническими трудностями, поэтому для определения запаздывания этих фаз зачастую прибегают к косвенным методам. Так, в работе [Souriau, Woodhouse, 1985] времена прихода вторичных волн определялись на основе математического моделирования. В работе [Vinnik et al., 1999] невязки времен прихода S-волн определялись по обменным волнам, образованным на границах переходной зоны мантии. Существенным достоинством использования обменных волн является то, что в определении невязки времени пробега фигурирует не средняя модель, а стандартная модель IASP91. В работах [Vinnik et al., 2009; 2016] показано, что в ряде регионов кроме прямой обменной волны P410s удается выделить кратную обменную волну P2p410s (см. рис. 1). Измеряя времена прихода обеих волн, мы можем определить невязки прихода как волн S, так и волн P, а также искомый коэффициент регрессии $a = {{\delta {{t}_{S}}} \mathord{\left/ {\vphantom {{\delta {{t}_{S}}} {\delta {{t}_{P}}}}} \right. \kern-0em} {\delta {{t}_{P}}}}.$
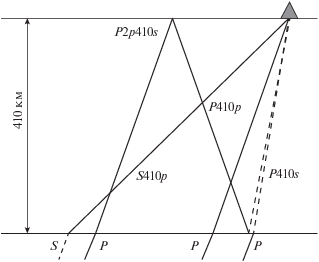
Рис. 1.
Лучевая схема фаз, обсуждаемых в статье: прямая волна P410p – продольная волна, преломленная на границе 410 км; P410s – прямая обменная волна, результат конверсии P в S на границе 410 км; P2p410s – кратная обменная волна, образованная преломлением волны P на границе 410 км, отражением от свободной поверхности и конверсией в S-волну при отражении от границы 410 км; S410p – обменная волна, результат конверсии из S в P на границе 410 км. Продольные волны изображены сплошной линией, поперечные – пунктиром.
В первой части данной работы на основе последовательного кинематического анализа уточнена связь между станционными аномалиями обменных и прямых волн, вычислен коэффициент регрессии a, а также выполнена оценка погрешности его определения. Во второй части на основании простой модели приведена оценка значений средних сейсмических параметров верхней мантии. Параметры модели определяются из условия, что расчетные времена пробега обменных волн должны совпадать с наблюдаемыми значениями. Такое построение может быть выполнено различными способами (см, напр., [Sengupta, Julian, 1978; Romanowicz, Cara, 1980; Souriau, Woodhouse, 1985; Vinnik et al., 1999]). Здесь мы ограничились простейшей двухслойной моделью, которая, тем не менее, позволяет выполнить необходимые оценки. В качестве демонстрации будут использованы данные по северной части Финляндии, представленные в работе [Vinnik et al., 2016].
КИНЕМАТИКА
В основе определения времен прихода прямой и кратной обменных волн от мантийной границы 410 км лежит процедура, предложенная в работе [Vinnik, 1977], в которой соответствующие фазы выделяются суммированием большого числа сейсмограмм разных событий. Для выделения прямой обменной волны, как правило, достаточно сложить трассы нескольких десятков событий, зарегистрированных на одной станции. Чтобы надежно выявить кратную фазу, необходимо перейти к суммированию десятков записей с нескольких станций [Vinnik et al., 2009]. Как правило, станции удалены друг от друга на 50–100 км, а область распространения кратной обменной волны составляет приблизительно 350 км (см. рис. 1). Поэтому сама возможность наблюдения этой фазы подразумевает значительную степень латеральной однородности мантии.
Как уже отмечалось во Введении, для иллюстрации мы будем использовать данные, полученные для северной Финляндии в работе [Vinnik et al., 2016]. В этом регионе обработка сейсмограмм позволяет выделить четыре обменные волны. Первая из них (время прихода приблизительно 5 с) образуется на границе Мохо. Три оставшиеся – мантийные фазы. Во-первых, это первичная обменная волна P410s от верхней границы переходной зоны на глубине 410 км со временем прихода ${{T}_{1}} = 43$ с. Во-вторых, обменная волна, образованная на границе 660 км, время прихода 67 с, в данной работе она не используется. Наконец, кратная обменная волна P2p410s, время прихода ${{T}_{2}} = 130.5$ с. За начало отсчета времени принят момент прихода исходной фазы Pp.
Наша задача состоит в том, чтобы, используя измеренные времена пробега первичной и кратной обменных волн от границы 410 км, определить время пробега прямых волн продольных ${{T}_{P}}$ и поперечных ${{T}_{S}}$ от той же границы до поверхности. Точнее говоря, мы будем искать не сами времена пробега, а соответствующие станционные аномалии:
Связь времен пробега обменных волн с временами пробега прямых (продольных и поперечных) волн определяется соотношениями:
(1)
$\begin{gathered} {{T}_{1}} = {{T}_{S}}\left( {{{p}_{1}}} \right)~\,\, - \,\,{{T}_{P}}\left( {{{p}_{0}}} \right) + \delta {{\tau }_{1}}, \\ {{T}_{2}} = {{T}_{S}}\left( {{{p}_{2}}} \right)~\,\, + 2~{{T}_{P}}\left( {{{p}_{2}}} \right)~\,\, - ~\,\,{{T}_{P}}\left( {{{p}_{0}}} \right) + \delta {{\tau }_{2}}. \\ \end{gathered} $Здесь явно указана зависимость от лучевого параметра p, и определены величины
которые равны разнице времен пробега двух P-волн от единого источника до глубины 410 км, одна из которых имеет лучевой параметр ${{p}_{0}},$ а другая – ${{p}_{k}}$. В рамках заданной модели, в нашем случае – это IASP91, лучевой параметр исходной волны ${{p}_{0}}$ (луч “Pp” на рис. 1) можно вычислить непосредственно, по заданному эпицентральному расстоянию ${{\Delta }_{0}}$. Чтобы оценить лучевые параметры обменных волн (лучи “P410s” и “P2p410s” на том же рисунке), с помощью формулы(2)
${{\Delta }_{1}} = {{\Delta }_{0}} + \delta {{\Delta }_{S}},~\,\,\,\,~{{\Delta }_{2}} = {{\Delta }_{0}} + \delta {{\Delta }_{S}} - 2\delta {{\Delta }_{P}}.$Здесь ${{\Delta }_{0}}$, ${{\Delta }_{1}}$, ${{\Delta }_{2}}$– эпицентральные расстояния падающей волны P, обменной P410s и кратной обменной волны P2p410s соответственно. В практически интересных случаях отличие величин лучевых параметров ${{p}_{1}}$, ${{p}_{2}}$ от ${{p}_{0}}$ невелико:
Поэтому формулы для времен пробега ${{T}_{1}}$, ${{T}_{2}}$ можно упростить, используя разложение в ряд Тейлора до линейных слагаемых:
(3)
$\begin{gathered} \left| {T_{S}^{'}\left( {{{p}_{0}}} \right) - \hat {T}_{S}^{'}\left( {{{p}_{0}}} \right)} \right| \sim O\left( {\delta {{p}_{1}}} \right), \\ ~\left| {T_{P}^{'}\left( {{{p}_{0}}} \right) - \hat {T}_{P}^{'}\left( {{{p}_{0}}} \right)} \right| \sim O\left( {\delta {{p}_{2}}} \right). \\ \end{gathered} $Перейдем от соотношений между временами пробега к соотношениям между невязками. Для этого из обеих частей уравнений (1) вычтем из каждого слагаемого время пробега соответствующей волны, рассчитанное по стандартной модели:
Для этих величин в линейном приближении по приращению медленностей $\delta {{p}_{k}},$ с учетом формул (3), получаем:
(4)
$\begin{gathered} \delta {{t}_{S}}\left( 0 \right) \approx \delta {{t}_{S}}\left( {{{p}_{0}}} \right)~\sqrt {1 - p_{0}^{2}~\bar {v}_{S}^{2}} = \\ = \sqrt {1 - p_{0}^{2}\bar {v}_{S}^{2}} ~~{{\left( {\delta {{T}_{2}} + \delta {{T}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {\delta {{T}_{2}} + \delta {{T}_{1}}} \right)} 2}} \right. \kern-0em} 2}, \\ \delta {{t}_{P}}\left( 0 \right) \approx \delta {{t}_{P}}\left( {{{p}_{0}}} \right)\sqrt {1 - p_{0}^{2}\bar {v}_{P}^{2}} = \\ = \sqrt {1 - p_{0}^{2}\bar {v}_{P}^{2}} ~{{\left( {\delta {{T}_{2}} - \delta {{T}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {\delta {{T}_{2}} - \delta {{T}_{1}}} \right)} 2}} \right. \kern-0em} 2}, \\ a = {{\delta {{t}_{S}}\left( 0 \right)} \mathord{\left/ {\vphantom {{\delta {{t}_{S}}\left( 0 \right)} {\delta {{t}_{S}}\left( 0 \right)}}} \right. \kern-0em} {\delta {{t}_{S}}\left( 0 \right)}} = \\ = {{\sqrt {1 - p_{0}^{2}~\bar {v}_{S}^{2}} ~\left( {\delta {{T}_{2}}\left( {{{p}_{0}}} \right) + \delta {{T}_{1}}} \right)} \mathord{\left/ {\vphantom {{\sqrt {1 - p_{0}^{2}~\bar {v}_{S}^{2}} ~\left( {\delta {{T}_{2}}\left( {{{p}_{0}}} \right) + \delta {{T}_{1}}} \right)} {\sqrt {1 - p_{0}^{2}\bar {v}_{S}^{2}} }}} \right. \kern-0em} {\sqrt {1 - p_{0}^{2}\bar {v}_{S}^{2}} }}~ \times \,\, \\ \times \,\,\left( {\delta {{T}_{2}}\left( {{{p}_{0}}} \right) - \delta {{T}_{1}}} \right). \\ \end{gathered} $Множители с радикалом введены, чтобы учесть разницу хода лучей. Мы использовали следующие средние скорости сейсмических волн в модели IASP91: ${{\bar {v}}_{P}} \approx 8.3$ км/с, ${{\bar {v}}_{S}} \approx 4.5~$ км/с. Усреднение проводилось по глубине от 0 до 410 км. Формально полученные выражения (4) решают поставленную задачу, однако использовать их непосредственно нельзя. Значение регрессионного коэффициента a, рассчитанное по этим формулам, существенно зависит от точности задания входных данных. При подстановке двух разных наборов входных данных, каждый из которых лежит в пределах погрешности измерений, можно получить значения параметра a, отличающиеся на порядок и даже имеющие разный знак. Математически это обусловлено наличием в знаменателе последней из формул (4) разницы величин, которые сравнимы и между собой, и с погрешностью измерений. Чтобы оценить значения коэффициента регрессии a и невязок $\delta {{t}_{P}}$ и $\delta {{t}_{S}},$ мы воспользовались вероятностным моделированием.
Сводка числовых значений величин для северной Финляндии [Vinnik et al., 2016], использованных в расчетах, приведена в табл. 1. Входящие в формулы (4) величины изменялись случайным образом. Значения ${{T}_{1}}$, ${{T}_{2}}$ и ${{p}_{0}}$ выбирались независимо, с помощью генератора псевдослучайных чисел. Мы использовали значения, равномерно распределенные вокруг средних значений в пределах, определяемых погрешностями измерений. В процессе моделирования полное число комбинаций параметров менялось от 104 до 5 × 106. Начиная приблизительно с 5 × 104 форма распределения перестает изменяться и приобретает вид, изображенный на рис. 2 (гистограммы “1”). Полученные распределения позволяют сделать статистические оценки искомых величин и их доверительные интервалы, в качестве которых были использованы медиана и интерквартиль распределений. Средние величины и доверительные интервалы приведены в табл. 2. Станционная аномалия первичной волны $\delta {{t}_{P}}$ совпадает с вычисленной в работе [Vinnik et al., 2016], в то время как аномалия волны S, а следовательно, и коэффициент корреляции оказались меньше. На наш взгляд, указанное расхождение вызвано тем, что в цитированной работе ошибочно учтены слагаемые, превышающие точность в принятом приближении (линейном по приращению лучевого параметра $\delta p$).
Таблица 1.
Лучевые параметры и времена пробега фаз обменных волн для северной части Финляндии по данным работы [Vinnik et al., 2016]
| Фаза | Медленность, с/град |
Погрешность, с/град | Время вступления, с | Время вступления по IASP91, с | Погрешность, с |
|---|---|---|---|---|---|
| Pms | 6.4 | 0.15 | 5.0 | – | 0.1 |
| P410s | 6.23 | 0.15 | 43.0 | 44.1 | 0.2 |
| P2p410s | 6.44 | 0.15 | 130.5 | 132.1 | 0.3 |
| S410P | 10.40 | 0.30 | 50.7 | 51.9 | 0.3 |
Примечания: начало отсчета времени соответствует приходу основной волны; Pms – обменная волна, образованная на границе Мохоровичича; обозначения остальных фаз соответствуют рис. 1.
Рис. 2.
Плотность распределения вероятности для невязок времен пробега: P‑волн ($\delta {{t}_{P}}$), S-волн ($\delta {{t}_{S}}$) и коэффициента регрессии a (${{\delta {{t}_{S}}} \mathord{\left/ {\vphantom {{\delta {{t}_{S}}} {\delta {{t}_{P}}}}} \right. \kern-0em} {\delta {{t}_{P}}}}$); 1 – результат численного моделирования на основе кинематических соотношений; 2 – результаты расчета, но выполненного с использованием двухслойной модели.
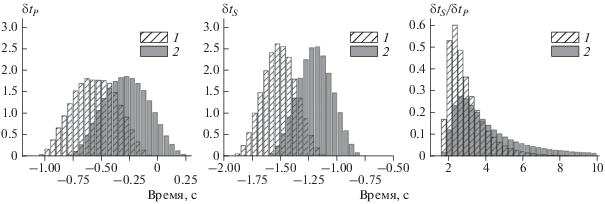
Таблица 2.
Результаты расчета станционных поправок и их отношения
| $\delta {{t}_{P}}$ | $\delta {{t}_{S}}$ | ${{\delta {{t}_{S}}} \mathord{\left/ {\vphantom {{\delta {{t}_{S}}} {\delta {{t}_{P}}}}} \right. \kern-0em} {\delta {{t}_{P}}}}$ | |
|---|---|---|---|
| [Vinnik et al., 2016] | $ - 0.6$ | $ - 2.0$ | 3.2 |
| Кинематика | $ - 0.6 \pm 0.3$ | $ - 1.5 \pm 0.2$ | $2.3 \pm 1.2$ |
| Модель | $ - 0.3 \pm 0.3$ | $ - 1.2 \pm 0.2$ | $2.8 \pm 1.6$ |
Формулы (4) исчерпывают возможности, предоставляемые простыми кинематическими соображениями, для дальнейшего анализа необходимо использование модели среды.
МОДЕЛЬ
Рассмотрим латерально однородную среду с переменными по глубине сейсмическими скоростями ${{v}_{P}} = {{v}_{P}}\left( x \right)$ и ${{v}_{S}} = {{v}_{S}}\left( x \right).$ Пусть нам известно время прохождения нескольких фаз с глубины ${{d}_{1}}$ до глубины ${{d}_{2}}.$ Построим модель этой среды для этого промежутка глубин в виде однородного слоя толщиной $H = {{d}_{2}} - {{d}_{1}}$. Сейсмические скорости $\left\langle {{{v}_{P}}~} \right\rangle $ и $\left\langle {{{v}_{S}}~} \right\rangle $ в слое выберем так, чтобы времена пробега соответствующих фаз через слой совпадали с истинными значениями. Введенные таким образом скорости можно рассматривать как результат усреднения. Процедура усреднения аналогична определению средней скорости в кинематике, где она рассчитывается как полный путь, деленный на время его прохождения. Поэтому будем называть результат такого усреднения кинематическим средним.
С другой стороны, рассматривая сейсмические скорости как материальные параметры, их среднее значение на промежутке глубин $\left[ {{{d}_{1}},{{d}_{2}}} \right]$ можно определить соотношением:
Очевидно, что для геофизического анализа интерес представляют именно такие величины. Определенные последней формулой средние скорости ${{\bar {v}}_{{P,S}}}$, вообще говоря, не совпадают со средними скоростями $\left\langle {{{v}_{{P,S}}}~} \right\rangle $, рассчитанными из кинематических соображений. Однако если на промежутке $\left[ {{{d}_{1}},{{d}_{2}}} \right]$ изменение скоростей ${{v}_{{P,S}}}\left( x \right)$ мало
(5)
$\begin{gathered} v = {{v}_{0}}\left( {1 + q\left( x \right)} \right),~\,\,\,\,{{v}_{0}} = v\left( {{{d}_{1}}} \right) = {\text{сonst}}, \\ ~~\underline {\left| {q\left( x \right)} \right|} \ll 1, \\ \end{gathered} $В то же время, при кинематическом определении средней скорости имеем:
То есть, в данном случае имеет место усреднение обратных скоростей. Если вариации скорости в слое подчиняются условию (5), то:
Отсюда следует искомое приближенное равенство $\bar {v} \approx v,$ которое, в частности, означает возможность интерпретации параметров модели, построенной по временам пробега волн, как усредненные значения параметров среды.
При построении модели будем исходить из времен пробега следующих фаз – прямой и кратной обменных волн P410s и P2p410s. Кроме того, здесь мы добавим к рассмотрению обменные волны, образованные при конверсии из волны S в волну P [Farra, Vinnik, 2000] (луч “S410p” на рис. 1]). Так как в интересующем нас интервале глубин на границе Мохо происходит резкое изменение скоростей, то будем исходить из двухслойной модели. Первый слой описывает кору, а второй – мантию от границы Мохо до верхней границы переходной зоны, расположенной на глубине 410 км. Времена пробега прямой и кратной обменных волн через однородный слой толщины h определяются соотношениями:
(6)
$\begin{gathered} {{\tau }_{1}}\left( {h,{{v}_{S}},{{v}_{P}},p} \right) = h~\left( {v_{S}^{{ - 1}}\sqrt {1 - {{p}^{2}}v_{S}^{2}} - v_{P}^{{ - 1}}\sqrt {1 - {{p}^{2}}v_{P}^{2}} } \right), \\ {{\tau }_{2}}\left( {h,{{v}_{S}},{{v}_{P}},p} \right) = h~\left( {v_{S}^{{ - 1}}\sqrt {1 - {{p}^{2}}v_{S}^{2}} + v_{P}^{{ - 1}}\sqrt {1 - {{p}^{2}}v_{P}^{2}} } \right). \\ \end{gathered} $Предположим, что в коре скорости продольных и поперечных волн совпадают со средними коровыми значениями в IASP91 и равны ${{v}_{{P,C}}} = 6.1~$ км/с, ${{v}_{{S,C}}} = 3.5$ км/с. Тогда мощность первого, верхнего слоя ${{h}_{C}}$ можно определить по времени пробега обменной волны, образованной на Мохо. Мощность мантии определяется соотношением ${{h}_{M}} = 410 - {{h}_{C}}.$ Для севера Финляндии, используя данные из табл. 1, получаем значения мощностей коры и мантии для нашей модели ${{h}_{C}} = 40~\,\,{\text{км}},\,\,{{h}_{M}} = 370{\text{\;км}}.$
Скоростные характеристики мантии определяются по временам пробега обменных волн от границы 410 км, которые мы обозначили как ${{T}_{1}}$ и ${{T}_{2}}$, а также временем пробега обменной волны S410P, которое мы обозначим ${{T}_{3}}$, а соответствующий лучевой параметр – ${{p}_{3}}$. Таким образом, используя формулы (7), получаем систему уравнений:
Индексами “C” и ”M” помечены величины, относящиеся к коре и мантии соответственно. Из-за ошибок при измерении времен пробега фазы ${{T}_{i}}~$ ($i = 1,2,3$) и при определении кажущихся медленностей ${{p}_{i}}$ эта система уравнений в общем случае не имеет точного решения. Поэтому искомые параметры определялись минимизацией функционала:
Как и в предыдущем разделе, чтобы оценить распределение параметров воспользуемся методом Монте-Карло, только теперь необходимо варьировать не только значения времен прихода фаз ${{T}_{1}},\,\,{{T}_{2}},\,\,{{T}_{3}},$ но и величину лучевых параметров ${{p}_{0}},{{p}_{3}}$. Значения для всех пяти параметров по-прежнему выбирались случайно, на основе равномерного распределения вблизи средних значений в пределах соответствующей погрешности (см. табл. 1). Лучевой параметр кратной обменной волны ${{p}_{2}}$ определялся на основании текущего значения ${{p}_{0}}$ по формулам (2). Созданный таким образом набор параметров использовался при минимизации функционала $\Phi $ методом Левенберг–Марквардта из библиотеки ALGLIB [Bochkanov, ALGLIB]. После получения результата – значений параметров ${{v}_{{S,M}}},{{v}_{{P,M}}}$, вычислялись синтетические времена пробега обменных волн $T_{i}^{{{\text{syn}}}}\left( {i = 1,2,3} \right).$ Если отличие всех трех величин от наблюденных значений не превышало соответствующую ошибку ${{\sigma }_{i}}$, то такое решение сохранялось для дальнейшего анализа, в противном случае решение отбрасывалось. При построении плотности распределения вероятности было использовано ${{10}^{7}}$ наборов входных параметров, около 40% полученных моделей были отброшены. Как и в предыдущем упражнении, при увеличении числа начальных моделей форма распределения практически перестает меняться, начиная с ${{10}^{5}}$ моделей.
Распределение значений невязок и коэффициента корреляции изображены на рис. 2 (гистограммы “2”), средние значения и доверительные интервалы приведены в табл. 2. Мы видим, что формы распределения невязок практически совпадают с кривыми, полученными на основе кинематического рассмотрения, но средние значения стали меньше по абсолютной величине. Эти отличия связаны с тем, что, используя двухслойную модель, мы получили возможность разделить время пробега волн через кору и мантию, в то время как кинематический анализ проводился без поправки за кору. Значение отношения невязок изменилось незначительно, но существенно вырос соответствующий доверительный интервал.
На рис. 3 изображены гистограммы с плотностью распределения вероятностей значений средних по мантии величин, их числовые значения равны (в скобках приведены значения, рассчитанные по модели IASP91):
Рис. 3
Плотности функций распределения средних значений упругих параметров в мантии: ${{{{v}_{P}}} \mathord{\left/ {\vphantom {{{{v}_{P}}} {{{v}_{S}}}}} \right. \kern-0em} {{{v}_{S}}}}$, ${{v}_{S}},$ ${{v}_{P}}$. Значения, соответствующие стандартной модели IASP91, отмечены вертикальными линиями.
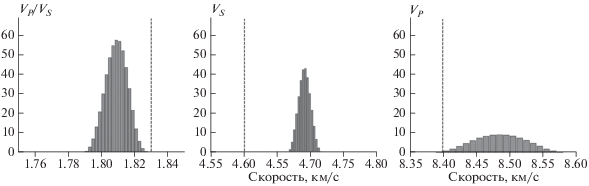
Из рисунка видно, что наиболее точно определяется отношение ${{{{v}_{P}}} \mathord{\left/ {\vphantom {{{{v}_{P}}} {{{v}_{S}}}}} \right. \kern-0em} {{{v}_{S}}}}$, которое для северной Финляндии заметно ниже стандартного значения, отмеченного на рисунке вертикальной пунктирной линией. Средние мантийные скорости ${{\bar {v}}_{P}}$ и ${{\bar {v}}_{S}}$ также заметно превышают значения, следующие из стандартной модели. Полученные результаты, в целом, согласуются с результатами, полученными на основе детального анализа данных обменных волн, проведенного в работе [Vinnik et al., 2016].
ЗАКЛЮЧЕНИЕ
Проведенный анализ показал, что оба метода определения станционных аномалий продольных и поперечных волн по данным обменных волн, образованных на верхней границе переходной зоны мантии, приводят к сравнимым значениям отношения невязок времен пробега. Использование сейсмической модели позволяет естественным образом учесть поправки за кору, сделать непосредственные оценки средних значений параметров мантии. В то же время, в ряде приложений, например, в задаче инверсии волновых форм приемных функций, предпочтение следует отдать данным, основанным на непосредственно измеренных величинах.
Список литературы
Cleary J., Hales A.L. An analysis of the travel times of P waves to North American Stations, in the distance range 32° to 100° // Bulletin of the Seismological Society of America. 1966. V. 56. № 2. P. 467–489.
Farra V., Vinnik L.P. Upper mantle stratification by P and S receiver functions // Geophysical J. International. 2000. V. 141. № 3. P. 699–712.
Hales A.L., Doyle H.A. P and S Travel Time Anomalies and their Interpretation // Geophysical J. Royal Astronomical Society. 1967. V. 13. № 4. P. 403–415.
Hales A.L., Herrin E. Travel times of seismic waves. The nature of the solid earth. McGraw-Hill New York, NY. 1972. P. 172–215.
Kennett B.L., Engdahl E.R. Traveltimes for global earthquake location and phase identification // Geophysical J. International. 1991. V. 105. № 2. P. 429–465.
Sengupta M.K., Julian B.R. Radial variation of compressional and shear velocities in the Earth’s lower mantle // Geophysical J. International. 1978. V. 54. № 1. P. 185–219.
Snoke J.A. Traveltime Tables for iasp91 and ak135 // Seismological Research Letters. 2009. V. 80. № 2. P. 260.
Robertson G.S., Woodhouse J.H. Comparison of P and S station corrections and their relationship to upper mantle structure // J. Geophysical Research: Solid Earth. 1997. V. 102. № B12. P. 27355–27366.
Romanowicz B., Cara M. Reconsideration of the relations between S and P Station anomalies in North America // Geophysical Research Letters. 1980. V. 7. № 6. P. 417–420.
Souriau A., Woodhouse J.H. A worldwide comparison of predicted S-wave delays from a three-dimensional upper mantle model with P-wave station corrections // Physics of the Earth and Planetary Interiors. 1985. V. 39. № 2. P. 75–88.
Vinnik L.P. Detection of waves converted from P to SV in the mantle // Physics of the Earth and Planetary Interiors. 1977. V. 15. № 1. P. 39–45.
Vinnik L.P., Chevrot S., Montagner J.-P., Guyot F. Teleseismic travel time residuals in North America and anelasticity of the asthenosphere // Physics of the Earth and Planetary Interiors. 1999. V. 116. № 1–4. P. 93–103.
Vinnik L.P., Oreshin S.I., Kosarev G.L., Kiselev S.G., Makeyeva L.I. Mantle anomalies beneath southern Africa: evidence from seismic S and P receiver functions // Geophysical J. International. 2009. V. 179. № 1. P. 279–298.
Vinnik L.P., Kozlovskaya E., Oreshin S.I., Kosarev G.L., Piiponen Katerina, Silvennoinen Hanna. The lithosphere, LAB, LVZ and Lehmann discontinuity under central Fennoscandia from receiver functions // Tectonophysics. 2016. V. 667. P. 189–198.
Bochkanov S. ALGLIB, доступно онлайн: http://www. alglib.net/
Дополнительные материалы отсутствуют.


