Физика Земли, 2020, № 2, стр. 69-88
Граничные значения параметров строения пустотного пространства петроупругих моделей карбонатных пород
М. Ф. Гасеми 1, *, **, И. О. Баюк 1, ***
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
* E-mail: mfgh_110@ifz.ru
** E-mail: mfgh_110@mail.ru
*** E-mail: ibayuk@yandex.ru
Поступила в редакцию 27.11.2018
После доработки 24.03.2019
Принята к публикации 25.03.2019
Аннотация
Данная работа посвящена построению параметрических математических моделей эффективных упругих свойств карбонатных пород на основе теории эффективных сред (петроупругих моделей). Такие модели в последнее время особенно востребованы в разведочной геофизике, поскольку позволяют связать упругие свойства пород-коллекторов углеводородов с параметрами пустотного пространства – формой и объемной концентрацией пор, трещин, каверн и степенью их связности. Эти параметры определяют по измеренным скоростям упругих волн. Однако, как правило, число неизвестных параметров модели больше, чем число измеренных величин, и такие задачи становятся недоопределенными. В этом случае обратная задача определения параметров модели может иметь бесконечное количество решений. Ограничение искомых параметров с учетом их физического смысла и имеющихся экспериментальных данных может значительно повысить надежность полученных результатов и уменьшить область возможных решений обратной задачи. В настоящей работе были предложены новые подходы для определения возможных границ изменения неизвестных параметров моделей, которые получить на основе прямых измерений невозможно, – параметра связности пустот, трещинной пористости и аспектного отношения трещин. Корреляция между параметром связности пустот с проницаемостью позволила разработать подход для оценки возможных границ изменения параметра связности пустот, который основан на использовании уравнения Козени–Кармана. Результаты трехосных испытаний образцов пород с помощью сервогидравлического нагружающего устройства (пресса) использованы для оценки верхней границы трещинной пористости и формы трещин. Характеристики микроструктуры исследуемых пород, полученные с помощью установленных ограничений, повышают достоверность построенных петроупругих моделей карбонатных пород. Данные модели можно использовать далее для различных геофизических исследований, предполагающих наличие связи изучаемых процессов или свойств с микроструктурой пород.
ВВЕДЕНИЕ
Определение физических свойств порово-трещиноватых углеводородосодержащих пластов является весьма сложной проблемой в отрасли разведочной геофизики. Хотя многочисленные работы были посвящены этому вопросу, неопределенность по-прежнему высока даже в предлагаемых современных методах.
Существующие подходы для моделирования эффективных физических свойств горных пород на основе их микроструктурных свойств можно классифицировать на три основные категории: 1) численное моделирование на основе метода дискретного элемента; 2) цифровой керн; 3) теория эффективных сред. Численное моделирование на основе метода дискретного элемента (метод ограниченных частиц – МОЧ) был впервые предложен [Potyondy et al., 2004]. При моделировании с помощью этого метода реальная порода заменяется случайным образом упакованными сферическими зернами с различными размерами.
Метод цифрового керна позволяет измерять локальную рентгеновскую абсорбцию в небольшом цилиндрическом образце породы с типичным диаметром в несколько миллиметров или менее. Концептуально вышеупомянутый метод МОЧ можно рассматривать как идеализированную ветвь цифрового керна, однако при моделировании пористых сред с помощью цифрового керна используются более сложные и современные методы, чтобы учесть реальную форму частиц в разных масштабах. Эти подходы могут в некоторой степени заменить прямые измерения физических параметров. Этой цели они, в основном, и служат. Однако для использования этих подходов для решения задачи о сопоставлении статических и динамических модулей необходимо иметь обобщенные характеристики микроструктуры породы. Поэтому необходима разработка целого цикла статистической обработки микроструктурных параметров и установления их качественного и количественного влияния на статические и динамические модули. Для этого нужны специальные программные средства типа Abacus, Avizo Fire и т.п. Однако таковые не всегда доступны, поскольку являются довольно дорогостоящими продуктами. Данные исследования, однако, являются также основой для построения моделей эффективных сред. Методы теории эффективных сред позволяют определить разные физические свойства, такие как скорости распространения упругих волн, гидравлические, тепловые, электрические и электромагнитные транспортные свойства на основе структурных или микроструктурных свойств горных пород (в зависимости от масштаба моделирования среды) [Bayuk, Chesnokov, 1998; 2000]. В состав этих параметров входят микроморфологические характеристики зерен, кристаллов и порового пространства (размер, форма и ориентация), объемная доля и степень гидравлической связности пустот, относительное пространственное распределение пустот и зерен. Методы теории эффективных сред позволяют решать прямую и также обратную задачу для среды, содержащей произвольное количество компонентов с произвольными контрастными свойствами и произвольными концентрациями. Методы теории эффективных сред позволяют учесть систему анизотропии компонентов среды и систему анизотропии результирующей среды. На основе этих методов можно определить одни физические свойства через другие, что имеет важное значение в случае невозможности экспериментального измерения каких-либо свойств. Метод обобщенного сингулярного приближения (ОСП) теории эффективных сред применялся в работе [Bayuk et al., 2007] для определения тензора упругости глинистой слоистой водонасыщенной анизотропной среды. Компоненты тензора упругости и микроструктурные свойства глины определились по методу ОСП на основе данных дипольного акустического каротажа в работе [Bayuk et al., 2008]. Методы теории эффективных сред применялись в работе [Chesnokov et al., 2009] для исследования влияния ориентации глинистых частиц и заполненных жидкостью трещин на скорости упругих волн в породах, содержащих глинистый минерал иллит. Методы теории эффективных сред также применялись для оценки транспортных свойств, в том числе, эффективной теплопроводности [Ялаев et al., 2016a; b], гидравлической проводимости [Shahraini et al., 2010] и электропроводности [Bayuk et al., 1998].
Целью настоящей работы является построение петроупругой модели породы-коллектора в сантиметровом масштабе, т.е. в масштабе образцов, которые обычно испытывают в лабораторных условиях. Эффективные упругие свойства определяются по характеристикам составляющих, которые имеют размер несколько миллиметров и микрон. Характеристиками этих составляющих являются: объемные концентрации компонентов, параметры, характеризующие упругие свойства составляющих (модули упругости), их морфологические характеристики (форму, ориентацию, степень связности). Причем, морфологические характеристики довольно сложно измерить экспериментально. Число известных параметров модели, как правило, больше числа неизвестных параметров. Вследствие этого задача определения характеристик микроструктуры породы является недоопределенной и имеет бесконечное число решений. Следовательно, необходимо разработать методы для ограничения диапазона поиска искомых параметров. Сужение диапазона поиска приводит к повышению достоверности и снижению неопределенности результатов.
В данной работе предложен способ ограничения параметра связности пустотного пространства и трещинной пористости в моделях карбонатных пород, построенных в масштабе керна, на основе данных лабораторных экспериментов по измерению фильтрационно-емкостных свойств керна и его геомеханических испытаний с помощью сервогидравлического нагружающего устройства (пресса).
ЭКСПЕРИМЕНТЫ
Исследования образцов проводились в рамках единого экспериментально-теоретического комплекса петрофизических работ, разработанного в ИФЗ РАН [Баюк и др., 2015; Tikhotsky et al., 2018]. Для исследований были отобраны шесть полноразмерных образцов керна карбонатных пород различного генезиса и один полноразмерный керн песчаника с большой долей карбонатного цемента (>40%), которые характеризуются различными упругими свойствами. Для дальнейших исследований из полноразмерного керна были выбурены 20 цилиндрических образцов диаметром 30 мм и максимальной длиной до 75 мм (стандартные образцы). Для цилиндрических образцов определялись фильтрационно-емкостные свойства (ФЕС) – пористость и проницаемость (по газу) с помощью стандартных методик. Результаты измерений ФЕС и характеристики микроструктуры образцов представлены в табл. 1. Литологическое изучение пород проводилось на оптическом лабораторном микроскопе Leica DM EP и микрозондовом комплексе на базе растрового (сканирующего) электронного микроскопа (РЭМ) “Jeol JSM-6480LV” с комбинированной системой рентгеноспектрального микроанализа (рис. 1). Для определения минерального состава изучаемых образцов применялся метод рентгено-фазового анализа (см. табл. 2). С целью изучения неоднородности внутреннего строения образцов полноразмерного керна проведена ультразвуковая томография (УЗТ) образцов в соответствии с методикой, предложенной в патенте В.А. Петрова и Р.М. Насимова [Петров, Насимов, 2008]. При проведении томографии использовалась УЗ-установка ИФЗ РАН, позволяющая получать волновые формы, на которых с помощью специального алгоритма выделялись вступления как продольных, так и поперечных волн. Согласно этой методике, образец прозвучивается вдоль вертикальной оси образца, а также в поперечном направлении, при постепенном перемещении линии “источник– приемник” от основания образца к его верху. Прозвучивание в поперечном направлении производится для разных азимутов. На основе результатов УЗТ рассчитаны значения скоростей упругих волн и их соответствующие стандартное квадратическое отклонение (СКО), результаты представлены в табл. 3.
Таблица 1.
Общие физические и петрофизические характеристики исследуемых образцов, измеренные в лабораторных условиях. Измерения фильтрационно-емкостных свойств выполнены группой Д.В. Короста (МГУ)
| Лаб. номер образца | Длина образца, см | Диаметр образца, см | Объем образца, см3 | Давление обжима, МПа | Объем пор, см3 | Кп*, % | Кпр**, мД | ККпр***, мД | КСК**** |
|---|---|---|---|---|---|---|---|---|---|
| С1-1 | 9.034 | 2.971 | 62.61 | 3.4 | 4.783 | 7.64 | 2.124 | 1.303 | 11.626 |
| С1-2 | 9.499 | 2.97 | 65.792 | 3.3 | 4.013 | 6.10 | 0.833 | 0.431 | 16.701 |
| С2-1 | 7.202 | 2.97 | 49.895 | 3.4 | 1.964 | 3.94 | 0.107 | 0.038 | 32.841 |
| С2-2 | 6.97 | 2.97 | 48.307 | 3.4 | 1.493 | 3.09 | 0.004 | 0.001 | 83.296 |
| С3-1 | 7.74 | 2.975 | 53.788 | 3.3 | 1.034 | 1.92 | 0.09 | 0.031 | 33.698 |
| С3-2 | 7.962 | 2.975 | 55.343 | 3.3 | 1.606 | 2.90 | 0.005 | 0.001 | 79.659 |
| С3-3 | 7.221 | 2.975 | 50.192 | 3.3 | 0.759 | 1.51 | 0.063 | 0.011 | 88.37 |
| С4-1 | 6.907 | 2.097 | 47.859 | 3.2 | 1.4 | 2.93 | 0.01 | 0.002 | 69.413 |
| С4-2 | 7.136 | 2.972 | 49.506 | 3.4 | 0.932 | 1.88 | 0.004 | 0.001 | 84.748 |
| С4-3 | 9.179 | 2.97 | 63.611 | 3.2 | 1.692 | 2.66 | 0.004 | 0.001 | 87.366 |
| С4-4 | 9.256 | 2.972 | 64.233 | 3.3 | 1.486 | 2.31 | 0.007 | 0.001 | 70.748 |
| С5-1 | Нет данных по измерению | ||||||||
| С5-2 | 7.661 | 2.966 | 52.921 | 3.3 | 6.108 | 11.54 | 0.114 | 0.037 | 37.068 |
| С5-3 | 7.73 | 2.966 | 53.409 | 3.2 | 7.46 | 13.97 | 0.156 | 0.054 | 33.681 |
| С5-4 | 9.989 | 2.964 | 68.905 | 3.3 | 8.697 | 12.62 | 0.125 | 0.038 | 41.353 |
| С6-1-1 | 7.568 | 2.964 | 52.208 | 3.3 | 11.85 | 22.70 | 9.478 | 7.564 | 4.516 |
| С6-1-2 | 6.191 | 2.965 | 42.739 | 3.3 | 9.3 | 21.76 | 8.114 | 6.364 | 4.9 |
| С6-2-1 | 7.167 | 2.964 | 49.444 | 3.4 | 11.352 | 22.96 | 9.965 | 7.966 | 4.481 |
| С6-2-2 | 6.952 | 2.964 | 47.97 | 3.4 | 10.891 | 22.70 | 9.746 | 7.8 | 4.457 |
| С6-2-3 | 7.284 | 2.964 | 50.259 | 3.4 | 11.102 | 22.09 | 6.794 | 5.225 | 5.363 |
Таблица 2.
Минеральный состав исследуемых образцов
| Образец | С1-1 | С1-2 | С2-1 | C3-3 | С4-2 | С4-2-1 | С5-2 | С5-3 | С6-1-2 |
|---|---|---|---|---|---|---|---|---|---|
| Кальцит, % | 52 | 59.5 | 97.6 | 100 | Следы | Следы | 82.4 | 52 | 99.5 |
| Доломит, % | 47.5 | 40.1 | 1.3 | 0 | 37 | 33.6 | 14.5 | 34.6 | 0 |
| Иллит, % | 0 | 0 | 0.5 | 0 | 5.5 | 4.8 | 0.7 | 4 | 0 |
| Хлорит, % | 0 | 0 | 0 | 0 | 1.9 | 3.4 | 0 | 2.3 | 0 |
| Кварц, % | 0.5 | 0.4 | 0.6 | 0 | 49.9 | 48.1 | 2.4 | 7.1 | 0.5 |
| КПШ, % (Ортоклаз, санидин) | 0 | 0 | 0 | 0 | 5.8 | 10 | 0 | 0 | 0 |
Таблица 3.
Скорости упругих волн исследуемых образцов, измеренные в лабораторных условиях
| Vp, км/с | σvp* | Vs1, км/с | σvs1 | Vs2, км/с | σvs2 | |
|---|---|---|---|---|---|---|
| C1-1 | 4.78 | 0.366 | 2.94 | 0.155 | 2.70 | 0.162 |
| C1-2 | 5.09 | 0.321 | 2.97 | 0.134 | 2.82 | 0.145 |
| C2-1 | 5.47 | 0.379 | 3.12 | 0.131 | 2.95 | 0.142 |
| C2-2 | 6.04 | 0.078 | 3.18 | 0.042 | 3.02 | 0.098 |
| C3-1 | 6.09 | 0.173 | 3.25 | 0.091 | 3.05 | 0.112 |
| C3-2 | 6.27 | 0.069 | 3.26 | 0.059 | 3.13 | 0.097 |
| C3-3 | 6.26 | 0.128 | 3.29 | 0.039 | 3.11 | 0.069 |
| С4-1 | 4.90 | 0.254 | 3.14 | 0.086 | 3.03 | 0.095 |
| С4-2 | 4.95 | 0.273 | 3.22 | 0.110 | 3.06 | 0.089 |
| С4-3 | 4.43 | 0.259 | 2.99 | 0.091 | 2.83 | 0.059 |
| С4-4 | 4.87 | 0.241 | 3.21 | 0.093 | 3.09 | 0.081 |
| С5-1 | 3.54 | 0.078 | 2.22 | 0.033 | 2.15 | 0.039 |
| С5-2 | 3.53 | 0.109 | 2.20 | 0.046 | 2.12 | 0.049 |
| С5-3 | 3.33 | 0.080 | 2.08 | 0.049 | 2.01 | 0.057 |
| С5-4 | 3.60 | 0.183 | 2.22 | 0.092 | 2.12 | 0.092 |
| С6-1-1 | 3.72 | 0.118 | 2.19 | 0.062 | 2.11 | 0.060 |
| С6-1-2 | 3.78 | 0.068 | 2.25 | 0.045 | 2.17 | 0.070 |
| С6-2-1 | 3.78 | 0.135 | 2.20 | 0.046 | 2.12 | 0.046 |
| С6-2-2 | 3.75 | 0.139 | 2.22 | 0.042 | 2.13 | 0.053 |
| С6-2-3 | 3.81 | 0.131 | 2.24 | 0.063 | 2.16 | 0.058 |
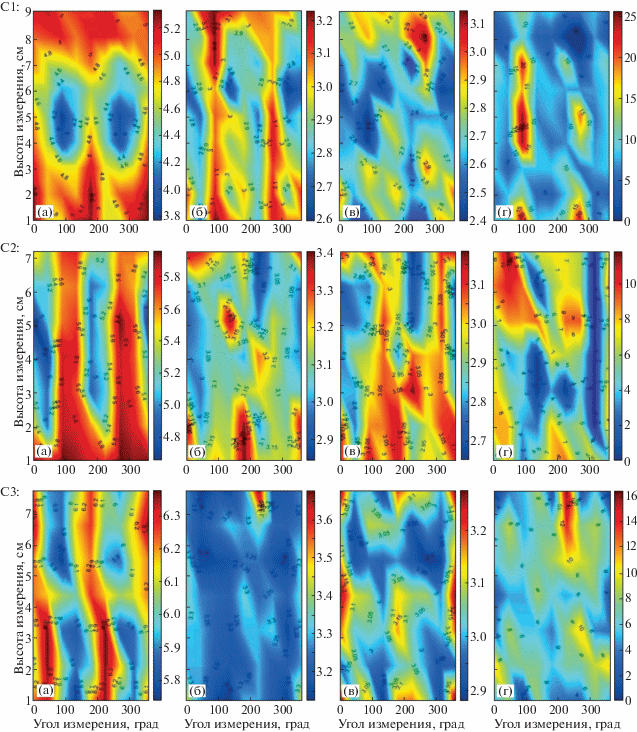
УЗТ позволяет определить степень неоднородности и тип анизотропии породы в масштабе образца. Тип анизотропии определяется путем сравнения характера поведения скоростей упругих волн с таковыми в кристаллах с известным типом анизотропии. Результаты УЗТ представлены на pис. 2.
ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ – ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ УПРУГИХ СВОЙСТВ
На основе анализа микроструктуры породы в разных масштабах были построены параметрические математические модели эффективных упругих свойств для исследуемых образцов. Основой такого моделирования является теория эффективных сред, которая позволяет в аналитической форме связать измеряемые физические свойства породы с параметрами ее микроструктуры. Для построения моделей пород, представленных образцами керна С1, С2, С4, С5, была использована модель двойной пористости (“Модель I”). Предполагалось, что пустотное пространство представлено пустотами двух видов – порами и трещинами. Для оолитового известняка, представленного керном С6, на основании анализа микроструктуры была построена математическая модель (“Модель II”), в основу которой положена иная модельная среда. Считалось, что модельная среда представлена двумя материалами: 1) трещиновато-пористой карбонатной вмещающей матрицей и 2) высокопористыми оолитами. Вторая среда (оолиты) в виде квазиизометричных включений находится в первой среде. Для выражения связи между эффективным тензором упругости и параметрами внутреннего строения среды использовался метод ОСП [Шермергор, 1977; Баюк, 2011]. Формула метода ОСП для определения эффективного тензора упругости произвольного типа анизотропии С* имеет вид (в тензорной форме):
(1)
${\mathbf{C}}* = \left\langle {{\mathbf{C}}\left( {\mathbf{r}} \right):{{{\left[ {{\mathbf{I}} - {\mathbf{\Gamma }}:\left( {\delta {\mathbf{C}}\left( {\mathbf{r}} \right)} \right)} \right]}}^{{ - {\mathbf{1}}}}}} \right\rangle :{{\left\langle {{{{\left[ {{\mathbf{I}} - {\mathbf{\Gamma }}:\left( {\delta {\mathbf{C}}\left( {\mathbf{r}} \right)} \right)} \right]}}^{{ - {\mathbf{1}}}}}} \right\rangle }^{{ - {\mathbf{1}}}}}.$В формуле (1) треугольные скобки означают объемное усреднение, которое проводится по всем компонентам породы, имеющим разные модули упругости, форму и ориентацию. Знак “:” обозначает операцию свертки тензоров. Далее даны пояснения к членам, входящим в формулу (1), в индексной форме (все индексы принимают значения от 1 до 3):
(2)
$\begin{gathered} \delta {{С}_{{ijkl}}}\left( {\mathbf{r}} \right) \equiv {{C}_{{ijkl}}}\left( {\mathbf{r}} \right) - C_{{ijkl}}^{C}, \\ {{\Gamma }_{{kmln}}} = \frac{1}{4}\left( {{{{\tilde {a}}}_{{klnm}}} + {{{\tilde {a}}}_{{mlnk}}} + {{{\tilde {a}}}_{{knlm}}} + {{{\tilde {a}}}_{{mnlk}}}} \right), \\ {{{\tilde {a}}}_{{kmln}}} = \frac{1}{{4\pi }}\int\limits_0^{2\pi } {\int\limits_0^\pi {n{}_{{mn}}\Lambda _{{kl}}^{{ - 1}}\sin \theta d\theta d\varphi } } , \\ {{\Lambda }_{{kl}}} \equiv C_{{kmln}}^{C}{{n}_{{mn}}},\,\,\,\,{{n}_{{mn}}} \equiv {{n}_{m}}{{n}_{n}}, \\ {{n}_{1}} = \frac{1}{{{{a}_{1}}}}\sin \theta \cos \varphi ,\,\,\,\,{{n}_{2}} = \frac{1}{{{{a}_{2}}}}\sin \theta \sin \varphi , \\ {{n}_{3}} = \frac{1}{{{{a}_{3}}}}\cos \theta . \\ \end{gathered} $В формуле (1) С (или соответствующее выражение с индексами в формуле (2)) – тензор упругости каждой компоненты (4-го ранга); r – радиус-вектор произвольной точки в объеме тела; I – единичный тензор 4-го ранга; а1, а2, а3 – полуоси эллипсоидов, моделирующих включения; ${{{\mathbf{С}}}^{С}}$ – тензор упругости тела сравнения, которое является однородным; ${\mathbf{\Gamma }}$ – симметризованная вторая производная тензора Грина тела сравнения. Согласно теории, выбор тела сравнения может быть произволен. Это позволяет выбрать тело сравнения в таком виде, чтобы учесть основные особенности взаимного расположения неоднородностей в породе. Выбор тензора упругости тела сравнения в виде ${{{\mathbf{С}}}^{С}} = \left( {1 - f} \right){{{\mathbf{C}}}^{m}} + f{{{\mathbf{C}}}^{{{\text{fluid}}}}},$ где ${{{\mathbf{С}}}^{С}}$, ${{{\mathbf{C}}}^{m}}$ и ${{{\mathbf{C}}}^{{{\text{fluid}}}}}$ – тензоры упругости тела сравнения, матрицы и флюида; а f – эмпирический параметр, показывающий степень связности порового пространства, позволяет рассматривать различные типы микроструктуры – от изолированных включений в минеральной матрице до экзотического случая, соответствующего эллипсоидальным частицам минерального вещества, окруженных флюидом.
Детали построенных петроупругих моделей представлены в работе [Гасеми, Баюк, 2018a; b].
Общий подход к определению параметров пустотного пространства
Построенные модели пород включают следующие параметры микроструктуры: коэффициент связности порового пространства (f), трещинную пористость (ϕс), аспектное отношение пор (αпор) и аспектное отношение микротрещин (αс). Эти параметры для исследованных в данной работе образцов были инвертированы из данных эксперимента. Заметим, что для оолитового известняка эти параметры были разными для трещиновато-пористой карбонатной вмещающей матрицы и высокопористых оолитов.
Для оценки параметров, представляющих характеристики микроструктуры, мы применили метод оптимизации прямого поиска [Nelder et al., 1965]. В нашем случае число неизвестных параметров, представляющих характеристики микроструктуры больше, чем число известных параметров (измеренные скорости упругих волн в атмосферных условиях). Это означает, что задача является недоопределенной. Для недоопределенной задачи число решений бесконечное. Ограничение диапазона поиска для каждого параметра может значительно повысить точность его оценки. В данной работе ограничения на искомые параметры вводились на основе анализа их физического смысла и имеющихся измеренных физических характеристик.
Ограничение параметра связности порового пространства (f-параметр)
Согласно теоретическим построениям, параметр f отражает связность пустотного пространства и, как показали результаты численного моделирования, проведенного нами, является одним из доминирующих параметров предложенных моделей при его высоких значениях (>0.6). Степень связности, в свою очередь, зависит от многочисленных параметров, включая пористость, размер и форму пор, содержание глины, напряженное состояние, поровое давление, тип жидкости, степень флюидонасыщения и т.д. Наряду с другими параметрами модели этот параметр определяет связь между упругими и транспортными свойствами пористых сред [Bayuk, Chesnokov, 1998; Chesnokov et al., 2010; Jiang et al., 2012]. В работе [Jiang, 2013] показано, что, строго говоря, параметр связности пустотного пространства является тензором второго ранга и прямо пропорционален тензорному коэффициенту Био–Гассмана α, который является тензором второго ранга. Имеет место соотношение ${\mathbf{f}} = {\mathbf{\alpha }}:{{({\mathbf{{\rm I}}} - {\mathbf{\Gamma }}:\delta {\mathbf{C}}]}^{{ - 1}}}.$ В этой же работе показано, что параметр связности пропорционален значению гидравлической проницаемости. В данной работе мы считали, что этот параметр является числом, значение которого соответствует шаровой части тензора второго ранга f, что вполне приемлемо для изотропных сред.
Большинство имеющихся публикаций, посвященных исследованию характеристик транспорта флюида в карбонатных породах, представляют описание и количественную оценку влияния текстурных и седиментологических параметров на зависимость проницаемости от пористости. Сложное строение и высокая степень неоднородности карбонатных пород, унаследованные от их комплексного постседиментационного диагенеза и метадиагенеза, приводит к значительным разбросам в эмпирических корреляционных зависимостях петрофизических свойств, таких как корреляция пористости и проницаемости [Ehrenberg et al., 2006; Gu et al., 2017]. Поскольку для карбонатных пород на основе представленного литературного обзора сложно найти связь между значением коэффициента общей пористости и проницаемости, мы предполагаем, что существует положительная корреляция коэффициента связности f и отношения проницаемости (k) к пористости ϕ. Отношение k/ϕ характеризует степень связности порового пространства и включает в себя структурные и седиментологические параметры, влияющие на пористость и проницаемость.
Для дальнейшего изучения гидравлических транспортных свойств исследуемых образцов и их зависимости от структурных и седиментологических параметров применялось полуэмпирическое уравнение Козени–Кармана [Carman, 1937]. В предположении, что карбонатная среда состоит из пучка изогнутых капиллярных труб с постоянной длиной и площадью поперечного сечения, уравнение Козени–Кармана позволяет вычислять проницаемость k из известной пористости ϕ и радиусов устьев пор. Проницаемость пропорциональна квадрату радиуса отдельных трубок (устьев пор) – d [Mavko et al., 1997]:
(3)
$k = \frac{{{{{\left( {\phi - {{\phi }^{{{\text{перк}}}}}} \right)}}^{3}}{{d}^{2}}}}{{36{{K}_{0}}{{\tau }^{2}}{{{\left( {1 - \phi + {{\phi }^{{{\text{перк}}}}}} \right)}}^{2}}}}$,Метод Данхэма применялся нами для классификации карбонатных образцов (для которых имеются в наличии изображения РЭМ – 8 образцов) по составу скелета и ее текстуре (см. табл. 4). В табл. 4 также представлены средние значения размера пор и макрокристаллов кальцита получены по анализу изображения РЭМ. Для изучаемых пород геометрический фактор и “пористость перколяции” были оценены с помощью метода N-мерных сеток (N – число параметров модели, который равняется 2 для данного случая, включая “пористость перколяции” и геометрический фактор), в узлах которых решена прямая задача. Узлы сеток являются набором неизвестных параметров уравнения (3) ( 1 ≤ K0 ≤ 3 и $0 \leqslant {{\phi }^{{{\text{перк}}}}} \leqslant \phi $) [Carman, 1937]). Параметр извилистости является функцией от размера и формы зерен и пустот, степени цементации и других седиментологических свойств. Однако существуют более простые формулы для оценки этого параметра на основе теории перколяции. Вид этих уравнений представлен далее. С помощью этого метода можно получить довольно много решений для совокупностей неизвестных параметров уравнения, по которым затем вычисляют статистические характеристики параметров (средние значения, матрицы ковариаций). Этот способ решения обратной задачи применяют, когда нет априорной информации о неизвестных параметрах или объем ее недостаточен для применения методов оптимизации [Баюк, 2013]. Результаты оценки неизвестных параметров уравнения Козени–Кармана представлены в табл. 5. На основе определений, представленных выше для геометрического фактора B и “пористости перколяции” ϕперк, оценка этих параметров может дать нам представление о морфологических характеристиках порового пространства и их степени связности.
Таблица 4.
Текстурные и микроморфологические характеристики исследуемых образцов, полученные на основе описаний изображений РЭМ
| Образец | Класс. Данхэма | Dпор, мм | Dзерен, мм | Vмик, % | ϕ, % | k, мД | k/ϕ |
|---|---|---|---|---|---|---|---|
| С1-1 | Разнозернистый биоспарит | 0.125–2.0 | 1.25 | 1 | 7.64 | 1.303 | 0.1705 |
| С1-2 | Разнозернистый биоспарит | 0.125–0.4 | 0.3–1.25 | 1 | 6.10 | 0.431 | 0.0707 |
| С2-1 | Ископаемый биомикрит | 0.06–2.5 | 0.06–0.6 | 90 | 3.94 | 0.038 | 0.0097 |
| С3-3 | Рыхлый биомикрит | 0.06–0.4 | 0.0025–0.02 | 80 | 1.51 | 0.011 | 0.0073 |
| С5-2 | Плотный биомикрит | 0.06–0.5 | 0.06–0.125 | 70 | 11.54 | 0.037 | 0.0032 |
| С5-3 | Плотный биомикрит | 0.05–0.1 | 0.06–0.126 | 50 | 13.97 | 0.054 | 0.0039 |
| С6-1-1 | Плотный оомикрит | 0.06–0.25 | 0.125 | 18 | 22.70 | 7.564 | 0.3332 |
| С6-2-1 | Плотный оомикрит | 0.06–0.26 | 0.125 | 20 | 22.96 | 7.966 | 0.3463 |
Таблица 5.
Параметры уравнения Козени–Кармана, полученные с помощью метода N-мерной сетки
| Образец | K0 | σk | ϕперк | σперк | τ | στ |
|---|---|---|---|---|---|---|
| C1-1 | 1.20 | 0.030 | 3.05 | 0.001 | 7.42 | 0.810 |
| C1-2 | 1.24 | 0.075 | 2.52 | 0.093 | 8.67 | 1.200 |
| C2-1 | 1.65 | 0.012 | 1.33 | 0.052 | 9.16 | 0.390 |
| C3-3 | 1.00 | 0.001 | 0.002 | 0.007 | 8.13 | 0.240 |
| C5-2 | 1.78 | 0.006 | 8.51 | 0.005 | 19.13 | 0.843 |
| C5-3 | 1.83 | 0.085 | 10.62 | 0.210 | 19.25 | 0.613 |
| C6-1-1 | 1.59 | 0.014 | 15.16 | 0.890 | 8.56 | 0.210 |
| C6-2-1 | 1.28 | 0.016 | 15.71 | 0.690 | 9.10 | 0.640 |
В настоящей работе данные о проницаемости и пористости были использованы для получения ограничений на параметр f. С точки зрения физической сути процесса фильтрации увеличение пористости должно приводить к увеличению проницаемости, поэтому отношение проницаемости к пористости в какой-то мере характеризует степень связности пустотного пространства. Основываясь на этой идее, отношение проницаемости к пористости было условно разделено на три общие категории: 0–10, 10–50 и более 50, которые в нашей терминологии представляют собой слабосвязанное, довольно связанное и хорошо связанное поровое пространство соответственно. На основании результатов исследования чувствительности модели к параметру f [Гасеми, Баюк, 2018a; b], возможная область изменения этого параметра для каждого образца была классифицирована следующим образом на три группы:
1. Слабосвязанное поровое пространство, k/ϕ < 10, 0.0 < f <0.6;
2. Довольно связанное поровое пространство, 10 < k/ϕ < 50, 0.6 < f < 0.9;
3. Хорошо связанное поровое пространство, 50 < k/ϕ, 0.9 < f < 1.0.
Результаты классификации образцов представлены в табл. 6. Затем, на основании построенной петроупругой модели была решена обратная задача по определению ее микроструктурных параметров для исследуемых образцов с учетом вышеуказанной классификации и соответствующих ограничений на параметр f. Как указано ранее, для решения обратной недоопределенной задачи использован метод нелинейной оптимизации прямого поиска.
Таблица 6.
Классификация исследуемых образцов для определения ограничений на параметр связности (f-параметра)
| Образец | ϕ, % | k, мД | k/ϕ | Категория | f-параметр |
|---|---|---|---|---|---|
| С1-1 | 7.64 | 2.124 | 27.8010 | 1 | 0.6 < f < 0.8 |
| С1-2 | 6.10 | 0.833 | 13.6580 | 1 | 0.6 < f < 0.8 |
| С2-1 | 3.94 | 0.107 | 2.7185 | 2 | f < 0.6 |
| С2-2 | 3.09 | 0.004 | 0.1294 | 2 | f < 0.6 |
| С3-1 | 1.92 | 0.09 | 4.6802 | 2 | f < 0.6 |
| С3-2 | 2.90 | 0.005 | 0.1723 | 2 | f < 0.6 |
| С3-3 | 1.51 | 0.063 | 4.1667 | 2 | f < 0.6 |
| С4-1 | 2.93 | 0.01 | 0.3419 | 2 | f < 0.6 |
| С4-2 | 1.88 | 0.004 | 0.2125 | 2 | f < 0.6 |
| С4-3 | 2.66 | 0.004 | 0.1503 | 2 | f < 0.6 |
| С4-4 | 2.31 | 0.007 | 0.3025 | 2 | f < 0.6 |
| С5-2 | 11.54 | 0.114 | 0.9877 | 2 | f < 0.6 |
| С5-3 | 13.97 | 0.156 | 1.1168 | 2 | f < 0.6 |
| С5-4 | 12.62 | 0.125 | 0.9904 | 2 | f < 0.6 |
| С6-1-1 | 22.70 | 9.478 | 41.7570 | 1 | 0.6 < f < 0.9 |
| С6-1-2 | 21.76 | 8.114 | 37.2869 | 1 | 0.6 < f < 0.9 |
| С6-2-1 | 22.96 | 9.965 | 43.4035 | 1 | 0.6 < f < 0.9 |
| С6-2-2 | 22.70 | 9.746 | 42.9264 | 1 | 0.6 < f < 0.9 |
| С6-2-3 | 22.09 | 6.794 | 30.7588 | 1 | 0.6 < f < 0.9 |
Рис. 1.
Фото шлифов, исследованных в данной работе карбонатных образцов, в миллиметровом (левые изображения, оптический микроскоп) и микрометровом (правые изображения, электронный сканирующий микроскоп) масштабах.
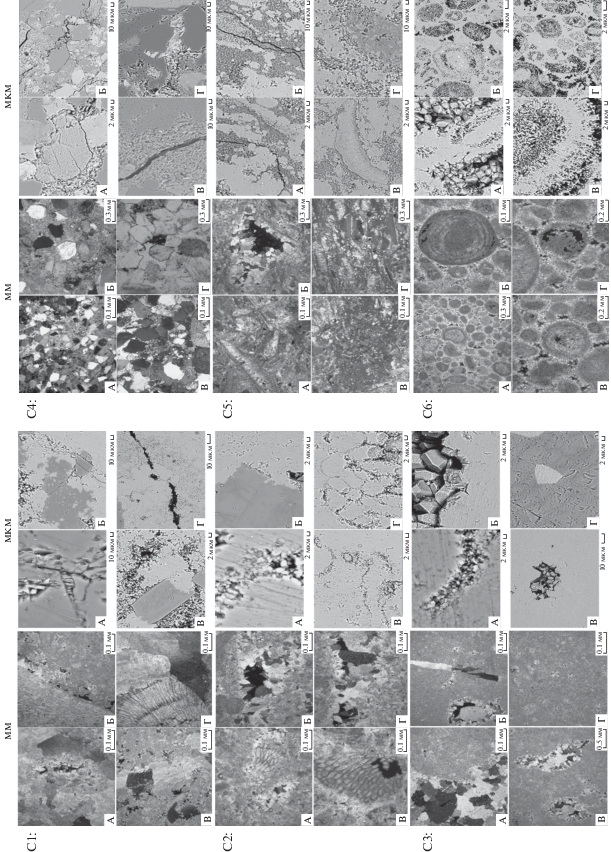
Рис. 2.
УЗТ образцов С1, С2 и С3. Для каждого образца: (а) – контуры скоростей продольных волн; (б) – контуры скоростей быстрых поперечных волн; (в) – контуры скоростей медленных поперечных волн; (г) – степень неоднородности.
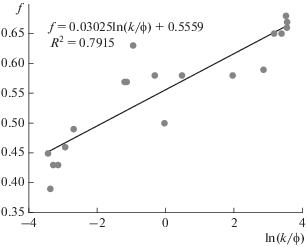
Результаты определения параметров модели представлены в табл. 7. Мы назвали приведенное выше разделение параметра связности на группы “примитивной системой классификации параметра связности”. На рис. 3 показана зависимость параметра f от логарифма отношения проницаемости к пористости. Исходя из этого рисунка, можно полагать, что зависимость значений отношения проницаемости к пористости от параметра f, экспоненциальная, поскольку $f \propto \ln \left( {{k \mathord{\left/ {\vphantom {k \phi }} \right. \kern-0em} \phi }} \right)$. Наши численные эксперименты показывают, что при изменении граничных значений примитивной системы классификации меняется лишь наклон линии аппроксимации, а конечная линейная зависимость $f \propto \ln \left( {{k \mathord{\left/ {\vphantom {k \phi }} \right. \kern-0em} \phi }} \right)$ остается справедливой.
Таблица 7.
Расчетные значения параметров модели на основе примитивной системы классификации параметра связности (f). Показаны параметры и их среднеквадратические отклонения
| Образец | f | σf | ϕс, % | ${{\sigma }_{{\phi c}}},$ % | ${{\alpha }_{p}}$ | ${{\sigma }_{{\alpha p}}}$ | ${{\alpha }_{с}} \times {{10}^{{ - 4}}}$ | ${{\sigma }_{{\alpha c}}} \times {{10}^{{ - 4}}}$ |
|---|---|---|---|---|---|---|---|---|
| С1-1 | 0.44 | 0.044 | 0.08 | 0.018 | 0.51 | 0.191 | 7.06 | 0.375 |
| С1-2 | 0.41 | 0.024 | 0.08 | 0.006 | 0.50 | 0.137 | 7.89 | 0.281 |
| С2-1 | 0.37 | 0.022 | 0.05 | 0.001 | 0.55 | 0.111 | 5.93 | 0.142 |
| С2-2 | 0.34 | 0.011 | 0.05 | 0.001 | 0.60 | 0.124 | 5.74 | 0.327 |
| С3-1 | 0.34 | 0.022 | 0.05 | 0.003 | 0.61 | 0.146 | 5.69 | 0.254 |
| С3-2 | 0.38 | 0.033 | 0.07 | 0.003 | 0.50 | 0.170 | 6.41 | 0.125 |
| С3-3 | 0.31 | 0.014 | 0.03 | 0.009 | 0.60 | 0.146 | 5.06 | 0.265 |
| С4-1 | 0.45 | 0.064 | 0.07 | 0.007 | 0.51 | 0.147 | 7.50 | 0.444 |
| С4-2 | 0.41 | 0.052 | 0.07 | 0.008 | 0.60 | 0.135 | 6.74 | 0.342 |
| С4-3 | 0.32 | 0.017 | 0.07 | 0.002 | 0.55 | 0.204 | 3.95 | 0.136 |
| С4-4 | 0.32 | 0.022 | 0.07 | 0.003 | 0.61 | 0.111 | 5.92 | 0.167 |
| С5-2 | 0.49 | 0.102 | 0.30 | 0.036 | 0.41 | 0.112 | 11.13 | 0.965 |
| С5-3 | 0.69 | 0.015 | 0.18 | 0.015 | 0.39 | 0.067 | 8.76 | 0.629 |
| С5-4 | 0.53 | 0.099 | 0.23 | 0.042 | 0.52 | 0.141 | 10.84 | 0.729 |
| С6-1-1 | 0.85 | 0.030 | 0.24 | 0.043 | 0.41 | 0.115 | 13.14 | 3.850 |
| С6-1-2 | 0.85 | 0.031 | 0.25 | 0.052 | 0.40 | 0.113 | 10.98 | 2.214 |
| С6-2-1 | 0.85 | 0.035 | 0.25 | 0.066 | 0.45 | 0.132 | 13.91 | 2.874 |
| С6-2-2 | 0.87 | 0.014 | 0.34 | 0.028 | 0.43 | 0.105 | 23.90 | 5.065 |
| С6-2-3 | 0.84 | 0.030 | 0.29 | 0.087 | 0.38 | 0.161 | 14.68 | 2.976 |
Рис. 3.
Результаты расчета параметра f на основе предложенной классификации связности пустотного пространства на три группы.
Как упоминалось ранее, уравнение Козени–Кармана отражает информацию о морфологических характеристиках порового пространства исследуемых образцов, в частности, о связности пустотного пространства. Эти характеристики (см. табл. 4) могут быть использованы для сужения границ для параметра f. Как указано в работе [Meredith, Tobias, 1962; Pisani, 2011], для пористого материала с идеально соединенным поровым пространством (чрезвычайно низкая “перколяционная пористость”) извилистость является функцией только пористости. Наиболее известным среди полуэмпирических выражений для расчета извилистости является соотношение Брюггемана [Meredith, Tobias, 1962]:
На основе теории перколяции для реальной среды уравнение (4) преобразуется следующим образом [Pisani, 2011]:
(5)
${{\tau }^{{{\text{(real)}}}}} = \phi {{\left[ {\frac{{\phi - {{\phi }^{{{\text{перк}}}}}}}{{1 - {{\phi }^{{{\text{перк}}}}}}}} \right]}^{{ - 1.5}}}.$Поскольку текстура предложенной идеальной среды является той же, как у реальной исследуемой среды, факторы формы (K0) у обеих сред аналогичны. Следовательно, геометрический фактор идеальной среды можно выразить следующим образом:
(6)
$\frac{{{{B}^{{{\text{(ideal)}}}}}}}{{{{B}^{{{\text{(real)}}}}}}} = \frac{{{{\tau }^{{{\text{(ideal)}}}}}}}{{{{\tau }^{{{\text{(real)}}}}}}} = {{\left[ {\frac{{\phi - {{\phi }^{{{\text{перк}}}}}}}{{\phi \left( {1 - {{\phi }^{{{\text{перк}}}}}} \right)}}} \right]}^{{1.5}}}.$Подставив геометрический фактор, полученный из уравнения (6) в выражение (3), и пренебрегая “пористостью перколяции” (считая ее бесконечно малой величиной), мы можем оценить максимальную возможную проницаемость для каждого образца (kmax).
Учитывая, что такая гипотетическая среда имеет различные микроструктурные параметры и, следовательно, различные значения проницаемости для разных образцов, мы называем эту гипотетическую модель “локальной идеальной средой”. Так как идеальная среда имеет идеальную гидравлическую проводимость для данной текстуры горной породы, значение коэффициента связности для этой идеальной среды близко к единице (максимальному значению).
Вышеупомянутая идеальная модель обеспечивает верхнюю границу значений проницаемости, причем минимальная возможная проницаемость для пористой среды является нулевой проницаемостью. Однако это является не совсем верным, поскольку нулевая проницаемость соответствует среде, которая полностью герметична. Согласно результатам работ [Neuzil, 1986; Stober, 1996; Manning et al., 1999; Jiang et al., 2010; Gleeson et al., 2011], минимальное значение проницаемости может быть принято равным 10–7 мД. Предполагается, что порода с минимальным значением проницаемости имеет изолированные поры и трещины, значение параметра f для таких сред составляет весьма низкое значение (~0).
В предположении, что линейная зависимость $f \propto \ln \left( {{k \mathord{\left/ {\vphantom {k \phi }} \right. \kern-0em} \phi }} \right)$ справедлива для каждого образца, можно оценить значение верхней границы параметра f для каждого образца путем построения линейной интерполяции между верхней границей системой уравнения {f = 1, ln(k/ϕ) = ln(kmax/ϕ)} и нижней границей системой уравнения {f = 0, ln(k/ϕ) = ln(kmin/ϕ)}. Линейное уравнение между этими двумя точками выражается следующим образом:
(7)
${{f}^{{\max }}} - 1 = \frac{{\ln ({{{{k}^{{{\text{real}}}}}} \mathord{\left/ {\vphantom {{{{k}^{{{\text{real}}}}}} {\phi )}}} \right. \kern-0em} {\phi )}} - \ln {{{{k}^{{\max }}}} \mathord{\left/ {\vphantom {{{{k}^{{\max }}}} {\phi )}}} \right. \kern-0em} {\phi )}}}}{{\ln ({{{{k}^{{\max }}}} \mathord{\left/ {\vphantom {{{{k}^{{\max }}}} {\phi )}}} \right. \kern-0em} {\phi )}} - \ln {{{{k}^{{\min }}}} \mathord{\left/ {\vphantom {{{{k}^{{\min }}}} {\phi )}}} \right. \kern-0em} {\phi )}}}}.$После ряда алгебраических преобразований уравнения (7) получаем следующее выражение для вычисления верхней границы параметра связности пустот:
(8)
${{f}^{{\max }}} = 1 - \frac{{\ln \left( {{{{{k}^{{{\text{max}}}}}} \mathord{\left/ {\vphantom {{{{k}^{{{\text{max}}}}}} {{{k}^{{{\text{real}}}}}}}} \right. \kern-0em} {{{k}^{{{\text{real}}}}}}}} \right)}}{{\ln \left( {{{{{k}^{{\max }}}} \mathord{\left/ {\vphantom {{{{k}^{{\max }}}} {{{k}^{{\min }}}}}} \right. \kern-0em} {{{k}^{{\min }}}}}} \right)}},$Результаты расчета ограничений на параметр f для образцов, по которым имелись данные РЭМ, представлены в табл. 8. На основе этих значений и значений ln(k/ϕ) для остальных образцов оценены величины максимального значения параметра f. Оценка параметра f на основе уравнения Козени–Кармана позволяет до некоторой степени учесть эффект размера пор и зерен, что невозможно сделать явно в методах теории эффективных сред.
Таблица 8.
Граничные значения искомых параметров моделей
| Образец | ${{f}^{{\max }}}$ | $\phi _{c}^{{\max }},$ % | $\phi _{c}^{{\min }},$ % | $\alpha _{с}^{{\min }} \times {{10}^{{ - 4}}}$ | $\alpha _{с}^{{\max }} \times {{10}^{{ - 4}}}$ |
|---|---|---|---|---|---|
| С1-1 | 0.81 | 0.08 | 0.30 | 2.00 | 8.00 |
| С1-2 | 0.84 | 0.08 | 0.30 | 2.00 | 8.00 |
| С2-1 | 0.79 | 0.05 | 0.20 | 1.50 | 6.00 |
| С2-2 | 0.71 | 0.05 | 0.20 | 1.50 | 6.00 |
| С3-1 | 0.80 | 0.07 | 0.26 | 1.50 | 6.00 |
| С3-2 | 0.71 | 0.07 | 0.28 | 1.50 | 6.00 |
| С3-3 | 0.78 | 0.06 | 0.24 | 1.50 | 6.00 |
| С4-1 | 0.73 | 0.07 | 0.26 | 2.00 | 8.00 |
| С4-2 | 0.72 | 0.07 | 0.26 | 1.75 | 7.00 |
| С4-3 | 0.71 | 0.07 | 0.26 | 1.00 | 4.00 |
| С4-4 | 0.72 | 0.07 | 0.26 | 1.50 | 6.00 |
| С5-2 | 0.76 | 0.08 | 0.32 | 3.50 | 14.00 |
| С5-3 | 0.77 | 0.09 | 0.34 | 4.00 | 16.00 |
| С5-4 | 0.76 | 0.08 | 0.30 | 3.00 | 12.00 |
| С6-1-1 | 0.87 | 0.11 | 0.44 | 5.00 | 20.00 |
| С6-1-2 | 0.87 | 0.11 | 0.44 | 5.00 | 20.00 |
| С6-2-1 | 0.87 | 0.10 | 0.41 | 4.00 | 16.00 |
| С6-2-2 | 0.87 | 0.13 | 0.50 | 7.00 | 28.00 |
| С6-2-3 | 0.87 | 0.13 | 0.50 | 5.00 | 20.00 |
Оценка трещинной пористости и формы трещин
Были проведены испытания нескольких серий образцов горных пород в условиях трехосного сжатия. В качестве основного режима испытания применялся режим с постоянной скоростью деформации 2 × 10–6 (1/с). Нагружение проводилось до начала этапа текучести. На основе первичных данных, полученных в результате серии экспериментов на прессе INOVA (ГО “Борок”, ИФЗ РАН), были рассчитаны кривые осевого напряжения, осевой, радиальной и объемной деформаций.
В этом исследовании мы ограничимся анализом кривой напряжений и деформаций для оценки плотности трещинной пористой среды. Более подробный анализ результатов трехосных испытаний будет представлен в другой публикации.
Полагая, что поровое пространство пористых материалов состоит только из трещин и частицы твердой фазы зафиксированы (зерна не скользят относительно друг от друга), в работе [Walsh, 1965b] автор предположил, что начальная нелинейная деформация пористых материалов при гидростатическом или трехосном испытании происходит за счет закрытия трещин. Однако твердая фаза вмещает сжимаемые минералы и зерна, которые могут быть прикрепленными слабо к вмещающей матрице. Таким образом, нелинейное поведение является результатом разнообразных процессов, таких как: деформация твердой фазы и пор [Zimmerman et al., 1986], вращение и перемещение нестабильных зерен [Wong, 1990; Zhang et al., 1990; DiGiovanni et al., 2000] и т.д. Следовательно, метод, разработанный в работе [Walsh, 1965a; b], даст максимальное значение трещинной пористости при гидростатической нагрузке изотропных пористых материалов, содержащих хаотически ориентированные трещины. Для негидростатической нагрузки линейное поведение наблюдается только по графикам зависимости осевого напряжения от осевой деформации. Тогда аналогично работе [Walsh, 1965b] для трехосного напряжения можно написать [Walsh, 1965a]:
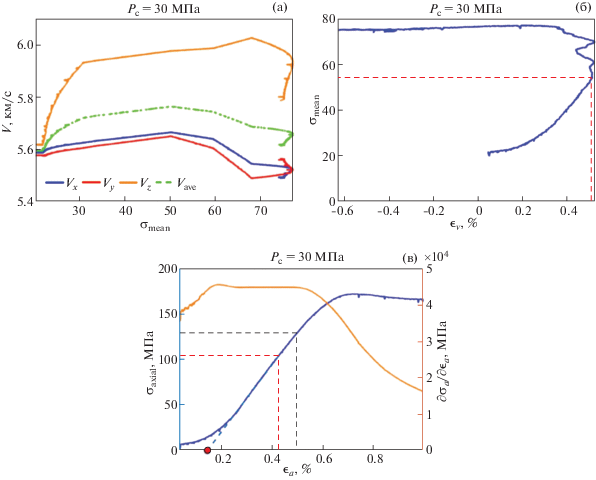
где: $\varepsilon _{v}^{c}$ и Smean – объемная деформация и среднее напряжение, соответствующие закрытию трещин; $\phi _{v}^{c}$ – доля трещин, закрытых при нагрузке образца; $K$ – эффективный модуль всестороннего объемного сжатия образца, который определялся для исследуемых образцов по зависимостям “среднее напряжение – объемная деформация”. Наклон прямых линий, показанных синими штрихами на рис. 4, определяет модуль Юнга исследуемых образцов, а точка пересечения с горизонтальной осью (красные кружки) – это осевая деформация, соответствующая закрытию трещин при нагрузке образца. Объемная деформация в уравнении (9) является объемной деформацией соответствующей осевой деформации, показанной красными кружками.Рис. 4.
Результаты одностадийного испытания образца С1-2: (а) – значения скоростей продольных волн, измеренные по направлению оси z (желтая линия), оси х (синяя линия) и оси y (красная линия). Зеленая линия представляет среднее значение скоростей по трем ортогональным направлениям; (б) – изменение объемной деформации относительно среднего напряжения; (в) – зависимость осевого напряжения от осевой деформации (синяя линия).
В работах [Berg, 1965; Walsh, 1965b] авторы показали, что при гидростатической нагрузке изотропных пористых материалов, содержащих хаотически ориентированные трещины, пористость закрытых трещин относится к трещинам определенного аспектного отношения. Согласно результатам этих авторов, максимальное возможное аспектное отношение трещин при гидростатическом испытании можно выразить следующим образом [Berg, 1965; Walsh, 1965b]:
где ${{\sigma }_{n}}$, ν и E – это гидростатическое напряжение, коэффициент Пуассона и модуль Юнга. Максимальное среднее аспектное отношение трещин, закрывшихся при трехосном или одноосном испытании для среды, содержащей трещины с функцией распределения ориентации и аспектного отношения $P\left( {\alpha ;\theta ,\varphi ,\psi } \right)$, выражается следующим уравнением [Nur, 1971].(11)
$\begin{gathered} \alpha _{c}^{{\max }} = \frac{{4\left( {1 - {{\nu }^{2}}} \right)}}{{\pi E}} \times \,\, \\ \times \,\,\frac{{\int\limits_0^{2\pi } {\int\limits_0^\pi {\int\limits_0^{2\pi } {\int\limits_{{{\alpha }_{1}}}^{{{\alpha }_{2}}} {\left[ {\left( {{{\sigma }_{1}}{{{\cos }}^{2}}\varphi + {{\sigma }_{2}}{{{\sin }}^{2}}\varphi } \right){{{\sin }}^{2}}\theta + {{\sigma }_{3}}{{{\cos }}^{2}}\theta } \right]P\left( {\alpha ;\theta ,\varphi ,\psi } \right)\sin \theta d\alpha d\varphi d\theta d\psi } } } } }}{{\int\limits_0^{2\pi } {\int\limits_0^\pi {\int\limits_0^{2\pi } {\int\limits_{{{\alpha }_{1}}}^{{{\alpha }_{1}}} {P\left( {\alpha ;\theta ,\varphi ,\psi } \right)\sin \theta d\alpha d\varphi d\theta d\psi } } } } }}, \\ \end{gathered} $В нашем случае, когда микроморфологические характеристики хаотически ориентированных монетообразных трещин описываются одним аспектным отношением и образец – цилиндрический, уравнение (11) упрощается следующим образом:
(12)
$\begin{gathered} \alpha _{c}^{{\max }} = \frac{{1 - {{\nu }^{2}}}}{{\pi E}}\int\limits_0^\pi {\left[ {{{P}_{c}}{{{\sin }}^{2}}\theta + {{\sigma }_{{axial}}}{{{\cos }}^{2}}\theta } \right]\sin \theta } d\theta = \\ = \frac{{2\left( {1 - {{\nu }^{2}}} \right)}}{{\pi E}}\left( {\frac{{2{{P}_{c}} + {{\sigma }_{{axial}}}}}{3}} \right) = \frac{{2\left( {1 - {{\nu }^{2}}} \right)}}{{\pi E}}{{\sigma }_{{mean}}}, \\ \end{gathered} $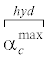 и
и 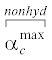 – аспектное отношение трещин при гидростатической и негидростатической всесторонних
нагрузках.
– аспектное отношение трещин при гидростатической и негидростатической всесторонних
нагрузках.
На основе проведенных всесторонних испытаний на исследуемых карбонатных образцах по данной методике получены значения верхней границы для значений трещинной пористости и аспектного отношения трещин как параметров, контролирующих пластическое поведение горных пород.
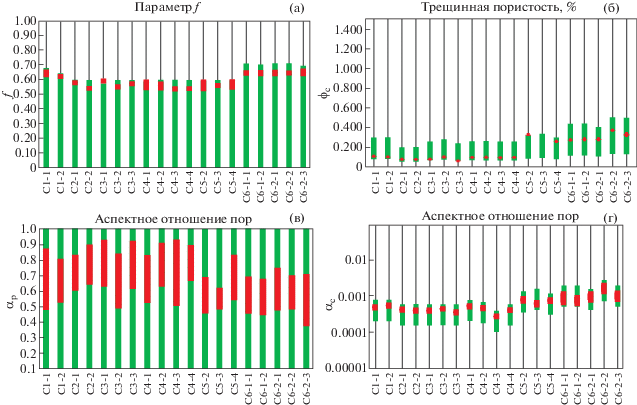
В данном исследовании мы приняли, что случайные ошибки различной природы при проведении эксперимента составляют 20% для при измерении фильтрационно-емкостных свойств и 35% при измерении напряжений и деформаций. Величины ограничений на параметр f (с учетом 20% полагаемой погрешности при измерении проницаемости и пористости), трещинную пористость и аспектное отношение трещин (с учетом 35% полагаемой погрешности при измерении напряжения и деформации), для всех исследуемых в данной работе образцов представлены в табл. 8. Несмотря на полезные результаты, которые представляет геометрический фактор B о структурных характеристиках порово-трещиноватых горных пород, не существует никакой физически обоснованной зависимости между значениями геометрического фактора и аспектного отношения пор и зерен. Как показывает анализ чувствительности построенных моделей к изменению ее параметров [Гасеми, Баюк, 2018a; b], область приемлемых значений параметра f довольно велика при разумных сочетаниях других параметров моделей. Введение ограничений на параметр связности пустотного пространства позволит значительно сузить область решений. На рис. 5 показано, как применение предложенных методов значительно сужает границы поиска метода оптимизации. На данном рисунке черные линии и зеленые столбцы иллюстрируют общий и ограниченный диапазон изменения искомых параметров соответственно. Красные столбцы показывают приемлемый диапазон определенных значений для искомых параметров в результате применения метода прямого поиска.
Рис. 5.
Диапазон изменения параметров построенных математических моделей. Черные линии и зеленые столбцы иллюстрируют общий и ограниченный диапазон изменения искомых параметров соответственно. Красные столбцы показывают приемлемый диапазон определенных значений для искомых параметров. Диапазон изменения: (а) – параметра связности пустот; (б) – трещинной пористости; (в) – аспектного отношения пор и (г) – аспектного отношения трещин.
В табл. 9 представлены средние значения и их стандартные отклонения (СКО) для каждого искомого параметра, полученные по примененному алгоритму оптимизации для модели I и II. Для петроупругой модели II, представляющей порово-трещиноватую среду исследуемых образцов выбуренных из полноразмерного керна С6, существует 6 неизвестных параметров, подлежащих определению (по сравнению с моделью I, для которой определяется 4 неизвестных параметра). Помимо параметров модели I, для модели II определяются параметры порового пространства внутри оолитовых зерен, включая аспектное отношение и объемную долю пор. Аспектное отношение пор, представляющее микроморфологические характеристики порового пространства для образцов С6, является средним по объемной концентрации значением аспектных отношений пор внутри оолитовых зерен и межзерновых пор. Результаты показывают, что оолитовые зерна включают в себя примерно 70% от общего объема порового пространства, а межзерновые поры составляют примерно 30% от общей пористости (обсуждение особенностей этой микроструктуры будет продолжено далее при анализе влияния объемной доли микрита).
Таблица 9.
Расчетные значения параметров моделей и их соответствующие среднеквадратические отклонения
| Образец | f | σf | ϕc, % | ${{\sigma }_{{\phi c}}},$ % | ${{\alpha }_{p}}$ | ${{\sigma }_{{\alpha p}}}$ | ${{\alpha }_{с}} \times {{10}^{{ - 4}}}$ | ${{\sigma }_{{\alpha c}}} \times {{10}^{{ - 4}}}$ |
|---|---|---|---|---|---|---|---|---|
| С1-1 | 0.59 | 0.053 | 8.23 × 10–3 | 2.25 × 10–5 | 0.87 | 0.194 | 3.51 | 3.89 × 10–5 |
| С1-2 | 0.70 | 0.039 | 3.61 × 10–3 | 1.56 × 10–5 | 0.36 | 0.175 | 3.40 | 3.33 × 10–5 |
| С2-1 | 0.54 | 0.049 | 6.81 × 10–3 | 2.04 × 10–5 | 0.68 | 0.245 | 1.98 | 2.73 × 10–5 |
| С2-2 | 0.48 | 0.028 | 1.78 × 10–3 | 1.22 × 10–5 | 0.41 | 0.162 | 2.95 | 1.49 × 10–5 |
| С3-1 | 0.66 | 0.048 | 1.23 × 10–3 | 8.77 × 10–6 | 0.55 | 0.199 | 2.95 | 1.52 × 10–5 |
| С3-2 | 0.43 | 0.046 | 1.07 × 10–3 | 4.17 × 10–6 | 0.94 | 0.136 | 2.95 | 3.85 × 10–5 |
| С3-3 | 0.56 | 0.032 | 1.17 × 10–3 | 5.16 × 10–6 | 0.63 | 0.155 | 2.95 | 2.9 × 10–5 |
| С4-1 | 0.52 | 0.017 | 9.47 × 10–3 | 3.53 × 10–5 | 0.31 | 0.206 | 2.77 | 3.87 × 10–5 |
| С4-2 | 0.46 | 0.010 | 1.28 × 10–2 | 3.82 × 10–5 | 0.89 | 0.127 | 5.86 | 5.84 × 10–5 |
| С4-3 | 0.42 | 0.023 | 1.84 × 10–2 | 2.18 × 10–5 | 0.78 | 0.195 | 1.63 | 1.39 × 10–5 |
| С4-4 | 0.43 | 0.020 | 1.71 × 10–2 | 3.5 × 10–5 | 0.86 | 0.145 | 2.17 | 3.47 × 10–5 |
| С5-2 | 0.60 | 0.015 | 2.58 × 10–2 | 1.61 × 10–4 | 0.18 | 0.085 | 8.34 | 9.02 × 10–5 |
| С5-3 | 0.58 | 0.026 | 9.03 × 10–2 | 1.09 × 10–4 | 0.28 | 0.195 | 8.34 | 4.99 × 10–5 |
| С5-4 | 0.58 | 0.027 | 4.56 × 10–2 | 2.78 × 10–4 | 0.28 | 0.192 | 8.34 | 1.05 × 10–4 |
| С6-1-1 | 0.76 | 0.016 | 5.66 × 10–3 | 2.68 × 10–4 | 0.26 | 0.060 | 8.08 | 9.09 × 10–5 |
| С6-1-2 | 0.77 | 0.004 | 6.64 × 10–2 | 7.96 × 10–5 | 0.10 | 0.002 | 8.97 | 1.27 × 10–4 |
| С6-2-1 | 0.78 | 0.001 | 4.48 × 10–2 | 9.25 × 10–5 | 0.14 | 0.022 | 5.38 | 3.94 × 10–5 |
| С6-2-2 | 0.76 | 0.002 | 1.48 × 10–2 | 2.76 × 10–4 | 0.29 | 0.060 | 11.59 | 1.87 × 10–4 |
| С6-2-3 | 0.75 | 0.001 | 8.28 × 10–2 | 7.37 × 10–5 | 0.11 | 0.002 | 9.02 | 1.32 × 10–4 |
Заметим, что в отечественной литературе исследованию пористоcти разного вида, включая трещинную, посвящен целый ряд современных работ (см., например, [Жуков, Моторыгин, 2017; 2018; Жуков и др., 2017]).
ОБСУЖДЕНИЕ
По результатам анализа чувствительности построенных петроупругих моделей пород была выявлена довольно широкая область возможной неопределенности в параметрах микроструктуры, экспериментальные значения для которых получить практически невозможно [Гасеми, Баюк, 2018a; b]. С целью уменьшения этой неопределенности проанализированы данные трехосных одностадийных и многостадийных испытаний на изучаемых образцах пород. На основе анализа начальной зоны нелинейного поведения при нагрузке образца определены максимальное значение аспектного отношения трещин и максимальное значение коэффициента трещинной пористости. Предложен метод для оценки ограничений сверху на параметр связности пустот (параметр f) путем построения идеализированной среды с максимальной проницаемостью. С использованием этого результата, а также ограничений на трещинную пористость и аспектное отношение трещин решена обратная задача по определению параметров микроструктуры шести изученных пород.
Размер пустот и зерен
Несмотря на то, что согласно работам [Fredrich et al., 1989; 1990; Menéndez et al., 1996; Ju et al., 2013; Zhao et al., 2014] размеры зерен и пор влияют на значения скоростей упругих волн и величины упругих модулей, методы теории эффективных сред не учитывают размер включений. На основе предложенного метода в этой работе для введения ограничений на параметр связности пустот мы применили уравнение Козени–Кармана чтобы в какой-то степени косвенно учесть влияние размера включений (пустот). Теме модификации методов теории эффективных сред для учета параметра размера включений посвящено мало работ [Sharma et al., 2004; Zhang et al., 2005a; Ma et al., 2011]. Но так как эта тема является весьма существенной, следует продолжать работать в этом направлении.
Цемент
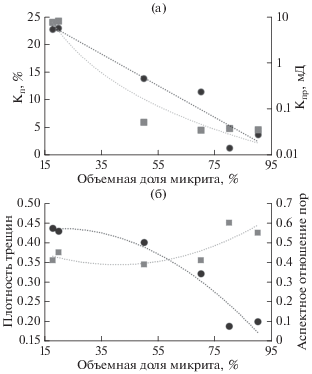
Объемная доля микрита является значимым параметром, контролирующим текстурные характеристики породы, такие как значение коэффициента общей пористости, проницаемости, размер и микроморфологические характеристики пустотного пространства. В данной работе объемная доля микрита определена для 6 образцов на основе анализа изображений РЭМ. Ограниченное количество данных не позволяет провести комплексный статистический анализ. Однако первичный анализ данных РЭМ позволяет сделать качественный вывод об отрицательном эффекте микрита на пористости и проницаемости. Микрит встречается в породах как цемент, содержащий круглые межкристаллические микропоры (диаметром меньше 36 μм [Fournier et al., 2009]), который обволакивает крупные кристаллы или оолитовые зерна, уменьшает размер пустот и блокирует устье пор.
Как показано на рис. 6, коэффициент общей пористости и проницаемости для образцов с большей объемной долей микрита меньше по сравнению с образцами, содержащими низкую объемную долю микрита. Гранулы микрокристаллов кальцита огибают поры и каналы пор и сокращают общий объем пустот, что приводит к уменьшению пористости и проницаемости среды. Согласно рис. 6б эффективное аспектное отношение пор выше для образцов с более высокой концентрацией микрита. На рис. 6б отображено влияние содержания микрита на плотность трещин $\left( {\frac{{3{{\phi }_{с}}}}{{4\pi {{\alpha }_{с}}}}} \right)$. Исходя из полученных результатов, можно заключить, что плотность трещин уменьшается за счет увеличения содержания микрита, то есть увеличение содержания микрита уменьшает как аспектное отношение трещин, так и пористость. РЭМ-изображения подтверждают этот вывод, показывая, что микрит осаждается в виде вторичного цемента и залечивает ранее существовавшие микротрещины.
Моделирование при пластовых условиях
Наличие жидкости в пористых породах может значительно изменить реакцию породы на приложенное напряжение при масштабе акустических деформаций (10–6) и при больших масштабах деформации трехосных испытаний (10–3–10–2). Локальный и глобальный поток жидкости во время движения акустических волн вызывает потерю энергии на средних и высоких частотах (от 100 кГц до 1 ГГц) [Jakobsen et al., 2009]. В результате этого затухания классические статические методы теории эффективных сред, такие как ОСП и Т-матрица [Jakobsen et al., 2003], недооценивают или переоценивают (в зависимости от пространственного распределения пор и трещин) скорость акустических волн. Механическое поведение горных пород может сильно измениться за счет присутствия жидкости в порах из-за герметизации и смазки [Hubbert et al., 1959; Paterson et al., 2005], вызывая эффекты уменьшения поверхности и, следовательно, уменьшения энергии трещинообразования [Lawn, 1993], растрескивания [Atkinson, 1984] и усиления диффузионных процессов, таких как растворение под давлением [Lehner, 1990; Zhang et al., 2005b; 2010]. В пластовых условиях основными механизмами, способствующими деформации, являются механическое двойникование и растворение минералов под давлением. Изменения в поведении пород при разных температурах могут быть связаны с взаимодействием растворимости минералов, скорости растворения и продолжительности деформационных процессов [Lizabeth et al., 2015]. Авторы этой работы также наблюдали, что компакция усиливается с увеличением температуры. При пластовых условиях (высокое давление и температура) растворение минералов под давлением является доминирующим механизмом компакции за счет усиления удаления минералов из точек их соприкосновения и их трансформации в поры и трещины. Высокая химическая активность поровой жидкости усиливает механическое двойникование, что препятствует образованию микротрещин. Следовательно, для жидкостей, химически уравновешенных с вмещающей матрицей, изменения объема порового пространства обусловлены пластичностью кристалла [Lizabeth et al., 2015].
Параметры микроструктуры пустотного пространства, исследованные выше, меняются в пластовых условиях при высоких давлениях и температурах за счет связанного влияния упомянутых явлений. Следовательно, результаты, полученные выше в лабораторных условиях, могут быть совершенно иными в пластовых условиях для горных пород, насыщенных разными флюидами. Для прогноза влияния пластовых условий на упругие свойства необходимо построить отдельные петроупругие модели для стадии линейной упругости и стадии после дилатации образца при нагрузке. Эти модели должны учитывать анизотропию, индуцированную при нагрузке образца. Имея скорости упругих волн (Vp, Vsv и Vsh) в трех основных ортогональных направлениях x, y и z (ось z расположена вертикально вдоль оси образца), при испытании можно оценить эволюцию параметров микроструктуры на разных стадиях поведения исследуемого образца. Таким образом, требуется провести более широкое исследование с большим количеством образцов.
ЗАКЛЮЧЕНИЕ
Экспериментальные результаты подтвердили теоретическое предположение о присутствии прямой связи между параметром связности пустот петроупругих моделей карбонатных пород, построенных с помощью метода ОСП, и гидравлической проницаемостью. Вследствие этого предложен метод для оценки ограничений сверху на параметр связности пустот (параметр f) путем построения идеализированной среды с максимальной проницаемостью.
Проведенные трехосные одностадийные и многостадийные испытания на образцах карбонатных пород позволили получить ограничения сверху на трещинную пористость и аспектное отношение трещин – важнейшие параметры, характеризующие пустотное пространство петроупругих моделей карбонатных пород. Ограничения на эти параметры моделей получены на основе анализа начальной зоны нелинейного поведения при нагрузке образцов.
Полученные ограничения приводят к уменьшению неопределенности решения обратной задачи путем сужения диапазона поиска параметров моделей при применении алгоритмов оптимизации. Это, в свою очередь, повышает достоверность полученных результатов по определению параметра связности пустот и характеристик трещиноватости (трещинной пористости и аспектного отношения трещин) полученных для исследованных карбонатных пород.
Анализ изображений РЭМ и параметров построенных петроупругих моделей карбонатных пород показал, что исследованные карбонатные образцы подверглись интенсивному вторичному диагенезу, в результате чего были залечены большинство ранее существовавших микротрещин, микритовые микропоры (с высокой сферичностью) и макропоры с “малой степенью сферичности” (малое значение аспектного отношения пустот). Микритовый цемент привел к уменьшению проницаемости исследованных образцов. Из-за вторичного диагенеза и доломитизации микропор микритового цемента коэффициент общей пористости для образцов с высокой долей микрита ниже по сравнению с коэффициентом общей пористости образцов с низкой долей коэффициента общей пористости.
Список литературы
Баюк И.О. Междисциплинарный подход к прогнозированию макроскопических и фильтрационно-емкостных свойств коллекторов углеводородов. Дис. ... докт. физ.-мат. наук. М.: ИФЗ РАН. 2013. 228 с.
Баюк И.О. Теоретические основы определения эффективных физических свойств коллекторов углеводородов // Акустика неоднородных сред. Ежегодник РАО. 2011. № 12. P. 107–120.
Баюк И.О., Белобородов Д.Е., Березина И.А., Гилязетдинова Д.Р., Краснова М.А., Корост Д.В., Патонин А.В., Пономарев А.В., Тихоцкий С.А., Фокин И.В., Хамидуллин Р.А., Цельмович В.А. Сейсмоакустические исследования керна при пластовых условиях // Технологии сейсморазведки. 2015. № 2. С. 36–45.
Гасеми М., Баюк И.О. Петроупругая модель оолитового известняка в масштабе керна // Экспозиция Нефть Газ. 2018a. № 3(63). С. 36–40.
Гасеми М., Баюк И.О. Петроупругое моделирование карбонатных пород-коллекторов с использованием модели двойной пористости // Экспозиция Нефть Газ. 2018b. № 5(65). С. 21–25.
Жуков В.С., Моторыгин В.В. Анализ некоторых способов оценки трещинной пористости // Научно-технический сборник Вести газовой науки. 2017. № 3 (31). С. 207–215.
Жуков В.С., Моторыгин В.В. Влияние межзерновой пористости и трещинной пустотности горных пород на скорость продольной волны // Научно-технический сборник Вести газовой науки. 2018. № 3(35). С. 249–255.
Жуков В.С., Моторыгин В.В. Влияние различных видов пористости на скорости упругих волн и электропроводность коллекторов чаяндинского месторождения // Научно-технический сборник Вести газовой науки. 2017. № 2(30). С. 223–233.
Петров В.А., Насимов Р.М. “Способ определения неоднородностей упругих и фильтрационных свойств горных пород”. Патент RU 2515332. 2008.
Шермергор. Т.Д. Теория упругости микронеоднородных сред. М.: Наука. 1977. 400 с.
Ялаев Т.Р., Баюк И.О., Тарелко Н.Ф., Абашкин В.В. Связь тепловых и упругих свойств песчаника // Технологии сейсморазведки. 2016. № 2. С. 76–82.
Atkinson B.K. Subcritical crack growth in geological materials // J. Geophysical Research: Solid Earth. 1984. V. 89. № B6. P. 4077–4114.
Bayuk I.O., Ammerman M., Chesnokov E.M. Elastic moduli of anisotropic clay // Geophysics. 2007. V. 72. № 5. P. D107–D117.
Bayuk I.O., Ammerman M., Chesnokov E.M. Upscaling of elastic properties of anisotropic sedimentary rocks // Geophysical J. International. 2008. V. 172. № 2. P. 842–860.
Bayuk I.O., Chesnokov E.M. Correlation between elastic and transport properties of porous cracked anisotropic media // Physics and Chemistry of the Earth. 1998. V. 23. № 3. P. 361–366.
Bayuk I.O., Chesnokov E.M. Transport properties of porous cracked anisotropic media. Porous Media: Physics, Models, Simulations / Eds. A. Dmitrievsky A., Panfilov M. 2000. World Scientific Publ. C. 325–336.
Berg C.A. Deformation of fine cracks under high pressure and shear // Journal of Geophysical Research. 1965. V. 70. № 14. P. 3447–3452.
Carman P.C. Fluid flow through granular beds // Chemical Engineering Research and Design. 1937. V. 75. P. S32–S48.
Chesnokov E., Bayuk I., Metwally Y. Inversion of shale microstructure parameters from permeability measurements // Expanded Abstracts of 80-th SEG Annual Meeting, 2010. P. 2634–2638.
Chesnokov E.M., Tiwary D.K., Bayuk I.O., Sparkman M.A., Brown R.L. Mathematical modelling of anisotropy of illite-rich shale // Geophysical J. International. 2009. V. 178. № 3. P. 1625–1648.
DiGiovanni A.A., Fredrich J.T., Holcomb D.J., Olsson W.A. Micromechanics of Compaction in an Analogue Reservoir Sandstone. Proceedings of 4th North American Rock Mechanics Symposium. Seattle, Washington. American Rock Mechanics Association. 2000.
Ehrenberg S.N., Gregor P. Eberli, G.P., Baechle G. Porosity–permeability relationships in Miocene carbonate platforms and slopes seaward of the Great Barrier Reef, Australia (ODP Leg 194, Marion Plateau) // Sedimentology. 2006. V. 53. № 6. P. 1289–1318.
Fournier F., Borgomano J. Critical porosity and elastic properties of microporous mixed carbonate-siliciclastic rocks // Geophysics. 2009. V. 74. № 2. P. E93–E109.
Fredrich J.T., Evans B., Wong T.-F. Effect of grain size on brittle and semibrittle strength: Implications for micromechanical modelling of failure in compression // J. Geophysical Research: Solid Earth. 1990. V. 95 № B7. P. 10907–10920.
Fredrich J.T., Evans B., Wong T.-F. Micromechanics of the brittle to plastic transition in Carrara marble // J. Geophysical Research: Solid Earth. 1989. V. 94. № B4. P. 4129–4145.
Gleeson T., Smith L., Moosdorf N., Hartmann J., Dürr H.H., Manning A.H., Van Beek L.P.H., Jellinek A.M. Mapping permeability over the surface of the Earth // Geophysical Research Letters. 2011. V. 38. № 2. Paper L02401.
Gu Y., Bao Z., Lin Y., Qin Z., Lu J., Wang H. The porosity and permeability prediction methods for carbonate reservoirs with extremely limited logging data: Stepwise regression vs. N-way analysis of variance // J. Natural Gas Science and Engineering. 2017. V. 42. P. 99–119.
Hubbert K., Rubey W.W. Role of fluid pressure in mechanics of overthrust faulting: I. Mechanics of fluid-filled porous solids and its application to overthrust faulting // GSA Bulletin. 1959. V. 70. № 2. P. 115–166.
Jakobsen M., Chapman M. Unified theory of global flow and squirt flow in cracked porous media // Geophysics. 2009. V. 74. № 2. P. WA65–WA76.
Jakobsen M., Hudson J.A., Johansen T.A. T-Matrix approach to shale acoustics // Geophysical Journal International. 2003. V. 154. № 2. P. 533–558.
Jiang T. Connection of elastic and transport properties: effective medium study in anisotropic porous media. PhD Thesis. University of Houston. 2013. 117 p.
Jiang T., Chesnokov E.M. Elastic moduli relation to microstructure properties in porous media using GSA modeling. Expanded Abstracts of 82-th SEG Annual Meeting. 2012. Paper segam2012-1038.1.
Jiang X.-W., Wang X.-S., Wan L. Semi-empirical equations for the systematic decrease in permeability with depth in porous and fractured media // Hydrogeology J. 2010. V. 18. № 4. P. 839–850.
Ju Y., Masce A., Yang Y., Peng R., Mao L. Effects of Pore Structures on Static Mechanical Properties of Sandstone // J. Geotechnical and Geoenvironmental Engineering. 2013. V. 139. № 10. P. 1745–1755.
Lawn B. Fracture of Brittle Solids. Cambridge: Cambridge University Press. 1993.
Lehner F.K. Thermodynamics of rock deformation by pressure solution, in Deformation Processes in Minerals, Ceramics and Rocks. Springer New York. 1990. P. 296–333.
Lisabeth H.P., Zhu W. Effect of temperature and pore fluid on the strength of porous limestone // J. Geophysical Research: Solid Earth. 2015. V. 120. № 9. P. 6191–6208.
Ma H.M., Gao X.-L. Strain gradient solution for a finite-domain Eshelby-type plane strain inclusion problem and Eshelby’s tensor for a cylindrical inclusion in a finite elastic matrix // International J. Solids and Structures. 2011. V. 48. № 1. P. 44–55.
Manning C.E., Ingebritsen S.E. Permeability of the continental crust: Implications of geothermal data and metamorphic systems // Reviews of Geophysics. 1999. V. 37. № 1. P. 127–150.
Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook. 2nd Edition. Tools for Seismic Analysis of Porous Media. Cambridge: Cambridge University Press. 2009. 511 p.
Mavko G., Nur A. The effect of a percolation threshold in the Kozeny-Carman relation // Geophysics. 1997. V. 62. № 5. P. 1480–1482.
Menéndez B., Zhu W., Wong T.-F. Micromechanics of brittle faulting and cataclastic flow in Berea sandstone // J. Structural Geology. 1996. V. 18. № 1. P. 1–16.
Meredith R.E., Tobias C.W. Conduction in heterogeneous systems. Advances in Electrochemistry and Electrochemical Engineering. V. 2. / Tobias C.W. (ed.). New York: Interscience Publishers. 1962. P. 15–47.
Nelder J.A., Mead R. A simplex method for function minimization // The Computer J. 1965. V. 7. № 4. P. 308–313.
Neuzil C.E. Groundwater flow in low-permeability environments // Water Resources Research. 1986. V. 22. № 8. P. 1163–1195.
Nur A. Effects of stress on velocity anisotropy in rocks with cracks // J. Geophysical Research. 1971. V. 76. № 8. P. 2022–2034.
Paterson M.S., Wong T.-F. Experimental Rock Deformation: The Brittle Field. New York: Springer. 2005. 348 p.
Pisani L. Simple Expression for the Tortuosity of Porous Media // Transport in Porous Media. 2011. V. 88. № 2. P. 193–203.
Potyondy D.O., Cundall P.A. A bonded-particle model for rock // International J. Rock Mechanics and Mining Sciences. 2004. V. 41. № 8. P. 1329–1364.
Shahraini A., Ali A., Jakobsen M. Characterization of fractured reservoirs using a consistent stiffness-permeability model: focus on the effects of fracture aperture // Geophysical Prospecting. 2010. V. 59. № 3. P. 492–505.
Sharma P., Ganti S. Size-dependent Eshelby’s tensor for embedded nano-inclusions incorporating surface/interface energies // Journal of Applied Mechanics. 2004. V. 71. № 5. P. 663–671.
Stober I. Researchers study conductivity of crystalline rock in proposed radioactive waste site // Eos, Transactions American Geophysical Union. 1996. V. 77. № 10. P. 93–94.
Tikhotsky S.A., Fokin I.V., Bayuk I.O., Beloborodov D.E., Berezina I.A., Gafurova D.R., Dubinya N.V., Krasnova M.A., Korost D.V., Makarova A.A., Patonin A.V., Ponomarev A.V., Khamidullin R.A., Tselmovich V.A. Comprehensive laboratory core analysis at CPGR IPE RAS // Seismic Instruments. 2018. V. 54. № 5. P. 586–597.
Walsh J.B. The effect of cracks in rocks on Poisson’s ratio // J. Geophysical Research. 1965a. V. 70. Issue 20. P. 5249–5257.
Walsh J.B. The effect of cracks on the compressibility of rock // J. Geophysical Research. 1965b. V. 70. № 2. P. 381–389.
Willis J.R. Variational and Related Methods for the Overall Properties of Composites // Advances in Applied Mechanics. 1981. V. 21. P. 1–78.
Wong T.-F. Mechanical compaction and the brittle-ductile transition in porous sandstones // Geological Society, London, Special Publications. 1990. V. 54. № 1. P. 111–122.
Yalaev T.R., Bayuk I.O., Tarelko N.F., Abashkin V.V. Connection of Elastic and Thermal Properties of Bentheimer Sandstone Using Effective Medium Theory (Rock Physics). 50th US Rock Mechanics/Geomechanics Symposium. Houston, Texas. 2016b. V. 1. P. 237–243.
Yalaev T.R., Bayuk I.O., Popov E.Y. Fluid Substitution Problem for Thermal Conductivity of Hydrocarbon Reservoirs Based on Rock Physics Methods. 7th EAGE Saint Petersburg International Conference and Exhibition. 2016a. P. 878–882.
Zhang J., Wong T.-F., Davis D.M. Micromechanics of pressure-induced grain crushing in porous rocks // J. Geophysical Research: Solid Earth. 1990. V. 95. № B1. P. 341–352.
Zhang X., Sharma P. Inclusions and inhomogeneities in strain gradient elasticity with couple stresses and related problems // International J. Solids and Structures. 2005a. V. 42. № 13. P. 3833–3851.
Zhang X., Spiers C.J. Compaction of granular calcite by pressure solution at room temperature and effects of pore fluid chemistry // International J. Rock Mechanics and Mining Sciences. 2005b. V. 42. № 7. P. 950–960.
Zhang X., Spiers C.J., Peach C.J. Compaction creep of wet granular calcite by pressure solution at 28°C to 150°C // J. Geophysical Research: Solid Earth. 2010. V. 115. Paper B09217.
Zhao H., Xiao Q., Huang D., Zhang S. Influence of Pore Structure on Compressive Strength of Cement Mortar // The Scientific World J. 2014. P. 247058.
Zimmerman R.W., Somerton W.H., King M.S. Compressibility of porous rocks // J. Geophysical Research: Solid Earth. 1986. V. 91. № B12. P. 12765–12777.
Дополнительные материалы отсутствуют.