Физика Земли, 2020, № 2, стр. 115-126
Особенности сравнительной оценки глобальных моделей гравитационного поля земли
В. Н. Конешов 1, В. Б. Непоклонов 1, 2, *, Е. С. Спиридонова 2, М. В. Максимова 2
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
2 Московский государственный университет геодезии и картографии
г. Москва, Россия
* E-mail: vbnep@miigaik.ru
Поступила в редакцию 21.03.2019
После доработки 29.10.2019
Принята к публикации 31.10.2019
Аннотация
Экспериментальным путем проведено сравнительное исследование современных глобальных моделей гравитационного поля Земли (ГПЗ) в виде сферических гармоник геопотенциала. Его актуальность связана с ростом числа моделей и повышением требований к результатам моделирования. Полученные сравнительные характеристики базируются на результатах статистической обработки модельных значений высот квазигеоида и аномалий силы тяжести в общеземном и региональном масштабах (на примере региона Арктики и территории России). Новизна полученных результатов обусловлена количеством исследованных моделей, их составом и методикой исследования. Исследованы 103 модели (3 – отечественные, 100 – зарубежные), в том числе модели низкого, среднего, высокого и сверхвысокого пространственного разрешения. Оценено влияние на статистические характеристики параметров ГПЗ сближения (непараллельности) меридианов расчетных точек, которое, по полученным оценкам, может быть значительным. Показано, что для его учета может использоваться модифицированный способ, предусматривающий введение весовых множителей. Проведен анализ расхождений между моделями в различных комбинациях, позволивший оценить вклад новых данных космической геодезии, полученных с использованием систем “спутник–спутник” и спутниковой градиентометрии. Показана целесообразность учета внутригрупповых, межгрупповых и межрегиональных различий между исследуемыми моделями.
ВВЕДЕНИЕ
В настоящее время в геодезии, геофизике, баллистике, навигации и других областях широко используются глобальные модели аномального гравитационного поля Земли (ГПЗ) в виде разложения геопотенциала в ряд по сферическим функциям. Практика показывает, что между моделями, созданными в разные годы, с использованием различной исходной информации, различных методов ее обработки, как и между моделями, имеющими различную детальность, могут наблюдаться существенные расхождения, которые, к тому же, варьируются в зависимости от географического положения расчетной области. Поэтому для указанных моделей актуально проведение их сравнительных исследований с точки зрения валидации результатов моделирования, оценки вклада новых данных о ГПЗ, в том числе измерений по линии “спутник–спутник” и спутниковой градиентометрии [Яшкин, 2009; Сугаипова, 2015], анализа и мониторинга динамики системы моделей ГПЗ как неотъемлемой составной части современной координатной основы пространственных данных [Непоклонов, 2016а; 2016б].
Сравнение глобальных моделей ГПЗ в виде сферических гармоник геопотенциала удобно проводить на регулярной сетке меридианов и параллелей. Однако из-за так называемого сближения (непараллельности) меридианов расстояние узлами сетки по параллелям уменьшается, а число узлов на единицу площади возрастает с увеличением модуля широты. Если не учитывать это обстоятельство, можно получить не вполне адекватные оценки как отдельно взятых моделей, так и расхождений между моделями. Поэтому целесообразно тем или иным способом сбалансировать вклад оценочных точек с высокими и низкими значениями широт, что не всегда должным образом делалось при проведении сравнительных исследований моделей ГПЗ. В опубликованных работах можно встретить различные подходы к устранению (уменьшению) отмеченного дисбаланса, но при этом результаты анализа и оценки их эффективности, как правило, отсутствуют.
Совокупность отмеченных выше обстоятельств, характеризующих особенности сравнительных исследований глобальных моделей ГПЗ указанного типа, послужила предпосылкой для проведения исследований, результаты которых представлены в данной работе.
ПОСТАНОВКА ЗАДАЧИ, МЕТОДИКА ИССЛЕДОВАНИЙ И ИСХОДНЫЕ ДАННЫЕ
Задача исследований предусматривала получение сравнительных оценок современных глобальных моделей ГПЗ в виде сферических гармоник геопотенциала по расхождениям одноименных статистических характеристик и статистическим характеристикам расхождений модельных значений параметров ГПЗ в заданных оценочных точках. При этом исследовалось возможное влияние на результаты сравнения следующих факторов: состава и способа вычисления статистических характеристик; географического положения области исследования; детальности (разрешающей способности) моделей; вида моделируемых параметров ГПЗ.
Область исследования
Сравнение моделей ограничивалось поверхностью Земли, за которую для удобства принималась поверхность общеземного эллипсоида (ОЗЭ). Были получены сравнительные оценки моделей как по всей Земле, так и по отдельным приоритетным регионам земного шара, к которым были отнесены территория Российской Федерации и зона Арктики. Расчеты выполнялись на регулярной сетке меридианов и параллелей с шагом 15' по обоим координатным направлениям.
Состав исследуемых моделей
Рассматривались модели различной разрешающей способности (детальности), определяемой наибольшим значением N-степени учитываемых сферических гармоник геопотенциала и выражается величиной [Xiong, 2001]:
где: ${{\lambda }_{N}}$ – предельно малое значение разрешаемых длин волн геоида; $R$ – радиус геосферы (в километрах). В зависимости от N исследуемые модели были разделены на четыре группы: модели низкого разрешения (МНР) – $N \leqslant 180$ (низкостепенные); модели среднего разрешения (МСР) – $180 < N \leqslant 330$ (среднестепенные); модели высокого разрешения (МВР) – $330 < N \leqslant 720$ (высокостепенные); модели сверхвысокого разрешения (МСВР) – $N > 720$ (ультравысокостепенные). Среднее по группе значение N будем называть размерностью группы.В программу исследований входило тестирование 103-х моделей, выпущенных с 1996 г., c выхода этапной модели EGM-96, официально принятой для поддержания и использования системы координат WGS-84. Это были три российские модели (ПЗ-2002/360, ГАО-2008 и ГАО-2012, все – высокого разрешения, до 360-й степени) и 100 зарубежных моделей из архива Международного центра глобальных моделей Земли (ICGEM) [ICGEM, 2019], в том числе: МНР – 39; МСР – 38; МВР – 16; МСВР – 7 (EGM2008, EIGEN-6C, EIGEN-6C2, EIGEN-6C3, EIGEN-6C4, GECO, SGG-UGM-1). Учитывая наличие российских моделей, группа МВР была разделена на две подгруппы – отечественные и зарубежные модели, соответственно МВР(О) и МВР(З).
Состав моделируемых параметров ГПЗ
Исследование проводилось на примере высоты квазигеоида (ВКГ) и аномалии силы тяжести (АСТ) как параметров аномального ГПЗ, имеющих наиболее широкое распространение в отечественной геодезической практике. Модельные значения ВКГ $\left( \zeta \right)$ и АСТ $\left( {\Delta g} \right)$ вычислялись по формулам [Мориц, 1983]:
(2)
$\begin{gathered} \zeta = \frac{{fM}}{{\gamma r}}\sum\limits_{n = 2}^N {{{{\left( {\frac{a}{r}} \right)}}^{n}}\sum\limits_{m = 0}^n {\overline {{{P}_{{nm}}}} \left( {\sin \varphi } \right)} } \times \\ \times \,\,\left( {{{{\bar {C}}}_{{nm}}}\operatorname{cosm} \lambda + {{{\bar {S}}}_{{nm}}}\sin m\lambda } \right), \\ \end{gathered} $(3)
$\begin{gathered} \Delta g = \frac{{fM}}{{{{r}^{2}}}}\sum\limits_{n = 2}^N {{{{\left( {\frac{a}{r}} \right)}}^{n}}\left( {n - 1} \right)\sum\limits_{m = 0}^n {{{{\bar {P}}}_{{nm}}}\left( {\sin \varphi } \right)} } \times \\ \times \,\,\left( {{{{\bar {C}}}_{{nm}}}\cos m\lambda + {{{\bar {S}}}_{{nm}}}\sin m\lambda } \right), \\ \end{gathered} $Состав оцениваемых статистических характеристик
В качестве оцениваемых статистических характеристик моделируемой величины $f$ использовались: экстремумы ${{f}_{{\min }}},{{f}_{{\max }}}$ (минимум, максимум), среднее $\mu $ и стандартное отклонение $\sigma $ ее модельных значений ${{f}_{i}}$$\left( {i = 1,...,n} \right)$, вычисленных на множестве оценочных точек по каждой отдельно взятой модели, где $n$ – число оценочных точек (вариант 1); аналогичные характеристики для отклонений ВКГ (АСТ), вычисленных по каждой исследуемой модели, от одноименных выходных данных модели, условно принимаемой за “эталон” (вариант 2). “Эталоном” служила модель EGM-2008 до 2190-й степени. Выбор “эталона” обусловлен, с одной стороны, тем, что модель EGM-2008 является официальной моделью системы координат WGS-84 [Pavlis, 2008], с другой стороны, тем, что результатами многочисленных проверок подтверждены ее высокие точностные характеристики. Следует отметить, что существенный вклад в обеспечение высоких точностных характеристик этой и следующих за ней моделей сверхвысокого разрешения вносят не только новые данные космической геодезии, но и результаты определения детальных характеристик ГПЗ в Мировом океане с использованием данных спутниковой альтиметрии.
Способ вычисления статистических характеристик
Граничные значения вычислялись путем перебора. Средние значения и стандартные отклонения вычислялись двумя способами с использованием известных формул математической статистики.
Первый способ – базовый (без учета сближения меридианов расчетной сетки):
(5)
$\sigma = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{{\left( {{{f}_{i}} - \mu } \right)}}^{2}}} } = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {f_{i}^{2}} - \mu _{{}}^{2}} .$Второй способ – модифицированный, обеспечивающий учет сближения меридианов с помощью соответствующих весовых коэффициентов:
(6)
$\mu = {{\left( {\sum\limits_{i = 1}^n {{{w}_{i}}} } \right)}^{{ - 1}}}\sum\limits_{i = 1}^n {{{w}_{i}}{{f}_{i}}} ;$(7)
$\sigma = \sqrt {{{{\left( {\sum\limits_{i = 1}^n {{{w}_{i}}} } \right)}}^{{ - 1}}}\sum\limits_{i = 1}^n {{{w}_{i}}f_{i}^{2}} - \mu _{f}^{2}} ;$Отметим, что учесть сближение меридианов можно было бы, располагая оценочные точки с шагом по параллелям, возрастающим по мере удаления от экватора и приближения к полюсам. Однако это ограничило бы возможность использования высокоэффективных алгоритмов гармонического синтеза параметров ГПЗ, в частности, алгоритмов, использующих быстрое преобразование Фурье [Hwang, 2006]. Удобство численной реализации процедуры гармонического синтеза в конечном итоге подталкивает к выбору оценочных точек в узлах полностью регулярной сетки меридианов и параллелей.
Следует отметить также, что использование весовых коэффициентов вида (8), учитывающих сближение меридианов, является частным случаем учета региональных особенностей при сравнении глобальных моделей ГПЗ. Возможны другие критерии дифференциации вклада различных регионов, например, гравитационная аномальность. Однако детальное рассмотрение данного вопроса выходит за рамки данной работы.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ИХ ОБСУЖДЕНИЕ
В табл. 1 и табл. 2 представлены оценки величин μ, $\sigma $ в виде, отражающем их зависимость от класса моделей, географического положения области исследования и способа вычисления (БС – базовый способ; МС – модифицированный способ). При этом, в связи с большим количеством исследованных моделей и лимитированным объемом статьи приведены только граничные значения этих оценок по группам моделей – максимальное (верхняя строка) и минимальное (нижняя строка). Влияние сближения меридианов можно оценить путем попарного сравнения этих значений для двух способов, используя для удобства анализа обобщенные (по всем группам моделей) показатели, приведенные в табл. 3: ${{M}_{\mu }}$ и ${{R}_{\mu }}$ – модуль медианы и размах граничных значений $\mu $; ${{M}_{\sigma }}$ и ${{R}_{\sigma }}$ – медиана и размах граничных значений $\sigma .$
Таблица 1.
Границы статистических характеристик модельных значений ВКГ и АСТ в зависимости от класса моделей и способа вычисления (вариант 1)
| Область исследования | Класс моделей | ВКГ, м | АСТ, мГал | ||||||
|---|---|---|---|---|---|---|---|---|---|
| БС | МС | БС | МС | ||||||
| $\mu $ | $\sigma $ | $\mu $ | $\sigma $ | $\mu $ | $\sigma $ | $\mu $ | $\sigma $ | ||
| Земной шар | МСВР | –0.808 | 29.207 | | µ | < 0.001 | 30.577 | –0.461 | 34.723 | | µ | < 0.001 | 35.453 |
| –0.813 | 29.204 | 30.576 | –0.485 | 33.281 | 34.628 | ||||
| МВР(З) | –0.808 | 29.230 | 30.601 | –0.363 | 32.354 | 33.222 | |||
| –0.843 | 29.178 | 30.553 | –0.673 | 25.458 | 26.241 | ||||
| МВР(О) | –0.804 | 29.209 | 30.676 | –0.389 | 32.632 | 31.263 | |||
| –0.826 | 29.188 | 30.573 | –0.462 | 27.083 | 27.964 | ||||
| МСР | –0.782 | 29.242 | 30.587 | –0.117 | 38.312 | 38.272 | |||
| –0.867 | 29.180 | 30.570 | –0.834 | 19.344 | 19.560 | ||||
| МНР | –0.775 | 29.243 | 30.620 | –0.083 | 45.692 | 50.752 | |||
| –0.848 | 29.122 | 30.497 | –0.714 | 16.180 | 16.331 | ||||
| Арктика | МСВР | 11.933 | 14.860 | 10.240 | 17.917 | 4.201 | 33.044 | 2.608 | 34.340 |
| 11.910 | 14.855 | 10.235 | 17.915 | 3.808 | 27.445 | 2.575 | 28.676 | ||
| МВР(З) | 11.941 | 14.862 | 10.248 | 17.941 | 4.234 | 26.374 | 2.626 | 27.649 | |
| 11.682 | 14.842 | 10.183 | 17.909 | 2.388 | 20.97 | 2.536 | 22.443 | ||
| МВР(О) | 11.952 | 14.860 | 10.245 | 17.917 | 4.221 | 30.36 | 2.577 | 31.937 | |
| 11.568 | 14.384 | 9.984 | 17.417 | 3.888 | 19.623 | 2.488 | 21.800 | ||
| МСР | 11.963 | 14.882 | 10.253 | 17.941 | 4.787 | 31.525 | 2.627 | 28.769 | |
| 11.749 | 14.843 | 10.181 | 17.912 | 2.493 | 20.493 | 2.395 | 22.619 | ||
| МНР | 12.079 | 14.981 | 10.281 | 18.006 | 7.344 | 40.658 | 2.895 | 33.601 | |
| 11.554 | 14.757 | 10.172 | 17.828 | 1.185 | 11.083 | 2.326 | 13.144 | ||
| Россия | МСВР | –5.354 | 18.018 | –5.636 | 18.696 | –1.437 | 32.777 | –1.392 | 33.913 |
| –5.356 | 18.017 | –5.638 | 18.695 | –1.460 | 31.405 | –1.427 | 32.743 | ||
| МВР(З) | –5.358 | 18.027 | –5.637 | 18.707 | –1.463 | 30.086 | –1.422 | 31.400 | |
| –5.405 | 17.969 | –5.684 | 18.643 | –1.656 | 22.519 | –1.602 | 23.676 | ||
| МВР(О) | –5.328 | 18.045 | –5.612 | 18.762 | –1.306 | 31.587 | –1.271 | 32.626 | |
| –5.381 | 18.030 | –5.685 | 18.714 | –1.552 | 26.372 | –1.495 | 27.587 | ||
| МСР | –5.328 | 18.030 | –5.610 | 18.708 | –1.344 | 33.775 | –1.321 | 34.872 | |
| –5.393 | 18.011 | –5.674 | 18.689 | –1.493 | 24.246 | –1.446 | 25.295 | ||
| МНР | –5.337 | 18.050 | –5.621 | 18.721 | –1.314 | 39.034 | –1.274 | 38.403 | |
| –5.401 | 17.913 | –5.676 | 18.585 | –1.733 | 11.716 | –1.652 | 12.033 | ||
Таблица 2.
Границы статистических характеристик модельных значений ВКГ и АСТ в зависимости от класса моделей и способа вычисления (вариант 2)
| Область исследования | Класс моделей | ВКГ, м | АСТ, мГал | ||||||
|---|---|---|---|---|---|---|---|---|---|
| БС | МС | БС | МС | ||||||
| $\mu $ | $\sigma $ | $\mu $ | $\sigma $ | $\mu $ | $\sigma $ | $\mu $ | $\sigma $ | ||
| Земной шар | МСВР | 0.000 | 0.192 | | µ | < 0.001 | 0.146 | 0.016 | 9.928 | | µ | < 0.001 | 7.603 |
| –0.002 | 0.115 | 0.103 | –0.008 | 3.132 | 2.904 | ||||
| МВР(З) | 0.009 | 1.524 | < 0.001 | 0.114 | 21.792 | 22.314 | |||
| –0.030 | 0.182 | < 0.001 | –0.196 | 12.302 | 12.816 | ||||
| МВР(О) | 0.009 | 1.524 | < 0.001 | 0.088 | 22.345 | 22.114 | |||
| –0.013 | 0.451 | < 0.001 | 0.015 | 19.051 | 18.717 | ||||
| МСР | 0.031 | 1.012 | 0.992 | 0.361 | 34.230 | 34.370 | |||
| –0.054 | 0.308 | 0.322 | –0.356 | 18.679 | 19.814 | ||||
| МНР | 0.038 | 1.976 | 2.071 | 0.835 | 42.908 | 48.730 | |||
| –0.035 | 0.442 | 0.470 | –0.236 | 21.281 | 22.886 | ||||
| Арктика | МСВР | 0.001 | 0.189 | 0.001 | 0.107 | 0.050 | 18.456 | 0.013 | 18.907 |
| –0.227 | 0.068 | –0.005 | 0.073 | –0.342 | 2.599 | –0.020 | 2.469 | ||
| МВР(З) | 0.008 | 1.450 | 0.008 | 1.061 | 0.084 | 21.79 | 0.030 | 19.679 | |
| –0.250 | 0.083 | –0.057 | 0.085 | –1.762 | 8.9 | –0.059 | 8.723 | ||
| МВР(О) | 0.019 | 1.070 | 0.005 | 1.040 | 0.070 | 19.888 | –0.019 | 19.04 | |
| –0.364 | 0.413 | –0.256 | 0.387 | –0.262 | 18.239 | –0.107 | 15.993 | ||
| МСР | 0.030 | 0.982 | 0.013 | 0.703 | 0.637 | 29.069 | 0.032 | 25.343 | |
| –0.183 | 0.298 | –0.059 | 0.283 | –1.658 | 14.425 | –0.200 | 13.327 | ||
| МНР | 0.147 | 2.140 | 0.031 | 1.941 | 3.194 | 41.027 | 0.300 | 33.772 | |
| –0.378 | 0.427 | –0.068 | 0.427 | –2.965 | 19.790 | –0.267 | 19.250 | ||
| Россия | МСВР | 0.001 | 0.082 | 0.001 | 0.082 | 0.001 | 9.309 | –0.001 | 8.674 |
| –0.001 | 0.069 | –0.001 | 0.069 | –0.023 | 1.632 | –0.035 | 1.637 | ||
| МВР(З) | 0.002 | 0.577 | 0.002 | 0.593 | –0.026 | 18.418 | –0.030 | 19.047 | |
| –0.367 | 0.090 | –0.047 | 0.092 | –0.218 | 9.258 | –0.210 | 9.626 | ||
| МВР(О) | 0.027 | 0.693 | 0.025 | 0.736 | 0.131 | 18.606 | 0.121 | 19.123 | |
| –0.026 | 0.328 | –0.048 | 0.337 | –0.114 | 14.658 | –0.103 | 15.247 | ||
| МСР | 0.026 | 0.874 | 0.027 | 0.893 | 0.115 | 30.26 | 0.071 | 31.048 | |
| –0.038 | 0.270 | –0.037 | 0.278 | –0.056 | 16.878 | –0.054 | 17.500 | ||
| МНР | 0.017 | 1.733 | 0.016 | 1.808 | 0.124 | 36.762 | 0.118 | 35.989 | |
| –0.047 | 0.455 | –0.039 | 0.473 | –0.596 | 20.582 | –0.260 | 21.434 | ||
Таблица 3.
Обобщенные показатели граничных оценок среднего и стандартного отклонения модельных значений ВКГ и АСТ
| Область исследования | Оцениваемый показатель | ВКГ, м | АСТ, мГал | ||||
|---|---|---|---|---|---|---|---|
| Способ оценки | Изменение “МС-БС”, % | Способ оценки | Изменение “БС-МС”, % | ||||
| БС | МС | БС | МС | ||||
| Вариант 1. Оценки по абсолютным значениям ВКГ и АСТ | |||||||
| Земной шар | ${{M}_{\mu }}$ | 0.82 | ≈0.00 | ≈–100 | 0.46 | ≈0 | ≈–100 |
| ${{M}_{\sigma }}$ | 29.20 | 30.58 | +4.7 | 32.49 | 32.24 | –0.8 | |
| ${{R}_{\mu }}$ | 0.01 | ≈0.00 | ≈–100 | 0.075 | ≈0 | ≈–100 | |
| ${{R}_{\sigma }}$ | 0.12 | 0.18 | +50.0 | 29.5 | 34.4 | +16.6 | |
| Арктика | ${{M}_{\mu }}$ | 11.92 | 10.24 | –14.1 | 4.04 | 2.58 | –36.1 |
| ${{M}_{\sigma }}$ | 14.85 | 17.92 | +20.7 | 26.91 | 28.16 | +4.4 | |
| ${{R}_{\mu }}$ | 0.52 | 0.30 | –42.3 | 6.16 | 0.57 | –90.7 | |
| ${{R}_{\sigma }}$ | 0.60 | 0.59 | –1.7 | 29.58 | 21.20 | –28.3 | |
| Россия | ${{M}_{\mu }}$ | 5.36 | 5.64 | +5.2 | 1.46 | 1.42 | –2.9 |
| ${{M}_{\sigma }}$ | 18.02 | 18.70 | +3.8 | 30.74 | 32.01 | +4.1 | |
| ${{R}_{\mu }}$ | 0.08 | 0.07 | –12.5 | 0.43 | 0.38 | –11.6 | |
| ${{R}_{\sigma }}$ | 0.14 | 0.18 | +28.6 | 28.35 | 29.25 | +3.2 | |
| Вариант 2. Оценки по относительным значениям ВКГ и АСТ | |||||||
| Земной шар | ${{M}_{\mu }}$ | ≈0 | ≈0 | < 0.051) | ≈0 | ≈0 | <0.051) |
| ${{M}_{\sigma }}$ | 0.45 | 0.12 | –73.5 | 20.17 | 20.96 | +3.4 | |
| ${{R}_{\mu }}$ | 0.09 | ≈0 | ≈–100 | 1.19 | ≈0 | ≈–100 | |
| ${{R}_{\sigma }}$ | 1.86 | 2.08 | +11.8 | 39.78 | 45.83 | +15.2 | |
| Арктика | ${{M}_{\mu }}$ | 0.09 | ≈0 | ≈–100 | 0.12 | 0.02 | –83.3 |
| ${{M}_{\sigma }}$ | 0.42 | 0.41 | –2.4 | 19.12 | 18.97 | –0.8 | |
| ${{R}_{\mu }}$ | 0.52 | 0.29 | –44.2 | 6.16 | 0.57 | –90.7 | |
| ${{R}_{\sigma }}$ | 2.07 | 1.87 | –9.7 | 38.43 | 31.30 | –18.6 | |
| Россия | ${{M}_{\mu }}$ | ≈0 | ≈0 | < 0.051) | 0.02 | 0.03 | +50.0 |
| ${{M}_{\sigma }}$ | 0.39 | 0.40 | +2.5 | 17.65 | 18.27 | +3.5 | |
| ${{R}_{\mu }}$ | 0.39 | 0.08 | –79.5 | 1.66 | 1.74 | +4.8 | |
| ${{R}_{\sigma }}$ | 0.73 | 0.38 | –47.9 | 35.13 | 34.35 | –2.2 | |
Вариант 1 – оценки по абсолютным значениям ВКГ и АСТ
Учет сближения меридианов вызвал:
– уменьшение ${{M}_{\mu }}$ по земному шару c 0.8 м для ВКГ и 0.5 мГал для АСТ практически до нулевого уровня (почти на 100%), что согласуется с теоретическими значениями, и достаточно резкое изменение (в сторону уменьшения) оценок средних значений ВКГ и АСТ в Арктике, причем это касается и ${{M}_{\mu }}$ (от 14 до 36%) и ${{R}_{\mu }}$ (от 40 до 90%);
– преобладающий рост значений ${{M}_{\sigma }}$ (от нескольких процентов до нескольких десятков процентов) при разнонаправленном изменении значений ${{R}_{\sigma }}$ – для земного шара они заметно увеличились как по ВКГ, так и по АСТ; для территории России также изменились в сторону увеличения, наиболее существенно – по ВКГ (примерно на 28%), а для Арктики, наоборот, уменьшились, в наибольшей степени – для АСТ (на уровне тех же 28%).
Вариант 2 – оценки по относительным значениям ВКГ и АСТ
Учет сближения меридианов характеризуется:
– сходным, но не столь заметным, как в варианте 1, эффектом для ${{M}_{\mu }}$ при более явном эффекте для ${{R}_{\mu }}$ по земному шару (уменьшение почти на 0.1 м для ВКГ и более чем на 1 мГал у АСТ), но при этом более заметным, по сравнению с вариантом 1;
– уменьшением значений и ${{M}_{\mu }}$ (от 80 до 100%) и ${{R}_{\mu }}$(от 44 до 90%) в Арктике, в то время как на территории России существенным можно считать только изменение ${{R}_{\mu }}$ для ВКГ – уменьшение с 0.39 до 0.08 м, почти на 80%;
– разнонаправленным изменением значений ${{M}_{\sigma }}$ и ${{R}_{\sigma }}$. Так, для ВКГ величина ${{M}_{\sigma }}$ по земному шару достаточно резко уменьшилась – на 0.3 м (более 70%), а на региональном уровне ее оценки, можно считать, практически не изменились. Для АСТ величина ${{M}_{\sigma }}$ по земному шару, наоборот, заметно увеличилась, почти на 0.8 мГал, хотя в процентном отношении рост составил всего 3.4%. Сходным образом (увеличение на 0.6 мГал, или на 3.5%) она изменилась и на территории России, а в Арктике ее значение, наоборот, несколько уменьшилось – на 0.15 мГал. Оценки ${{R}_{\sigma }}$ для земного шара они увеличили свои значения на 12–15%, в остальных случаях– уменьшились. В наибольшей степени это уменьшение затронуло: в Арктике – АСТ (более чем на 7 мГал, в относительной мере – 18.6%), на территории России – ВКГ (0.3 м, почти 48%).
В совокупности табл. 1–табл. 3 показывают, что учет сближения меридианов может оказывать существенное влияние на статистические характеристики модельных значений ВКГ и АСТ как абсолютных, так и относительных (для ВКГ – от нескольких дециметров до нескольких метров; для АСТ – от нескольких десятых долей до нескольких единиц миллигал) и для земного шара в целом, и для отдельных регионов, таких как Арктика и территория России. Однако какие-либо явные закономерности изменения оценок, отражающие этот эффект, практически не прослеживаются ни в том, ни в другом варианте, за исключением достаточно четко выраженного и вполне ожидаемого уменьшения их средних значений (по модулю), а также для абсолютных значений увеличения их стандартных отклонений по земному шару.
Дальнейшая задача сводилась к тому, чтобы выяснить, как при корректном учете сближения меридианов соотносятся между собой различные модели ГПЗ по статистическим характеристикам модельных значений ВКГ и АСТ.
Пределы изменения статистики модельных значений ВКГ и АСТ по всем отобранным моделям характеризуются на глобальном и региональном уровнях оценками, приведенными в табл. 4. Согласно этим оценкам, граничные значения могут варьироваться в пределах: для ВКГ – нескольких (2–6) метров по абсолютным значениям, нескольких (1–2) десятков метров по относительным значениям, причем это свойственно и глобальным, и региональным оценкам; для АСТ (как абсолютных, так и относительных) – в пределах нескольких (2–5 и более) сотен миллигал. Средние значения ВКГ и АСТ для земного шара в обоих вариантах близки к нулевым отметкам. Для сравнения, региональные оценки средних значений ВКГ меняются в пределах от нескольких сантиметров на территории России до нескольких дециметров в Арктике. Для АСТ диапазон их изменения в обоих случаях составляет около 0.5 мГал. При этом тренды абсолютных значений ВКГ и АСТ в Арктике положительны, а на территории России – отрицательны (по обеим границам средних значений). В отличие от этого, для относительных ВКГ и АСТ границы их средних значений знакопеременны. Стандартные отклонения варьируются в пределах: для ВКГ от нескольких (2–6) дециметров по абсолютным значениям до нескольких (1.5–2) метров по относительным значениям; для АСТ – нескольких (3–5) десятков мГал.
Таблица 4.
Пределы изменения статистических характеристик модельных значений ВКГ и АСТ
| Область | ВКГ, м | АСТ, мГал | ||||||
|---|---|---|---|---|---|---|---|---|
| ${{f}_{{\min }}}$ | ${{f}_{{\max }}}$ | $\mu $ | $\sigma $ | ${{f}_{{\min }}}$ | ${{f}_{{\max }}}$ | $\mu $ | $\sigma $ | |
| Вариант 1. Оценки по абсолютным значениям ВКГ и АСТ | ||||||||
| Земной шар | –108.10 | 82.03 | ≈0.00 | 30.50 | –417.9 | 85.8 | ≈0.0 | 16.3 |
| –106.20 | 87.98 | 30.68 | –60.8 | 749.5 | 50.8 | |||
| Арктика | –30.71 | 58.61 | 9.98 | 17.42 | –233.5 | 38.8 | 2.3 | 13.1 |
| –27.03 | 62.63 | 10.28 | 18.01 | –40.1 | 215.3 | 2.9 | 34.3 | |
| Россия | –47.33 | 25.68 | –5.68 | 18.58 | –282.1 | 33.0 | –1.6 | 12.0 |
| –42.17 | 28.55 | –5.61 | 18.76 | –27.4 | 238.1 | –1.3 | 38.4 | |
| Вариант 2. Оценки по относительным значениям ВКГ и АСТ | ||||||||
| Земной шар | –24.43 | 3.25 | ≈0.00 | 0.00 | –753.4 | 74.2 | ≈0.0 | 2.9 |
| 2.76 | 22.66 | 2.07 | –57.8 | 478.8 | 48.7 | |||
| Арктика | –10.63 | 0.42 | –0.26 | 0.07 | –240.7 | 18.3 | –0.3 | 2.5 |
| –0.43 | 10.03 | 0.03 | 1.94 | –24.7 | 298.4 | 0.3 | 33.8 | |
| Россия | –10.31 | 0.57 | –0.05 | 0.07 | –307.5 | 14.3 | –0.3 | 1.6 |
| –0.78 | 14.52 | 0.03 | 1.81 | –19.1 | 286.1 | 0.1 | 36.0 | |
Оценивая по той же таблице общий фон отклонений глобальных моделей ГПЗ, созданных в разные годы, от “эталонной” модели EGM-2008 до 2190-й степени по ВКГ и АСТ, можно отметить, что в целом по земному шару амплитуды отклонений по всем показателям, за исключением среднего, существенно выше, чем по отдельно взятым регионам Арктики и территории России. В свою очередь, амплитуды отклонений по всем показателям, за исключением части граничных значений, в зоне Арктики больше (от нескольких процентов до нескольких раз), чем на территории России. Это можно связать с улучшением изученности гравитационного поля в Арктике благодаря реализации новых методов космической геодезии и развитию гравиметрических съемок, в том числе в рамках международного сотрудничества [McAdoo, 2013].
Также в задачи данной работы входил анализ особенностей выявленных различий между исследуемыми моделями. Проведенный анализ показал, что эти различия могут быть разделены на внутригрупповые, межгрупповые и межрегиональные.
К внутригрупповым различиям можно отнести вариации оценок величин ${{f}_{{\min }}},\,\,{{f}_{{\max }}},\,\,\mu ,\,\,\sigma $, отдельно для ВКГ и АСТ, в определенной группе моделей для определенной области. Показателем таких различий может служить величина размаха ${{R}_{\varepsilon }}\left( {i\left| k \right.} \right)$ оцениваемой величины $\varepsilon $ в i-й группе моделей по k-й области исследования. По внутригрупповым различиям можно судить о влиянии на расхождения между моделями состава исходной информации, ее качества и методов обработки.
Межгрупповые различия можно характеризовать расхождениями оценок величины $\varepsilon $ в двух различных группах моделей для одной и той же исследуемой области. Показателем межгрупповых различий может служить величина:
(9)
$\Delta {{R}_{\varepsilon }}\left( {i,j\left| k \right.} \right) = \left| {{{R}_{\varepsilon }}\left( {i\left| k \right.} \right) - {{R}_{\varepsilon }}\left( {j\left| k \right.} \right)} \right|,$Межрегиональные различия можно характеризовать разностями значений одного и того же показателя по каждой, отдельно взятой группе моделей в каждой паре сравниваемых областей исследования. Для оценки межрегиональных различий может использоваться формула вида (9), где ${{R}_{\varepsilon }}\left( {i\left| k \right.} \right)$ и ${{R}_{\varepsilon }}\left( {j\left| k \right.} \right)$ – соответственно значения размаха оцениваемой величины в i-й и j-й области для k-й группы моделей. Анализ межрегиональных различий может использоваться, в частности, для оценки влияния на расхождения между моделями таких факторов как неоднородность гравитационного поля по его аномальности и изученности в различных регионах земного шара.
Для анализа различий между моделями ГПЗ могут использоваться данные, приведенные в табл. 5, а также графики, приведенные на рис. 1 и рис. 2. В табл. 5 представлены сгруппированные оценки размаха статистических характеристик ${{f}_{{\min }}},{{f}_{{\max }}}$, $\mu ,\,\,\sigma $ модельных значений ВКГ и АСТ, базирующиеся на полученных экспериментальных данных. Графики представляют в наглядном виде эмпирическую зависимость размаха ${{R}_{\sigma }}$ стандартных отклонений модельных значений ВКГ (рис. 1а, рис. 2а) и АСТ (рис. 1б, рис. 2б) от группы моделей, идентифицируемой номером (1 – МСВР; 2 – МВР(З); 3 – МВР(О); 4 – МСР; 5 – МНР), и области исследования, идентифицируемой типом линии графика (сплошная – земной шар; штрихпунктирная – Арктика; пунктирная – Россия).
Рис. 1
Зависимость размаха стандартных отклонений модельных ВКГ и АСТ (абсолютные значения) от группы моделей и области исследования: (а) – ВКГ; (б) – АСТ.
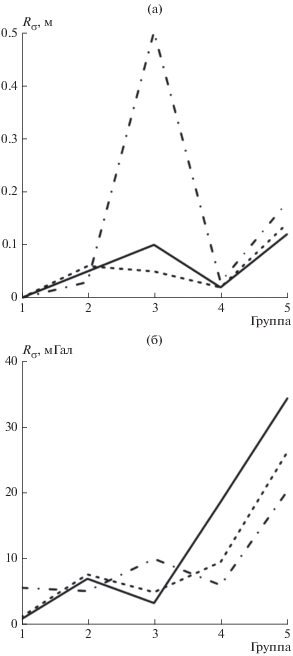
Рис. 2.
Зависимость размаха стандартных отклонений модельных ВКГ и АСТ (относительные значения) от группы моделей и области исследования: (а) – ВКГ; (б) – АСТ.
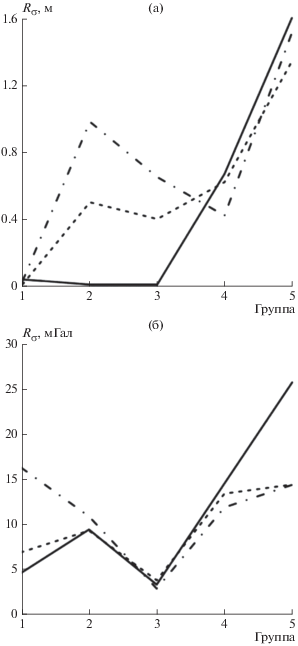
Таблица 5.
Групповые оценки размаха статистических характеристик модельных значений ВКГ и АСТ
| Область исследования | Группа моделей | ВКГ, м | АСТ, мГал | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ${{f}_{{\min }}}$ | ${{f}_{{\max }}}$ | $\mu $ | $\sigma $ | ${{f}_{{\min }}}$ | ${{f}_{{\max }}}$ | $\mu $ | $\sigma $ | ||
| Вариант 1. Оценки по абсолютным значениям ВКГ и АСТ | |||||||||
| Земной шар | МСВР | 0.06 | 0.13 | ≈0.00 | 0.00 | 4.0 | 40.5 | ≈0.0 | 0.8 |
| МВР(З) | 1.73 | 5.32 | 0.05 | 45.1 | 219.6 | 7.0 | |||
| МВР(О) | 0.84 | 1.49 | 0.10 | 32.3 | 242.1 | 3.3 | |||
| МСР | 1.69 | 1.97 | 0.02 | 270.2 | 361.8 | 18.7 | |||
| МНР | 1.89 | 5.95 | 0.12 | 357.2 | 346.9 | 34.4 | |||
| Арктика | МСВР | 0.04 | 0.13 | 0.01 | 0.00 | 44.9 | 15.9 | 0.0 | 5.7 |
| МВР(З) | 0.48 | 0.94 | 0.06 | 0.03 | 42.0 | 89.3 | 0.1 | 5.2 | |
| МВР(О) | 0.94 | 1.67 | 0.26 | 0.50 | 70.0 | 99.0 | 0.1 | 10.1 | |
| МСР | 1.10 | 0.97 | 0.07 | 0.03 | 28.5 | 55.9 | 0.2 | 6.1 | |
| МНР | 3.68 | 4.01 | 0.11 | 0.18 | 136.9 | 121.6 | 0.6 | 20.4 | |
| Россия | МСВР | 0.20 | 0.05 | 0.00 | 0.00 | 7.2 | 15.5 | 0.0 | 1.2 |
| МВР(З) | 1.85 | 0.54 | 0.05 | 0.06 | 64.2 | 85.4 | 0.2 | 7.7 | |
| МВР(О) | 1.47 | 1.15 | 0.07 | 0.05 | 35.3 | 84.0 | 0.2 | 5.0 | |
| МСР | 1.53 | 1.27 | 0.06 | 0.02 | 10.0 | 36.4 | 0.1 | 9.6 | |
| МНР | 5.16 | 3.17 | 0.06 | 0.14 | 160.7 | 163.2 | 0.4 | 26.3 | |
| Вариант 2. Оценки по относительным значениям ВКГ и АСТ | |||||||||
| Земной шар | МСВР | 6.76 | 1.56 | ≈0.00 | 0.04 | 238.0 | 207.8 | ≈0.0 | 4.7 |
| МВР(З) | 18.24 | 11.83 | ≈0.00 | 206.7 | 171.7 | 9.5 | |||
| МВР(О) | 14.51 | 8.39 | ≈0.00 | 282.9 | 60.1 | 3.4 | |||
| МСР | 6.67 | 7.83 | 0.67 | 118.7 | 31.7 | 14.6 | |||
| МНР | 16.06 | 17.72 | 1.60 | 270.2 | 98.9 | 25.8 | |||
| Арктика | МСВР | 0.63 | 0.26 | 0.00 | 0.03 | 57.8 | 77.0 | 0.0 | 16.4 |
| МВР(З) | 6.68 | 5.04 | 0.05 | 0.98 | 96.2 | 77.1 | 0.1 | 11.0 | |
| МВР(О) | 3.24 | 2.25 | 0.07 | 0.65 | 54.4 | 41.1 | 0.1 | 3.0 | |
| МСР | 3.10 | 2.95 | 0.06 | 0.42 | 44.9 | 117.5 | 0.2 | 12.0 | |
| МНР | 7.47 | 7.26 | 0.06 | 1.51 | 49.5 | 57.9 | 0.6 | 14.5 | |
| Россия | МСВР | 0.50 | 0.30 | 0.00 | 0.01 | 51.9 | 69.0 | 0.0 | 7.0 |
| МВР(З) | 4.06 | 3.23 | 0.00 | 0.50 | 127.5 | 85.1 | 0.2 | 9.4 | |
| МВР(О) | 4.20 | 10.31 | 0.02 | 0.40 | 83.8 | 112.7 | 0.2 | 3.9 | |
| МСР | 1.79 | 1.28 | 0.03 | 0.62 | 53.6 | 48.3 | 0.1 | 13.5 | |
| МНР | 5.71 | 12.90 | 0.02 | 1.34 | 63.1 | 46.5 | 0.4 | 14.5 | |
Приведенные оценки и графики показывают, что в статистическом смысле между моделями ГПЗ, в том числе полученными относительно недавно, имеются довольно значительные различия всех трех видов – внутригрупповые, межгрупповые, межрегиональные, причем эти различия заметно варьируются не только в зависимости от вида моделируемой величины (ВКГ или АСТ) и оцениваемого статистического показателя, но и от того, по каким значениям ВКГ и АСТ, абсолютным (вариант 1) или относительным (вариант 2), вычисляются статистические характеристики.
В первом варианте наименьшие внутригрупповые различия, как правило, характерны для МСВР: ВКГ – не более 20 см по ${{R}_{f}}$, около 1 см по ${{R}_{\mu }}$, не более нескольких миллиметров по ${{R}_{\sigma }}$; АСТ – в пределах 45, 1 и 6 мГал соответственно. Это существенно, в ряде случаев – многократно меньше по сравнению с другими группами моделей. Следующую позицию по внутригрупповым различиям разделили между собой МВР и МСР, причем, по земному шару в целом – отечественные модели, по Арктике и территории России – зарубежные модели. Наибольшие внутригрупповые различия продемонстрировали МНР: по ${{R}_{f}}$ – до 3–5 м и 150–350 мГал, по ${{R}_{\sigma }}$ – до 15–20 см и 25–30 мГал, соответственно для ВКГ и АСТ. Такой расклад обусловливается: в части МСВР – отсутствием резких изменений в составе используемой исходной информации; в части МВР – относительной малочисленностью отечественных моделей, а также различием отечественных и зарубежных моделей по составу исходной спутниковой и гравиметрической информации, в том числе в регионах Арктики и Российской Федерации; в части МНР – варьированием состава исходной спутниковой информации – только наземные траекторные измерения; только измерения по линии “спутник–спутник”; комбинированные варианты.
Межгрупповые различия в обоих случаях (ВКГ, АСТ) выражаются в тенденции к увеличению вариации одноименных показателей с уменьшением размерности моделей, особенно для АСТ, что достаточно хорошо иллюстрируют графики, приведенные на рис. 1 . Вместе с этим, графики подчеркивают и такую специфику, как относительно большие по сравнению с моделями других групп, значения $\Delta {{R}_{\sigma }}$ для отечественных моделей, особенно в сравнении с зарубежными моделями высокого и среднего разрешения. К этому следует добавить и относительно высокий в целом уровень межрегиональных различий у МВР(O) по сравнению с аналогичными зарубежными моделями, в основном за счет Арктики. Последнее также можно объяснить особенностями исходной информации в части использования новых данных космической геодезии, полученных низкоорбитальными космическими аппаратами с близкой к 100% степенью покрытия земного шара, включая его полярные районы. Вообще говоря, межрегиональные различия в первом варианте сильнее проявляются по АСТ, чем по ВКГ, что обусловлено влиянием структуры аномального ГПЗ.
Во втором варианте в целом наименьшие внутригрупповые различия показали: по ВКГ – МСВР (${{R}_{f}}$ – от нескольких дециметров до нескольких метров; ${{R}_{\sigma }}$ – на уровне нескольких сантиметров), особенно на региональном уровне; по АСТ –МВР, причем отечественные (${{R}_{f}}$ – как правило, на уровне нескольких десятков миллигал; ${{R}_{\sigma }}$ – до 3–4 мГал). Отмеченный характер внутригрупповых различий МСВР можно объяснить тем, что модели, выпущенные после 2008 г., хотя и реализуют в той или иной степени новую измерительную информацию, включая данные спутниковой альтиметрии и спутниковой градиентометрии в Арктике, все же в значительной мере опираются на исходную модель EGM-2008. Внутригрупповая близость МВР(О), видимо, обусловлена использованием этими моделями относительно стабильного, по сравнению с зарубежными моделями, массива исходной информации о средних значениях АСТ.
Специфика межгрупповых различий в части отклонений от модели EGM-2008, судя по рис. 2 , в наибольшей степени проявляется в диапазоне моделей сверхвысокого и высокого разрешения, причем существенный вклад в это вносит Арктика. С учетом интенсивности обновления исходной информации о гравитационных аномалиях в Арктике данный факт можно считать вполне закономерным. Межрегиональные различия по ВКГ в данном варианте наиболее заметны у МВР, по АСТ –у МСВР и МНР, что также в определенной мере обусловлено спецификой исходной информации.
Сравнение двух вариантов показывает, что для ВКГ при переходе от их абсолютных к относительным значениям и внутригрупповые и межгрупповые и межрегиональные различия моделей в целом возрастают, а для АСТ, наоборот, ослабевают. Так, межгрупповые различия между МСВР и МНР по стандартным отклонениям ВКГ увеличились, в зависимости от области исследования, в 8–13 раз, а по стандартным отклонениям АСТ уменьшились, в 1.5–3 раза и более. Как показывает сравнение графиков, приведенных на рис. 1 и рис. 2 , по характеру межгрупповых и межрегиональных различий статистические характеристики модельных ВКГ и АСТ в двух вариантах в целом согласуются в диапазоне МСР и МНР, но заметно расходятся в диапазоне МСВР и МВР. При этом обращает на себя внимание особое, по отношению к моделям других групп, поведение российских МВР. Также из сопоставления графиков видно, что в статистическом смысле межгрупповые различия моделей ГПЗ по АСТ, по крайней мере, по региональным оценкам, причем как в абсолютных, так и в относительных величинах, выглядят менее интенсивными по сравнению с вариациями соответствующих оценок этих моделей по ВКГ. Вероятно, это также в определенной мере является следствием динамики объемов и видового разнообразия новой исходной информации, полученной с использованием систем “спутник–спутник” и спутниковой градиентометрии.
ЗАКЛЮЧЕНИЕ
Проведенные в данной работе исследования по сравнительной оценке глобальных моделей ГПЗ в виде сферических гармоник геопотенциала позволяют сделать следующие основные выводы:
1) результаты сравнительной оценки моделей указанного типа зависят от ряда особенностей проведения исследований такого рода, к числу которых можно отнести: географическое положение области исследования, расположение оценочных точек, состав исследуемых моделей, набор оцениваемых показателей (статистических характеристик расхождений между моделями) и способы их вычисления. Новизна данной работы определяется составом исследуемых моделей, включающим не только большое число (100) современных зарубежных, но и ряд отечественных моделей, использованием при сравнении моделей как абсолютных, так и относительных значений параметров ГПЗ, в том числе ВКГ и АСТ, сравнительным анализом модельных значений ВКГ и АСТ как по земному шару в целом, так и по отдельным регионам, таким как Арктика и территория России, а также оценкой эффекта, обусловленного учетом сближения меридианов расчетных точек;
2) сравнительный анализ моделей удобно проводить на регулярной сетке меридианов и параллелей для использования эффективных в вычислительном отношении алгоритмов расчета модельных значений параметров аномального ГПЗ. При этом сближение меридианов оценочных точек (узлов сетки) может относительно просто учитываться в процессе статистической обработки модельных значений параметров ГПЗ путем замены базового способа вычисления средних значений и стандартных отклонений по формулам (4), (5) модифицированным вариантом (6), (7) с весовыми коэффициентами (8);
3) полученные экспериментальные данные показывают, что расхождения между статистическими характеристиками одних и тех же модельных значений параметров ГПЗ, вычисленными двумя описанными способами, могут быть значительными: для ВКГ – от нескольких дециметров до нескольких метров; для АСТ – от нескольких десятых долей до нескольких единиц миллигал. Поэтому при сравнении современных глобальных моделей ГПЗ целесообразно использовать модифицированный способ оценки средних значений и стандартных отклонений моделируемых величин на равномерной сетке меридианов и параллелей как по земному шару в целом, так и по отдельным областям, включающим районы средних и высоких широт;
4) представленные результаты сравнительного исследования моделей, созданных в разные годы, с использованием различных видов исходной информации и методик ее обработки, актуализируют общее представление о том, насколько при корректном учете сближения меридианов оценочных точек, велики или, наоборот, малы различия между моделями различной размерности (разрешающей способности), между моделями, созданными по зарубежным и отечественным технологиям, а также между моделями, созданными без использования и с использованием новых данных космической геодезии, полученных с помощью систем “спутник–спутник” и спутниковой градиентометрии. При этом в методике сравнительного исследования целесообразно в общем случае учитывать наличие внутригрупповых, межгрупповых и межрегиональных различий между исследуемыми моделями.
Список литературы
Мориц Г. Современная физическая геодезия. Пер. с англ. М.: Недра. 1983. 392 с.
Непоклонов В.Б., Максимова М.В. Координатная основа пространственных данных как объект геоинформационного анализа и моделирования // Изв. вузов. Геодезия и аэрофотосъемка. 2016а. № 1. С. 22–28.
Непоклонов В.Б., Максимова М.В., Абакушина М.В. Анализ динамики системы математических моделей гравитационного поля Земли // Изв. вузов. Геодезия и аэрофотосъемка. 2016б. № 3. С. 8–14.
Сугаипова Л.С. О планируемых проектах спутниковой гравиметрии // Изв. вузов. Геодезия и аэрофотосъемка. 2015. № 6. С. 3–8.
Яшкин С.Н. Спутниковая градиентометрия и системы “спутник–спутник”. М.: изд-во МИИГАиК. 2009. 112 с.
Hwang C., Yu-Chi Kao. Spherical harmonic analysis and synthesis using FFT: Application to temporal gravity variation // Computers and Geosciences. 2006. V. 32. P. 442–451.
International Centre for Global Earth Models (ICGEM) – URL: http://icgem.gfz-potsdam.de/home. (Дата обращения: 28.10.2019 г.).
McAdoo D.C., Farrell S.L., Laxon S., Ridout A., Zwally H.J., Donghui Yi. Gravity of the Arctic Ocean from satellite data with validations using airborne gravimetry: Oceanographic implications // J. geophysical research: oceans. 2013. V. 118. P. 917–930.
Pavlis N.K., Holmes S.A., Kenyon S.C., Factor J.K. An Earth Gravitational Model to Degree 2160: EGM2008 / EGU General Assembly 2008. Vienna, Austria, April 13–18, 2008. URL: http://earth-info.nga.mil/GandG/wgs84/gravitymod/ egm2008
Xiong Li, Götze H.-J. Tutorial. Ellipsoid, geoid, gravity, geodesy, and geophysics // Geophysics. 2001. V. 66. № 6. P. 1660–1668.
Дополнительные материалы отсутствуют.


