Физика Земли, 2020, № 2, стр. 3-9

Методика комплексирования поверхностно-волновой томографии и результатов метода приемных функций при изучении скоростного разреза верхней мантии

Т. Б. Яновская^*

Санкт-Петербургский государственный университет
г. Санкт-Петербург, Россия

Поступила в редакцию 24.10.2019
После доработки 30.10.2019
Принята к публикации 01.11.2019

DOI: 10.31857/S0002333720020118

Аннотация

С целью совместной инверсии данных о дисперсии скоростей поверхностных волн, измеряемых на протяженных трассах, и результатов метода приемных функций предлагается метод, основанный на модификации процедуры поверхностно-волновой томографии, позволяющий использовать данные не только по трассам, но и получаемые в отдельных изолированных точках. Вначале данные приводятся к одному типу: либо к скорости поверхностной волны путем вычисления дисперсионной кривой для разреза, полученного методом приемных функций, либо к скорости поперечной волны путем одномерной инверсии наблюдаемых на трассах дисперсионных кривых поверхностной волны. Таким образом, в вычислительном аспекте задача сводится к следующей: определить двумерное сглаженное распределение функции по данным значений этой функции в отдельных точках и средних по линиям (трассам), которые можно принимать прямыми. Прямое применение процедуры поверхностно-волновой томографии в предположении, что точки являются линиями нулевой длины, бесполезно, так как решение оказывается сингулярным в точках. Для устранения этого недостатка предложено заменять точки окружностями малого радиуса вокруг них. Тогда задача томографии расширяется от использования данных только по линейным трассам до включения данных по круговым трассам. Модельные расчеты показали, что добавление данных в точках приводит к увеличению разрешения.

Ключевые слова: дисперсия скорости, поверхностно-волновая томография, одномерная инверсия.

1. ВВЕДЕНИЕ

В настоящее время существуют два основных метода исследования распределения скоростей сейсмических волн в верхней мантии – это поверхностно-волновая томография (Surface Wave Tomoraphy – SWT) [Дитмар и др., 1987; Яновская, 2015; Barmin et al., 2001] и метод приемных функций (Receiver Function Method – RF) [Vinnik, 1977; Винник и др., 1981; Винник, 2019]. Методы принципиально различаются как по типам используемых данных, так и по окончательным результатам. В SWT исходными данными являются дисперсионные кривые групповых скоростей поверхностных волн, измеряемые по протяженным трассам (очаг–станция или станция–станция), тогда как в RF – это сигналы в объемных волнах, подходящие к приемной станции от удаленных источников почти вертикально. Результатом SWT являются либо локально-сглаженные дисперсионные кривые, либо построенные по ним локально-сглаженные скоростные разрезы поперечных волн, причем степень сглаженности зависит от количества и взаимной ориентации трасс. В то время как результатом RF является локальный скоростной разрез под станцией. Точнее, не разрез непосредственно под точкой расположения станции, а средний в некоторой узкой ее окрестности. Следует отметить, что практически отсутствуют работы, в которых бы выполнялась совместная интерпретация данных SWT и RF. В работах, где делались попытки использовать те и другие данные, распределение скорости подбиралось так, чтобы удовлетворить по возможности всем данным [Винник и др., 2014]. В то же время очевидно, что поскольку конечной целью и того, и другого метода является получение сведений о распределении сейсмических скоростей в коре и верхней мантии, то представляется желательным разработать такую методику, которая бы позволяла обрабатывать данные двух методов совместно и получать такое распределение скорости, которое бы удовлетворяло обоим типам данных.

Такой подход и предлагается в данной работе.

МЕТОД

По методу приемных функций P-волн определяется скоростной разрез поперечных волн под станцией. А по данным, используемым для SWT, – дисперсионным кривым поверхностной волны по трассам – можно определить средний по трассе скоростной разрез поперечной волны. Таким образом, для каждой конкретной глубины мы будем иметь скорости S-волн средние по трассам и их значения в отдельных точках. Поэтому задача сведется к тому, чтобы определить двумерные (сглаженные) распределения скорости S-волн на последовательных глубинах по средним значениям на трассах и по значениям в точках.

Возможен и другой подход, сводящийся к такой же задаче. Построенный по методу RF скоростной разрез поперечных волн дает возможность вычислить дисперсионную кривую поверхностной волны в точке под станцией. В результате, объединяя данные двух методов, мы будем иметь дисперсионные кривые по трассам (SWT) и дисперсионные кривые в точках расположения станций. И задача опять же сводится к расширению процедуры SWT путем включения в блок данных помимо средних значений по трассам еще и данные в точках.

На первый взгляд может показаться, что к таким данным можно было бы применить обычную процедуру SWT, принимая при этом нулевыми длины “трасс”, отвечающих точкам. Однако такой способ приводит к тому, что исходные данные – временны́е невязки на таких трассах – оказываются нулевыми.

Очевидно, что способ модификации процедуры SWT должен зависеть от метода, положенного в основу этой процедуры. Методы можно разделить на два класса: (1) параметризация модели и поиск параметров модели [Nakanishi et al., 1982; Mantovani et al., 1985; Zhang et al., 1989; Ritzwoller et al., 1998; Barmin et al., 2001]; (2) наложение условий на решение [Tarantola et al., 1984; Дитмар и др., 1987]. Большинство из первой группы методов состоит в разбиении территории на блоки (ячейки) и оценке средних значений искомой функции в каждом из блоков. Этот метод оказывается эффективным в случае очень большого количества данных по трассам и их равномерного распределении по азимутам. Более широкое применение получила методика, основанная на предположении о гладкости искомой функции [Дитмар и др., 1987], так как она не накладывает ограничений на количество и качество исходных данных: просто в тех участках, где данных недостаточно, разрешение оказывается низким.

Итак, автоматическая замена данных в точках данными по трассам нулевой длины приведет к нулевым временным невязкам, а именно временные невязки являются входными данными в системе линейных уравнений, к которым и сводится в конечном итоге процедура SWT. Поэтому для возможности использования таких данных в процедуре томографии предлагается данные в точках заменить их средними значениями по окружностям малого радиуса, окружающим данные точки. Эти окружности можно рассматривать как трассы круговой формы в отличие от прямолинейных трасс очаг–станция (или станция–станция), по которым измерены скорости поверхностных волн. Такая замена вполне правомерна, поскольку разрезы, получаемые из RF, фактически отвечают не точке, а некоторой ее окрестности. Таким образом, оказывается достаточным модифицировать процедуру SWT так, чтобы включить данные по круговым трассам в процедуру SWT, основанную на естественных предположениях – о гладкости искомой функции (относительной поправки к скорости) и конечности этой поправки на бесконечности.

Будем обозначать искомую поправку $m({\mathbf{r}}) = \frac{{\delta V({\mathbf{r}})}}{{{{V}_{0}}}},$ где: r = (x, y); V₀ – средняя скорость для рассматриваемого периода волны на изучаемой территории. Таким образом, искомая функция должна удовлетворять следующим условиям:

(1)

$\iint {(\nabla m,\nabla m)d{\mathbf{r}}} = \min $

(условие гладкости);

(2)

$\int\limits_{{{L}_{i}}} {m({\mathbf{r}})\frac{{d{{s}_{i}}}}{{{{V}_{0}}}}} = \delta {{t}_{i}} = {{t}_{i}} - {{t}_{{0i}}},\,\,\,\,i = 1,2,...N$

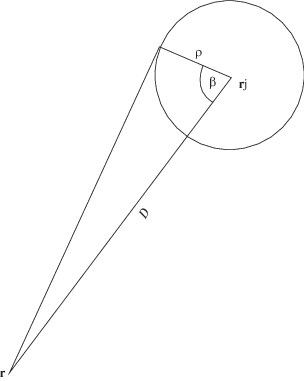
(временные невязки по N-прямолинейным трассам L_i);

(3)

$\oint\limits_{{{S}_{j}}} {m({\mathbf{r}})\frac{{d{{s}_{{}}}}}{{{{V}_{0}}}}} = \delta {{t}_{j}} = 2\pi \rho \left( {\frac{1}{{{{V}_{j}}}} - \frac{1}{{{{V}_{o}}}}} \right)\,\,\,\,j = 1,....,n$

(невязки по n круговым трассам S_j);

(4)

$m({\mathbf{r}}) = {\text{const}}\,\,\,\,{\text{при}}\,\,\,\,\left| {\mathbf{r}} \right| \to \infty $

(условие конечности решения на бесконечности).

Здесь через t_0i обозначено время пробега по i-й (j-й) трассе в начальном приближении V₀, а ρ обозначает радиус окружности вокруг n точек. В принципе эти радиусы могут для разных точек быть разными, но здесь для простоты они приняты одинаковыми.

Как и в стандартной процедуре SWT, решение представляется в виде разложения по базисным функциям, которые определяются из условия гладкости (1), а коэффициенты при них – из условий (2)–(4).

Базисные функции, отвечающие линейным трассам, те же самые, что и в стандартной процедуре SWT [Дитмар и др., 1987; Яновская, 2015], т.е.

(5)

${{\psi }_{i}}({\mathbf{r}}) = \int\limits_{{{L}_{i}}} {\ln \left| {{\mathbf{r}} - {{{\mathbf{r}}}_{i}}} \right|} d{{s}_{i}},$

а функции, отвечающие круговым трассам, определяются аналогично, но при этом имеют более простой вид. Это иллюстрируется рис. 1:

$\begin{gathered} {{\varphi }_{j}}({\mathbf{r}}) = \frac{R}{{{{V}_{0}}}}\int\limits_0^{2\pi } {\ln \sqrt {{{D}^{2}} + {{\rho }^{2}} - 2D\rho \cos \vartheta } d\vartheta } = \\ = \frac{{2\pi \rho }}{{{{V}_{0}}}}\left. {\left( \begin{gathered} \ln D{\text{ }}D > \rho \hfill \\ \ln \rho {\text{ }}D < \rho \hfill \\ \end{gathered} \right.} \right), \\ \end{gathered} $

где $D = \left| {{\mathbf{r}} - {{{\mathbf{r}}}_{j}}} \right|$ [Прудников и др., 1981]. Таким образом, базисная функция оказывается постоянной внутри круга и возрастает как логарифм расстояния от текущей точки до центра круга.

Рис. 1.

Иллюстрация вывода базисной функции для круговой трассы.

Решение, таким образом, представляется в виде линейной комбинации базисных функций:

(6)

$m({\mathbf{r}}) = \sum\limits_{i = 1}^N {{{\lambda }_{i}}{{\psi }_{i}}({\mathbf{r}})} + \sum\limits_{j = 1}^n {{{\mu }_{j}}{{\varphi }_{j}}({\mathbf{r}})} + C.$

Константа С, как и в стандартной процедуре SWT, добавлена для того, чтобы обеспечить конечность решения на бесконечности.

Коэффициенты при базисных функциях определяются из уравнений, вытекающих из (2)–(4):

(7)

$\begin{gathered} \delta {{t}_{k}} = \sum\limits_{i = 1}^N {{{\lambda }_{i}}\int\limits_{{{L}_{k}}} {{{\psi }_{i}}(x,y){{ds} \mathord{\left/ {\vphantom {{ds} {{{V}_{{\text{0}}}}}}} \right. \kern-0em} {{{V}_{{\text{0}}}}}}} } + \\ + \,\,\sum\limits_{j = 1}^n {{{\mu }_{j}}\int\limits_{{{L}_{k}}} {{{\varphi }_{j}}} (x,y)} {{ds} \mathord{\left/ {\vphantom {{ds} {{{V}_{{\text{0}}}}}}} \right. \kern-0em} {{{V}_{{\text{0}}}}}} + {{C}_{0}}{{t}_{{0k}}} \\ (k = 1,2, \ldots .N), \\ \end{gathered} $

(8)

$\begin{gathered} \delta {{t}_{q}} = \sum\limits_{i = 1}^N {{{\lambda }_{i}}\oint\limits_{{{S}_{q}}} {{{\psi }_{i}}(x,y){{d{{s}_{q}}} \mathord{\left/ {\vphantom {{d{{s}_{q}}} {{{V}_{{\text{0}}}}}}} \right. \kern-0em} {{{V}_{{\text{0}}}}}}} } + \\ + \,\,\sum\limits_{j = 1}^n {{{\mu }_{j}}\oint\limits_{{{S}_{q}}} {{{\phi }_{j}}(x,y)} } {{d{{s}_{q}}} \mathord{\left/ {\vphantom {{d{{s}_{q}}} {{{V}_{{\text{0}}}}}}} \right. \kern-0em} {{{V}_{{\text{0}}}}}} + 2\pi \rho {C \mathord{\left/ {\vphantom {C {{{V}_{{\text{0}}}}}}} \right. \kern-0em} {{{V}_{{\text{0}}}}}}, \\ (q = 1.2, \ldots n), \\ \end{gathered} $

(9)

$\sum\limits_{i = 1}^N {{{\lambda }_{i}}{{t}_{{0i}}} + \sum\limits_{j = 1}^n {{{\mu }_{j}}} } \frac{{2\pi \rho }}{{{{V}_{0}}}} = 0.$

Таким образом, задача сводится к решению системы N + n + 1 линейных уравнений и построению решения в точках сетки (x,y) по формуле (6).

ОЦЕНКА РАЗРЕШЕНИЯ

Как и в стандартной процедуре SWT, разрешающую способность данных проще всего оценивать величиной эффективного радиуса области сглаживания R [Дитмар и др., 1987; Яновская, 2015]. Оценка R производится по той же процедуре, как и в SWT, путем нахождения коэффициентов ${{a}_{i}}({\mathbf{r}})$ в представлении решения в виде разложения по всем невязкам времен пробега (по линейным и круговым трассам)

$m({\mathbf{r}}) = \sum\limits_1^{N + n} {{{a}_{i}}({\mathbf{r}})\delta {{t}_{i}}} .$

Разрешение зависит только от расположения трасс и точек и не зависит от величин временных невязок. При этом очевидно, что в точках территории, где заданы значения искомой функции, эффективный радиус области сглаживания должен быть порядка радиуса окружности, по которой принимаются средние значения скорости, т.е. ρ. В следующем разделе будет показано, что это действительно имеет место.

МОДЕЛЬНЫЙ ПРИМЕР

В программе, реализующей описанный алгоритм, предусмотрена возможность любых соотношений между числом данных по линейным трассам и заданных в точках, в том числе n = 0 (только трассы) и N = 0 (только точки). Прежде всего, отметим, что решение оказывается практически независящим от выбора радиуса окружности ρ, однако слишком малые значения ρ приводят к трудностям вычислительного характера: коэффициенты в линейных уравнениях (7)–(9) оказываются различающимися на несколько порядков.

Для проверки работоспособности и возможностей метода были выполнены восстановления двумерного распределения скорости по синтетическим данным для нескольких вариантов линейных и круговых трасс. Модель распределения скорости и трассы изображены на рис. 2. Радиус окружности вокруг точек ρ был принят равным 1.5 и 2 км, при этом результаты практически не отличались друг от друга.

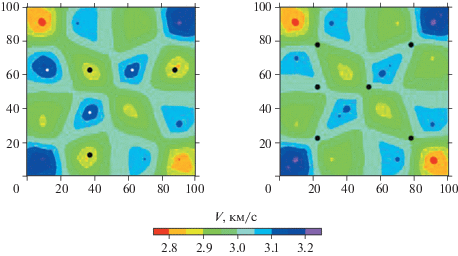
Рис. 2

Модельное распределение скоростных аномалий, схема трасс и расположение точек, в которых задана искомая функция.

Решение строилось для трех выборок данных – только по 40 линейным трассам, только по данным в 40 точках и по всем 80 данным. Результаты таких построений показаны на рис. 3. В левом столбце изображены решения по этим выборкам, в правом – радиус R эквивалентной круговой области сглаживания. Как и следовало ожидать, в случае использования данных только по трассам, которые более или менее равномерно и полно заполняют всю исследуемую область, величина линейного размера области сглаживания (2R) практически одинакова для всей территории и составляет ~ 30–36 км. Это значение несколько больше, чем размер аномалии (25 км), что и приводит к искажению формы аномальных областей.

Рис. 3.

Восстановленное распределение скорости (левая панель) и оценка радиуса эквивалентной области сглаживания (правая панель) по данным только линейных трасс (верхняя панель), по данным только в точках (средняя панель) и по всем данным (нижняя панель).

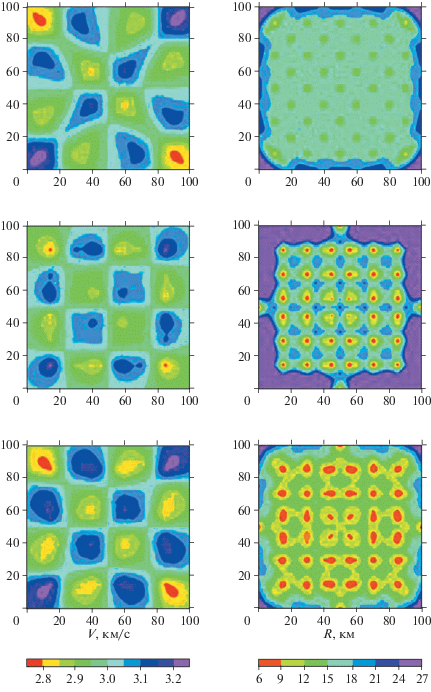
В случае, когда данные приняты только в точках, высокое разрешение достигается только в близкой окрестности точек, что и следовало ожидать, а в остальных частях области решение получается фактически интерполяцией между данными в точках: информация о скорости в этих частях отсутствует, и разрешение оказывается низким.

В случае использования данных и по линейным трассам, и по точкам линейные размеры областей сглаживания варьируют от 12 до 30 км, и скорость восстанавливается достаточно удовлетворительно.

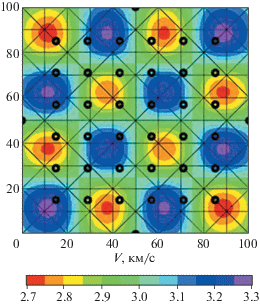
Можно возразить, что улучшение решения произошло за счет увеличения объема выборки. Но, с другой стороны, хотелось бы понять, каким образом добавление данных в точках изменяет решение. С этой целью были построены решения для той же модели, при этом данные по трассам взяты теми же самыми (40 трасс), и к ним добавлены данные по 6 точкам в двух вариантах. Расположение точек и решения для них изображены на рис. 4. В первом варианте точки помещены в центры аномалий скорости, а во втором – между ними, т.е. там, где скорости близки к средней по всей области. Хотя в обоих вариантах добавлено одно и то же количество данных в точках (т.е. 6) решения оказываются различными и отличающимися от того, в котором использовались данные только по трассам. В первом случае конфигурация и значения аномалий улучшились в окрестности точек, где были заданы значения, а во втором варианте формы аномалий остались практически без изменений, но значения аномалий уменьшились, т.е. решение получилось более сглаженным.

Рис. 4.

Решения по данным 40 трасс, изображенных на рис. 2, и двух вариантов расположения точек. Сравнить с данными только по трассам (рис. 3 верхний).

Таким образом, оказывается, что качество решения зависит не от количества точек, в которых задаются данные, а от их местоположения по отношению к аномалиям скорости в среде.

ВЫВОДЫ И ОБСУЖДЕНИЕ

Разработан метод, на основе которого модифицирована программа SWT , в основу которой принято предположение о гладкости искомой функции. Такой функцией может быть скорость поперечной волны на заданной глубине, либо групповая скорость поверхностной волны, соответствующая определенному периоду.

Расчеты для модельного примера показывают, что добавление данных в точках может существенно улучшить решение за счет повышения разрешения. Это представляется важным еще и потому, что добавление данных в точках может расширить информацию о распределении скоростей на больших глубинах. Дело в том, что в SWT по средним трассовым значениям такая информация получается, если выборка содержит достаточно большое количество длинных трасс, а при изучении небольших по размерам регионов приходится использовать лишь короткие трассы. Заметим еще, что такой подход к комбинированию данных SWT и RF для исследования верхней мантии имеет смысл в тех регионах, где трудно получить большое количество данных о скоростях поверхностных волн по трассам разного направления из-за отсутствия землетрясений и малого числа станций. В частности, к таким регионам относятся Восточно-Европейская и Западно-Сибирская платформы. В случае же данных по большому числу трасс добавление данных в точках метод SWT практически не изменяет результаты.

По-видимому, предлагаемый метод может найти применение и в сейсморазведке для определения строения верхней толщи методом MASW, если известны результаты измерения скорости по скважинам.

Список литературы

Винник Л.П. Сейсмология приемных функций// Физика Земли. 2019 № 1. С. 16–27.
Винник Л.П. Косарев Г.Л. Определение параметров коры по наблюдениям телесейсмических объемных волн // Докл. АН СССР. 1981. Т. 261. № 5. С. 1091–1095.
Дитмар П.Г, Яновская Т.Б. Обобщение метода Бейкуса–Гильберта для оценки горизонтальных вариаций скорости поверхностных волн // Изв. АН СССР. Сер. Физика Земли. 1987. № 6. С. 30–40.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. 1981. М.: Наука. 797 с.
Яновская Т.Б. Поверхностно-волновая томография в сейсмических исследованиях. СПб: Наука. 2015.167 с.
Barmin M.P., Ritzwoller M.H., Levshin A.L. A fast and reliable method for surface wave tomography // Pure Appl. Geophys. 2001. V. 158(8). P. 1351–1375.
Mantovani E., Nolet G., Panza G.F. Lateral heterogeneity in the crust of the Italian region from regionalized Rayleigh wave group velocities // Ann. Geoph. 1985. V. 3. № 4. P. 519–530.
Nakanishi, Anderson Don.L. 1982 Wourld wide distribution of group velocity of mantle Rayleigh waves as determined by spherical harmonic analysis // Bull. Seism. Soc. Am. V. 72. № 4. P. 1185–1194.
Ritzwoller M.H., Levshin A.L. Eurasian surface wave tomography: group velocities // J. Geophys. Res. 1998. V. 103. P. 4839–4878.
Tarantola A., Nersessian A. Three-dimensional inversion without blocks // Geophys. J. Roy. astr. Soc. 1984. V. 76. P. 299–306.
Vinnik L.P. Detection of waves converted from P to S in the mantle // Phys. Earth planet. Inter. 1977. V. 15. P. 39–45.
Zhang Y.S., Tanimto T. Three-dimensional modeling of upper mantle structure under the Pacific ocean and surrounding area // Geoph. J. Int. 1989. V. 98. P. 255–269.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал