Физика Земли, 2020, № 4, стр. 161-171
Современные движения земной поверхности и распространение напряжений в верхней упругой коре
Б. И. Биргер *
Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
* E-mail: birgerbor@mail.ru
Поступила в редакцию 09.01.2019
После доработки 09.07.2019
Принята к публикации 27.01.2020
Аннотация
Земная кора моделируется как тонкая упругая пластина, а подстилающая ее литосфера – как полупространство с реологией вязкой жидкости. Для такой системы с помощью преобразования Фурье по горизонтальным координатам и преобразования Лапласа по времени получены решения уравнений механики сплошной среды в виде волн диффузионного типа, которые, сильно затухая, распространяются из области начального возмущения по земной поверхности и вызывают ее смещения. В случае точечного начального возмущения найдено аналитическое выражение для этих волн, дающее явную зависимость смещений земной поверхности и напряжений в упругой коре от горизонтальных координат и времени. Диффузионные волны (безынерционные волны Рэлея и Лява) можно рассматривать как механизм современных вертикальных и горизонтальных движений земной коры. Безынерционные волны Рэлея приводят к восстановлению изостатического равновесия земной коры, которое нарушается начальным вертикальным смещением земной поверхности. В том случае, когда безынерционная волна Лява распространяется вдоль запертого разлома из участка разлома, где произошло вспарывание разлома, сопровождаемого землетрясением, эта волна снижает нормальное напряжение, приложенное к борту разлома, и поэтому уменьшает силу трения, способствуя вспарыванию на удаленном участке запертого разлома и вызывая новое землетрясение.
ВВЕДЕНИЕ
Лабораторные эксперименты с образцами горных пород показывают, что, когда деформации ползучести малы, имеет место неустановившаяся ползучесть: при постоянных приложенных напряжениях скорость деформаций ползучести уменьшается со временем. Тектоника плит допускает только малые деформации в литосферных плитах, поэтому ползучесть литосферы является неустановившейся. Здесь и далее термин “литосфера” означает литосферную плиту, а границы между плитами, где деформации велики, исключаются из рассмотрения. Литосферная плита представляет собой холодный пограничный слой, образуемый мантийной конвекцией, а толщина континентальных плит может превосходить 200 км. Деформации литосферы складываются из ползучих, упругих и хрупких (псевдопластических) деформаций. Эти реологические механизмы конкурируют между собой, и доминирует тот механизм, который при фиксированном сдвиговом напряжении вызывает сдвиговую деформацию, значительно превышающую деформации, связанные с остальными механизмами. Реологическая модель степенной неньютоновской жидкости, которая описывает установившуюся ползучесть и обычно используется в современных геофизических исследованиях, приводит к очень высокой эффективной вязкости, характеризующей ползучесть при малых деформациях. При такой высокой эффективной вязкости реологию литосферы можно описывать упруго-хрупкой реологической моделью, пренебрегая ползучестью. Неустановившейся ползучести соответствует намного более низкая эффективная вязкость, чем установившейся ползучести. Поэтому неустановившуюся ползучесть необходимо учитывать при рассмотрении геофизических процессов в литосфере. Эффективная вязкость, соответствующая неустановившейся ползучести, зависит от характерной продолжительности рассматриваемого геофизического процесса. В работах [Birger, 1998; 2000; 2012; 2013] был рассмотрен процесс образования осадочных бассейнов на континентальных кратонах. Характерное время этого процесса – порядка 108 лет. В работе [Биргер, 2017] рассматривается восстановление изостатического равновесия после начального мелкомасштабного возмущения рельефа земной поверхности. В результате процесса восстановления земная поверхность возвращается к плоскому положению, которое соответствует равновесному состоянию при однородном по горизонтали распределении плотности. Характерная продолжительность этого процесса не превышает 1000 лет, и поэтому распределение реологических свойств по глубине литосферы и коры отличается от того распределения, которое соответствует более медленным процессам, связанным с конвективным движением. Процесс восстановления изостазии сопровождается безынерционными волнами Рэлея, которые, сильно затухая, распространяются из области начального возмущения вдоль земной поверхности и вызывают ее вертикальные смещения.
Литосфера, определяемая как холодный пограничный слой, формируемый мантийной конвекцией, значительно толще, чем ее верхний упругий слой (упругая кора). Конвективная литосфера, определяемая таким образом, включает в себя не только упругую кору, но и астеносферу (слой с пониженной эффективной вязкостью, расположенный под упругой корой), которая соответствует послеледниковым данным. Несогласованности, возникающие из-за различных определений понятия “литосфера”, подробно обсуждаются в работах [Anderson, 1995; Karato, 2008; Биргер, 2016].
Процесс с характерным временем порядка 1000 лет является достаточно быстрым адиабатическим процессом, при исследовании которого можно не учитывать влияние вертикального градиента температуры, присутствующего в литосфере, поскольку термомеханические эффекты связаны с очень медленно происходящей теплопроводностью. Но, в то же время, процесс с характерной продолжительностью порядка 1000 лет является достаточно медленным для того, чтобы можно было пренебречь упругостью, сжимаемостью и инерционностью. Медленное течение в вязкой среде, связанное с таким процессом, называют ползущим.
В настоящей работе будут рассмотрены современные движения земной поверхности и связанные с ними напряжения в упругой коре, вызванные недавними (с точки зрения геологии) начальными вертикальными и горизонтальными смещениями земной поверхности. Эти начальные возмущения будут считаться точечными, т.е. сосредоточенными на бесконечно малой площади поверхности. Реальное возмущение, охватывающее конечную площадь поверхности, можно считать точечным, если рассматривать смещения поверхности и напряжения в коре на достаточном удалении от начального возмущения. Характерные скорости современных движений значительно выше, чем скорости геологических движений в том же самом регионе. Это неудивительно, поскольку эти движения обусловлены разными механизмами, и нельзя считать, что современные движения являются унаследованными по отношению к древним геологическим движениям [Кузьмин, 2013].
ПОСТАНОВКА ЗАДАЧИ. ПРЕОБРАЗОВАНИЯ ФУРЬЕ И ЛАПЛАСА
Рассматривается упругая тонкая пластина, лежащая на полупространстве, имеющем реологию вязкой ньютоновской несжимаемой жидкости, в которой девиаторные напряжения ${{\tau }_{{ij}}}$ связаны со скоростями деформации ${{\dot {\varepsilon }}_{{ij}}}$ и с компонентами скорости ${{v}_{i}}$ соотношениями:
(1)
${{\tau }_{{ij}}} = 2\eta {{\dot {\varepsilon }}_{{ij}}},\,\,\,\,~{{\dot {\varepsilon }}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{v}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{v}_{j}}}}{{\partial {{x}_{i}}}}} \right),\,\,\,\,~i,~j = 1,~2,~3,$(2)
$ - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {{\tau }_{{xx}}}}}{{\partial x}} + \frac{{\partial {{\tau }_{{xy}}}}}{{\partial y}} + \frac{{\partial {{\tau }_{{xz}}}}}{{\partial z}} = 0,$(3)
$ - \frac{{\partial p}}{{\partial y}} + \frac{{\partial {{\tau }_{{yx}}}}}{{\partial x}} + \frac{{\partial {{\tau }_{{yy}}}}}{{\partial y}} + \frac{{\partial {{\tau }_{{yz}}}}}{{\partial z}} = 0,$(4)
$ - \frac{{\partial p}}{{\partial z}} + \frac{{\partial {{\tau }_{{zx}}}}}{{\partial x}} + \frac{{\partial {{\tau }_{{zy}}}}}{{\partial y}} + \frac{{\partial {{\tau }_{{zz}}}}}{{\partial z}} = 0,$(5)
$\frac{{\partial {{v}_{x}}}}{{\partial x}} + \frac{{\partial {{v}_{y}}}}{{\partial y}} + \frac{{\partial {{v}_{z}}}}{{\partial z}} = 0,$На верхней поверхности полупространства (z = 0) наложены граничные условия, определяемые силовым воздействием упругой пластины:
(6)
$\begin{gathered} \left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right){{u}_{x}} + \frac{{\left( {1 + \nu } \right)}}{{\left( {1 - \nu } \right)}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial {{u}_{x}}}}{{\partial x}} + \frac{{\partial {{u}_{y}}}}{{\partial y}}} \right) + \\ + \,\,\frac{1}{{\mu h}}{{\tau }_{{xz}}} = 0, \\ \end{gathered} $(7)
$\begin{gathered} \left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right){{u}_{y}} + \frac{{\left( {1 + \nu } \right)}}{{\left( {1 - \nu } \right)}}\frac{\partial }{{\partial y}}\left( {\frac{{\partial {{u}_{x}}}}{{\partial x}} + \frac{{\partial {{u}_{y}}}}{{\partial y}}} \right) + \\ + \,\,\frac{1}{{\mu h}}{{\tau }_{{yz}}} = 0, \\ \end{gathered} $(8)
$N{{\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)}^{2}}{{u}_{z}} + \rho g{{u}_{z}} + {{\tau }_{{zz}}} - p = 0,$Применяя преобразование Фурье по координатам $x$, y и преобразование Лапласа по времени $t$ к уравнениям (1)–(10) и исключая все физические переменные, кроме вертикальной скорости, приходим к соотношениям:
(11)
$V_{x}^{*} = \frac{{i{{k}_{x}}}}{{{{k}^{2}}}}DV_{z}^{*},\,\,\,\,V_{x}^{*} = \frac{{i{{k}_{y}}}}{{{{k}^{2}}}}DV_{z}^{*},$(12)
$T_{{zz}}^{*} = 2\eta DV_{z}^{*},\,\,\,\,P* = \frac{\eta }{{{{k}^{2}}}}({{D}^{3}} - {{k}^{2}}D)V_{z}^{*},$(13)
$\begin{gathered} T_{{xz}}^{*} = \frac{{i{{k}_{x}}}}{{{{k}^{2}}}}\eta ({{D}^{2}} + {{k}^{2}})V_{z}^{*}, \\ T_{{yz}}^{*} = \frac{{i{{k}_{y}}}}{{{{k}^{2}}}}\eta ({{D}^{2}} + {{k}^{2}})V_{z}^{*}, \\ \end{gathered} $Решение уравнения (15), удовлетворяющее условию ограниченности при $z \to - \infty $, записывается как
(16)
$V_{z}^{*} = \left[ {{{C}_{1}}\left( s \right) + {{C}_{2}}\left( s \right)z} \right]{\text{exp}}\left( {\left| k \right|z} \right),$(17)
$\begin{gathered} V_{z}^{*} = {{C}_{1}}\left( s \right),\,\,\,\,V_{x}^{*} = \frac{{i{{k}_{x}}}}{{{{k}^{2}}}}[{{C}_{1}}(s)k + {{C}_{2}}(s)], \\ V_{y}^{*} = \frac{{i{{k}_{y}}}}{{{{k}^{2}}}}\left[ {{{C}_{1}}\left( s \right)k + {{C}_{2}}\left( s \right)} \right]. \\ \end{gathered} $Применяя преобразования Фурье и Лапласа к соотношению (10), получаем
где ${{U}_{{0i}}}$ – изображения Фурье компонент начального (t = 0) смещения пластины. Из (17) и (18) следует:(19)
$\begin{gathered} U_{x}^{*} = \frac{1}{s}\left[ {\frac{{i{{k}_{x}}}}{{{{k}^{2}}}}\left( {{{C}_{1}}k + {{C}_{2}}} \right) + {{U}_{{0x}}}} \right], \\ U_{y}^{*} = \frac{1}{s}\left[ {\frac{{i{{k}_{y}}}}{{{{k}^{2}}}}\left( {{{C}_{1}}k + {{C}_{2}}} \right) + {{U}_{{0y}}}} \right], \\ \end{gathered} $Подставляя решение (16) в преобразованные по Фурье и Лапласу граничные условия (6)–(8) и учитывая соотношения (12), (13) и (19), находим:
(21)
$\begin{gathered} 2i{{k}_{x}}\left( {\frac{1}{{1 - \nu }} - s\frac{\eta }{{\mu hk}}} \right)\left( {{{C}_{1}}k + {{C}_{2}}} \right) = \\ = - \left( {{{k}^{2}} + \frac{{1 + \nu }}{{1 - \nu }}k_{x}^{2}} \right){{U}_{{0x}}} - \frac{{1 + \nu }}{{1 - \nu }}{{k}_{x}}{{k}_{y}}{{U}_{{0y}}}, \\ \end{gathered} $(22)
$\begin{gathered} 2i{{k}_{y}}\left( {\frac{1}{{1 - \nu }} - s\frac{\eta }{{\mu hk}}} \right)\left( {{{C}_{1}}k + {{C}_{2}}} \right) = \\ = - \left( {{{k}^{2}} + \frac{{1 + \nu }}{{1 - \nu }}k_{y}^{2}} \right){{U}_{{0y}}} - \frac{{1 + \nu }}{{1 - \nu }}{{k}_{x}}{{k}_{y}}{{U}_{{0x}}}, \\ \end{gathered} $(23)
$\left( {N{{k}^{4}} + \rho g + 2k\eta s} \right){{C}_{1}} = - \left( {N{{k}^{4}} + \rho g} \right){{U}_{{0z}}}.$Как следует из (23), если ${{U}_{{0z}}} = 0,$ то ${{C}_{1}} = 0.$ Таким образом, как видно из (20) и (23), вертикальное смещение развивается только в том случае, когда имеется начальное вертикальное смещение. Если начального вертикального смещения нет, но есть начальное горизонтальное смещение, то в коре развиваются горизонтальные смещения. Этот процесс описывается уравнениями (21) и (22), в которых следует положить ${{C}_{1}} = 0$.
ДВУМЕРНЫЕ ЗАДАЧИ
Начнем с рассмотрения двумерных задач, пренебрегая зависимостью решения от координаты $y$. При этом следует отбросить уравнение (22) и положить ${{k}_{y}} = 0$ и ${{k}_{x}} = k$ в уравнениях (21) и (23). В случае, когда в начальный момент возникает вертикальное смещение земной поверхности, а начальных горизонтальных смещений нет, определяя ${{C}_{1}}$ из (23) и воспользовавшись (20), получаем лапласовское изображение вертикального смещения верхней поверхности $(z = 0$):
(24)
$U_{z}^{*} = \frac{{2\left| k \right|\eta {{U}_{{0z}}}\left( k \right)}}{{\rho g + N{{k}^{4}} + 2\left| k \right|\eta s}}.$Обращение лапласовсого изображения (24) дает:
(25)
${{U}_{z}}\left( t \right) = {{U}_{{0z}}}\left( k \right){\text{exp}}\left( { - \frac{{\rho g + N{{k}^{4}}}}{{2\left| k \right|\eta }}t} \right).$Когда ${{U}_{{0x}}} = {{U}_{{0y}}} = 0$, из (21) и (22) следует соотношение:
при выполнении которого, как следует из (13), (16) и (19), на верхней поверхности (z = 0) отсутствуют горизонтальные смещения и напряжения.Чтобы обратить изображение Фурье (25), нужно определить начальное возмущение земной поверхности. Пусть в начальный момент $t = 0~$ вертикальное смещение поверхности (z = 0) задано:
Изображение Фурье функции (27) записывается в виде:
(28)
${{U}_{{0z}}}\left( k \right) = \int\limits_{ - \infty }^\infty {{{u}_{{0z}}}} \left( x \right)\exp \left( { - ikx} \right)dx,$(29)
${{u}_{{0z}}}\left( x \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {{{U}_{{0z}}}} \left( k \right)\exp \left( {ikx} \right)dk.$Пусть начальное смещение имеет форму “ступеньки” шириной $l$:
(30)
$\begin{gathered} {{u}_{{0z}}}\left( x \right) = {{u}_{0}},~\,\,\,\,~{\text{если}}~\,\,\,\,{{ - l} \mathord{\left/ {\vphantom {{ - l} 2}} \right. \kern-0em} 2} < x < {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}, \\ {{u}_{{0z}}}\left( x \right) = 0,~\,\,\,\,{\text{\;если}}\,\,\,{\text{\;}}~x < - {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}\,\,~{\text{или}}\,\,x > {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}. \\ \end{gathered} $Преобразование Фурье для такой “ступеньки” имеет вид
(31)
${{U}_{{0z}}}\left( k \right) = 2{{u}_{0}}\frac{{{\text{sin}}\left( {{{lk} \mathord{\left/ {\vphantom {{lk} 2}} \right. \kern-0em} 2}} \right)}}{k}.$Как следует из (31), когда ширина начального возмущения мала ($lk$ $ \ll $ 1), изображение Фурье не зависит от k:
Изображение (32) соответствует точечному начальному возмущению:
(33)
${{u}_{{0z}}}\left( x \right) = {{u}_{0}}l\delta \left( x \right),\,\,\,\,\delta \left( x \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\exp } \left( {ikx} \right)dk,$(34)
${{u}_{z}}\left( {x,t} \right) = \frac{{{{u}_{0}}l}}{{2\pi }}\int\limits_{ - \infty }^\infty {{\text{exp}}\left( { - \frac{{\rho g + N{{k}^{4}}}}{{2\left| k \right|\eta }}t + ikx} \right)dk} .$Функция
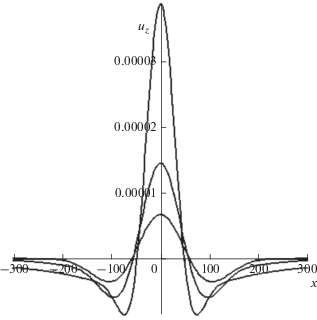
имеет резко выраженный минимум при k = km= $ = {{\left( {{{\rho g} \mathord{\left/ {\vphantom {{\rho g} {3N}}} \right. \kern-0em} {3N}}} \right)}^{{1/4}}}$. Окрестность точки $k = {{k}_{m}}$ дает основной вклад в интеграл (34) и определяет его значение.Даваемая формулой (34) зависимость вертикальных смещений поверхности от горизонтальной координаты в различные моменты времени показана на рис. 1. В рассмотренном случае начального точечного вертикального смещения переход к трехмерной постановке задачи вносит мало нового в понимание рассматриваемого процесса: на рис. 1 достаточно заменить координату $x$ полярной координатой r (при точечном вертикальном возмущении решение не зависит от угловой полярной координаты).
Рис. 1.
Три кривые на этом рисунке показывают зависимость вертикальных смещений земной поверхности от горизонтальной координаты в различные моменты времени (10, 30 и 50 лет). По вертикальной оси отложено безразмерное смещение ${{u}_{z}}$, измеряемое в масштабе ${{{{u}_{0}}} \mathord{\left/ {\vphantom {{{{u}_{0}}} {2\pi }}} \right. \kern-0em} {2\pi }}$, где ${{u}_{0}}$ – начальное вертикальное смещение. На этом и на всех последующих рисунках в центре начального возмущения все смещения и напряжения убывают со временем, линейный размер области начального возмущения l = 1 км, а расстояние $x$ от центра начального возмущения измеряется в километрах.
В случае, когда возникает начальное горизонтальное смещение, а ${{U}_{{0y}}}$ = ${{U}_{{0z}}} = 0$, из уравнений (21) и (23) следует:
(35)
${{C}_{1}} = 0,\,\,\,\,{{C}_{2}} = {{{{U}_{{0x}}}ik} \mathord{\left/ {\vphantom {{{{U}_{{0x}}}ik} {\left( {1 - s\frac{{\eta \left( {1 - \nu } \right)}}{{\mu h\left| k \right|}}} \right)}}} \right. \kern-0em} {\left( {1 - s\frac{{\eta \left( {1 - \nu } \right)}}{{\mu h\left| k \right|}}} \right)}}.$Подставляя (35) в (19), получаем после несложных алгебраических преобразований
(36)
$U_{x}^{*} = {{{{U}_{{0x}}}} \mathord{\left/ {\vphantom {{{{U}_{{0x}}}} {\left( {s - \frac{{\mu h\left| k \right|}}{{\eta \left( {1 - \nu } \right)}}} \right)}}} \right. \kern-0em} {\left( {s - \frac{{\mu h\left| k \right|}}{{\eta \left( {1 - \nu } \right)}}} \right)}}.$Обращая лапласовское изображение (36), находим:
(37)
${{U}_{x}} = {{U}_{{0x}}}{\text{exp}}\left( { - \left| k \right|\lambda t} \right),\,\,\,\,\lambda = \frac{{\mu h}}{{\eta \left( {1 - \nu } \right)}}.$Введенный параметр λ оценивается как $\lambda \approx {{10}^{{ - 3}}}\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ ≈ $30\,\,{{{\text{км}}} \mathord{\left/ {\vphantom {{{\text{км}}} {{\text{год}}}}} \right. \kern-0em} {{\text{год}}}}$. В случае точечного начального возмущения
обращение изображения Фурье (37) дает(39)
${{u}_{x}}\left( x \right) = \frac{{{{u}_{0}}l}}{{2\pi }}\int\limits_{ - \infty }^\infty {\exp \left( { - \left| k \right|\lambda t + ikx} \right)dk} .$Интегрируя правую часть уравнения (39), получаем:
(40)
${{u}_{x}}\left( x \right) = \frac{{{{u}_{0}}l}}{{2\pi }}\frac{{\lambda t}}{{{{\lambda }^{2}}{{t}^{2}} + {{x}^{2}}}}.$Согласно теории тонкой упругой пластины (см., например, [Ландау, Лифшиц, 1965]), при смещениях ${{u}_{x}}\left( x \right)$ и ${{u}_{y}} \equiv 0$ в упругой коре возникают напряжения:
(41)
$\begin{gathered} {{\sigma }_{{xx}}} = 2\frac{\mu }{{1 - \nu }}{{\varepsilon }_{{xx}}},\,\,\,\,{{\sigma }_{{yy}}} = 2\frac{{\mu \nu }}{{1 - \nu }}{{\varepsilon }_{{xx}}}, \\ {{\varepsilon }_{{xx}}} = \frac{{\partial {{u}_{x}}}}{{\partial x}}. \\ \end{gathered} $Напомним, что $\mu = {E \mathord{\left/ {\vphantom {E 2}} \right. \kern-0em} 2}\left( {1 + \nu } \right)$, где $E$ – модуль Юнга. Подставляя (40) в (41), находим:
(42)
${{\sigma }_{{xx}}} = 4\frac{\mu }{{1 - \nu }}\frac{{{{u}_{0}}l}}{\pi }\frac{{\lambda tx}}{{{{{({{\lambda }^{2}}{{t}^{2}} + {{x}^{2}})}}^{2}}}},\,\,\,\,{{\sigma }_{{yy}}} = \nu {{\sigma }_{{xx}}}.$Формулы (40) и (42) справедливы при $t > 0$. При $t = 0$, как следует из (39), смещение ${{u}_{x}}\left( x \right)$ описывается соотношением (38), а напряжения принимают вид:
(43)
${{\sigma }_{{yy}}} = \nu {{\sigma }_{{xx}}} = 4\mu \frac{\nu }{{1 - \nu }}\frac{{{{u}_{0}}l}}{\pi }\frac{d}{{dx}}\delta \left( x \right).$Зависимости ${{u}_{x}}$ и ${{\sigma }_{{yy}}}$ от $x$, даваемые формулами (40) и (42), показаны на рис. 2 и рис. 3 в различные моменты времени. Функция ${{\sigma }_{{xx}}}\left( {x,t} \right)$ в любой момент времени имеет максимум, достигаемый при $x = {{ - t} \mathord{\left/ {\vphantom {{ - t} \lambda }} \right. \kern-0em} \lambda },$ и симметричный относительно $x = 0$ минимум. Дифференцирование правой части уравнения (42) показывает, что максимум и минимум напряжения ${{\sigma }_{{xx}}}$, затухая по закону ${1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0em} t},$ удаляются от точки начального возмущения $x = 0$ со скоростью $\lambda \sqrt 3 \approx 50\,\,{{{\text{км}}} \mathord{\left/ {\vphantom {{{\text{км}}} {{\text{год}}}}} \right. \kern-0em} {{\text{год}}}}$. В рассмотренном случае горизонтального начального смещения имеет смысл перейти к трехмерной постановке задачи.
Рис. 2.
Зависимость горизонтального смещения земной поверхности от горизонтальной координаты в различные моменты времени (1, 2 и 3 года) после возникновения возмущения для двумерной задачи. По вертикальной оси отложено безразмерное смещение ${{u}_{x}}$, измеряемое в масштабе ${{{{u}_{0}}} \mathord{\left/ {\vphantom {{{{u}_{0}}} {2\pi }}} \right. \kern-0em} {2\pi }}$, где ${{u}_{0}}$ – начальное горизонтальное смещение вдоль оси $x$.
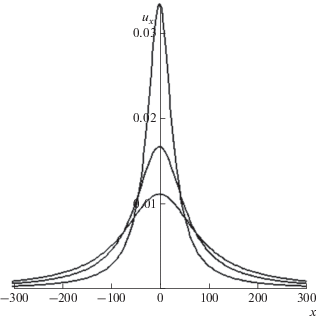
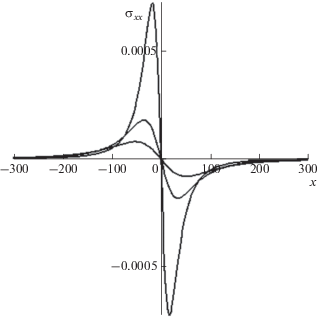
Рис. 3.
Зависимость напряжения в коре от горизонтальной координаты в различные моменты времени (1, 2 и 3 года) после возникновения возмущения для двумерной задачи. По вертикальной оси отложено безразмерное напряжение ${{\sigma }_{{xx}}}$, измеряемое в масштабе $\frac{{4\mu }}{{1 - \nu }}\frac{{{{u}_{0}}}}{{\pi l}},$ где ${{u}_{0}}$ – начальное горизонтальное смещение вдоль оси $x$.
ТРЕХМЕРНАЯ ЗАДАЧА
Используемое при решении двумерных задач начальное возмущение, заданное в виде $\delta \left( x \right)$, соответствует случаю, когда в начальный момент времени возникает смещение в очень узкой полосе, бесконечно протяженной вдоль оси $y$. В рамках двумерной постановки задачи такое возмущение можно называть точечным. Переходя к трехмерной постановке задачи, следует рассматривать точечное возмущение в начальный момент времени, которое можно представить как:
(44)
$\begin{gathered} {{u}_{{x0}}}\left( {x,~y} \right) = {{u}_{0}}{{l}^{2}}\delta \left( x \right)\delta \left( y \right) = \\ = \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\exp \left( {i{{k}_{x}}x + i{{k}_{y}}y} \right)d{{k}_{x}}d{{k}_{y}}} } . \\ \end{gathered} $Изображение Фурье точечного горизонтального смещения (44) имеет очень простой вид и не зависит от волновых чисел ${{k}_{x}}$ и ${{k}_{y}}{\kern 1pt} :$
Как следует из (6), (7), (21) и (22), в начальный момент времени, когда приложенные к пластине касательные напряжения ${{\sigma }_{{xz}}}$ и ${{\sigma }_{{yz}}}~$ равны нулю, возмущение (45) сопровождается мгновенно возникающим смещением:
Когда начальное горизонтальное смещение определено соотношением (46), формула (37), полученная в рамках двумерной постановки аналогичной задачи, остается справедливой и для трехмерной задачи.
Обращение изображения Фурье ${{U}_{x}}\left( {{{k}_{x}},{{k}_{y}}} \right)$ определяется двойным интегралом:
(47)
$\begin{gathered} {{u}_{x}}\left( {x,y} \right) = \frac{1}{{4{{\pi }^{2}}}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{U}_{x}}\left( {{{k}_{x}},{{k}_{y}}} \right)} } \exp \left( {i{{k}_{x}}x + i{{k}_{y}}y} \right)d{{k}_{x}}d{{k}_{y}}. \\ \end{gathered} $Подставляя (37) в (47), получаем в случае точечного начального горизонтального смещения:
(48)
${{u}_{x}} = \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\exp \left( { - \left| k \right|\lambda t + i{{k}_{x}}x + i{{k}_{y}}y} \right)} } d{{k}_{x}}d{{k}_{y}}.$Представим волновые числа как:
и перейдем к полярным координатам в уравнении (48), переписав это уравнение как(49)
$\begin{gathered} {{u}_{x}}\left( {x,y,t} \right) = \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}} \times \\ \times \,\,\int\limits_0^{2\pi } {\int\limits_0^\infty {\exp \left( { - k\lambda t + ixk~{\text{cos}}\varphi + iyk~{\text{sin}}\varphi } \right)} } kdkd\varphi . \\ \end{gathered} $Проведя интегрирование по переменной $k$ при $t > 0$, находим:
(50)
$\begin{gathered} \int\limits_0^\infty {\exp } \left( { - k\lambda t + ixk~{\text{cos}}\varphi + iyk~{\text{sin}}\varphi } \right)kdk~ = \\ = {1 \mathord{\left/ {\vphantom {1 {{{{\left( { - \lambda t + ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi } \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( { - \lambda t + ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi } \right)}}^{2}}}}. \\ \end{gathered} $С учетом (50) перепишем (49) в виде:
(51)
${{u}_{x}}\left( {x,y,t} \right) = \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\frac{{d\varphi }}{{{{{\left( { - \lambda t + ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi } \right)}}^{2}}}}} .$Как и равенства (40) и (42), уравнение (51) справедливо при $t > 0$.
Из (46) следует, что для y-компоненты смещения уравнение (37) заменяется уравнением:
Обращая изображение Фурье (52) и проведя преобразования, аналогичные тем, которые привели к формуле (51) для смещения ${{u}_{x}}\left( {x,y,t} \right)$, находим:
(53)
${{u}_{y}}\left( {x,y,t} \right) = \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\frac{{{\text{tg}}\varphi }}{{{{{\left( { - \lambda t + ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi } \right)}}^{2}}}}} d\varphi .$В тонкой упругой пластине напряжения связаны со смещениями соотношениями (см., например, [Ландау, Лифшиц, 1965]):
(54)
$\begin{gathered} {{\sigma }_{{xy}}} = \mu \left( {\frac{{\partial {{u}_{x}}}}{{\partial y}} + \frac{{\partial {{u}_{y}}}}{{\partial x}}} \right),\,\,\,\,{{\sigma }_{{xx}}} = \frac{{2\mu }}{{1 - \nu }}\left( {\frac{{\partial {{u}_{x}}}}{{\partial x}} + \nu \frac{{\partial {{u}_{y}}}}{{\partial y}}} \right), \\ ~{{\sigma }_{{yy}}} = \frac{{2\mu }}{{1 - \nu }}\left( {\frac{{\partial {{u}_{y}}}}{{\partial y}} + \nu \frac{{\partial {{u}_{x}}}}{{\partial x}}} \right). \\ \end{gathered} $Подставляя (51) и (53) в (54), получаем:
(55)
${{\sigma }_{{xy}}} = - i\mu \frac{{{{u}_{0}}{{l}^{2}}}}{{{{\pi }^{2}}}}\int\limits_0^{2\pi } {\frac{{{\text{sin}}\varphi }}{{{{{\left( { - \lambda t + ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi } \right)}}^{3}}}}} d\varphi ,$(56)
${{\sigma }_{{xx}}} = - i\mu \frac{{{{u}_{0}}{{l}^{2}}}}{{{{\pi }^{2}}\left( {1 - \nu } \right)}}\int\limits_0^{2\pi } {\frac{{~{\text{cos}}\varphi + \nu {\text{tg}}\varphi ~{\text{sin}}\varphi ~}}{{{{{\left( { - \lambda t + ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi } \right)}}^{3}}}}} d\varphi ,$(57)
$\begin{gathered} {{\sigma }_{{yy}}} = - i\mu \frac{{{{u}_{0}}{{l}^{2}}}}{{{{\pi }^{2}}\left( {1 - \nu } \right)}} \times \\ \times \,\,\int\limits_0^{2\pi } {\frac{{~{\text{tg}}\varphi ~{\text{sin}}\varphi + \nu {\text{cos}}\varphi }}{{{{{\left( { - \lambda t + ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi } \right)}}^{3}}}}} d\varphi . \\ \end{gathered} $В правых частях равенств (51), (53) и (55)–(57) перейдем к полярным координатам:
Тогда выражение $ix~{\text{cos}}\varphi + iy~{\text{sin}}\varphi ,$ входящее в эти уравнения, заменяется на $ir\cos \left( {\varphi - \alpha } \right).$ Численное интегрирование показывает, что смещения и напряжения, определяемые выражениями
(51), (53), (55)–(57), действительны (их мнимые части равны нулю). Смещение ${{u}_{x}}$ не зависит от угла ${\alpha }$, смещения ${{u}_{y}}$ зависит от угла $\alpha $ как $~{\text{sin}}2\alpha $, напряжение ${{\sigma }_{{xy}}}$ – как ${\text{sin}}\alpha $, напряжение ${{\sigma }_{{yy}}}$ – как ${\text{cos}}\alpha $. Таким образом, в направлении оси $x$ (${\alpha } = 0)$, т.е. вдоль разлома, распространяется смещение ${{u}_{x}}$ и напряжение ${{\sigma }_{{yy}}}$, а смещение ${{u}_{y}}$ и напряжение ${{\sigma }_{{xy}}}$ равны нулю. В направлении оси $y$ 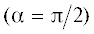 , т.е. перпендикулярно разлому, распространяется смещение ${{u}_{x}}$ и напряжение ${{\sigma }_{{xy}}}$, а смещение ${{u}_{y}}$ и напряжение ${{\sigma }_{{xx}}}$ равны нулю. В других направлениях распространяются смещения ${{u}_{x}},$ ${{u}_{y}}$ и напряжения ${{\sigma }_{{xy}}}$, ${{\sigma }_{{xx}}}$.
, т.е. перпендикулярно разлому, распространяется смещение ${{u}_{x}}$ и напряжение ${{\sigma }_{{xy}}}$, а смещение ${{u}_{y}}$ и напряжение ${{\sigma }_{{xx}}}$ равны нулю. В других направлениях распространяются смещения ${{u}_{x}},$ ${{u}_{y}}$ и напряжения ${{\sigma }_{{xy}}}$, ${{\sigma }_{{xx}}}$.
Трансформный разлом представляет собой такой тип границы литосферных плит, при котором плиты скользят относительно друг друга, двигаясь в горизонтальном направлении, не создавая и не уничтожая земную кору. Разлом Сан-Андреас в Калифорнии, вдоль которого происходит скольжение Североамериканской плиты относительно Тихоокеанской плиты, является типичным примером трансформного разлома. Скольжение по трансформному разлому является прерывистым: движение вдоль разлома происходит только во время землетрясений, а остальное время разлом заперт (соседние плиты сцеплены между собой). Вдали от запертого разлома плиты двигаются в противоположных направлениях с постоянными скоростями порядка 5 см/год. Это движение создает растущие со временем сдвиговые деформации и напряжения в зоне, примыкающей к разлому. В этой зоне совершается подготовка землетрясения, которое происходит тогда, когда сдвиговое напряжение на разломе достигает порогового значения, определяемого трением покоя. При землетрясении участок запертого разлома вспарывается, и накопленная энергия упругой деформации частично уносится сейсмическими волнами (упругая отдача), а частично переходит в тепло, что обусловлено трением скольжения. Имеющиеся сейсмологические данные позволяют предположить, что возмущения напряжений распространяются вдоль запертого разлома со скоростью порядка 50 км/год и действуют как “спусковой механизм” землетрясений. Теоретическая модель распространения напряжений была предложена Эльзассером [Elsasser, 1969], получила дальнейшее развитие в ряде исследований, обзор которых представлен в статье [Быков, 2018], и стала одним из классических разделов геодинамики [Теркот, Шуберт, 1985].
Начальные горизонтальные смещения в земной коре связаны с проскальзыванием литосферных плит на участке разлома в момент землетрясения. Одну из двух плит можно считать неподвижной: на границе этой плиты с зоной разлома отсутствует начальное смещение. Начальное смещение, вызванное землетрясением, возникает на границе ($y = 0)~$ второй плиты с зоной разлома. Смещения и вызванные ими напряжения распространяются в одну сторону ($y \geqslant 0)$ от разлома, и в выписанных выше выражениях для смещений и напряжений следует положить, что $y \geqslant 0$ и, следовательно, угол ${\alpha }$ лежит в интервале $0 \leqslant {\alpha } \leqslant {\pi }$. В частности, смещения и напряжения распространяются вдоль самого разлома ($y = 0$), что может вызвать землетрясения на удаленных участках разлома. Смещение вдоль разлома ($y = 0$) записываются как:
(58)
${{u}_{x}} = \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\frac{{2\lambda \pi t}}{{{{{({{x}^{2}} + {{\lambda }^{2}}{{t}^{2}})}}^{{3/2}}}}},\,\,\,\,{{u}_{y}} = 0,$(59)
${{\sigma }_{{xy}}} = 0,\,\,\,\,{{\sigma }_{{yy}}} = - 2\mu \frac{\nu }{{1 - \nu }}\frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\frac{{6\lambda \pi xt}}{{{{{({{x}^{2}} + {{\lambda }^{2}}{{t}^{2}})}}^{{5/2}}}}}.$Напомним, что параметр $\lambda = \frac{{\mu h}}{{\eta \left( {1 - \nu } \right)}}$ оценивается как $\lambda \approx 30\,\,~{{{\text{км}}} \mathord{\left/ {\vphantom {{{\text{км}}} {{\text{год}}}}} \right. \kern-0em} {{\text{год}}}}.$
Положительное напряжение ${{\sigma }_{{yy}}}$ снижает нормальное напряжение, приложенное к борту разлома, и поэтому уменьшает силу трения, способствуя проскальзыванию на участке запертого разлома, которое вызывает землетрясение. Дифференцируя по $t$ выражение в правой части равенства (59), нетрудно заметить, что напряжение ${{\sigma }_{{yy}}}$, затухая со временем как ${{t}^{{ - 3}}}$, распространяется вдоль разлома со скоростью $2\lambda \approx 60\,\,~{{{\text{км}}} \mathord{\left/ {\vphantom {{{\text{км}}} {{\text{год}}}}} \right. \kern-0em} {{\text{год}}}}$. Соответствующая формулам (58) и (59) зависимость смещения ${{u}_{x}}$ и напряжения ${{\sigma }_{{yy}}}$ от координаты $x$ в различные моменты времени показана на рис. 4 и рис. 5. Соотношения (58) и (59) уточняют соотношения (40) и (42), полученные в рамках двумерной модели. Как видно из рис. 5, положительное напряжение ${{\sigma }_{{yy}}}$ распространяется вдоль разлома в сторону отрицательных координат $x$ (по лучу α = π), т.е. в направлении, противоположном направлению начального точечного горизонтального смещения на разломе.
Рис. 4.
Зависимость горизонтального смещения земной поверхности от горизонтальной координаты в различные моменты времени (1, 2 и 3 года) после возникновения возмущения на линии $y = 0$, вдоль которой направлено начальное горизонтальное смещение. По вертикальной оси отложено безразмерное смещение ${{u}_{x}}$, измеряемое в масштабе $\frac{{{{u}_{0}}}}{{4{{\pi }^{2}}}}$, где ${{u}_{0}}$ – начальное горизонтальное смещение вдоль оси $x$.
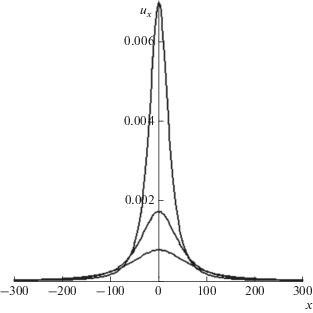
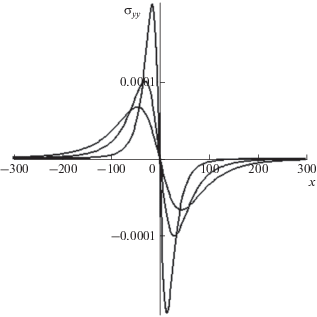
Рис. 5.
Зависимость напряжения ${{\sigma }_{{yy}}}$ в коре от горизонтальной координаты в различные моменты времени (1, 2 и 3 года) после возникновения возмущения на линии $y = 0$, вдоль которой направлено начальное горизонтальное смещение. По вертикальной оси отложено безразмерное напряжение ${{\sigma }_{{xx}}}$, измеряемое в масштабе 2µ $\frac{\nu }{{1 - \nu }}\frac{{{{u}_{0}}}}{{4{{\pi }^{2}}l}},$ где ${{u}_{0}}$ – начальное горизонтальное смещение вдоль оси $x$. Для того, чтобы был лучше виден эффект распространения максимального напряжения, на этом рисунке уменьшен эффект затухания (вместо затухания, происходящего по закону ${{t}^{{ - 3}}},$ для наглядности используется зависимость ${{t}^{{ - 1}}}$).
В перпендикулярном разлому направлении (α = = π/2) смещения и напряжения принимают вид
(60)
$\begin{gathered} {{u}_{x}} = \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\frac{{2\lambda \pi t}}{{{{{({{y}^{2}} + {{\lambda }^{2}}{{t}^{2}})}}^{{3/2}}}}},\,\,\,\,{{u}_{y}} = 0,\,\,\,\,{{\sigma }_{{xx}}} = 0, \\ {{\sigma }_{{xy}}} = - \mu \frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\frac{{6\lambda \pi yt}}{{{{{({{y}^{2}} + {{\lambda }^{2}}{{t}^{2}})}}^{{5/2}}}}}. \\ \end{gathered} $Напряжение ${{\sigma }_{{xy}}}$ распространяется перпендикулярно разлому вдоль оси $y$ точно так же, как напряжение ${{\sigma }_{{yy}}}$ распространяется вдоль разлома.
Напряжение трения покоя между бортами разлома представимо в виде:
(61)
$2\mu {{\dot {\varepsilon }}_{{xy}}}t = \sigma _{{fr}}^{{\left( 0 \right)}} - f2\mu \frac{\nu }{{1 - \nu }}\frac{{{{u}_{0}}{{l}^{2}}}}{{4{{\pi }^{2}}}}\frac{{6\lambda \pi xt}}{{{{{({{x}^{2}} + {{\lambda }^{2}}{{t}^{2}})}}^{{\frac{5}{2}}}}}}~,$Если ${{u}_{0}}{{l}^{2}} \approx 1\,\,{\text{к}}{{{\text{м}}}^{3}}$, что справедливо, например, в случае, когда ${{u}_{0}} \approx 10~\,\,{\text{м}} = 0.01\,\,{\text{км,}}$ а $l \approx 10\,\,{\text{км}}$, уравнение (62) имеет решение $t \approx 100\,\,~{\text{лет}}$, что конечно не более, чем оценка порядка величины. Однако ясно, что диффузионная волна, распространяющаяся вдоль запертого разлома, слабо снижает трение между бортами разлома, и время, прошедшее между двумя последовательными землетрясениями, определяется движением смежных литосферных плит. Диффузионная волна определяет не момент следующего землетрясения, а тот участок разлома, на котором оно происходит.
ЗАКЛЮЧЕНИЕ
В настоящей работе для решения задачи о распространении смещений и напряжений в земной коре начальное распределение смещений преобразуется по Фурье и прослеживается зависимость от времени для моды с фиксированным значением волнового числа k. Чтобы получить зависимость смещения от горизонтальной координаты, совершается обратное преобразование Фурье, которое позволяет обнаружить распространение возмущения от его начального положения вдоль земной поверхности. Такое распространение связано с тем, что моды с различными значениями волнового числа k затухают с различными скоростями. Уменьшение смещений в начальной области сопровождается распространением смещений за ее пределы, что видно на рис. 1, рис. 2 и рис. 4.
Простое аналитическое решение задачи получено в результате использования тонкой упругой пластины, подстилаемой вязким полупространством, в качестве модели верхней упругой земной коры и подстилающей ее астеносферы (как отмечено во Введении, астеносфера представляет собой нижний слой литосферной плиты). Кроме того, рассматриваются только начальные смещения земной поверхности, которые охватывают малые участки площади поверхности, т.е. точечные начальные возмущения. В рамках такой постановки задачи можно исследовать распространение как вертикальных, так и горизонтальных начальных смещений. Задача о начальном вертикальном смещении и его распространении есть, по сути, классическая задача о восстановлении изостазии, происходящем, в частности, при мелкомасштабных послеледниковых течениях в астеносфере [Cathles, 1975]. Если в какой-то ограниченной области земной поверхности произошло вертикальное смещение, нарушившее изостатическое равновесие коры, то процесс восстановления изостазии сводится не только к постепенному уменьшению начальных вертикальных смещений в этой области, но и к распространению смещений за ее пределы, что видно на рис. 1. Сравнение результатов теоретического решения задачи о мелкомасштабных послеледниковых течениях с данными наблюдений позволяет оценить эффективную вязкость астеносферы. Поскольку при небольших деформациях среда демонстрирует неустановившуюся ползучесть, ее эффективная вязкость зависит от характерной длительности рассматриваемого процесса. Поэтому оценку эффективной вязкости, полученную при исследовании мелкомасштабных послеледниковых течений, нельзя использовать для изучения значительно более медленных или быстрых процессов в астеносфере, но конечно можно применять для решения задачи о распространении начального горизонтального смещения.
Применение преобразования Фурье по горизонтальной пространственной координате является необходимым для решения задач, рассматриваемых в настоящей работе. Преобразование Лапласа по времени, которое также применяется в настоящей работе, не является необходимым математическим аппаратом при использовании ньютоновской вязкой жидкости в качестве упрощенной реологической модели астеносферы, но если использовать более адекватную реологическую модели Андраде, преобразование Лапласа становится необходимым [Биргер, 1989].
Процесс распространения напряжений в коре называют иногда быстрыми тектоническими волнами, противопоставляя их медленным тектоническим волнам, существование которых предполагают геологические данные [Белоусов, 1978]. Периодами порядка ${{10}^{8}}$ лет, характерными для медленных тектонических волн, обладают малоамплитудные термоконвективные волны. Эти волны распространяются в литосфере, ползучесть которой при малых деформациях является неустановившейся и описывается реологической моделью Андраде [Birger, 2000]. Скорость распространения термоконвективных волн – около 1 см/год. Скорость распространения напряжений в коре – порядка 50 км/год, что почти на 7 порядков выше скорости термоконвективных волн и почти на 7 порядков ниже скорости сейсмических волн. Процессы распространения напряжений и смещений в коре можно назвать волнами диффузионного типа. Такого типа волны появляются при решении параболических уравнений теории диффузии и теплопроводности. Эти волны описывают процесс распространения возмущения температуры из области, где произошло возмущение, в окружающую среду. Постепенно повышается температура во все более удаленных областях, а температура в начально возмущенной области понижается. Распространение возмущения сопровождается его сильным затуханием, и со временем возмущение температуры везде исчезает. Именно так и протекает процесс распространения смещения в упругой коре, где смещение выступает как аналог возмущения температуры. Распространение смещения сопровождается распространением напряжения, которое пропорционально производной смещения по горизонтальной координате. В каждый момент времени распределение напряжения по горизонтальной координате имеет максимум (по абсолютной величине). Как видно из рис. 5, этот максимум со временем удаляется от точки, где произошло начальное смещение. Движение максимума напряжения происходит с сильным затуханием, но с постоянной скоростью. При использованных в настоящей работе оценках физических параметров земной коры эта скорость приближенно оценивается как $60\,{{\,~{\text{км}}} \mathord{\left/ {\vphantom {{\,~{\text{км}}} {{\text{год}}}}} \right. \kern-0em} {{\text{год}}}}$.
В настоящей статье рассмотрены только точечные начальные возмущения, т.е. возмущения, сосредоточенные на бесконечно малой площади поверхности и описываемые с помощью δ-функции. Реальное возмущение, охватывающее конечную площадь поверхности, можно считать точечным, если рассматривать смещения поверхности и напряжения в упругой коре на достаточном удалении от начального возмущения. Диффузионная волна, распространяясь из области начального возмущения, достигает удаленных участков разлома только через достаточно большое время. Таким образом, полученное значение является асимптотической оценкой скорости распространения возмущения, достигаемой на достаточно больших временах, прошедших с момента возникновения возмущения (на меньших временах скорость распространения возмущения выше [Райс, 1982]). Однако, если размеры области начального возмущения малы, движение, соответствующее найденному асимптотическому решению, быстро устанавливается, т.е. это решение становится справедливым уже на малых временах.
Впервые исследуя распространение напряжений в литосфере, вызываемое начальными горизонтальными смещениями, Эльзассер [Elsasser, 1969] предполагал, что в вязком слое, подстилающем верхний упругий слой, реализуется горизонтальное течение Куэтта, а на подошве вязкого слоя скорости течения обращаются в нуль. Это искусственное граничное условие использовалось и в последующих исследованиях [Теркот, Шуберт, 1985]. В настоящей работе исследование диффузионных волн напряжения проводится в рамках типичной для поверхностных волн постановки задачи: среда, подстилающая упругую тонкую кору, моделируется как полупространство, а в качестве граничного условия накладывается требование ограниченности смещений на большой глубине. Если на верхней горизонтальной границе, т.е. на земной поверхности, смещения вертикальны, рассматриваемые диффузионные волны можно назвать безынерционными волнами Рэлея, а если на верхней границе происходят горизонтальные смещения, то возникающие диффузионные волны можно назвать безынерционными волнами Лява [Биргер, 1989].
Начальное вертикальное смещение может быть вызвано как впадиной, образовавшейся после растаявшего ледника или высохшего соляного озера, так и промышленной деятельностью человечества. За несколько тысяч последних лет вертикальные смещения, нарушающие изостазию, происходили в разных регионах земной поверхности. Генерируемые этими начальными смещениями безынерционные волны Рэлея распространяются по всей земной поверхности и являются механизмом современных вертикальных движений земной коры. Эти современные движения, происходящие несколько тысяч последних лет, хорошо наблюдаются, а их скорость оценивается как 1–10 мм/год.
Начальное горизонтальное смещение может быть вызвано проскальзыванием литосферных плит по участку запертого поверхностного разлома, которое происходит во время землетрясения. Современные горизонтальные движения земной поверхности, генерируемые начальными горизонтальными смещениями, наблюдаются в последние годы с помощью спутниковых навигационных систем GPS и ГЛОНАСС.
Поскольку в упругой коре, подстилаемой вязкой астеносферой, диффузионная волна быстро затухает, в ряде исследований, обзор которых представлен в статье [Быков, 2018], предлагались механизмы, приводящие к распространению вдоль разлома незатухающей уединенной волны (солитон или кинк). Такие волны получаются как решения некоторых нелинейных уравнений (например, уравнения sin-Гордона). Однако эти нелинейные уравнения невозможно вывести из уравнений механики сплошной среды без дополнительных предположений [Быков, 2018]. В настоящей работе предложен простой механизм, позволяющий объяснить последовательность землетрясений на разломе с помощью механики сплошной среды и представлений тектоники плит.
Список литературы
Белоусов В.В. Эндогенные режимы материков. М.: Недра. 1978. 232 с.
Биргер Б.И. Распространение напряжений в литосфере Земли // Изв. АН СССР. Сер. Физика Земли. 1989. № 12. С. 3–18.
Биргер Б.И. Динамика литосферы Земли. М.: Ленанд. 2016. 256 с.
Биргер Б.И. Восстанавливающие изостазию течения в литосфере // Геофизические исследования. 2017. Т. 18. № 4. С. 17–31.
Быков В.Г. Предсказание и наблюдение деформационных волн Земли // Геодинамика и тектонофизика. 2018. Т. 9. № 3. С. 721–754.
Кузьмин Ю.О. Современная геодинамика разломов и парадоксы скоростей деформаций // Физика Земли. 2013. № 5, с. 28-46.
Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука. 1965. 202 с.
Теркот Д., Шуберт Дж. Геодинамика. Геологические приложения физики сплошных сред. М.: Мир. 1985. 730 с.
Райс Дж. Механика очага землетрясения. М.: Мир. 1982. 217 с.
Anderson D. Lithosphere, asthenosphere, and perisphere // Reviews of Geophysics. 1995. V. 31. P. 125–149.
Birger B.I. Rheology of the Earth and thermoconvective mechanism for sedimentary basins formation // Geophys. J. Inter. 1998. V. 134. P. 1–12.
Birger B.I. Excitation of thermoconvective waves in the continental lithosphere // Geophys. J. Inter. 2000. V. 140. P. 24–36.
Birger B.I. Transient creep and convective instability of the lithosphere // Geophys. J. Inter. 2012. V. 191. P. 909–922.
Birger B.I. Temperature-dependent transient creep and dynamics of cratonic lithosphere // Geophys. J. Inter. 2013. V. 195. P. 695–705.
Karato S. Deformation of Earth Materials. An Introduction to the Rheology of Solid Earth. Cambridge university press. 2008. 463 p.
Cathles L.M. The viscosity of the Earth’s mantle. Princeton university press. 1975. 386 p.
Elsasser W.H. Convection and stress propagation in the upper mantle // Appl. Modern Phys. Earth Planet. Inter. N.Y.: Wiley, 1969. P. 223–246.
Дополнительные материалы отсутствуют.


