Физика Земли, 2020, № 5, стр. 3-22
О взаимосвязи параметров Омори и Гутенберга–Рихтера в афтершоковых последовательностях
В. Б. Смирнов 1, 2, *, Т. И. Карцева 1, 2, А. В. Пономарев 2, А. В. Патонин 4, P. Bernard 3, В. О. Михайлов 1, 2, М. Г. Потанина 1, 2
1 Московский государственный университет им. М.В. Ломоносова, физический факультет
г. Москва, Россия
2 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
3 Institut de Physique du Globe de Paris
Paris, France
4 Геофизическая обсерватория “Борок” ИФЗ РАН
п. Борок, Россия
* E-mail: vs60@mail.ru
Поступила в редакцию 15.01.2020
После доработки 10.03.2020
Принята к публикации 10.03.2020
Аннотация
Проведено исследование вопроса о связи двух показателей самоподобия – параметров Гутенберга–Рихтера b и Омори p – в афтершоковых последовательностях. В лабораторных экспериментах, при инициации разрушения в горных породах под воздействием резких скачков осевого напряжения обнаружена корреляционная связь p и b в сходных с афтершоками релаксационных режимах разрушения. Корреляция для обводненных образцов песчаника с предварительно сформированными разломами оказалась отрицательной и выражена ярко. Для “сухих” образцов мигматита и бетона корреляция оказалась положительной, но статистическая значимость ее ниже, чем для обводненных образцов. Анализ литературных данных свидетельствует о разнородности результатов выявления связи параметров p и b в натурных афтершоковых последовательностях. Одни авторы делают вывод о наличии связи параметров, причем отмечается как корреляция, так и антикорреляция. Другие приводят данные об отсутствии корреляции. Проведенное нами исследование натурных афтершоков по данным региональных каталогов землетрясений показало, что статистические оценки параметров Гутенберга–Рихтера и Омори весьма чувствительны к качеству и однородности исходных данных. Были выделены основные факторы, влияющие на качество оценки этих параметров, и выработана методика отбора каталогов афтершоков для предметного анализа. Результаты статистических оценок параметров Гутенберга–Рихтера и Омори в афтершоковых процессах в регионах с различными типами тектонических режимов – в зонах субдукции и в областях сдвиговых трансформных разломов – показало, что в зонах субдукции взаимосвязь этих параметров может быть как положительной, так и отрицательной. В зонах сдвиговых трансформных разломов связь параметров не выявлена. Обобщена высказанная К. Шольцем идея объяснения закона Омори суперпозицией процессов релаксации с различными временами. Согласно этой обобщенной модели, различный знак корреляции показателей самоподобия афтершоковых процессов соответствует различным механизмам релаксации с различными типами зависимости времени релаксации от “ размера” релаксатора. Вопрос о реализации тех или иных механизмов в афтершоковых процессах остается в настоящее время открытым. Обнаруженная в проведенных лабораторных и натурных исследованиях связь параметров Омори и Гутенберга–Рихтера (корреляция, антикорреляция и отсутствие корреляции), возможно, свидетельствует о реализации разных механизмов релаксации в тех или иных условиях.
ВВЕДЕНИЕ
Многочисленные работы по анализу сейсмического режима выявили несколько принципиальных проблем, одной из которых является недостаточная изученность закономерностей и физики переходных режимов как проявлений общей динамики сейсмичности в ответ на различные возбуждающие факторы. Сейсмический процесс охвачен действием различного рода обратных связей, формирующих и регулирующих эволюцию сейсмичности. Переходный режим сейсмического процесса является откликом геофизической среды на воздействия различного происхождения, выводящие ее из стационарного состояния. Выявление закономерностей переходного режима дает возможность прояснить характер и особенности тех ключевых свойств среды и действующих в ней физических механизмов, которые управляют динамикой сейсмичности.
Афтершоковые процессы представляют переходный режим, возбужденный наиболее сильными природными воздействиями. С точки зрения физики сейсмического процесса исследование переходных режимов выигрышно в методическом отношении тем, что приближает геофизическое исследование к физическому эксперименту, который подразумевает контролируемость условий и повторяемость опытов. В случае переходных режимов мы имеем представление об источнике возмущения и можем говорить о повторяемости натурных опытов. Аналогия, конечно, неполная, поскольку основные параметры среды и ее состояния (такие, как напряжения, деформации, температура, внутрипоровое давление, структура неоднородностей и др.) неизвестны. Естественным развитием идеи физического исследования натурных переходных режимов является натурное и лабораторное моделирование.
Лабораторные исследования позволяют выявить принципиальные физические закономерности исследуемых процессов, что составляет основу для развития адекватных физических представлений и определяет обоснованные направления, подходы и методы натурных исследований. Лабораторное моделирование процесса разрушения горных пород не учитывает, однако, все многообразие естественных процессов и не в полной мере выполняет критерии подобия. Горные породы в лабораторном эксперименте не могут в строгом смысле моделировать самих себя в естественных условиях, поэтому лабораторный эксперимент не позволяет в полной мере воспроизвести натурные условия, оставаясь качественной или полуколичественной (подобной не по всем параметрам) моделью.
Конструктивным в этой ситуации является совместное изучение натурных переходных режимов и их лабораторных моделей: выявление характерных закономерностей в натурных условиях и выяснение их физической природы в лаборатории; выявление и оценка в лаборатории закономерностей, исследование которых недоступно в натурных условиях, и проверка действенности этих закономерностей в натурных условиях.
ЛАБОРАТОРНОЕ МОДЕЛИРОВАНИЕ АФТЕРШОКОВОЙ РЕЛАКСАЦИИ
В работе [Смирнов и др., 2019] представлены результаты экспериментальных исследований релаксационных процессов при разрушении образцов песчаника, ассоциируемых с афтершоковыми явлениями в натурных условиях. Целью экспериментов было выявление характера релаксации процесса разрушения, инициированного внешним воздействием, и выяснение зависимости параметров релаксации от уровня действующих напряжений.
Эксперименты осуществлялись по сценарию ступенчатой инициации разрушения [Смирнов, Пономарев, 2004; Смирнов и др., 2010] при варьировании осевых напряжений и различных величинах давления всестороннего сжатия в условиях насыщения образцов водой перед началом эксперимента и дальнейшего поддержания заданного порового давления. Ступеньки нагрузки формировались в режиме управления прессом по деформации – прессовое оборудование обеспечивало заданную скорость нарастания деформации ступеньки и последующую неизменность величины деформации вплоть до момента начала следующей ступеньки (скорость нарастания ступеньки всегда была одной и той же – равной 10–3 1/с). Такой режим был выбран на основании представлений о процессах в очагах землетрясений. В механике землетрясения очаг в первом приближении моделируется ступенчатой функцией деформации (функцией нарастания) [Kostrov, Das, 1988], которая и вызывает дальнейшую эволюцию напряженно-деформированного состояния и процесса разрушения (проявляющегося в натурных условиях в виде афтершокового процесса).
В натурных условиях афтершоковые процессы, как правило, рассматриваются в зонах, приуроченных к крупным разломным структурам, таким, например, как сдвиговые Калифорнийская и Северо-Анатолийская зоны, зоны субдукции в западной части Тихоокеанского кольца и др. Землетрясения, возникающие вне разломных структур, достаточно редки, и особенности их афтершоковых последовательностей не систематизированы. В связи с этим в экспериментах афтершоковые последовательности моделировались в образцах, в которых были сформированы макроразрывы, имитирующие природные трансформные разломы. В одном опыте из работы [Смирнов и др., 2019] (шифр BS02) формирование макроразрыва выполнялось в режиме ступенчатого увеличения осевой нагрузки с управлением по деформации. В другом (шифр BS03) – на стадии формирования макроразрыва использовался режим нагружения с обратной связью по акустической эмиссии [Lockner et al., 1991; 1992].
Инициирующие ступеньки деформации задавались при различных увеличивающихся уровнях осевых напряжений. При некотором уровне осевых напряжений увеличение деформаций, задаваемое прессом, переставало приводить к увеличению напряжений, что можно объяснить переходом контакта сформированного разлома в режим проскальзывания, когда имеющиеся на контакте зацепы (asperity) оказывались разрушенными. В этой ситуации ступенчатое нагружение приостанавливалось и производилось увеличение давления всестороннего сжатия, в результате чего на контакте формировались новые зацепы. После этого ступенчатое нагружение возобновлялось.
По данным системы акустических датчиков, смонтированных на поверхности образца, (аналогичной сети сейсмических станций в натурных условиях) в экспериментах формировались каталоги акустических событий (аналогичные каталогам землетрясений), содержащих информацию о времени и координатах источника, а также об усредненной амплитуде поступающих с акустических датчиков электрических сигналов, приведенной к выбранной референц-сфере вокруг события (абсолютная калибровка механо-электрического преобразователя не проводилась). По аналогии с сейсмологией амплитуда A пересчитывалась в условный энергетический класс по формуле $K = 2\lg A$. В предположении малого различия спектров импульсов и неизменности контакта датчика с образцом величина A2 пропорциональна сейсмической энергии, и в этом случае K сходен по смыслу с энергетическим классом, применяемым в сейсмологии.
Первичная обработка акустических каталогов проводилась по методике, разработанной для оценки однородности данных сейсмических каталогов [Смирнов, 1997; 2009; Смирнов, Габсатарова, 2000] и применявшейся ранее к анализу данных лабораторных экспериментов [Смирнов, Пономарев, 2004; Смирнов и др., 2010].
В качестве параметров акустического режима в работе [Смирнов и др., 2019] использовались параметр Гутенберга–Рихтера $b$ (наклон графика повторяемости) и параметры модифицированного закона Омори p и c: $\lambda \left( t \right) = \frac{{{{I}_{0}}}}{{{{{\left( {t + c} \right)}}^{p}}}}.$
Для наклона графика повторяемости использовалась оценка максимального правдоподобия с учетом усечения распределения в области больших магнитуд [Page, 1968; Pickering et al., 1995; Смирнов, Завьялов, 2012]. Эта методика позволяет получить оценки сверху и снизу для истинного значения наклона графика повторяемости и работает корректно даже в случае небольших динамических диапазонов энергий событий (что актуально для условий лабораторных экспериментов).
Для оценки параметров Омори p и c использовался алгоритм, разработанный в работе [Holschneider et al., 2012] (и снабженный открытым кодом), позволяющий получить как оценки параметров, так и их статистические погрешности, и хорошо зарекомендовавший себя в сейсмологических исследованиях [Ommi et al., 2016; Баранов, Шебалин, 2018; Баранов и др., 2019].
На рис. 1 представлены истории нагружения и зависимости исследуемых параметров от напряжений для двух экспериментов.
Рис. 1.
История нагружения (а), (б) и зависимость от напряжений параметров Гутенберга–Рихтера и Омори (в), (г) – компиляция из работы [Смирнов и др., 2019]. На всех рисунках соответствующими цветами показаны оценки при разных давлениях всестороннего сжатия (подписаны на рисунке (в)). Залитыми кружками показаны результаты эксперимента BS02, открытыми – BS03 (в), (г). На рисунках (а) и (б) отмечены подготовительная (I, целый образец) и рабочая (II, сформирован макроразрыв) стадии; (в) – зависимость параметров от дифференциального напряжения (разности осевой нагрузки и давления всестороннего сжатия); (г) – зависимость параметров от среднего по образцу кулоновского напряжения.
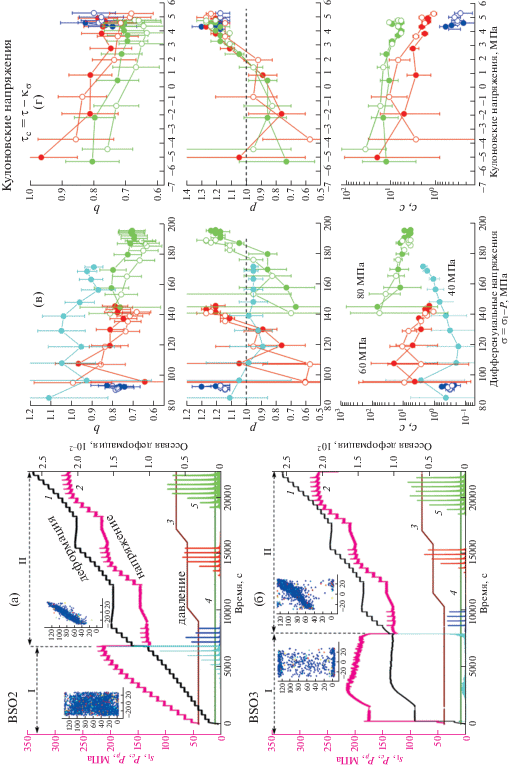
В работе [Смирнов и др., 2019] сделан вывод о закономерном изменении параметров Омори и Гутенберга–Рихтера в зависимости от уровня осевых напряжений и давления всестороннего сжатия. На рабочей стадии (стадия II на рис. 1) при наличии макроразрыва параметр p увеличивается с ростом действующих напряжений – в пределах каждого уровня давления всестороннего сжатия тенденция видна во всем диапазоне. Зависимость от давления всестороннего сжатия проявляется в том, что с увеличением давления те же значения параметра p достигаются при более высоких уровнях осевых напряжений. На подготовительной стадии, при целом образце, параметр Омори p существенно не меняется (голубые кривые на рис. 1в).
Параметр b уменьшается с увеличением действующих напряжений. При этом разброс значений, полученный в двух экспериментах, больше, чем для параметров закона Омори.
Разнознаковые изменения параметров $p$ и $b$ при увеличении напряжений свидетельствует об их антикорреляции. На рис. 2а, 2б представлены диаграммы рассеяния этих параметров – $pb$-диаграммы, построенные по данным из работы [Смирнов и др., 2019], с соответствующими прямыми регрессий (табл. 1). На рис. 2а, 2б и в табл. 1 для образцов с разломами видна антикорреляция $p$ и $b$, тогда как для целого образца значимая корреляция отсутствует (этот случай выделен в табл. 1 затенением). Таким образом, в рассмотренных опытах связь значений параметров $p$ и $b$ оказалась различной для целых образцов и образцов с разломами.
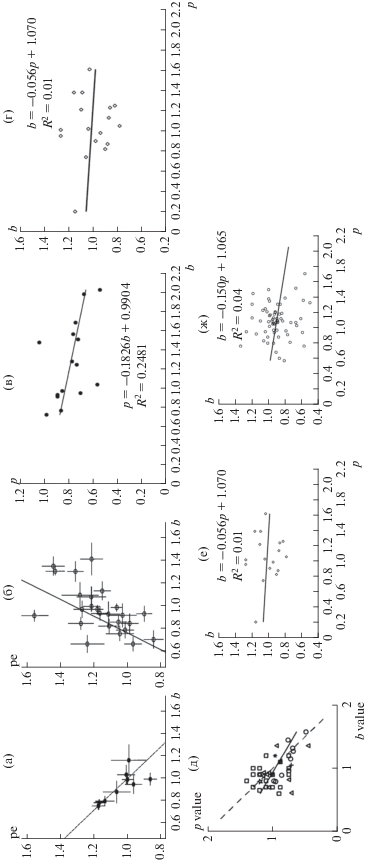
Рис. 2.
pb-диаграммы по лабораторным данным: (а) – опыты BS02 и BS03, цвета соответствуют рис. 1; (в), (г) – опыт МГМ, 1 и 2 соответствуют циклам 1 и 2 на рисунке (в); (д), (е) – опыт БЕТ.

Таблица 1.
Параметры регрессии $p = {\alpha }b + {\beta }$ по данным лабораторных опытов
| Давление всестороннего сжатия, МПа |
Поровое давление, МПа |
Параметр α |
Погрешность параметра α |
Параметр β |
Погрешность параметра β |
Опыт | Рисунок (прямая) |
Примечание |
|---|---|---|---|---|---|---|---|---|
| 40 | 10 | –0.6 | 0.6 | 1.6 | 0.4 | BS02 | 2а (1) | Целый обр. |
| 60 | 10 | –5.0 | 1.7 | 4.6 | 1.2 | BS02 | 2а (2) | Разлом |
| 80 | 10 | –3.9 | 0.5 | 3.5 | 0.3 | BS02 | 2а (3) | Разлом |
| 60 | 10 | –3.9 | 0.9 | 3.8 | 0.6 | BS03 | 2б (2) | Разлом |
| 80 | 10 | –4.3 | 1.7 | 3.6 | 1.0 | BS03 | 2б (3) | Разлом |
| 30 | – | 2.6 | 1 | –0.5 | 0.8 | МГМ | 2г (1) | Разлом |
| 30 | – | 1.3 | 0.7 | –0.2 | 0.6 | МГМ | 2г (2) | Разлом |
| 0 | – | 0.2 | 0.1 | 0.9 | 0.1 | БЕТ | 2е | Целый |
На рис. 2г представлены $pb$-диаграммы, построенные по данным аналогичного эксперимента, но выполненного на другом материале [Vilhelm et al., 2017]. Использовался образец крупнозернистого мигматита, обводнение которого не проводилось (шифр опыта МГМ). История нагружения показана на рис. 2в. На начальной стадии эксперимента в образце был сформирован макроразрыв, после чего давление всестороннего сжатия было увеличено, но далее в эксперименте не менялось. На рис. 2г видна некоторая корреляция параметров, хотя разброс точек достаточно велик и значимость ортогональных регрессий (линии которых показаны на рис. 2г пунктиром, а параметры приведены в табл. 1) невелика – коэффициенты корреляции составляют 0.3 для первого цикла инициации и 0.5 для второго.
На рис. 2е представлена $pb$-диаграмма по данным эксперимента, выполненного на искусственном образце, изготовленном из бетона [Потанина и др., 2015] (шифр опыта БЕТ). История нагружения показана на рис. 2д. Обводнение образца на исследованной стадии не производилось. Видна положительная корреляция параметров (параметры регрессии приведены в табл. 1), коэффициент корреляции равен 0.7.
Таким образом, лабораторные исследования выявили разнознаковую связь параметров Гутенберга–Рихтера и Омори в процессе релаксации разрушения после его инициации скачком осевой нагрузки. Для обводненных образцов с разломами обнаружена ярко выраженная антикорреляция (рис. 2а, 2б). Для “сухих” образцов мигматита и бетона характерна положительная корреляция (рис. 2г, 2е), но статистическая значимость ее ниже, чем для антикорреляции в обводненных образцах.
Отметим, что сопоставление параметров $p$ и $b$ в экспериментах на песчанике (рис. 2а, 2б) выявило их антикорреляцию в случае разрушения в “разломной” зоне и отсутствие значимой корреляции при разрушении целого образца. Этот результат указывает, что даже в модельных условиях экспериментов на относительно однородном материале характер связи параметров $p$ и $b$ оказывается существенно различным в разных условиях разрушения.
ПАРАМЕТРЫ ГУТЕНБЕРГА–РИХТЕРА И ОМОРИ В ПОСЛЕДОВАТЕЛЬНОСТЯХ АФТЕРШОКОВ
Лабораторные исследования, выявившие связь параметров релаксации разрушения в режимах, моделирующих афтершоковые процессы, побуждают провести аналогичное исследование связи параметров афтершоковых последовательностей в тектонической сейсмичности.
Анализ литературы показал, что исследованию связи параметров $p$ и $b$ посвящены немногочисленные работы, результаты которых разнородны и свидетельствуют об отсутствии ясности в этом вопросе. Одни авторы делают вывод о наличии связи $p$ и $b$, причем отмечается как корреляция, так и антикорреляция. Другие приводят данные об отсутствии корреляции. В качестве примера на рис. 3 скомпилированы графики из нескольких публикаций.
Рис. 3.
pb-диаграммы из литературных источников: (а) – Япония, “межплитовая сейсмичность” [Guo, Ogata, 1997]; (б) – Япония, “внутриплитовая сейсмичность” [Guo, Ogata, 1997]; (в) – Мексика [Avila-Barrientos et al., 2015]; (г) – Италия [Gasperini, Lolli, 2006]; (д) – Япония и Китай [Wang, 1994]; (е) – Новая Зеландия [Gasperini, Lolli, 2006]; (ж) – Калифорния [Gasperini, Lolli, 2006].
С целью прояснения вопроса о наличии или отсутствии статистической связи параметров Гутенберга–Рихтера и Омори в афтершоковых последовательностях нами было проведено систематическое исследование этого вопроса по данным региональных каталогов землетрясений. Учитывая, что в лабораторных экспериментах было обнаружено различие связи $p$ и $b$ при различных режимах и условиях разрушения образцов, мы отобрали афтершоковые последовательности в регионах с различными типами тектонических режимов – в зонах субдукции и в областях сдвиговых трансформных разломов. Первые были представлены каталогами Аляски, Камчатки, Курильских островов, Японии и Новой Зеландии. Вторые – каталогами Северной и Южной Калифорнии (область разлома Сан-Андреас), Турции и Греции (область Северо-Анатолийского разлома).
Исходные сейсмические каталоги
Все региональные каталоги были получены из открытых источников в Интернете. Афтершоки выделялись по алгоритму Молчана–Дмитриевой с помощью авторского программного обеспечения [Смирнов, 2009]. Сводка сведений об объемах каталогов и афтершоковых последовательностях представлена в табл. 2. Рассматривались последовательности после главных событий с магнитудами M5+, но 90% магнитуд главных событий оказалось M6+.
Таблица 2.
Сведения о региональных каталогах и каталогах афтершоков
| Регион | Период | Количество событий в каталоге | Количество афтершоковых последовательностей |
|---|---|---|---|
| Аляска (включая Алеутскую дугу) | 2010–2018 | 148 900(6.5%) | 150 (6) |
| Камчатка | 1962–2015 | 156 500(9%) | 20 (14) |
| Курилы | 1962–2016 | 40 350(13%) | 79 (11) |
| Япония | 1981–2012 | 59 500(28%) | 14 (9) |
| Новая Зеландия | 1991–2010 | 326 600(1.5%) | 315 (8) |
| Северная Калифорния | 1984–2011 | 513 500(13%) | 51 (17) |
| Южная Калифорния | 1981–2016 | 590 150(18%) | 68 (29) |
| Турция | 1900–2003 | 84 700(4%) | 164 (10) |
| Греция | 1964–2006 | 55 800(11%) | 152 (8) |
В табл. 2 в столбце “Количество событий в каталоге” в скобках указана доля выделенных афтершоков. В столбце “Количество афтершоковых последовательностей” указано полное количество выделенных последовательностей, в скобках – количество последовательностей, удовлетворяющих требованиям для их анализа (см. ниже).
Источники погрешностей оценок и стратегия селекции данных
Анализ литературных данных и наши пилотные исследования, выполненные ранее, показали, что оценки параметров афтершоковых последовательностей весьма чувствительны к качеству и однородности исходных каталогов афтершоков. В связи с этим этот вопрос был специально изучен, были выделены основные факторы, влияющие на качество оценки параметров, и выработана методика отбора каталогов афтершоков для дальнейшего предметного анализа.
Повторные афтершоки и ошибки идентификации. Используемый алгоритм идентификации афтершоков Молчана–Дмитриевой не выделяет вторичные афтершоки, что иногда проявляется в резких повышениях активности в середине или в конце афтершоковой последовательности, когда алгоритм относит к данной афтершоковой последовательности повторные афтершоки либо афтершоки от другого близкого главного события. Такие последовательности отбраковываются или обрезаются по времени, если повторная активизация приходится на конец последовательности.
Нелинейность графика повторяемости и систематическая ошибка при селекции по магнитуде. На рис. 4а показан типичный график повторяемости афтершоков. Различия оценок наклона графика повторяемости $b$ при различных выборах порога селекции по магнитудам снизу вблизи загиба графика повторяемости оказывается, как правило, существенно выше статистической погрешности их оценок. Для того, чтобы представить различие оценок $b$ нестатистической природы (связанное с криволинейностью графика повторяемости, а не с конечностью выборки) мы варьировали для каждой последовательности значение магнитуды селекции и представляли на pb-диаграммах полученные облака оценок и их среднее значение (рис. 4б).
Рис. 4.
Иллюстрация метода усреднения по варьированным пороговым значениям магнитуды: (а) – график повторяемости, варьирование магнитуд селекции осуществляется в диапазоне от ${{M}_{1}}$ до ${{M}_{3}}$; (б) – соответствующий разброс точек на pb-диаграмме.
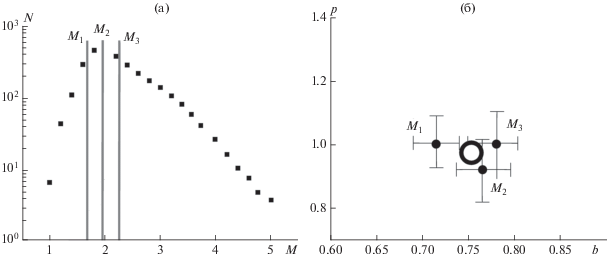
Неоднородность наклона графика повторяемости афтершоков во времени. В течение некоторого интервала времени после главного события, обычно от нескольких часов до нескольких суток, оценки наклона графика повторяемости имеют меньшие значения, чем в последующее время (рис. 5а). Этот интервал, как правило, соответствует времени установления степенного спада афтершоковой активности (рис. 5б). Природу эффекта связывают как с перегруженностью сейсмической сети на начальной стадии афтершоков, так и с изменениями в физических параметрах афтершокового процесса (краткий обзор см. в работе [Смирнов и др., 2019]).
Рис. 5.
Изменение оценки наклона графика повторяемости (а), афтершоковой активности (б) и представительной магнитуды (в) во времени (на примере афтершоков землетрясения М7.3 Ландерс, Калифорния). На врезке (а) показан график повторяемости для всей последовательности, вертикальная линия – порог селекции $M = 2$ для расчета наклона графика повторяемости. Пунктирной вертикальной линией на всех рисунках показана оценка параметра с модифицированного закона Омори.
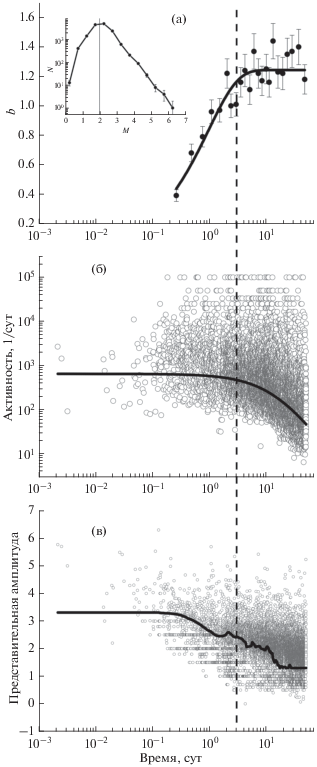
Для идентификации аномального интервала в начале афтершоковых последовательностей можно рассматривать зависимости наклона графика повторяемости от времени и находить моменты времени, начиная с которых параметр $b$ перестает заметно увеличиваться (рис. 5а). По этому времени можно выполнять селекцию, исключая неоднородную начальную часть каталога. Такой подход полезен и тем, что второй параметр – $p$ в законе Омори – определяется, в основном, по спадающей по степенной функции части афтершоковой активности (алгоритм оценки параметров модифицированного закона Омори работает по всему каталогу, но основной вклад в оценку $p$ дает падающая ветвь [Holschneider et al., 2012]). Эта часть определяется условием $t \gg c$, которое обычно соответствует интервалу выхода параметра $b$ из области неоднородности. Селекцию можно производить и на основании оценок представительной магнитуды в скользящих временных окнах (рис. 5в). Однако такие оценки требуют большей статистики по сравнению с оценками $b$ и на них не всегда хватает объемов выборок афтершоков.
Объем выборки. Относительные погрешности статистических оценок параметров Гутенберга–Рихтера и Омори определяются, в первую очередь, объемами выборок (количеством афтершоков), по которым они оцениваются. На рис. 6 показаны зависимости относительных погрешностей (отвечающих 96-процентному доверительному интервалу) параметров $p$ (рис. 6а) и $b$ (рис. 6б) от объемов выборок по данным каталога Японии. Каждая точка соответствует некоторой афтершоковой последовательности. Перед оцениванием параметров осуществлялась селекция каталогов афтершоков в соответствии с описанными выше правилами.
Рис. 6.
Зависимость относительных погрешностей оценок параметров $p$ (а) и $b$ (б) от количества событий в афтершоковых последовательностях и pb-диаграммы (в)–(д) для Японии. Горизонтальные линии – выбранные уровни относительной погрешности параметров; pb-диаграммы приведены для последовательностей, в которых относительные погрешности не превосходят 10% (в), 25% (г) 40% (д).
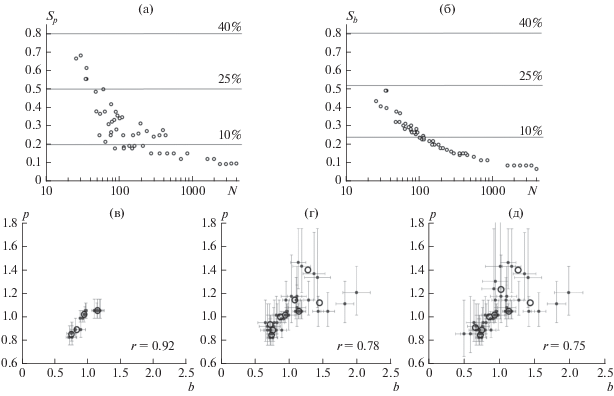
На рис. 6а, 6б видно ожидаемое уменьшение относительной погрешности с увеличением объема выборки. На рис. 6в–6д представлены pb-диаграммы для трех выбранных уровней погрешностей оценок: 10-процентный уровень является слишком жестким, поскольку только небольшая доля афтершоковых последовательностей имеет необходимое количество событий; pb-диаграммы для 25- и 40-процентных уровней – схожи, но разброс точек на 40-процентной диаграмме выше. Исходя из этого, при проведении предметного анализа отбраковывались последовательности, объем которых был недостаточен для получения оценок хуже, чем с 25-процентной относительной погрешностью.
Концепция селекции исходных каталогов афтершоков. Рассмотренные выше источники погрешностей оценок исследуемых параметров афтершоковых последовательностей позволили сформировать концепцию селекции исходных данных и построения pb-диаграмм. Каталоги афтершоков отбраковываются при наличии явных повторных афтершоковых последовательностей и, при возможности, селектируются по времени, если артефактная активизация (обусловленная грубостью работы алгоритма идентификации) попадает на конец последовательности. Далее каталоги афтершоков селектируются по магнитуде, при этом порог селекции варьируется вблизи загиба графика повторяемости, и на pb-диаграмму наносятся соответствующие точки и их средние значения. При необходимости, начальные участки афтершоковых последовательностей исключаются из анализа. Объемы отселектированных афтершоковых последовательностей, допускаемых для дальнейшего анализа, ограничиваются величинами, обеспечивающими достижение полученными по ним оценками $p$ и $b$ относительных “двухсигмовых” погрешностей не более 25%.
Исследованные регионы
На рис. 7 и рис. 8 представлены карты областей зон субдукции и трансформных разломов с нанесенными на них эпицентрами афтершоков из последовательностей, прошедших процедуру отбора и селекции для дальнейшего предметного анализа.
Рис. 7.
Карты областей зон субдукции. Разноцветными точками показаны эпицентры афтершоков последовательностей, отобранных для анализа (для Аляски – 6 последовательностей, Новой Зеландии – 8, Японии – 9, Камчатки – 14, для Курил ни одна последовательность не удовлетворила требованиям отбора). Синими линиями показаны положения желобов.
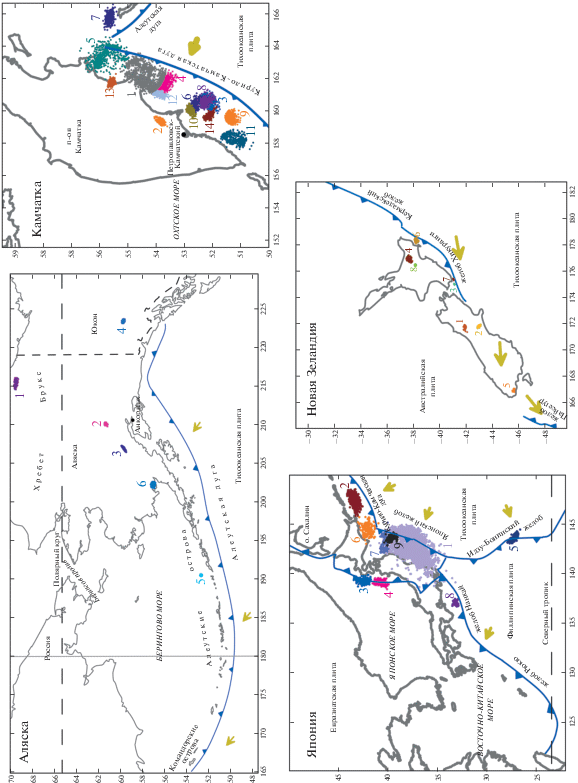
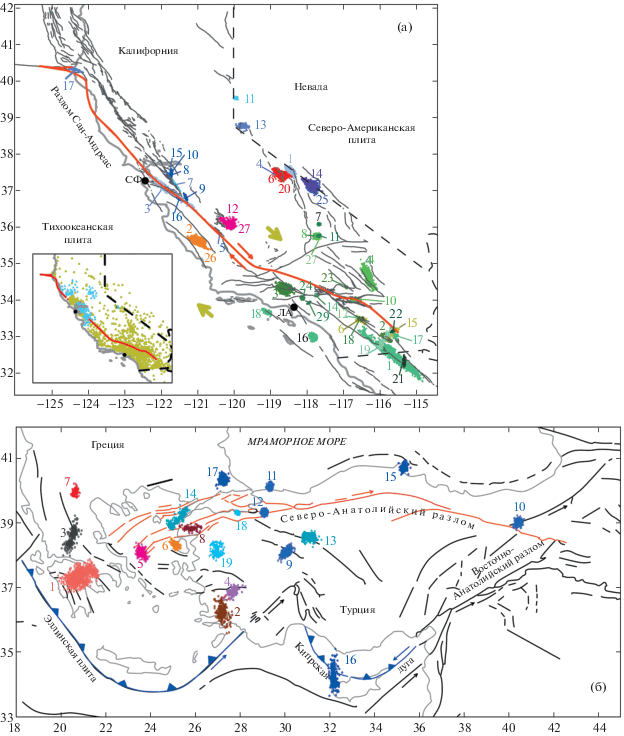
Рис. 8.
Карты областей зон сдвиговых трансформных разломов (положения разломов показаны красными линиями, красные стрелки – направления смещения берегов разломов): (а) – область разлома Сан-Андреас; (б) – область Северо-Анатолийского разлома. Разноцветными точками показаны эпицентры афтершоков последовательностей, отобранных для анализа (в области Северо-Анатолийского разлома: 1–8 – из каталога Греции, 9–18 – из каталога Турции; в области разлома Сан-Андреас: 1–17 – из каталога Северной, 18–29 – Южной Калифорнии).
РЕЗУЛЬТАТЫ
Унификация шкалы магнитуд. Для сопоставления pb-диаграмм, построенных по различным каталогам, необходимо привести оценки наклона графика повторяемости к единой магнитудной шкале (в разных каталогах используются, вообще говоря, разные магнитуды). Процедура унификации магнитудных шкал региональных каталогов землетрясений описана в работе [Смирнов, 2009]. Она заключается в сопоставлении записей о землетрясениях в региональном каталоге и Гарвардском каталоге тензоров сейсмического момента. После выявления пар записей, относящихся к одному и тому же землетрясению, строится ортогональная регрессия магнитуды регионального каталога и моментной магнитуды из Гарвардского каталога.
Выбор записей из двух каталогов, относящихся к одному землетрясению, осуществляется путем задания пространственно-временных окон, определяющих допустимое различие координат эпицентров (или, реже, гипоцентров) и времен землетрясений. Размеры окон подбираются эмпирически, исходя из следующих соображений. Варьирование размеров окон может приводить как к увеличению, так и к уменьшению количества формально совпавших пар записей из двух каталогов. Увеличение означает, что окно слишком велико, и в него попадают не только пары записей, относящиеся к одному событию, а записи о нескольких близких землетрясениях. Уменьшение означает, что окно слишком маленькое, и записи, относящиеся к одному событию, не попадают в него из-за погрешностей гипоцентрии. В работе [Смирнов, 2009] показано, что обычно имеется диапазон оптимальных размеров окон, в пределах которого количество совпадающих пар остается примерно постоянным при небольшом варьировании размеров окон. Для подбора оптимальных окон производится варьирование их размеров в некотором диапазоне значений и находится область стабильных количеств выделяемых пар записей.
В табл. 3 сведены полученные по соответствующим ортогональным регрессиям оценки коэффициента пересчета $k$ значений наклона графика повторяемости ${{b}_{l}}$ в магнитудах региональных каталогов к значению ${{b}_{w}}$ в моментных магнитудах: ${{b}_{w}} = k{{b}_{l}}$.
Таблица 3.
Унификация шкал магнитуд
| Регион | Окно, R°; Тс | Количество пар | Коэфф. корр. | $k$ |
|---|---|---|---|---|
| Аляска | 0.5°; 1с | 75 | 0.8 | 1.08 |
| Камчатка | 0.5°; 1с | 71 | 0.86 | 1.95 |
| Япония | 0.1°; 1с | 166 | 0.92 | 1.23 |
| Новая Зеландия | 0.5°; 1с | 54 | 0.86 | 1.05 |
| Северная Калифорния | 0.5°; 2с | 63 | 0.93 | 1.05 |
| Южная калифорния | 0.3°; 1с | 48 | 0.95 | 1.10 |
| Турция | 0.5°; 2с | 93 | 0.85 | 0.97 |
| Греция | 0.5°; 2с | 99 | 0.83 | 1.01 |
pb-диаграммы. На рис. 9 представлены сводные pb-диаграммы для исследованных зон субдукции и областей сдвиговых трансформных разломов.
Рис. 9.
Сводные pb-диаграммы для зон субдукции (а) и сдвиговых трансформных разломов (б). Эллипсами охвачены облака точек, по которым рассчитывались коэффициенты корреляции для различных районов (подписаны на рисунках). Цветные области оконтуривают области погрешностей оценок параметров $p$ и $b$ (включая погрешности унификации магнитудных шкал).
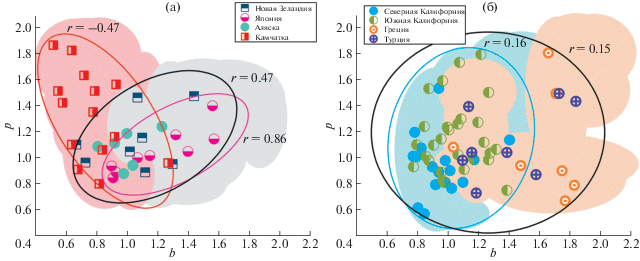
На рис. 9а видно, что для зон субдукции имеется корреляционная связь между параметрами Омори и Гутенберга–Рихтера. Наиболее надежно такая связь обнаружена для регионов Камчатки и Японии, причем для Камчатки связь отрицательная (антикорреляция), а для Японии – положительная (корреляция). В работе [Guo, Ogata, 1997] использовался каталог Японии до 1995 года, у нас – до 2012 года, 5 последовательностей из нашего каталога присутствуют и в работе [Guo, Ogata, 1997], причем все они относятся к внутриплитовым событиям. Авторы работы [Guo, Ogata, 1997] обнаруживают в этом случае, как и мы, положительную корреляцию (см. рис. 9а).
Рисунок 9б свидетельствует, что в исследованных областях сдвиговых трансформных разломов статистическая связь параметров $p$ и $b$ отсутствует.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
В литературе дискутируются различные физические механизмы релаксации афтершоковой активности (см. например, общую характеристику афтершоковых процессов в работе [Scholz, 2019] и подробный обзор возможных механизмов в диссертации [Helmstetter, 2002].) Механизмы можно условно разделить на два класса: “пассивная” релаксация на тех или иных структурных элементах (трение на контактах блоков, вязко-упругая релаксация, течение вязкого порового флюида) и “активная” – разрушение тех или иных структурных элементов, вызванное или инициированное главным событием (субкритический рост трещин, механическая коррозия, усталостное разрушение, эпидемические модели). И те, и другие механизмы предполагают наличие неких релаксаторов, действие которых формирует спад афтершоковой активности $I\left( t \right)$ согласно закону Омори:
или модифицированному закону Омори:Механизмы афтершоковой релаксации можно обобщить, рассматривая формально спад афтершоковой активности как процесс релаксации в системе релаксаторов, обладающей некоторым спектром времен релаксации ${\tau }\left( l \right)$, определяемым параметром релаксатора $l$, и соответствующей функцией плотности распределения релаксаторов ${\text{Pr}}\left( l \right)$ [Smirnov, Ponomarev, 2013]. Параметр $l$ будем называть “размером” релаксатора. Многие физические механизмы релаксации ассоциируются с системой неоднородностей среды (контакты блоков, трещины, очаги землетрясений, система пор и т.д.), в таких случаях параметр $l$ может быть связан с реальным геометрическим размером релаксатора.
Спад афтершоковой активности можно представить как суперпозицию процессов релаксации с временами ${\tau }\left( l \right)$, причем вклад каждого релаксатора “размера” $l$ определяется долей ${\text{Pr}}\left( l \right)$ таких релаксаторов в системе:
(3)
$I\left( t \right)\sim \int\limits_{{{l}_{1}}}^{{{l}_{2}}} {{\text{Pr}}\left( l \right)} {{e}^{{ - \frac{t}{{{\tau }\left( l \right)}}}}}dl,$Согласно представлениям о самоподобии сейсмического процесса и иерархичном характере структуры неоднородностей литосферы примем для функции плотности распределения релаксаторов ${\text{Pr}}\left( l \right)$ степенной вид:
В этом случае $d$ в (4) является показателем самоподобия распределения релаксаторов по “размерам”. Если же $l$ является реальным геометрическим размером той или иной структуры среды, то во многих случаях $d$ можно рассматривать как некоторую фрактальную размерность системы релаксаторов.
Релаксация согласно (3) при условии (4) для неограниченного спектра релаксаторов и зависимостей ${\tau }\left( l \right)$ в виде экспоненциальной и степенной функций рассмотрена в работе [Narteau et al., 2002] в предположении, что “размером” релаксатора $l$ (в нашей терминологии) является величина перенапряжений. Обе рассмотренные в работе [Narteau et al., 2002] зависимости ${\tau }\left( l \right)$ полагают уменьшение $\tau $ с увеличением $l$ – уменьшение времени релаксации с увеличением перенапряжений. Мы рассматриваем (3), не ограничиваясь только убывающим с ростом $l$ спектром времен релаксации, поэтому приведем соответствующие общие результаты, хотя часть из них совпадает с результатами работы [Narteau et al., 2002].
Неограниченный спектр релаксаторов
Рассмотрим сначала частный случай – (3) в пределе ${{l}_{1}} = 0$ и ${{l}_{2}} = \infty $:
(5)
$I\left( t \right)\sim {{\int\limits_0^\infty {{{l}^{{ - d}}}e} }^{{ - \frac{t}{{{\tau }\left( l \right)}}}}}dl.$Примем, что времена релаксации можно описать самоподобной функцией c показателем самоподобия $m$ так, что:
Если $m > 0$, то время релаксации увенчивается с увеличением “размера” релаксатора $l$, в противном случае – уменьшается.
Подставляя (6) в (5) при $m > 0$ и производя замену переменной интегрирования $x = {{{\tau }\left( l \right)} \mathord{\left/ {\vphantom {{{\tau }\left( l \right)} t}} \right. \kern-0em} t}$, получаем:
(7)
$I\left( t \right)\sim {{t}^{{ - \frac{{d - 1}}{m}}}}\int\limits_0^\infty {{\theta }{{{\left( x \right)}}^{{ - d}}}} {\theta }\left( x \right){\kern 1pt} '{{e}^{{ - \frac{1}{x}}}}dx,$Интеграл в (7) не зависит от $t$, поэтому окончательно получаем:
Аналогично, при $m < 0$ находим:
(9)
$I\left( t \right)\sim {{t}^{{ - \frac{{d - 1}}{m}}}}\int\limits_0^\infty {\frac{{{\theta }{{{\left( {\frac{1}{x}} \right)}}^{{ - d}}}{\theta }\left( {\frac{1}{x}} \right){\kern 1pt} '{{e}^{{ - x}}}}}{{{{x}^{2}}}}} dx~~\sim ~~{{t}^{{ - \frac{{d - 1}}{m}}}}.$Таким образом, для любых значений $m \ne 0$ выражение (5) сводится к закону Омори (1) при
Из (10) видно, что в рамках рассматриваемой модели параметр Омори определяется показателями самоподобия распределения по “размерам” $d$ и спектра релаксаторов $m$ и не зависит от конкретного вида функции ${\tau }\left( l \right)$. Следовательно, при степенной функции распределения ${\text{Pr}}\left( l \right)$ степенной спад активности получается при любом физическом механизме релаксации ${\tau }\left( l \right)$, обладающем свойством самоподобия. Из (9) и (10) видно также, что характер связи параметра Омори $p$ с показателем распределения релаксаторов по “размерам” $d$ существенно различен при $m > 0$ и $~m < 0$: в первом случае $p$ и $~d$ коррелируют, во втором – антикоррелируют.
Ограниченный спектр релаксаторов
Рассмотренный выше неограниченный спектр релаксаторов физически не оправдан уже потому, что афтершоковые процессы локализованы в пространстве и во времени. Вернемся к выражению (3) и рассмотрим общий случай, когда спектр релаксаторов ограничен “размерами” ${{l}_{1}}$ и ${{l}_{2}}$:
(11)
$I\left( t \right)\sim \int\limits_{{{l}_{1}}}^{{{l}_{2}}} {{{l}^{{ - d}}}} {{e}^{{ - \frac{t}{{{\tau }\left( l \right)}}}}}dl.$а). Узкий диапазон “размеров” релаксаторов: ${{{{l}_{2}}} \mathord{\left/ {\vphantom {{{{l}_{2}}} {{{l}_{1}}}}} \right. \kern-0em} {{{l}_{1}}}} \approx 1$.
В этом случае зависимостью ${\tau }\left( l \right)$ можно пренебречь и положить ${\tau }\left( l \right) \approx {\tau }\left( {\bar {l}} \right)$, где $\bar {l}\epsilon \left[ {{{l}_{1}},~{{l}_{2}}} \right]$. Тогда из (11) получаем:
(12)
$I\left( t \right)\sim {{e}^{{ - \frac{t}{{{\tau }\left( {\bar {l}} \right)}}}}}\int\limits_{{{l}_{1}}}^{{{l}_{2}}} {{{l}^{{ - d}}}} dl~~\sim ~~{{e}^{{ - \frac{t}{{{\tau }\left( {\bar {l}} \right)}}}}}.$В случае небольшого диапазона “размеров” релаксаторов суммарная релаксация имеет экспоненциальный характер, и стенной закон Омори не реализуется.
б). Широкий диапазон “размеров” релаксаторов: ${{{{l}_{2}}} \mathord{\left/ {\vphantom {{{{l}_{2}}} {{{l}_{1}}}}} \right. \kern-0em} {{{l}_{1}}}} = k \gg 1$.
Пусть, по-прежнему, ${\tau }\left( l \right)$ является самоподобной функцией (6).
Рассмотрим (12) для $m > 0$. В этом случае после замены переменных $x = {{{\tau }\left( l \right)} \mathord{\left/ {\vphantom {{{\tau }\left( l \right)} t}} \right. \kern-0em} t}$ получаем из (12):
где(14)
${\varphi }\left( t \right) = \int\limits_{\frac{{{{{\tau }}_{1}}}}{t}}^{\frac{{{{{\tau }}_{2}}}}{t}} {{\theta }{{{\left( x \right)}}^{{ - d}}}} ~{\theta }\left( x \right){\kern 1pt} '{{e}^{{ - \frac{1}{x}}}}~dx,$Если $t \gg {{{\tau }}_{1}}$, то нижний предел в (14) можно положить равным нулю. Если $t \ll {{{\tau }}_{2}}$, то верхний предел в (14) можно считать бесконечным. Таким образом, в диапазоне времен зависимостью ${\varphi }$ от $t$ в (14) можно пренебречь. В это ${{{\tau }}_{1}} \ll t \ll {{{\tau }}_{2}}$. В этом случае (13) переходит в (8), и спад активности имеет степенной вид, т.е. закон Омори реализуется в диапазоне ${{{\tau }}_{1}} \ll t \ll {{{\tau }}_{2}}$ при $p = \frac{{d - 1}}{m}$, что отвечает (10).
Для $m < 0$, делая замену $x = {t \mathord{\left/ {\vphantom {t {{\tau }\left( l \right)}}} \right. \kern-0em} {{\tau }\left( l \right)}}$, получаем из (12):
где(16)
${\psi }\left( t \right) = \int\limits_{\frac{{{{{\tau }}_{2}}}}{t}}^{\frac{{{{{\tau }}_{1}}}}{t}} {\frac{{{\theta }{{{\left( {\frac{1}{x}} \right)}}^{{ - d}}}{\theta }\left( {\frac{1}{x}} \right){\kern 1pt} '{{e}^{{ - x}}}}}{{{{x}^{2}}}}~} dx$В этом случае, если ${{{\tau }}_{2}} \ll t \ll {{{\tau }}_{1}}$, то верхний и нижний пределы в интеграле (16) можно считать равными нулю и бесконечности, соответственно. Тогда (26) тоже переходит в (8), т.е. при $m < 0$ закон Омори реализуется в диапазоне ${{{\tau }}_{2}} \ll t \ll {{{\tau }}_{1}}$.
Далее, для единообразного обсуждения случаев $m > 0$ и $m < 0$ обозначим минимальное и максимальное время релаксации как ${{{\tau }}_{{{\text{min}}}}}$ и ${{{\tau }}_{{{\text{max}}}}}$. В случае $m > 0$: ${{{\tau }}_{{{\text{min}}}}} = {\tau }\left( {{{l}_{1}}} \right)$ и ${{{\tau }}_{{{\text{max}}}}} = \tau \left( {{{l}_{2}}} \right)$, в случае $m < 0$: ${{{\tau }}_{{{\text{min}}}}} = {\tau }\left( {{{l}_{2}}} \right)$ и ${{{\tau }}_{{{\text{max}}}}} = {\tau }\left( {{{l}_{1}}} \right)$. И в том, и в другом случае ${{{{{\tau }}_{{{\text{max}}}}}} \mathord{\left/ {\vphantom {{{{{\tau }}_{{{\text{max}}}}}} {{{{\tau }}_{{{\text{min}}}}}}}} \right. \kern-0em} {{{{\tau }}_{{{\text{min}}}}}}} = {{k}^{{\left| m \right|}}} \gg 1.$
В этих обозначениях степенной спад активности (закон Омори) реализуется в диапазоне ${{{\tau }}_{{{\text{min}}}}} \ll t \ll {{{\tau }}_{{{\text{max}}}}}.$
Пусть теперь $t \ll {{{\tau }}_{{{\text{min}}}}}$. В этом случае ${{e}^{{ - \frac{t}{{{\tau }\left( l \right)}}}}} \approx 1 - \frac{t}{{{\tau }\left( l \right)}}$ и (11) принимает вид:
где(18)
$B = \int\limits_{{{l}_{1}}}^{{{l}_{2}}} {{{l}^{{ - d}}}dl} = \frac{{l_{1}^{{1 - d}}}}{{1 - d}}\left( {{{k}^{{1 - d}}} - 1} \right)$(19)
$A = \int\limits_{{{l}_{1}}}^{{{l}_{2}}} {\frac{{{{l}^{{ - d}}}}}{{\tau \left( l \right)}}} dl = \frac{1}{{{{\tau }_{0}}}}\frac{{l_{1}^{{1 - \left( {d + m} \right)}}}}{{1 - \left( {d + m} \right)}}\left( {{{k}^{{1 - \left( {d + m} \right)}}} - 1} \right).$В (19) принято, что ${\tau }\left( l \right) = {\tau }\left( {l \times 1} \right) = {{{\tau }}_{0}}{{l}^{m}},$ где ${{{\tau }}_{0}} = {\tau }\left( 1 \right)$.
Следовательно, в диапазоне времен $t \ll {{{\tau }}_{{{\text{min}}}}}$ спад активности происходит по линейному закону.
Для некоторых реалистичных условий можно показать, что второе слагаемое в (17) пренебрежимо мало по сравнению с первым. Действительно, положим ${{t}_{{max}}} = {\delta }{{{\tau }}_{{{\text{min}}}}}$, где ${\delta } \ll 1$ в соответствии с условием $t \ll {{{\tau }}_{{{\text{min}}}}}$, примем для определенности ${{{\tau }}_{{{\text{min}}}}} = {{{\tau }}_{0}}l_{1}^{m}$ и оценим отношение ${{\left| {A{{t}_{{{\text{max}}}}}} \right|} \mathord{\left/ {\vphantom {{\left| {A{{t}_{{{\text{max}}}}}} \right|} {\left| B \right|}}} \right. \kern-0em} {\left| B \right|}}$. При $d > 1$ и $k \gg 1$: ${{k}^{{1 - d}}} \ll 1$ и ${{k}^{{1 - \left( {d + m} \right)}}} \ll 1$, и этими слагаемыми в (18) и (19) можно пренебречь. Тогда получим:
(20)
$\frac{{\left| {A{{t}_{{{\text{max}}}}}} \right|}}{{\left| B \right|}} = \frac{{d - 1}}{{d + m - 1}}{\delta }{\text{.}}$Из (20) видно, что в рассмотренном случае, при ${\delta } \ll 1$ отношение ${{\left| {A{{t}_{{{\text{max}}}}}} \right|} \mathord{\left/ {\vphantom {{\left| {A{{t}_{{{\text{max}}}}}} \right|} {\left| B \right|}}} \right. \kern-0em} {\left| B \right|}} \ll 1$. Следовательно, в диапазоне $t \ll {{{\tau }}_{{{\text{min}}}}}$ активность $I\left( t \right)$ можно считать постоянной:
Наконец, рассмотрим случай $t \gg {{{\tau }}_{{{\text{max}}}}}$. В этом случае зависимостью ${\tau }$ от $l$ в (11) можно пренебречь, положив ${\tau }\left( l \right) = {{{\tau }}_{{{\text{max}}}}}$. Тогда:
(22)
$I\left( t \right)\sim \int\limits_{{{l}_{1}}}^{{{l}_{2}}} {{{l}^{{ - d}}}} {{e}^{{ - \frac{t}{{{{{\tau }}_{{{\text{max}}}}}}}}}}dl = {{e}^{{ - \frac{t}{{{{{\tau }}_{{{\text{max}}}}}}}}}}\int\limits_{{{l}_{1}}}^{{{l}_{2}}} {{{l}^{{ - d}}}} dl~~\sim ~~{{e}^{{ - \frac{t}{{{{{\tau }}_{{{\text{max}}}}}}}}}}.$Следовательно, в диапазоне времен $t \gg {{{\tau }}_{{{\text{max}}}}}$ активность спадает экспоненциально, и степенной закон Омори не реализуется.
Подведем итог. Результаты, полученные при анализе наиболее общего выражения (11), сводятся к следующему.
В диапазоне $t \ll {{{\tau }}_{{{\text{min}}}}}$ спад активности отсутствует: $I\left( t \right) \approx {\text{const}}$ (выражение (21)).
В диапазоне ${{{\tau }}_{{{\text{min}}}}} \ll t \ll {{{\tau }}_{{{\text{max}}}}}$ активность спадает по степенному закону – реализуется закон Омори с параметром, определяемым формулой (10).
В диапазоне $t \gg {{{\tau }}_{{{\text{max}}}}}$ активность спадает по экспоненциальному закону (22).
Отметим, что такие выводы были сделаны ранее в работе [Narteau et al., 2002] для одного из типов распределения релаксаторов по их “размерам”. Наши результаты свидетельствуют, что эти три типа спада активности универсальны и реализуются при любом самоподобном распределении релаксаторов по “размерам” ${\tau }\left( l \right)$.
Полученные результаты можно проинтерпретировать следующим образом.
В диапазоне $t \ll {{{\tau }}_{{{\text{min}}}}}$ даже самые быстрые релаксаторы, имеющие время релаксации ${{{\tau }}_{{{\text{min}}}}}$, не успевают срелаксировать (более медленные релаксаторы с временами релаксации ${\tau }\left( l \right) \in \left[ {{{{\tau }}_{{{\text{min}}}}},{\kern 1pt} {\text{\;}}{{{\tau }}_{{{\text{max}}}}}} \right]$ тем более не успевают срелаксировать). Тем самым, в этом диапазоне времен $t \ll {{{\tau }}_{{{\text{min}}}}}$ релаксации фактически нет, и поэтому активность остается неизменной.
В диапазоне $t \gg {{{\tau }}_{{{\text{max}}}}}$ все релаксаторы успевают срелаксировать и для спада активности мы получаем экспоненциальную асимптоту с временем релаксации ${{\tau }_{{{\text{max}}}}}$.
В промежуточном случае ${{{\tau }}_{{{\text{min}}}}} \ll t \ll {{{\tau }}_{{{\text{max}}}}}$ вклад релаксаторов с различными временами релаксации ${\tau }\left( l \right)$ определяется распределением релаксаторов по “размеру” ${\text{Pr}}\left( l \right)$. Для самоподобных функций ${\tau }\left( l \right)$ и ${\text{Pr}}\left( l \right)$ реализуется степенной спад активности – закон Омори.
Заметим, что результаты, полученные для случаев $t \ll {{{\tau }}_{{{\text{min}}}}}$ и ${{{\tau }}_{{{\text{min}}}}} \ll t \ll {{{\tau }}_{{{\text{max}}}}}$, можно объединить в модифицированный закон Омори (2). Действительно, в объединенном диапазоне $t \ll {{{\tau }}_{{{\text{max}}}}}$ спад активности подчиняется (2) при $p = \frac{{d - 1}}{m}$ и $c = {{{\tau }}_{{{\text{min}}}}}$.
Примеры релаксаторов со спектрами времен разного типа
Вопрос о спектре “размеров” релаксаторов и характере их распределения по “размерам” остается в настоящее время открытым. Если принять, что время релаксации определяется “временем жизни” (долговечностью) дефекта размера $l$ в постоянном поле напряжений, то обратную зависимость времени релаксации от размера дефекта можно на качественном уровне объяснить в рамках кинетической концепции разрушения. Действительно, чем больше дефект, тем выше на нем концентрация напряжений. А согласно концепции Журкова [Журков, 1968], чем выше напряжения, тем меньше долговечность. Следовательно, чем больше размер дефекта, тем меньше его “время жизни” в поле напряжений.
Зависимость ${\tau }\sim {1 \mathord{\left/ {\vphantom {1 l}} \right. \kern-0em} l}$ получается также для времен релаксации деформации вязкой жидкости в областях характерного размера $l$ под действием градиента напряжений [Артюшков, 1979]. Такой механизм может быть актуален в моделях релаксации за счет перетекания вязкой жидкости в поровом или трещиноватом пространстве. В этом случае под размером релаксатора $l$ можно понимать размер “канала”, по которому движется жидкость – размер пор или трещин. Скорость течения жидкости в таком случае будет пропорциональна $l$, а соответствующее время выравнивания давлений при перетекании жидкости – обратно пропорционально $l$.
Оба указанных механизма для зависимости типа ${\tau }\sim {1 \mathord{\left/ {\vphantom {1 l}} \right. \kern-0em} l}$ имеют кинетическую природу – задержка обусловлена процессом, развивающимся во времени с конечной скоростью. В первом случае, это, согласно концепции Журкова, – кинетика разрушения, во втором – динамика вязкого течения флюида.
К этому же типу зависимости $\tau \left( l \right)$ относятся спектры времен релаксации, рассмотренные в работе [Narteau et al., 2002], где, напомним, в качестве параметра “размера” релаксатора рассматриваются перенапряжения в среде, созданные главным событием.
Прямая зависимость ${\tau }$ от $l$ рассматривалась в геомеханике неоднородной (блоковой) среды [Родионов и др., 1986]. Размер релаксатора в таком случае определяется размером неоднородности. Скорость релаксации в такой среде принимается пропорциональной градиенту напряжений на неоднородностях. Характерный градиент задается отношением разницы напряжений к размеру неоднородности $l$. Соответственно, время релаксации оказывается пропорциональным $l$.
В предположении, что распределение релаксаторов по размерам определяется теми или иными структурными неоднородностями среды, можно принять, что показатель самоподобия распределения релаксаторов по “размерам” $d$ связан с показателем самоподобия сейсмического режима – параметром Гутенберга–Рихтера $b$. Если релаксаторы ассоциируются с реальными неоднородностями среды (такими, например, как очаги афтершоков в сценарии ETAS [Ogata, 1988]), то показатель $d$ имеет смысл фрактальной размерности системы неоднородностей. В этом случае его можно связать с параметром $b$ по формуле Аки ${\alpha }b = d$. В таком случае, вместо связи $p$ и $d$ в (10) можно рассматривать связь $p$ и $b$.
В лабораторных экспериментах на обводненных образцах была обнаружена антикорреляция параметров $p$ и $b$. Согласно (10) это указывает на обратную зависимость времени релаксации от “размера” релаксатора. Теоретически такой вид спектра времен релаксации может быть обусловлен движением вязкой жидкости в поровом пространстве. Другой возможный механизм, отвечающий этому типу, был предложен в работе [Narteau et al., 2002].
В экспериментах оценки параметров $p$ и $b$ получены при различных уровнях напряжений, а различие типов корреляции $p$ и $b$ фактически определяется различием зависимости параметра Омори от напряжений, поскольку, как отмечалось в работе [Смирнов и др., 2019], наклон графика повторяемости $b$ в целом всегда уменьшается с ростом уровня действующих напряжений. Из (10) следует, что изменения параметра Омори могут быть вызваны как изменением структуры релаксаторов – изменением параметра самоподобия распределения релаксаторов по “размерам” $d$, так и изменением свойств релаксаторов – изменением параметра $m$. Обнаруженные в работе [Смирнов и др., 2019] разнознаковые, но синхронные изменения параметра Омори $p$ и наклона графика повторяемости $b$ свидетельствуют в пользу первого механизма, поскольку параметр $b$ характеризует самоподобие структуры процесса разрушения.
В натурных условиях статистическая связь $p$ и $b$ обнаружена в зонах субдукции, причем она оказалась разных знаков – антикорреляция для Камчатки и корреляция для Японии. Такое различие для сходных в тектоническом отношении регионов оказалось неожиданным, и авторы не могут в настоящее время дать ему обоснованное объяснение.
ЗАКЛЮЧЕНИЕ
Сопоставление результатов статистических оценок параметров Омори и Гутенберга–Рихтера в афтершоковых процессах показало, что в зонах субдукции взаимосвязь этих параметров может быть как положительной, так и отрицательной. В зонах сдвиговых трансформных разломов связь параметров отсутствует. Лабораторные эксперименты по моделированию афтершоко-подобной релаксации процесса разрушения также обнаруживают как положительную, так и отрицательную их корреляцию, знак и степень которой различаются в экспериментах на разных материалах и в разных условиях: сухие или обводненные образцы, целые или со сформированным макроразрывом.
“Интеграл Шольца” (3) – высказанная К. Шольцем идея объяснения закона Омори суперпозицией процессов релаксации с различными временами – позволяет связать параметр Омори степенного спада $p$ с показателем самоподобия распределения релаксаторов по их “размерам” $d$. В зависимости от типа спектра времен релаксации – нарастающего или убывающего с увеличением “размера” релаксатора – связь $p$ и $d$ имеет разный знак. В случае возрастающего спектра $p$ и $d$ коррелируют, в случае убывающего – антикоррелируют. Теоретически известны механизмы релаксации, которые допускают и тот, и другой виды спектров времен релаксации.
Вопрос о реализации тех или иных механизмов афтершоковой релаксации в зонах субдукции и сдвиговых разломов остается в настоящее время открытым.
Список литературы
Артюшков Е.В. Геодинамика. М.: Наука. 1979. 327 с.
Баранов С.В., Шебалин П.Н. О прогнозировании афтершоковой активности. 3. Динамический закон Бота // Физика Земли. 2018. № 6. С. 129–136.
Баранов С.В., Павленко В.А., Шебалин П.Н. О прогнозировании афтершоковой активности. 4. Оценка максимальной магнитуды последующих афтершоков // Физика Земли. 2019. № 4. С. 15–32.
Журков С.Н. Кинетическая концепция прочности твердых тел // Вестник АН СССР. 1968. № 3. С. 46–52.
Потанина М.Г., Смирнов В.Б., Пономарев А., Бернар П., Любушин А., Шозиёев Ш. Особенности акустической эмиссии при флюидной инициации разрушения по данным лабораторного моделирования // Физика Земли. 2015. № 2. С. 126–138.
Родионов В.Н., Сизов И.А., Цветков В.М. Основы геомеханики. М.: Недра. 1986. 301 с. / с. 67.
Смирнов В.Б. Опыт оценки представительности данных каталогов землетрясений // Вулканология и сейсмология. 1997а. № 4. С. 93–105.
Смирнов В.Б. Прогностические аномалии сейсмического режима. I. Методические основы подготовки исходных данных // Геофизические исследования. 2009. Т. 10. № 2. С. 7–22.
Смирнов В.Б., Габсатарова И.П. Представительность каталога землетрясений северного Кавказа: расчетные данные и статистические оценки // Вестник ОГГГГН РАН. 2000. Т. 14. № 4. С. 35–41.
Смирнов В.Б., Завьялов А.Д. К вопросу о сейсмическом отклике на электромагнитное зондирование литосферы Земли // Физика Земли. 2012. № 7–8. С. 63-88.
Смирнов В.Б., Пономарев А.В. Закономерности релаксации сейсмического режима по натурным и лабораторным данным // Физика Земли. 2004. № 10. С. 26–36.
Смирнов В.Б., Пономарев А.В., Бернар П., Патонин А.В. Закономерности переходных режимов сейсмического процесса по данным лабораторного и натурного моделирования // Физика Земли. 2010. № 2. С. 17–49.
Смирнов В.Б., Пономарев А.В., Станчиц С.А., Потанина М.Г., Патонин А.В., Dresen G., Narteau C., Bernard P., Строганова С.М. Лабораторное моделирование афтершоковых последовательностей: зависимость параметров Омори и Гутенберга–Рихтера от напряжений // Физика Земли. 2019. № 1. С. 169–165. https://doi.org/10.31857/S0002-333720191149-165
Avila-Barrientos L., Zunigac F.R., Rodríguez-Perezac Q., Guzman-Spezialec M. Variation of b and p values from aftershocks sequences along the Mexican subduction zone and their relation to plate characteristics // J. South American Earth Sciences. 2015. V. 63. P. 162–171.
Gasperini P., Lolli B. Correlation between the parameters of aftershock rate equation: Implications for the forecasting of future sequences // PEPI. 2006. V. 156 P. 41–58.
Guo Z., Ogata Y. Statistical relations between the parameters of aftershocks in time, space, and magnitude // J. Geophysical Research: Solid Earth. 1997. T. 102. № B2. P. 2857–2873.
Helmstetter A. Ruptures et instabilit’es: sismicit’e et mouvements gravitaires. These de Doctorat de l’Universite le Joseph Fourier – Grenoble I. 2002. 387 p.
Holschneider M., Narteau C., Shebalin P., Peng Z., Schorlemmer D. Bayesian analysis of the modified Omori law // J. Geophys. Res. 2012. V. 117. B06317. https://doi.org/10.1029/2011JB009054
Jeen-Hwa Wang. On the correlation of observed Gutenberg-Richter’s b value and Omori’s p value for aftershocks // Bull. Seismol. Soc. Am. 1994 V. 84. P. 2008–2011.
Kostrov B.V., Das S. Principles of earthquake source mechanics. Cambridge Univ. Press, 1988. 286 p.
Lockner D.A., Byerlee J.D., Kuksenko V., Ponomarev A., Sidorin A. Quasi-static fault growth and shear fracture // Nature. 1991. V. 350. № 6313. P. 39–42.
Lockner D.A., Byerlee J.D., Kuksenko V., Ponomarev V., Sidorin A. Observations of Quasistatic Fault Growth from Acoustic Emissions / Fault Mechanics and Transport Properties of Rocks / Editors Evans B., Wong T.F. London: Academic Press. 1992. P. 3–31.
Narteau C., Byrdina S., Shebalin P., Schorlemmer D. Common dependence on stress for the two fundamental laws of statistical seismology // Nature. 2009. V. 462. № 3. P. 642–646. https://doi.org/10.1038/nature08553
Narteau C., Shebalin P., Holschneider M. Temporal limits of the power law aftershock decay rate // J. Geophys. Res. 2002. V. 107. P. B2359. https://doi.org/10.1029/2002JB001868
Ogata Y. Statistical models for earthquake occurrence and residual analysis for point processes // J. Am. Stat. Assoc. 1988. V. 83. P. 9–27. https://doi.org/10.2307/2288914
Ommi S., Zafarani H., Smirnov V.B. Bayesian estimation of the Modified Omori Law parameters for the Iranian Plateau // J. Seismology. 2016. V. 20. P. 953–970. https://doi.org/10.1007/s10950-016-9574-8
Page R. Aftershocks and microaftershocks of the Great Alaska Earthquake of 1964 // Bull. Seismol. Soc. Am. 1968. V. 58. № 3. P. 1131–1168.
Pickering G., Bull J.M., Sanderson D.J. Sampling power-low distribution // Tectonophysics. 1995. V. 248. P. 1–20.
Scholz C.H. Microfracturing and the inelastic deformation of rocks in compression // J. Geophys. Res. 1968. V. 73. P. 1417–1432.
Scholz C.H. The mechanics of earthquakes and faulting. Cambridg Univ. Press. 2019. 493 p.
Shebalin P., Narteau C., Holschneider M., Schorlemmer D. Short-Term Earthquake Forecasting Using Early Aftershock Statistics // Bull. Seismol. Soc. Am. 2011. V. 101. № 1. P. 297–312. https://doi.org/10.1785/0120100119
Smirnov V., Ponomarev A. Modeling of transient seismic process - laboratory and field scales // Joint Assembly of IAHS-IAPSO-IASPEY, Gothenburg, Sweden, 2013. Book of Abstracts. 2013. S301S1.01.
Vilhelm J., Rudajev V., Ponomarev A.V., Smirnov V.B., Lokajíček T. Statistical study of acoustic emissions generated during the controlled deformation of migmatite specimens // International Journal of Rock Mechanics and Minings Sciences. 2017. V. 100. P. 83–89. https://doi.org/10.1016/j.ijrmms.2017.10.011
Wang J-H. On the correlation of observed Gutenberg-Richter’s b value and Omori’s p value for after-shocks // Bull. Seismol. Soc. Am. 1994. V. 84. P. 2008–2011.
Дополнительные материалы отсутствуют.
Инструменты
Физика Земли


