1. На главную
  2. Электронные версии
  3. Физика Земли
  4. № 6, 2020

Физика Земли, 2020, № 6, стр. 11-23

Обнаружение и оценка моды Шлихтера по наблюдениям землетрясения в Чили 27.02.2010 г. на лазерном интерферометре-деформографе

В. К. Милюков 1, 2, *, М. П. Виноградов 1, А. П. Миронов 1, А. В. Мясников 1

1 Государственный астрономический институт им. П.К. Штернберга, МГУ им. М.В. Ломоносова
г. Москва, Россия

2 Владикавказский научный центр РАН
г. Владикавказ, Россия

* E-mail: vmilyukov@yandex.ru

Поступила в редакцию 03.03.2020
После доработки 21.04.2020
Принята к публикации 23.04.2020

Полный текст (PDF)

Аннотация

Мода Шлихтера (1S1) является самой длиннопериодной модой собственных колебаний Земли. Период моды Шлихтера непосредственно зависит от разницы в плотности между внешним жидким и внутренним твердым ядром, что делает ее обнаружение очень важным для уточнения внутреннего строения Земли. Достоверные экспериментальные данные об обнаружении моды отсутствуют, что связано с ее незначительной амплитудой на поверхности. В работе впервые для обнаружения моды Шлихтера используются деформографические данные Баксанского лазерного интерферометра-деформографа ГАИШ МГУ с длиной измерительного плеча 75 м (Приэльбрусье, Северный Кавказ), записанные во время крупнейшего землетрясения в Чили 2010 г. Разработан асимптотически-оптимальный алгоритм анализа данных с учетом свойств сейсмического шума и особенностей моды, позволяющий одновременно с обнаружением осуществлять оценку ее параметров (частоту и величину расщепления). Выполнена оценка статистической достоверности обнаружения, определены параметры моды Шлихтера и соответствующий скачок плотности между внутренним и внешним ядром Земли.

Ключевые слова: ядро Земли, собственные колебания Земли, мода Шлихтера, лазерный интерферометр-деформограф, асимптотически-оптимальный алгоритм.

ВВЕДЕНИЕ

Самая длиннопериодная мода собственных колебаний Земли 1S1 возникает во время перемещения твердого внутреннего ядра Земли относительно жидкого внешнего ядра и мантии, о ее существовании впервые было указано Шлихтером [Slichter, 1961]. Частота моды Шлихтера в значительной степени зависит от скачка плотности на границе внутреннего ядра, т.к. основной восстанавливающей силой при колебаниях является отрицательная плавучесть твердого внутреннего ядра. Эта особенность делает определение ее периода очень важным для понимания структуры ядра.

Основные “классические” модели строения Земли (в частности, PREM) и их модификации дают значения периодов моды Шлихтера в диапазоне 3–9 ч, в частности, стандартная модель PREM – 5.5 ч (325 мин). Следует отметить, что наблюдения в данном диапазоне усложняются за счет когерентных помех в виде нелинейных приливных гармоник. Даже после “удаления” из данных прилива остаточный сигнал на его частотах может быть ошибочно воспринят как проявление моды 1S1. Из-за вращения Земли мода должна наблюдаться в виде триплета, причем из-за большой величины периода абсолютная величина расщепления значительна [Busse, 1974].

В настоящее время нет точного понимания возможных механизмов возбуждения моды Шлихтера. Если раньше рассматривались только сейсмические механизмы [Smith, 1976; Crossley, 1992a; Rosat, 2007], то в последние годы стали появляться альтернативные теории, в частности, поверхностное атмосферное давление, столкновение с метеороидами. По оценке, данной в работах [Rosat, Rogister, 2012; Rosat et al., 2014] наибольшую амплитуду может вызвать механизм потока давления через границы ядра, однако сама возможность такого потока в необходимых пространственно-временных масштабах остается неясной.

Гипотезы основного механизма затухания также различны, хотя все теории дают для добротности оценку Q более 2000. В работе [Crossley et al., 1992b] основной причиной затухания указывается сейсмическая неупругость, в работе [Mathews, Guo, 2005] – вязкость внешнего ядра, авторы работ [Buffett, Goertz, 1995; Buffett, 2010] предполагают магнитную природу затухания.

Первые серьезные экспериментальные попытки обнаружения моды Шлихтера были начаты в конце 90-х гг. с развитием сети Global Geodynamic Project (GGP), состоящей из сверхпроводящих гравиметров.

В большинстве наблюдений [Smylie, 1992; Crossley et al., 1992c; Hinderer et al., 1995; Smylie, McMillan, 2000; Courtier et al., 2000; Rosat et al., 2003; 2006; Xu et al., 2010; Rosat, Rogister, 2012; Jiang et al., 2013; Shen, Luan, 2015; Ding, Chao, 2015] были сделаны выводы о возможном наличии возбуждения. В других наблюдениях [Jensen et al., 1995; Guo et al., 2007; Abd El-Gelil, Pagiatakis, 2009; Ding, Shen, 2013] мода Шлихтера не была обнаружена. Во многом данная неопределенность связана с недостаточной чувствительностью используемых приборов [Rosat et al., 2003] и с отсутствием точного понимания механизмов возбуждения и затухания моды. На данный момент достоверные наблюдения моды Шлихтера отсутствуют.

Целью работы является поиск и оценка параметров моды Шлихтера, возбуждение которой могло быть вызвано Чилийским землетрясением 2010 года, по деформографическим данным Баксанского лазерного интерферометра-деформографа ГАИШ МГУ.

ДЕФОРМАЦИОННЫЕ ДАННЫЕ

Баксанская станция ГАИШ МГУ (Северный Кавказ, Приэльбрусье, координаты N 43.27252° и E 42.69749°) оснащена лазерным интерферометром-деформографом с длиной измерительного плеча 75 м и инструментальной разрешающей способностью к измерению деформаций 3 × 10–13 [Милюков, Мясников, 2005]. Деформограф размещен в подземной галерее Баксанской нейтринной обсерватории ИЯИ РАН. Ориентация главного измерительного плеча относительно направления на север составляет 150°37′. В штатном режиме деформограф производит мониторинг литосферных деформаций по пяти частотным каналам. Непрерывная запись деформаций осуществляется с 2004 г.

Данные Баксанского деформографа успешно использовались авторами работы для обнаружения большого числа сфероидальных и тороидальных мод СКЗ, возбуждаемых крупными землетрясениями [Милюков, 2005; Милюков и др., 2015a; 2015b; 2018].

Величина возбуждения моды Шлихтера зависит от типа землетрясения (особенностей распределения сейсмического момента по компонентам), его глубины; также при регистрации имеет значение расположение приемника относительно источника [Dahlen, Tromp, 1998]. Теоретический расчет возможного возбуждения моды Шлихтера от крупнейших землетрясений за последние 20 лет (2000–2019 гг.) показал, что наибольшую амплитуду деформации при наблюдении на Баксане должно было вызвать землетрясение, произошедшее на территории Чили 27.02.2010 г. Это землетрясение, также известное как землетрясение Mauli на офшоре Bio-Bio, произошло на глубине 23 км [Duputel et al., 2012]. По величине магнитуды 8.8 Mw находится оно на шестом месте в списке наиболее значительных за историю наблюдений.

АЛГОРИТМ ОБНАРУЖЕНИЯ

Обнаружение моды Шлихтера в деформографических данных является типичной задачей обнаружения слабого сигнала на фоне помех. Если шум является гауссовским, то решением подобной задачи является согласованная фильтрация. Однако реальный сейсмический шум отличается от гауссовского, что требует другого подхода.

Авторами был предложен асимптотически-оптимальный алгоритм для одновременного обнаружения и оценки параметров моды Шлихтера с учетом свойств полезного сигнала (моды Шлихтера) и сейсмического шума, основанный на методе максимального правдоподобия [Виноградов и др., 2019]. Было показано, что свойства шума можно учесть безынерционным нелинейным преобразованием исходного сигнала перед осуществлением согласованной фильтрации. В компьютерном эксперименте была подтверждена эффективность использования алгоритма при поиске моды Шлихтера после крупнейших землетрясений. В данной работе мы модифицировали предложенный алгоритм, добавив в него определение параметра расщепления b, который, как и частота моды Шлихтера, зависит от особенностей внутреннего строения Земли.

Представим исследуемый деформационный сигнал в виде аддитивной смеси полезного сигнала (моды Шлихтера) и сейсмического шума:

(1)
${{y}_{i}} = {\lambda }{{S}_{i}} + {{{\xi }}_{i}},$
где: Si – деформация, вызываемая модой Шлихтера; λ = 1 в случае наличия моды Шлихтера и λ = 0 в случае ее отсутствия; ξ – деформационный сигнал в отсутствие моды Шлихтера (сейсмический шум); i – номер отсчета данных от 1 до N.

В качестве основной гипотезы для проверки предположим, что полезный сигнал, обусловленный триплетом Шлихтера, представляет собой три косинусоиды, частоты которых связаны между собой и однозначно вычисляются через параметры расщепления триплета и фиксированное значение вырожденной частоты. Тогда деформацию, обусловленную модой Шлихтера для изотропных моделей Земли, можно представить как

(2)
${{S}_{i}} = {{S}_{0}}\sum\limits_{m\, = \, - 1,\,0,\,1} {\cos } \left( {2{\pi }{{f}_{{\text{в}}}}\left( {1 + a + bm + c{{m}^{2}}} \right)i{\tau }} \right),$
где: S0 – амплитуда моды; а, b и c – параметры расщепления; fв – вырожденная (нерасщепленная) частота моды; m – угловой номер синглета; τ – время (интервал) дискретизации деформографических данных.

Если все входящие в (2) параметры (fв, a, b, c) известны и постоянны, то описанная задача является задачей обнаружения детерминированного когерентного сигнала на фоне шума.

Решение задачи может быть найдено методом максимального правдоподобия [Сосулин, 1992]. Суть метода состоит в построении так называемой достаточной статистики – функции наблюдаемой реализации случайного процесса, позволяющей найти оптимальное решающее правило для принятия решения о наличии или отсутствии сигнала. В методе максимального правдоподобия в качестве достаточной статистики Z используется отношение плотности вероятности в присутствии полезного сигнала к плотности вероятности в его отсутствии. Оптимальное правило обнаружения сводится к сравнению Z с константой h (порогом обнаружения): при Z > h принимается решение о присутствии полезного сигнала в данных, при Z < h – решение о его отсутствии. В случае, если априорные вероятности наличия или отсутствия полезного сигнала неизвестны, для определения h используют критерий Неймана–Пирсона, в соответствии с которым порог обнаружения может быть определен через вероятность ложной тревоги ${{F}_{{\alpha }}}$.

Если помеха является белым гауссовским шумом, то оптимальный обнаружитель представляет собой согласованный фильтр [Сосулин, 1992]. Структура обнаружителя не меняется, если гауссовский шум не является белым – в этом случае достаточно выполнить так называемое “обеление” сигнала. Обеляющий фильтр осуществляет декорреляцию помехи, обеспечивая на выходе статистическую независимость выборок сигнала, что позволяет получить точное решение для отношения правдоподобия.

Регистрируемый деформографом сейсмический шум имеет негауссовский характер – его плотность распределения характеризуется т. н. “тяжелыми” хвостами, связанными с присутствием импульсных помех. Наилучшие результаты для представления шума обеспечивает нестандартизированное распределение Стьюдента [Korn G.A., Korn T.M., 1974]:

(3)
$p\left( {\left. y \right|{\mu },{\sigma },n} \right) = \frac{{{\Gamma }\left( {\frac{{n + 1}}{2}} \right)}}{{{\Gamma }\left( {\frac{n}{2}} \right){\sigma }\sqrt {{\pi }n} }}{{\left( {1 + \frac{1}{n}{{{\left( {\frac{{y - {\mu }}}{{\sigma }}} \right)}}^{2}}} \right)}^{{ - \frac{{n + 1}}{2}}}},$
где: Г(..) означает Гамма-функцию; ${\mu },{\sigma },n$ – соответственно коэффициенты сдвига (аналог среднего значения), масштаба (аналог дисперсии) и формы (число степеней свободы).

Для негауссовского шума перед согласованным фильтром ставится безынерционный нелинейный преобразователь (БНП), определяемый плотностью вероятности шума ${{p}_{{\xi }}}$. Так как полезный сигнал много меньше амплитуды помехи (ожидаемое отношение сигнал/шум для моды Шлихтера составляет не более 10–2 [Milyukov et al., 2018b]), то в качестве первого приближения можно ограничиться только первым членом ряда – поэтому данный метод является асимптотически оптимальным. В этом случае структура БНП для распределения (3) будет определяться уравнением:

(4)
${{f}_{1}}\left( {{{y}_{i}}} \right) = - \frac{d}{{d{{y}_{i}}}}\ln {{p}_{{\xi }}}\left( {{{y}_{i}}} \right) = - \frac{{p_{{\xi }}^{'}\left( {{{y}_{i}}} \right)}}{{{{p}_{{\xi }}}\left( {{{y}_{i}}} \right)}},$
а окончательная формула для достаточной статистики принимает вид [Виноградов и др., 2019]:

(5)
$Z = \sum\limits_{i = 1}^N {\frac{{\left( {n + 1} \right)\left( {\frac{{{{y}_{i}} - {\mu }}}{\sigma }} \right)}}{{n + {{{\left( {\frac{{{{y}_{i}} - {\mu }}}{\sigma }} \right)}}^{2}}}}} {{S}_{i}} \gtrless h.$

Обнаружитель (3) позволяет определить, присутствует или нет мода Шлихтера с конкретно выбранными параметрами (fв, a, b, c) в наблюдаемых данных. Этого достаточно для проверки какой-то отдельной гипотезы, например, в рамках выбранной модели Земли, для которой мы можем точно рассчитать указанные параметры. Однако в общем случае ни частота моды, ни параметры расщепления неизвестны. Для решения общей задачи при постоянных, но неизвестных параметрах сигнала задачу обнаружения можно совместить с задачей оценивания параметров моды Шлихтера. В этом случае оптимальный приемник необходимо сделать многоканальным: для каждого неизвестного параметра определяется диапазон возможных значений, он разбивается на большое число интервалов с заданной дискретизацией, и для каждого канала строится свой согласованный фильтр. Значение, при котором достигается максимальная величина достаточной статистики, принимается за оценку параметра, а соответствующий максимум Z сравнивается с порогом h.

В общем случае для моды Шлихтера в представлении (2) мы имеем четыре неизвестных параметра, это вырожденная частота fв и параметры расщепления, от которых зависит смещение частот отдельных синглетов триплета относительно вырожденной частоты:

(6)
${\delta }{{f}_{{ - 1,\,0,\,1}}} = \left\{ \begin{gathered} {{f}_{{\text{в}}}}\left( {1 + a - b + c} \right) \hfill \\ {{f}_{{\text{в}}}}\left( {1 + a} \right) \hfill \\ {{f}_{{\text{в}}}}\left( {1 + a + b + c} \right) \hfill \\ \end{gathered} \right.,~$
где: a, b и c определяются моделью Земли, причем параметры a и с зависят от эллиптичности Земли 1-го и 2-го порядков, параметр b – от вращения Земли (силы Кориолиса) 1-го порядка [Dahlen, Tromp, 1998].

Так как параметр a входит во все синглеты с постоянным знаком, фактически его учет сводится к постоянной поправке к вырожденной частоте. Поэтому на характер достаточной статистики его изменение не влияет – ошибка в его определении лишь смещает оценку частоты на соответствующую величину. Влиянием возможного отклонения параметра c можно в первом приближении пренебречь, т.к. его значение для моды Шлихтера в 30 раз меньше параметра a и почти в 200 раз меньше параметра b. Таким образом, наиболее критичным следует ожидать влияние параметра b как в силу величины его значения, так и по причине того, что именно он определяет удаление боковых синглетов триплета друг от друга. Из формулы (2) непосредственно следует, что

(7)
$b = \frac{{{{f}_{1}} - {{f}_{{ - 1}}}}}{{2{{f}_{{\text{в}}}}}}.$

Вопрос разности частот между боковыми синглетами неоднократно обсуждался в литературе (см., например, [Smylie, McMillan, 2000; Rieutord, 2002; Rosat et al., 2006]), в частности, выдвигались различные модификации моделей PREM с учетом изменения вязкости и расчетом соответствующего “разброса” синглетов мод Шлихтера и контраста плотности в ядре. Поэтому определение параметра b наряду с периодом моды также имеет важное значение для подтверждения той или иной модели строения Земли.

В монографии [Dahlen, Tromp, 1998] приводится следующая формула для коэффициента b:

(8)
$b = {\chi }\left( {\frac{{\Omega }}{{2{\pi }{{f}_{{\text{в}}}}}}} \right),$
где: ${\Omega }$ – угловая скорость вращения Земли; ${\chi } = \frac{1}{2}\int_0^R {{\rho }\left( r \right)} $ × $\left( {{{V}^{2}} + 2\sqrt 2 UV + {{W}^{2}}} \right){{r}^{2}}dr$ – кориолисов параметр расщепления, зависящий от собственных функций V, U, W моды Шлихтера и плотности Земли ${\rho }$; R – радиус Земли.

Следует отметить, что величина коэффициента b зависит от периода моды, поэтому корректный подход к определению моды Шлихтера должен позволять одновременно оценивать оба параметра – и период, и параметр расщепления. С точки зрения теории обнаружения параметр b также является неизвестным постоянным и информационным параметром, как и период моды.

Таким образом, при применении алгоритма мы будем осуществлять максимизацию достаточной статистики Z как функции двух переменных Z = Z(fв, b). Параметры a и c мы будем предполагать известными, взяв их значения соответствующими модели Земли 1066A. Такое приближение позволяет без заметных потерь для результата значительно сократить время расчетов.

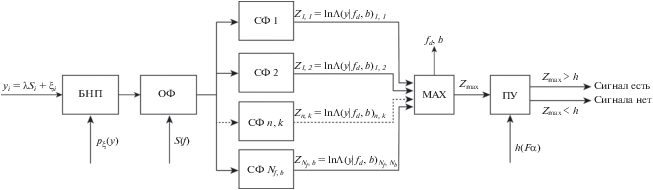
Итоговая структурная схема асимптотически-оптимального обнаружителя для поиска моды Шлихтера на фоне негауссовских помех с независимыми значениями приведена на рис. 1. Его отличие от предложенного в работе [Виноградов и др., 2019] состоит в максимизации достаточной статистики одновременно по двум параметрам – вырожденной частоте и параметру расщепления b. Эта особенность алгоритма позволяет учесть априорную информацию о моде Шлихтера, связанную с расщеплением моды на синглеты.

Рис. 1.

Структурная схема асимптотически-оптимального обнаружителя для поиска моды Шлихтера в негауссовом шуме: ОФ – обеляющий фильтр; СФ – согласованный фильтр; MAX – выбор максимального значения; ПУ – пороговое устройство.

Форма БНП для реальных деформографических данных после чилийского землетрясения показана на рис. 2. Как следует из данного рисунка, оптимальная обработка сигнала в случае негауссовских шумов значительно отличается от обычного согласованного фильтра за счет существенно нелинейной формы входного преобразователя. При формировании достаточной статистики преобразователь практически не изменяет малые значения, в которых отношение сигнал–шум максимально, и эффективно подавляет большие амплитуды, связанные с импульсной помехой.

Рис. 2.

Вид БНП для сейсмического шума Баксанского деформографа после Чилийского землетрясения (сплошная кривая). Пунктиром показана линейная функция в случае, если бы шум имел гауссовское распределение.

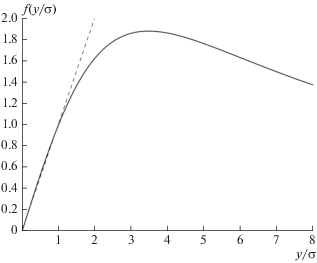
Указанное свойство преобразователя позволяет не только подавлять импульсные шумы, но и эффективно бороться с когерентными помехами – такими, как нелинейные приливы, несколько мод которых (например, M6, S4, MK4, S4, M4) находятся в возможном диапазоне значений моды Шлихтера.

ПРИМЕНЕНИЕ АЛГОРИТМА К ДЕФОРМОГРАФИЧЕСКИМ ДАННЫМ ПОСЛЕ ЧИЛИЙСКОГО ЗЕМЛЕТРЯСЕНИЯ

Предварительная обработка деформографических данных включала в себя полосовую фильтрацию исходного сигнала в диапазоне от 3.5 до 7.8 ч. Выбор данного диапазона соответствует основным теоретическим предположениям о периоде моды Шлихтера [Busse, 1974; Crossley et al., 1992], а также позволяет исключить влияние высокоамплитудной 8-часовой приливной гармоники.

После фильтрации осуществлялось усреднение исходных данных до периода дискретизации 30 минут посредством процедуры децимации.

Важное значение для применения алгоритма имеет оптимальный выбор длительности наблюдения. Для периодических сигналов его можно оценить через произведение добротности и периода: при малых значениях накопление периодического сигнала может быть недостаточно эффективным, а при больших – слишком малое отношение сигнал/шум. Т.к. ожидаемая добротность моды Шлихтера достаточно высока (от 3 до 5 тыс. единиц), то оптимальное время наблюдения может составлять до двух лет. Однако на таких длинных интервалах мы сталкиваемся с проявлением нестационарности сейсмического шума, в том числе, в связи с регистрацией других сильных землетрясений. Кроме того, при формулировке гипотезы обнаружения мы предположили постоянство амплитуды полезного сигнала, то есть, не учитывали его затухание. Поэтому было принято решение ограничиться длительностью в 10 тыс. получасовых интервалов, что составляет примерно 208 сут. Первые 300 интервалов не использовались с целью исключения влияния широкополосного шума сразу после землетрясения. Таким образом, длительность используемого ряда данных после землетрясения составила 202.3 сут (9700 отсчетов).

Подбор методом наименьших квадратов нестандартизированного распределения Стьюдента для полученного описанным выше способом 202-суточного интервала данных позволил определить следующие значения параметров распределения:

(9)
$\begin{gathered} \sigma = {\text{ }}8.8 \times {{10}^{{ - 10}}},\,\,\,\,\mu = 1.1 \times {{10}^{{ - 11}}}, \\ n = {\text{ }}12. \\ \end{gathered} $

На рис. 3 представлено сравнение эмпирической кумулятивной плотности вероятности сейсмического шума с наиболее близким гауссовским распределением и с нестандартизированным распределением Стьюдента при параметрах (9). Видно, что нестандартизированное распределение Стьюдента с указанными параметрами гораздо лучше описывает реальный шум, чем гауссовское, особенно в диапазоне больших амплитуд (свыше 2 × 10–9, см. график на врезке) – то есть на ее “хвостах”.

Рис. 3.

Кумулятивные плотности вероятности сейсмического шума: эмпирическая и ее аппроксимации: гауссовским распределением и обобщенным распределением Стьюдента. На врезке серым фоном показан 95% доверительный интервал для эмпирической функции распределения.

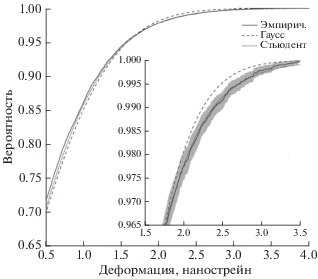
Дискретизация по частоте при поиске моды Шлихтера была выбрана опытным путем на уровне 10–9 Гц, что для диапазона периодов от 3 до 7.8 ч дает 55 тыс. возможных значений частоты. Для возможных значений параметра b был выбран диапазон ±10% относительно значения, предсказываемого моделью 1066A, с интервалом дискретизации 5 × 10–5. Таким образом, общее количество каналов при согласованной фильтрации (см. рис. 1) с учетом двух неизвестных параметров составило более 21 миллиона.

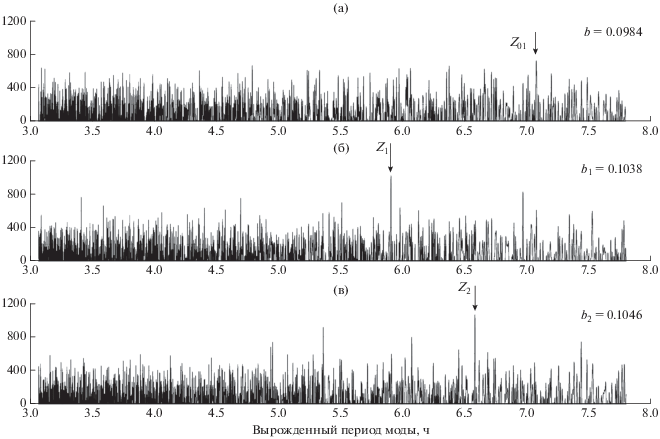
На рис. 4 приведены результаты поиска максимума достаточной статистики Z. Наибольшие по амплитуде значения Z1 = 1022 и Z2 = 1061 (абсолютный максимум) достигаются, соответственно, при b1 = 0.1038 и b2 = 0.1046.

Рис. 4.

Абсолютный максимум достаточной статистики Zmax как функция двух переменных: вырожденного периода T и параметра расщепления b.

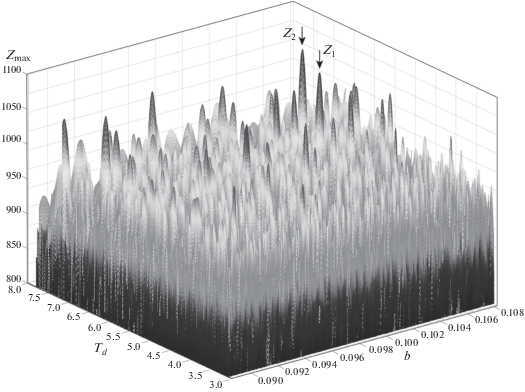
На рис. 5 приводится вид достаточной статистики для параметров расщепления в соответствии с моделью Земли 1066A (рис. 5а) и для значений b, полученных в данной работе (рис. 5б, 5в). Как уже упоминалось выше, значения параметров a и c использовались согласно модели 1066A. В первом случае (модель 1066A) наиболее вероятное значение вырожденного периода для моды Шлихтера соответствует абсолютному максимуму достаточной статистики, достигающемуся при периоде 7.075 ч (Z01 = 723). Если мы предполагаем, что параметр расщепления b не известен точно, а находится в диапазоне [0.0885…0.1082], то наиболее вероятными оценками периода моды Шлихтера с точки зрения метода максимального правдоподобия являются значения периодов T1 = = 5.905 ч (амплитуда Z1 = 1022 при b1 = 0.1038), T2 = 6.581 ч (амплитуда Z2 = 1061 при b2 = 0.1046).

Рис. 5.

Достаточная статистика Z для чилийского землетрясения для различных значений параметра расщепления b: график (а) рассчитан для модели 1066A; графики (б) и (в) соответствуют параметрам b для двух самых больших значений амплитуд Zmax в рассматриваемом диапазоне параметров b и T.

СТАТИСТИЧЕСКАЯ ДОСТОВЕРНОСТЬ ОБНАРУЖЕНИЯ

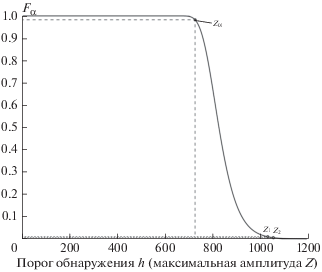
Для определения статистической достоверности наблюдаемых на рис. 5 максимумов можно воспользоваться связью величины порогового значения h и вероятности ложной тревоги ${{F}_{\alpha }}$. Для критерия Неймана–Пирсона она определяется формулой [Сосулин, 1992]:

${{F}_{\alpha }} = \int\limits_h^\infty p \left( {\left. {\ln {\Lambda }} \right|0} \right)d{\Lambda },$
где: $p\left( {\ln \left. {\Lambda } \right|0} \right)$ – плотность вероятности шума в отсутствии полезного сигнала на выходе приемника.

Для расчета необходимо знать функцию распределения максимума достаточной статистики. Прямой способ ее определения по реальным данным предполагает проведение большого числа отдельных испытаний, на каждом из которых определяется максимум на интервале. Для этого требуются огромные объемы экспериментальных данных, которые просто отсутствуют. Альтернативным вариантом является формирование статистики по искусственным данным, по параметрической модели сейсмического шума [Виноградов и др., 2019]. В этом случае мы не ограничены длительностью, т.к. по имеющимся параметрам шума мы можем сформировать модельный сигнал неограниченного размера. Недостатком данного метода будет зависимость результатов от выбранных параметров модели шума.

Однако есть существенно более простой вариант расчета статистики максимума. Так как достаточная статистика формируется суммированием большого числа случайных величин (их число в формуле (5) составляет N = 9700), то в соответствии с центральной предельной теоремой распределение достаточной статистики будет гауссовым.

Этот факт позволяет нам аналитически вычислить плотность распределения абсолютного максимума Z на заданном интервале. Решение этой задачи рассматривается в теории выбросов случайных процессов и приведено в работе [Тихонов, 1970]. Если мы имеем гауссовский случайный процесс с N независимыми значениями Zi и плотностью вероятности ${{w}_{{{{Z}_{i}}}}} = \frac{1}{{\sigma \sqrt {2\pi } }}{{e}^{{ - \frac{{Z_{i}^{2}}}{{2{{\sigma }^{2}}}}}}}$, нулевым средним и дисперсией ${{\sigma }^{2}}$, то плотность распределения абсолютного максимума Zmax такого процесса будет определяться формулой:

(10)
${{W}_{{{{Z}_{{{\text{max}}}}}}}} = \left( {N + 1} \right){{w}_{{{{Z}_{i}}}}}\left( {{{Z}_{{{\text{max}}}}}} \right){{{\Phi }}^{N}}\left( {\frac{{{{Z}_{{{\text{max}}}}}}}{\sigma }} \right),$
где ${\Phi }\left( x \right) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^x {{{e}^{{ - \frac{1}{2}{{x}^{2}}}}}} dx$ – интеграл вероятности.

Подставляя значения дисперсии и числа отсчетов в интервале (σ = 216 и N = 9700 соответственно), получаем представленную на рис. 6 кривую обнаружения – зависимость вероятности ложной тревоги от порога достаточной статистики. Кривая обнаружения позволяет определить вероятности ложной тревоги для найденных ранее оценок периода моды Шлихтера (табл. 1).

Рис. 6.

Зависимость порога обнаружения и вероятности ложной тревоги.

Таблица 1.  

Оценки параметров моды Шлихтера и вероятности ложной тревоги их определения

Обозначение максимума Амплитуда максимума достаточной статистики Период, ч Параметр расщепления b Вероятность ложной тревоги
Z01 723 7.075 0.0984 0.984
Z1 1022 5.905 0.1038 0.012
Z2 1061 6.581 0.1046 0.005

Наиболее вероятными кандидатами на моду Шлихтера являются значения периодов 5.905 и 6.581 ч, причем вторая оценка имеет меньшую вероятность ложной тревоги. Также в табл. 1 для сравнения приведена амплитуда максимума Z01, полученного для параметра расщепления b = = 0.984 в соответствии с моделью 1066A (рис. 5а). Вероятность ложной тревоги для этой оценки существенно хуже (близка к единице), поэтому соответствующая ей гипотеза должна быть отклонена.

Для сравнения предложенного алгоритма с обычным гауссовским приемником была вычислена достаточная статистика при использовании согласованного фильтра без нелинейного преобразователя, т.е. без учета негауссовости сейсмического шума. Общий вид статистики в негауссовом приближении очень близок к гауссовскому случаю, однако амплитуда абсолютного максимума имеет меньшее значение (Zмах_гаусс = 1002), что соответствует вероятности ложной тревоги 0.018%. Таким образом, учет негауссовости шума позволил заметно улучшить показатели обнаружения, снизив вероятность ложной тревоги в 3.5 раза.

Следует подчеркнуть, что представленные на рис. 5 графики, хотя и имеют по оси абсцисс значения периода, представляют собой не спектр, а достаточную статистику. Она содержит вероятностную информацию о наличии сигнала в исходной выборке: чем выше амплитуда пика, тем больше вероятность присутствия сигнала с соответствующими этому максимуму значениями неизвестных параметров. Значимость пиков определяется кривой обнаружения (рис. 6), которая существенно нелинейна, причем вероятность ложной тревоги изменяется от нуля до единицы в достаточно узком диапазоне амплитуд Zmax (от 700 до 1000). Поэтому даже небольшая разница в амплитуде пиков Zmax может приводить к разным выводам о наличии или отсутствии полезного сигнала в наблюдаемых данных.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Метод максимального правдоподобия с учетом особенностей сейсмического шума в рамках выбранной гипотезы позволил определить оценку двух наиболее вероятных значений вырожденной частоты, которые могут быть вызваны возбуждением моды Шлихтера после чилийского землетрясения. Соответствующие им значения периодов триплета приведены в табл. 2. Также в эту таблицу включены теоретические значения, полученные по различным моделям, и экспериментальные оценки моды по гравиметрическим наблюдениям.

Таблица 2.  

Оценки моды Шлихтера различными авторами

№ п/п Автор/Источник Модель/эксперимент T–1 T0 T+1 Тв
1 [Smith, 1976] DG579 4.0550 4.4410 4.9160 4.5060
2 [Dahlen, Sailor, 1979] 1066A 4.1284 4.5338 5.0140 Н.д.*
3 [Dziewonski, Anderson, 1981] PREM 4.6776 5.1814 5.7991 5.2384
4 [Gilbert, Dziewonski, 1985] 1066A 4.0491 4.4199 4.8603 4.4547
5 [Bullen, Bolt, 1985] Cal8 3.5168 3.7926 4.1118 3.8247
6 [Widmer et al., 1988] Core11 5.1280 5.7412 6.5114 5.8197
7 [Crossley et al., 1992] 1066A 3.9500 4.4380 4.8960 Н.д.
8 [Crossley, 1992] PREM модиф. 4.7770 5.3100 5.9790 Н.д.
9 [Peng, 1997] PREM модиф. 4.7640 5.3090 5.9780 Н.д.
10 [Courtier et al., 2000] Эксперим. 3.5822 3.7656 4.0150 3.7985
11 [Rieutord, 2002] 1066A модиф. 3.8940 4.2550 4.6870 Н.д.
12 [Rogister, 2003] PREM модиф. 4.7700 5.3090 5.9910 5.4200
13 [Rogister, 2003] 1066A модиф. 4.1290 4.5290 5.0240 4.5990
14 [Rosat et al., 2006]** PREM модиф. Δρ = 300 г/см3 6.2439 7.1984 8.4952 Н.д.
15 [Rosat et al., 2006] PREM модиф. Δρ = 300 г/см3 6.1482 6.9855 8.2590 Н.д..
16 [Rosat et al., 2006] PREM модиф. Δρ = 600 г/см3 4.7606 5.2971 5.9766 Н.д.
17 [Rosat et al., 2006] PREM модиф. Δρ = 600 г/см3 4.6911 5.1837 5.8511 Н.д.
18 [Rosat et al., 2006] PREM модиф. Δρ = 800 г/см3 4.2290 4.6494 5.1705 Н.д.
19 [Rosat et al., 2006] PREM модиф. Δρ = 800 г/см3 4.1685 4.5607 5.0719 Н.д.
20 [Rosat et al., 2006] PREM модиф. Δρ = 900 г/см3 4.0264 4.4069 4.8750 Н.д.
21 [Rosat et al., 2006] PREM модиф. Δρ = 900 г/см3 3.9695 4.3268 4.7858 Н.д.
22 [Guo et al., 2006] Эксперим. 5.2527 6.0200 7.0573 6.1761
23 [Guo et al., 2006] Эксперим. 3.0095 3.3042 3.6388 3.3274
24 [Smylie, Palmer, 2007] Cal8 (с учетом вязкости) 3.5840 3.7731 4.0168 3.8247
25 [Pagiatakis, 2007] Эксперим. 4.2690 4.5160 4.8890 Н.д.
26 [Xu et al., 2010] Эксперим. 4.3442 4.7746 5.3104 4.8473
27 [Xu et al., 2010] Эксперим. 4.0928 4.5045 5.0110 4.5733
28 [Xu et al., 2010] Эксперим. 3.7318 4.0928 4.5159 4.1552
29 [Shen, Ding, 2013] Эксперим. 4.7280 5.2080 5.8940 Н.д.
30 [Jiang et al., 2013] Эксперим. 4.8170 5.2944 5.8624 5.3769
31 [Jiang et al., 2013] Эксперим. 4.3539 4.8170 5.2944 4.8859
32 [Jiang et al., 2013] Эксперим. 4.1377 4.5376 5.0080 4.6049
33 [Jiang et al., 2013] Эксперим. 3.9654 4.3539 4.8170 4.4250
34 [Jiang et al., 2013] Эксперим. 3.7982 4.1377 4.5813 4.5880
35 [Jiang et al., 2013] Эксперим. 3.7219 4.0900 4.5376 4.1440
36 [Ding, Chao, 2015] Эксперим. 4.8900 5.4152 6.0729 5.5325
37 [Ding, Chao, 2015] Эксперим. 3.9735 4.2918 4.6729 4.3470
38 [Ding, Chao, 2015] Эксперим. 3.9735 4.2918 4.7695 4.3470
39 [Ding, Chao, 2015] Эксперим. 3.9735 4.2918 4.7809 4.3470
40 [Ding, Chao, 2015] Эксперим. 3.5566 3.8660 4.2076 3.9037
41 [Shen, Luan, 2015] Эксперим. 4.7536 5.2161 5.8307 Н.д.
42 Данная работа Эксперим. 5.2791 5.8160 6.4822 5.9050
43 Данная работа Эксперим. 5.8793 6.4818 7.2307 6.5810

Примечание: Периоды отдельных синглетов триплета T–1, 0, 1 и вырожденного периода Tв в часах (* – значения вырожденного периода не приводятся; ** – разные модели, в т.ч. разные значения скачка плотности и разные методы расчета). * Нет данных.

Из сравнения с теоретическими моделями обращает внимание относительная близость одного из кандидатов (T1 = 5.905 ч) к периоду модели CORE11 T = 5.820 ч [Widmer et al., 1988]. Отличие составляет менее полутора процентов. При этом для модели CORE11 значение коэффициента расщепления b отличается в большую сторону от модели 1066A, так же, как и для найденных оценок в нашей работе.

Следует отметить, что степень расщепления во многих экспериментальных оценках и в теоретических моделях отличается друг от друг в значительных пределах. Этот вопрос требует детального анализа и, возможно, отдельного исследования. В литературе по обнаружению моды Шлихтера расчету и/или оценке коэффициентов расщепления практически не уделяется внимания – как правило, приводятся значения для модели 1066A, впервые полученной в работе [Dahlen, Sailor, 1979]. Однако приведенные в работе [Rosat et al., 2006] значения частот боковых синглетов триплета предполагают значительные отличия коэффициента b от модели 1066A, особенно при меньших значениях скачка плотности (0.3 г/см3).

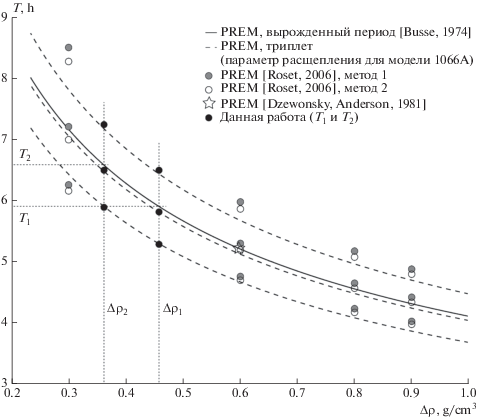
Знание периода моды позволяет получить оценку скачка плотности на границе между внутренним и внешним ядром Земли. Для расчета использовалась модель [Busse, 1974], коэффициенты расщепления в соответствии с моделью 1066A [Dahlen, Tromp, 1998] и найденные в данной работе (табл. 1). На рис. 7 показана общая зависимость периода моды Шлихтера от скачка плотности, теоретические значения классической модели PREM [Dziewonski, Anderson, 1981] и модифицированных моделей [Rosat, 2006], а также полученные результаты в данной работе. Период T1 = 5.905 ч соответствует скачку плотности Δρ1 = 0.456 г/см3, T2 = 6.581 ч соответствует Δρ2 = 0.360 г/см3.

Рис. 7.

Зависимость периода моды Шлихтера от скачка плотности между внутренним и внешним ядром Земли по различным источникам и результатам данной работы.

ЗАКЛЮЧЕНИЕ

Традиционно поиск моды Шлихтера осуществляется на основе данных, получаемых на сверхпроводящих гравиметрах международной сети GGP. В настоящее время сеть включена в сервис IGETS (International Geodynamics and Earth Tide Service).

Амплитуда предполагаемых гравитационных сигналов, вызываемых модой Шлихтера на поверхности Земли, составляет порядка 1 нГал [Rosat et al., 2014]. Это меньше уровня шумов лучших сверхпроводящих гравиметров, что не позволяет непосредственно выделить моду Шлихтера при спектральном оценивании. Для борьбы с шумами исследователи использовали процедуру “стекинга” – оптимальной совместной обработки нескольких приборов.

В данном исследовании впервые предпринята попытка обнаружения и оценки моды Шлихтера по записи Чилийского землетрясения 23.02.2010 г. Баксанским лазерным интерферометром-деформографом. Теоретическая величина деформации по модели PREM, вызываемой модой Шлихтера от данного землетрясения в месте регистрации должна составлять около 10–13 стрейн. Стандартное отклонение регистрируемого деформографом сейсмического шума на частоте, соответствующей периоду моды Шлихтера (5.5 ч), составляет 5 × 10–11 стрейн [Milyukov, 2018], то есть для обнаружения моды должны быть разработаны алгоритмы, имеющие чувствительность по отношению “сигнал/шум” не ниже 10–2.

Для решения этой задачи нами разработан асимптотически-оптимальный алгоритм обработки деформационных данных для обнаружения и оценки моды Шлихтера при отношениях сигнал/шум в диапазоне 10–2–10–4, основанный на методе максимального правдоподобия.

Включение в процедуру обработки нелинейного преобразователя, учитывающего негауссовское распределение сейсмического шума, позволяет повысить эффективность обнаружения моды Шлихтера после крупнейших землетрясений и снизить вероятность принятия ошибочного решения о наличии сигнала (уменьшить вероятность ложной тревоги).

Преимущество предложенного алгоритма заключается в том, что он основан на фундаментальных принципах теории оптимального приема сигналов на фоне шумов, что обеспечивает наиболее эффективное обнаружение сигнала в соответствии с выбранным критерием оптимальности. Алгоритм позволяет четко сформулировать проверяемую гипотезу (с учетом предполагаемых характеристик полезного сигнала и имеющихся особенностей приемника) и оценить количественно вероятность присутствия полезного сигнала (моды Шлихтера) в наблюдаемых данных. При формулировке гипотез можно не только рассматривать различные периоды моды, но и включать в них другие параметры, зависящие от выбранной модели строения Земли. Получаемые в результате применения алгоритма вероятности оценок позволяют выбрать наиболее вероятную гипотезу, а следовательно, получить оценки заложенных при ее формулировке параметров – добротности, вязкости и др.

Это существенно отличает разработанный алгоритм от широко применяемых при анализе гравиметрических данных эмпирических процедур на основе “стекинга”, которые по своей сути представляют собой параметрические модели спектрального оценивания большого объема данных с нескольких станций. При этом выбор того или иного “набора” периодов триплета осуществляется, как правило, по степени близости характеристик расщепления к какой-либо теории, то есть по субъективному критерию.

Одновременно с оценкой периода моды предложенный алгоритм позволяет оценивать также параметры расщепления, в частности, параметр b, зависящий от вязкости внешнего ядра. Поскольку величина коэффициента b зависит от периода моды, в корректном подходе к определению моды Шлихтера должны одновременно оцениваться оба неизвестных – и период, и параметр расщепления.

Разработанный алгоритм был применен для поиска моды Шлихтера по деформационным наблюдениям Чилийского землетрясения 2010 г. Поиск абсолютных максимумов достаточной статистики выделил в качестве наиболее вероятных значений два набора параметров моды Шлихтера: T1 = 5.905 ч при b1 = 0.1038; и T2= 6.581 ч при b2 = = 0.1046. Найденные параметры моды Шлихтера имеют вероятность ложной тревоги, равную 0.012 и 0.005 соответственно. В то же время вероятность ложной тревоги для оценок моды Шлихтера с фиксированным значением b = 0.984 (в соответствии с моделью 1066A) практически равна единице, поэтому соответствующая им гипотеза должна быть отклонена. Отметим также, что учет негауссовости шума позволил заметно улучшить показатели обнаружения, снизив вероятность ложной тревоги в 3.5 раза.

Сравнение наших результатов с теоретическими моделями и результатами экспериментальных определений периода моды Шлихтера, полученные ранее, показывает близкое соответствие периода T1 = 5.905 ч периоду модели CORE11 [Widmer et al., 1988], отличие составляет менее 1.5%. В случае моделей PREM [Rosat et al., 2006] найденным оценкам периодов соответствуют скачки плотности между внутренним и внешним ядром: Δρ1 = 0.456 г/см3 при T1 = 5.905 ч и Δρ2 = 0.360 г/см3 при T2 = 6.581 ч.

Список литературы

  1. Акимов П.С., Бакут П.А., Богданович В.А. и др. Теория обнаружения сигналов. М.: Радио и связь. 1984.

  2. Виноградов М.П., Милюков В.К., Миронов А.П., Мясников А.В. Асимптотически оптимальный алгоритм для поиска и оценки моды Шлихтера по долговременным деформационным данным // Вестник Московского университета. Серия 3: Физика, астрономия. 2019. № 2. С. 89–94.

  3. Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. М.: Наука. 1974.

  4. Милюков В.К. Наблюдение тонкой структуры основной сфероидальной моды Земли 0S2 // Физика Земли. 2005. № 4. С. 16–22.

  5. Милюков В.К., Мясников А.В. Метрологические характеристики Баксанского лазерного интерферометра // Измерительная техника. 2005. № 12. С. 26–30.

  6. Милюков В.К., Виноградов М.П., Лагуткина А.В., Миронов А.П., Мясников А.В., Перелыгин Н.А., Пустовитенко Б.Г., Боборыкина О.В., Вольфман Ю.М., Насонкин В.А. Наблюдения собственных колебаний Земли лазерными интерферометрами-деформографами // Измерительная техника. 2015a. № 12. С. 25–29.

  7. Милюков В.К., Виноградов М.П., Миронов А.П., Мясников А.В., Перелыгин Н.А. Собственные колебания Земли, возбужденные тремя крупнейшими землетрясениями последнего десятилетия, по деформационным наблюдениям // Физика Земли. 2015b. № 2. С. 21–36. https://doi.org/10.7868/S0002333715010093

  8. Милюков В.К., Виноградов М.П., Миронов А.П., Мясников А.В. Собственные колебания Земли, возбужденные глубокофокусным землетрясением 2013 г. в Охотском море // Геофизические процессы и биосфера. 2018. Т. 17. № 4. С. 127–140. https://doi.org/10.21455/GPB2018.4-7

  9. Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации. М.: Радиоисвязь. 1992.

  10. Тихонов В.И. Выбросы случайных процессов. М.: Наука. 1970.

  11. Abd El-Gelil M., Pagiatakis S. Least squares self-coherence for sub-nGal signal detection in the superconducting gravimeter records // Journal of Geodynamics. 2009. V. 48(3). P. 310–315.

  12. Buffett B., Goertz D.E. Magnetic damping of the translational oscillations of the inner core // Geophys. J. Int. 1995. V. 120. P. 103–110.

  13. Buffett B.A. Tidal dissipation and the strength of the Earth’s internal magnetic field // Nature. 2010. V. 468. P. 952–954. https://doi.org/10.1038/nature09643

  14. Bullen K.E., Bolt B.A. An Introduction to the Theory of Seismology, 4th ed. Cambridge, Univ. Press. Cambridge, UK. 1985. 499 p.

  15. Busse F.H. On the Free Oscillations of the Earth’s Inner Core // J. Geophysical Research. 1974. V. 79(5). P. 753–757.

  16. Courtier N., Ducarme B., Goodkind J., Hinderer J., Imanishi Y., Seama N., Sun H., Merriam J., Bengert B., Smylie D.E. Global superconducting gravimeter observations and the search for the translational modes of the inner core // Phys. Earth Planet. Inter. 2000. V. 117. P. 3–20.

  17. Crossley D.J. Eigen solutions and seismic excitation of the Slichter mode triplet for a fully rotating Earth model // EOS. 1992a. V. 73 43). P. 60.

  18. Crossley D.J., Hinderer J., Legros H. On the excitation, detection and damping of core modes // Phys. Earth Planet. Int. 1992b. V. 68. P. 97–116.

  19. Crossley D., Rochester M., Peng Z. Slichter modes and Love numbers // Geophys. Res. Lett. 1992c. V. 19. P. 1679–1682.

  20. Dahlen F., Tromp J. Theoretical Global Seismology. U.S., Princeton, New Jersey: Princeton University Press. 1998. 944 p.

  21. Dahlen F.A., Sailor R.V. Rotational and elliptical splitting of the free oscillations of the Earth // Geophys. J. R. Astron. Soc. 1979. V. 58. P. 609–623.

  22. Ding H., Chao B.F. The Slichter mode of the Earth: Revisit with optimal stacking and autoregressive methods on full superconducting gravimeter dataset // J. Geophysical Research: Solid Earth. 2015. V. 48. P. 7261–7272. https://doi.org/10.1002/2015JB012203

  23. Ding H., Shen W.-B. Search for the Slichter modes based on a new method: Optimal sequence estimation // J. Geophys. Res. Solid Earth. 2013. V. 118. P. 5018–5029. https://doi.org/10.1002/jgrb.50344

  24. Duputel Z., Rivera L., Kanamori H., Hayes G. W phase source inversion for moderate to large earthquakes (1990–2010) // Geophys. J. Int. 2012. V. 189(2). P. 1125–1147.

  25. Dziewonski A.M., Anderson D.L. Preliminary reference Earth model // Phys. Earth Planet. Int. 1981. V. 25. P. 297–356.

  26. Gilbert F., Dziewonski A. An application of normal mode theory to the retrieval of structural parameters and source mechanisms from seismic spectra // Phil. Trans. R. Soc. Lond. 1975. V. A278. P. 187–269.

  27. Guo J.Y., Dierks O., Neumeyer J., Shum C.K. A search for the Slichter modes in superconducting gravimeter records using a new method // Geophys. J. Int. 2007. V. 168. P. 507–517.

  28. Hinderer J., Crossley D., Jensen O. A search for the Slichter triplet in superconducting gravimeter data // Phys. Earth Planet. Int. 1995. V. 90. P. 183–195.

  29. Jiang Y., Xu J., Sun H. Detection of Inner Core Translational Oscillations Using Superconducting Gravimeters // Journal of Earth Science. 2013. V. 24(5). P. 750–758. https://doi.org/10.1007/s12583-013-0370-x

  30. Jensen O.G., Hinderer J., Crossley D.J. Noise limitations in the core-mode band of superconducting gravimeter data // Phys. Earth Planet. Int.1995. V. 90. P. 169–181.

  31. Mathews P.M., Guo J.Y. Viscoelectromagnetic coupling in precession-nutation theory // J. Geophys. Res. 2005. V. 110. B02402. https://doi.org/10.1029/2003JB002915

  32. Milyukov V.K., Vinogradov M.P., Mironov A.P., Myasnikov A.V. Detection and estimation of the Slichter mode based on the data of the Baksan long-base laser strainmeter (the Northern Caucasus, Russia) // Geophysical Research Abstracts of General Assemblies of the European Geosciences Union (EGU). 2018. V. 20. P. EGU2018–3964.

  33. Peng Z. Effects of a mushy transition zone at the inner core boundary on Slichter modes // Geophys. J. Int. 1997. V. 131. P. 607–617.

  34. Rieutord M. Slichter modes of the Earth revisited // Phys. Earth Planet. Inter. 2002. V. 131. P. 269–278. https://doi.org/10.1016/S0031-9201(02)00039-0

  35. Rogister Y. Splitting of seismic-free oscillations and of the Slichter triplet using the normal mode theory of a rotating, ellipsoidal Earth // Phys. Earth Planet. Inter. 2003. V. 140. P. 169–182.

  36. Rosat S. Optimal Seismic Source Mechanisms to Excite the Slichter Mode // Int. Assoc. of Geod. Symposia, Dynamic Planet, Cairns (Australia). 2007. V. 130. P. 571–577.

  37. Rosat S., Boy J.-P., Rogister Y. Surface atmospheric pressure excitation of the translational mode of the inner core // Phys. Earth Planet. Inter. 2014. V. 227. P. 55–60. https://doi.org/10.1016/j.pepi.2013.12.005

  38. Rosat S., Hinderer J., Crossley D.J., Rivera L. The search for the Slichter mode: comparison of noise levels of superconducting gravimeters and investigation of a stacking method // Phys. Earth Planet. Int. 2003. V. 140(13). P. 183–202.

  39. Rosat S., Rogister Y. Excitation of the Slichter mode by collision with a meteoroid or pressure variations at the surface and core boundaries // Phys. Earth Planet. Inter. 2012. V. 190–191. P. 25–31.

  40. Rosat S., Rogister Y., Crossley D., Hinderer J. A search for the Slichter Triplet with Superconducting Gravimeters: Impact of the Density Jump at the Inner Core Boundary // J. Geodyn. 2006. V. 41. P. 296–306.

  41. Shen W.B., Ding H. Detection of the inner core translational triplet using superconducting gravimetric observations // J. Earth Sci. 2013. V. 24. P. 725–735.

  42. Shen W.B., Luan W. Feasibility Analysis of Searching for the Slichter Triplet in Superconducting Gravimeter Records // Geodesy and Geodynamics.2015. V. 6(5). P. 307–315. https://doi.org/10.13039/501100001809

  43. Slichter L.B. The fundamental free mode of the Earth’s inner core // Proc. Natl. Acad. Sci. U. S. A. 1961. V. 47. P. 186–190.

  44. Smith M.L. Translational inner core oscillations of for a rotating, slightly elliptical Earth // J. Geophysical Research. 1976. V. 81(17). P. 3055–3064.

  45. Smylie D.E. The inner core translational triplet and the density near Earth’s centre // Science. 1992. V. 255. P. 1678–1682.

  46. Smylie D.E., McMillan D.G. The inner core as a dynamic viscometer // Phys. Earth Planet. Inter. 2000. V. 117. P. 71–79. https://doi.org/10.1016/S0031-9201(99)00088-6

  47. Smylie D.E., Palmer A. Viscosity of Earth’s Outer Core // Published electronically in arXiv.org> physics >physics.geo-ph, Cornell University Library, Ithaca, N. Y. February 2, 2008

  48. Widmer R., Masters G., Gilbert F. The spherical Earth revisited // 17th International Conference on Mathematical Geophysics. June 1988. Blanes, Spain, IUGG

  49. Xu J.Q., Sun H.P., Zhou J.C. Experimental detection of the inner core translational triplet // Chin. Sci. Bull. 2010. V. 55(3). P. 276–283.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал