Физика Земли, 2021, № 1, стр. 61-68
Роль давления анизотропных протонов в генерации геомагнитных пульсаций герцового диапазона
Ф. З. Фейгин 1, *, Ю. Г. Хабазин 1
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
* E-mail: feygin@ifz.ru
Поступила в редакцию 07.11.2019
После доработки 16.06.2020
Принята к публикации 04.07.2020
Аннотация
Проведено исследование влияния горячей анизотропной плазмы на развитие циклотронной неустойчивости в околоземной космической плазме при конечных значениях плазменного давления ${{\beta }_{ \bot }}$. Показано, что учет конечных значений ${{\beta }_{ \bot }}$ приводит к модификации не только мнимой части дисперсионного уравнения, связанной с усилением волн, но и к модификации реальной части этого уравнения, связанной с распространением волн вдоль силовых линий. Это приводит как к изменению инкремента циклотронной неустойчивости, так и к вариации параметров распространения электромагнитных ионно-циклотронных (ЭМИЦ) волн вдоль силовой линии. Полученные результаты позволяют сделать вывод, что при генерации ЭМИЦ волн в околоземной плазме предпочтительны малые значения перпендикулярного плазменного давления протонов (${{\beta }_{ \bot }}$), большие значения анизотропии (A) и большие значения параметра ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}}$.
ВВЕДЕНИЕ
Циклотронная неустойчивость протонов радиационного пояса Земли, приводящая к генерации геомагнитных пульсаций герцового диапазона, исследовалась многими авторами (см., например, [Тверской, 1968; Фейгин, Якименко, 1969; Feygin, Yakimenko, 1971; Gendrin et al., 1971; Гульельми, 1979; Bespalov, Trakhtengerts, 1986; Guglielmi, Pokhotelov, 1996; Kangas et al., 1998; Guglielmi et al., 2000; Demekhov, 2007]). Наиболее известными из этого класса пульсаций являются Рс1 (“жемчужины”). Эти пульсации представляют собой волновые пакеты электромагнитных ионно-циклотронных (ЭМИЦ) волн, распространяющиеся вдоль силовых линий между сопряженными точками. По мере раскачки волн в источнике (экваториальная область силовых линий) они начинают все сильнее рассеивать протоны в конус потерь, обеспечивая устойчивость радиационного пояса [Тверской, 1968]. Это предположение подтверждено в работе [Yahnin et al., 2007], где проведен анализ одновременных наблюдений геомагнитных пульсаций Рс1 на Земле и протонных полярных сияний на спутнике IMAGE и показано, что протонные полярные сияния могут быть следствием высыпания энергичных протонов в результате циклотронной неустойчивости. Протонный радиационный пояс в спокойном состоянии характеризуется тем, что давление энергичных анизотропных протонов (~100 Кэв) много меньше магнитного давления магнитного поля (т.е. ${{\beta }_{ \bot }} = 8\pi {{n}_{h}}{{T}_{ \bot }}/{\kern 1pt} B_{0}^{2} \ll 1$) и концентрация горячей плазмы мала по сравнению с плотностью холодной плазмы $\left( {{{n}_{h}} \ll {{n}_{0}}} \right)$. Эти условия и были положены в основу теоретического исследования механизма генерации Рс1 в результате циклотронной неустойчивости протонов радиационного пояса Земли. Однако в работе [Berko et al., 1975] утверждается, что в области 4–6 радиусов Земли, где генерируются и откуда распространяются “жемчужины”, давление плазмы может быть равным давлению геомагнитного поля. Мы проверили это утверждение, построив зависимость ${{\beta }_{ \bot }}$ от $L$ для протонов с энергией ~100 Кэв во время магнитной бури 17–20 июня 1972 года по данным [Berko et al., 1975] (рис. 1). Для этой цели были использованы данные спутника Explorer 45 (S3-A) [Longanecker, Hoffman, 1973; Smith, Hofinan, 1973; Konradi et al., 1973]. Как видно из рис. 1, действительно, в магнитосфере Земли возможны периоды, когда давление горячей протонной плазмы близко к давлению магнитного поля. По-видимому, такая геофизическая ситуация наиболее характерна в периоды сильной магнитной активности. Таким образом, необходимо распространить существующую теорию генерации геомагнитных пульсаций герцового диапазона на случай анизотропных протонов с конечными ${{\beta }_{ \bot }}$.
Влияние горячей плазмы на генерацию ЭМИЦ волн в мультиионной (${{{\text{H}}}^{ + }},{\text{H}}{{{\text{e}}}^{ + }},{{{\text{O}}}^{ + }}$) магнитосферной плазме рассматривалось в работах [Wang et al., 2016; Ni et al., 2017; Tang et al., 2017]. В этих работах в основном исследовалось взаимодействие ЭМИЦ волн с ультрарелятивистскими электронами электронного радиационного пояса Земли. Эти волны оказывают существенное влияние на степень питч-углового рассеяния в конус потерь мэвных электронов радиационного пояса Земли [Ni et al., 2017]. Кроме того, в этих работах проведен детальный анализ влияния концентрации тяжелых ионов на развитие циклотронной неустойчивости ЭМИЦ волн в полосах непрозрачности (вблизи гирочастот ${{{\text{H}}}^{ + }},{\text{H}}{{{\text{e}}}^{ + }},{{{\text{O}}}^{ + }}$) [Wang et al., 2016; Tang et al., 2017], в которых эти волны не могут распространяться.
Целью нашей работы является исследование влияния горячей анизотропной плазмы на развитие циклотронной неустойчивости в протонном радиационном поясе Земли при конечных ${{\beta }_{ \bot }}$. Будет показано, что учет конечных значений ${{\beta }_{ \bot }}$ приводит к модификации не только мнимой части дисперсионного уравнения, но и к модификации реальной части этого уравнения. Это приводит как к изменению инкремента циклотронной неустойчивости, так и к вариации параметров распространения ЭМИЦ волн вдоль силовой линии. Приведенный теоретический анализ полезен также в методическом отношении, так как позволяет глубже понять природу и динамику ультранизкочастотных электромагнитных волн.
ОСНОВНЫЕ УРАВНЕНИЯ
Рассмотрим влияние конечного давления плазмы на генерацию и распространение геомагнитных пульсаций герцового диапазона (Рс1-пульсации). Протоны, попадающие в область захваченной радиации под влиянием нестационарных полей геомагнитных возмущений, дрейфуют по направлению к Земле. Рост энергии движения частиц поперек и вдоль магнитного поля при этом дрейфе определяется сохранением соответственно первого и второго адиабатических инвариантов. Это обстоятельство и наличие конуса потерь, характерной для любой плазменной ловушки с магнитными пробками, приводит к тому, что в области внешнего протонного пояса ($L$ = 4–6) средняя энергия поперечного движения горячих протонов становится больше средней энергии вдоль силовой линии. Наличие такой анизотропии $A = ({{{{T}_{ \bot }}} \mathord{\left/ {\vphantom {{{{T}_{ \bot }}} {{{T}_{\parallel }}}}} \right. \kern-0em} {{{T}_{\parallel }}}}) - 1$ предопределило создание теории генерации “жемчужин” [Kennel, Petschek, 1966; Cornwall, 1966; Тверской, 1968; Фейгин, Якименко, 1969]. Если в спокойном состоянии горячие протоны в магнитосфере Земли имеют би-максвелловское распределение с ${{T}_{ \bot }} > {{T}_{\parallel }}$ и если плотность горячих частиц много меньше плотности холодных частиц $({{n}_{h}} \ll {{n}_{0}})$, то для волн, распространяющихся вдоль магнитной силовой линии (волновой вектор ${{k}_{ \bot }} = 0$), решение дисперсионного уравнения [Шафранов, 1963] при ${{\beta }_{ \bot }} = 0$, приводит к коэффициенту линейного усиления (инкремент) в виде [Фейгин, Якименко, 1969; Feygin, Yakimenko, 1971; Gendrin at al., 1971; Гульельми, 1979]:
(1)
$\begin{gathered} \frac{\gamma }{\Omega } = {{\pi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{n}_{h}}}}{{{{n}_{o}}}}\left( {\frac{{{{c}_{A}}}}{{{{v}_{{\parallel h}}}}}} \right)\frac{{(A + 1)(\tilde {A} - x){{{(1 - x)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}{{{{x}^{2}}(2 - x)}} \times \\ \times \,\,\exp \left[ { - \frac{{{{{(1 - x)}}^{3}}}}{{{{x}^{2}}}}{{{\left( {\frac{{{{c}_{A}}}}{{{{v}_{{\parallel h}}}}}} \right)}}^{2}}} \right], \\ \end{gathered} $При конечном давлении плазмы параметры, которые определяют распространение пакета волн и их усиление, существенно отличаются от приближения холодной плазмы. Формально это означает, что изменяется как мнимая, так и действительная часть частоты ($\omega \to \omega + i\gamma $).
Дисперсионное уравнение для рассматриваемых волн, вывод которого представлен в Приложении 1, имеет вид:
(2)
$\begin{gathered} {{k}^{2}}F = \frac{{{{x}^{2}}}}{{(1 - x)}} - i\sqrt \pi \frac{{{{n}_{h}}}}{{{{n}_{0}}}}\frac{{{{{(1 - x)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{x}\frac{{{{c}_{A}}}}{{{{v}_{{\parallel h}}}}}{{F}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,(A + 1)(\tilde {A} - x)\exp \left[ { - \frac{{{{{(1 - x)}}^{3}}}}{{{{x}^{2}}}}{{{\left( {\frac{{{{c}_{A}}}}{{{{v}_{{\parallel h}}}}}} \right)}}^{2}}F} \right], \\ \end{gathered} $Дисперсионное уравнение (2) отличается от аналогичного уравнения в холодно-плазменном приближении (${{n}_{h}} \ll {{n}_{0}}$) множителем:
Рассмотрим отличие в формулах при учете ${{\beta }_{ \bot }} \ne 0$. Уравнение для реальной части частоты имеет дополнительный множитель:
Из дисперсионного уравнения (2) выводится выражение для инкремента, вывод которого мы вынесли в Приложение 2, и которое имеет вид:
(5)
$\begin{gathered} \frac{\gamma }{\Omega } = {{\pi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{n}_{h}}}}{{{{n}_{o}}}}\left( {\frac{{{{c}_{A}}}}{{{{v}_{{\parallel h}}}}}} \right)\frac{{(A + 1)(\tilde {A} - x){{{(1 - x)}}^{{5/2}}}{{F}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{x}^{2}}(2 - x)\left[ {1 - \frac{{x(1 - x)}}{{2 - x}}\frac{{\partial \ln F}}{{\partial x}}} \right]}} \times \\ \times \,\,\exp \left[ { - \frac{{{{{(1 - x)}}^{3}}F}}{{{{x}^{2}}}}{{{\left( {\frac{{{{c}_{A}}}}{{{{v}_{{\parallel h}}}}}} \right)}}^{2}}} \right]. \\ \end{gathered} $Таким образом, из формул (3), (5) следует, что зависимость инкремента от ${{\beta }_{ \bot }}$ входит только в $F$.
РЕЗУЛЬТАТЫ
Для оценки численных результатов мы будем использовать типичные параметры магнитосферной плазмы в области протонного радиационного пояса (4–6 радиусов Земли) с энергичными анизотропными протонами (~100 Кэв) и холодной плазмы с температурой $\sim {\kern 1pt} 1\,\,ev$ [Тверской, 1968; Feygin, Yakimenko, 1971; Gendrin et al., 1971]: $A \approx 0.5{\kern 1pt} - {\kern 1pt} 3$, ${{{{n}_{h}}} \mathord{\left/ {\vphantom {{{{n}_{h}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} \approx {{10}^{{ - 3}}}$, ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}} \approx 2{\kern 1pt} - {\kern 1pt} 10$. Эти параметры использовались для оценки инкремента в работе [Gendrin et al., 1971]. Мы построили графики зависимости нормированного инкремента ${\gamma \mathord{\left/ {\vphantom {\gamma \Omega }} \right. \kern-0em} \Omega }$ (5) от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega \Omega }} \right. \kern-0em} \Omega }$, которые учитывает конечность ${{\beta }_{ \bot }}$ для разных значений ${{\beta }_{ \bot }}$ при постоянном ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}} = 2.5,$ $A = 1$ и ${{{{n}_{h}}} \mathord{\left/ {\vphantom {{{{n}_{h}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = {{10}^{{ - 3}}}$ (рис. 2) и графики зависимости нормированного инкремента (2) от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega \Omega }} \right. \kern-0em} \Omega }$ при постоянном ${{\beta }_{ \bot }}$ и разных значений A и ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}}$ (рис. 3, 4).
Рис. 2.
Зависимость нормированного инкремента ${\gamma \mathord{\left/ {\vphantom {\gamma {{\kern 1pt} \Omega }}} \right. \kern-0em} {{\kern 1pt} \Omega }}$ от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega {{{\Omega }_{i}}}}} \right. \kern-0em} {{{\Omega }_{i}}}}{\kern 1pt} $ для разных значений ${{\beta }_{ \bot }}$ (0, 0.3, 0.5, 1) при постоянных $A = 1$${{\,{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{\,{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}} = 2.5$, ${{{{n}_{h}}} \mathord{\left/ {\vphantom {{{{n}_{h}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = {{10}^{{ - 3}}}$.
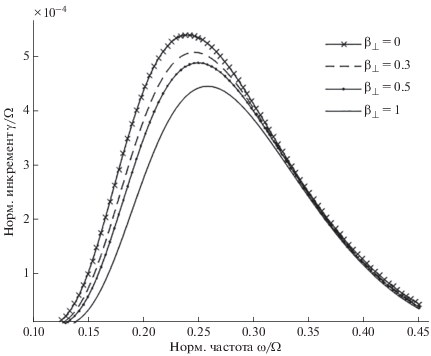
Рис. 3.
Зависимость нормированного инкремента ${\gamma \mathord{\left/ {\vphantom {\gamma {{\kern 1pt} \Omega }}} \right. \kern-0em} {{\kern 1pt} \Omega }}$ от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega {{{\Omega }_{i}}}}} \right. \kern-0em} {{{\Omega }_{i}}}}{\kern 1pt} $ при увеличении А от 0.7 до 2 для ${{\beta }_{ \bot }}{\kern 1pt} = 0.1$, ${{n}_{h}}{\kern 1pt} /{\kern 1pt} {{n}_{0}} = {{10}^{{ - 3}}}$ и ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}} = 2.5$.
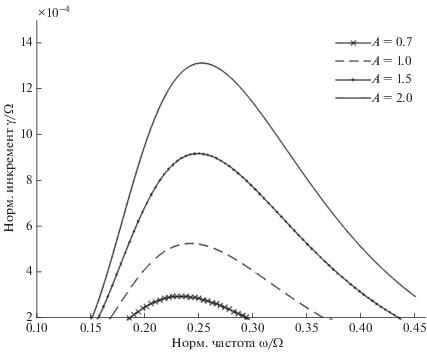
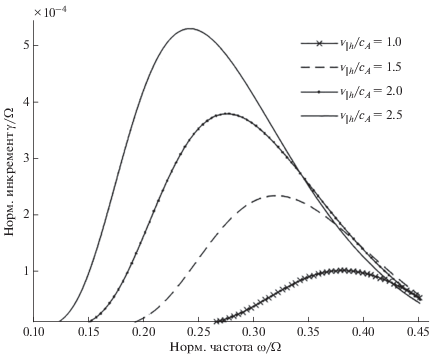
Рис. 4.
Зависимость нормированного инкремента ${\gamma \mathord{\left/ {\vphantom {\gamma {{\kern 1pt} \Omega }}} \right. \kern-0em} {{\kern 1pt} \Omega }}$ от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega {{{\Omega }_{i}}}}} \right. \kern-0em} {{{\Omega }_{i}}}}{\kern 1pt} $ при А = 1, ${{\beta }_{ \bot }}{\kern 1pt} = 0.1$, ${{n}_{h}}{\kern 1pt} /{\kern 1pt} {{n}_{0}} = {{10}^{{ - 3}}}$и изменяющемся ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}}$ от 1 до 2.5.
На рис. 2 представлена зависимость нормированного инкремента (5) от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega \Omega }} \right. \kern-0em} \Omega }$ для разных ${{\beta }_{ \bot }}$ при ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}} = 2.5$ и $A = 1$. Как видно из рис. 2, при увеличении ${{\beta }_{ \bot }}$ значение максимального инкремента уменьшается. При этом значения оптимальной частоты ${{x}_{0}} = {{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} \Omega }} \right. \kern-0em} \Omega }$, соответствующей максимуму инкремента, сдвигаются в сторону больших значений. Таким образом, для эффективной генерации Рс1 пульсаций предпочтительны малые значения ${{\beta }_{ \bot }}$.
Рисунок 3 показывает, как изменяются максимальный инкремент и оптимальная частота при увеличении А от 0.7 до 2 при ${{\beta }_{ \bot }}{\kern 1pt} = 0.1$ и ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}} = 2.5$. При этих параметрах максимальный инкремент с увеличением А увеличивается (по сравнению с рис. 2).
Рисунок 4 представляет зависимость нормированного инкремента ${\gamma \mathord{\left/ {\vphantom {\gamma \Omega }} \right. \kern-0em} \Omega }{\kern 1pt} $ от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega {{{\Omega }_{i}}}}} \right. \kern-0em} {{{\Omega }_{i}}}}$ при А = 1, ${{\beta }_{ \bot }}{\kern 1pt} = 0.1$ и изменяющемся ${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}}$ от 1 до 2.5. Из рисунка видно, что оптимальная частота при этих параметрах сдвигается в сторону больших значений.
ОБСУЖДЕНИЕ И ВЫВОДЫ
1. Полученные результаты показывают, что наиболее эффективно усиление ЭМИЦ волн происходит при малых значениях ${{\beta }_{ \bot }}$. Но это характерно при низкой магнитной активности. В периоды повышенной магнитной активности, как показывают наши результаты, при рассмотрении усиления ЭМИЦ волн необходимо учитывать конечные значения ${{\beta }_{ \bot }}$ (рис. 1).
2. Зависимость нормированного инкремента ${\gamma \mathord{\left/ {\vphantom {\gamma \Omega }} \right. \kern-0em} \Omega }$ от нормированной частоты ${\omega \mathord{\left/ {\vphantom {\omega \Omega }} \right. \kern-0em} \Omega }{\kern 1pt} $, которая учитывает конечность ${{\beta }_{ \bot }}$, полученная на основе выведенного нами аналитического выражения (5), представлена на рис. 2. Анализ полученных результатов показал, что при учете конечных ${{\beta }_{ \bot }}$ значение максимального инкремента снижается по сравнению со случаем ${{\beta }_{ \bot }}{\kern 1pt} = 0$. Динамика значений оптимальной частоты ${{x}_{0}} = {{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} \Omega }} \right. \kern-0em} \Omega }$, соответствующей максимальному инкременту, показывает смещение в сторону больших значений.
3. Анализ всех результатов (рис. 2–рис. 4) позволяет сделать вывод, что при генерации ЭМИЦ волн в околоземной плазме предпочтительны малые значения перпендикулярного плазменного давления анизотропных протонов (${{\beta }_{ \bot }}$), большие значения анизотропии (А) и большие значения отношения продольной скорости горячих анизотропных протонов к альвеновской скорости в области протонного радиационного пояса Земли (${{{{v}_{{\parallel h}}}} \mathord{\left/ {\vphantom {{{{v}_{{\parallel h}}}} {{{c}_{A}}}}} \right. \kern-0em} {{{c}_{A}}}}$).
Список литературы
Гульельми А.В. МГД волны в околоземной плазме. М.: Наука. 1979. 139 с.
Стикс Т. Теория плазменных волн. М.: Атомиздат. 1965. 344 с.
Тверской Б.А. Динамика радиационных поясов Земли. М.: Наука. 1968. 223 с.
Фейгин Ф.З., Якименко В.Л. Механизм генерации и развитие “жемчужин” при циклотронной неустойчивости внешней протонной зоны // Геомагнетизм и аэрономия. 1969. Т. 9. С. 700–705.
Шафранов В.Д. Вопросы теории плазмы. Вып. 3. М.: Госатомиздат. 1963. С. 3–140.
Berko F.M., Cahill I.J., Jr Fritz T.A. // J. Geophys. Res. 1975. V. 80. P. 3539–3552.
Bespalov P.A., Trakhtengerts V.Y. The cyclotron instability in the Earth radiation bets. // In: Leonovich M.A. (Ed.), Reviews of plasma Physics. 1986. V.10. Plenum, New York. P. 155–192.
Cornwall J.M. Micropulsations and the outer radiation zone // J. Geophys. Res. 1966. V. 71. P. 2185–2199.
Demekhov A.G. Recent progress in understanding Pc1 pearl formation // J. Atmos. Solar-Terr. Phys. 2007. V. 69. P. 1609–1622.
Feygin F.Z, Yakimenko V.L. Appearance and development of geomagnetic Pc1 type micropulsations (“pearls”) due to cyclotron instability of proton belt // Ann. Geophys. 1971. V. 27. P. 49–55.
Gendrin R., Lacourly S., Roux A., Solomon J., Feygin F.Z., Gokhberg M.B., Troitskaya V.A., Yakimenko V.L. Wave packet propagation in an amplifying medium and its application to the dispersion characteristics and to the generation mechanism of Pc1 events // Planet. Space Sci. 1971. V. 19. P. 165–194.
Guglielmi A.V., Polhotelov O.A. Geoelectromagnetic Waves. IOP Publ. Ltd. Bristol. 1996.
Kangas J., Guglielmi A., Pokhotelov O. Morphology and physics of the short period magnetic pulsations // Space Sci. Rev. 1998. V. 83. P. 435–512.
Kennel C.F., Petschek H.E. Limit on stably trapped particle fluxes // J. Geophys. Res. 1966. V. 71. P. 1–28.
Konradi, A., Williams D.J., Fritz T.A. Energy spectra and pitch angle distributions of storm time and substorm-injected protons // J. Geophys. Res. 1973. V. 78. P. 4739–4744.
Longanecker G.W., Hoffman R.A. S-A spacecraft and experiment description // J. Geophys. Res. 1973. V. 78. P. 4711–4717.
Ni B., Cao X., Shprits Y., Summers D., Gu X., Fu S., Lou Y. Hot Plasma Effects on the Cyclotron-Resonant Pitch-Angle Scattering Rates of Radiation Belt Electrons Due to EMIC Waves // Geophysical Research Letters. 2017. V. 45. P. 21–30.
Smith P.H., Hoffman R.A. Direct observations in the dusk hours of the characteristics of the storm time ring current particles during the beginning of magnetic storms // J. Geophys. Res. 1974. V. 79. P. 966–971.
Tang Y., Jinsong Zhao J., Sun H., Lu J., Wang M. Effects of ion thermal pressure on wave properties of electromagnetic ion cyclotron waves in a H+–He+–O+ plasma // Phys. Plasmas. 2017. V. 24. P. 052120. https://doi.org/10.1063/1.4983622
Wang Q., Cao X., Gu X., Ni B., Zhou C., Shi R., Zhao Z. A parametric study of the linear growth of magnetospheric EMIC waves in a hot plasma // Phys. Plasmas. 2016. V. 23. P. 062903. https://doi.org/10.1063/1.4953565
Yahnin A.G., Yahnina T.A., Frey H.U. Subauroral proton spots visualize the Pc1 source // J. Geophys. Res. 2007. V. 112. A10223. https://doi.org/10.1029/2007JA012501
Yahnina T.A., Frey H.U., Bцsinger T., Yahnin A.G. Evidence for subaroral proton flashes on the dayside as the result of the ion cyclotron interaction // J. Geophys. Res. 2008. V. 113. P. A07209. https://doi.org/10.1029/2008JA013099
Дополнительные материалы отсутствуют.



