Физика Земли, 2021, № 1, стр. 133-143
Моделирование поля упругих напряжений земной коры Центральной Азии по данным об ориентациях осей главных напряжений
Ш. А. Мухамедиев 1, А. Н. Галыбин 1, *
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
* E-mail: a.n.galybin@gmail.com
Поступила в редакцию 29.06.2020
После доработки 06.07.2020
Принята к публикации 01.09.2020
Аннотация
В работе проведены реконструкции полей упругих напряжений по дискретным данным о главных направлениях тензора напряжений в Центральной Азии. Методика предусматривает оптимизацию нормы отклонений расчетных и натурных данных, а также непрерывность вектора напряжений на разломе в случае, когда он явно учитывается в модели. Построены поля траекторий главных напряжений и изолиний максимальных касательных напряжений для двух областей. На примере показано, что в модели, учитывающей разлом, поля напряжений в окрестности разлома существенно отличаются от полей напряжений в модели, не учитывающей разлом.
1. ВВЕДЕНИЕ
Данная работа была инициирована Ш.А. Мухамедиевым, который был рецензентом статьи И.У. Атабекова, опубликованной в этом же номере журнала [Атабеков, 2021]. На формирование мнения о рецензируемой статье и возможности ее публикации повлияли следующие соображения. Исследуемый регион Центральной Азии является одним из важнейших в мире для понимания новейшей геодинамики и сейсмотектоники земной коры. Для него накоплено много сейсмологических и геодезических данных, позволяющих делать выводы о современных деформационных процессах. К сожалению, результатов моделирования напряженного состояния для данного региона явно недостаточно. Результаты опубликованных в последние годы работ методами локальной кинематической реконструкции напряжений и палеонапряжений являются сомнительными. Потенциально корректных подходов, основанных на решении нелокальных краевых задач, насколько нам известно, нет. Такие подходы, используемые, в том числе, и российскими исследователями, посвящены другим регионам (например, Калифорнии). Поэтому важным представляется приложение таких подходов к Центральной Азии. Статья И.У. Атабекова является первым опытом.
С другой стороны, доступны независимые данные по ориентациям осей главных напряжений, которые аккумулированы в мировой базе данных по напряжениям – WSMP [Headache et al., 2016]. В работах [Galybin, Mukhamediev, 2004a; 2004b; Mukhamediev et al., 2006; Galybin, 2009] были разработаны алгоритмы реконструкции полей упругих напряжений, использующие дискретные данные по ориентациям главных напряжений в качестве входных, при этом никакие другие данные как граничные, так и полевые не используются. Указанные алгоритмы успешно применялись для реконструкций полей напряжений различных регионов Земли в статьях [Мухамедиев и др., 2005а; Мухамедиев и др., 2005б; Мухамедиев, Галыбин, 2006; Irša, Galybin, 2010; Haderka et al., 2009; Irša, Galybin, 2011]. В данной работе эти алгоритмы используются для реконструкции поля напряжений той же области, которая была рассмотрена И.У. Атабековым. В отличие от работы [Атабеков, 2021] здесь предпринята попытка промоделировать влияние разломов на поле тектонических напряжений, для чего в модель явно введен один из крупных геологических разломов Центральной Азии.
2. ВХОДНЫЕ ДАННЫЕ И МЕТОДЫ РЕКОНСТРУКЦИИ ПОЛЕЙ НАПРЯЖЕНИЙ
2.1. Натурные данные
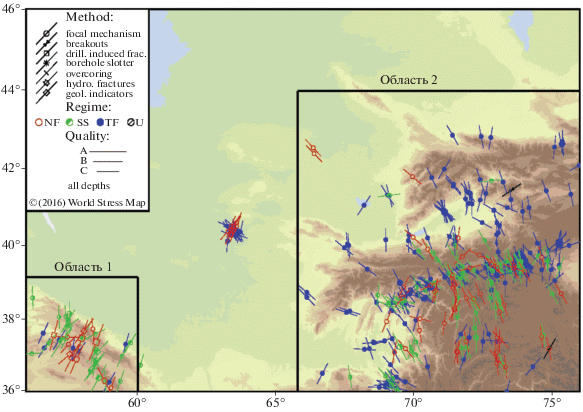
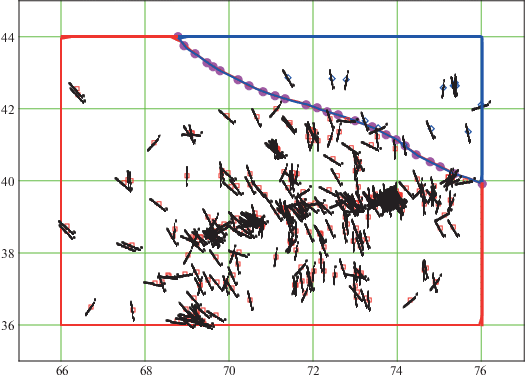
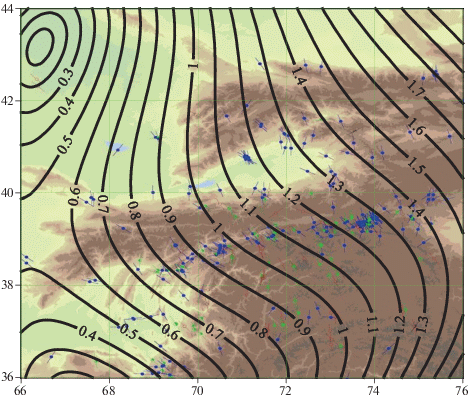
Мировая база данных по напряжениям WSMP 2016 содержит 42 870 ориентаций главных напряжений, полученных различными методами, в большинстве по механизмам очагов землетрясений. Качество данных различно: так данные качества А указывают ориентации с ошибкой ±15°; качество B – ±20°; качество C – ±25°. Таких данных в базе более 32000, другие данные для моделирования обычно не используются. На рис. 1 показаны ориентации главных сжимающих горизонтальных напряжений в области, ограниченной географическими координатами 36:46 с.ш., 56:76 в.д., т.е. той же, что рассмотрена и в статье И.У. Атабекова. Следует отметить, что число данных высшего качества А всего 4, данных качества В – 16, остальные 381 ориентации имеют качество С. Также следует отметить отсутствие данных в большой части данного региона, что вызывает необходимость рассмотрения нескольких областей меньшего размера. Далее рассматриваются две: первая область ограничена географическими координатами 36:39 с.ш., 56:60 в.д., где находятся 43 данных (показаны в левом нижнем углу на рис. 1); вторая область ограничена географическими координатами 36:44 с.ш., 66:76 в.д., где находятся 334 данных. Следует отметить, что во второй области расположено около ста геологических разломов, в частности глубинные Северо-Тянь-Шаньский, Нарынский, Таласо-Ферганский, Южно-Тянь-Шаньский, Памиро-Гиндукушский и второстепенные разломы [Уломов, 1974], которые могут рассматриваться как активные. Учет всех разломов в моделировании нецелесообразен, поскольку алгоритмы для многосвязных областей используют непрерывность векторов напряжений на разломах в некотором (достаточно большом) числе точек. Если число данных по ориентациям относительно невелико, например, как в данном случае 3–4 данных (в среднем) на каждую подобласть, ограниченную разломами, то количество уравнений из-за условий непрерывности значительно больше, чем число уравнений, порождаемых данными, что приводит к практически непрерывным полям напряжений. Однако непрерывные поля могут быть получены, если пренебречь влиянием разломов, что значительно упрощает расчеты. Ранее проведенные реконструкции полей напряжений в некоторых регионах (см. [Мухамедиев, Галыбин, 2006; Irša, Galybin, 2011]), показали, что существенное различие в результатах реконструкции напряжений возникает, если данных в каждой подобласти десятки, поэтому далее вторая область рассматривается в виде двух связных подобластей с границей вдоль Таласо-Ферганского разлома, как показано на рис. 2. Выбор данного разлома объясняется тем, что он полностью пересекает вторую область, что облегчает проведение моделирования. Несмотря на то, что в отличие от других крупных разломов сейсмическая активность вдоль этого разлома ниже, он, как будет показано в дальнейшем, оказывает существенное геомеханическое влияние на поле напряжений рассматриваемой области.
2.2. Описание алгоритма
Подробные описания алгоритмов приведены в цитированных выше работах. Кратко их можно сформулировать следующим образом.
Предполагается, что вертикальное сжимающее напряжение ${{S}_{V}}$ является главным и определяется весом вышележащих пород. Главные горизонтальные напряжения ${{S}_{H}}$ и ${{S}_{h}}$, действующие в плоскости пласта, являются сжимающими и при этом $\left| {{{S}_{H}}} \right| \geqslant \left| {{{S}_{h}}} \right|$. В соответствии с представлениями Колосова–Мусхелешвили вводятся гармоническая функция $P = \frac{1}{2}\left( {{{S}_{H}} + {{S}_{h}}} \right)$ – среднее давление и комплекснозначная функция девиатора напряжений $D = \frac{1}{2}\left( {{{S}_{H}} - {{S}_{h}}} \right){{e}^{{i{\alpha }}}},$ где аргумент $\alpha = \pi - 2\theta $ выражается через главные направления плоского тензора напряжений – функцию θ. Далее используются выражения напряжений через два комплексных потенциала $\Phi (z)$ и $\Psi (z)$ в виде $P(z,\bar {z}) = 2\operatorname{Re} \left( {\Phi (z)} \right)$, которые подлежат нахождению из следующих условий.
Пусть Ω – односвязная упругая область (конечная или бесконечная), ограниченная несамопересекающимся замкнутым контуром Γ. Эта область может быть подобластью большей области, которая необязательно односвязная или ограниченная. Пусть данные о главных направлениях θj тензора напряжений известны в точках zj (j = 1…N), которые расположены как внутри области, так и могут быть на ее границе.
Требуется определить двумерное поле напряжений в Ω, которое:
− обеспечивает наилучшее согласие данных θj и расчетных главных направлений в заданных точках zj;
− удовлетворяет всем уравнениям плоской теории упругости, сформулированным в напряжениях.
Поскольку главные направления определяются только аргументом комплекснозначной биголоморфной функции девиатора напряжений $D = D(z,\bar {z})$, то задача может быть рассмотрена как задача определения биголоморфной функции D с последующим нахождением гармонической функции $P = P(z,\bar {z})$ из уравнений равновесия. Таким образом, исходная задача эквивалентна нахождению комплексных потенциалов $\Phi (z)$ и $\Psi (z)$, которые обеспечивают минимизацию суммы квадратов отклонений аргумента комплекснозначной функции девиатора напряжений от углов ${{\alpha }_{j}} = \pi - 2{{\theta }_{j}}$, т.е.:
(1)
$\sum\limits_{j = 1}^N {{{{\left\{ {\operatorname{Im} \left[ {\exp ( - i{{\alpha }_{j}})\left( {{{{\bar {z}}}_{j}}\Phi {\kern 1pt} '({{z}_{j}}) + \Psi ({{z}_{j}})} \right)} \right]} \right\}}}^{2}}} \Rightarrow \min .$Отметим, что если считать, как это принято в геомеханике, что максимальное главное напряжение есть наибольшее сжимающее напряжение (геомеханическое соглашение), то надо положить ${{\alpha }_{j}} = - 2{{\theta }_{j}}$, что не приводит к изменению в виде (1).
Комплексные потенциалы ищутся в виде многочленов:
(2)
$\Psi \left( z \right) = \sum\limits_{k = 0}^n {{{c}_{k}}{{z}^{k}}} ,\,\,\,\,\Phi {\kern 1pt} '\left( z \right) = \sum\limits_{k = 0}^{n - 1} {{{c}_{{k + n + 1}}}{{z}^{k}}} .$Комплексные константы ck неизвестны и должны определяться из решения задачи (1), после чего аргумент биголоморфной функции D становится известным, как и сама эта функция. Количество комплексных неизвестных, 2n + 1, не должно превосходить половины числа данных N, в противном случае разрешающая система линейных уравнений будет недоопределенной.
Отметим, что можно использовать разное количество членов для комбинаций голоморфных функций в (2). Здесь представление для Φ′(z) имеет на один член меньше, чем для Ψ(z), что не является обязательным, но обеспечивает одинаковое количество членов в функциях напряжений Р и D.
Использование (2) приводит к следующему выражению для функции девиатора напряжений:
(3)
$\begin{gathered} D\left( {z,\bar {z}} \right) = \sum\limits_{k = 0}^{2n} {{{c}_{k}}{{F}_{k}}\left( {z,\bar {z}} \right)} , \\ {{F}_{k}}\left( {z,\bar {z}} \right) = \left\{ {\begin{array}{*{20}{c}} {{{z}^{k}},}&{0 \leqslant k \leqslant n} \\ {\bar {z}{{z}^{{k - n - 1}}},}&{n < k \leqslant 2n} \end{array}} \right.. \\ \end{gathered} $Поскольку ${\text{Im}}({{e}^{{ - i{\alpha }}}}D) = 0,$ то подстановка из (3) приводит к функциональному уравнению:
(4)
$\operatorname{Im} \sum\limits_{k = 0}^{2n} {{{c}_{k}}{{e}^{{ - i\alpha \left( {z,\bar {z}} \right)}}}{{F}_{k}}\left( {z,\bar {z}} \right)} = 0,\,\,\,\,z \in \Omega .$Уравнение (4) далее сводится к системе линейных алгебраических уравнений относительно неизвестных констант ck. Поскольку функция аргумента α известна в точках zj, то методом коллокаций получаем следующую систему N реальных уравнений для определения 2n + 1 комплексных констант:
(5)
$\operatorname{Im} \sum\limits_{k = 0}^{2n} {{{e}^{{ - i{{\alpha }_{j}}}}}{{F}_{k}}({{z}_{j}},{{{\bar {z}}}_{j}}){{c}_{k}}} = 0,\,\,\,\,j = 1 \ldots N.$Уравнение (5) является однородным, таким образом, по крайней мере одно дополнительное условие необходимо для того, чтобы найти нетривиальное решение системы. Как видно, умножение системы (5) на любую положительную постоянную не нарушает этой системы, что означает, что любое решение, удовлетворяющее (5), можно нормировать на константу. Эта константа может быть выбрана из условия, что средний модуль D по области равен единице. Так как |D| = e-iαD, то дополнительное уравнение принимает вид:
(6)
$\sum\limits_{j = 1}^N {\sum\limits_{k = 0}^{2n} {{{e}^{{ - i{{\alpha }_{j}}}}}{{F}_{k}}({{z}_{j}},{{{\bar {z}}}_{j}}){{c}_{k}}} } = N.$Удобно переписать систему (5)–(6) в вещественной матричной форме, записывая комплексные константы как ck = Xk + iX2n +k+ 1 (следовательно, вводя вектор С из 4n + 2 вещественных неизвестных), что приводит к выражению:
где: A – (N + 1)(4n + 2) матрица системы с вещественными коэффициентами Ak,j, которые определены ниже; С – (4n + 2) вектор вещественных неизвестных Xk; b – (N + 1) вектор, все компоненты которого равны нулю за исключением последнего, равного N, как следует из (6):(8)
$\begin{gathered} {{A}_{{j,k}}} = \left\{ \begin{gathered} \operatorname{Im} \left[ {{{e}^{{ - i{{\alpha }_{j}}}}}{{F}_{k}}({{z}_{j}},{{{\bar {z}}}_{j}})} \right],\,\,\,\,0 \leqslant k \leqslant 2n \hfill \\ \operatorname{Im} \left[ {i{{e}^{{ - i{{\alpha }_{j}}}}}{{F}_{{k - 2n - 1}}}({{z}_{j}},{{{\bar {z}}}_{j}})} \right],\,\,\,\,2n < k \leqslant 4n + 1 \hfill \\ \end{gathered} \right.,\,\,j = 1 \ldots N \\ {{A}_{{N + 1,k}}} = \left\{ \begin{gathered} \sum\limits_{j = 1}^N {{{e}^{{ - i{{\alpha }_{j}}}}}} {{F}_{k}}({{z}_{j}},{{{\bar {z}}}_{j}}),\,\,\,\,0 \leqslant k \leqslant 2n \hfill \\ \sum\limits_{j = 1}^N {i{{e}^{{ - i{{\alpha }_{j}}}}}} {{F}_{{k - 2n - 1}}}({{z}_{j}},{{{\bar {z}}}_{j}}),\,\,\,\,2n < k \leqslant 4n + 1 \hfill \\ \end{gathered} \right.. \\ \end{gathered} $Переопределенная система (8) решается далее методом наименьших квадратов, при этом для ее разрешимости необходимо, чтобы N ≥ 4n + 2.
В случае, когда область Ω состоит из М подобластей, необходимо записать уравнения (5) для каждой подобласти и добавить к уравнениям (6) условия непрерывности вектора напряжений на всех внутренних границах Γj между соседними подобластями, j = 1…Nint. Формально задача сводится к оптимизации целевой функции:
(9)
$\begin{gathered} \sum\limits_{m = 1}^N {{{{\left\{ {\operatorname{Im} \left[ {{{e}^{{2i{{\theta }_{m}}}}}D({{z}_{m}},{{{\bar {z}}}_{m}})} \right]} \right\}}}^{2}}} + \\ + \,\,{\text{weigth}}\,\,\sum\limits_{j = 1}^{{{N}_{{\operatorname{int} }}}} {\int\limits_{{{\Gamma }_{j}}} {{{{\left[ {\left\langle {P(\zeta )} \right\rangle + \tfrac{{d\zeta }}{{d\bar {\zeta }}}\left\langle {D(\zeta )} \right\rangle } \right]}}^{2}}d\zeta } } \Rightarrow \min , \\ \left( {{\text{при условии }}\left( {\text{6}} \right)} \right), \\ \end{gathered} $Приближенное решение системы (7) по методу наименьших квадратов есть:
(10)
${\mathbf{C}}* = {{({{{\mathbf{A}}}^{T}}{\mathbf{A}})}^{{ - 1}}}{{{\mathbf{A}}}^{T}}{\mathbf{b}}.$Однако этот метод сам по себе не в состоянии обеспечить устойчивость полученного решения, неустойчивость может возникнуть из-за некорректности задачи. Для контроля точности и устойчивости решения используются соответственно невязка R и число обусловленностей CN. При высоком числе обусловленностей используется SVD-регуляризация. Невязка подсчитывается по формуле:
(11)
${{R}^{2}} = \sum\limits_{k = 1}^N {{{{\left| {{{e}^{{i\arg {{D}_{{rec}}}({{z}_{k}},{{{\bar {z}}}_{k}})}}} - {{e}^{{ - 2i{{\theta }_{k}}}}}} \right|}}^{2}}} ,$Как уже отмечалось, Drec из-за нормировки определяется с точностью по произвольной положительной мультипликативной постоянной. Поскольку ее аргумент определяется однозначно, то эта постоянная относится к модулю комплексного девиатора, который представляет собой функцию максимального касательного напряжения ${{\tau }_{{\max }}}(z,\bar {z})$ в горизонтальной плоскости. Следовательно, среднее давление (которое получается интегрированием уравнений равновесия) зависит от двух параметров, которые не влияют на траектории поля напряжений. Соответственно общее решение в терминах главных напряжений представляется в следующем виде:
(12)
$\begin{gathered} \tfrac{1}{2}({{S}_{H}} - {{S}_{h}}) = {{\tau }_{{\max }}}(z,\bar {z}) = b\tau (z,\bar {z}), \\ \tfrac{1}{2}({{S}_{H}} + {{S}_{h}}) = a + bp(z,\bar {z}), \\ \end{gathered} $Следует отметить, что как только определена функция комплексного девиатора, то по ее аргументу α$(z,\bar {z})$ определяются главные направления, после чего поле траекторий наибольших главных напряжений однозначно находится путем интегрирования системы дифференциальных уравнений первого порядка:
второе семейство траекторий ортогонально к первому. В случае использования “геомеханического соглашения” эти траектории меняются местами. Интегрирование (13) не встречает значительных трудностей и везде далее выполняется численно. Поэтому, когда аргумент D известен в любой точке области, поле траекторий можно считать известным везде, за исключением особых (изотропных) точек, которые могут быть определены в процессе решения.3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
3.1. Область 1
Расчеты для первой области проводились для n = 0…4, при этом обнаружилось, что невязки при n = 1–3 приблизительно одинаковы и округленно равны 4, при n = 2 невязка минимальна, при n = 4 R = 7, числа обусловленностей невысоки (n = 1: CN = 30; n = 2: CN = 70; n = 3: CN = 166; n = 4: CN = 540). Поэтому все иллюстрации приведены для n = 2. На рис. 3 показаны траектории главных напряжений, а на рис. 4 – изолинии максимальных касательных напряжений в первой области. Средние углы наклона траекторий получаются при использовании n = 0 и составляют 64о.
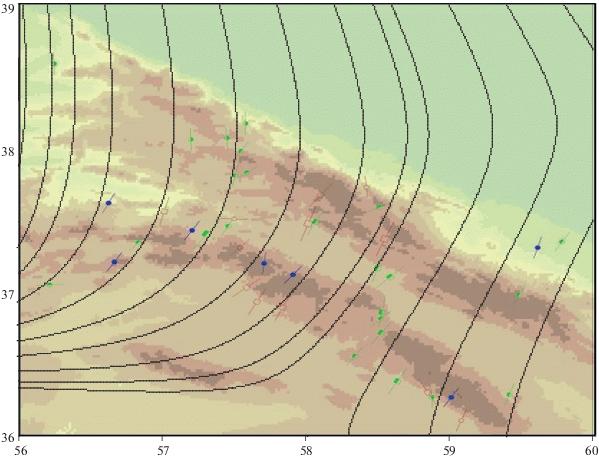
Рис. 4.
Изолинии максимальных горизонтальных касательных напряжений ${{\tau }_{{\max }}}$в области 1.
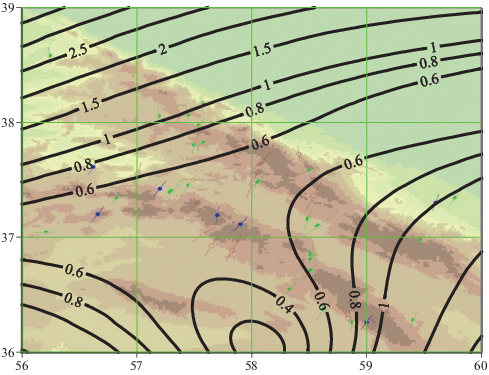
Как видно из рис. 3, реконструированные траектории удовлетворительно коррелируют с данными WSMP. Рис. 4 показывает, что ${{\tau }_{{\max }}}$ минимально в точке с координатами 36° с.ш., 58° в.д. и по мере удаления возрастает в любом направлении, достигая максимума в правой верхней части области. Следует отметить, что здесь и далее напряжения на всех графиках приводятся в нормализованной (безразмерной) форме, т.е. в формулах (12) a = 0 и b = 1, при этом среднее значение по области всегда ${{\tau }_{{\max }}}$ = 1.
3.2. Область 2
3.2.1. Без учета разлома. Невязки при n = 1–4 различаются незначительно, с округлением R = 17, числа обусловленности также низкие (n = 1: CN = 46; n = 2: CN = 98; n = 3: CN = 181; n = 4: CN = 319). Ниже приведены результаты для n = 2. На рис. 5 показаны траектории главных напряжений в области 2 без учета разлома и данные WSMP. Несмотря на то, что данные имеют существенный разброс, траектории в целом соответствуют дискретным направлениям. На рис. 6 показана карта изолиний максимальных касательных напряжений в горизонтальной плоскости, из которой видно, что интенсивность ${{\tau }_{{\max }}}$ возрастает в направлении с запада на восток.
3.2.2. С учетом разлома. При расчетах с учетом разлома число точек коллокаций на разломе, в которых выполнялись условия непрерывности вектора напряжений, выбиралось равным половине числа данных, а именно 167. Таким образом, число уравнений, ответственных за непрерывность, совпадало с числом уравнений, использующих данные, т.е. суммарное число уравнений было равным 669, из которых только одно неоднородное, которое обеспечивает условие равенства единице среднего девиатора напряжений (функции D) по всем точкам данных. Число неизвестных коэффициентов в каждой подобласти варьировалось в диапазоне n = 1–4, при этом было установлено, что невязки изменяются незначительно и составляют порядка 17, в то время как числа возрастают или число возрастает от 318 при n = 1, далее 1535 при n = 2, 5687 при n = 3 и до 15 510 при n = 4. Оптимальное число коэффициентов достигается при n = 2, что обеспечивает наилучшую устойчивости к разбросу данных. При этом система вещественных уравнений имеет матрицу размерности 669 × 21.
Результаты расчетов для n = 2 показаны на рис. 7 и рис. 8. На рис. 7 представлены поля траекторий главных напряжений. Как видно из рисунка, траектории напряжений в нижней подобласти качественно совпадают с траекториями, показанными на рис. 5, где разлом не учитывался. Однако они существенно отличаются в верхней подобласти, где имеют другую кривизну, хотя и сохраняют тенденцию загибания на север. На рис. 8 приведены изолинии максимальных горизонтальных касательных напряжений ${{\tau }_{{\max }}}$. Интенсивность ${{\tau }_{{\max }}}$ в нижней подобласти меньше, чем в верхней, но сохраняет тенденцию возрастания в направлении с запада на восток, как и в случае, когда разлом не учитывался (см. рис. 6). В верхней подобласти изолинии практически параллельны разлому, около которого они имеют минимальное значение, а затем быстро возрастают в направлении на северо-восток, где остаются похожими на изолинии, приведенные на рис. 6.
Рис. 7.
Траектории главных напряжений в области 2, состоящей из двух связных подобластей, и данные WSMP.
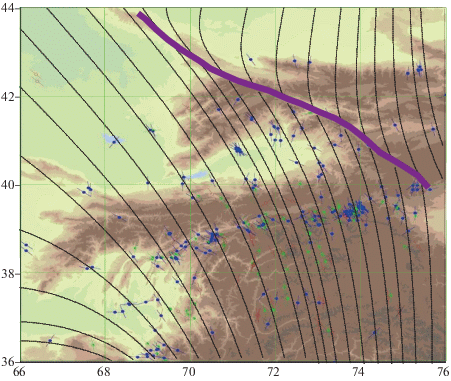
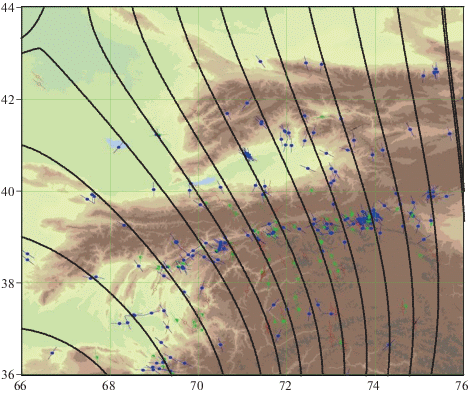
Рис. 8.
Изолинии главных касательных напряжений ${{\tau }_{{\max }}}$ в области 2, состоявшей из двух связных подобластей.
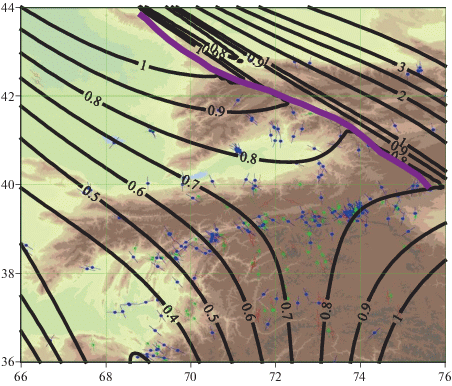
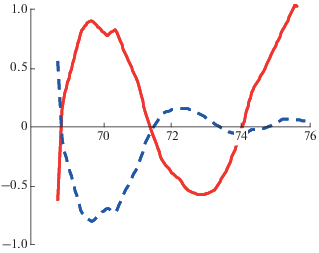
Таким образом, существенное изменение напряжений наблюдается только в окрестности разлома. При переходе через него нормальная и касательная компоненты напряжения остаются непрерывными, а латеральная (тангенциальная) компонента ${{\sigma }_{t}}$ терпит разрыв, также как и максимальное касательное напряжение и оба главных напряжения ${{S}_{H}},{{S}_{h}}$. Разрыв тангенциальной компоненты совпадает с разрывом удвоенных средних напряжений (поскольку нормальная компонента непрерывна), соответственно получаем $\left\langle {{{\sigma }_{t}}} \right\rangle = \left\langle {{{S}_{H}} + {{S}_{h}}} \right\rangle $. На рис. 9 показаны эпюры разрывов латеральных и максимальных касательных напряжений вдоль разлома в зависимости от долготы. Как отмечалось выше оба напряжения даны в безразмерной форме, что соответствует случаю a = 0 и b = 1.
4. ОБСУЖДЕНИЕ И ВЫВОДЫ
Полученные поля напряжений отличаются от результатов моделирования, проведенного [Атабековым, 2021], однако неплохо коррелируют с данными по направлениям главных осей напряжений. В работе И.У. Атабекова такие результаты не приводятся. В данном подходе нет необходимости использовать смещения или скорости смещений, что требуется при постановке краевой задачи, рассмотренной И.У. Атабековым. Для сравнения можно только рассмотреть карту интенсивности напряжений в Центральной Азии на глубине 20 км, приведенной И.У. Атабековым в его работе на рис. 3. Как видно, оно качественно отличается от полей максимальных касательных напряжений в горизонтальной плоскости, представленных в нашей работе на рис. 4, рис. 6 и рис. 8. Это может быть объяснено тем фактом, что приведенные нами поля максимальных касательных напряжений соответствуют случаю режима напряжений “Strike-Slip, SS” (т.е. скольжению в горизонтальной плоскости). Как следует из базы WSMP, таких данных достаточно много в рассматриваемом регионе, они показаны зеленым на рис. 1. В данном регионе больше данных режима “Thrust Faulting, TF” (надвиг), которые показаны синим цветом, и значительно меньше данных режима “Normal Faulting, NF” (сброс, красный цвет). На глубинах свыше 15 км число данных TF – 69, данных SS – 42 и данных NF – 10, а также 8 комбинированных.
Исходя из этих наблюдений в исследуемом регионе наиболее вероятными являются режимы TF и SS. Режим SS соответствует случаю, когда вертикальное главное напряжение является промежуточным между горизонтальными главными, $\left| {{{S}_{H}}} \right| > \left| {{{S}_{V}}} \right| > \left| {{{S}_{h}}} \right|$. В этом случае максимальные касательные есть ${{\tau }_{{\max }}}$, рассчитанные выше. Режим TF соответствует соотношению$\left| {{{S}_{H}}} \right| > \left| {{{S}_{V}}} \right| > \left| {{{S}_{h}}} \right|$, т.е. максимальные касательные напряжения ${{T}_{{\max }}}$ есть разница ${{T}_{{\max }}} = \tfrac{1}{2}\left( {\left| {{{S}_{H}}} \right| - \left| {{{S}_{V}}} \right|} \right)$. В рассматриваемой модели вертикальные главные напряжения являются постоянными на заданной глубине, поэтому с учетом (12) ${{T}_{{\max }}}$ можно представить к виде ${{T}_{{\max }}} = b\left( {p(z,\bar {z}) - \tau (z,\bar {z})} \right) + C$, где С = a + SV – произвольная постоянная. На рис. 10 приведены изолинии полей напряжений ${{T}_{{\max }}}$, рассчитанные без учета разлома (слева) и с учетом разлома (справа) при b = 1 и С = 0. Следует отметить, что поле напряжений на правой картинке качественно не противоречит результату И.У. Атабекова, если выбрать, например, b = 1 и С = –3, в этом случае области, где располагаются изолинии максимального сжатия в обоих моделях, неплохо коррелируют.
Рис. 10.
Максимальные касательные напряжения ${{T}_{{\max }}}$, обеспечивающие режим TF, слева рассчитанные без учета разлома, справа с учетом разлома.
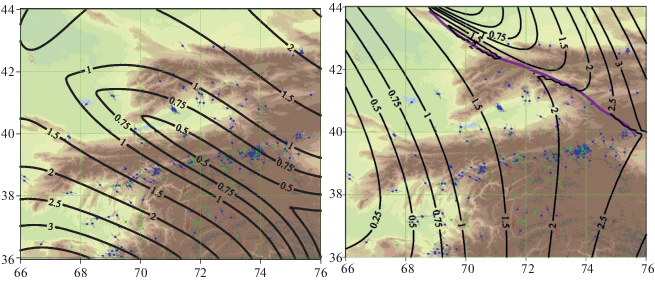
В отличие от работы И.У. Атабекова, данный подход позволяет напрямую учесть механическое влияние геологических разломов. Это, в частности, приводит к тому, что одна из компонент напряжений является разрывной при переходе через разлом, что существенно влияет на распределение напряжений вблизи разлома. Проведенные расчеты позволяют оценить величину разрыва напряжений вдоль разлома и, таким образом, определить опасные участки, по которым возможны скольжения в соответствии с режимами напряжений TF и SS.
Список литературы
Атабеков И.У. Опыт моделирования сейсмотектонического течения земной коры Центральной Азии // Физика Земли. 2021. № 1. С. 00–00.
Мухамедиев Ш.А., Галыбин А.Н., Белоусов Т.П. От дискретных ориентаций главных осей палеонапряжений к реконструкции полей палеонапряжений в упругой литосфере // Докл. РАН. 2005а. Т. 403. № 1. С. 101–105.
Мухамедиев Ш.А., Белоусов Т.П., Галыбин А.Н. Теоретическое моделирование полей упругих палеонапряжений по данным натурных индикаторов // Физика Земли. 2005б. № 11. С. 47–61.
Мухамедиев Ш.А., Галыбин А.Н. Где и как зародились разрывы землетрясений 26.12.04 и 28.03.05 у о. Суматра // Докл. РАН. 2006. Т. 406. № 1. С. 95–98. https://doi.org/10.1134/S1028334X06010132
Уломов В.И. Динамика земной коры Средней Азии и прогноз землетрясений. Ташкент: ФАН. 1974. 218 с.
Galybin A.N. Mukhamediev Sh.A. Determination of elastic stresses from discrete data on stress orientations // Int. J. Solids and Structures. 2004a. V. 41. № 18–19. P. 5125–5142. https://doi.org/10.1016/j.ijsolstr.2004.04.007
Galybin A.N. Mukhamediev Sh.A. On the problem of stress reconstruction from discrete orientations of principal stresses // Bollettino di Geofisica Teorica ed Applicata. An International J. Earth Sciences. 2004b. V. 45(1). P. 338–342.
Galybin A.N. On stress reconstruction in composite domains from discrete data on principal directions // WIT Transactions on Modelling and Simulation. 2009. V. 49. P. 35–43. https://doi.org/10.2495/BE090041
Haderka P., Galybin A.N., Mukhamediev Sh.A. Stress Field in Antarctic Tectonic Plate: Elastic and Plastic Models // WIT Transactions on Modelling and Simulation. 2009. V. 49. P. 257–267. https://doi.org/10.2495/BE090231
Heidbach O., Rajabi M., Reiter K., Ziegler M. WSM Team (2016): World Stress Map Database Release 2016. GFZ Data Services. https://doi.org/10.5880/WSM.2016.001
Irša J., Galybin A.N. On STEM modelling of tectonic stress fields in tsunamigenic regions // WIT Transactions on Modelling and Simulation. 2011. V. 52. P. 203–214. https://doi.org/10.2495/BE110181
Irša J., Galybin A.N. Stress Trajectories Element Method for stress determination from discrete data on principal directions // Engineering Analysis with Boundary Elements. 2010. V. 34 (5). P. 423–432. https://doi.org/10.1016/j.enganabound.2009.12.004
Mukhamediev Sh.A., Galybin A.N., Brady B.H.G. Determination of stress fields in elastic lithosphere by methods based on stress orientations // International J. Rock Mechanics and Mining Sciences. 2006. V. 43(1). P. 66–88. https://doi.org/10.1016/j.ijrmms.2005.04.008
Дополнительные материалы отсутствуют.