1. На главную
  2. Электронные версии
  3. Физика Земли
  4. № 2, 2021

Физика Земли, 2021, № 2, стр. 153-163

Связь мультифрактальных и энтропийных свойств сейсмического шума на Камчатке с неравномерностью вращения Земли

А. А. Любушин 1, *, Г. Н. Копылова 2, **, Ю. К. Серафимова 2, ***

1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия

2 Камчатский филиал Федерального исследовательского центра “Единая геофизическая служба Российской академии наук”
г. Петропавловск-Камчатский, Россия

* E-mail: lyubushin@yandex.ru
** E-mail: gala@emsd.ru
*** E-mail: yulka@emsd.ru

Поступила в редакцию 11.02.2020
После доработки 08.08.2020
Принята к публикации 08.08.2020

Полный текст (PDF)

Аннотация

Исследуется связь свойств сейсмического шума, непрерывно регистрируемого на сети из 21 широкополосной сейсмической станции на Камчатке в течение 9 лет наблюдений, 2011–2019 гг., с неравномерностью вращения Земли. Рассматриваются ежесуточные временные ряды медианных значений, вычисленных по всем станциям сети, трех параметров шума: ширины носителя мультифрактального спектра сингулярности, обобщенного показателя Херста и минимальной энтропии распределения квадратов ортогональных вейвлет-коэффициентов. Для выделения общих составляющих вариаций этих параметров вычислялась их адаптивная первая главная компонента в полугодовом скользящем временном окне. Вычислялся квадратичный спектр когерентности между первой главной компонентой свойств сейсмического шума и временным рядом длины дня в скользящем временном окне длиной 182 сут. Рассматривалась частотно-временная диаграмма спектра когерентности, которая характеризуется последовательностью всплесков когерентности, сконцентрированных в узкой частотной полосе с периодами от 11 до 14 сут. Оцениваются временные задержки между всплесками когерентности и выделением сейсмической энергии на Камчатке в скользящем временном окне длиной 5 лет.

Ключевые слова: сейсмический шум, мультифракталы, энтропия, метод главных компонент, когерентность, неравномерность вращения Земли.

ВВЕДЕНИЕ

Свойство неравномерного вращения Земли традиционно привлекается внимание геофизиков. В основном объяснение этого эффекта основано на оценках влияния процессов в атмосфере [Левицкий и др., 1995; Сидоренков, 2002; Zotov et al., 2017]. В то же время многие исследователи неоднократно указывали на связь неравномерности вращения Земли и сейсмичности [Губерман, 1976; Сасорова, Левин, 2017; Shanker et al., 2001; Levin et al., 2017]. При этом основное внимание уделялось возможному триггерному механизму воздействия вариаций скорости вращения планеты на сейсмический процесс [Bendick, Bilham, 2017]. Заметим, что при такой интерпретации возникает закономерный вопрос о воздействии атмосферных процессов (в том числе и вариаций климата) через неравномерность вращения Земли на сейсмический процесс.

В данной статье рассматривается связь между сейсмическим шумом на полуострове Камчатка, являющемся одним из наиболее сейсмически активных регионов планеты, с параметром LOD (length of day), представляющим последовательность значений длины суток и характеристику неравномерности вращения Земли. Связь свойств глобального сейсмического шума с временным рядом LOD ранее была исследована в работах [Lyubushin, 2020a; 2020b], где было показано, что середина 2003 г. является точкой перелома в трендах и корреляциях свойств глобального сейсмического шума. После 2003 г. тренды приобретают характер, присущий областям с увеличивающейся сейсмической опасностью. Заметим, что после Суматранского мегаземлетрясения 26.12.2004 г., М = 9 произошло резкое возрастание числа сильнейших землетрясений по всему миру. Новизна данного исследования заключается в применении ранее разработанного подхода к анализу данных Камчатки.

Сейсмический шум рассматривается как проявление внутренней жизни планеты и как важный “канал связи”, позволяющий исследовать процессы в литосфере, в том числе предваряющие сильные землетрясения [Любушин, 2007; 2009; 2014; Соболев, 2014; Lyubushin, 2018]. Прогностические свойства сейсмического шума на Камчатке были ранее рассмотрены в работах [Касимова и др. 2018; Любушин и др., 2015].

ИСХОДНЫЕ ДАННЫЕ

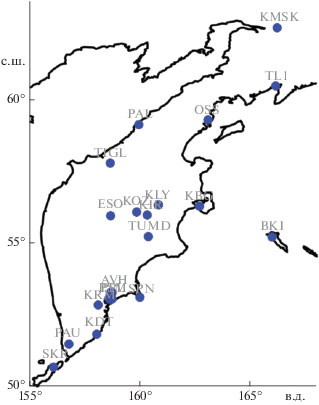
На территории Камчатского края имеется сеть цифровых широкополосных сейсмических станций, данные с которых в режиме реального времени поступают в Информационно-обрабатывающий центр КФ ФИЦ ЕГС РАН по спутниковым и другим каналам связи [Чебров, 2013; Чебров и др., 2013]. В качестве источников сейсмических данных в работе использовались записи вертикальных компонент движений грунта на канале BHZ с частотой оцифровки 100 Гц c 01.01.2011 по 31.12.2019 гг., полученные на 21 широкополосной сейсмической станции Геофизической службы РАН, расположенных на территории Камчатского края и о-ва Парамушир, Курильские о-ва (рис. 1).

Рис. 1.

Кружками показаны положения 21-й сейсмической станции на Камчатке. Рядом с каждой станцией указаны их сокращенные идентификаторы.

Для создания 1-минутных временных рядов низкочастотного шума, зарегистрированного на каждой станции, вычислялись средние значения исходных записей в последовательных интервалах времени длиной 6000 отсчетов. Получаемые 1-минутные временные ряды для всех 21 станции хранятся в пополняемой базе данных на сервере КФ ФИЦ ЕГС РАН с доступом по локальной сети. Типы широкополосных сейсмических датчиков – CMG-6TD, CMG-3TВ, KS2000, информация о них была приведена в статьях [Касимова и др., 2018; Любушин и др., 2015].

Важным вопросом дискуссионного характера в применении используемой методики для исследования свойств фоновых низкочастотных шумов является то, что формально частотный диапазон сигналов, записанных сейсмометрическими датчиками, не включает в себя периоды от 2 до примерно 1000 мин, которые фактически исследуются после перехода к шагу по времени 1 мин на временных интервалах длиной одни сутки. Возникает закономерный вопрос о правомерности перехода в столь низкочастотную область записей сейсмического сигнала.

Здесь мы исходим из предположения, что аппаратурные ограничения по низкой частоте сигнала приводятся исключительно для корректного отображения движений грунта при отдельных землетрясениях и количественного определения их параметров. Следует заметить, что разработчиками широкополосной сейсмометрической аппаратуры не рассматривались задачи использования непрерывно регистрируемых сейсмических записей в более широком диапазоне частот, превышающем частоты сигналов от землетрясений, и не предполагалось, что сейсмометрические датчики можно бы было использовать также, как обычный наклономер, т.е. регистрировать изменения сигнала в приливной полосе частот. Мы полагаем, что при решении задач геофизического мониторинга имеется принципиальная возможность более широкого применения широкополосной сейсмометрической аппаратуры, превышающая формальные ограничения на рабочую полосу частот, которая традиционно используется при изучении отдельных землетрясений.

Ранее в работах авторов [Касимова и др., 2018; Любушин и др., 2015] этот вопрос уже обсуждался. В частности, были приведены оценки спектров мощности сейсмических записей при переходе к шагу по времени 1 ч, то есть при существенно более глубоком усреднении, чем используется для анализа в данной статье, и было продемонстрировано, что эти спектры содержат стандартные приливные гармоники, то есть фактически широкополосные сейсмометры могут работать как наклономеры в частотном диапазоне, значительно выходящим за их формальные границы.

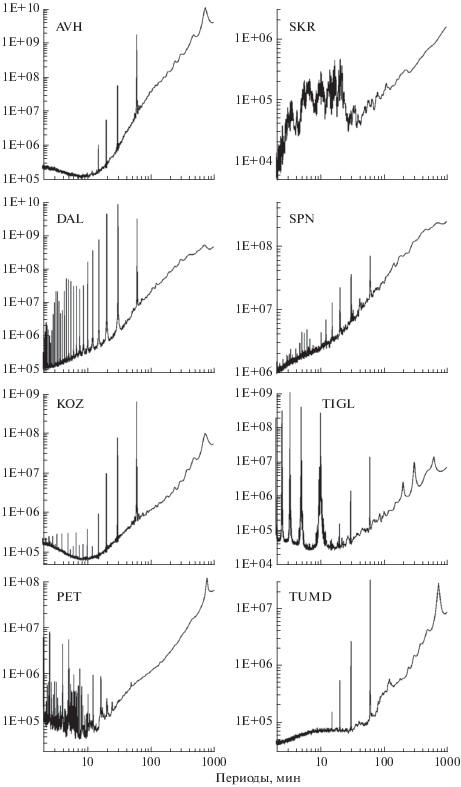
Возвращаясь к этому вопросу в настоящей статье, оценим спектры мощности записей после перехода к шагу по времени 1 мин в частотном диапазоне, являющемся “промежуточным” между сейсмологическим и наклономерным, с периодами от 2 до 1000 мин. Известно, что этот частотный диапазон содержит спектральные пики, соответствующие собственным колебаниям Земли, постоянно возбуждаемым землетрясениями в фоновом режиме [Милюков и др., 2015]. Возникает вопрос о том, присутствуют ли эти пики в спектре сейсмических записей после перехода к шагу по времени 1 мин? На рис. 2 представлены оценки спектров мощности для 8 сейсмических станций. Видно, что почти все они содержат набор монохроматических гармоник, соответствующих различным модам собственных колебаний Земли, возбуждаемых в результате сейсмических событий, в частности самую низкочастотную гармонику собственных колебаний Земли с периодом, близким к 60 мин.

Рис. 2.

Графики оценок спектров мощности сейсмических записей после перехода к шагу по времени 1 мин для 8-ми станций сети в частотном диапазоне с периодами от 2 до 1000 мин.

Таким образом, мы полагаем, что переход в низкочастотную часть спектра путем усреднения сейсмических записей и приведения их к шагу по времени 1 мин, не влечет за собой полное уничтожение полезной информации, содержащейся в записях. Более того, именно переход в низкочастотную часть спектра позволяет уйти от большей части помех антропогенного характера и исследовать прогностические свойства собственного шума Земли. Этот переход многократно использовался ранее в работах [Любушин, 2007; 2009; 2014; Lyubushin, 2010; 2012; 2013; 2014; 2018; 2020a; 2020b] при анализе непрерывных записей сейсмического шума широкополосных сетей.

ИСПОЛЬЗУЕМЫЕ СВОЙСТВА СЕЙСМИЧЕСКОГО ШУМА

Ниже дается описание 3 безразмерных свойств сейсмического шума, которые вычислялись для вертикальных колебаний после перехода к шагу по времени 1 мин для каждой станции в последовательных окнах длиной 1 сут (1440 минутных отсчетов). Перед вычислением этих свойств из волновых форм сейсмического шума в каждом временном окне удалялись тренды ортогональным полиномом 8-го порядка. Удаление трендов направлено на подавление влияния приливных и термических деформаций земной коры в вариациях сейсмического шума и является необходимой процедурой при исследовании его статистических характеристик. Использование ортогонального полинома обеспечивает устойчивость оценки значений тренда в точках отсчетов. При этом порядок полинома (8-й) был выбран в результате численных экспериментов как наименьший порядок, позволяющий гарантировано устранять суточные и полусуточные вариации на интервалах времени длиной одни сутки.

Мультифрактальные параметры $\Delta \alpha $ и $\alpha {\text{*}}$

Рассмотрим некоторое случайное колебание $x(t)$ на интервале времени $[t - {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2},\,\,t + {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2}]$ длиной $\delta $ с центром во временной точке $t$. Рассмотрим размах $\mu (t,\delta )$ случайного колебания на этом интервале, то есть разницу между максимальным и минимальным значениями:

(1)
$\mu (t,\delta ) = \mathop {\max }\limits_{t - {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2} \leqslant \,s\, \leqslant \,t + \,{\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2}} x(s)\,\,\,\, - \,\,\,\mathop {\min }\limits_{t - {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2} \leqslant \,s \leqslant \,t + {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2}} x(s).$

Если устремить $\delta \to 0$, то $\mu (t,\delta )$ будет также стремиться к нулю, но здесь важна скорость этого убывания. Если скорость определяется законом ${{\delta }^{{\;h(t)}}}$: $\mu (t,\delta )$ ~ ${{\delta }^{{h(t)}}}$ при $\delta \to 0$, или если существует предел $h(t) = \mathop {\lim }\limits_{\delta \to 0} \frac{{\lg (\mu (t,\delta ))}}{{\lg (\delta )}}$, то величина $h(t)$ называется экспонентой Гельдера–Липшица. Если величина $h(t)$ не зависит от момента времени $t$: $h(t) = {\text{const}} = H$, то случайное колебание $x(t)$ называется монофрактальным, а величина $H$ – экспонентой Херста. Если же экспоненты Гельдера–Липшица $h(t)$ существенно различаются для разных моментов времени $t$, то случайное колебание называется мультифракталом и для него можно определить понятие спектра сингулярности $F(\alpha )$ [Feder, 1988]. Для этого мысленно выделим множество $C(\alpha )$ таких моментов времени $t$, которые имеют одно и то же значение $\alpha $ экспоненты Гельдера–Липшица: $h(t) = \alpha $. Множества $C(\alpha )$ существуют, т.е. содержат какие-то элементы и не являются пустыми множествами не для всех значений $\alpha $. То есть существуют некоторые минимальное ${{\alpha }_{{\min }}}$ и максимальное ${{\alpha }_{{\max }}}$, такие, что лишь для ${{\alpha }_{{\min }}} < \alpha < {{\alpha }_{{\max }}}$ множества $C(\alpha )$ непустые. Мультифрактальный спектр сингулярности $F(\alpha )$ – это фрактальная размерность множества точек $C(\alpha )$. Параметр $\Delta \alpha = {{\alpha }_{{\max }}} - {{\alpha }_{{\min }}}$, называемый шириной носителя спектра сингулярности, представляется наиболее важной мультифрактальной характеристикой. Кроме того, значительный интерес представляет аргумент $\alpha {\text{*}}$, доставляющий максимум спектру сингулярности: $F(\alpha *) = \mathop {\max }\limits_{{{\alpha }_{{\max }}} \leqslant \alpha \leqslant {{\alpha }_{{\min }}}} F(\alpha )$, называемый обобщенным показателем Херста. Максимум спектра сингулярности не может превосходить 1 – размерности вмещающего множества или оси времени, $0 < F(\alpha *) \leqslant 1$, обычно $F(\alpha *) = 1$. Заметим, что для монофрактального сигнала $\Delta \alpha = 0$, $\alpha * = H$. По своему определению $\Delta \alpha $ является мерой разнообразия случайного поведения сигнала, которая отражает число экспонент Гельдера–Липшица. В простом монофрактальном случайном сигнале есть только один показатель Гельдера–Липшица, он же показатель Херста. Поэтому уменьшение $\Delta \alpha $ является признаком подавления определенных степеней свободы системы, генерирующей изучаемый сигнал, и уменьшения их числа. Используемый метод вычисления параметров $\Delta \alpha $, $\alpha {\text{*}}$ подробно изложен в работах [Любушин, 2007; 2009; 2014; Lyubushin, 2010; 2018].

Минимальная нормализованная энтропия вейвлет-коэффициентов $En$

Пусть $x(t)$ – конечная выборка некоторого случайного сигнала, $t = 1,...,N$ – индекс, нумерующий последовательные отсчеты (дискретное время). Определим нормализованную энтропию конечной выборки формулой:

(2)
$\begin{gathered} En = - \sum\limits_{k = 1}^N {{{p}_{k}}{{\lg ({{p}_{k}})} \mathord{\left/ {\vphantom {{\lg ({{p}_{k}})} {\lg (N)}}} \right. \kern-0em} {\lg (N)}}} , \\ {{p}_{k}} = {{c_{k}^{2}} \mathord{\left/ {\vphantom {{c_{k}^{2}} {\sum\limits_{j = 1}^N {c_{j}^{2}} }}} \right. \kern-0em} {\sum\limits_{j = 1}^N {c_{j}^{2}} }},\,\,\,\,0 \leqslant En \leqslant 1. \\ \end{gathered} $

Здесь ${{c}_{k}},\;k = 1,N$ – коэффициенты ортогонального вейвлет-разложения с некоторым базисом. Ниже использовались 17 ортогональных вейвлетов Добеши: 10 обычных базисов с минимальным носителем с числом обнуляемых моментов от 1 до 10 и 7 так называемых симлетов Добеши [Mallat, 1999], с числом обнуляемых моментов от 4 до 10. Для каждого из базисов вычислялась нормализованная энтропия распределения квадратов коэффициентов (2) и находился базис, обеспечивающий минимум величине (2). Заметим, что в силу ортогональности вейвлет-преобразования сумма квадратов коэффициентов равна дисперсии (энергии) сигнала $x(t)$. Таким образом, величина (2) вычисляет энтропию распределения энергии колебаний на различных частотных и временных масштабах.

Статистики $\Delta \alpha $, $\alpha {\text{*}}$ и $En$ использовались в работах [Любушин, 2007; 2009; 2014; Lyubushin, 2010; 2012; 2013; 2014; 2018; 2020c] при исследовании свойств синхронизации глобального поля сейсмических шумов и прогностических свойств сейсмического шума на Японских островах и Калифорнии.

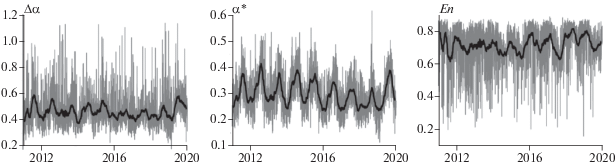
Для каждого свойства и для каждых суток вычислялись медианные значения свойств $(En,\Delta \alpha ,\alpha *)$ по всем работоспособным станциям. В результате были получены 3 временных ряда с шагом по времени 1 сут в течение 2011–2019 гг., графики которых представлены на рис. 3.

Рис. 3.

Графики ежесуточных медианных значений 3-х безразмерных параметров сейсмического шума на Камчатке; толстыми линиями представлены значения скользящих средних в окне длиной 57 сут.

АДАПТИВНЫЙ МЕТОД ГЛАВНЫХ КОМПОНЕНТ

Существует необходимость в агрегировании временных рядов $(En,\Delta \alpha ,\alpha *)$ в один временной ряд, который несет наиболее общие свойства из начального набора параметров свойств шума. Мы использовали здесь модификацию популярного метода главных компонентов [Айвазян и др., 1989; Jolliffe, 1986], предложенную в работе [Lyubushin, 2018]. Пусть $P(t) = {{({{P}_{1}}(t),...,{{P}_{m}}(t))}^{T}}$, $t = 0,\,\,1,...$ – несколько временных рядов суммарной размерности $m$. В нашем случае $m = 3$. Пусть $L$ – число отсчетов в пределах временного окна, которое движется слева направо с минимальным взаимным сдвигом 1, который мы назовем “окном адаптации”. Пусть $s$ – номер отсчета, соответствующего правому концу движущегося временного окна. Это означает, что временное окно содержит выборки с временными индексами, которые подчиняются условию $s - L + 1 \leqslant t \leqslant s$. Вычислим корреляционную матрицу $\Phi (s)$ размера $m \times m$ в каждом временном окне после нормализации компонентов временных рядов:

(5)
$\begin{gathered} \Phi (s) = \left( {\varphi _{{ab}}^{{(s)}}} \right),\,\,\,\,\varphi _{{ab}}^{{(s)}} = \sum\limits_{t = s - L + 1}^s {{{q_{a}^{{(s)}}(t)q_{b}^{{(s)}}(t)} \mathord{\left/ {\vphantom {{q_{a}^{{(s)}}(t)q_{b}^{{(s)}}(t)} L}} \right. \kern-0em} L},} \\ a,b = 1,...,m, \\ \end{gathered} $
где:

(6)
$\begin{gathered} q_{a}^{{(s)}}(t) = {{({{P}_{a}}(t) - \bar {P}_{a}^{{(s)}})} \mathord{\left/ {\vphantom {{({{P}_{a}}(t) - \bar {P}_{a}^{{(s)}})} {\sigma _{a}^{{(s)}}}}} \right. \kern-0em} {\sigma _{a}^{{(s)}}}}, \\ \bar {P}_{a}^{{(s)}} = \sum\limits_{t = s - L + 1}^s {{{{{P}_{a}}(t)} \mathord{\left/ {\vphantom {{{{P}_{a}}(t)} L}} \right. \kern-0em} L},} \\ {{\left( {\sigma _{a}^{{(s)}}} \right)}^{2}} = \sum\limits_{t = s - L + 1}^s {({{P}_{a}}(t) - {{\bar {P}_{a}^{{(s)}}{{)}^{2}}} \mathord{\left/ {\vphantom {{\bar {P}_{a}^{{(s)}}{{)}^{2}}} {(L - 1)}}} \right. \kern-0em} {(L - 1)}}} , \\ a = 1,...,m. \\ \end{gathered} $

Первая главная компонента ${{\psi }^{{(s)}}}(t)$ вычисляется по формуле:

(7)
${{\psi }^{{(s)}}}(t) = \sum\limits_{\alpha = 1}^m {\theta _{a}^{{(s)}}q_{a}^{{(s)}}(t)} .$

Здесь $m$-мерный вектор ${{\theta }^{{(s)}}} = {{(\theta _{{\;1}}^{{(s)}},...,\theta _{{\;m}}^{{(s)}})}^{T}}$ является собственным вектором корреляционной матрицы $\Phi (s)$, соответствующим максимальному собственному числу. Определим скалярный временной ряд адаптивной первой главной компоненты $\psi (t)$ в скользящем окне длиной $L$ отсчетов по формуле:

(8)
$\psi (t) = \left\{ \begin{gathered} {{\psi }^{{(L - 1)}}}(t),\,\,\,\,{\text{ }}0 \leqslant t \leqslant (L - 1) \hfill \\ {{\psi }^{{(t)}}}(t),\,\,\,\,t \geqslant L \hfill \\ \end{gathered} \right..$

Операции, представленные формулами (5)–(7), осуществляются независимо в каждом временном окне длиной $L$ отсчетов. Таким образом, в пределах 1-го временного окна адаптации временной ряд $\psi (t)$ состоит из значений, рассчитанных по (7), тогда как для всех последующих временных индексов равен значению (7), соответствующему наиболее правому концу временного окна, то есть за пределами 1-го окна адаптации $\psi (t)$ зависит только от прошлых значений $P(t)$.

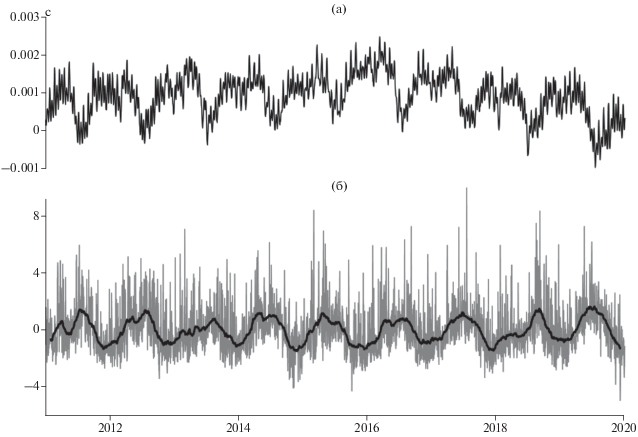
На рис. 4 представлены графики временного ряда длины дня (LOD – length of day), характеризующего неравномерность вращения Земли и главной компоненты ежесуточных временных рядов 3 свойств $(En,\Delta \alpha ,\alpha *)$ в скользящем окне адаптации длиной $L = 182$ сут (полгода). Данные о длине суток взяты из базы данных International Earth rotation and Reference systems Service (IERS) по адресу https://hpiers.obspm.fr/iers/eop/eopc04/eopc04.62-now.

Рис. 4.

(а) – Временной ряд длины суток (LOD); (б) – первая главная компонента 3 ежесуточных медианных значений сейсмического шума на Камчатке, вычисленная в окне длиной 182 сут; толстой линией представлены значения скользящего среднего в окне длиной 57 сут.

ОЦЕНКА СПЕКТРА КОГЕРЕНТНОСТИ

Для анализа связи между свойствами сейсмического шума и неравномерностью вращения Земли воспользуемся аппаратом вычисления спектра когерентности между временным рядом LOD и первой главной компонентой.

На рис. 5 представлена частотно-временная диаграмма эволюции квадратичного спектра когерентности между 2 временными рядами, графики которых представлены на рис. 3. Оценка была произведена в скользящем временном окне длиной 182 сут со смещением 5 сут с использованием 2-мерной векторной авторегрессионной модели 5-го порядка [Marple, 1987] с предварительным удалением линейных трендов и переходом к приращениям. Этот подход уже был использован в работах [Lyubushin, 2020a; 2020b] при анализе трендов свойств глобального сейсмического шума и их связей с неравномерностью вращения Земли. Из рис. 5 видно, что всплески когерентности сосредоточены в узкой частотной полосе с периодами от 11 до 14 сут.

Рис. 5.

Частотно-временная диаграмма квадратичного спектра когерентности между LOD и первой главной компонентой 3-х свойств сейсмического шума в скользящем временном окне длиной 182 сут со смещением 5 сут.

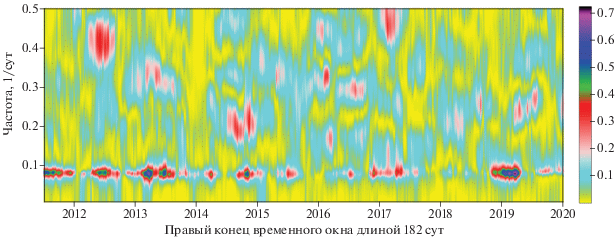
На рис. 6 представлены графики максимумов всплесков когерентности в каждом временном окне для периодов от 11 до 14 сут и график логарифма энергии (джоули), выделившейся в результате сейсмических событий в Камчатском регионе также в скользящем временном окне длиной 182 сут со смещением 5 сут.

Рис. 6.

(а) – Максимум квадрата когерентности между LOD и первой главной компонентой 3-х ежесуточных свойств сейсмического шума; (б) – десятичный логарифм энергии (джоули), выделившейся в результате сейсмических событий в прямоугольной области 50°−60° с.ш. и 153°−170° в.д. (https://www.usgs.gov/; http://glob.emsd.ru/).

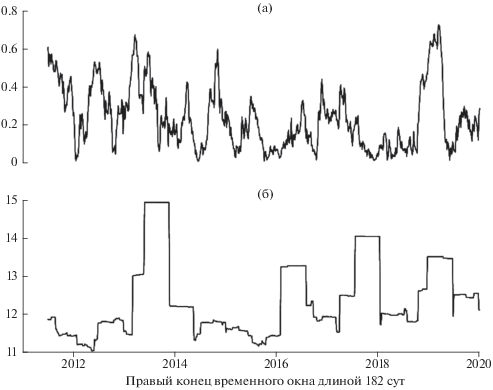
На рис. 6 визуально заметно, что кривая логарифма выделившейся энергии часто запаздывает относительно кривой максимумов спектра когерентности при их оценивании в скользящем временном окне длиной 182 сут со смещением 5 сут. Оценим количественно это смещение путем вычисления кросскорреляционной функции, график которой представлен на рис. 7.

Рис. 7.

Коэффициенты корреляции между логарифмом энергии, выделившейся в результате сейсмических событий в Камчатском регионе в скользящем окне длиной 182 сут со смещением 5 сут, и максимальным значением квадратичного спектра когерентности между LOD и первой главной компонентой 3-х ежесуточных медианных свойств сейсмического шума.

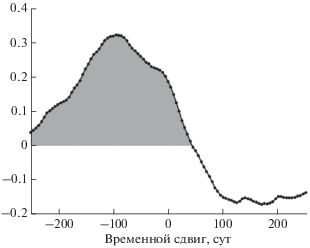
На рис. 7 значения кросскорреляционной функции берутся с временным сдвигом от –250 до 250 сут (±50 отсчетов с шагом по времени 5 сут). Максимум коэффициента корреляции между величинами максимальной когерентности вариаций LOD и сейсмического шума приходится на 95 сут (19 сдвигов по времени), показывая, что “в среднем” эффект увеличения их когерентности опережает выделение сейсмической энергии в Камчатском регионе.

Из графиков на рис. 6 заметно, что временной сдвиг между сравниваемыми кривыми является не постоянным, а может изменяться. Дополним среднюю оценку взаимной корреляции, представленную на рис. 7, аналогичной оценкой в скользящем временном окне. Следует отметить, что в наших оценках уже присутствует временное окно длиной 182 сут. Назовем его “коротким”. Теперь же мы хотим получить оценки взаимной корреляции в “длинном” временном окне, которое состоит из некоторого числа “коротких” окон. При выборе “длинного” окна следует учитывать, что когерентности получены путем оценки в “коротких” временных окнах длиной 182 сут, взятых со смещением 5 суток. Таким образом, если взять смежные $L$-значений когерентностей, то размерная длина “длинного” временного окна будет равна $N = 182 + (L - 1) \times 5$ сут. При выборе $L = 330$ значение $N = 1827$ сут. Число дней в 5 смежных годах равно 1826 или 1827 сут с учетом того, что в каждом интервале длиной 5 лет либо один, либо два года являются високосными. Поэтому выбор $L = 330$ обеспечивает длину временного окна 5 лет с большой точностью.

На рис. 8а представлен график изменения максимальных значений коэффициента корреляции между когерентностями и логарифмами выделившейся энергии в скользящем временном окне длиной 330 смежных значений (примерно 5 лет) с минимальным смещением в одно значение (5 сут). Максимумы берутся по взаимным временным сдвигам внутри “большого окна” ±50 отсчетов с шагом по времени 5 сут.

Рис. 8.

(а) – График максимального по модулю коэффициента корреляции между когерентностями и логарифмами выделившейся энергии в окне длиной 5 лет при возможных сдвигах от –250 до 250 сут; (б) – график сдвига в сутках внутри временного окна длиной 5 лет, реализующего максимальные значения модуля коэффициента корреляции, заштрихованы отрицательные значения временного сдвига, соответствующие опережению всплесками когерентности выделению сейсмической энергии.

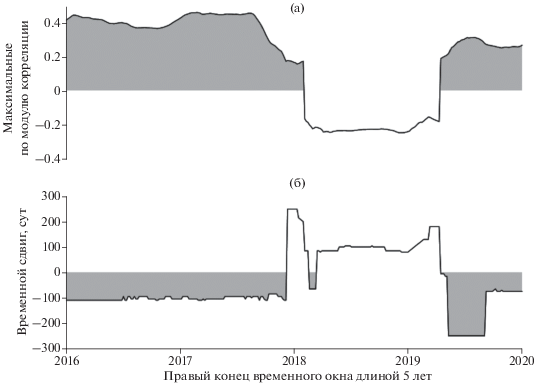
Что же касается оценки временного сдвига, реализующего максимум модуля взаимной корреляции, то она представлена на графике на рис. 8б. Из этого графика видно, что в течение большей части рассматриваемого интервала временной сдвиг является отрицательным, что соответствует опережению всплесками когерентности выделения сейсмической энергии. Следует отметить, что медианное значение оптимальных временных сдвигов на рис. 8б равно 95 сут, то есть равно значению, реализующему максимум средней взаимной корреляции на рис. 7.

ВЫВОДЫ

Разработан метод, позволяющий исследовать частотно-временную связь между набором медианных свойств сейсмического шума, регистрируемого сетями сейсмических станций в заданном регионе и временным рядом длины суток, характеризующим неравномерность вращения Земли. В результате применения метода к данным непрерывной регистрации в течение 2011–2019 гг. сейсмического шума на сети станций на Камчатке, получен временной ряд всплесков когерентности при оценке в скользящем временном окне длиной полгода. Кросскорреляционный анализ вариаций максимумов когерентности и логарифма энергии, выделившейся в результате сейсмических событий в Камчатском регионе, во временном окне той же длины обнаружил преимущественное запаздывание интенсивности сейсмического процесса относительно изменений когерентности. Этот факт интерпретируется как проявление триггерного воздействия неравномерности вращения Земли на сейсмический процесс.

Список литературы

  1. Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности. М.: Финансы и статистика. 1989.

  2. Губерман Ш.А. D-волны и неравномерность вращения Земли // Докл. АН СССР. 1976. Т. 230. № 4. С. 811–814.

  3. Касимова В.А., Копылова Г.Н., Любушин А.А. Вариации параметров фонового сейсмического шума на стадиях подготовки сильных землетрясений в Камчатским регионе // Физика Земли. 2018. № 2. С. 269–283.

  4. Левицкий Л.С., Рыхлова Л.В., Сидоренков Н.С. Южное колебание Эль-Ниньо и неравномерность вращения Земли // Астрон. журн. 1995. Т. 72. Вып. 2. С. 272–276.

  5. Любушин А.А. Анализ данных систем геофизического и экологического мониторинга. М.: Наука. 2007. 228 с.

  6. Любушин А.А. Тренды и ритмы синхронизации мультифрактальных параметров поля низкочастотных микросейсм // Физика Земли. 2009. № 5. С. 15–28.

  7. Любушин А.А. Анализ когерентности глобального сейсмического шума, 1997–2012 // Физика Земли. 2014. № 3. С. 18–27.

  8. Любушин А.А., Копылова Г.Н., Касимова В.А., Таранова Л.Н. О свойствах поля низкочастотных шумов, зарегистрированных на Камчатской сети широкополосных сейсмических станций // Вестник КРАУНЦ. Науки о Земле. 2015. № 2. Вып. 26. С. 20–36. http://www.kscnet.ru/kraesc/2015/2015_26/art3.pdf

  9. Милюков В.К., Виноградов М.П., Миронов А.П., Мясников А.В., Перелыгин Н.А. Собственные колебания Земли, возбужденные тремя крупнейшими землетрясениями последнего десятилетия, по деформационным наблюдениям // Физика Земли. 2015. № 2. С. 21–36.

  10. Сасорова Е.В., Левин Б.В. О связи вариаций скорости вращения Земли и ее сейсмической активности. Вступление Земли в новую фазу уменьшения угловой скорости вращения // Вестник КРАУНЦ. Физ.-мат. науки. 2017. № 4(20). С. 91–100. https://doi.org/10.18454/2079-6641-2017-20-4-91-100

  11. Сидоренков Н.С. Атмосферные процессы и вращение Земли. СПб.: Гидрометеоиздат. 2002. 366 с.

  12. Соболев Г.А. Сейсмический шум. М.: ООО “Наука и образование”. 2014. 272 с.

  13. Чебров В.Н. Региональная система сейсмического мониторинга. Проблемы комплексного геофизического мониторинга Дальнего Востока России. Тр. Четвертой научно-техн. конф. Обнинск: ГС РАН. 2013. С. 8–15.

  14. Чебров В.Н., Дрознин Д.В., Кугаенко Ю.А. и др. Система детальных сейсмологических наблюдений на Камчатке в 2011 г. // Вулканология и сейсмология. 2013. № 1. С. 18–40.

  15. Bendick R., Bilham R. Do weak global stresses synchronize earthquakes? // Geophys. Res. Lett. 2017. V. 44. P. 8320–8327. https://doi.org/10.1002/2017GL074934

  16. Feder J. Fractals. London, New York: Plenum Press. 1988. (Русский перевод: Федер Е. Фракталы. М.: Мир. 1991. 254 с.)

  17. Levin B.W., Sasorova E.V., Steblov G.M., Domanski A.V., Prytkov A.S., Tsyba E.N. Variations of the Earth’s rotation rate and cyclic processes in geodynamics // Geodesy and Geodynamics. 2017. № 8. P. 206–212. https://doi.org/10.1016/j.geog.2017.03.007

  18. Lyubushin A.A. Multifractal Parameters of Low-Frequency Microseisms In: Geoplanet: Earth and Planetary Sciences, Synchronization and Triggering: from Fracture to Earthquake Processes / V. de Rubeis, Z. Czechowski and R. Teisseyre (Eds.). Berlin: Springer. 2010. P. 253–272. https://doi.org/10.1007/978-3-642-12300-9_15

  19. Lyubushin A.A. Prognostic Properties of Low-Frequency Seismic Noise // Nat. Sci. 2012. V. 4. P. 659–666. https://doi.org/10.4236/ns.2012.428087

  20. Lyubushin A.A. How Soon Would the Next Mega-Earthquake Occur in Japan? // Nat. Sci. 2013. № 5. P. 1–7. https://doi.org/10.4236/ns.2013.58A1001

  21. Lyubushin A.A. Dynamic Estimate of Seismic Danger Based on Multifractal Properties of Low-Frequency Seismic Noise // Nat. Hazards. 2014. V. 70. P. 471–483. https://doi.org/10.1007/s11069-013-0823-7

  22. Lyubushin A. Synchronization of Geophysical Fields Fluctuations. Complexity of Seismic Time Series. Measurement and Applications / T.Chelidze, L. Telesca, F. Vallianatos (Eds.). Oxford, Cambridge, Amsterdam: Elsevier. 2018. Ch. 6. P. 161–197. https://doi.org/10.1016/B978-0-12-813138-1.00006-7

  23. Lyubushin A.A. Trends of Global Seismic Noise Properties in Connection to Irregularity of Earth’s Rotation // Pure Appl. Geophys. 2020a. V. 177. № 2. P. 621–636. https://doi.org/10.1007/s00024-019-02331-z

  24. Lyubushin A. Connection of Seismic Noise Properties in Japan and California with Irregularity of Earth’s Rotation // Pure Appl. Geophys. 2020b. V. 177. P. 4677–4689.https://doi.org/10.1007/s00024-020-02526-9

  25. Lyubushin A.A. Seismic Noise Wavelet-Based Entropy in Southern California // J. Seismology. 2020c. https://doi.org/10.1007/s10950-020-09950-3

  26. Mallat S.A. Wavelet Tour of Signal Processing. Second edition. Academic Press. San Diego, London, Boston, New York, Sydney, Tokyo, Toronto. 1999. (Русский перевод: Малла С. Вейвлеты в обработке сигналов. М.: Мир. 2005).

  27. Marple S.L. Digital spectral analysis with applications. Prentice-Hall, Inc., Englewood Cliffs, New Jersey. 1987. (Русский перевод: Марпл С.Л. Цифровой спектральный анализ и его приложения. М.: Мир. 1990. 584 с.).

  28. Jolliffe I.T. Principal Component Analysis. Springer-Verlag. 1986. https://doi.org/10.1007/b98835

  29. Shanker D., Kapur N., Singh V. On the spatio temporal distribution of global seismicity and rotation of the Earth – A review // Acta Geod. Geoph. Hung. 2001. V. 36. P. 175–187. https://doi.org/10.1556/AGeod.36.2001.2.5

  30. Zotov L., Sidorenkov N.S., Bizouard C., Shum C.K., Shen W. Multichannel singular spectrum analysis of the axial atmospheric angular momentum // Geodesy and Geodynamics. 2017. V. 8. № 6. P. 433–442. https://doi.org/10.1016/j.geog.2017.02.010

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал