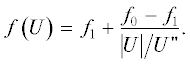Физика Земли, 2021, № 5, стр. 146-154

ВВЕДЕНИЕ

Движение крупных блоков земной коры определяется силами, действующими между блоками. В длинном списке механизмов, определяющих эти силы, одним из главных является сухое трение горных пород. В широком смысле сухое трение можно определить как зависимость сопротивления сдвигу по границе блоков от давления окружающей среды. Для медленных движений в горных породах применимо классическое определение коэффициента трения как коэффициента пропорциональности между предельным сдвиговым напряжением и нормальным напряжением на площадке скольжения. Для описания движения при высоких скоростях деформации часто необходимо предположить, что сила сухого трения зависит от скорости сдвига и, во многих случаях, от амплитуды сдвига бортов разлома. Наиболее известные примеры крупномасштабных движений с динамически уменьшающимся трением дают дальнопробежные лавины [Adushkin, 2006] и коллапсирующие в поле тяжести переходные полости крупных ударных кратеров [Melosh, Ivanov, 1999]. В этих случаях применяются феноменологические модели динамического снижения сухого трения без детального описания условий на площадке скольжения. Эти модели помогают оценить эффективное сопротивление скоростного деформирования через псевдовязкость, описывающую снижение сопротивления сдвигу в условиях сложного динамического процесса.

Такие модели удобны в моделировании, но требуют калибровки по результатам наблюдений. Хотя феноменологические модели снижения трения позволяют воспроизвести в численной модели многие стороны динамических процессов, необходимо продолжать поиски возможности обосновать эти модели из первых принципов и лабораторных экспериментальных данных. В данной публикации мы рассматриваем процесс калибровки одной из моделей и попытку ввести в модель некоторые результаты прямых экспериментов.

МОДЕЛЬ АКУСТИЧЕСКОЙ ФЛЮИДИЗАЦИИ

Изначально модель снижения сухого трения была предложена для объяснения аномально низкого теплового потока в области активного разлома Сан-Андреас (США), который свидетельствовал о низком уровне сдвиговых напряжений, препятствующих смещению бортов разлома – порядка 10 МРа по изначальным оценкам [Brune et al., 1969] вместо ожидаемого уровня ~100 МПа для обычного коэффициента сухого трения [Rice, 1992]. Даже бурение через разлом не дало прямого ответа на этот вопрос [Zoback et al., 2010]. Интересная альтернатива объяснения низкого уровня сдвиговых напряжений была предложена в работе [Melosh, 1979], где периодические колебания среднего давления в материале, заполняющем разлом, предполагались достаточно сильными, чтобы сдвиговая прочность на короткий промежуток времени оказывалась меньше сдвиговых напряжений. То есть в отличие от гипотезы “малопрочного материала” в работе [Rice, 1992] в модели из работы [Melosh, 1979] предполагалось динамическое снижение эффективного коэффициента трения за счет колебаний среднего давления. Этот эффект получил название “акустической флюидизации” (АФ-модель). В дальнейшем автор работы [Melosh, 1986] предложил использовать аналогичный подход для объяснения дальнопробежных лавин. Наиболее удобной АФ-модель динамического снижения сухого трения оказалась в численном моделировании образования крупных метеоритных кратеров [Melosh, Ivanov, 1999].

Модель предполагает, что: 1) горные породы вокруг формирующегося кратера движутся как набор блоков со средним размером h; 2) в статических условиях прочность на сдвиг по границе двух соседних блоков определяется коэффициентом сухого трения f и нормальным напряжением σ; 3) при наличии внутренних колебаний в системе блоков величина σ осциллирует вокруг величины среднего (статического) значения с амплитудой p_vib и периодом T_osc; 4) амплитуда колебаний затухает со временем экспоненциально с характерным временем T_dec [Ivanov, Artemieva 2002]. В итоге, сила трения,  f × σ, противостоящая сдвиговому напряжению τ, периодически оказывается ниже критической,

и соседние блоки проскальзывают друг относительно друга в условиях, когда без дополнительных внутренних колебаний (p_vib = 0) это проскальзывание было бы невозможно (f × σ > τ). Авторы работы [Melosh, Ivanov, 1999] привели несколько формулировок соотношения параметров АФ-модели, но на практике часто используется предположение о предельном механизме – в положительной фазе внутреннего колебания (блоки прижаты друг к другу) относительное перемещение отсутствует, в отрицательной фазе (блоки разжаты) – один блок перемещается относительно соседнего блока с ускорением: где h² – оценка площади контакта двух блоков, а ρ × h³ – оценка массы блока. Тогда за один цикл внутренних колебаний два блока переместятся на некоторое расстояние Δl ~ 0.5 × a_lim × (T_osc/2)², и приращение сдвиговой деформации составит величину ~Δl/h. Таким образом, модель предполагает, что АФ-движение носит “stick-slip” характер, при котором постоянное среднее сдвиговое напряжение вызывает рост сдвиговой деформации с постоянной скоростью. Такое движение может быть описано как квазивязкая деформация с постоянным (в простейшем приближении) коэффициентом кинематической вязкости: где c_af – модельный коэффициент в диапазоне от 4 до 8. Согласно модели, внутренние колебания блоков затухают экспоненциально с характерным временем затухания T_dec и, соответственно, уменьшается амплитуда местных колебаний давления: где начальная амплитуда внутренних колебаний давления вычисляется для каждой расчетной ячейки как p_vib0 = c_vib × ρ × c × v_max, а максимальная массовая скорость в расчетной ячейке v_max определяется только во время прохождения ударной волны.

Описанные выше принципы АФ-модели основаны на упрощенном описании движения блоков горной породы как несжимаемых твердых тел. В численных моделях ударного кратерообразования учет сжимаемости среды является базовым элементом, без которого невозможно воспроизведение ударных волн. Стандартная модель постепенного разрушения горных пород также построена для сжимаемой упругопластической среды [Collins et al., 2004]. “Сшивание” моделей несжимаемых блоков и упругопластической среды в настоящее время производится в очень приближенной форме – используемый нами численный алгоритм для каждой расчетной ячейки вычисляет прочность на сдвиг по стандартной упругопластической модели (сцепление плюс сухое трение) для среднего давления, уменьшенного на величину p_vib (4), добавляет квазивязкие напряжениями для локальной расчетной скорости сдвига и “вязкости” (3). Такую модель можно назвать “бингамовской” [Bingham, 1917] – предельные напряжения, разделяющие упругое и пластическое поведение материала, определяются некоторым “сцеплением” и “вязкими” напряжениями.

КАЛИБРОВКА МОДЕЛИ АКУСТИЧЕСКОЙ ФЛЮИДИЗАЦИИ

АФ-модель представляет собой попытку построить внутренне непротиворечивое описание набора наблюдательных фактов, которые удобно объяснять в предположении о временном уменьшении величины сухого трения в горных породах, вовлеченных в динамический процесс. Однако до сих пор модель является эмпирической, а подбор параметров осуществляется методом проб и ошибок.

Для ударных кратеров такой подход к калибровке параметров модели состоит в сравнения результатов численного модулирования с данными геологических и геофизических исследований изученных структур. Одной из наиболее изученных структур является Пучеж-Катункский метеоритный кратер на левом берегу Волги южнее Нижнего Новгорода. Знаменитый в геологических кругах Воротиловский выступ представляет собой поднятие пород архейского фундамента, прорывающего 2-км толщу осадочных пород. Исследование структуры, завершившиеся бурением глубокой 5-км скважины в центре поднятия, показало, что Воротиловский выступ является центральной горкой ударного кратера исходным диаметром ~40 км [Масайтис, Певзнер, 1999].

В 2020 г. сотрудники ВСЕГЕИ подготовили сводку результатов исследований по Пучеж-Катункскому кратеру и Воротиловской скважине в виде коллективной монографии [Masaitis, Naumov, 2020]. Для этого издания было проведено новое исследование параметров переменного динамического трения в давно разрабатываемой в ИДГ РАН компьютерной модели образования ударных кратеров на Земле, Луне и других планетах [Ivanov, 2005; Ivanov, Melosh, 2013; Ivanov et al., 2010]. Здесь мы используем для иллюстрации некоторые результаты, не вошедшие в работу [Iva-nov, 2020].

Путем параметрического моделирования мы оценили для Пучеж-Катункского случая характерный размер блоков h в диапазоне от 100 до 150 м, период колебания блоков T_osc от 0.5 до 1 с, что дает эффективную кинематическую вязкость порядка 10⁵ м²/с.

Отношение периода колебаний ко времени затухания позволяет оценить добротность колебательной системы блоков. Ее можно интерпретировать как число колебаний, которое каждый блок совершит до эффективного затухания:

Для Пучеж-Катункского случая Q находится в диапазоне от 50 до 100. Это значит, что предполагаемые модельные блоки совершают 50–100 колебаний до того момента, когда внутренние колебания затухнут, и коэффициент сухого трения восстановится до нормальных (статических) значений.

В результате проведенных расчетов были подобраны параметры ударников для двух возможных скоростей соударения и параметры модели динамического снижения трения, наилучшим образом воспроизводящие профиль конечного кратера и распределение по глубине величины максимального ударного давления, оцененное по микродеформациям минералов в образцах керна Воротиловской скважины [Ivanov, 2020].

Путем метода проб и ошибок для простейшего случая вертикального удара астероида в двуслойную мишень (осадочный слой поверх кристаллического фундамента) были подобраны размеры ударников, D_proj, при двух возможных скоростях удара v_imp (D_proj ~ 4 км при v_imp = 10 км/с и D_proj ~ 3.2 км при v_imp = 16 км/с) – см. детали в работе [Ivanov, 2020]. На рис. 1 показан вариант подбора времени затухания внутренних АФ-колебаний. Видно, что без АФ-модели породы под дном кратера оказываются вдавленными вниз, а изначальная полость переходного кратера частично заполняется веществом оползней со склонов кратера. При включении АФ-модели начинает наблюдаться подъем дна переходного кратера, уменьшающий возможности для оползания бортов. Наилучшими в данном ряду параметрического исследования были признаны варианты, в которых характерное время затухания внутренних АФ-колебаний T_dec составляло 40–45 с. Рисунок 1 демонстрирует, что в случае с быстрым затуханием АФ (или в отсутствие АФ) ударный расплав остается зажатым в центре кратера обрушенным материалом со стенок кратера. При эффективно действующей АФ дно кратера успевает подняться, вытесняя расплав в тонкую поверхностную линзу.

На рис. 2 показаны модельные профили кратеров при увеличении параметра T_dec. Повторим, что Воротиловская скважина в центре кратера вскрыла 5 км архейских гнейсов. Согласно модели, нерасплавленный материал на поверхности Воротиловского выступа был поднят с глубины от 4 до 5 км. Таким образом, предположение о временном (примерно на 40 с) снижении сухого трения в горных породах вокруг формирующегося ударного кратера позволяет воспроизвести строение хорошо изученной структуры.

ПОИСК МОДЕЛИ ЛОКАЛЬНОГО СНИЖЕНИЯ ТРЕНИЯ

Открытие и исследование ударных кратеров на Луне и других планетах земного типа позволили расширить наши представления о формировании сложных ударных кратеров на иные, чем на Земле, условия образования и существования горных пород. Отсутствие воды и другая сила тяготения позволяют нам ограничить круг причин, определяющих явление динамического снижения трения в горных породах. Такие сопоставления Земли и Луны в отношении ударных кратеров начались давно [Pike, 1977]. К настоящему времени появились хорошо обоснованные сравнения земных и инопланетных дальнопробежных лавин [Lucas et al., 2014].

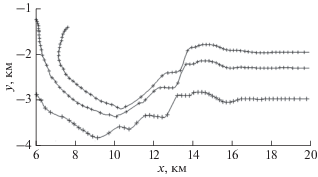
Во многих сложных инопланетных кратерах на внутреннем склоне кратеров наблюдается серия концентрических террас, свидетельствующих об оседании бортов сложного кратера по серии концентрических разломов. Такие же концентрические разломы часто наблюдаются (скорее – предполагаются) вокруг крупных земных кратеров. На рис. 3 показаны примеры двух лунных кратеров диаметром около 40 км с хорошо заметными множественными террасами шириной 2–3 км. Профили высот вдоль диаметра, пересекающего кратеры, показаны на рис. 4. При невысоком пространственном разрешении здесь видна только одна кольцевая терраса шириной порядка 2 км и амплитудой сброса от 100 до 200 м.

Ранее кольцевые террасы в ударных кратерах Луны и Меркурия с точки зрения механики грунтов рассматривались в работах [Leith, McKinnon, 1991; Pearce, Melosh, 1986]. Использование нашей АФ-модели очень редко приводит к появлению локализованных полос деформаций – модель сводит все процессы к простому снижению сухого трения в породах под кратером. Локальные модели снижения трения относительно редко использовались при численном моделировании кратерообразования. В данной работе мы провели предварительные эксперименты, следуя работе [Senft, Stewart, 2009]. В этой работе предполагалось, что локальный коэффициент сухого трения уменьшается с ростом локальной скорости сдвиговой деформации [Beeler et al., 2008; Rice, 2006]. В поисках отправной точки для задания аналитического вида зависимости трения от скорости смещения соседних блоков мы обратили внимание на работу [Lucas et al., 2014], в которой моделировалась дальность пробега лавин на Земле и Марсе. Здесь было предложено соотношение для коэффициента трения между двумя блоками f в зависимости от скорости перемещения одного блока относительно соседнего блока U. В статике и при малых скоростях смещения, меньших некоторого критического значения U ", коэффициент сухого трения равен f₀. Переход от f₀ к пониженному значению f₁ (авторы называют это значение “пониженным из-за нагрева” – “thermally weakened friction coefficient”) происходит, если абсолютное значение скорости перемещения |U| > U ". Тогда:

Для моделирования дальнопробежных лавин [Lucas et al., 2014] подобрали значения f₀ = 0.75, f₁ = 0.08, U " = 4 м/с.

Используемая нами эйлерова модель движения сплошной среды не позволяет просто выделить направление плоскости скольжения в каждой ячейке на каждом шаге по времени, поэтому мы попытались переписать (5) в терминах, стандартных для нашей компьютерной модели. Девиаторная (упругая) часть программы SALEB, как и ее модернизированный вариант iSALE (https://isale-code.github.io) по полю скоростей вычисляет тензор скоростей деформаций и его второй инвариант (скорость сдвига) e'. При простом сдвиге скорость перемещения одной грани ячейки шириной Δx относительно противоположной грани ячейки U ~ Δx × e'. Однако ширина ячейки Δx в моделях движения сплошной среды определяется соображениями о полном размере расчетной сетки, пространственного разрешения ударника и возникающих ударных волн, поэтому пока не представляется возможным одновременно моделировать образование кратера диаметром в десятки километров и тонкие эффекты скольжения вдоль узких разломов. Поэтому мы подобрали методом проб и ошибок соотношение:

в котором величина критической скорости сдвиговой деформации e" варьировалась от 0.01 до 0.05 1/с. Если формально сопоставить U " из (5) с величиной Δx × e", мы получим, например для Δx ~ 60 м (типичная величина для использованного масштаба моделей, описанных в предыдущем разделе), что скорости сдвига в (6) примерно соответствуют параметрам в (5): U  " ~ Δx × e" ~ 60 × × (0.01–0.05) = 0.6–3 м/с. Мы оставляем на будущее вопросы влияния величины Δx и иного уровня давлений при образовании кратеров диаметром в десятки километров по сравнению с задачами, рассмотренными в работе [Lucas et al., 2014], и обратимся к качественным результатам использования (6) в расчетах удара того же масштаба, что и Пучеж-Катункский кратер.

Для пробных расчетов мы использовали однородную мишень без осадочного слоя. Сферический ударник диаметром 2.15 км падал на мишень со скоростью 16 км/с. При отключении АФ-модели в материале мишени с динамически уменьшающимся сухим трением (6) возникали отчетливо видимые узкие полосы сдвига/скольжения (“разломы”) толщиной в 1–3 расчетных ячейки, однако ни одна из систем полос скольжения не возникла ниже уровня дна переходного кратера (рис. 5), и обрушение кратера произошло по модели простого кратера (аналогично изображенным на рис. 1 и рис. 2).

Повторение этого же варианта расчета с включением АФ-модели привело к образованию модельного кратера, более похожего на ожидаемый кратер такого размера (рис. 6), но с сохранением основных деталей локализации сдвига вдоль нескольких искривленных поверхностей скольжения.

В данном случае нас интересовали поверхности локализованных сдвиговых деформаций. Чтобы лучше их визуализировать, на рис. 7 показан “рельеф” поля деформаций под кратером, построенный путем “освещения” трехмерной карты параметра z(x, y) источником света, распложенным слева сверху. Это позволяет лучше видеть локализованные полосы параметров. Слева на рис. 7 показаны сдвиговые деформации, рассчитанные по смещению лагранжевых частиц-маркеров. Справа на рис. 7 показан нагрев вещества за счет механической работы, величина которой суммируется в каждой ячейке на каждом шаге по времени, если напряжения выходят за предел прочности (точнее – остаются на предельной поверхности). Для краткости эта энергия часто называется пластической работой.

Сравнение распределения деформаций и пластической работы показывает, что хотя в зонах локализованного сдвига предполагается динамическое уменьшение коэффициента трения, пластическая энергия работы против сил трения локализуется именно в этих ячейках. В дальнейшем мы планируем детально изучить детали движения зонах сдвига.

Наши надежды на воспроизведение террас на внутренних склонах кратера оправдались неполностью: с одной стороны, в нашей двумерной модели с цилиндрической симметрией локализованные полосы сдвига не вышли на поверхность. С другой стороны, на глубине более 2 км можно определить расстояние между полосами сдвига (рис. 8) – оно оказалось порядка 2.3 км, как и в лунных кратерах сходного размера.

ЗАКЛЮЧЕНИЕ

Проблема изменения коэффициента сухого трения между блоками горных пород возникает при рассмотрении многих динамических явлений в земной коре. Случай формирования ударных кратеров сложной формы, которую пока удалось объяснить только предположив временное снижение трения в интенсивно деформируемых породах вокруг растущего ударного кратера, представляет особый интерес, так как последовательность изменения строения кратеров (от простых чашеобразных к сложным кратерам с центральным поднятием и далее к многокольцевым бассейнам) повторяется на всех планетных телах с твердой корой (содержащей воду и лед на Земле и Марсе и более “сухой” – на Луне, Венере и Меркурии). Это доказывает, что влияние порового давления флюидов и наличие “мягких” гидросиликатов на снижение трения между блоками не является универсальной причиной снижения трения между блоками. С другой стороны, чисто механические модели типа модели акустической флюидизации пока разработаны на чисто феноменологическом уровне и требуют определенной осторожности при переходе от планеты к планете. Мы попытались частично скомпенсировать недостатки АФ-модели путем добавления локальной модели снижения трения при быстром сдвиге соседних блоков. Использованное здесь условие динамического снижения трения пока носит чисто феноменологический характер, так как модель пытается учесть процессы, происходящие на гораздо меньших масштабах, чем это разрешается на имеющихся расчетных сетках. С учетом этих проблем для анализа в будущем, нам показалось интересным, что введение даже упрощенной модели динамического разупрочнения привело к “самозарождению” системы локализованных поверхностей скольжения. В некотором диапазоне глубин под модельным кратером диаметром ~40 км расстояние между двумя-тремя поверхностями скольжения оказались сопоставимы с шириной кольцевых террас, наблюдаемых во многих лунных кратерах. Нам представляется, что наблюдательные данные о строении природных ударных кратеров могут послужить для подбора параметров моделей трения между крупными блоками земной коры.