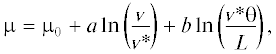Физика Земли, 2021, № 5, стр. 55-73
Моделирование индуцированной сейсмичности на основе двухпараметрического закона rate-and-state
В. Ю. Рига 1, *, С. Б. Турунтаев 1, 2, 3, **
1 Всероссийский научно-исследовательский институт автоматики им. Н.Л. Духова
г. Москва, Россия
2 Институт динамики геосфер имени академика М.А. Садовского РАН
г. Москва, Россия
3 Московский физико-технический институт
г. Москва, Россия
* E-mail: rigavu92@gmail.com
** E-mail: s.turuntaev@gmail.com
Поступила в редакцию 23.03.2021
После доработки 16.04.2021
Принята к публикации 16.04.2021
Аннотация
Рассматривается вопрос численного моделирования сейсмичности, индуцированной закачкой флюида в недра. Одним из важных факторов, определяющих динамику скольжения тектонических разломов в процессе воздействия, является вид закона трения, действующего на берегах разломов. Путем численного анализа, проведенного в рамках слайдер-модели в сопоставлении с результатами лабораторных экспериментов, показано, что двухпараметрическая форма закона трения типа rate-and-state позволяет описывать наиболее широкий спектр наблюдаемых режимов скольжения. На основе модели двойной пористости, а также слайдер-модели трещин моделируется индуцированная сейсмичность в районе г. Базель, Швейцария, возникшая в ходе реализации проекта по использованию геотермальной энергии. Представлена физически полная модель вложенных трещин, позволяющая моделировать процесс фильтрации флюида в породе, содержащей трещины или разломы, с учетом изменения фильтрационных свойств последних. Процесс деформации разлома описывается с использованием метода разрывных смещений. Модель применяется для анализа результатов натурного эксперимента по закачке воды в разлом на юге Франции. Исследуется развитие подвижек разлома в зависимости от различных параметров: свойств разлома, фильтрационных свойств породы, параметров закачки. Найдены условия, при которых в рамках предложенной модели возможно возникновение сейсмических подвижек.
ВВЕДЕНИЕ
Задача моделирования и прогнозирования развития сейсмических процессов техногенного характера в настоящее время является весьма актуальной. Это связано с наблюдением все большего количества случаев индуцированной и триггерной сейсмичности, вызванной деятельностью человека, а также с необходимостью оценки последствий такого воздействия при добыче углеводородов, использовании геотермальной энергии и др. [McGarr et al., 2002; Ellsworth et al., 2015; Адушкин, Турунтаев, 2015]. В настоящее время для оценки риска возникновения опасной сейсмичности и принятия мер для предотвращения такой ситуации используется так называемый “светофорный” принцип [Bommer et al., 2006], согласно которому воздействие должно быть уменьшено или прекращено, если магнитуда индуцированных сейсмических событий достигает определенных критических значений (обычно порядка 2 и 3 соответственно). Недостатком такого подхода является отсутствие обоснованной оценки развития сейсмичности в случае продолжения закачки и оценки ожидаемой максимальной магнитуды землетрясения, что в ряде случаев приводит как к переоценке, так и к недооценке опасности. К примеру, из-за возникновения сейсмичности в результате закачки воды на глубину более 5 км с целью использования геотермальной энергии в районе г. Базель [Häring et al., 2008] данный проект был закрыт, что привело к значительным убыткам (порядка 100 млн евро). В ходе закачки воды в тех же целях в г. Пхохан в Южной Корее была отмечена умеренная сейсмичность, однако проект не был остановлен, и произошло одно из крупнейших для этого региона землетрясений [Ellsworth et al., 2019]. Эти и другие примеры наглядно показывают необходимость предварительного моделирования последствий флюидного воздействия на разломные зоны и оценки рисков с целью минимизации последующих издержек.
Наиболее распространенная модель землетрясения (в упрощенном виде) заключается в том, что существующее на отдельных участках разлома трение препятствует взаимному движению его берегов и способствует накоплению сдвиговых напряжений до критического уровня [Brace, Byerlee, 1966], после достижения которого происходит подвижка по разлому и землетрясение. Модели, которые бы описывали весь спектр физических явлений, происходящих при закачке флюида и подвижкам по трещинам/разломам, достаточно трудоемки в вычислительном плане, ими стали активно заниматься относительно недавно. Помимо вычислительных проблем, актуальны и вопросы выбора адекватной физической модели закона трения, действующего на берегах разлома [Lay, 2009].
В настоящей статье приводится краткий обзор вариантов закона трения типа rate-and-state и на основе численного анализа и сопоставления с данными экспериментов [Будков и др., 2015; Kocharyan et al., 2014] показывается, что двухпараметрический закон трения [Gu et al., 1984] с введением вязкого слагаемого позволяет описывать наиболее широкий спектр скольжений. Предложена модель влияния закачки на развитие сейсмичности, в которой влияние раскрытия трещин на процесс фильтрации учитывается, как увеличение проницаемости породы с ростом давления, а подвижки по трещинам описываются с использованием двухпараметрического закона трения. Эта модель применяется к анализу сейсмичности в районе Базельского геотермального проекта. Также рассмотрена модель фильтрации, описывающая явно процесс изменения проницаемости протяженного разлома с ростом порового давления. Для этого предложена модель вложенных трещин, которая позволяет корректно описывать процесс фильтрации в малопроницаемой породе, вмещающей высокопроницаемый разлом. Рассмотрены случаи, когда давление жидкости не превышает нормального напряжения, действующего на разлом, но при этом происходит его деформация в касательном направлении. Данный подход использован применительно к результатам натурного эксперимента, который проводился на юге Франции [Guglielmi et al., 2015]. Рассматривается единичный разлом (неоднородный по параметрам закона трения) в бесконечной однородной упругой слабопроницаемой среде. Для того, чтобы воссоздать натурные условия, в модели из экспериментальных данных были взяты геомеханические параметры среды, история закачки воды, начальная ширина трещины. Посредством численного моделирования было выявлено, каково влияние различных параметров модели (нормальной жесткости разлома, проницаемости коллектора, параметров законов трения) на деформацию разлома. Рассматривались различные модельные случаи, в которых варьировалось расположение зоны разупрочнения на разломе и параметры закачки: удаление скважины от разлома, темпы закачки, суммарный объем закачки, начальное значение касательных напряжений, действующих на разломе. В результате анализа результатов численного эксперимента получены закономерности, определяющие зависимость параметров деформации разлома от упомянутых величин.
ВЫБОР ВИДА ЗАКОНА ТРЕНИЯ НА ОСНОВЕ ЛАБОРАТОРНЫХ ЭКСПЕРИМЕНТОВ
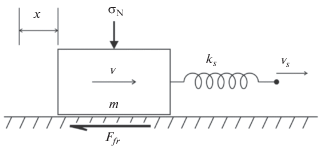
Для выбора вида закона трения, позволяющего наиболее адекватно описывать сейсмогенерирующие и асейсмичные подвижки по разломам, воспользуемся так называемой слайдер-моделью (рис. 1) и результатами лабораторных экспериментов, описанных в работе [Budkov, Kocharyan, 2017]. Блок, лежащий на подложке и находящийся под действием постоянной нормальной силы ${{\sigma }_{N}}{{\sigma }_{N}}$, приводится в движения посредством силы натяжения пружины, конец которой движется с постоянной скоростью vs (скорость протяжки). Трение между блоком и подложкой определяется законом трения rate-and-state, т.е. зависит от скорости скольжения блока (v) и параметра состояния контакта θ. Движение блока описывается в общем виде системой уравнений:
(1)
$\left\{ \begin{gathered} m\ddot {x} = {{k}_{s}}\left( {{{v}_{s}}t - x} \right) - {{F}_{{fr}}} \hfill \\ {{F}_{{fr}}} = {{\sigma }_{N}}\mu \left( {v,{{\theta }}} \right) \hfill \\ {{\dot {\theta }}} = \theta \left( v \right) \hfill \\ \end{gathered} \right..$Для описания трения наиболее часто используется однопараметрический вариант уравнения rate-and-state [Dieterich et al., 1979; Ruina et al., 1998; Budkov et al., 2017; Кочарян, 2014], который можно записать в виде:
где: μ, μ0 – коэффициенты трения движения и покоя; v – скорость скольжения; a, b, $v{\text{*}}$ и L – параметры; θ – переменная состояния, значение которой характеризует состояние скользящих поверхностей и эволюция которой во времени определяется уравнением:Помимо (3) существуют и другие формы уравнения состояния, например [Gu et al., 1984]:
(5)
$\dot {\theta } = - \frac{v}{L}\left[ {\theta + b\ln \left( {\frac{v}{{v{\text{*}}}}} \right)} \right].$Если блок скользит со скоростью протяжки, и при этом параметр состояния не меняется, то такое скольжение является стационарным. Если система в процессе стационарного скольжения испытает небольшое возмушение, например изменение скорости протяжки, то скольжение может стать нестабильным (т.е. система не перейдет в новое стационарное состояние, скорость блока будет постоянно меняться). Для этого должны выполниться два условия: a < b и ks < kcr, где kcr – критическое значение жесткости, определяемое параметрами закона трения. Если же какое-либо их этих условий не выполняется, то скольжение будет стабильным.
В работе [Gu et al., 1984] приведен пример экспериментальных данных, которые не удается описывать в рамках однопараметрического закона, и возникает необходимость использовать двухпараметрический:
(6)
$\mu = {{\mu }_{0}} + a{\text{ln}}\left( {\frac{v}{{v{\text{*}}}}} \right) + {{{{\theta }}}_{1}} + {{{{\theta }}}_{2}},$(7)
${{{{\dot {\theta }}}}_{i}} = - \frac{v}{{{{L}_{i}}}}\left[ {{{{{\theta }}}_{i}} + {{b}_{i}}{\text{ln}}\left( {\frac{v}{{v{\text{*}}}}} \right)} \right].$В двухпараметрическом законе трения величина b1 + b2 выполняет такую же роль, как и величина b в однопараметрическом законе. Двухпараметрический закон трения не нашел широкого применения, за исключением ряда случаев описания лабораторных экспериментов. Однако наблюдаемые как в природе, так и в лабораторных экспериментах процессы скольжения обычно характеризуются хаотическим (апериодическим) движением. В работе [Erickson et al., 2008] рассматривается слайдер-модель с законом трения, описываемым однопараметрическим уравнением. Авторы в результате численных экспериментов смогли получить реализацию хаотического движения, однако оно наблюдалось при значении безразмерного параметра $\varepsilon = \frac{{b - a}}{a}$ > 11. Такое значение параметра ε значительно превышает значения, полученные в экспериментальных работах, согласно которым эта величина очень часто меньше 1 [Okazaki, Katayama, 2015; Capenter et al., 2014; 2015; Marone, Saffer, 2015]. Двухпараметрический закон трения позволяет получать реализации хаотического движения при значительно меньших величинах параметра ε.
Анализ наличия хаотических решений систем дифференциальных уравнений и условий появления таких решений удобно проводить с помощью отображения Пуанкаре [Guckenheimer, Holmes, 1983], представляющего собой проекцию фазовых траекторий на гиперплоскость в фазовом пространстве, осуществляемую вдоль траекторий. Для рассматриваемой задачи в качестве гиперплоскости была взята поверхность, на которой скорость скольжения блока равна скорости протяжки. На рис. 2 показана зависимость количества точек отображения Пуанкаре от параметра $\varepsilon $ при фиксированном значении других параметров и разных значениях величины $\rho = {{{{L}_{2}}} \mathord{\left/ {\vphantom {{{{L}_{2}}} {{{L}_{1}}}}} \right. \kern-0em} {{{L}_{1}}}}$. По оси ординат отложены безразмерные координаты блока $\left( {{{x}_{{{\text{dim}}}}} = \frac{x}{{{{L}_{1}} + {{L}_{2}}}}} \right)$ для точек пересечения. Фазовые орбиты с единичным периодом на таком графике представляются одной точкой, с двойным периодом – двумя и т.д. Хаотические орбиты отображаются набором произвольно распределенных точек. Из представленных графиков видна тенденция: по мере приближения параметра ρ к 1 увеличивается критическое значение величины ε, начиная с которого наблюдается хаотическое движение. При ρ = 1 двухпараметрический закон трения вырождается в однопараметрический, чем больше ρ отличается от 1, тем больше разница параметров состояния θ1 и θ2. Результаты остаются верными при других значениях остальных величин (b1/b2, ks/kcr и пр.). Полученные результаты свидетельствуют, что для описания хаотического движения надо использовать как минимум двухпараметрический закон трения.
Рис. 2.
По вертикальной оси – карта безразмерных координат блока точек отображения Пуанкаре; по горизонтальной – значение величины ε. Показаны случаи для различных соотношений величины L2/L1.

Рассмотренные выше “классические” законы трения не позволяют описывать медленные события. Поэтому была рассмотрена модификация закона трения путем введения дополнительного члена типа вязкости (8) и изменением закона эволюции параметра θ (9) [Budkov et al., 2017; Kato et al., 2001]:
(8)
$\tau = \tau {\text{*}} + {{\sigma }_{n}}\left( {A\ln \left( {\frac{v}{{v{\text{*}}}}} \right) + {{\theta }_{1}} + {{\theta }_{2}}} \right) + \eta {\text{*}}v,$(9)
$\left\{ \begin{gathered} \tau = \tau {\text{*}} + {{\sigma }_{n}}\left( {A\ln \left( {\frac{v}{{v{\text{*}}}}} \right) + {{b}_{1}}{\text{ln}}\left( {\frac{{v{\text{*}}{{{{\theta }}}_{1}}}}{{{{L}_{1}}}}} \right) + {{b}_{1}}{\text{ln}}\left( {\frac{{v{\text{*}}{{{{\theta }}}_{2}}}}{{{{L}_{2}}}}} \right)} \right) \hfill \\ {{{{{\dot {\theta }}}}}_{i}} = {{e}^{{ - \,\frac{v}{{{{v}_{c}}}}}}} - \frac{{v{\text{*}}{{{{\theta }}}_{i}}}}{{{{L}_{i}}}}\left( {\frac{{v{\text{*}}{{{{\theta }}}_{i}}}}{{{{L}_{i}}}}} \right) \hfill \\ \end{gathered} \right.,$На рис. 3 представлено изменение эпюры скорости по мере изменения параметра vc и параметра η.
Рис. 3.
Изменение профиля скорости смещения блока при различных значениях ${{v}_{c}}$ (слева) или η (справа) при неизменных других параметрах.

Как видно на рис. 3, новый параметр в уравнении для ${{\dot {\theta }}_{i}}$ оказывает слабое влияние на ширину пика скорости смещения блока, при этом значительно влияет на максимальное значение скорости. Модификация закона трения путем введения дополнительного слагаемого позволяет достаточно эффективно изменять ширину пика скорости, “растягивая” его по мере увеличения параметра вязкости. При этом уменьшается максимальная скорость. Т.к. параметры a, b1, b2 в основном влияют на амплитуду, но не на длительность импульса, использование вязкого слагаемого позволяет достаточно эффективно “подстраиваться” под конкретную эпюру скорости.
Рисунок 4 демонстрирует эпюры скорости движения блока для однопараметрического закона при изменении параметра b и для 2-параметрического при изменении параметра b1. Наличие двух параметров позволяет менять форму пика.
Рис. 4.
Изменение эпюры скорости по мере изменения параметра B (слева) для однопараметрического закона трения или параметра B1 (справа) при фиксированном B2 для двухпараметрического закона трения ($B = b{{\sigma }_{n}}$).

Стоит отметить, что по мере увеличения вязкого слагаемого уменьшается вероятность развития хаотических подвижек, а для описания “медленных” скольжений величина безразмерной вязкости должна быть достаточно большой. Поэтому критерием успешного описания скольжения является воспроизведение эпюры скорости единичного скачка и усредненного периода повторяемости событий.
Для периодического скольжения удается достаточно хорошо воспроизвести как форму скачка, так и их повторяемость (рис. 5). Для апериодического сложного движения удается получить среднюю повторяемость и форму скачка.
ИНДУЦИРОВАННАЯ СЕЙСМИЧНОСТЬ В РАЙОНЕ БАЗЕЛЬСКОГО ГЕОТЕРМАЛЬНОГО ПРОЕКТА
Характеристика геотермальной системы Базель 1
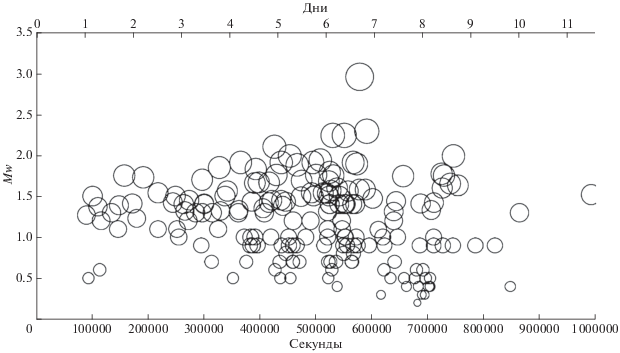
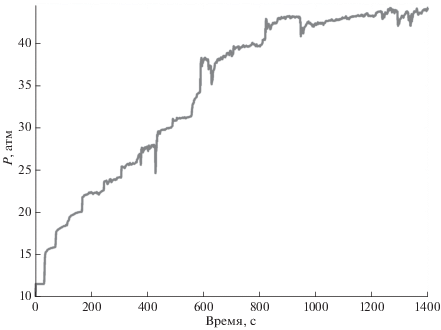
Проект по производству геотермальной энергии в городе Базель был начат в 2006 г. В регионе предварительно была создана сеть сейсмического мониторинга, начавшая функционировать в феврале 2006 г. В период между маем и октябрем была пробурена скважина Basel 1 на глубину около 5 км, 2 декабря началась закачка воды. Планировалось проводить закачку в течение 21 дня, но в первые шесть дней наблюдалось повышение сейсмической активности, в том числе произошло землетрясение с магнитудой ML 2.6, и было решено прекратить закачку. Спустя пять часов произошло сейсмическое событие с магнитудой ML 3.4, в течение следующего года было зафиксировано порядка 3700 событий [Diechmann et al., 2014].
Регион, в котором располагается г. Базель, характеризуется следующими величинами компонент напряжений на глубине 4900 м [Häring et al., 2008]: ${{S}_{{h{\text{min}}}}} = 84\,\,~{\text{МПа}}$, ${{S}_{V}} = 122~\,\,{\text{МПа}}$, ${{S}_{{H{\text{max}}}}} = 160\,\,~{\text{МПа}}$, где ${{S}_{{H{\text{max}}}}}$, ${{S}_{{h{\text{min}}}}}$ – максимальное и минимальное горизонтальные напряжения, ${{S}_{V}}$ – вертикальное напряжение. Азимут ${{S}_{{H{\text{max}}}}}$ равен 144° ± 14°, азимут ${{S}_{{h{\text{min}}}}}$ равен 54° ± 14°. На основе акустического каротажа было получено азимутальное распределение трещин, соответствующее ориентации максимальной горизонтальной компоненты напряжений.
В ноябре 2006 г. был проведен 75-часовой тест по закачке воды, интерпретация полученных данных дала среднее значение эффективной проницаемости 1 × 10–17 м2. Дальнейший анализ показал, что течение в породе является билинейным (течение по порам и по системе трещин), причем преобладающим является течение по трещинам. Во время закачки давление в резервуаре увеличивается, что приводит к раскрытию трещин и увеличению их проводимости до 400 раз [Häring et al., 2008]. В работе [Dinske, 2011] на основе микросейсмических данных определен усредненный тензор коэффициентов проницаемости породы в предположении, что порода обладает пористой проводимостью $~k = \left( {\begin{array}{*{20}{c}} {14}&0&0 \\ 0&{67.7}&0 \\ 0&0&{121.3} \end{array}} \right)\,\,\left[ {{\text{мкД}}} \right]$. Ось Z (3-я главная ось тензора) практически вертикальна (составляет угол в 1° с вертикалью), азимут оси Y равен 150°, т.е. ось Y практически совпадает с направлением максимального горизонтального напряжения. Основываясь на распределении сейсмических событий по глубине в первые часы и в первый день, автор работы [Dinske, 2011] пришел к выводу, что лишь 46 м отрытой части ствола скважины непосредственно гидродинамически связаны с резервуаром. Учитывалось, что необсаженная часть ствола начинается с глубины 4379 м.
Моделирование фильтрационных и сейсмических процессов в районе Базельского геотермального проекта
Для моделирования фильтрации флюида в настоящей работе использовался симулятор MATLAB [Lie, 2016]. В силу сложности фильтрационных процессов в резервуаре и ограниченности имеющихся данных сделано несколько упрощений. Так, проницаемость породы и объем, охваченный фильтрацией (расчетная область), подбирались такими, чтобы по известным расходам при закачке получить соответствие между рассчитанным и измеренным забойным давлением в скважине. По аналогии с [Dinske, 2011] при моделировании примем, что резервуар обладает пористой проводимостью, но для имитации эффекта увеличения проводимости трещин вследствие увеличения давления, будем считать, что, начиная с некоторого давления, часть компонент тензора проницаемости в рассматриваемой расчетной ячейке растет пропорционально давлению (простейшая линейная аппроксимация). Отношение проницаемости при максимальном забойном давлении к начальной проницаемости будем считать равным нескольким сотням. Примем, что расход обратного тока воды через скважину после остановки закачки постоянен, суммарный объем откачанной воды равен исходному. Данный подход проиллюстрирован на рис. 6, там же показано сопоставление рассчитанного и измеренного забойного давления.
Рис. 6.
Слева – темпы закачки и темпы отбора воды. Справа – изменение забойного давления (факт и модель).

Разломную зону представим в виде набора трещин, которые не связаны между собой. Каждую трещину, в соответствии со слайдер-моделью, представим набором упруго связанных блоков. [McClure, 2016; Kato, 2003; 2004] предлагают разбиение разломных зон на множество дискретных элементов и рассмотрение безынерционной системы. По аналогии с этим подходом будем рассматривать безынерционные системы, что значительно ускоряет вычислительный процесс. Каждую трещину представим в виде набора трех блоков. Для крайних двух выполняется соотношение a > b1 + b2 (скольжение с упрочнением), для среднего блока a < b1 + b2 скольжение с разупрочнением), также вводится слагаемое, учитывающее динамическую вязкость контакта. Вначале все трещины неактивны. Для того, чтобы избежать неопределенностей из-за наличия логарифма в законе трения и неопределенности в начальных значениях параметров состояния (${{{{\theta }}}_{i}}$), задано условие, что до активации трещины скользят стабильно с пренебрежимо малой скоростью. При повышении порового давлением происходит “срыв” трещины – она активируется и начинает скользить.
Таким образом, система уравнений, описывающих безынерционное движение блоков, составляющих каждую трещину, становится следующей (закон трения взят в форме (8)):
(10)
$\left\{ \begin{gathered} 0 = {{k}_{1}}\left( {{{u}_{0}}t - {{x}_{1}}} \right) - {{k}_{{12}}}\left( {{{x}_{1}} - {{x}_{2}}} \right) - {{\tau }_{{fr1}}}\left( {{{v}_{1}},{{\theta }}_{1}^{{1,2}}} \right) \hfill \\ 0 = {{k}_{2}}\left( {{{u}_{0}}t - {{x}_{2}}} \right) + {{k}_{{12}}}\left( {{{x}_{1}} - {{x}_{2}}} \right) - \hfill \\ - \,\,{{k}_{{23}}}\left( {{{x}_{2}} - {{x}_{3}}} \right) - {{\tau }_{{fr2}}}\left( {{{v}_{2}},{{\theta }}_{1}^{{1,2}}} \right) \hfill \\ 0 = {{k}_{3}}\left( {{{u}_{0}}t - {{x}_{3}}} \right) - {{k}_{{23}}}\left( {{{x}_{2}} - {{x}_{3}}} \right) - {{\tau }_{{fr3}}}\left( {{{v}_{2}},{{\theta }}_{1}^{{1,2}}} \right) \hfill \\ \end{gathered} \right..$Система уравнений решалась с помощью явного метода Рунге–Кутта четвертого порядка с адаптивным шагом по времени [Press et al., 2007]. Скорость каждого блока вычислялась при помощи итеративного метода Ньютона. В начале расчета все блоки покоятся, затем, как только касательное напряжение превышает силу трения, блоки начинают свое движение. Если в результате движения и изменения поля давлений сила трения вновь превышает касательное напряжение, блок останавливается.
На основе данных [Haring et al., 2008] принята следующая оценка диапазона начальной разности между касательным напряжением вдоль берега трещины и силой трения на единицу площади: ${{\Delta }}\tau = 6{\kern 1pt} - {\kern 1pt} 10$ МПа (на глубине закачки). Для каждой трещины значение бралось случайным образом из указанного промежутка. Для моделирования неоднородности трещин параметры закона трения брались случайным образом в диапазоне ±5% от среднего. Результаты сейсмических наблюдений показали, что источники сейсмических сигналов находились практически в одной плоскости [Häring et al., 2008]. Соответственно, было принято упрощение, что трещины распределены по расчетным ячейкам центральной плоскости, проходящей через скважину, случайным образом, площадь каждого сегмента равна площади соответствующей ячейки, общее количество трещин в расчетах варьировалось. После проведения расчетов анализировалась зависимость скорости блоков от времени, выделялись случаи срывов – “сейсмические события”, совпадающие по времени события в близких ячейках расчетной сетки объединялись в одно крупное событие. Сейсмический момент события рассчитывался по формуле:
где: G – модуль сдвига; S – площадь поверхности блока; Δx – смещение блока при срыве.
Были проведены расчеты для различного количества блоков: 300, 600 и 1000. Пример набора параметров закона трения, использовавшихся в расчете, приведен в табл. 1. Примеры результатов вычислений показаны на рис. 7–рис. 8.
Таблица 1.
Средние значения параметров модели приведены для двух примеров расчетов
| Параметр | Количество сегментов | |
|---|---|---|
| 300 | 600 | |
| ${{L}_{1}}$ | 135 мкм | 56 мкм |
| ${{L}_{2}}$ | 150 мкм | 159 мкм |
| ${{b}_{1}}$ | 0.00149 | 0.00072 |
| ${{b}_{2}}$ | 0.0009 | 0.00107 |
| $a$ | Центральный блок: 0.00225 Крайние блоки: 0.00275 |
Центральный блок: 0.00169 Крайние блоки: 0.00205 |
| η | 11 803 Па/(м/с) | 6910 Па/(м/с) |
| ${{k}_{s}}$ | 3.44 × 109 Н/(м ⋅ м2) | 1.58 × 109 Н/(м ⋅ м2) |
| ${{k}_{1}}$ | 5.36 × 108 Н/(м ⋅ м2) | 1.41 × 108 Н/(м ⋅ м2) |
Рис. 8.
Верхние рисунки – расчетные значения моментных магнитуд сейсмических событий. Нижние – накопленный сейсмический момент для фактического и смоделированного каталогов событий.

Видно, что характер поведения модельной сейсмичности схож с характером фактической сейсмичности: первое событие происходит приблизительно спустя день после начала закачки, пик сейсмичности приходится практически на момент окончания закачки (4500 с), далее сейсмичность идет на убыль. Как видно из графиков накопленного сейсмического момента, модель с достаточным количеством сегментов (600) хорошо качественно и количественно воспроизводит фактические данные. Для смоделированной сейсмичности также наблюдается резкий рост накопленного момента в узкий интервал времени, но по сравнению с фактическими данными, этот рост более плавный и заканчивается несколько раньше. Данные отличия вполне ожидаемы в рамках используемой модели и могут быть объяснены тем, что использованная модель сейсмичности упрощенная. Главным эффектом, который не учитывается, является наличие дальней упругой связи блоков.
ВЛИЯНИЕ ЗАКАЧКИ НА ЕДИНИЧНЫЙ РАЗЛОМ
Описание модели
Рассматривается единичный разлом в бесконечной однородной упругой слабопроницаемой среде (рис. 9). Разлом высокопроницаем и его проницаемость растет по мере увеличения порового давления. Решается несвязанная задача фильтрации флюида и деформации разлома с пренебрежением изменения поля полных напряжений: считается, что из-за изменения порового давления меняются лишь эффективные напряжения. Данные для моделирования (геомеханические параметры среды, история закачки воды, начальная ширина разлома) брались из данных натурного эксперимента по закачке воды в разлом на юге Франции [Cappa et al., 2018; Guglielmi et al., 2015].
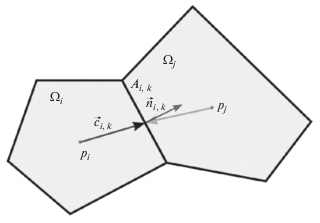
Для моделирования фильтрации использовался метод вложенных трещин, в котором сетки для матрицы породы и для трещин создаются независимо, что позволяет избежать проблемы создания сложных сеток с увеличением разрешения сетки в районе разлома. Метод был реализован на основе пакета Matlab Simulation Toolbox (MRST). Процесс фильтрации описывается уравнением неразрывности и уравнением Дарси:
(12)
$\frac{\partial }{{\partial t}}\left( {\varphi \rho } \right) + \nabla \left( {\rho {\mathbf{v}}} \right) = q,$Для определения проницаемости разлома использовался кубический закон течения между двумя плоскостями, но в качестве ширины зазора использовалось не расстояние между берегами разлома, а эффективная гидродинамическая ширина, которая меняется при изменении давления вследствие деформации контактной зоны разлома [Witherspoon et al., 1980]:
где: ${{a}_{{h0}}}$ – начальное значение ширины; ${{k}_{n}}$ – нормальная жесткость разлома.Взаимодействие матрицы и разлома осуществлялось посредством перетока жидкости между этими двумя системами. Для описания перетока использовалась двухточечная схема аппроксимации, когда объемный поток жидкости пропорционален перепаду давлений в центрах ячеек:
где ${{T}_{{ik}}}$ – проводимость между ячейками i и k.Метод определения проводимости между двумя ячейками зависит от типа этих ячеек. Для двух матричных ячеек имеем:
(17)
${{T}_{{i,k}}} = {{A}_{{i,k}}}{{k}_{i}}\frac{{{{{\mathbf{c}}}_{{i,k}}} \cdot {{{\mathbf{n}}}_{{i,k}}}}}{{{{{\left| {{{{\mathbf{c}}}_{{i,k}}}} \right|}}^{2}}}},$Для скважины и элемента разлома используется следующая формула [McClure, 2012]:
где: ${{a}_{k}}$ – динамическая ширина элемента разлома; ${{l}_{k}}$ – длина элемента.Для моделирования процесса деформации разлома использовался метод разрывных смещений [Shou, Crouch, 1995], рассматривалось только смещение элементов разлома вдоль его плоскости. При вычислении общей матрицы жесткости отбрасывались элементы строк матрицы, значение которых меньше на 4 порядка, чем соответствующий диагональный элемент. Таким образом, данная матрица получалась разреженной. Для каждого элемента скорость скольжения определяется как производная смещений по времени. Изначально по разлому скольжения нет (численно это описывается как скольжение с очень маленькой скоростью 10–10 м/с). Закон трения, действующего на разломе, используется в виде (5), (6). При описании скольжения применяется безынерционное приближение, трение на разломе уравновешивается касательным напряжением:
где: τ – касательное напряжение; ηv – слагаемое, позволяющее аппроксимировать инерционные эффекты при высоких скоростях деформации; $\eta = \frac{G}{{2{{v}_{s}}}}$ [Rice, 1993; Segall, 2010]; ${{v}_{s}}$ – скорость поперечных волн; ${{S}_{0}}$ – коэффициент сцепления.Для определения давления на каждом новом временном шаге использовалась неявная схема второго порядка точности:
(20)
$\frac{{{{{\left( {{{\varphi }}\rho } \right)}}^{{n + 1}}} - {{{\left( {{{\varphi }}\rho } \right)}}^{n}}}}{{{{{\left( {\Delta t} \right)}}^{n}}}} + {\text{div}}{{\left( {\rho v} \right)}^{{n + 1}}} = {{q}^{{n + 1}}},$(21)
${{{\mathbf{v}}}^{{n + 1}}} = - \frac{K}{{{{\mu }^{{{\text{n}} + 1}}}}}\left( {{\text{grad}}\left( {{{p}^{{n + 1}}}} \right) - g{{\rho }^{{n + 1}}}{\text{grad}}\left( z \right)} \right).$Данная система уравнений решалась с использованием метода Ньютона. Градиент и дивергенция вычислялись для каждой ячейки в интегральном смысле: слагаемое с дивергенцией – суммарный поток вещества из ячейки через все ее грани, градиент для каждой грани – разница давлений между давлениями в ячейках, для которых грань является общей.
Жидкость и поры считались сжимаемыми с постоянным коэффициентом сжатия, соответственно плотность флюида выражается:
(22)
$\frac{{d\rho }}{{dp}} = c\rho \Rightarrow {{\rho }}\left( p \right) = {{\rho }_{r}}{{e}^{{c\left( {p - {{p}_{r}}} \right)}}},$(23)
${{V}_{{pore}}}\left( p \right) = {{V}_{{pore,r}}}{{e}^{{{{c}_{r}}\left( {p - {{p}_{r}}} \right)}}},$В формуле (20) используется плотность флюида, но так как плотность в ячейках различается, используется средняя плотность для ячеек, которые имеют общую поверхность. Для решения задачи деформации разлома применялся метод Рунге–Кутта 3-го порядка точности с адаптивным шагом на основе решения 2-го порядка точности с обновлением скорости скольжения на каждом временном подшаге в соответствии с работой [Noda et al., 2009].
Параметры модели и результаты
Геометрические размеры исследуемой области 800 × 200 м, история забойного давления представлена на рис. 11. Рассмотрено несколько случаев, в которых проницаемость породы менялась от 0 до 2 мкД, начальная толщина разлома составляла 9 мкм, модуль сдвига G = 9 ГПа, нормальная жесткость разлома менялась в пределах от 8 × 1011 до 0.25 × 1011 а/м, что соответствует изменению проницаемости разлома в результате закачки от ~2 до ~270 раз. Начальное значение нормального напряжения на разломе $\sigma _{{n,0}}^{'}$ было 4.25 МПа, коэффициент ${{\mu }_{0}}$ был равен 0.6 [Cappa et al., 2018; Guglielmi et al., 2015]. Было использовано три значения для начального касательного напряжения на разломе (1.65, 1.8 и 2 МПа) и различные значения параметров закона трения: $a - \left( {{{b}_{1}} + {{b}_{2}}} \right) = 0.002$, $a = 0.015$, $\frac{{{{b}_{2}}}}{{{{b}_{1}}}} = 1{\kern 1pt} - {\kern 1pt} 10$, $\frac{{{{L}_{2}}}}{{{{L}_{1}}}} = 0.5{\kern 1pt} - {\kern 1pt} 10.$
Полученные в модели смещения являются достаточно медленными и асейсмичными. На рис. 12 показано, как меняется касательное напряжение вдоль разлома на момент времени 1400 с при изменении нормальной жесткости разлома и проницаемости породы. Для непроницаемого коллектора нормальная жесткость практически не влияет на значение максимального касательного напряжения (рис. 13а). Для слабопроницаемого коллектора увеличение нормальной жесткости ведет к росту максимального касательного напряжения, и эта зависимость более явная для больших значений поровой проводимости. Схожее поведение наблюдается для смещения в центре разлома (рис. 13в): для случая непроницаемой матрицы смещение не зависит от нормальной жесткости, но существует явно выраженная зависимость смещения от жесткости для слабопроницаемой матрицы. Положение максимума касательного напряжения (рис. 13б) зависит от нормальной жесткости во всех случаях, но в большей степени для непроницаемой матрицы. В целом зависимость этих величин от проницаемости матрицы нелинейная.
Рис. 12.
Профили вдоль полудлины для касательного напряжения и порового давления в конце расчета для различных значений нормальной жесткости и поровой проницаемости породы $({{\tau }_{0}} = 1.8~\,\,{\text{МПа)}}$): (a) – непроницаемая порода; (б) – малопроницаемая порода. Положение максимального касательного напряжения (${{L}_{{\tau ~{\text{ma}}x}}}$) и фронта давления (${{L}_{{{\text{pres}}}}})$ показано вертикальными линиями.
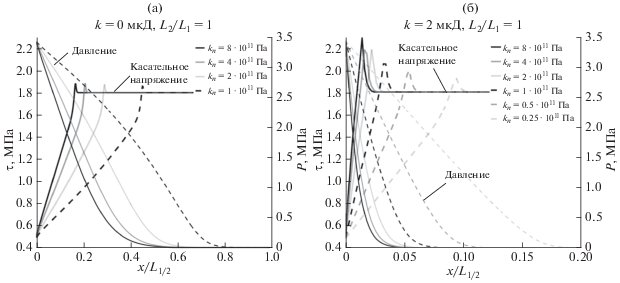
Рис. 13.
Влияние нормальной жесткости разлома, поровой проницаемости породы $({{\tau }_{0}} = 1.8~\,\,{\text{МПа)}}$ на: (а) – максимальное значение касательного напряжения в конце расчета; (б) – положения максимума касательного напряжения относительно длины фронта давления; (в) – смещение в центре разлома.

Параметры закона трения не влияют столь значительно на деформацию разлома в силу того, что в рассматриваемом случае скольжение всегда было асейсмическим. Если взять однопараметрический случай как базовый (${{{{L}_{2}}} \mathord{\left/ {\vphantom {{{{L}_{2}}} {{{L}_{1}}}}} \right. \kern-0em} {{{L}_{1}}}} = 1$), то максимальное изменение параметров деформации разлома относительно него не более чем ~2%.
Начальное значение касательного напряжения τ0 ожидаемо влияет на значение смещения разлома и длину смещения разлома (характеризуемую положением максимума касательного напряжения): с увеличением τ0 значения этих параметров возрастают. Но разница ${{\tau }_{{{\text{max}}}}} - {{\tau }_{0}}$ при этом практически не зависит от значения τ0. Стоит отметить, что рост смещения разлома (~32%) больше, чем соответствующий рост τ0 (21%), таким образом можно ожидать, что по мере приближения τ0 к критическому значению рост деформации разлома будет значительнее. Смещение разлома в центре в эксперименте [Guglielmi et al., 2015] было порядка 1.2 мм, что находится в соответствии с полученными результатами. Отметим, что в данной постановке вид закона трения не играет существенной роли.
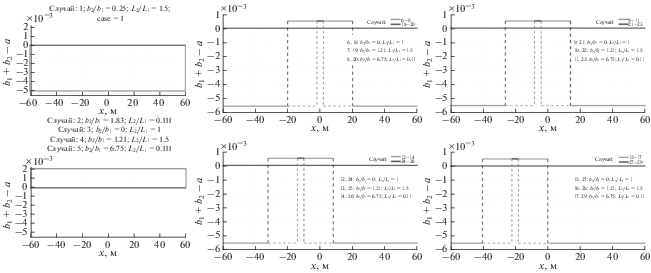
Рассмотрим, какое влияние на подвижки по разлому оказывают расстояние от разлома до скважины, скорость закачки флюида, расположение и длина зоны разупрочнения на разломе (рис. 14), параметры закона трения (b2/b1 и L2/L1 при неизменном значении величин b1+ b2 и L1+ L2). При этом значения касательного напряжения, действующего на разломе, варьировались так, чтобы во всех случаях условия получались сходными.
Пусть темп закачки постоянен, и закачка прекращается, как только суммарный объем достигает заданной величины. В такой постановке при выбранном наборе параметров максимальная скорость скольжения достигается вскоре после начала процесса скольжения. Это говорит о том, что на максимальную скорость скольжения не может влиять суммарный объем закачки (который определяет максимальное давление и время начала его падения), а влияют условия, сложившиеся на момент начала скольжения.
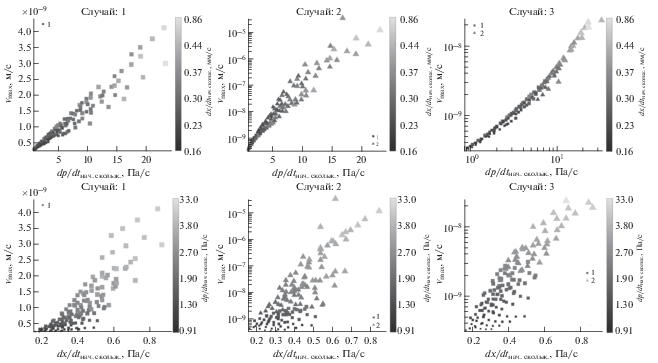
Примеры результатов расчетов представлены на рис. 15–рис. 17. Условимся называть линию, соединяющую скважину и ее проекцию на разлом, осью симметрии, а характеристики, обладающие симметрией относительно этой линии, будем называть симметричными. Из графиков видно (случаи 1, 2, 5), что, в случае симметричного расположения области разупрочнения на разломе при медленном скольжении, максимум скорости один и расположен в точке симметрии (рис. 16). При скоростях, больших примерно 10–9 м/с, таких максимумов два (рис. 16). При значительном смещении области разупрочнения влево (случаи 13–15 на рис. 14) максимум практически всегда один. Максимально достигаемая скорость подвижки зависит от совокупности двух параметров на момент начала скольжения: скорости роста давления и скорости роста длины части разлома, для которой перестает выполняться критерий Кулона–Мора из-за роста давления. Чем больше скорость роста зоны скольжения, тем больше максимально достигаемая скорость скольжения, а при прочих равных она больше при большей скорости роста давления (рис. 15, рис. 17).
Рис. 15.
Зависимость максимальной скорости скольжения от параметров в центре разлома в начале старта скольжения: по горизонтальной оси – скорость изменения давления в момент старта скольжения в центре разлома; по вертикальной – скорость роста области разлома, для которой не выполняется критерий Кулона–Мора (форма маркера характеризует, была ли максимальная скорость достигнута в единственной точке или в двух).

Рис. 16.
Пример динамики скорости скольжения и изменения касательного напряжения, вызванного деформацией разлома, вдоль длины разлома для двух случаев.

Рис. 17.
Максимально достигаемая скорость скольжения в зависимости от скорости изменения давления для различных случаев параметров закона трения. В легенде кривые с разными параметрами расположены в порядке убывания скорости.

При трении с упрочнением скорости скольжения получаются близкими к медленному крипу, возмущение давления не приводит к сейсмическим подвижкам. Скорости, близкие к сейсмическому режиму скольжения, реализуются, если трение на разломе описывается разупрочняющим законом, чему также способствует больший размер разупрочняющей области около центра разлома. В табл. 2 приведены критические жесткости, полученные для рассматриваемого набора параметров закона трения с разупрочнением, и соответствующие длины части разлома, начиная с которых его жесткость становится меньше критической жесткости. Если сопоставить эти величины с графиком на рис. 17, то видно, что чем меньше критическая длина части разлома, тем больше достигаемая скорость. Более того, для заданных условий при критической длине 43 м максимальные скорости практически не различаются для случаев, когда зона разупрочнения полностью покрывает разлом или достигает больших размеров (40 м). Для длины критической зоны в 45 м разница будет уже более заметной. Так же стоит отметить, что минимальные скорости скольжения наблюдались не тогда, когда весь разлом обладал упрочняющими свойствами, а когда присутствовала небольшая область разупрочнения в стороне от центра разлома.
Таблица 2.
Значение критической жесткости и критической длины разлома, при которой жесткость участка разлома становится равной критической жесткости, для разных случаев
| Случай | 2 | 3, 6, 9, 12, … | 4, 7, 10, 13, … | 5, 8, 11, 14, … |
|---|---|---|---|---|
| kcr, Па/м | 8.94 × 108 | 1.6 × 108 | 3.03 × 108 | 3.16 × 108 |
| Lcr, м | 15.3 | 85 | 45 | 43 |
Теперь обратимся к численным экспериментам, в которых менялись темпы и объем закачки. В этом случае значение величины критической жесткости так же играет основную роль. При одинаковом значении величины $\mu \sigma _{{n,0}}^{'}{\kern 1pt} - {\kern 1pt} {{\tau }_{0}}$ большая скорость скольжения наблюдается при большей скорости закачки, что соответствует более интенсивному возмущению на разломе (рис. 18). При этом зависимость максимальной скорости от скорости изменения давления в момент старта практически линейна (рис. 19). Если сравнивать с предыдущим набором расчетов, то в данном случае около половины точек находится в области, где dp/dt больше 10 Па/с. В данном диапазоне можно наблюдать нелинейность, при близких значениях скорости возрастания давления большая скорость скольжения не всегда наблюдается при большей скорости роста области скольжения, причем такая зависимость наблюдается лишь для случая, когда критическая длина области разлома составляет 43 м (случай 2).
Рис. 18.
Зависимость максимальной скорости скольжения от разницы начального значения силы трения и касательного напряжения. Показано для разных случаев темпа закачки.

Рис. 19.
Зависимость максимальной скорости скольжения от параметров в центре разлома в начале старта скольжения. Для верхних графиков: по горизонтальной оси – скорость изменения давления в момент старта скольжения в центре разлома (тон и размер маркера – скорость роста области разлома, для которой не выполняется критерий Кулона–Мора; форма маркера характеризует, была ли максимальная скорость достигнута в единственной точке или в двух). Для нижних графиков: по горизонтальной оси – скорость роста области скольжения (тон и размер маркера – скорость изменения давления).
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
При использовании закономерностей, предложенных как обобщение экспериментальных наблюдений, всегда остаются вопросы, связанные с возможностью использования тех или иных форм уравнений для описания широких классов явлений. Рассмотренный в настоящей работе 2‑параметрический закон трения rate-and-state впервые появился в работе [Gu et al., 1986], однако широко не использовался, не исследовались особенности поведения систем, которые им описываются. Для сложных динамических систем, к которым относятся геофизические системы, характерны хаотические процессы. Возможность описания хаотического движения в рамках слайдер-системы для однопараметрической версии закона трения рассматривалась в работе [Erickson et al., 2007], а для двухпараметрического закона – в работе [Hobbs, 1990]. Однако в первой работе хаотические решения были получены для нереально больших значений параметра $\varepsilon = \frac{{b - a}}{a}$, а во второй работе получены лишь два значения параметров, дающих хаотические движения. Анализ решений уравнений для слайдер-системы с двухпараметрическим законом трения, выполненный в настоящей работе, показал возникновение хаотических решений при значениях параметра ε, соответствующих наблюдениям. Сравнение с экспериментальными результатами, приведенными в работе [Будков и др., 2015], показывает, что двухпараметрический закон трения с модификацией путем введения вязкого слагаемого позволяет наиболее корректно описывать данные лабораторных экспериментов. Потенциальный интерес могут представлять модели и с большим числом переменных состояния, но ситуации, в которых дальнейшее усложнение уравнений rate-and-state было бы необходимо, авторам не известны.
Двухпараметрический закон трения дал возможность смоделировать сейсмичность, индуцированную закачкой жидкости при реализации Базельского геотермального проекта. Рассмотренная модель схожа по основным принципам с моделями, предложенными в работах [Baisch et al., 2010; Gisching et al., 2013], в которых сейсмичность также получалась в результате роста порового давления в зоне трещин, распределенных случайным образом в пространстве. Однако в этих работах сейсмический момент оценивался на основе известной статистики естественной сейсмичности в рассматриваемой области. В настоящей статье индуцированная сейсмичность моделируется без использования статистики наблюдаемой ранее естественной сейсмичности.
Исследования влияния закачки на сейсмичность проводились в работах [Norbeck, Horn, 2016; 2018] с использованием схожего с примененным в настоящей статье метода вложенных трещин в связанной постановке. Случай закачки в разлом рассматривался в работе [Cappa et al., 2018], изучался вопрос влияния нормальной жесткости на область деформации разлома. Рассматриваемые нами случаи касаются анализа влияния порового давления на характеристики деформации разлома и, в отличие от представленных ранее работ, также включают вопрос о влиянии фрикционных свойств разлома на возможность реализации сейсмической подвижки.
ЗАКЛЮЧЕНИЕ
Показано, что двухпараметрический закон трения rate-and-state позволяет описывать особенности развития подвижек по разломам и процесса возникновения сейсмических явлений при закачке жидкости, которые не удается описать с помощью однопараметрического закона трения. Так, уже при небольших значениях параметра, отвечающего за величину сброса напряжений при воздействии на разлом, удается получить режим хаотического скольжения, что согласуется с наблюдениями.
Предложен подход, позволяющий описывать процесс возникновения индуцированной сейсмичности при закачке флюида в недра. Расчеты, выполненные с использованием характеристик пород и условий закачки в ходе реализации Базельского геотермального проекта, позволили получить результаты, качественно и количественно близкие к наблюдавшейся сейсмичности.
Исследован вопрос влияния различных параметров на процесс деформации тектонического разлома в результате закачки. Показано, что нормальная жесткость разлома играет роль только в случае, если порода проницаема. Найдены условия, при которых в рамках предложенной модели возможно возникновение сейсмических подвижек. Показано, что определяющими параметрами, влияющими на параметры подвижки по разлому, возникающей при закачке, являются скорость изменения возмущения, скорость увеличения области разлома, подверженной скольжению. Свою роль играют также расположение зоны разупрочнения на разломе и параметры закона трения. Последние определяют критическую жесткость разлома и критическую длину, эти параметры играют ключевую роль в вопросе возможности возникновения сейсмического скольжения. Полученные результаты могут быть использованы для построения реалистичных сценариев развития сейсмической активности в районах воздействия на подземные флюидные системы.
Список литературы
Адушкин В.В., Турунтаев С.Б. Техногенная сейсмичность – индуцированная и триггерная. М.: ИДГ РАН. 2015. 364 с.
Будков А.М., Кочарян Г.Г., Новиков В.А., Крашенинников А.В. Модификация эмпирического закона трения “Rate and State friction law” для моделирования эпизодов медленного скольжения // Динамические процессы в геосферах. 2015. Выпуск 7. M.: ГЕОС. С. 22–30.
Кочарян Г.Г., Кишкина С.Б., Новиков В.А. Остапчук А.А. Медленные перемещения по разломам: параметры, условия возникновения, перспективы исследований // Геодинамика и тектонофизика. 2014. № 5(4). С. 863–891.
Рига В.Ю., Турунтаев С.Б., Остапчук А.А. Численное моделирование сейсмогенерирующих подвижек на основе модели rate-state экспериментов межблокового скольжения // Динамические процессы в геосферах. 2018. № 10. С. 99–109.
Baisch S., Voros R., Rothert E Stang H., Jung R., Schellschmidt R. A numerical model for fluid injection induced seismicity at Soultz-sousForets // International J. Rock Mechanics and Mining Sciences. 2010. V. 47. № 3. P. 405–413.
Budkov A.M., Kocharyan G.G. Experimental Study of Different Modes of Block Sliding along Interface. Part 3. Numerical Modeling // Physical Mesomechanics. 2017. V. 20. № 2. P. 203–208. https://doi.org/10.1134/S1029959917020102
Cappa F., Guglielmi Y., Nussbaum C., Birkholzer J. On the Relationship Between Fault Permeability Increases, Induced Stress Perturbation, and the Growth of Aseismic Slip During Fluid Injection // Geophys. Res. Lett. 2018. V. 45. № 11. P. 11–20.
Carpenter B.M., Saffer D.M., Marone C. Frictional properties of the active San Andreas Fault at SAFOD: Implications for fault strength and slip behavior // J. Geophys. Res.: Solid Earth. 2015. V. 120. № 7. P. 5273–5289.
Carpenter B.M., Scuderi M.M., Collettini C., Marone C. Frictional heterogeneities on carbonate-bearing normal faults: Insights from the Monte Maggio Fault, Italy // J. Geophys. Res.: Solid Earth. 2014. V. 119. № 12. P. 9062–9076.
Diechmann N., Kraft T., Evans K.F. Identification of faults activated during the stimulation of the Basel geothermal project from cluster analysis and focal mechanics of the larger magnitude events // Geothermics, Elsevier. 2014. V. 52. P. 84–97. https://doi.org/10.1016/j.geothermics.2014.04.001
Dieterich J.H. Modeling of rock friction: 1. Experimental results and constitutive // J. Geophys. Res. 1979. V. 84. № B5. P. 2161–2168.
Dinske C. Interpretation of fluid induced seismicity and hydrocarbon of Basel and Cotton Valley. Doctoral dissertation, Free University of Berlin. 2011. 151 p. https://doi.org/10.17169/refubium-15993
Ellsworth W., Llenos A., McGarr A., Michael A., Rubinstein J., Mueller C., Petersen M., Calais E. Increasing seismicity in the U.S. midcontinent: Implications for earthquake hazard // The Leading Edge. 2015. V. 34. № 6. P. 618–626. https://doi.org/10.1190/tle34060618.1
Ellsworth W.L., Giardini D., Townend J., Ge S., Shimamoto T. Triggering of the Pohang, Korea, Earthquake (Mw 5.5) by Enhanced Geothermal System Stimulation // Seismological Research Letters. 2019. V. 90. № 5. P. 1844–1858. https://doi.org/10.1785/0220190102
Erickson B., Birnir B., Lavallée D. A model for aperiodicity in earthquakes // Nonlin. Processes Geophys. 2008. V. 15. P. 1–12. https://doi.org/10.5194/npg-15-1-2008
Gischig V.S., Wiemer S. A stochastic model for induced seismicity based on non-linear pressure diffusion and irreversible permeability enhancement // Geophys. J. Int. 2013. V. 194. №2. P. 1229–1249.
Gu J.-C., Rice J.R., Ruina A.L., Tse S.T. Slip motion and stability of a single degree of freedom elastic system with rate and state dependent friction // Apl. Mech. Phys. Solids. 1984. V. 32. № 3. P. 167–196.
Guckenheimer J., Holmes P. Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. Springer-Verlag, New York. 1st edition. 1983. 462 p.
Guglielmi Y., Cappa F., Avouac J.-P., Henry P., Elsworth D. Seismicity triggered by fluid injections induced aseismic slip // Science. 2015. V. 348. № 6240. P. 1224–1226.
Häring M.O., Schanz U., Ladner F. Characterisation of the Basel 1 enhanced geothermal // Geothermics. 2008. V. 37. № 5. P. 469–495.
Hobbs B.E. Chaotic behaviour of frictional shear instabilities // Rockbursts and Seismicity in Mine. Mineapolis. 1990. P. 87–91.
Kanamori H. The energy release in great earthquakes // J. Geophys. Res. 1977. V. 82. № 20. P. 2981–2987. https://doi.org/10.1029/JB082i020p02981
Kato N. Interaction of slip on asperities: Numerical simulation of seismic cycles on a two-dimensional planar fault with nonuniform frictional property // J. Geophysical Res. 2004. V. 109. B12306. 17 p. https://doi.org/10.1029/2004JB003001
Kato N. Repeating Slip Events at a Circular Asperity: Numerical simulation with a rate-and-state-dependent friction law // Bull. Earthq. Res. Inst. Univ. Tokyo. 2003. V. 78. P. 151–166.
Kato N., Tullis T.E. A composite rate-and state dependent law for rock friction // Geophys. Res. Lett. 2001. V. 28(6). P. 1103–1106.
Kocharyan G.G., Markov V.K., Ostapchuk A.A., Pavlov D.V. Mesomechanics of shear Resistance along a Filled Crack // Phys Mesomech. 2014. V. 17. № 2. P. 123–133. https://doi.org/10.1134/S1029959914020040
Lay T. Seismological Grand Challenges in Understanding Earth’s Dynamic Systems. Report to the National Science Foundation – Iris Consortium. 2009. 84 p.
Lie K.-A. An introduction to reservoir simulation using MATLAB: User Guide for the Matlab Reservoir Simulation Toolbox (MRST). SINTED ICT. 2016. 392 p.
Marone C., Saffer D.M. The Mechanics of Frictional Healing and Slip Instability During the Seismic Cycle // Treatise on Geophysics. Elsevier. 2015. P. 111–138.
McClure M.W. Modeling and characterization of hydraulic stimulation and induced seismicity in geothermal and shale gas reservoirs: Doctoral dissertation. Stanford University. 2012. 369 p.
McGarr A., Simpson D., Seeber L. Case histories of induced and triggered seismicity / W.H.K. Lee, H. Kanamori, eds. International handbook of earthquake and engineering seismology: Academic Press. 2002. V. 81A. P. 647–660.
Noda H., Dunham E., Rice J.R. Earthquake ruptures with thermal weakening and the operation of major faults at low overall stress levels // J. Geophys. Res. 2009. V. 114. B07302. 27 p. https://doi.org/10.1029/2008JB006143
Norbeck J., Horne R. Maximum magnitude of injection-induced earthquakes: A criterion to assess the influence of pressure migration along faults // Tectonophysics. 2018. V. 733. P. 108–118. https://doi.org/10.1016/j.tecto.2018.01.028
Norbeck J.H., Horne R.N. Evidence for a transient hydromechanical and frictional faulting response during the 2011 Mw 5.6 Prague, Oklahoma earthquake sequence // J. Geophys. Res.: Solid Earth. 2016. V. 121. P. 8688–8705, https://doi.org/10.1002/2016JB013148
Okazaki K., Katayama I. Slow stick slip of antigorite serpentinite under hydrothermal conditions as a possible mechanism for slow earthquakes // Geophys. Res. Lett. 2015. V. 42. № 4. P. 1099–1104.
Press W.H., Teukolsky S.A., Vatterling W.T., Flannery B.P. Numerical recipes 3rd edition: the art of scientific computing. Cambridge University Press New York. 2007. 1276 p.
Rice J.R. Spatio-temporal complexity of slip on a fault // J. Geophys. Res. 1993. V. 98. № B6. P. 9885–9907.
Segall P. Earthquake and Volcano Deformation. Princeton University Press. Princeton. 2010. 456 p.
Shou K.J., Crouch S.L. A higher order Displacement Discontinuity Method for analysis of crack problems // Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995. V. 32. № 1. P. 49–55.
Witherspoon P.A., Wang J.S.Y., Iwai K., Gale J.E. Validity of cubic law for fluid flow in a deformable rock fracture // Water Resour. Res. 1980. V.16. P. 1016–1024.
Дополнительные материалы отсутствуют.