Физика Земли, 2022, № 6, стр. 175-191
Интегральная формула решения задачи теплового сопряжения для слоистых сред. Структура интегрального оператора
И. В. Ладовский 1, Д. Д. Бызов 1, П. С. Мартышко 1, *
1 Институт геофизики им. Ю.П. Булашевича УрО РАН
г. Екатеринбург, Россия
* E-mail: pmart3@mail.ru
Поступила в редакцию 23.03.2022
После доработки 27.04.2022
Принята к публикации 30.04.2022
- EDN: GRZXQN
- DOI: 10.31857/S0002333722060084
Аннотация
В пространстве обобщенных функций, заданном на множестве преобразований свертки, получено в интегральной форме решение задачи теплового сопряжения для модели слоистых сред с кусочно-однородным распределением теплопроводности и интегрируемой функцией тепловых источников. При малом контрасте теплопроводности сопредельных слоев выписано аналитическое представление температуры и теплового потока в виде суммы составляющих от внутренних (коровых) и внешних (мантийных) источников поля. Получено интегральное уравнение и разработан численный алгоритм пересчета мантийной составляющей теплового потока с уровня земной поверхности на границу “кора–мантия” через слоисто-неоднородную по теплопроводности среду.
1. ВВЕДЕНИЕ
Тепловой поток как индикатор кондуктивного теплообмена в твердых телах является важнейшей энергетической характеристикой термического состояния литосферы и определяет направление развития глубинных тектонических процессов.
Необходимость изучения строения низов коры и верхней мантии определяет актуальность создания трехмерных математических образов неоднородной геологической среды с использованием, в том числе, данных геотермических методов геофизических исследований [Crough, Thompson, 1976]. Интерпретация геотермических данных во взаимосвязи с полями иной эндогенной природы снижает степень неоднозначности геолого-геофизических моделей и повышает надежность представлений о глубинном строении и вещественном составе структурно геологических комплексов на разных иерархических уровнях ее организации.
Энергетический баланс земной коры по суммарному тепловому потоку формируют объемные источники радиогенной теплогенерации; перераспределение теплового потока в неоднородной по теплопроводности среде контролирует параметр теплопроводной контрастности. Мантийный тепловой поток обобщает глубинные теплопотери всей планеты в целом и обеспечивает тепловое взаимодействие между корой и мантией [Sclater et al., 1980]. Поэтому, исходя из целеполагающей идеи комплексирования гравитационных и тепловых полей, мы предварительно разработали новый аналитический метод решения задачи теплового сопряжения как граничной задачи теории потенциала, а затем построили алгоритм расчетов, близкий по технологии к вычислительным схемам количественной интерпретации гравитационных аномалий.
2. ИСХОДНЫЕ ДАННЫЕ ДЛЯ ГЕОТЕРМИЧЕСКИХ МОДЕЛЕЙ
Примем соглашение о терминологии для уточнения названия “поток”. Тепловой поток – это интегральная характеристика, равная количеству тепловой энергии, проходящей через поверхность в единицу времени. Стационарный тепловой поток не меняется на любом временном интервале. Тепловой поток с единицы поверхности называется плотностью теплового потока (мВт/м2). В практике геотермических измерений плотность теплового потока принято называть “тепловым потоком”. Хотя на образцах конечных размеров измеряется именно тепловой поток, а затем пересчитывается в его плотность. Отсюда общеприняты определения: “данные теплового потока”, “карты теплового потока” и т.д. В этом контексте здесь и далее мы принимаем сокращение “тепловой поток”, понимая при этом его плотность.
Геотермическая модель верхней части литосферы аппроксимируется неоднородным пластом с горизонтальными границами внешнего обрамления. Плотностная и геотермическая модели заданы в одинаковом формате. За основу нами принята авторская модель трехмерного распределения сеточной плотности до глубины 80 км и площадью раскрытия на земной поверхности в пределах градусной трапеции 60°–68° с.ш., 48°–72°в.д. [Martyshko et al., 2019]. Трехмерное распределения теплофизических параметров (теплогенерации и теплопроводности) пересчитываются по базе сеточной плотностной модели ${{\rho }}\left( {x,y,z} \right)$ и данных статистической зависимости “плотность – теплогенерация” и “плотность–теплопроводность” [Булашевич, 1983; Голованова, 2005]. Их конфигурация образует пространственные формы, соответствующие блочной структуре распределения источников теплогенерации $Q\left( {x,y,z} \right)$ в земной коре и послойному распределению коэффициента теплопроводности ${{\lambda }}\left( {x,y,z} \right)$ в коре и мантии.
Геологическая информативность интерпретации тепловых полей проявляется в сопоставлении расчетных и “наблюденных” значений тепловых потоков, редуцированных на изотермическую граничную плоскость “нейтрального” слоя. В отличие от глубинных температур, накопленный массив данных о поверхностных тепловых потоках и сопутствующий им картографический материал находятся в открытом доступе и могут использоваться для всестороннего геотермического анализа, с возможностью виртуальной корректировки при сопоставлении с результатами математического моделирования.
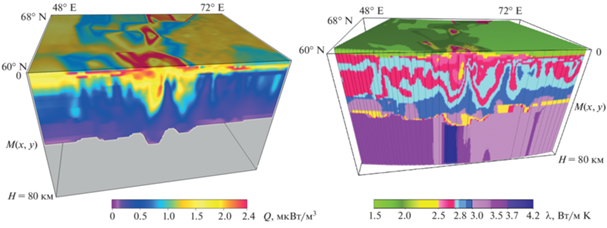
Рис. 1.
Сеточная 3D-модель распределения источников радиогенной теплогенерации в земной коре (слева) и послойного распределение теплопроводности в земной коре и верхней мантии (справа) для основных породообразующих комплексов горных пород.
Приповерхностный тепловой поток вычислен по результатам измерений температуры и теплопроводности в параметрических (или разведочных) скважинах глубокого бурения и привязан к разреженной градусной сети геотермических пикетов. Выборка экспериментальных данных для Северного и Приполярного Урала получена по результатам скважинных геотермических исследований В.А. Щапова и существенно дополнены сходными данными И.В. Головановой и А.Д. Дучкова [Щапов, 2000; Голованова, 2005; Дучков и др., 2013]. В пределах градусной трапеции 60°–68° с.ш., 48°–72° в.д. наблюденные 234 значения теплового потока пересчитаны на регулярную сетку 11 зоны картографической проекции Гаусса–Крюгера с шагом (10 × 10) км2. Соответствующая карта в изолиниях, скомпонованная в виде рельефа трехмерной поверхности, изображена на (рис. 2).
Рис. 2.
Карта наблюденных значений теплового потока (в изолиниях), отнесенная к верхней изотермической граничной плоскости (плоскости “наблюдений”). Точками нанесено плановое положение скважин, по разрезу которых измерялись распределения температур.
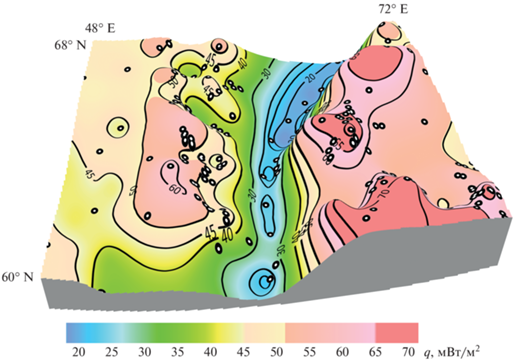
Осевая зона Приуральского прогиба (Уральская геосинклиналь) характеризуется очень низким тепловым потоком 20–30 мВт/м2 в сравнении с платформенными областями, где плотность теплового потока достигает 40–70 мВт/м2 [Булашевич, Щапов, 1983]. Резкое увеличение теплового потока при переходе от Восточно-Уральской складчатой системы герцинского возраста к палеозойскому фундаменту сравнительно молодой Западно-Сибирской плиты подчеркивает возможное существование коллизионного надвига в процессе тектонической эволюции [Дучков, Соколова, 1997].
3. ОСНОВЫ ОБОБЩЕННО-НЕПРЕРЫВНОГО АНАЛИТИЧЕСКОГО АЛГОРИТМА
Методы количественной интерпретации стационарных тепловых и гравитационных полей очень близки. Это потенциальные поля, которые удовлетворяют уравнению Пуассона и относятся к классу субгармонических интегрируемых функций. Коэффициенты (и свободные члены) соответствующих уравнений аппроксимируются распределением плотностных и теплофизических параметров неоднородной среды. В задаче гравиметрии не предусмотрена явная постановка граничных условий, кроме асимптотических. В связи с чем, ее решение записывается напрямую в виде интеграла Пуассона по области сосредоточения аномальных масс [Martyshko et al., 2020].
В геотермических моделях стационарных температур важную роль играет верхняя граничная плоскость, на которую замыкаются все силовые линии теплового поля. Это плоскость в “нейтральном слое” вблизи земной поверхности. Обычно геотермические исследования градиентов температуры и тепловых потоков производятся ниже “нейтрального слоя”; до того же уровня ведутся модельные расчеты. “Нейтральный слой” определяется как зона постоянных годовых температур или зона максимального проникновения сезонных колебаний температуры солнечной радиации. Он вводится чисто из методических соображений, чтобы обосновать наличие изотермической границы как граничной поверхности задачи Дирихле для расчета стационарных температур и тепловых потоков в верхней части литосферы. Любая поверхность (но, желательно, плоскость) в “нейтральном слое” будет поверхностью постоянных температур. И несущественно, на какой поверхности в “нейтральном слое” будет задано граничное условие Дирихле. В частности, подошва слоя может приниматься за изотермическую граничную плоскость.
Стационарная модель кондуктивной (или молекулярной) теплопроводности учитывает распределение только двух теплофизических параметров среды: радиогенной теплогенерации $Q$ и теплопроводности ${{\lambda }}$. Их связывает условие неразрывности для стационарного теплового потока q [Карслоу, Егер, 1964]:
При постоянной теплопроводности λ любое (но интегрируемое) распределение объемных источников Q не создает принципиальных затруднений при решении тепловых задач, поскольку алгоритмически они тождественны задачам для гравитационного потенциала (γ – гравитационная постоянная) с эквивалентной массовой плот-ностью 4πγQ/λ [Тихонов 1999]. Если теплопроводность переменна, то к эндогенным аномалиям тепловых источников добавляются аномалии теплопроводной контрастности, связанные с рефракцией теплового потока на контакте разно-теплопроводных сред. Это тип краевых задач линейного сопряжения с граничными условиями IV рода [Лыков, 1967; Светов, Губатенко, 1988]. Решение граничной задачи для полупространства в “гравитермическом” приближении элементарно и записывается через обычный интеграл Пуассона для трехмерного потенциала (потенциала Ньютона); решение задачи теплового сопряжения требует разработки специальных аналитических алгоритмов. Поэтому, исходя из целеполагающей идеи комплексирования гравитационных и тепловых полей, мы предварительно разработали новый аналитический метод решения задачи теплового сопряжения как граничной задачи теории потенциала, а затем построили алгоритм расчетов, близкий по технологии к вычислительным схемам количественной интерпретации гравитационных аномалий.
Определим метрические и теплофизические параметры геотермической модели слоистой среды с кусочно-однородным распределением коэффициента теплопроводности ${{\lambda }}$ и интегрируемой функцией тепловых источников $Q$. Модельная (расчетная) область D представляет собой пласт бесконечного простирания мощности Н с горизонтальными границами внешнего обрамления. В системе прямоугольных координат $\left( X \right) = \left( {x,y,z} \right)$ горизонтальная плоскость $\left( {x,0,y} \right)$ совпадает с верхней граничной плоскостью, ось $\left( {0,z} \right)$ направлена вертикально вниз по глубине пласта. Верхняя граница ${{S}_{0}}:~\left( {z = 0} \right)$ условно принята за уровень земной поверхности, точнее за изотермическую граничную плоскость в “нейтральном” слое; нижняя граница ${{S}_{H}}\,:\,\left( {~z = H} \right)$ – вспомогательная адиабатическая плоскость задания внешней (восходящей) составляющей глубинного теплового потока. Внутренние граничные поверхности $~{{S}_{k}}:\left( {z = {{z}_{k}}\left( {x,y} \right)} \right);~$ $\left( {k = 1 \ldots {\text{M}}} \right)$ разделяют область D на (M + 1) криволинейных слоев. Выше границы ${{S}_{k}}$ теплопроводность постоянна и равна ${{{{\lambda }}}_{k}}$; ниже равна ${{{{\lambda }}}_{{k + 1}}}$. Из семейства внутренних контактных границ особо выделена граница ${{S}_{M}}:\left( {z = {{z}_{{\text{M}}}}\left( {x,y} \right)} \right)$– граница раздела “кора–мантия” (“М” или поверхность Мохо). Выше границы “М”, т.е. только в земной коре, сосредоточены эндогенные источники тепла ${{Q}_{k}}$; их плотность $Q\left( X \right) = \bigcup\nolimits_{\left( k \right)} {{{Q}_{k}}} $ предполагается интегрируемой.
Принцип редукции Дюамеля предписывает включение граничных условий в операторную часть дифференциального уравнения [Тихонов, Самарский, 1999]. В работе [Ладовский и др., 2019] предложен способ преобразования двусторонних контактных условий теплового сопряжения в плотность источников эквивалентного простого слоя. В его основе лежит функциональное представление разрывного коэффициента обратной теплопроводности слоистой среды с последующим переходом к дифференциальным операциям в континуальном пространстве обобщенно-непрерывных функций.
Обобщенно-непрерывный оператор для уравнения теплопроводности (3.1) с разрывными коэффициентами, по существу, является уравнением Пуассона с двумя типами источников в его правой части:
(3.2)
${{\nabla }^{2}}T = - \nabla \left( {\frac{1}{{\hat {\lambda }}}} \right){\mathbf{q}} - \left( {\frac{1}{{\hat {\lambda }}}Q} \right).$Объемные источники $\left[ {{{Q\left( X \right)} \mathord{\left/ {\vphantom {{Q\left( X \right)} {\lambda \left( X \right)}}} \right. \kern-0em} {\lambda \left( X \right)}}} \right]$ – источники первичного поля для модели слоисто-неоднородного пласта; поверхностные источники $\left[ {\nabla \left( {{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0em} \lambda }} \right){\mathbf{q}}} \right]$ – это вторичные источники эквивалентного простого слоя с подлежащей определению поверхностной плотностью.
Разрыв функции обратной теплопроводности задан ступенчатой функцией области $H\left( {{{{{\Phi }}}_{k}}} \right)$, [Гельфанд, Шилов, 1959]. Аргумент функции области – неявное уравнение контактной поверхности ${{S}_{k}}:\left( {{\text{\;}}{{{{\Phi }}}_{k}}\left( X \right) = z - {{z}_{k}}\left( {x,y} \right) = 0} \right)$
(3.3)
$\frac{1}{{{{\hat {\lambda }}}\left( X \right)}} = \frac{1}{{{{{{\lambda }}}_{1}}}} + \mathop \sum \limits_{k = 1}^M \left( {\left( {\frac{1}{{{{{{\lambda }}}_{{k + 1}}}}} - \frac{1}{{{{{{\lambda }}}_{k}}}}} \right)H\left( {{{{{\Phi }}}_{k}}\left( X \right)} \right)} \right).~$Обобщенная производная для функции области $H\left( {{{{{\Phi }}}_{k}}} \right)$ равна поверхностной дельта-функции ${{\delta }}\left( {{{{{\Phi }}}_{k}}} \right);~$градиент уравнения границы ${{{{\Phi }}}_{k}}$ сориентирован по направлению оси глубин и пропорционален вектору единичной нормали ${{{\mathbf{N}}}_{k}}$ к поверхности ${{S}_{k}}$:
(3.4)
$H_{{{\Phi }}}^{'}\left( {{{{{\Phi }}}_{k}}} \right) = {{\delta }}\left( {{{{{\Phi }}}_{k}}} \right);\,\,\,\,{{~\nabla {{{{\Phi }}}_{k}}} \mathord{\left/ {\vphantom {{~\nabla {{{{\Phi }}}_{k}}} {\left\| {\nabla {{{{\Phi }}}_{k}}} \right\|}}} \right. \kern-0em} {\left\| {\nabla {{{{\Phi }}}_{k}}} \right\|}} = {{{\mathbf{N}}}_{k}}\left( {{{S}_{k}}} \right).$Источники простого слоя в уравнении (3.2) заданы комбинацией формул (3.3)–(3.4):
Скачок нормальных производных температуры (или электрического потенциала) в двусторонней окрестности контакта ${{S}_{k}}$ приравнивается к поверхностной плотности простого слоя ${{\nu }_{k}}\left( {{{S}_{k}}} \right)$ [Мартышко, 1986]:
(3.5)
$\begin{gathered} {{\nu }_{k}}\left( {{{S}_{k}}} \right) = - {{{\mathbf{N}}}_{k}}\left( {\frac{{\mathbf{q}}}{{{{\lambda }_{{k + 1}}}}} - \frac{{\mathbf{q}}}{{{{\lambda }_{k}}}}} \right) = \\ = - {{{\mathbf{N}}}_{k}}\left( {\nabla {{T}_{{k + 1}}} - \nabla {{T}_{k}}} \right) = 2{{\varepsilon }_{k}}\left( {{{{\mathbf{N}}}_{k}} \cdot \nabla T} \right).~ \\ \end{gathered} $Здесь $\left( {{{{\mathbf{N}}}_{k}} \cdot \nabla T} \right)$ – прямое значение нормальной составляющей градиента температуры на поверхности ${{S}_{k}}$, равное полусумме Дирихле его лево- и правосторонних значений; ${{{{\varepsilon }}}_{k}}$ – параметр теплопроводной контрастности k-го и (k + 1)-го сопредельных слоев:
Двусторонние условия теплового сопряжения в формате эквивалентного простого слоя (3.5) заложены в обобщенно непрерывный оператор редуцированного уравнения теплопроводности (3.2):
(3.6)
${{\nabla }^{2}}T - \mathop \sum \limits_{k = 1}^M {{{{\nu }}}_{k}}\left( {{{S}_{k}}} \right)\left\| {\nabla {{{{\Phi }}}_{k}}} \right\|*{{\delta }}\left( {{{{{\Phi }}}_{k}}} \right) + \frac{{Q\left( X \right)}}{{{{\lambda }}\left( X \right)}} = 0.~$Для замыкания области решения уравнения (3.6) достаточно постановки односторонних условий на внешних границах ${{S}_{0}}$ и ${{S}_{H}}$ неоднородного пласта:
(3.7)
${{\left. {T\left( X \right)} \right|}_{{X \in {{S}_{0}}}}} = {{\theta }}\left( {{{S}_{0}}} \right);\,\,\,\,~{{\left. {\left( {{{{\mathbf{N}}}_{{{{S}_{H}}}}} \cdot \nabla T} \right)} \right|}_{{X \in {{S}_{H}}}}} = {{\mu }}\left( {{{S}_{H}}} \right).~$Здесь ${{\theta }}\left( {{{S}_{0}}} \right) = {{{{\theta }}}_{0}}$ – постоянная температура на верхней границе пласта $\left( {{{S}_{0}}\,:~z = 0} \right)$; $~{{\mu }}\left( {{{S}_{H}}} \right)$ – геотермический градиент на его нижней границе $\left( {{{S}_{H}}\,:~z = H} \right)$.
Стационарность краевого режима обеспечивает верхнее граничное условие постоянства температуры (внутренняя задача Дирихле) и нижнее – по восходящему глубинному тепловому потоку (внутренняя задача Неймана). Условие Неймана опосредованно учитывает стационарный теплообмен на границе “кора–мантия”. Если температура в “нейтральном слое” равна нулю, а поток тепла через нижнюю границу пласта отсутствует, то смешанные условия внутренней краевой задачи становятся однородными. Однородные условия по температуре или тепловому потоку можно рассматривать, как предельную реализацию контактных условий теплового сопряжения при бесконечно больших или малых значениях коэффициентов теплопроводности в сопредельных областях, внешних по отношению к обрамляющим границам модельного пласта.
4. ИНТЕГРАЛЬНАЯ ФОРМУЛА ЗАДАЧИ СОПРЯЖЕНИЯ ДЛЯ СЛОИСТОГО ПЛАСТА
Совокупность интегральных преобразований свертки редуцированного уравнения (3.6) образует линейное подпространство обобщенных функций. Ядром преобразования является функция Грина, структура и вид которой находятся из граничных условий (3.7) однородной задачи Дирихле–Неймана. В нашей предыдущей работе [Martyshko et al., 2020] обосновано решение задачи теплового сопряжения при помощи обобщенной формулы Грина и получены аддитивные интегральные формулы, разделенные по аномалиям от источников и граничным условиям.
Пусть $A\left( X \right)$ – параметрическая точка вычисления поля внутри пласта, $C\left( X \right)$– точка локализации источников и ${{P}_{k}}\left( X \right)$ – точка на контактной поверхности ${{S}_{k}}$. Функция Грина $G\left( {A,C} \right)$ приравнивается к потенциалу точечного источника внутри однородного пласта с однородными граничными условиями Дирихле–Неймана на его замкнутой внешней поверхности ${{S}_{0}} \cup {{S}_{H}}$. Выполнив преобразования, предписанные интегральной формулой Грина [Тихонов, Самарский, 1999; Владимиров, Жаринов, 2000], выделим из общего решения две составляющие для температуры. Это потенциал первичного поля тепловых источников и вторичный потенциал источников простого слоя:
(4.1)
$T\left( A \right) = W\left( A \right) - \frac{1}{{4{{\pi }}}}\sum\limits_{k = 1}^M {\iint\limits_{{{S}_{k}}} {{{{{\nu }}}_{k}}}} \left( {{{S}_{k}}} \right)G\left( {A,{{P}_{k}}} \right)d{{S}_{k}}.$Здесь $W\left( A \right)$ – аддитивное решение для температуры в “гравитермическом” приближении, заданное суммой внутренних ${Q \mathord{\left/ {\vphantom {Q {{\lambda }}}} \right. \kern-0em} {{\lambda }}}$ и внешних ${{\mu }}\left( H \right)$ источников теплового поля:
(4.2)
$\begin{gathered} W\left( A \right) = {{\theta }_{0}} + \frac{1}{{4\pi }}\iiint\limits_D {\frac{{Q\left( C \right)}}{{\lambda \left( C \right)}}}G\left( {A,C} \right)d{{\tau }_{C}} + \\ + \,\,\frac{1}{{4\pi }}\iint\limits_{{{S}_{H}}} {\mu \left( {{{P}_{H}}} \right)}G\left( {A,~{{P}_{H}}} \right)d{{S}_{H}}. \\ \end{gathered} $Неизвестные плотности простых слоев ${{{{\nu }}}_{k}}\left( {{{S}_{k}}} \right)$ для вторичной составляющей потенциала (4.1) можно найти из системы интегральных уравнений (3.5). В приближении малого контраста теплопроводностей сопредельных слоев систему уравнений (3.5) заменяет список интегральных формул:
(4.3)
${{\nu }_{k}}\left( {{{S}_{k}}} \right) = 2{{\varepsilon }_{k}}\left( {{{{\mathbf{N}}}_{k}} \cdot {{\nabla }_{{{{P}_{k}}}}}} \right)W\left( {{{P}_{k}}} \right).~$Неявное решение для температуры (4.1) в линейном по ε приближении (4.3) принимает тот же вид интегральной свертки с аддитивной структурой, что и первичный потенциал (4.2):
(4.4)
$\begin{gathered} T\left( A \right) = \frac{1}{{4\pi }}\iiint\limits_D {\frac{{Q\left( {{{\tau }_{C}}} \right)}}{{\lambda \left( {{{\tau }_{C}}} \right)}}}K\left( {A,C} \right)d{{V}_{C}} + \\ + \,\,\frac{1}{{4\pi }}\iint\limits_{{{S}_{H}}} {\mu \left( {{{P}_{H}}} \right)}K\left( {A,{{P}_{H}}} \right)d{{S}_{H}}.~ \\ \end{gathered} $Но в отличие от функции Грина, ядро K(A, C) преобразующего оператора (4.4) учитывает рефракцию теплового поля на всех внутренних границах слоистого пласта:
(4.5)
$\begin{gathered} K\left( {A,C} \right) = G\left( {A,C} \right) - \\ - \,\,\frac{1}{{2\pi }}\mathop \sum \limits_{k = 1}^M {{\varepsilon }_{k}}\iint\limits_{{{S}_{k}}} {G\left( {A,{{P}_{k}}} \right)}\left( {{{{\mathbf{N}}}_{k}} \cdot {{\nabla }_{{{{P}_{k}}}}}} \right)G\left( {{{P}_{k}},C} \right)d{{S}_{{{{P}_{k}}}}}. \\ \end{gathered} $Как видим, в поле температур влияние аномалиеобразующих факторов разделено: эндогенные аномалии тепловых источников и глубинный тепловой поток формируют однотипные рефракционные картины силовых линий. Это дает возможность использовать двухэтапную схему количественной интерпретации тепловых полей в слоисто-неоднородных средах. Сначала вычисляется первичный “гравитермический” потенциал $W$ и его градиент проектируется по нормали на все поверхности тепловых контактов. Затем вычисляются плотности простых слоев (4.3) и находится общее решение для температуры (4.4)–(4.5). Поскольку гравитационные и расчетные тепловые поля удовлетворяют общему принципу суперпозиции, то вариации плотностных и теплофизических параметров можно аппроксимировать сеточными функциями. Сеточный аддитивный алгоритм заложен в основе комплексирования гравитационных и геотермических полей при построении моделей глубинного строения земной коры и верхней мантии.
5. УРАВНЕНИЕ ОБРАТНОЙ ЗАДАЧИ АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ ТЕПЛОВЫХ ПОЛЕЙ
Интерпретация тепловых полей и ее геолого-геофизическая информативность, прежде всего, проявляется в сопоставлении расчетных и “наблюденных” значений тепловых потоков, редуцированных на верхнюю изотермическую граничную плоскость “нейтрального” слоя. В отличие от глубинных температур, измеренных по редкой сети выстоявших скважин вдоль их одномерных разрезов, накопленный массив данных о поверхностных тепловых потоках и сопутствующий им картографический материал находятся в открытом доступе и могут использоваться для всестороннего количественного анализа.
Решение прямой задачи геотермии для обособленной части верхней литосферы возможно лишь в том случае, когда искомые распределения температур (или тепловых потоков) расчетной модели замкнуты граничными условиями. Верхнее граничное условие Дирихле соответствует постоянной температуре в “нейтральном слое”; нижнее граничное условие Неймана задается по восходящему тепловому потоку, что косвенно учитывает тепловое взаимодействие между корой и мантией. Но тепловой поток из мантии (за исключением тривиального случая) является неизвестной граничной функцией прямой задачи для вышележащих слоев. В таких случаях обычно используют схемы многократного интуитивного подбора. Меняя распределение мантийного потока на глубинной границе, добиваются совпадения наблюденных и вычисленных значений потока на земной поверхности [Kukkonen et al., 1997]. Мы предлагаем детерминированный и более наглядный способ вычисления глубинной составляющей теплового потока на границе “кора–мантия”. Способ основан на решении обратной задачи аналитического продолжения тепловых полей с граничного уровня земной поверхности на требуемую глубину. Сам алгоритм аналитического продолжения является неотъемлемой частью полученного выше общего решения прямой задачи теплопроводности для модели слоистого пласта.
Восходящая составляющая теплового потока на поверхности ${{S}_{i}}$ антинаправлена к оси глубин, т.е. совпадает по знаку с градиентом температуры:
На земной поверхности ${{S}_{{0~}}}\,:~{{A}_{i}} = {{A}_{0}}\left( {x,y,0} \right)$. При этом следует уточнить, что оператор поверхностного градиента температуры вычисляется по мнемоническому правилу:
Здесь и далее будем использовать принятые сокращения.
Как и в формуле для температуры (4.4), суммарный тепловой поток разделяется на составляющие от источников радиогенной теплогенерации Q в земной коре и от поверхностных источников μ с подошвы мантийного слоя, $q\left( {{{A}_{0}}} \right) = {{q}_{Q}}\left( {{{A}_{0}}} \right) + {{q}_{\mu }}\left( {{{A}_{0}}} \right)$:
(5.1)
${{q}_{Q}}\left( {{{A}_{0}}} \right) = \frac{{{{\lambda }_{1}}}}{{4\pi }}\left( {{{{\mathbf{N}}}_{0}} \cdot {{\nabla }_{{{{A}_{0}}}}}} \right)\iiint\limits_D {\frac{{Q\left( C \right)}}{{\lambda \left( C \right)}}}K\left( {{{A}_{0}},C} \right)d{{V}_{C}},$(5.2)
${{q}_{\mu }}\left( {{{A}_{0}}} \right) = \frac{{{{\lambda }_{1}}}}{{4\pi }}\left( {{{{\mathbf{N}}}_{0}} \cdot {{\nabla }_{{{{A}_{0}}}}}} \right)\iint\limits_{{{S}_{H}}} {\mu \left( {{{P}_{H}}} \right)}K\left( {{{A}_{0}},{{P}_{H}}} \right)d{{S}_{H}}.$Глубинный тепловой поток ${{q}_{\mu }}\left( H \right) = {{\lambda }_{{M + 1}}}*\mu \left( {{{P}_{H}}} \right)$ на нижней граничной плоскости $z = H$ не является априори известной функцией. Но “след” этой функции однозначно прослежен в решении для верхней границы пласта–плоскости, на которой заданы редуцированные значения “наблюденного” теплового потока. Разность между “наблюденным” и модельным тепловым потоком от источников теплогенерации в земной коре приравнена к целевой функции подбора обратной задачи аналитического продолжения гармонических функций. Полагая ${{q}_{Q}}\left( {{{A}_{0}}} \right) + {{q}_{\mu }}\left( {{{A}_{0}}} \right) = {{q}_{{observ}}}$, получаем интегральное уравнение относительно граничной составляющей глубинного теплового потока:
(5.3)
$\begin{gathered} {{q}_{\mu }}\left( {{{A}_{0}}} \right) = {{q}_{{observ}}} - {{q}_{Q}}\left( {{{A}_{0}}} \right) = \\ = \frac{1}{{4\pi }}\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{{M + 1}}}}}\left( {{{{\mathbf{N}}}_{0}} \cdot {{\nabla }_{{{{A}_{0}}}}}} \right)\iint\limits_{{{S}_{H}}} {K\left( {{{A}_{0}},{{P}_{H}}} \right)}~{{q}_{\mu }}\left( {{{P}_{H}}} \right)d{{S}_{H}}. \\ \end{gathered} $Правая часть выражения (5.3) является интегральным оператором типа свертки прямого пересчета поля ${{q}_{\mu }}\left( {{{P}_{H}}} \right)$ с уровня $z = H$ “на высоту” $~z = 0$. Инверсия интегрального оператора (5.3) дает решение обратной задачи аналитического продолжения мантийной составляющей теплового потока через слоисто-неоднородную среду с уровня земной поверхности на нижнюю граничную плоскость $z = H$. Пересчет поля ${{q}_{{{\mu }}}}\left( {{{P}_{H}}} \right)$ вверх на криволинейную границу $~z = {{z}_{M}}\left( {x,y} \right),~$ ${{A}_{M}} = A\left( {x,y,{{z}_{M}}} \right)$ находится из решения прямой задачи, аналога интегральной формулы (5.2):
(5.4)
$\begin{gathered} {{q}_{\mu }}\left( {{{A}_{M}}} \right) = \,\,~\frac{1}{{4\pi }}\frac{{{{\lambda }_{M}}}}{{{{\lambda }_{{M + 1}}}}}\left( {{{{\mathbf{N}}}_{M}} \cdot {{\nabla }_{{{{A}_{M}}}}}} \right) \times \\ \times \,\,\iint\limits_{{{S}_{H}}} {K\left( {{{A}_{M}},{{P}_{H}}} \right)}{{q}_{\mu }}\left( {{{P}_{H}}} \right)d{{S}_{H}}.~ \\ \end{gathered} $Формулы пересчета (5.3)–(5.4) позволяют исключить граничное условия Неймана по тепловому потоку из решения прямой задачи и выразить поток ${{q}_{\mu }}\left( {{{A}_{M}}} \right)$ на кровле верхней мантии через его значение ${{q}_{\mu }}\left( {{{A}_{0}}} \right)$ на поверхности Земли.
Модельный тепловой поток (5.1) (прямая задача) от источников в земной коре вычислен в плоскости “нейтрального слоя” $\left( {z = 0} \right)$; мантийная составляющая поверхностного потока (5.3) (обратная задача) приравнена к разности между наблюденными и вычисленными значениями. Разделение общего теплового потока на коровую и мантийную составляющую для территории 60°–68° с.ш., 48°–72° в.д. приведены на рис. 3:
Рис. 3.
Наблюденный тепловой поток (1); расчетные значения теплового потока для кристаллической коры и осадочного чехла в плоскости z = 0 (2); разностный тепловой поток (мантийная составляющая) на том же (верхнем) граничном уровне (3).
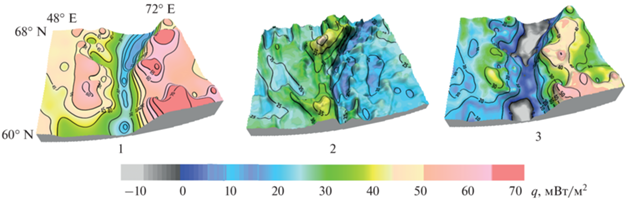
Аналитическое продолжение мантийной составляющей теплового потока через слоисто-неоднородную среду с уровня земной поверхности на границу “кора–мантия” выполняется двумя этапами: сначала решается интегральное уравнение (5.3) обратной задачи относительно неизвестной составляющей потока на нижней граничной плоскости, а затем найденный глубинный поток пересчитывается по прямой интегральной формуле (5.4) на любую вышележащую поверхность. Последовательность пересчетов соответствует схеме $z = 0\mathop \to \limits_{{\text{вниз}}} z = H\mathop \to \limits_{{\text{вверх}}} {{z}_{M}}\left( {x,y} \right)$. Оптимальный параметр регуляризации в задаче численного аналитического продолжения выбирается по критерию стационарности пересчета гармонических функций: продолженная функции по любому замкнутому контуру в области ее гармоничности возвращается к первоначальным исходным значениям. Фактически, оптимальный параметр регуляризации соответствует минимуму невязки исходного и пересчитанного поля с глубины $H$ на земную поверхность. Детали сеточного алгоритма последовательных пересчетов гравитационного поля “вверх–вниз” изложены в работах [Martyshko et al., 2021]. Для теплового потока алгоритм пересчета “вниз–вверх” будет таким же. Последовательность схемы пересчетов и восходящая (вертикальная) составляющая теплового потока на границе “кора–мантия” показана на рис. 4:
Рис. 4.
Численный пересчет мантийной составляющей теплового потока с уровня земной поверхности на глубину границы “кора–мантия” при оптимальном параметре регуляризации. Последовательность вычислений соответствует решению интегрального уравнения (5.3) и применению интегральной формулы (5.4).
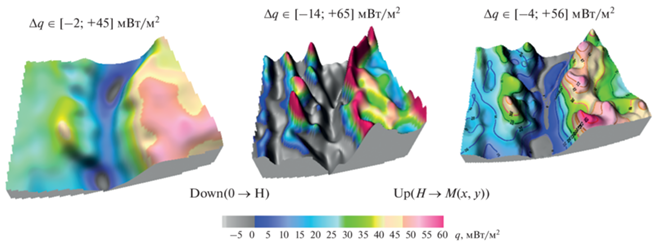
Мантийная составляющая потока на верхней граничной плоскости меняется в широких пределах: от нормальных (средних) значений (20–30) мВт/м2 в пределах щитов и древних платформ (ВЕП + ТПП) [Гордиенко, 1980; Gordienko, Pavlenkova, 1985] до высоких (40–50) мВт/м2 (и более) на западной окраине молодой Западно-Сибирской плиты (ЗП) [Дучков, Соколова, 1997]. На Урале мантийный поток частично отрицательный. С одной стороны это связано с экстремально низкими значениями измеряемых градиентов температур (и вычисляемых тепловых потоков) по скважинам в пределах Уральской эвгеосинклинали [Булашевич, Щапов, 1983]; с другой – сравнительно высокой теплогенерацией в корнях гор Уральской складчатой системы [Kukkonen et al., 1997]. Отрицательные значения стационарного теплового потока на земной поверхности становятся заведомо нереальными величинами при их аналитическом продолжении на глубину. Это противоречит стационарному геотермическому режиму в земной коре и на границе раздела “кора–мантия”, что, вероятно, потребует введения в наблюденные данные теплового потока дополнительной корректирующей добавки за счет палеоклиматической редукции [Голованова и др., 2012].
6. РАЗЛОЖЕНИЕ ЯДРА ИНТЕГРАЛЬНОГО ОПЕРАТОРА ЗАДАЧИ СОПРЯЖЕНИЯ
Интегральная формула (4.4) решения задачи теплового сопряжения для слоистого пласта с неоднородными условиями Дирихле–Неймана на его внешних границах представлена сверткой внутренних и внешних тепловых источников поля с “контактной” функцией Грина $K\left( {A,C} \right)$ – решения (4.5) подобной задачи, но для точечного источника с сингулярной плотностью и однородными краевыми условиями:
Производная контактной функции Грина $K_{z}^{{\text{'}}}\left( {0,C} \right)$ является ядром интегральной формулы прямой задачи для расчета поверхностного теплового потока (5.1) от источников земной коры; ее примем за коровую составляющую потока. Производная $K_{z}^{{\text{'}}}\left( {0,H} \right)$ входит в ядро интегрального оператора (5.3) обратной задачи аналитического продолжения разностной мантийной составляющей потока с уровня земной поверхности на глубину границы “кора–мантия”.
6.1. Функция Грина для однородного пласта. Формула удвоения
Здесь и далее используется индексированная система условных обозначений для аргументов и параметров функции обратных расстояний между двумя точками. В прямоугольных координатах $\left( X \right) = \left( {x,y,z} \right)$ определим пространственное расстояние между точкой наблюдения ${{X}_{A}}$ и точкой источника ${{X}_{C}}$:
Проекцию расстояния между двумя точками ${{R}_{{AC}}}$ на горизонтальную плоскость примем за параметр функции расстояний, а приращение аппликат этих точек – за аргумент функции:
(6.1)
$\begin{gathered} \sqrt {{{{\left( {{{x}_{A}} - {{x}_{C}}} \right)}}^{2}} + {{{\left( {{{y}_{A}} - {{y}_{C}}} \right)}}^{2}}} = {{R}_{{AC}}}, \hfill \\ {{X}_{{AC}}}\left( {{{z}_{A}} - {{z}_{C}}} \right) = \sqrt {R_{{AC}}^{2} + {{{\left( {{{z}_{A}} - {{z}_{C}}} \right)}}^{2}}} . \hfill \\ \end{gathered} $В обозначениях (6.1) функция Грина двух переменных для однородной полосы $z \in \left[ {0,~H} \right]$ записывается в виде разложения по рекурсивным разностям обратных расстояний от точек изображений источников $~C\left( {2nH \mp {{z}_{C}}} \right)$ до точки наблюдения $A\left( {{{z}_{A}}} \right)$ [Франк, Мизес, 1937]:
(6.2)
$\begin{gathered} G\left( {A,C} \right) = \mathop \sum \limits_{n = - \infty }^{ + \infty } {{\left( { - 1} \right)}^{n}} \times \\ \times \,\left[ {\frac{1}{{{{X}_{{AC}}}\left( {{{z}_{A}}\, + \,2nH\, - \,{{z}_{C}}} \right)}}\, - \,\frac{1}{{{{X}_{{AC}}}\left( {{{z}_{A}}\, + \,2nH\, + \,{{z}_{C}}} \right)}}} \right]~. \\ \end{gathered} $При $H \to \infty $ полоса конечной мощности “раскрывается” до модели нижнего однородного полупространства $z \geqslant 0$ с изотермической верхней границей. В этом приближении сохраняется единственный член ряда (6.2) с индексом n = 0:
Для полупространства функция Грина равна потенциалу двух зеркально симметричных (и противоположных по знаку) источников относительно изотермической плоскости $z = 0$. И, сравнительно с фундаментальным решением $\mathcal{E}\left( {A,C} \right)$ для точечного источника в безграничной среде, вертикальный градиент от зеркальной пары источников удваивается на границе полупространства:
(6.3)
${{\left. {\frac{{\partial {{G}_{0}}\left( {A,C} \right)}}{{\partial {{z}_{A}}}}} \right|}_{{{{z}_{A}} = 0}}} = {{\left. {2\frac{\partial }{{\partial {{z}_{A}}}}\mathcal{E}\left( {A,C} \right)} \right|}_{{{{z}_{A}} = 0}}} = 2\frac{{{{z}_{C}}}}{{~X_{{AC}}^{3}\left( {{{z}_{C}}} \right)}}~.$На распределение температур в верхней части геотермического разреза наибольшее влияние оказывает граничное условие постоянства температуры в плоскости “нейтрального слоя”. И формула для производной (6.3) в формате зеркальной пары интерпретируется как “формула удвоения” [Лыков, 1967]. Близкий результат можно получить из разложения функции Грина (6.2) по полной системе изображений источников однородной полосы $\left[ {0,~H} \right]$. Продифференцируем ряд (6.2) по $z$ – координате первого аргумента функции $~G\left( {A,C} \right)$:
(6.4)
$\begin{gathered} \frac{{\partial G\left( {A,C} \right)}}{{\partial {{z}_{A}}}} = \mathop \sum \limits_{n = - \infty }^{ + \infty } {{\left( { - 1} \right)}^{n}} \times \\ \times \,\,\left[ {\frac{{{{z}_{A}}\, + \,2nH\, + \,{{z}_{C}}}}{{X_{{AC}}^{3}\left( {{{z}_{A}}\, + \,2nH\, + \,{{z}_{C}}} \right)}}\, - \,\frac{{{{z}_{A}}\, + \,2nH\, - \,{{z}_{C}}}}{{X_{{AC}}^{3}\left( {{{z}_{A}}\, + \,2nH\, - \,{{z}_{C}}} \right)}}} \right]~. \\ \end{gathered} $При $z = 0$ ряд для производной (6.4) инвариантен относительно смены знака индекса “n”. Ряду источников из нижнего полупространства с положительными индексами будет соответствовать зеркально-симметричный ряд источников из верхнего полупространства с отрицательными индексами. Следовательно, при $\left( {m \geqslant 0 = \left| n \right|} \right)$ для всех зеркальных пар справедлива формула “удвоения” градиентов на изотермической плоскости $z = 0$:
(6.5)
$\begin{gathered} {{\left. {\frac{{\partial G\left( {A,C} \right)}}{{\partial {{z}_{A}}}}} \right|}_{{{{z}_{A}} = 0}}} = 2\frac{{{{z}_{C}}}}{{~X_{{AC}}^{3}\left( {{{z}_{C}}} \right)}} + 2\mathop \sum \limits_{m = 1}^{ + \infty } {{\left( { - 1} \right)}^{m}} \times \\ \times \,\,\left[ {\frac{{\left( {2mH + {{z}_{C}}} \right)}}{{X_{{AC}}^{3}\left( {2mH + {{z}_{C}}} \right)}} - \frac{{\left( {2mH - {{z}_{C}}} \right)}}{{X_{{AC}}^{3}\left( {2mH - {{z}_{C}}} \right)}}} \right]. \\ \end{gathered} $Отношение рядов (6.5) и (6.3) показывает влияние нижней границы пласта $z = H$ на геотермический режим в верхней части разреза. Их зависимость от общего числа членов разложения обозначим через $G_{z}^{{\text{'}}}\left( m \right)$ и $G_{z}^{{\text{'}}}\left( 0 \right).$
На рисунке 5 приведен расчетный график эпицентральных значений вертикального градиента ${{G_{z}^{{\text{'}}}\left( m \right)} \mathord{\left/ {\vphantom {{G_{z}^{{\text{'}}}\left( m \right)} {G_{z}^{{\text{'}}}\left( 0 \right)}}} \right. \kern-0em} {G_{z}^{{\text{'}}}\left( 0 \right)}}$ в относительных единицах как функции глубины ${{{{z}_{C}}} \mathord{\left/ {\vphantom {{{{z}_{C}}} H}} \right. \kern-0em} H}$:
Рис. 5.
График изменений вертикального градиента функции Грина $G_{z}^{'}\left( m \right) = G_{z}^{'}\left( {0,C} \right)$ в эпицентре точечного источника, нормированного на величину градиента “формулы удвоения”. Переменный параметр суммы ряда – относительная глубина залегания источника ${{{{z}_{C}}} \mathord{\left/ {\vphantom {{{{z}_{C}}} H}} \right. \kern-0em} H}$. Число членов суммы знакопеременного ряда m = 100.
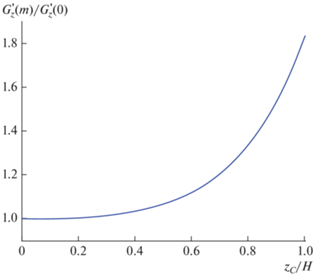
Как видно из рис. 5, сравнительно с “формулой удвоения”, наибольший эффект (увеличение почти в два раза) наблюдается для источников, соприкасающихся с нижней границей слоя ${{z}_{C}} = H$. С уменьшением глубины источника эффект нижней границы значительно ослабевает и, например, при ${{z}_{C}} = {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}$ не будет превышать 10%.
6.2. Контактная функция Грина для слоистого пласта
На изотермической граничной плоскости $z = 0$ (условная граница радела “земля–воздух”) восходящий тепловой поток (5.1), (5.2) пропорционален вертикальной составляющей градиента температуры. Последний вычисляется через вертикальный градиент “контактной” функции Грина $K\left( {A,C} \right)$ по точке А (первому аргументу):
(6.6)
$\begin{gathered} {{\left. {\frac{\partial }{{\partial {{z}_{A}}}}K\left( {A,C} \right)} \right|}_{{{{z}_{A}} = 0}}} = {{\left. {\frac{\partial }{{\partial {{z}_{A}}}}G\left( {A,C} \right)} \right|}_{{{{z}_{A}} = 0}}} - \frac{1}{{2\pi }}\mathop \sum \limits_{k = 1}^M {{\varepsilon }_{k}} \times \\ \times \,\,\iint\limits_{{{S}_{k}}} {\frac{\partial }{{\partial {{z}_{A}}}}}G\left( {A,{{P}_{k}}} \right)\left( {{{{\mathbf{N}}}_{k}} \cdot {{\nabla }_{{{{P}_{k}}}}}} \right)G\left( {{{P}_{k}},C} \right){{\left. {d{{S}_{{{{P}_{k}}}}}} \right|}_{{{{z}_{A}} = 0}}}. \\ \end{gathered} $В выражение (6.6) входят сама производная функции $G_{z}^{{}}$ и интеграл-свертка от комбинации ее производных. Однако на криволинейной поверхности ${{S}_{k}}$ существуют все три компоненты вектора-градиента и свертка нормальных производных функций Грина, в общем случае, может быть найдена только численно. Чередование слоев с различной теплопроводностью приводит к эффекту теплового экранирования. По порядку величины его можно оценить в рамках упрощенной модели горизонтально слоистой среды. Пусть ${{S}_{k}}$ – горизонтальные плоскости с уравнениями$~z = {{z}_{{Pk}}}$. Нормаль к этой плоскости сориентирована вдоль оси глубин, а производная по нормали от функции $G$ имеет только вертикальную составляющую.
Выполним все вычисления, предписанные формулой (6.6). Граничные значения производной $G_{z}^{{}}\left( {0,C} \right)$ заданы в формате ряда “формулы удвоения” (6.5). Тому же ряду соответствует граничная производная $G_{z}^{{}}\left( {0,{{P}_{k}}} \right)$ при ${{z}_{C}} = {{z}_{{Pk}}}$:
(6.7)
$\begin{gathered} {{\left. {\frac{\partial }{{\partial {{z}_{A}}}}G\left( {A,{{P}_{k}}} \right)} \right|}_{{{{z}_{A}} = 0}}} = G_{z}^{'}\left( {0,{{P}_{k}}~} \right) = 2\sum\limits_{m = 0}^{ + \infty } {{{{\left( { - 1} \right)}}^{m}}} {{\delta }_{{m,0}}} \times \\ \times \,\,\left[ {\frac{{\left( {2mH + {{z}_{{Pk}}}} \right)}}{{X_{{AC}}^{3}\left( {2mH + {{z}_{{Pk}}}} \right)}} - \frac{{\left( {2mH - {{z}_{{Pk}}}} \right)}}{{X_{{AC}}^{3}\left( {2mH - {{z}_{{Pk}}}} \right)}}} \right]. \\ \end{gathered} $Здесь слагаемое с $m = 0$ включено в общую сумму ряда с декрементом ${{\delta }_{{m,0}}} = \left\{ \begin{gathered} {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},~\,\,\,\,m = 0~ \hfill \\ 1,\,\,\,m \geqslant 1 \hfill \\ \end{gathered} \right..$
Подобным образом можно вычислить градиент функции $G\left( {{{P}_{k}},C} \right)~$по первому аргументу “точки наблюдения” ${{P}_{k}}$ для горизонтального контакта. Нормаль к плоскости контакта сориентирована вдоль оси глубин, а производная по нормали от функции $G\left( {{{P}_{k}},C} \right)~$ имеет только вертикальную составляющую:
(6.8)
$\begin{gathered} \frac{{\partial G\left( {{{P}_{k}},C} \right)}}{{\partial {{z}_{{{{P}_{k}}}}}}} = G_{z}^{'}\left( {{{P}_{k}},C} \right) = \mathop \sum \limits_{n = - \infty }^{ + \infty } {{\left( { - 1} \right)}^{n}} \times \\ \times \,\,\left[ {\frac{{\left( {{{z}_{{{{P}_{k}}}}}\, + \,2nH\, + \,{{z}_{C}}} \right)}}{{X_{{PC}}^{3}\left( {{{z}_{{{{P}_{k}}}}}\, + \,2nH\, + \,{{z}_{C}}} \right)}}\, - \,\frac{{{{z}_{{{{P}_{k}}}}}\, + \,2nH\, - \,{{z}_{C}}}}{{X_{{PC}}^{3}\left( {{{z}_{{{{P}_{k}}}}}\, + \,2nH\, - \,{{z}_{C}}} \right)}}} \right]. \\ \end{gathered} $В разложениях (6.5), (6.7) и (6.8) приращения аппликат точек источника ${{z}_{C}}$ и контактных границ ${{z}_{{Pk}}}$ являются рекурсивными переменными глубины $H$. Определим их как рекурсивные аргументы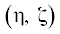 
функций расстояний ${{X}_{{AC}}}\left( {{{{{\eta }}}_{m}}} \right)$ и ${{X}_{{PC}}}\left( {{{{{\zeta }}}_{n}}} \right)$:
(6.9)
$\begin{gathered} {{\eta }_{m}} = {{\eta }_{m}}\left( {P \oplus C} \right):\, = \eta _{m}^{ \pm } = 2mH \pm \left( {{{z}_{P}} \oplus {{z}_{C}}} \right); \\ m \in \left[ {\left. {0,~ + \infty } \right)} \right., \\ {{\zeta }_{n}} = {{\zeta }_{n}}\left( {P,C} \right):\, = \zeta _{n}^{ \pm } = {{z}_{{{{P}_{k}}}}} + \left( {2nH \pm {{z}_{C}}} \right); \\ n \in \left( { - \infty ,~ + \infty } \right). \\ \end{gathered} $Здесь индексированные параметры ${{{{\eta }}}_{m}}\left( {P \oplus C} \right)$ принимают два возможных значения, а индексированные параметры ${{{{\zeta }}}_{n}}\left( {P,C} \right)$– четыре значения; $ \oplus $ – операция исключающего “или”.
Перемножим ряды (6.7) и (6.8); ${{\eta }}_{m}^{ \pm } = {{\eta }}_{m}^{ \pm }\left( P \right)$:
Применим символы подстановки (6.9) и выпишем интеграл от произведения рядов:
Для плоских границ ${{S}_{k}}$ интеграл ${{I}_{{m,n}}}$ вычисляется в явном виде [Мартышко et al., 2020]:
(6.10)
$\begin{gathered} {{I}_{{m,n}}}\left( {{{\eta }_{m}},~{{\zeta }_{n}}} \right) = \frac{1}{{2\pi }}\int\limits_ - ^ + {\int\limits_\infty ^\infty {\frac{{{{\eta }_{m}}{{\zeta }_{n}}~d{{x}_{P}}d{{y}_{P}}}}{{X_{{AP}}^{3}\left( {{{\eta }_{m}}} \right)X_{{PH}}^{3}\left( {{{\zeta }_{n}}} \right)}}} } = \\ ~ = {\text{sign}}\left( {~{{\eta }_{{m~}}}} \right){\text{sign}}\left( {{{\zeta }_{n}}} \right)\frac{{\left| {~{{\eta }_{m}}} \right| + \left| {{{\zeta }_{n}}} \right|}}{{X_{{AH}}^{3}\left[ {\left( {\left| {~{{\eta }_{m}}} \right| + \left| {{{\zeta }_{n}}} \right|} \right)} \right]}}~. \\ \end{gathered} $Объединим все преобразованные фрагменты формулы (6.6) и запишем результирующий ряд для производной $K_{z}^{{\text{'}}}\left( {A,C} \right)$ в компактном свернутом виде:
(6.11)
$\begin{gathered} {{\left. {\frac{\partial }{{\partial {{z}_{A}}}}K\left( {A,C} \right)} \right|}_{{{{z}_{A}} = 0}}} = K_{z}^{'}\left( {m,n} \right) = 2\sum\limits_{m = 0}^{ + \infty } {{{{\left( { - 1} \right)}}^{m}}} {{\delta }_{{m,0}}}\left[ {\left. {\frac{{{{\eta }_{m}}}}{{X_{{AC}}^{3}\left( {{{\eta }_{m}}} \right)}}} \right|_{{\eta _{m}^{ - }\left( C \right)}}^{{\eta _{m}^{ + }\left( C \right)}}} \right] + ~ \\ + \,\,\sum\limits_{k = 1}^M {{{\varepsilon }_{k}}} \left\{ {2\sum\limits_{m = 0}^\infty {{{\delta }_{{m,0}}}} {{{\left( { - 1} \right)}}^{m}}{\text{sign}}\left( {~{{\eta }_{{m~}}}} \right)\sum\limits_{n = - \infty }^{ + \infty } {{{{\left( { - 1} \right)}}^{n}}~} {\text{sign}}\left( {{{\zeta }_{n}}} \right)\left[ {\left. {\left. {\frac{{\left| {~{{\eta }_{m}}} \right| + \left| {{{\zeta }_{n}}} \right|}}{{X_{{AC}}^{3}\left( {\left| {~{{\eta }_{m}}} \right| + \left| {{{\zeta }_{n}}} \right|} \right)}}} \right|_{{\eta _{m}^{ - }\left( P \right)}}^{{\eta _{m}^{ + }\left( P \right)}}} \right|_{{\zeta _{n}^{ - }}}^{{\zeta _{n}^{ + }}}} \right]} \right\}. \\ \end{gathered} $Подстановка (6.9) переменных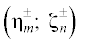 
на верхних и нижних пределах дает полную сумму, состоящую из [(2m + 1) + (2m + 1)2(2n + 1)] = (2m + 1)(4n + 3) слагаемых. Далее примем, что замещающие индексы в аргументах функции $K_{z}^{'}\left( {A,C} \right) = K_{z}^{'}\left( {m,n} \right)$ указывают на число членов суммы внешнего и внутреннего рядов (6.11). Частичные суммы
ряда вычисляются по однотипным рекуррентным формулам при любых значениях индексов
$m~\,{\text{и\;}}n$. Погрешность вычисления частичных сумм знакопеременных рядов не превышает абсолютной
величины первого неучтенного слагаемого.
6.3. Приближение формулы “удвоения” для источников земной коры
Изотермическая плоскость в “нейтральном слое” служит тепловым стоком, на которую замыкаются все силовые линии восходящего теплового потока. Условие Неймана по восходящему потоку на глубинной граничной плоскости $z = H$ является вспомогательным и несущественно меняет общую картину поля от источников в верхней части земной коры. Влияние этого граничного условия нетрудно оценить, сопоставив решение для полосы $z \in \left[ {0,H} \right]$ с решением для полупространства $z \geqslant 0$.
При $H \to \infty $ полоса конечной мощности преобразуется в модель слоистого полупространства. И в решении (6.11) для $K_{z}^{{\text{'}}}\left( {m,n} \right)$ остается только три члена с $m = n = 0$, которые отличны от нуля. По аналогии с (6.3) этим трем слагаемым придадим смысл “формулы удвоения” геотермического градиента в слоистой среде:
(6.12)
$\begin{gathered} K_{z}^{'}\left( {0,0} \right) = 2~\frac{{{{z}_{C}}}}{{{{{\left[ {R_{{AC}}^{2} + {{z}_{C}}^{2}} \right]}}^{{3/2}}}}} + 2\sum\limits_{k = 1}^M {{{\varepsilon }_{k}}} \times \\ \times \,\,\left[ {{\text{sing}}\left( {{{z}_{{Pk}}}\, - \,{{z}_{C}}} \right)\frac{{\left( {{{z}_{{Pk}}}\, + \,\left| {{{z}_{{Pk}}}\, - \,{{z}_{C}}} \right|} \right)}}{{{{{\left[ {R_{{AC}}^{2}\, + \,{{{\left( {{{z}_{{Pk}}}\, + \,\left| {{{z}_{{Pk}}}\, - \,{{z}_{C}}} \right|} \right)}}^{2}}} \right]}}^{{3/2}}}}}} \right. - \\ ~\left. { - \,\,\frac{{2{{z}_{{Pk}}} + {{z}_{C}}}}{{{{{\left[ {R_{{AC}}^{2} + {{{\left( {2{{z}_{{Pk}}} + {{z}_{C}}} \right)}}^{2}}} \right]}}^{{3/2}}}}}} \right]. \\ \end{gathered} $Знак параметра теплопроводной контрастности ${{\varepsilon }_{k}}$ задает тенденцию изменения градиента в большую или меньшую сторону. Функции модуля и знака разности $\left( {{{z}_{{Pk}}} - {{z}_{C}}} \right)$ показывают, что при заданных ${{{{\varepsilon }}}_{k}}$ величина самого градиента зависит от положения источников ${\text{\;}}{{z}_{C}}$ относительно границ ${{z}_{{Pk}}}$ тепловых контактов.
Так при ${{z}_{C}} < {{z}_{{Pk}}}$:
При ${{z}_{C}} > {{z}_{{Pk}}}$
(6.13)
$\begin{gathered} K_{z}^{'}\left( {0,0} \right) = 2\left( {1 - \mathop \sum \limits_{k = 1}^M {{\varepsilon }_{k}}} \right)~\frac{{{{z}_{C}}}}{{{{{\left[ {R_{{AC}}^{2} + {{z}_{C}}^{2}} \right]}}^{{3/2}}}}} - \\ - \,\,2{\kern 1pt} \mathop \sum \limits_{k = 1}^M {{\varepsilon }_{k}}\left[ {\frac{{2{{z}_{{Pk}}} + {{z}_{C}}}}{{{{{\left[ {R_{{AC}}^{2} + {{{\left( {2{{z}_{{Pk}}} + {{z}_{C}}} \right)}}^{2}}} \right]}}^{{3/2}}}}}} \right]. \\ \end{gathered} $В схемах количественной интерпретации приповерхностного теплового потока целесообразно разделить влияние глубинных и приповерхностных источников и оценить погрешность замены полного решения (6.11) на его усеченный вариант “формулы удвоения” (6.12). На рис. 6 приведен расчетный график эпицентральных значений вертикального градиента ${{K_{z}^{'}\left( {m,n} \right)} \mathord{\left/ {\vphantom {{K_{z}^{'}\left( {m,n} \right)} {K_{z}^{'}\left( {0,0} \right)}}} \right. \kern-0em} {K_{z}^{'}\left( {0,0} \right)}}$ в относительных единицах (синяя линия 1), как функции глубины ${{{{z}_{C}}} \mathord{\left/ {\vphantom {{{{z}_{C}}} H}} \right. \kern-0em} H}$. Здесь же для сравнения дано отношение ${{G_{z}^{{\text{'}}}\left( m \right)} \mathord{\left/ {\vphantom {{G_{z}^{{\text{'}}}\left( m \right)} {G_{z}^{{\text{'}}}\left( 0 \right)}}} \right. \kern-0em} {G_{z}^{{\text{'}}}\left( 0 \right)}}$ (красная линия 2). Аргумент вычисляемых функций – глубина залегания источника ${{{{z}_{C}}} \mathord{\left/ {\vphantom {{{{z}_{C}}} H}} \right. \kern-0em} H}$. Число членов в суммах знакопеременных рядов (6.5) и (6.11) $m = n$ = = 100. Вертикальными темными линиями нанесены две границы разно теплопроводных слоев $({{{\text{z}}}_{{P1}}}~$ = 6 км; ${{{{\varepsilon }}}_{1}}$ = –0.167) и $({{{\text{z}}}_{{P2}}}~$ = 40 км; ${{{{\varepsilon }}}_{2}}$ = –0.235). Эти границы условно разделяют верхнюю литосферу на три слоя: низко теплопроводный осадочный чехол с ${{{{\lambda }}}_{1}} = 2~\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\left( {{\text{м}} \cdot {\text{К}}} \right)}}} \right. \kern-0em} {\left( {{\text{м}} \cdot {\text{К}}} \right)}}$, кристаллическая кора со средневзвешенной теплопроводностью ${{{{\lambda }}}_{2}} = 2.6\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\left( {{\text{м}} \cdot {\text{К}}} \right)}}} \right. \kern-0em} {\left( {{\text{м}} \cdot {\text{К}}} \right)}}$ и относительно теплопроводная мантия с теплопроводностью ${{{{\lambda }}}_{3}} = 4.2\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\left( {{\text{м}} \cdot {\text{К}}} \right)}}} \right. \kern-0em} {\left( {{\text{м}} \cdot {\text{К}}} \right)}}$.
Рис. 6.
График эпицентральных значений вертикального градиента контактной функции Грина $K_{z}^{'}\left( {m,n} \right)$ (синяя линия 1), отнесенных к величине $K_{z}^{{\text{'}}}\left( {0,0} \right)$. Для сравнения приведен график отношения ${{G_{z}^{{\text{'}}}\left( m \right)} \mathord{\left/ {\vphantom {{G_{z}^{{\text{'}}}\left( m \right)} {G_{z}^{{\text{'}}}\left( 0 \right)}}} \right. \kern-0em} {G_{z}^{{\text{'}}}\left( 0 \right)}}$ (красная линия 2). Аргумент вычисляемых функций – относительная глубина залегания источника ${{{{z}_{C}}} \mathord{\left/ {\vphantom {{{{z}_{C}}} H}} \right. \kern-0em} H}$. Индексы вычисляемых сумм рядов $m = n$ = 100.
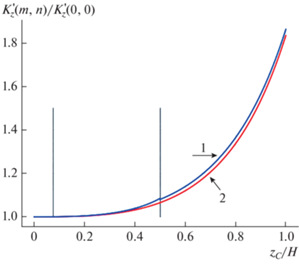
Практическое совпадение линий (1) и (2) на рис. 6 свидетельствует лишь о близости скоростей затухания градиентов для точечного источника в однородной и слоистой среде. Чтобы оценить эффект теплопроводного экранирования источников, сравним отношение эпицентральных градиентов ${{K_{z}^{{\text{'}}}\left( {m,n} \right)} \mathord{\left/ {\vphantom {{K_{z}^{{\text{'}}}\left( {m,n} \right)} {G_{z}^{{\text{'}}}\left( m \right)}}} \right. \kern-0em} {G_{z}^{{\text{'}}}\left( m \right)}}$ контактной и однородной функций Грина. Аргумент вычисляемых функции тот же – относительная глубина залегания источника ${{{{z}_{C}}} \mathord{\left/ {\vphantom {{{{z}_{C}}} H}} \right. \kern-0em} H}$. На рис. 7 приведен график этого отношения для эпицентральной точки земной поверхности (синяя линия 1). Теплопроводность нарастает с глубиной; возрастает и вклад источников, лежащих в более теплопроводных слоях. Эффект теплопроводного экранирования весьма устойчив и слабо зависит от влияния теплоизолированной нижней границы пласта $~z = H$. Так для модели полупространства с изотермической верхней границей отношение приповерхностных градиентов ${{K_{z}^{{\text{'}}}\left( {0,0} \right)} \mathord{\left/ {\vphantom {{K_{z}^{{\text{'}}}\left( {0,0} \right)} {G_{z}^{{\text{'}}}\left( 0 \right)}}} \right. \kern-0em} {G_{z}^{{\text{'}}}\left( 0 \right)}}$ в приближении формулы “удвоения” (зеленая линия 2) фактически повторяет полное решение, незначительно уменьшаясь на глубинах $z \geqslant {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}$, характерных для высокотеплопроводной верхней мантии.
Рис. 7.
График изменений вертикального градиента контактной функции Грина $K_{z}^{'}\left( {m,n} \right)$ в эпицентре точечного источника, нормированного на величину градиента однородной функции Грина $G_{z}^{{\text{'}}}\left( m \right)$ (синяя линия 1). Для сравнения приведен график отношения ${{K_{z}^{{\text{'}}}\left( {0,0} \right)} \mathord{\left/ {\vphantom {{K_{z}^{{\text{'}}}\left( {0,0} \right)} {G_{z}^{{\text{'}}}\left( 0 \right)}}} \right. \kern-0em} {G_{z}^{{\text{'}}}\left( 0 \right)}}$ (зеленая линия 2). Аргумент вычисляемых функций – относительная глубина залегания источника ${{{{z}_{C}}} \mathord{\left/ {\vphantom {{{{z}_{C}}} H}} \right. \kern-0em} H}$. Индексы вычисляемых сумм рядов $m = n$ = 100.
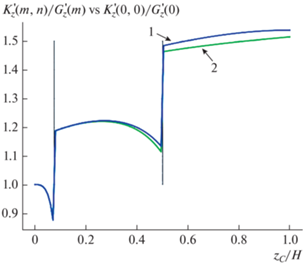
В практике геотермических исследований измеряемый по скважинам вертикальный геотермический градиент используется для определения интегральной величины теплового потока. Точность определения последнего не менее 15% [Булашевич, Щапов, 1983]. Погрешность замены точного решения приближенным не превышает апостериорную точность исходных данных. Поэтому в практических схемах количественной интерпретации вполне допустимо использование приближенной “формулы удвоения” (6.12) при условии, что восходящий (мантийный) тепловой поток задан на глубине, превышающей двукратную мощность слоя тепловых источников в земной коре. Такое требование заведомо выполнимо, если учесть, что в низах коры мощность источников радиогенной теплогенерации на два порядка ниже, чем в приповерхностном осадочном и нижележащем гранито-гнейсовом слое коренных пород.
6.4. Мантийная составляющая теплового потока
Мантийная составляющая теплового потока задана своим граничным значением на вспомогательной
глубинной плоскости $z = H$. Решение прямой задачи (5.2) записывается через интеграл Пуассона, ядро которого
приравнено к градиенту контактной функции Грина в направлении нисходящей нормали.
При пересчете потока с нижней плоскости $z = H$ на верхнюю плоскость $z = 0$ нормальная проекция градиента совпадает с вертикальной производной для функции Грина.
Для сокращения письма введем символические обозначения точек внешних границ пласта,
z – координаты которых равны 0 или H: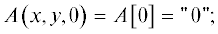 
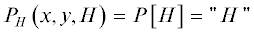. В этих обозначениях ядро интегральной формулы пересчета представим в виде:
(6.14)
$\begin{gathered} K_{z}^{'}\left( {0,H} \right) = G_{z}^{'}\left( {0,H} \right) - \\ - \,\,\frac{1}{{2\pi }}\mathop \sum \limits_{k = 1}^M {\kern 1pt} {{\varepsilon }_{k}}\iint\limits_{{{S}_{k}}} {G_{z}^{'}}\left( {0,{{P}_{k}}} \right)G_{z}^{'}\left( {{{P}_{k}},H} \right)d{{S}_{k}}. \\ \end{gathered} $Три комбинации для рядов производных $G_{z}^{{\text{'}}}\left( {0,H} \right),G_{z}^{{\text{'}}}\left( {0,{{P}_{k}}} \right),G_{z}^{{\text{'}}}\left( {{{P}_{k}},H} \right),$ входят в градиент контактной функции Грина (6.14). Их можно построить на основе известных разложений для источников (6.5), (6.7) и (6.8), выполнив преобразование перехода $~{{z}_{C}} \to H$. Симметрия аргументов функций по параметру $H$ существенно упрощает вид этих преобразований.
1. Индексы рядов рекурсивных аргументов $\left( {{{{{\eta }}}_{m}},~{{{{\zeta }}}_{n}}} \right)$ чередуются на единицу:
(6.15)
$\begin{gathered} {{\eta }_{m}} = {{\eta }_{m}}\left( {P \oplus \,H} \right):\, = \eta _{m}^{ \pm } = 2mH \pm \left( {{{z}_{P}} \oplus H} \right); \\ ~m \in \left[ {\left. {0,~ + \infty } \right)} \right.;~ \\ {{\zeta }_{n}} = {{\zeta }_{n}}\left( {P,H} \right):\, = ~\zeta _{n}^{ \pm } = {{z}_{P}} + \left( {2n \pm 1} \right)H; \\ n \in \left( { - \infty ,~ + \infty } \right).~~ \\ \end{gathered} $2. Для аргументов ${{\eta }_{m}}\left( H \right):\, = \eta _{m}^{ \pm } = \left( {2m \pm 1} \right)H$ просто уравняем индексы одинаковых частей рядов (6.5) и приведем подобные слагаемые:
(6.16)
$G_{z}^{'}\left( {0,H} \right) = 4{\kern 1pt} \mathop \sum \limits_{m = 0}^{ + \infty } {{\left( { - 1} \right)}^{m}}\left[ {\frac{{\left( {2m + 1} \right)H}}{{X_{{AH}}^{3}\left( {\left( {2m + 1} \right)H} \right)}}} \right].$3. Для аргументов ${{\eta }_{m}}\left( P \right):\, = \eta _{m}^{ \pm } = 2mH \pm {{z}_{P}}$ ряд (6.7) не изменится:
(6.17)
$\begin{gathered} G_{z}^{'}\left( {0,~{{P}_{k}}} \right) = 2{\kern 1pt} \mathop \sum \limits_{m = 0}^{ + \infty } {{\left( { - 1} \right)}^{m}}{{\delta }_{{m,0}}} \times \\ \times \,\,\left[ {\frac{{\left( {2mH + {{z}_{{Pk}}}} \right)}}{{X_{{AP}}^{3}\left( {2mH + {{z}_{{Pk}}}} \right)}} - \frac{{\left( {2mH - {{z}_{{Pk}}}} \right)}}{{X_{{AP}}^{3}\left( {2mH - {{z}_{{Pk}}}} \right)}}} \right]~. \\ \end{gathered} $4. Ряд (6.8) для $~G_{z}^{'}\left( {{{P}_{k}},H} \right)$ перегруппируем к односторонней сумме с положительными индексами ${{{{\zeta }}}_{n}}\left( {P,H} \right): = ~{{\zeta }}_{n}^{ \pm } = {{z}_{P}} \pm \left( {2n + 1} \right)H;~$ $~n \in \left[ {\left. {0,~ + \infty } \right)} \right.$. При этом число членов удвоится:
(6.18)
$\begin{gathered} G_{z}^{'}\left( {{{P}_{k}},H} \right) = 2\,\mathop \sum \limits_{n = 0}^{ + \infty } {{\left( { - 1} \right)}^{n}} \times \\ \times \,\,\left[ {\frac{{\left( {2n + 1} \right)H + {{z}_{{Pk}}}}}{{X_{{PH}}^{3}\left[ {\left( {2n + 1} \right)H + {{z}_{{Pk}}}} \right]}}} \right. + \\ \left. { + \,\,\frac{{\left( {2n + 1} \right)H - {{z}_{{Pk}}}}}{{X_{{PH}}^{3}\left[ {\left( {2n + 1} \right)H - {{z}_{{Pk}}}} \right]}}} \right].~ \\ \end{gathered} $5. Перемножим ряды (6.17) и (6.18) и проинтегрируем полученное произведение по плоскости ${{S}_{k}}$, применив свертку (6.10).
6. Соберем воедино все части формулы (6.14) для производной $K_{z}^{{\text{'}}}\left( {0,H} \right)$:
Здесь, как и ранее, замещающие индексы в аргументах функции $K_{z}^{'}\left( {0,H} \right) = K_{z}^{'}\left( {m,n} \right)$ указывают на число членов внешнего и внутреннего рядов.
Скорость сходимости знакопеременных рядов достаточно высока и последовательность частичных
сумм $K_{z}^{{\text{'}}}\left( {m,n} \right)$ сходится к своему пределу уже на пятой итерации по индексу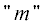 
для всех $n \geqslant 0$. Меньшая скорость сходимости у одинарного ряда по “m”. Для него абсолютная погрешность m-итерации (порядок следующего отброшенного члена) составит ${{\Delta }_{m}} \leqslant \left| {{1 \mathord{\left/ {\vphantom {1 {{{{\left( {2m + 1} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {2m + 1} \right)}}^{2}}}}{{H}^{2}}} \right|$. Двойной ряд по “m” и “n” сходится быстрее, а его абсолютная погрешность заведомо меньше ${{\Delta }_{{m,n}}} \leqslant \left| {{1 \mathord{\left/ {\vphantom {1 {{{{\left[ {2\left( {m + n} \right) + 1} \right]}}^{2}}}}} \right. \kern-0em} {{{{\left[ {2\left( {m + n} \right) + 1} \right]}}^{2}}}}{{H}^{2}}} \right|$. Если в решении оставить два слагаемых при m = 1; n = 0, то абсолютная погрешности частичной суммы $K_{z}^{{\text{'}}}\left( {0,0} \right)$ не будет превышать ${{\Delta }_{1}} \leqslant {1 \mathord{\left/ {\vphantom {1 {9{{H}^{2}}}}} \right. \kern-0em} {9{{H}^{2}}}}$:
(6.19)
$\begin{gathered} K_{z}^{'}\left( {0,0} \right) = 4\left( {1 - \mathop \sum \limits_{k = 1}^M {{\varepsilon }_{k}}} \right)\frac{H}{{{{{\left[ {R_{{AH}}^{2} + {{H}^{2}}} \right]}}^{{3/2}}}}} - \\ - \,\,4\mathop \sum \limits_{k = 1}^M {{\varepsilon }_{k}}\frac{{2{{z}_{{Pk}}} + H}}{{{{{\left[ {R_{{AH}}^{2} + {{{\left( {2{{z}_{{Pk}}} + H} \right)}}^{2}}} \right]}}^{{3/2}}}}}~. \\ \end{gathered} $Имеем очевидное совпадение приближенной формулы (6.19) с прямыми вычислениями градиентов контактной функции Грина на глубине (см. рис. 6). При одних и тех же значениях аппликат контактных границ ${{z}_{{Pk}}}$ и параметров теплопроводной контрастности ${{{{\varepsilon }}}_{k}}$ мантийная составляющая градиента $K_{z}^{{\text{'}}}\left( {0,0} \right)$ на плоскости $z = H$ вдвое выше, чем для источников в земной коре на глубинах $\left( {~{{z}_{C}} \leqslant {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}} \right)$.
Ядро (6.13) мы применили для вычисления коровой составляющей теплового потока при решении прямой задачи (5.1); ядро (6.19) – для решения обратной задачи (5.3) при пересчете мантийной составляющей потока на глубину. Теплопроводность геотермического разреза возрастает с глубиной, т.е. параметры теплопроводной контрастности будут отрицательными ${{{{\varepsilon }}}_{P}} < 0$. Это означает, что сравнительно с моделью безграничной среды рост теплопроводности разреза увеличивает ядро интегральных формул для температурных градиентов. Следовательно, составляющая потока из решения прямой задачи от источников в земной коре будет больше, а мантийная составляющая обратной задачи аналитического продолжения будет меньше. Контраст теплопроводностей слоистой среды меняет расчетные соотношение между поверхностным и глубинным тепловыми потоками, что затрагивает энергетику стационарного теплообмена между корой и мантией.
7. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Настоящие исследования включают в себя три этапа: создание аналитического метода решения геотермических задач стационарной теплопроводности для моделей кусочно-однородных сред; разработку универсальной схемы количественной интерпретации тепловых и гравитационных аномалий; построение практических примеров интерпретации тепловых полей на основе численных алгоритмов математической модели.
1. Граничные задачи линейного (теплового) сопряжения, несмотря на прозрачность их физической постановки, обладают довольно сложной математической структурой [Светов, Губатенко, 1988]. В их постановочную часть не входят явные значения граничных функций; указана лишь степень гладкости сопрягаемых на границах тепловых полей. Ветви кусочно-гладких частных решений удовлетворяют системе уравнений Пуассона, каждое из которых задано в своей области пространства, но не замкнуто граничными условиями. В результате утрачивается математический формализм “сквозных” алгоритмов при построении общего решения задачи и, в частности, ограничивается применение метода интегральных преобразований.
Эти проблемы снимаются в рамках предложенной нами алгоритмической схемы. Преобразования двусторонних условий теплового сопряжения в плотность источников эквивалентного простого слоя опирается на функциональные представление разрывного коэффициента обратной теплопроводности слоистой среды. Решение определяется интегральной сверткой по обобщенной формуле Грина.
2. В практике количественной интерпретации тепловых полей допускается упрощенный вариант постановки задачи сопряжения для моделей слабоконтрастных сред: перепад теплопроводностей в сопредельных слоях не должен быть более двух. В реальном разрезе контраст теплопроводностей литологических разностей горных пород еще ниже и меняется в диапазоне (1.1–1.5) относительных единиц. В таких случаях безразмерный параметр теплопроводной контрастности становится малым, а система уравнений Фредгольма для плотности простых слоев допускает итеративное разложение по малому параметру. В линейном приближении искомая плотность простых слоев вычисляется по интегральной формуле в явном виде. При этом появилась дополнительная возможность разделить вклад от глубинных и приповерхностных источников поля в суммарном тепловом потоке.
3. Аддитивное решение для температуры записывается в виде суммы интегралов Пуассона от распределения источников в земной коре и верхней мантии. Последние приравниваются к восходящей составляющей глубинного теплового потока. Такое приближение решения называется “гравитермическим”. В нем разделяются тектонические аномалии глубинного теплового потока и приповерхностные аномалии от источников земной коры. Это дает возможность использовать упрощенный алгоритм количественной интерпретации тепловых полей в слоисто-неоднородных средах, близкий в методическом плане к задачам гравиметрии. В его основе лежит общий принцип суперпозиции тепловых и гравитационных полей, реализованный при решении двух типов краевых задач.
4. Глубинный тепловой поток из мантии (за исключением тривиального случая) не является априори заданной граничной функцией прямой задачи геотермии. Но “след” этой функции однозначно прослежен на верхней границы пласта – плоскости, на которой заданы редуцированные значения “наблюденного” теплового потока. Разность между “наблюденными” и вычисленными значениями коровой составляющей потока приравнивается к целевой функции подбора мантийной составляющей на требуемой глубине. Алгоритм пересчетов “вниз” основан на решении обратной задачи численного аналитического продолжении гармонической функции с уровня земной поверхности на границу “кора–мантия”. По аналогии с интегралом Пуассона для однородной среды, в формулу пересчетов тепловых потоков входит производная контактной функции Грина для слоистого пласта. Оптимальный параметр регуляризации численной схемы аналитического продолжения выбирается по критерию стационарности схемы пересчетов гармонических функций: продолжение по любому замкнутому контуру в области гармоничности функции возвращает ее исходные значения. Возможность корректного вычисления мантийного теплового потока на глубине по исходным геотермическим данным на дневной поверхности позволяет лучше понять энергетику глубинных геотермических процессов.
5. Ядром интегрального решения для температуры (и ее градиента) является контактная функция Грина K слоистой по теплопроводности среды. Функция Грина геотермической задачи полностью учитывает рефракцию теплового потока на всех внутренних границах неоднородного пласта. Теплопроводность геотермического разреза возрастает с глубиной. И, сравнительно со своим производящим аналогом – функцией Грина G для однородного пласта, темп нарастания производной $K_{z}^{{}}$ по глубине будет больше. Это означает, что при прочих равных условиях, вычисленный градиент температуры в земной коре (прямая задача геотермии) будет выше, а пересчитанный градиент на мантию (обратная задача аналитического продолжения) будет ниже. Та же тенденция будет наблюдаться и в тепловых потоках. Геотермическое картирование тепловых потоков (см. рис. 2) содержит тектонические признаки индикатора глубинного теплообмена. В тектонически-активных структурах молодых палеозойских платформ индикативное отношение тепловых потоков в коре и мантии стремится к равновесному значению порядка единицы. И, как следствие, уменьшение теплового потока на границе “кора–мантия” способствует общей стабилизации теплового режима в нижней части земной коры.
8. ЗАКЛЮЧЕНИЕ
Развитие методов количественной интерпретации гравитационных полей с построением трехмерных сеточных моделей распределения плотности предопределило возможность верификации искомых параметров в полях принципиально иной эндогенной природы – полях стационарных температур и тепловых потоков. Сохранение преемственности алгоритмов количественных вычислений потребовало решения прямой задачи геотермии для модели неоднородной по теплопроводности слоистой среды.
Теория решения граничных задач теплового сопряжения базируется на аналитической аппроксимации обратного коэффициента теплопроводности на сопредельных границах кусочно-однородных сред и континуальном представлении дифференциального оператора с разрывными коэффициентами для уравнения стационарной теплопроводности. На границах разрыва коэффициента теплопроводности образуются “тепловые” источники эквивалентного простого слоя, плотность которых находится из решения системы интегральных уравнений Фредгольма. Для слабоконтрастных по теплопроводности слоистых сред плотности источников простого слоя находится в явном виде, а общее решение для температур и тепловых потоков становится аддитивным.
Интегральная формула решения задачи сопряжения представлена сверткой внутренних и внешних тепловых источников поля с “контактной” функцией Грина – ядром преобразования свертки для слоистой среды. Структура и вид ядра как функции распределения источников поля в коре и мантии задана двойным знакопеременным рядом по рекурсивным расстояниям от изображений источников. Для плоских границ тепловых контактов ядро приобретает замкнутый аналитический вид, близкий (по форме) к ядру интеграла Пуассона для однородной среды.
За основу количественных расчетов тепловых полей использовалась авторская модель трехмерного распределения плотности верхней части литосферы Уральского региона. По стохастической выборке из массива данных о связи плотностных и теплофизических параметров неоднородных сред, выполнено трехмерное макетирование материальных коэффициентов уравнения теплопроводности с тем, чтобы решить прямую задачу геотермии на сетках слоисто-блочного распределения теплопроводности и теплогенерации. Показана возможность практического применения аддитивных схем количественных расчетов. Принцип суперпозиции полей лежит в основе комплексной интерпретации тепловых и гравитационных аномалий. Построен сеточный алгоритм решения прямых и обратных задач стационарной теплопроводности для геотермических моделей слоистых сред.
Разработан метод аналитического продолжения мантийной составляющей теплового потока с уровня земной поверхности на кровлю верхней мантии через слоистую по теплопроводности среду. Определен вклад мантийной составляющей в приповерхностный тепловой поток. Показано, что в реальном геотермическом разрезе рост теплопроводности с глубиной увеличивает коровую и уменьшает мантийную составляющую в суммарном балансе тепловых потоков.
Таким образом, выбранная стратегия континуального подхода к постановке и решению граничных задач сопряжения для моделей кусочно-однородных сред (граничных задач с условиями IV рода) позволяет записать единую интегральную формулу явного решения задачи в классе моделей с криволинейными границами раздела и построить унифицированный аддитивный алгоритм вычисления стационарных тепловых полей в неоднородных средах. Комплексирование гравитационных и тепловых аномалий повышает надежность имитационного математического моделирования и снижает степень неоднозначности полученных результатов при решении обратных задач гравиметрии и геотермии.
Список литературы
Булашевич Ю.П. Информативность геотермии при изучении земной коры Уральской эвгеосинклинали // Изв. АН СССР. Сер. Физика Земли. 1983. № 8. С. 76–83.
Булашевич Ю.П., Щапов В.А. Геотермическая характеристика Урала. Применение геотермии в региональных и поисково–разведочных исследованиях. Свердловск: УНЦ АН СССР. 1983. С. 3–17.
Владимиров В.С., Жаринов В.В. Уравнения математической физики. М.: Физматлит. 2000. 400 с.
Гельфанд И.М., Шилов Г.Е. Обобщенные функции и действия над ними. М.: Физматгиз. 1959. 470 с.
Голованова И.В. Тепловое поле Южного Урала. М.: Наука. 2005. 190 с.
Голованова И.В., Сальманова Р.Ю., Демежко Д.Ю. Реконструкции климата на Урале по геотермическим данным // Геология и геофизика. 2012. Т. 53. № 12. С. 1776–1785.
Гордиенко В.В. Радиогенная теплогенерация в земной коре и тепловой поток из мантии древних платформ // Геофизический журн. 1980. Т. 2. № 3. С. 29–34.
Дучков А.Д., Соколова Л.С. Термическая структура литосферы Сибирской платформы // Геология и геофизика. 1997. Т. 38. № 2. С. 494–503.
Дучков А.Д., Соколова Л.С., Горнов П.Ю., Веселов В.В. Электронный геотермический атлас Сибири и Дальнего Востока (2009–2012). Новосибирск.: ИГиГ. 2013. URL: http://maps.nrcgit.ru/geoterm/
Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука. 1964. 488 с.
Ладовский И.В., Мартышко П.С., Бызов Д.Д., Цидаев А.Г. Задача сопряжения стационарных тепловых полей // Докл. РАН. 2019. Т. 488. № 8. С. 81–85. https://doi.org/10.31857/S0869-5652488181-85
Лыков А.В. Теория теплопроводности. М.: Высшая школа. 1967. 600 с.
Мартышко П.С. О решении обратной задачи электроразведки на постоянном токе для произвольных классов потенциалов // Изв. АН СССР. Сер. Физика Земли. 1986. № 1. С. 87–92.
Светов Б.С., Губатенко В.П. Аналитические решения электродинамических задач. М.: Наука. 1988. 344 с.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука. 1999. 979 с.
Франк Ф., Мизес Р. Дифференциальные и интегральные уравнения математической физики. Москва–Ленинград: ОНТИ. 1937. 998 с.
Щапов В.А. Тепловое поле Урала // Уральский геофизический вестник. 2000. № 1. С. 126–130.
Gordienko V.V., Pavlenkova N.I. Combined geothermal-geophysical models of the earth’s crust and upper mantle for the European continent // J. Geodyn. 1985. V. 4(1–4). P. 75–90. https://doi.org/10.1016/0264-3707(85)90053-5
Crough S.T., Thompson G.A. Thermal model of continental lithosphere // Journal of Geophysical Research. 1976. V. 81. P. 4857–4862.
Kukkonen I.T., Golovanova I.V., Khachay Yu.V., Druzhinin V.S., Kosarev A.M., Schapov V.A. Low Geothermal heat flow of the Urals fold belt – implication of low heat production, fluid circulation or palaeoclimate? // Tectonophysics. 1997. V. 276. P. 63–85.
Ladovskii I.V., Martyshko P.S., Tsidaev A.G., Byzov D.D. A Method for Quantitative Interpretation of Stationary Thermal Fields for Layered Media // Geosciences. 2020. V. 10. № 5. № 199. https://doi.org/10.3390/geosciences10050199
Martyshko P., Ladovskii I., Byzov D., Tsidaev A. On solutions of forward and inverse problem for potential geophysical fields: Gravity inversion for Urals region. AIP Conference Proceedings 2019. V. 2164. 120010. Albena. https://doi.org/10.1063/1.5130870
Martyshko P.S., Ladovskii I.V., Byzov D.D., Tsidaev A.G. On a solution of forward and inverse problems of potential geophysical fields. AFSID-2020. AIP Conference Proceedings 2312, 040002 (2020). https://doi.org/10.1063/5.0035417
Martyshko P., Ladovskii I., Byzov D. Parallel Algorithms for Solving Inverse Gravimetry Problems: Application for Earth’s Crust Density Models Creation // Mathematics. 2021. V. 9. P. 2966. https://doi.org/10.3390/math9222966
Sclater J.G., Jaupart C., Galson D. The heat flow through oceanic and continental crust and the heat loss of the Earth // Rev. Geophys. Space Phys. 1980. V. 18. P. 269–311.
Дополнительные материалы отсутствуют.
Пн.-пт.: 10.00-19.00