Физика Земли, 2023, № 2, стр. 212-223

ВВЕДЕНИЕ

В настоящее время наблюдается повышенный интерес к интерес к разработке нетрадиционных коллекторов углеводородов. В частности, к таким коллекторам относятся нефтематеринские отложения баженовской свиты. Углеводороды, содержащиеся в нефтематеринских породах, как правило, находятся под действием повышенного пластового давления. Это приводит к ряду проблем при бурении и, как следствие, необходимости более точного определения границ допустимых давлений бурового раствора, особенно при бурении горизонтальных стволов или наклонно-направленных стволов с большим отходом от вертикали. Повышение точности моделирования неизбежно приводит к вопросу о соответствии моделей горной породы реальному ее поведению. Многие исследователи [Лехницкий, 1977; Аннин, 2009; Батугин, Ниренбург, 1972; Тихоцкий, 2017] отмечают, что некоторые породы, слагающие, в том числе, баженовскую свиту, обладают анизотропией упругих свойств. В частности, к таким породам необходимо отнести сланцы, а также различные типы глин.

Настоящее исследование посвящено вопросу о влиянии выбора модели на результат прогноза безопасного окна давления бурового раствора, а также сопутствующих параметров бурения. Для построения моделей в работе использованы действительные данные керновых исследований, выполненных в разное время на образцах пород, слагающих баженовскую свиту. Поскольку исследования не проводились целенаправленно на изучение анизотропных свойств, полученные корреляционные зависимости между упругими свойствами стоит рассматривать скорее как иллюстрацию подхода. Однако полученные в результате анализа данные говорят об анизотропии, характерной для баженовской свиты по данным других источников. Таким образом, в настоящей работе, не претендуя на безусловную точность построения моделей, авторы попытались описать возможные ошибки, к которым приводит неверный выбор модели, а также показать ряд эффектов, которые невозможно описать с использованием моделей изотропных упругих свойств горных пород.

АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ

Анизотропия – это изменение свойств материала в зависимости от направления. В общем виде закон Гука для пороупругих анизотропных тел можно записать в виде:

где: $\sigma _{{ij}}^{{eff}}$, ${{\sigma }_{{ij}}}$ – эффективное и полное напряжение соответственно; $p$ –пластовое давление; ${{{{\alpha }}}_{{ij}}}$ – тензор пороупругости; ${{{{\varepsilon }}}_{{kl}}}$ – тензор деформации; ${{c}_{{ijkl}}}$ – тензор упругости 4-го ранга. Для того, чтобы представить закон Гука (1) в удобном для записи виде, часто применяют представление Ламе:

Здесь ${\mathbf{\sigma }},{{{\mathbf{\sigma }}}^{{eff}}},{\mathbf{\alpha }}$ – вектора размерности 6, полученные из соответствующих тензоров в записи (1) согласно правилу Ламе: $xx \to 1$, $yy \to 2$, $zz \to 3$, $yz \to 4$, $xz \to 5$, $xy \to 6$. Вектор деформации ${\mathbf{\varepsilon }}$ также состоит из компонент тензора деформаций, но классически имеет другой вид: ${{\varepsilon }_{{1,2,3}}} = {{\varepsilon }_{{xx,yy,zz}}}$, ${{\varepsilon }_{{4,5,6}}} = 2{{\varepsilon }_{{yz,xz,xy}}}$. Матрица упругости ${\mathbf{\hat {C}}}$ получается из тензора упругости с учетом правила Ламе и вида вектора деформаций ${\mathbf{\varepsilon }}$. Введем также матрицу податливости ${\mathbf{\hat {S}}} = {{{\mathbf{\hat {C}}}}^{{ - 1}}}$, обратную матрице упругости. В общем случае матрица упругости с учетом симметрии имеет 21 компоненту. Здесь необходимо упомянуть, что введенные такими правилами вектора и матрицы при повороте системы координат имеют собственные законы преобразования, не совпадающие с классическими законами преобразований в трехмерном пространстве [Лехницкий, 1977]. Далее будем использовать оба способа нумерации в зависимости от контекста.

Наиболее распространенным типом симметрии среди горных пород является слоистая симметрия. К этому типу относятся алевролиты, глинизированные песчаники, сланцы и другие горные породы [Аннин, 2009; Батугин, Ниренбург, 1972]. Слоистые горные породы имеют выделенную ось симметрии или ось изотропии, направленную поперек напластования. При этом по отношению к географической системе отсчета ось изотропии может быть расположена произвольным образом.

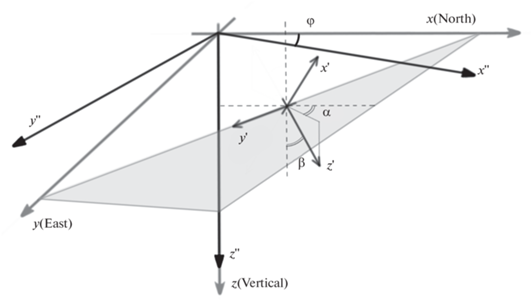
Будем далее различать географическую систему координат и систему координат, связанную с напластованием (рис. 1). Географическая система координат – это система координат, у которой ось $z$ направлена по вертикали вниз, а ось $x$ направлена на север. Система координат, связанная с напластованием, имеет ось $z{\kern 1pt} '$, направленную поперек напластования, а ось $y{\kern 1pt} '$ лежит в плоскости напластования параллельно дневной поверхности $z = 0$.

Слоистые породы, каждый слой которых представлен изотропной породой, относятся к трансверсально-изотропным телам. Также к трансверсально-изотропным телам можно отнести любые породы с изотропными включениями, вытянутыми или сплюснутыми только в одном направлении. Такие породы характеризуются пятью модулями упругости. Матрица податливости трансверсально-изотропного тела в системе напластования имеет вид:

где: ${{E}_{{H,V}}}$ – вдоль и поперек напластования; ${{{{\nu }}}_{{12}}}$ – коэффициент Пуассона вдоль напластования; ${{{{\nu }}}_{{31}}}$ – коэффициент Пуассона поперек напластования; $G{\kern 1pt} '$ – модуль поперечного сдвига. Введем углы ${{\alpha }}$ и ${{\beta }}$ – азимут падения и наклон оси напластования (рис. 1). Матрица податливости в географической системе отсчета может быть получена при помощи преобразования поворота: где: ${\mathbf{\hat {S}}}{\kern 1pt} '$ – матрица податливости в системе отсчета, связанной с напластованием, определенная соотношением (3); ${\mathbf{\hat {S}}}$ – матрица податливости в географической системе отсчета; ${\mathbf{q}}\left( {{{\alpha }},{{\beta }}} \right)$ – матрица преобразования поворота (см. [Лехницкий, 1977]).

Таким образом, любая слоистая трансверсально-изотропная порода должна быть охарактеризована пятью упругими модулями: ${{E}_{H}},{{E}_{V}},{{\nu }_{{12}}},{{{{\nu }}}_{{31}}},G{\kern 1pt} '$, а также двумя углами ${{\alpha }},{{\beta }}$, определяющими положение оси изотропии.

АНАЛИЗ КЕРНОВОГО МАТЕРИАЛА

Общий подход к определению статических модулей упругости включает в себя определение связи между статическими и динамическими модулями упругости на керновом материале и последующем применении полученной корреляционной зависимости к данным акустического каротажа. При существенном отличии акустических свойств, полученных при исследовании на керне и в скважине, вводят дополнительную “ремасштабирующую” корреляцию между акустическими исследованиями разного масштаба. В случае с восстановлением статических параметров анизотропного тела возможно сохранение такого же подхода при определении модулей вертикального нагружения. Продольная и поперечная скорости звука в трансверсально-изотропной среде, распространяющиеся вдоль оси изотропии, зависят только от этих модулей. Для восстановления остальных трех модулей упругости можно воспользоваться их корреляционными зависимостями от двух модулей вертикального нагружения. В настоящей работе рассмотрен способ получения параметров анизотропии пород баженовской свиты по данным проведенных ранее лабораторных испытаний керна месторождений А и Б.

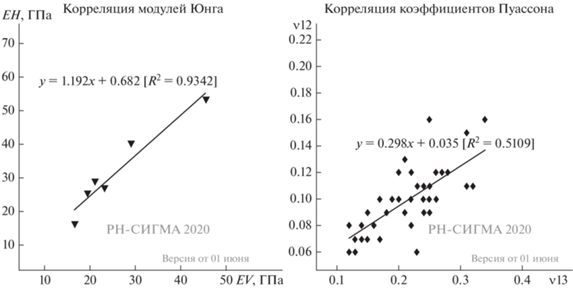
Образцы керна месторождения А были использованы для получения корреляционной зависимости между модулями Юнга ${{E}_{V}}$ и ${{E}_{H}}$. Тесты были проведены на цилиндрических образцах диаметром 30 мм и отношением длины к диаметру равным 2. Часть образцов была выбурена перпендикулярно напластованию, часть образцов – параллельно.

Статические модули Юнга определены стандартным способом, как коэффициенты пропорциональности на линейном сегменте зависимости деформации от нагрузки по ветви разгрузки [ASTM D7012-07, 2007]. Для оценки степени анизотропии были выбраны пары образцов с близких глубин (среднее значение разницы глубин 0.16 м), выбуренных в двух взаимно перпендикулярных направлениях. На рис. 2 показаны результаты эксперимента.

Результаты исследований керна А месторождения не позволяют определить коэффициенты Пуассона, поскольку выполнены на цилиндрических образцах. При этом использование цепного датчика не дает возможности учесть различие в деформации вдоль оси изотропии и поперек нее при нагружении образца вдоль напластования. Для измерения коэффициентов Пуассона ${{{{\nu }}}_{{12}}}$ и ${{{{\nu }}}_{{13}}}$ был использован иной подход. К сожалению, полного комплекса исследований на образцах одного месторождения в распоряжении авторов не нашлось, поэтому вторая часть лабораторных исследований основана на результатах испытаний керна месторождения Б.

Образцы керна месторождения Б исследованы на испытательной системе трехосного неравнокомпонентного нагружения ИСТНН. Методика исследования описана в работе [Karev, 2013]. Из кернового материала были изготовлены кубические образцы с гранью 40 либо 50 мм. Образцы маркируются следующим образом: ось 3 образца совпадает с осью изотропии керна (ось $z{\kern 1pt} '$), ориентация осей 2 и 1 произвольна.

Нагружение образцов проведено в два этапа. На первом этапе образец равномерно обжимается по всем трем осям до заданных значений напряжения. На втором этапе нагрузка по осям 1 и 3 образца поддерживаются постоянными, а нагрузка вдоль оси 2 в плоскости напластования увеличивается. Увеличение нагрузки на втором этапе продолжается до разрушения образца. В ходе испытания измеряются деформации образца по трем взаимно перпендикулярным осям.

По данным испытания был рассчитан коэффициента Пуассона ${{{{\nu }}}_{{12}}}$, характеризующий деформации вдоль плоскости изотропии при действии нагрузок вдоль плоскости изотропии, а также коэффициент Пуассона ${{{{\nu }}}_{{13}}}$, характеризующий деформации в направлении оси изотропии при действии нагрузок вдоль плоскости изотропии [Karev, 2020]. Результаты эксперимента показаны на рис. 2.

Итогом проведенных испытаний стали две корреляционные зависимости, позволяющие восстановить два из трех недостающих модуля упругости:

Последнее соотношение – это прямая связь модулей Юнга и коэффициентов Пуассона трансверсально-изотропного тела [Лехницкий, 1977]. На примере изученного кернового материала видно, что упругие свойства – модуль Юнга и коэффициент Пуассона горной породы баженовской свиты зависят от направления. При нагружении поперек напластования модуль Юнга имеет меньшее значение, чем при нагружении вдоль напластования.

Приведенные исследования позволяют восстановить четыре упругих модуля: два модуля Юнга и два коэффициента Пуассона. Но для полноценного описания среды необходимо знать также модуль поперечного сдвига $G{\kern 1pt} '$ (3). Для его прямого измерения необходимо привлечение исследований на керне, выбуренном по направлению под углом к оси напластования [Amadei, 1983]. В изученной выборке такие исследования отсутствуют. Однако в работе [Батугин, Ниренбург, 1972] приведена корреляция модуля поперечного сдвига от модулей Юнга и коэффициентов Пуассона, с инженерной точностью описывающая этот модуль для большого количества пород. Приведем здесь эту корреляцию:

Авторы понимают, что подобный подход может вызвать вопросы о состоятельности использования данных с разных месторождений. Важнейшим моментом здесь является идентичность образцов. Стоит, однако, заметить, что подобные вопросы часто возникают даже в случае использования кернового материала из протяженного однородного материала, извлеченного из одной скважины. Более того, в дальнейшем при построении модели полученные корреляционные зависимости будут распространены на весь интервал баженовской свиты. Как будет видно далее, это сделано намеренно для того, чтобы подчеркнуть разнообразие эффектов, к которым приводит анизотропия упругих свойств. Подобный подход преследовал и еще одну цель: показать, что, несмотря на отсутствие данных (что часто встречается в инженерной практике), оценку следствия наличия анизотропии часто можно провести и на существующем наборе. Безусловно, при построении модели на месторождениях с анизотропными пластами авторы настоятельно рекомендуют проводить лабораторные испытания кернового материала, направленные на изучение анизотропии конкретных горных пород. Таким образом, результаты, полученные в настоящем разделе, стоит воспринимать как иллюстрацию подхода. Полученные при этом параметры анизотропии не противоречат данным других исследователей о степени анизотропии баженовской свиты [Тихоцкий, 2017; Шустов, 2019; Lu, 2015].

НАПРЯЖЕНИЯ В ДЕФОРМАЦИОННО-ОГРАНИЧЕННОЙ СРЕДЕ

Далее рассмотрим задачу о напряженном состоянии анизотропного пласта в деформационно-ограниченной постановке. Пусть пласт находится под действием веса вышележащих горных пород ${{{{\sigma }}}_{V}}$. Со стороны вмещающей плиты в латеральном направлении на пласт действуют некоторые тектонические силы. Здесь необходимо ввести еще одну вспомогательную систему координат, связанную с направлением главных тектонических воздействий. Под тектоническим воздействием будем понимать силы, действующие на вмещающую месторождение литосферную плиту со стороны мантии. Эти силы действуют на масштабе, существенно превышающем масштаб месторождения. Для описания эффекта от тектонического воздействия часто прибегают к модели деформационно-ограниченной среды [Зобак, 2018; Jeager, Cook, 2007]. Данная модель предполагает, что тектонические силы на масштабе, большем, чем масштаб месторождения, но меньшем, чем масштаб литосферной плиты, приводят к появлению заданной тектонической деформации. Как и любой тензор, тензор тектонической деформации можно привести к главным осям. Будем предполагать далее, что одна из главных осей этого тензора направлена вертикально вниз, а ось максимальной тектонической деформации направлена под углом ${{\varphi }}$ к направлению на север или к оси $x$ географической системы координат. Угол ${{\varphi }}$ при этом называют азимутом регионального напряжения. Таким образом, система отсчета, связанная с тектоническим воздействием, получается из географической системы координат поворотом последней вокруг оси $z$ на угол ${{\varphi }}$. При расчете тензора восприимчивости в этой системе отсчета можно воспользоваться формулой (4), заменив азимут падения напластования $\alpha $ разностью этого азимута и азимута регионального напряжения ${{\alpha }} - {{\varphi }}$.

Обозначим максимальную тектоническую деформацию ${{{{\varepsilon }}}_{{{\text{max}}}}}$, а минимальную – ${{{{\varepsilon }}}_{{{\text{min}}}}}$. Предположим, также, что касательные тектонические напряжения отсутствуют: ${{\varepsilon }_{4}} = {{\varepsilon }_{5}} = 0$. Также, в системе отсчета тектонического воздействия касательная деформация равна нулю: ${{\varepsilon }_{6}} = 0$, а вертикальное напряжение равно горному давлению: ${{\sigma }_{3}} = {{\sigma }_{V}}$

Запишем закон Гука в системе, связанной с тектоническим воздействием с учетом сделанных предположений, а также выражения (1):

Здесь ${{C}_{{ij}}}$ – компоненты тензора упругости в системе отсчета, связанной с тектоническими напряжениями; ${{{{\alpha }}}_{i}}$ – компоненты тензора пороупругости в этой же системе отсчета, перенумерованные согласно правилу Ламе. Звездочкой для удобства помечены величины, известные из граничных условий. Величины без звездочки – неизвестные, подлежащие определению. При записи компонентов матрицы упругости также учтена ее симметрия по отношению к перестановке индексов, а также ее наиболее общий вид. Выражая из третьего уравнения (7) величину ${{\varepsilon }_{3}}$ и подставляя ее в остальные уравнения, можно записать решение в форме:

где индекс $K = 1,2,4,5,6$.

Анализируя формулу (8) можно сделать несколько важных выводов:

1. Компонента ${{\sigma }_{6}} = {{\sigma }_{{xy}}} \ne 0$. В этом случае оси главных напряжений не совпадают с осями главных деформаций. Эффект тем больше, чем выше разница главных деформаций.

2. Компоненты ${{\sigma }_{4}} = {{\sigma }_{{yz}}} \ne 0$, ${{\sigma }_{5}} = {{\sigma }_{{xz}}} \ne 0$. В этом случае вертикальная ось не является осью главного напряжения. Эффект тем меньше, чем больше разность горного и горизонтального напряжения. Для нормального режима с большой разницей напряжений эффектом можно пренебречь.

3. Даже в случае равенства тектонических деформаций ${{\varepsilon }_{1}} = {{\varepsilon }_{2}}$ при наличии наклона оси изотропии возможно появление разности главных напряжений. Эффект тем выше, чем выше анизотропия и разница в направлениях осей главных деформаций и оси изотропии.

4. Возможно также проявление эффекта, обратного предыдущему: допустимо ${{\sigma }_{1}} = {{\sigma }_{2}}$ при неравных тектонических деформациях. И если прямое равенство главных напряжений следует считать скорее совпадением, то проявление снижения контраста напряжений относительно случая со строго вертикальным направлением оси главного напряжения в данном случае может сказаться на результатах дальнейшего моделирования.

МОДЕЛИ НАПРЯЖЕННОГО СОСТОЯНИЯ ПЛАСТА

Исследование процесса устойчивости ствола скважины можно условно разделить на две части:

1. Построение модели напряженного состояния пласта с заданными свойствами.

2. Расчет напряженного состояния в околоскважинном пространстве и на стенке скважины.

В предыдущем разделе приведен способ расчета регионального тензора напряжения в анизотропном пласте. Для иллюстрации работы алгоритмов, а также для выявления некоторых особенностей итоговых моделей были построены три варианта моделей напряженного состояния пласта:

1. Первая модель (ISO) предполагает изотропный пласт, модули упругости которого получены стандартным измерением с использованием образцов, выбуренных поперек напластования. Иными словами, в качестве упругих параметров выбраны модули ${{E}_{V}}$ и ${{{{\nu }}}_{{31}}}$.

2. Вторая модель (VTI) предполагает трансверсально-изотропный пласт, модули упругости которого получены на основании данных стандартного акустического каротажа в вертикальной скважине, а также корреляционных зависимостей (5), (6). Ось изотропии в этой модели направлена строго вверх ${{\beta }} = 0$.

3. Третья модель (TTI) предполагает трансверсально-изотропный пласт, модули упругости которого определены согласно той же процедуре, что и во втором случае, но азимут падения пласта $\alpha $ равен 65°, а наклон слоистости $\beta $ равен 20°.

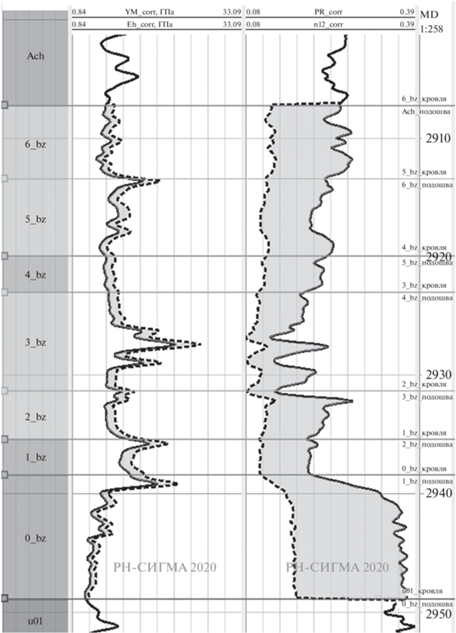
Поскольку данных о различных пропластках баженовской свиты в распоряжении авторов нет, все корреляции распространены на весь интервал баженовской свиты с целью оценки величин возможных ошибок при определении компонент напряженного состояния. Профили восстановленных упругих свойств в баженовской свите изображены на рис. 3. Обращает на себя внимание большая разница в коэффициентах Пуассона: ${{\nu }_{{31}}} - {{\nu }_{{12}}} \sim 0.15$. Контраст модулей Юнга при этом достаточно умеренный (~15%). Помимо модулей упругости важным параметром для построения корректной модели являются величины деформаций и азимут максимального тектонического воздействия. Для построения моделей в баженовской свите эта информация была взята из моделей, построенных для вышележащих ачимовских отложений, поскольку с глубиной величины тектонических деформаций изменяются слабо. Приведем здесь значения этих параметров: ${{\varepsilon }_{{{\text{max}}}}} = 4 \times {{10}^{{ - 4}}}$, ${{\varepsilon }_{{\min }}} = 2 \times {{10}^{{ - 4}}}$, $\varphi = - 40^\circ $.

Метод получения тектонических деформаций – это подбор таких значений этих параметров, которые не противоречат результатам исследований на скважинах. Исследования включают в себя измерение давления смыкания трещин гидроразрыва на нескольких скважинах, а также анализ результатов работы микроимиджера. Первый тип исследования дает информацию о минимальном горизонтальном напряжении, а второй тип исследования позволяет определить направление действия максимального горизонтального напряжения по данным о направлении вывалов на стенке скважины или направлении техногенной трещиноватости, а также оценить максимальное горизонтальное напряжение по данным о ширине вывалов при прочих известных параметров. Такой процесс называется калибровкой напряжений и по сути является обратной задачей. Более подробное его описание можно найти в работе [Зобак, 2018].

На рис. 4 приведены результаты построения модели компонент напряженного состояния $~{{\sigma }_{{\max }}}$ и ${{\sigma }_{{\min }}}$, а также контраста напряжений $\Delta \sigma = {{\sigma }_{{\max }}} - {{\sigma }_{{\min }}}$. Подробное рассмотрение модели показывает следующие особенности:

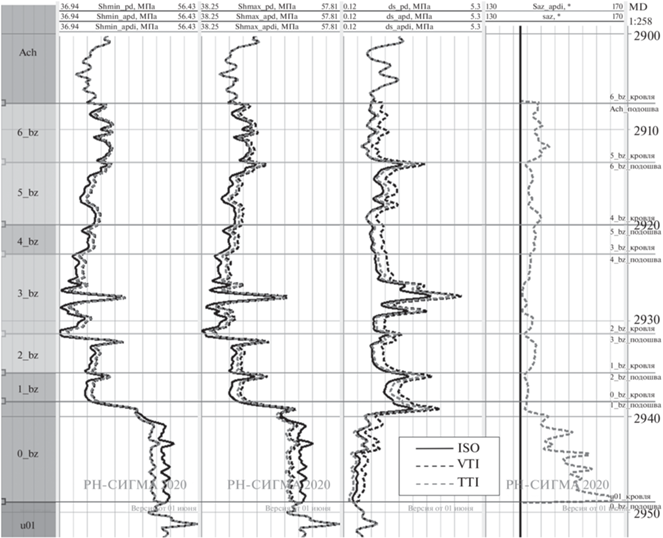
1. Компоненты минимального и максимального горизонтальных напряжений в анизотропных моделях отличаются от таковых в изотропной модели на величину порядка 1–2 МПа. Контраст напряжений при этом отличается на величину порядка 0.5–1 МПа.

2. Присутствие анизотропии в нижней части баженовских отложений приводит к снижению величин напряжений, тогда как в остальной части разреза – к их повышению.

3. Контраст напряжений для модели с наклоном оси изотропии (TTI) на большей части разреза баженовской свиты практически совпадает с контрастом в изотропной модели.

4. В модели с наклоном оси изотропии наблюдается сильное отклонение направления локального действия максимального напряжения от регионального направления (~22°).

Как видно из сравнения трех различных моделей, анизотропия оказывает существенное влияние на компоненты напряжения. При этом проявления анизотропии весьма разнообразны и сложно предсказуемы. Далее рассмотрим проявления анизотропии упругих свойств горной породы на устойчивость ствола скважины.

МОДЕЛИ УСТОЙЧИВОСТИ СТВОЛА СКВАЖИНЫ

Моделирование подобных задач требует привлечения нестандартных алгоритмов для решения задач о напряженном состоянии скважины, заполненной жидкостью под давлением в предварительно нагруженной среде с анизотропными упругими свойствами. Такая задача решена в программном комплексе “РН-СИГМА”. Основой решения задачи является общее решение [Лехницкий, 1977], реализованное в виде алгоритма. Кроме того, решение этой задачи используется для определения оптимального окна плотности бурового раствора при проводке ствола скважины. Формат данной статьи, а также трудоемкость записи решения не позволяют авторам привести здесь алгоритм решения этой задачи. Стоит, однако, упомянуть, что сам алгоритм основан на решении задачи в комплексных потенциалах и позволяет выписать решение задачи для вмещающей среды, описывающейся произвольной физически корректной матрицей упругости [Amadei, 1983]. В текущей версии ПК “РН-СИГМА” реализована инициализация матрицы упругости не сложнее трансверсально-изотропной среды с произвольным наклоном оси изотропии. Это связано с тем, что данные для описания материалов с более сложной формой анизотропии, как правило, у инженеров отсутствуют.

Для расчета критической плотности обрушения необходимо выбрать критерий разрушения породы. Вообще говоря, выбор критерия разрушения также является вопросом для отдельного изучения, но этот вопрос не является целью настоящей работы. Исследование влияния критерия разрушения на результат моделирования можно найти в работе [Rahimi, 2014]. Для иллюстрации влияния анизотропии на устойчивость ствола скважины был выбран критерий Кулона–Мора как наиболее часто использующийся при моделировании этого процесса.

В настоящей работе приведены результаты моделирования устойчивости для двух скважин: первая скважина – вертикальная, вторая скважина – горизонтальная. На рис. 5 представлены результаты моделирования окна безопасной плотности бурового раствора для обеих скважин. На левом треке представлено окно для вертикальной скважины, а на правом – для горизонтальной. Областями с более светлой заливкой показаны области, в которых анизотропия предсказывает изменение окна бурового раствора.

Вертикальная скважина фактически проведена без осложнений, что и подтверждает моделирование. Необходимо, однако, отметить несколько особенностей. Во-первых, анизотропия не оказывает практически никакого влияния на критическую плотность обрушения, за исключением небольшой области в нижней части разреза. Здесь учет анизотропии позволяет выбрать более низкую плотность бурового раствора для прохождения этого интервала. Снижение критической плотности составляет <0.04 г/см³. Критическая плотность поглощения при этом показывает повышение в большей части интервала, за исключением нижней (глубины от 2940 до 2950 м), где она становится существенно ниже. Размер изменений приблизительно одинаков и составляет ~0.05 г/см³ в обе стороны. В целом необходимо отметить, что в данном случае все модели дают приблизительно одинаковый результат.

Иная ситуация наблюдается в случае горизонтальной скважины. Из рис. 5 (справа) видно, что в модели изотропной среды интервал поглощения и интервал обрушения существенно перекрываются, что затрудняет бурение и может привести к ряду осложнений. В данном случае стратегия выбора плотности бурового раствора может заключаться в прохождении интервалов несовместимости с плотностью ниже плотности поглощения. Это приведет к образованию вывалов на стенке скважины. В данном случае контраст напряжений в плоскости, поперечной ее оси велик. Одно из напряжений практически совпадает с горным давлением, а второе – с максимальным горизонтальным напряжением. Следовательно, угловая ширина вывалов будет небольшой, и скважина останется устойчивой [Зобак, 2018]. Выбор плотности бурового раствора выше критического значения плотности поглощения приведет к необходимости изменений состава бурового раствора для формирования вокруг скважины зоны с низкой проницаемостью, что приведет к необходимости дополнительной работы по очистке околоскважинной зоны перед вводом ее в эксплуатацию.

В рассматриваемом случае в модели анизотропной среды общий размер интервалов перекрытия существенно меньше, чем в модели изотропной среды. Критическая плотность поглощения выше на величину $ \leqslant {\kern 1pt} 0.04\,{{\,{\text{г}}} \mathord{\left/ {\vphantom {{\,{\text{г}}} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}$, а критическая плотность обрушения ниже на величину $ \leqslant {\kern 1pt} 0.025\,\,{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}~$. На практике это приведет к меньшему объему выноса дополнительного шлама из-за образования вывалов при выборе одинаковой плотности бурового раствора, а также к более гибкому выбору плотности бурового раствора до момента начала поглощения. В данном примере различия между анизотропией с вертикальной осью и наклоном оси несущественны.

Горизонтальная скважина в данном примере в действительности не была пробурена, поэтому проверить достоверность модели напрямую невозможно. Однако через интервал баженовской свиты была пробурена горизонтальная скважина на нижележащий интервал. Баженовскую свиту эта скважина пересекала под углом >75°. Осложнений на этой скважине не выявлено.

ЭФФЕКТЫ АНИЗОТРОПИИ

Выше было показано, что выбор модели, описывающей упругие свойства породы, существенно влияет на результат расчета параметров безопасного бурения. Необходимо также обратить внимание на еще один немаловажный аспект – потерю симметрии при моделировании в анизотропных средах. Пусть необходимо оценить окно безопасной плотности бурового раствора для двух стволов. Если оба ствола имеют равный наклон, а азимут стволов различается на 180°, то результат моделирования в изотропной среде будет абсолютно одинаков. Тот же результат можно ожидать и в трансверсально-изотропной среде, со строго вертикальной осью изотропии (VTI). В случае же, когда ось изотропии наклонена относительно вертикали, этот вывод уже не будет верным (см. рис. 6). Таким образом, при моделировании устойчивости ствола в такой среде необходимо с осторожностью переносить опыт моделирования в более простых средах.

Другой немаловажный факт состоит в том, что потеря симметрии сказывается и на уровне скважины. Как было отмечено ранее, направление максимального горизонтального напряжения на уровне скважины может не совпадать с направлением регионального напряжения. Это приводит к вращению направления вывала, что с одной стороны может быть неверно интерпретировано, а с другой является косвенным признаком наличия анизотропии. Форма вывалов в изотропной однородной среде всегда близка к симметричной независимо от направления ствола относительно вертикали. При этом на стенке скважины образуется ровно два вывала, расположенных друг напротив друга. Это является следствием симметрии полей напряжения на стенке скважины в изотропной среде. Ряд методов интерпретации вывалов основаны на предположении о симметрии вывалов [Зобак, 2018]. В случае, когда ось симметрии не совпадает с осью скважины, такого рода симметрия исчезает, а областей вывалов может быть более двух (см. рис. 7). Эти факты ставят совершенно новую проблему перед исследователями: калибровка модели устойчивости ствола скважины в анизотропной среде должна учитывать все особенности получаемых имиджей.

ВЫВОДЫ

В настоящей работе показан процесс построения модели с учетом трансверсально-изотропных свойств пород, слагающих баженовскую свиту. На основании разнородных лабораторных исследований построены корреляции, позволяющие оценить все компоненты тензора упругости слагающих пород. Не претендуя на точность модели, на основании этих общих корреляций построены модели напряженного состояния для трех различных вариантов: изотропной породы, трансверсально-изотропной породы с вертикальной осью изотропии и наклонной осью изотропии. Показано, что уже на уровне модели напряженного состояния их различия нельзя игнорировать, поскольку поведение тензора напряжений в разных моделях отличается не только на уровне величин, но и на качественном уровне: в модели с наклоном оси изотропии может появляться эффект вращения осей главных горизонтальных напряжений.

Для оценки влияния анизотропии на прогноз устойчивости ствола скважины в работе были построены модели устойчивости ствола скважины во всех трех вариантах моделей для двух скважин: вертикальной и горизонтальной. Для построения были использованы инструменты программного комплекса “РН-СИГМА”. На уровне скважин отличия также проявляются в существенном изменении параметров окна безопасной плотности бурового раствора. Особенно сильно это сказывается на критической плотности поглощения, хотя и изменения в критической плотности обрушения для горизонтальной скважины также могут быть ощутимы. Более детальный анализ также показал, что эффекты анизотропии горной породы сказываются и на применимости методов, разработанных для изотропных сред. Так, стереограммы критических плотностей более не являются симметричными, а вывалы на стенках скважины могут приобретать специфическую геометрию. В частности, при прохождении анизотропных интервалов может появляться эффект вращения вывала.

Таким образом, при изучении устойчивости ствола скважины в анизотропных средах необходимо применение совершенно новых, нетрадиционных подходов и алгоритмов для построения моделей напряженного состояния как на региональном уровне, так и на уровне скважин. Кроме того, требуются новые подходы к интерпретации скважинных имиджей и других специфических исследований, применяемых в геомеханике при калибровке моделей.