Физика Земли, 2023, № 5, стр. 114-130
Глубинные аномалиии электропроводности в районе Чаунской губы по данным магнитовариационного зондирования
С. С. Старжинский 1, *, Д. А. Сормаков 2, **
1 Тихоокеанский океанологический институт им. В.И. Ильичева ДВО РАН
г. Владивосток, Россия
2 Арктический и антарктический научно-исследовательский институт
г. , Санкт-Петербург, Россия
* E-mail: ss_stars@poi.dvo.ru
** E-mail: dimsoa@aari.ru
Поступила в редакцию 17.10.2022
После доработки 23.01.2023
Принята к публикации 24.01.2023
- EDN: WAWRAP
- DOI: 10.31857/S0002333723050137
Аннотация
В статье рассматриваются результаты магнитовариационных зондирований в двух пунктах в восточной Арктике в районе Чаунской губы, на метеостанциях “Певек” и “Валькаркай”, посредством выполнения 3D-инверсии типперов по программе ModEM. В результате инверсии была получена геоэлектрическая модель района в подповерхностной области размером 300 × 300 × 200 км. Модули типперов в обеих пунктах принимают значения в диапазоне 0.2–0.85, достигая максимальных значений на периоде 1000 с. На метеостанции “Певек” реальная индукционная стрелка в конвенции Паркинсона ориентирована в западном направлении во всем диапазоне периодов. Во втором пункте ее азимут изменяется от 30° на СВ до –30° на СЗ с увеличением периода вариаций. Во всем диапазоне глубин проводящие неоднородности располагаются западнее и севернее Чаунской складчатой зоны. В области глубин 8–12 км они узкой полосой протягиваются под западной и северной прибрежными участками зоны. При увеличении глубины отмечается их разбиение на блоки, достигающие максимальных размеров в горизонтальной плоскости в диапазоне глубин 20–30 км. Среди них наиболее заметен проводящий блок под южной частью Чаунской губы. Корни этих блоков различимы на глубинах до 100 км. Чаунская складчатая зона представляется высокоомным блоком вплоть до глубин 150 км и с удельным электрическим сопротивлением более 1000 Ом м. При сравнении полученной геоэлектрической модели с ранее выполненными здесь геофизическими исследованиями отмечается корреляция между расположением проводящих образований и положением слабоположительных аномалий в гравитационном поле в редукциях Буге и изостатической в районе прибрежных акваторий.
ВВЕДЕНИЕ
Предметом исследования настоящей статьи является глубинное строение еще недостаточно изученного геофизическими методами района Чаунской губы в восточной области арктического бассейна России. В этой части Арктики геологическое строение лучше изучено геофизическими методами в глубоководной акватории Восточно-Сибирского моря, где выполнен большой объем сейсмических исследований. Параллельно выполнялись гравиметрические и гидромагнитные измерения с борта научно-исследовательских судов. При этом, согласно схеме геофизической изученности Восточно-Сибирского и Чукотского морей [Заварзина и др., 2017; Глебовский и др., 2018] прибрежные шельфовые области в районе Чаунской губы на удалениях от берега на 50–100 км не были исследованы вследствие мелководья. Эта область покрывалась гравитационными и магнитными измерениями как со спутников на высотах их орбит [Sandwell et al., 2013; Flechtner et al., 2021], так и на меньших высотах путем выполнения аэросъемки в аэровариантах этих методов.
Применение вышеперечисленных геофизических методов позволяет оценивать скоростные, плотностные и магнитные характеристики глубинного разреза и на их основе производить геологические реконструкции, в той или иной мере отражающие геологическое строение, картировать границы блоков земной коры (ЗК), производить тектоническое районирование территории с ограничением глубинности характерном для каждого метода.
В последнее время на основе выполненных в Арктическом бассейне магнитных измерений в спутниковых, наземных и аэросъемочных вариантах построены цифровые модели глобального аномального магнитного поля EMAG2v3 [Meyer et al., 2017], WDMAM 2 [Dyment et al., 2015], CAMP-M [Gaina et al., 2011] в циркумполярной области Арктики. Развитые на этой основе алгоритмы оценки глубины положения точки Кюри в разрезе [Li et al., 2017; Lu et al., 2022] позволяют, используя корреляцию между глубиной точки Кюри и величиной теплового потока, охарактеризовать термическое состояние недр и косвенным образом на качественном уровне судить об удельном электрическом сопротивлении (УЭС) блоков в геологическом разрезе. Это следует из того, что в активных областях Земли с аномальным тепловым потоком, как правило, МТ методами в ЗК определяются зоны повышенной электрической проводимости, обусловленной частичным плавлением горных пород внедряющихся магматических интрузий [Pace et al., 2022].
Известно, что электрическая проводимость горных пород является весьма важным физическим параметром, позволяющим оценивать их термический режим, пористость, насыщенность флюидами или проводящими расплавами. Среди геофизических методов для этой цели наиболее широко используются магнитотеллурические (МТ) методы геоэлектрики, позволяющие исследовать геоэлектрическое строение разреза в диапазоне глубин от первых сотен метров до сотен км. Но в арктических областях России они пока применяются недостаточно широко, что связано с труднодоступностью района и суровыми климатическими условиями.
Для изучения геоэлектрического разреза региона в последние годы на северо-востоке России были выполнены МТ зондирования вдоль региональных профилей 2-ДВ (Магадан–Билибино) и 2-ДВ-А (Певек–Валунистое–Хатырка) [Соловьев и др., 2016; Antashchuk et al., 2020]. Последний профиль 2-ДВ-А начинается вблизи г. Певека, и начальная часть полученного здесь до глубин 80 км геоэлектрического разреза располагается в области Чаунской складчатой зоны к востоку от Чаунской губы.
Чтобы дополнить выполненные МТ зондирования магнитовариационными (МВ) зондированиями мы воспользовались записями геомагнитных вариаций, полученными на длительном временном интервале вблизи метеостанций “Певек” и “Валькаркай” Арктическим и антарктическим научно-исследовательским институтом (ФГБУ “ААНИИ”). Так как МТ зондирования выполнялись в пределах складчатой области, горные породы которых, как правило, обладают высокими УЭС, вызывающими интенсивные гальванические искажения и локальность отклика разреза в электрических вариациях, то МВ зондирование может дать дополнительную информацию о геоэлектрическом разрезе. Это связано с тем, что отклик разреза в поле геомагнитных вариаций носит интегральный характер и менее подвержен действию локальных геоэлектрических неоднородностей. МВ зондирования чувствительны к контрастам пород по УЭС и могут трассировать границы блоков (разломы) и фиксировать проводящие слои в глубинном разрезе [Campanya et al., 2016; Jorgensen et al., 2015; Бердичевский, Дмитриев, 2009].
Нельзя не отметить, что район исследований находится в области действия полярного электроджета. Возможности его влияния на результаты зондирований были детально проанализированы в работе [Старжинский и др., 2020] по данным обс. “Тикси”. В результате был сделан вывод о возможности выделения проводящих блоков в геоэлектрическом разрезе полярных областей.
Таким образом, целью исследований являлось построение пилотной модели глубинного геоэлектрического строения в районе Чаунской губы, что важно для обоснования построения различных геодинамических моделей региона [Лавёров и др., 2013]. Особая значимость геологического строения арктической континентальной окраины Чукотки для этих целей подчеркивалась и в работе [Sokolov et al., 2014].
Смена геодинамических обстановок в процессе раскрытия арктического бассейна могла приводить к интенсификации механизмов сжатия и растяжения в ЗК, способствующих развитию сдвиговых деформаций, создающих зоны разуплотнения по границам участвующих в движении геоблоков. Эти зоны разуплотнения на протяжении геологического времени могли заполняться мантийными проводящими флюидами, расплавами пород, водными рассолами, графитной минерализацией и т. д., которые в случае их сохранения в современную эпоху будет фиксироваться методами МТ и МВ зондирований.
Следует заметить, что в работе под магнитовариационным зондированием (МВЗ) будет использоваться его модификация, предложенная в работах М.Н. Бердичевского [Бердичевский и др., 2003] (т.е. когда в первичном возбуждающем поле отсутствует вертикальная компонента магнитной вариации), основанная на расчетах магнитного типпера.
ГЕОЛОГО-ГЕОФИЗИЧЕСКИЕ ОСОБЕННОСТИ СТРОЕНИЯ ИССЛЕДУЕМОГО РАЙОНА
Исследуемый район располагается за Северным полярным кругом в области пассивной континентальной окраины Северного Ледовитого океана. Он включает в себя акватории Чаунской губы, Восточно-Сибирского моря и прибрежные участки азиатского континента. Глубины мелководного моря в пределах района не превышают 50 м. Чаунская губа располагается на месте молодой Чаунской депрессии, сформировавшейся в позднечетвертичное время. Континентальные и морские осадки впадины имеют мощность до 70 м [Геологическая …, 1979]. На мелководье примыкающего к району прибрежного шельфа Восточно-Сибирского моря мощность осадков не превышает 2 км [Petrov et al., 2016; Gaina et al., 2014] и только в области материкового склона, располагающегося в северо-восточном направлении от Чаунской губы, она увеличивается до 7–8 км [Miller, Verzhbitsky, 2009].
С восточной стороны Чаунской губы располагается наиболее изученная в геологическом отношении Чаунская складчатая зона [Luchitskaya et al., 2014] с меловыми магматическими центрами, сформировавшимися в режиме расширения земной коры и перекрытых терригенными осадками. С севера она ограничивается Восточно-Сибирским морем, а с юга и востока Раучуанским и Певекским прогибами (соответственно) [Ватрушкина и др., 2019]. Складчатые образования эоны продолжаются и под шельфом моря. Предполагается [Miller, Verzhbitsky, 2009], что Чаунская складчатая зона сформировалась в результате коллизии Чукотской микроплиты с Евразийским континентом в процессе субширотного расширения земной коры, простирающегося в субмеридиональном направлении. В зоне широко развиты интрузии калиевых и ультракалиевых гранитоидов, генерация которых происходила с участием мантийных источников [Efremov, Travin, 2021]. Часто интрузии представлены изометричными батолитами, при углублении сливающимися в единый массив. Согласно данным геотермобарометрии [Tikhomirov et al., 2009] кристаллизация гранитов происходила на глубинах 1.5–3 км при температурах около 700°С.
Магнитное поле района согласно глобальной модели магнитного поля Земли EMAG2V3 (Earth Magnetic Anomaly Grid) ровное слабоотрицательное [Meyer et al., 2017] в пределах акватории Чаунской губы и континентальной области, что предполагает слабую намагниченность осадков и пород фундамента, а также отсутствие заметного проявления базальтового магматизма, вызывающего интенсивные магнитные аномалии.
В то же время со стороны моря с севера до Шелагского мыса в меридиональном направлении спускается полоса слабоположительных аномалий, которая, не доходя до мыса, поворачивает на восток и оканчивается, не доходя до мыса Кибера.
Закартированные в арктической области аномальные магнитные поля, заданные глобальной моделью EMAG2, были использованы для оценки глубины точки Кюри в арктическом регионе [Lu et al., 2022]. Согласно полученной карте глубин точки Кюри в Арктике в районе Чаунской губы эта точка находится в области глубин 35–40 км. Учитывая, что толщина земной коры в районе Чаунской губы, оцененная в работе [Petrov et al., 2016], составляет около 30 км можно ожидать здесь на подкоровых глубинах максимальных температур, близких к точке Кюри магнетита ≈580°С.
Толщина литосферы в регионе согласно карте рельефа [Карта…, 1995] составляет около 60–70 км. В районе нет данных по тепловому потоку из недр Земли. В ближайшей северо-восточной прибрежной области Аляски он по измерениям составляет 50–70 мВт/м2 [Petrov et al., 2016].
Гравитационное поле района исследований согласно глобальной модели WGM2012 международного гравиметрического бюро (BGI, http://bgi.obs-mip.fr) слабо дифференцированное и плавно изменяющееся представлено небольшими положительными аномалиями, особенности распределения которых по площади хорошо видны в редукциях Буге и в изостатической. Эти аномалии узкой полосой протягиваются под дном Чаунской губы и, расширяясь, выходят в Восточно-Сибирское море, огибая Шелагский полуостров в восточном направлении. Под северо-западной оконечностью Чаунской складчатой зоны просматриваются локальные отрицательные аномалии малой интенсивности.
Приведенный в работах [Gaina et al., 2014; Яковлев и др., 2012] анализ результатов сейсмотомографических исследований, выполненных в Арктическом регионе для глубин 20–100 км показывает, что под Чаунской губой фиксируется обширная область пониженных сейсмических скоростей, охватывающая континентальные и шельфовые территории, что может свидетельствовать о разуплотнении в верхней мантии региона.
Выполненная на северо-востоке азиатского континента сеть опорных геолого-геофизических профилей [Соловьев и др., 2016] включает и профиль 2-ДВ-А (г. Певек–п. Валунистое–г. Анадырь–п. Хатырка), начинающийся вблизи г. Певека, и в своей начальной части проходящего по Чаунской складчатой зоне. По результатам магнитотеллурических зондирований на этом участке профиля построен геоэлектрический разрез до глубин 80 км [Antashchuk et al., 2020]. Основными особенностями разреза являются наличие вертикального проводящего блока с удельным электрическим сопротивлением (УЭС) ≈ 2 Ом м, начинающегося с глубины около 2 км и протягивающегося от 20-го до 40-го км профиля и низкоомной верхней мантии с УЭС ≈ 60 Ом м, подстилающей земную кору толщиной около 30 км. Проводящий блок в земной коре вертикально продолжается до глубины 14 км и при дальнейшем углублении полого погружается до глубины 20 км под Чаунскую губу в северо-западном направлении.
ИСПОЛЬЗУЕМЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
Для выполнения магнитовариационного зондирования были использованы цифровые записи магнитных вариаций, выполнявшиеся в течение ряда лет в пунктах вблизи метеостанций “Певек” (PBK, 69.69965° N, 170.25667° E) и “Валькаркай” (VLK, 70.08755° E , 170.94625° N) Арктическим и антарктическим научно-исследовательским институтом (ААНИИ, https://www.aari.ru). Пункты удалены друг от друга на расстояние ≈50 км. Магнитометр в пункте PBK располагался в городской черте приблизительно в 130 м от здания Росгидромета в юго-западной оконечности полуострова Певек вблизи берега одноименного пролива, отделяющего полуостров от островов Роутан. Ширина пролива ≈4 км, глубина 15–25 м.
Запись магнитных вариаций осуществлялась трехкомпонентными феррозондовыми магнитометрами: датским FGE-89D в пункте PBK с дискретностью по времени 1 мин и львовским LEMI-22 (https://kmstechnologies.com/Files/Flyer%20for%20 website/LEMI-022_Brochure.pdf ) во втором пункте VLK с секундным разрешением по времени. Ввиду действия интенсивных технологических помех в короткопериодной области на станции “Певек” в 2018 г. пункт наблюдения магнитных вариаций был перенесен на станцию “Валькаркай”, свободной от их влияния, с заменой магнитометра на LEMI-22.
В пункте VLK постамент магнитометра располагается на прибрежной косе приблизительно в 100 м от уреза воды Восточно-Сибирского моря. С противоположной стороны находится морская лагуна. В этом пункте техногенные помехи могут возникать только за счет недостаточного удаления датчика от питающего дизель-генератора-источника помех. В обоих пунктах постаменты располагаются на скальных основаниях, вследствие чего подвижки грунта при оттаивание будут мало влиять на наклоны и повороты постамента, искажая показания магнитных датчиков. Магнитометры ориентировались по магнитному полю т.е. функционировали в локальной геомагнитной системе координат [Laundal, Richmond, 2017]. Это учитывалось при обработке данных, когда компоненты вариаций пересчитывались в географическую систему координат.
Отмеченные выше особенности постановок приборов в пунктах PBK и VLK в должной мере проявились при обработке данных, когда для выделения полезного сигнала в пункте PBK выбирались интервалы наблюдений, выполненные в возмущенных геомагнитных условиях, при которых отношение сигнал/шум возрастает. Этому же способствовало и увеличение длин реализаций, выбираемых для обработки.
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
В частотной области между компонентами геомагнитных вариаций ${{H}_{{x,}}}{{H}_{{y,}}}{{H}_{z}}$ выполняется линейная связь вида:
где все величины комплексные. Что в матричной форме можно записать как(2)
${{H}_{z}} = \left[ {{{W}_{x}}{{W}_{y}}} \right]{\kern 1pt} \left[ \begin{gathered} {{H}_{x}} \hfill \\ {{H}_{y}} \hfill \\ \end{gathered} \right] = \left[ {\mathbf{W}} \right]{{{\mathbf{H}}}_{h}}.$Представляя матрицу $\left[ {\mathbf{W}} \right]$типпера в векторной форме, определим комплексный вектор ${\mathbf{W}}$с компонентами, ${{W}_{x}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {{W}_{y}}$:
где ${\mathbf{j}}$ и ${\mathbf{k}}$ – реальные направляющие векторы вдоль осей $x$ и $y$, соответственно, называемые векторами типпера или индукционной стрелками, следуя определениям в работе [Бердичевский, Дмитриев, 2009]. Аналогичным образом может быть определен и вектор горизонтального магнитного поля ${{{\mathbf{H}}}_{h}}$. Если рассматривать выражение (1) как скалярное произведение двух этих векторов:то можно вывести соотношение для модуля типпера $\left| {\mathbf{W}} \right|$ (см. [Старжинский и др., 2022]):
(5)
$\left| {\mathbf{W}} \right| = {{(A_{r}^{2} + A_{i}^{2} + B_{r}^{2} + B_{i}^{2})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{{\left| {{{H}_{z}}} \right|}}{{\left| {{{{\mathbf{H}}}_{h}}} \right|}}.$В выражении (5) нижние индексы $r$ и $i$ обозначают реальные и мнимые части комплексного числа. Таким образом, модуль типпера обозначает отношение модуля вертикальной компоненты вариации к модулю горизонтальной компоненты. В данном случае он является инвариантом, т.е. не зависит от ориентации системы координат.
Для представления результатов МВ исследований вводятся реальный $\operatorname{Re} {\mathbf{W}}$ и мнимый $\operatorname{Im} {\mathbf{W}}$ – индукционные векторы (индукционные стрелки), определяемые как
Здесь в выражениях (6) и (7), в отличие от определения Визе, знаки инвертированы. В этом случае реальная индукционная стрелка указывает на области с высокой электрической проводимостью в конвенции по Паркинсону. Поведение мнимой индукционной стрелки гораздо сложнее и труднее поддается простой интерпретации.
Обычно при представлении результатов МВ работ величины и направления стрелок вычерчиваются на картах для выбранного периода вариации. В нашем исследовании будут использоваться графики зависимостей углов ориентации реальной ${{\alpha }_{r}}$ и мнимой ${{\alpha }_{i}}$ стрелок от периода. Углы определяются как
и на интервале $0{\kern 1pt} - {\kern 1pt} 2\pi $. Положительные значения углов отсчитываются от направления на север (от оси x) по часовой стрелке. При первичной качественной интерпретации будут использоваться модуль типпера и углы ориентации индукционных стрелок. Наличие минимума на зависимостях модуля типпера от периода может трактоваться как наличие проводящего слоя в геоэлектрическом разрезе [Бердичевский, Дмитриев, 2009], а ориентация индукционных стрелок определяет положение проводящей неоднородности в горизонтальной плоскости относительно пункта измерений. Для того, чтобы оценить к какому типу геоэлектрических разрезов 1D, 2D, 3D относится исследуемый разрез, рассчитывалась ассиметрия типпера (Tipper Skew) как(10)
$Sk = 2\frac{{{{W}_{x}}_{r}{{W}_{y}}_{i} - {{W}_{x}}_{i}{{W}_{y}}_{r}}}{{{{{\left| {\mathbf{W}} \right|}}^{2}}}},$Для оценки выше определенных интерпретационных параметров была использована несколько модифицированная программа, ранее описанная в работе [Старжинский, 2004]. Она включает следующие операции: удаление линейного тренда из данных; коррекцию частотной характеристики каналов в высокочастотной области; расчет спектров трех компонент по алгоритму быстрого преобразования Фурье (БПФ); выполнение полосовой фильтрации в частотной области путем умножения спектров компонент на частотную характеристику полосового гауссовского фильтра; получение оценок функций множественной, частной и обычной когерентностей. После обратного преобразования Фурье рассчитывались огибающие и фазы узкополосного аналитического сигнала во временной области и вычислялись коэффициенты ${{W}_{x}}$ и ${{W}_{y}}$ на заданном временном отрезке, скользящем по реализации. В завершение производилась робастная селекция рассчитанных коэффициентов с использованием медианных оценок и селекция по шести значениям рассчитанных функций когерентностей. Величины ${{W}_{x}}$ и ${{W}_{y}}$вычислялись как по методу наименьших квадратов по данным на выбранном временном интервале, так и по двухточечной схеме, когда использовались значения компонент ${{H}_{{x,}}}{{H}_{{y,}}}{{H}_{z}}$ в уравнение (1) в два различных момента времени, разнесенных на варьируемый временной интервал. Оказалось, что при использовании робастной селекции эти два подхода дают практически одинаковый результат. Максимальная длина входных последовательностей составляла 6 суток, при интервале дискретизации $dt = 1$ с. В длиннопериодной области использовались децимированные реализации, длительность которых измерялась месяцами.
КАЧЕСТВЕННЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ ОБРАБОТКИ ДАННЫХ
Интерпретационные параметры, полученные в результате обработки данных по пунктам PBK, VLK изображены в виде графиков на рис. 2. Модули типперов, представленные в верхней части рисунка, принимают значения в пределах 0.2–0.85 (рис. 2а). При этом надо отметить, что в области длинных периодов, начиная с периода ≈200 с графики модулей типперов в обеих пунктах практически совпадают. Их довольно большие значения, превышающие здесь 0.7, указывают на присутствие в глубинной части разреза контрастных электрических неоднородностей вблизи обеих пунктов.
В области коротких периодов минимальные значения модуля типпера около 0.2 отмечаются в пункте VLK на периоде 20 с. Учитывая, что пункт располагается в непосредственной близости от мелководного шельфа Восточно-Сибирского моря (см. рис. 1), и учитывая направление реальной индукционной стрелки в этом пункте, необходимо допустить, что его величина модуля типпера определяется конфигурацией береговой черты и мощностью осадков в пределах прибрежного шельфа в окрестности пункта VLK. Глубокое море находится здесь на расстоянии нескольких сотен км на северо-восток от Чаунской губы.
Рис. 1.
Расположение центральной области моделирования (квадрат со стороной 300 км), осей системы координат, реальных индукционных стрелок в конвенции Паркинсона (черные стрелки) на периодах: 1 – 20.0 с, 2 – 1260.0 с в пунктах PBK и VLK (треугольники) на местности. Синей линией обозначено положение МТЗ профиля 2-ДВ-А. Красной линией оконтурено положение вертикальной проекции центров проводящих блоков в области глубин 25–30 км, а красной пунктирной линией обозначено положение менее контрастной проводящей аномалии. Три оттенка синего цвета по мере возрастания их насыщенности обозначают глубины 10, 25 и 50 м. Масштабная индукционная стрелка указана в левой нижней части рисунка. Данные для рисунка были получены с сайта https://www.gebco.net/.
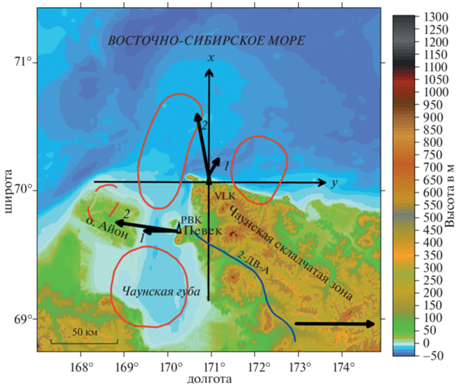
Рис. 2.
Графики зависимостей от периода вариаций модулей типпера |W|, азимутов αr реальных и αi мнимых индукционных стрелок и асимметрии типпера sk для пунктов PBK (точки) и VLK (кубики).
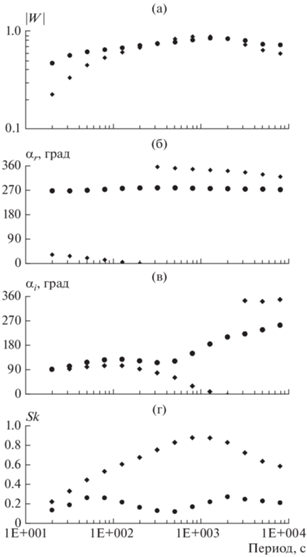
Несколько отличная картина наблюдается на этом периоде в пункте PBK, где значение модуля типпера примерно в два раза больше. Учитывая ограниченность площади акватории мелководной Чаунской губы, ближайшей здесь к пункту наблюдений, следует допустить, что повышенные значения модулей типперов здесь вызываются присутствием в верхах ЗК проводящих неоднородностей западнее пункта PBK.
Это подтверждается и ориентацией реальной индукционной стрелки в этом пункте, представленной на рис. 2б, которая примерно перпендикулярна восточному берегу Чаунской губы во всем диапазоне периодов. Такое устойчивое западное направление реальной индукционной стрелки указывает на присутствие в геологическом разрезе под акваторией губы протяженного проводящего образования. Ориентация мнимой индукционной стрелки в этом пункте, представленная на рис. 2в, непостоянна. На коротких периодах до 200–300 с она примерно противоположна ориентации реальной стрелки, а с увеличением периода поворачивается по часовой стрелке, приближаясь на самых длинных периодах к ориентации реальной стрелки.
В пункте VLK на коротких периодах реальная индукционная стрелка ориентирована в направлении ≈30° на СВ и с увеличением периода поворачивается против часовой стрелки, устанавливаясь на самых длинных периодах в направлении ≈330° на СЗ. Мнимая индукционная стрелка на коротких периодах направлена на восток и составляет угол ≈60° с реальной стрелкой на этих периодах. С увеличением периода она также поворачивается против часовой стрелки, приближаясь к ориентации реальной стрелки на длинных периодах, устанавливаясь в северном направлении. Ориентация реальной и мнимой стрелок на длинных периодах в пункте VLK отличается на ≈30°, т.е. стрелки указывают в одном и том же направлении.
Если рассматривать рис. 2г, на котором изображены графики изменения параметра асимметрии для двух пунктов при изменении периода вариаций, то можно заметить, что они значительно отличаются. Малые значения параметра в пункте PBK, не превышающие значений 0.3, указывают на то, что здесь разрез можно рассматривать как квазидвухмерный, что свидетельствует о выше сделанном для этого пункта заключении о контакте здесь двух контрастных по проводимости вытянутых структур. В пункте VLK об этом можно говорить только на самых коротких периодах. В остальной же области периодов разрез в этом пункте должен рассматриваться как трехмерный.
3D-ИНВЕРСИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ТИППЕРОВ
Для выполнения 3D-инверсии типперов была использована программа трехмерного моделирования методом конечных разностей ModEM, разработанная в Орегонском университете США [Egbert, Kelbert, 2012; Kelbert et al., 2014]. Она успешно применяется для инверсии профильных и площадных МТ и МВ исследований [Samrock et al., 2015; Tietze et al., 2015]. Программа ModEM использует метод конечных разностей для численного решения уравнений Максвелла прямой задачи и нелинейный метод сопряженных градиентов для решения проблемы минимизации процесса инверсии. Для нахождения модели разреза, отвечающей экспериментальным данным, минимизируется целевая функция Ψ
(11)
$\begin{gathered} \Psi ({\mathbf{m}},{\mathbf{d}}) = {\mathbf{d}} - {\mathbf{f}}({\mathbf{m}}){{)}^{T}}{\mathbf{C}}_{{\mathbf{d}}}^{{ - 1}}({\mathbf{d}} - {\mathbf{f}}({\mathbf{m}}) + \\ + \,\,\lambda {{({\mathbf{m}} - {{{\mathbf{m}}}_{0}})}^{T}}{\mathbf{C}}_{{\mathbf{m}}}^{{ - 1}}({\mathbf{m}} - {{{\mathbf{m}}}_{0}}), \\ \end{gathered} $(12)
$CKO = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {\frac{{{{{(d_{i}^{{obs}} - d_{i}^{{pred}})}}^{2}}}}{{e_{i}^{2}}}} } ,$Программа реализуется на быстродействующих многопроцессорных системах, что позволяет рассчитывать сложные модели геоэлектрических разрезов. Входными данными программы могут быть все компоненты импедансной матрицы или ее главные элементы, типперы, горизонтальные МВ отклики, определяемые на интервале периодов. В качестве априорной (стартовой) модели разреза задается трехмерная матрица удельных электрических сопротивлений, обычно однородное полупространство, в которое может быть включено море или иные области с фиксированными начальными электрическими сопротивлениями, меняющими или сохраняющими свои значения в процессе инверсии. Также задаются параметры сглаживания, начальное значение параметра регуляризации и характер его изменения в итерациях, максимальное количество итераций и другие параметры.
В нашем случае входными данными для инверсии служили экспериментальные значения типперов, рассчитанные по записям геомагнитных вариаций на пунктах PBK и VLK. 3D-инверсия выполнялась с использованием оборудования ЦКП “Дальневосточный вычислительный ресурс” ИАПУ ДВО РАН на многопроцессорном вычислительном кластере IRUS17 ( https://www.cc.dvo.ru ) с пиковой производительностью 56.3 терафлопс.
Размерность используемой сетки была 90 × 90 × 53 ячеек по осям x, y, z, соответственно, без учета ячеек в верхнем полупространстве. Начало модельной системы координат помещалось в месте нахождения магнитометра на пункте VLK. Местоположение пункта PBK относительно начала координат определялось реальными расстояниями между пунктами, вследствие чего этот пункт размещался вне узлов используемой сетки.
В горизонтальной плоскости в центральной части сетки размером 60 × 60 ячеек размер ячейки был 5 × 5 км и к краям сетки он увеличивался в геометрической прогрессии со знаменателем 1.24, что определяет область моделирования ≈1114 × 1114 км. По оси z размер первой ячейки был задан 15 м и увеличивался вниз с глубиной в геометрической последовательности со знаменателем 1.2.
Стартовые модели разреза задавались полупространством с УЭС ρ = 100 Ом м и ориентацией модельной x оси по меридиану без учета моря и с его введением в стартовую модель. В последнем случае ввиду мелководья и ограниченности размеров Чаунской губы ее водный слой не учитывался. Так как глубоководная область Восточно-Сибирского моря находится на большом удалении от района исследований и не влияет на результаты, то его шельфовая часть была задана в модели в виде прямоугольной области, вытянутой в широтном направлении. Водный слой в ее пределах аппроксимировался двумя слоями толщиной 15 и 18 м с учетом батиметрии моря, взятой с сайта https://maps.ngdc.noaa.gov/viewers/bathymetry/. УЭС водной толщи задавалось равным 0.3 Ом м.
Параметры сглаживания модели по трем осям осям принимались равными 0.1 или 0.3. Экспериментальные значения типперов задавались на 14-ти периодах на интервале 20–8000 с. Их ошибка принималась равной 0.05. Близость экспериментальных значений типперов к предсказанным значениям по результирующей модели оценивалась по (12). На рис. 3 приведены графики, демонстрирующие близость экспериментальных и модельных типперов в пунктах PBK и VLK в зависимости от периода вариаций с СКО равным 1.45 после последней 69-й итерации при сглаживание, равном 0.1, в стартовой модели с включением моря.
Рис. 3.
Сравнение реальных и мнимых частей экспериментальных типперов (звездочки) с типперами результирующей модели геоэлектрического разреза (точки) для пунктов PBK и VLK при среднеквадратическом отклонении, равном 1.45.
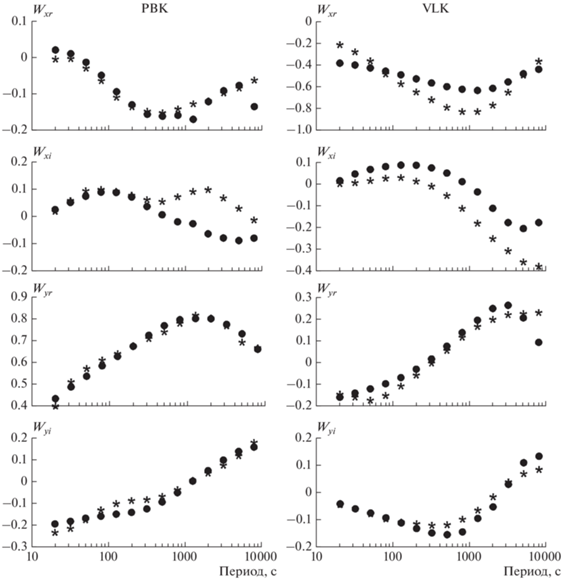
При использовании стартовой модели, задаваемой однородным полупространством и с теми же входными параметрами, в результирующей модели несколько понижалась контрастность проводящих и непроводящих глубинных блоков и незначительно изменялись их размеры. В то время как в стартовой модели с включением моря контрастность повышалась, аномальные области несколько уменьшались в размерах, но их пространственное положение выдерживалось при использовании обеих стартовых моделей. Кроме того, в этом случае контрастнее представлялись наиболее глубинные части модели. Включение моря несколько повысило среднеквадратическое отклонение результирующей модели до значения 1.45 против 1.33 без него.
При задании в стартовой модели с морем и сглаживания по всем осям равным 0.3 положение аномальных областей сохраняется, но их границы становятся менее изрезанными, плавными и в подкоровых областях их контрастность уменьшается, сохраняя свои высокие значения до глубины около 45 км. В двух других случаях при сглаживании равном 0.1 аномалии контрастно просматриваются до глубины ≈100 км в модели с морем и ≈60 км без него.
Принимая во внимание, что в модели с включением моря учитывается реально существующая и оконтуренная поверхностная геоэлектрическая неоднородность и наблюдается более детальная прорисовка локальных особенностей границ блоков в результирующей модели, в последующем будут анализироваться результаты инверсии для этой стартовой модели с заданным сглаживанием, равным 0.1.
Возможность локализации глубинных проводящих блоков с использованием только измерений магнитных вариаций в одном или нескольких пунктах анализировалась путем 3D-инверсии частотных зависимостей типперов, рассчитанных для конкретных моделей среды. Учитывая, что измерения проводились на побережье мелководного моря, модель включала его аппроксимацию слоем воды с УЭС, равным 0.3 Ом м, и глубинный проводящий блок в виде параллелепипеда со сторонами 70 × 30 × 20 км по осям x, y, z, соответственно, и сопротивлением 1.0 Ом м, залегающего на глубине 20 км. Для выполнения инверсии к рассчитанным типперам добавлялся гауссовский шум с нулевым средним и заданным стандартным отклонением. При этом нормированная среднеквадратическая ошибка аппроксимации составляла около 1.03. Оказалось, что блок может быть локализован не только по профильным данным, но и по данным нескольких и даже одного удаленного пункта. Разумеется, что в последнем случае его локализация несколько размыта.
РЕЗУЛЬТАТЫ 3D-ИНВЕРСИИ
Рассматривая графики на рис. 3, на которых представлено сравнение экспериментальных типперов с типперами результирующей модели можно отметить близость их значений в диапазоне используемых периодов вариаций. Заметное расхождение наблюдается только для мнимой компоненты Wxi в длиннопериодной области в пункте PBK, что, по-видимому, вызвано действием техногенных помех при оценке экспериментальных типперов.
Анализируя все полученные горизонтальные срезы результирующей модели, можно заметить, что проводящие неоднородности наиболее ярко выражены и занимают наибольшие площади в области глубин 20–30 км, как это изображено на рис. 4. Характерно, что с дальнейшим увеличением глубины аномально проводящие блоки С1 и С3 отделяются от блока C2 и, не меняя своего положения, но с понижением электрической проводимости, просматриваются до глубины около 100 км. В то же время блок C2 при этом смещается в северо-западном направлении, теряя различимость центральной части.
Рис. 4.
Распределение УЭС в результирующей модели в горизонтальном слое в области глубин 25–30 км. Треугольниками обозначены пункты наблюдений. Светло-серой линией нанесено положение региональной береговой черты в районе Чаунской губы. Тонкими пронумерованными пунктирными линиями обозначены положения меридиональных и широтных вертикальных разрезов модели. С1–С3 – проводящие блоки, R – высокоомный блок.
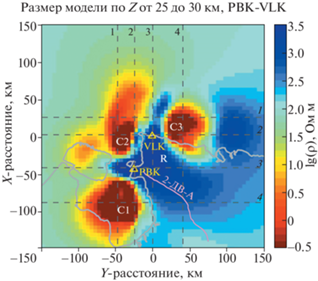
При движении вверх по разрезу блоки сближаются, уменьшаясь в размерах. И в области глубин 8–12 км их центральные части сливаются вместе, узкой полосой протягиваясь от восточного берега губы южнее г. Певек до южной оконечности о. Айон и затем под акваторией Чаунской губы доходят до Шелагского полуострова, огибая который под побережьем и шельфом Восточно-Сибирского моря несколько не доходят до мыса Кибера. Далее, приближаясь к поверхности, эта аномальная зона разбивается на две части, локализующиеся вблизи пунктов измерений. Одна располагается северо-восточнее пункта VLK в прибрежной области, другая западнее пункта PBK под примыкающей акваторией Чаунской губы, что указывает на их обусловленность мелководьями ближайших акваторий, реакция на которые в геомагнитных вариациях превалирует в области коротких периодов, обеспечивая локальность аномалии.
Положение высокоомного блока R (рис. 4) пространственно совпадает с положением Чаунской складчатой зоны. В глубинной части он мало меняет как свои размеры, так и конфигурацию во всех используемых стартовых моделях, в то время как в горизонтальных срезах, приближающихся к поверхности, он уменьшается в размерах, разделяется на две части, локализирующиеся вблизи пунктов измерений.
Для анализа довольно сложного распределения по глубине непроводящих и проводящих неоднородностей в результирующей модели были построены широтные и меридиональные вертикальные разрезы. Положение наиболее характерных из них, проходящих через пункты измерений и вне них через области контрастных по проводимости блоков, помечено цифрами на рис. 4, а их вид представлен на рис. 5, рис. 6.
Рис. 5.
Вертикальные меридиональные разрезы распределения УЭС в результирующей модели в районе Чаунской губы в плоскостях XZ. Разрезы пронумерованы (цифры в кружках) согласно рис. 4. Треугольники указывают положение пунктов наблюдений. Разрезы 2 и 3 проходят через пункты PBK и VLK, соответственно. Вид с восточной стороны.
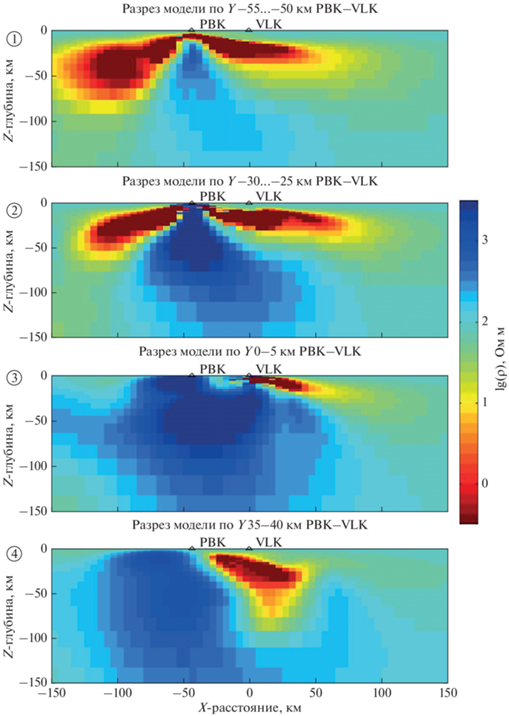
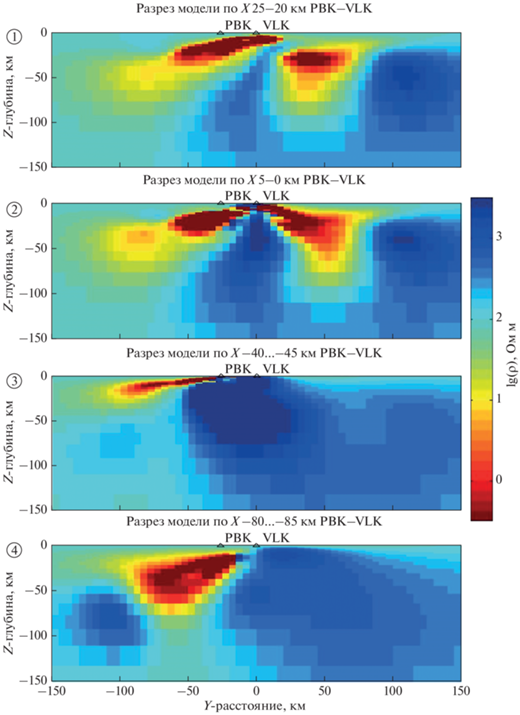
Рис. 6.
Вертикальные широтные разрезы распределения УЭС в результирующей модели в районе Чаунской губы в плоскостях YZ. Разрезы пронумерованы (цифры в кружках) согласно рис. 4. Треугольники указывают положение пунктов наблюдений. Разрезы 2 и 3 проходят через пункты VLK и PBK, соответственно. Вид с южной стороны.
Рассматривая последовательно полученные меридиональные разрезы с запада на восток, можно заметить, что западная часть модели более низкоомная, по сравнению с восточной и с приближением к восточному берегу губы представляется двумя глубинными проводящими аномалиями в северной и южной частях губы, смыкающимися вместе в области глубин не более 5–7 км под акваторией Чаунской губы как это можно видеть на рис. 5.1 . При дальнейшем приближении к восточному берегу губы в районе полуострова Певек связь этих двух аномалий прерывается, и за восточным побережьем губы глубинные проводящие аномалии представлены только севернее и восточнее пункта VLK под шельфом и побережьем, что обусловлено огибанием проводящей аномалией Шелагского полуострова. Южнее располагается Чаунская складчатая область, которая в модели выражается высокоомным блоком вплоть до глубин 150 км и с удельным электрическим сопротивлением ρ > 1000 Ом м.
Наибольшая глубинность проводящих аномалий достигается под шельфом моря и под южной частью Чаунской губы, где они проникают до глубин 100 км, как это можно видеть из рис. 5.1, 5.4 (блоки C1, C3 на рис. 4). Причем в последнем случае проводящий блок просматривается и на глубинах до 150 км с понижением своей электрической проводимости. В то же время в континентальной области восточнее полуострова Певек и южнее пункта VLK во всем диапазоне глубин располагается массивный высокоомный блок, проникающий в глубинной части и в область шельфа (см. рис. 5.3 и рис. 4).
Рассматривая широтные разрезы последовательно с севера на юг, отметим, что на первом профиле, располагающемся под шельфом моря на удалении 20–25 км от пункта VLK к северу, видны две проводящие неоднородности. Одна из них начинается в прибрежной части шельфа с самых верхов разреза и плавно погружается в западном направлении до глубин более 50 км на удалении от пункта VLK около 100 км. Другая располагается восточнее пункта, начинаясь с глубины ≈20 км, она углубляется до глубины ≈100 км. Здесь она контактирует с высокоомными нижележащими слоями в отличие от первой, плавно уменьшающей свою проводимость при увеличении глубины. На втором широтном профиле, проходящем через пункт VLK, конфигурация проводящих и высокоомных блоков сохраняется, за исключением того, что они несколько изменяют свои размеры и соединяются в верхней части по системе проводящих блоков сложной конфигурации.
Заметные изменения в распределении УЭС в разрезе происходят на третьем профиле, изображенном на рис. 6.3 и проходящем через пункт PBK. Здесь определяется локальный проводящий блок, начинающийся от п-ва Певек с самых верхов разреза и медленно погружающийся в западном направлении до глубин около 30 км на удалении ≈100 км. Восточная часть профиля во всем интервале глубин содержит высокоомный блок с наибольшими значениями УЭС под восточным побережьем Чаунской губы.
Разрез вдоль четвертого профиля на рис. 6.4 отличается от предыдущего тем, что на этих удалениях от пункта VLK он пересекает глубинную проводящую аномалию под южной частью Чаунской губы. Здесь эта аномалия проводимости в глубинной области в окружении высокоомных пород погружается до глубин в 150 км. В верхней части разреза, до глубин около 50 км, она контактирует с проводящим блоком к западу от нее, а при дальнейшем погружении просматривается ее пространственно локализованное продолжение, по-видимому, в область еще больших глубин.
Таким образом на основе полученных результатов можно сделать вывод о том, что в континентальной области восточнее Чаунской губы в результирующей модели представлены высокоомные породы вплоть до глубин в 150 км. В отличие от этого к западу и северу от губы глубинный разрез составляют породы со значительно меньшими УЭС.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ ИНВЕРСИИ
На графиках ориентации реальных индукционных стрелок на рис. 2б и на рис. 1 можно отметить, что в пункте PBK с изменением периода вариаций они практически не меняют своего положения, ориентируясь в западном направлении. Принимая во внимание большие значения типперов в этом пункте во всем диапазоне периодов, мелководье прилегающей губы, можно заключить, что не последняя является причиной этих значений, а какая-то глубинная протяженная проводящая аномалия западнее пункта PBK.
В отличие от этого в пункте VLK с увеличением периода ориентация реальной индукционной стрелки меняется в секторе ≈70°. На коротких периодах ее ориентация будет определяться конфигурацией береговой черты, водным слоем и мощностью осадков в море, которая достигает здесь 2 км [Petrov et al., 2016]. С увеличением периода вариаций ее поворот против часовой стрелки с одновременным увеличением значений типпера свидетельствует о влияние глубинной проводящей неоднородности, погружающейся к северо-западу или западу от этого пункта.
Отмечающееся по результатам инверсии декомпенсационных аномалий силы тяжести глобальной модели EIGEN-6C4 [Sidorov et al., 2021; Förste et al., 2014] за западной оконечностью о. Айон увеличение мощности осадков в области, в 2–4 раза превышающей площадь этого острова, не может обеспечить такого увеличения типперов. Это обеспечивается тем, что мощность осадков в этом случае не превышает 2-х км и тем, что нельзя допустить высоких горизонтальных градиентов УЭС в приповерхностном осадочном слое, которые вызывают увеличение типперов на удалении от них. К тому же этот осадочный бассейн удален от пунктов наблюдений на расстояние более 150 км.
Такое поведение реальных индукционных стрелок может быть обусловлено существованием глубинной проводящей неоднородности, протягивающейся пол-дном Чаунской губы с выходом в Восточно-Сибирское море и являющейся причиной больших значений типперов в обоих пунктах. Ранее такой величины типперы наблюдались на обсерватории “Тикси” в области активного рифтогенеза [Старжинский и др., 2020].
Результирующая модель геоэлектрического строения района, полученная в результате 3D-инверсии данных, не противоречит этому, определяя аномальную проводящую зону с изменяющейся электрической проводимостью на ее протяжении, вследствие чего выделяются области с высокими значениями проводимостей. Положение вертикальной проекции этих аномально проводящих блоков в области глубин 25–30 км на местности оконтурено и представлено на рис. 1. Общий вид распределения УЭС в этом диапазоне глубин, где проводящие области занимают максимальные площади, изображен на рис. 4. Из рисунка видно, что УЭС этих аномально проводящих блоков принимают значения меньше 1.0 Ом м, что характерно для расплавов горных пород или трещинных зон, насыщенных концентрированными рассолами [Sanmyo, Keppler, 2017]. Однако необходимо заметить, что это значение УЭС аномальных зон, вследствие использования только двух пунктов измерений, необходимо уточнять, увеличивая их количество.
Положение проводящих блоков C1, C2 на рис. 4 находится в области слабоположительной аномалии гравитационного поля в редукциях Буге и изостатической согласно глобальной модели WGM2012 международного гравиметрического бюро (BGI, http://bgi.obs-mip.fr/data-products/gravity-databases/land-gravity-data/ ). Причем в случае изостатической редукции положительная аномалия (≈10 мГал) в районе п-ва Певек разбивается на два блока широтной полосой слабых отрицательных аномалий такой же интенсивности. Пространственное положение этих слабоположительных аномалий в гравитационном поле перекрывается с расположением проводящих блоков C1, C2. Обособленный блок C3 располагается под прибрежным шельфом моря на границе этой гравитационной аномальной зоны, продолжающейся здесь к востоку от Шелагского мыса в области Куветского регионального разлома [Рекант и др., 2020].
Вся континентальная исследуемая площадь и акватория Чаунской губы располагаются в области однородного слабоотрицательного магнитного поля согласно мировым цифровым картам аномального магнитного поля WDMAM2 и EMAG2V3, представляющих значения поля приведенные к высотам 5 и 4 км, соответственно. Эта область продолжается и в Восточно-Сибирское море западнее Шелагского мыса. Восточнее его наблюдаются интенсивные магнитные аномалии, под которыми определяется проводящий блок C3.
Детальность аномалий на акватории губы несколько повышается в модели аномального магнитного поля CAMP-M, представляющей значения поля на высоте 1.0 км, что позволяет выделять локальные слабоположительные аномалии в этой области. Это может свидетельствовать о существовании базальтоидных пород в глубинной части разреза под акваторией и их расплавов на еще больших углублениях.
Глубины нижней границы магнитоактивных масс под Восточно-Сибирским морем и Чукотским складчатым поясом, оцененные в работе [Середкина, Филиппов, 2021], составляют ≈28 и ≈33 км.
Учитывая, что согласно работе [Lu et al., 2022] точка Кюри в районе Чаунской губы находится на глубине 35–40 км, можно ожидать, принимая во внимание эти оценки, присутствие расплавов горных пород в разрезе ниже подкоровых глубин в региональном масштабе, что могло бы обеспечить низкие УЭС. Полученное же в результате инверсии типперов положение проводящих блоков C1–C3 пространственно локализовано. И кроме того, глубинный разрез модели представляет собой сочетание проводящих и непроводящих блоков.
Результаты инверсии можно сравнить с геоэлектрическим разрезом, полученным вдоль профиля 2-ДВ-А до глубин 80 км по результатам интерпретации магнитотеллурических зондирований [Antashchuk et al., 2020]. Прежде всего необходимо отметить, что по результатам интерпретации диапазон значений УЭС пород составляет от первых Ом м до 105 Ом м в пределах начальной части профиля, проходящего по Чукотской складчатой зоне. Здесь так же в ЗК располагаются как непроводящие, так и проводящие блоки. Причем наиболее массивный проводящий блок располагается вблизи п-ва Певек в области Певекского разлома и погружается в северо-западном направлении до глубин 20 км под Чаунскую губу, под которой по результатам инверсии типперов определены проводящие образования, включающие блоки C1 и C2.
Полученное в результате инверсии типперов интегральное распределение УЭС в модели геоэлектрического разреза характеризуется высокоомным блоком под Чаунской складчатой областью (блок R на рис. 4) и расположением проводящих блоков C1-C3 по его периферии. В блоке R в пределах начальной части профиля, проходящего по складчатой зоне, значения УЭС почти на два порядка ниже по сравнению с их максимальными значениями, определяемыми при интерпретации данных МТЗ. Внутри блока R не определяются локальные проводящие образования в верхах ЗК, что, по-видимому, является следствием отсутствия точек измерения вариаций магнитного поля в его пределах. Можно отметить, что в обоих случаях проводящие блоки располагаются вблизи восточного борта Чаунской губы.
Глубинные интервалы довольно сложного распределения проводящих образований в полученной модели представлены на меридиональных и широтных разрезах модели, положение которых изображено на рис. 4 и помечено цифрами 1–4. Разрезы 2 и 3 как меридиональные, так и широтные проходят через пункты измерений остальные через характерные особенности близлежащих проводящих аномалий. Сами разрезы представлены на рис. 5 и рис. 6. Согласно рис. 4 начальная часть профиля МТЗ 2-ДВ-А находится в квадрате, ограниченном меридиональными 2, 4 и широтными 3, 4 профилями. В области глубин от подкоровых до 80 км здесь по данным МТЗ представлены проводящие образования с УЭС ≈60 Ом м. В то же время, как следует из рассмотрения разрезов модели, изображенных на рис. 5 и рис. 6, удельное электрическое сопротивление пород в этом диапазоне глубин и глубже составляет около 1000 Ом м. Возможно такое расхождение связано с тем, что МТЗ чувствительно к вертикальным градиентам УЭС в разрезе, в то время как типперы более чувствительны к горизонтальным градиентам [Tietze et al., 2015]. Поэтому для обеспечения высоких значений наблюденных типперов на длинных периодах горизонтальные градиенты должны сохраняться и на больших глубинах, что и обеспечивается в модели наличием проводящих и непроводящих блоков в глубинном разрезе.
Как видно из рис. 5, рис. 6 проводящие блоки просматриваются в разрезе модели до глубин около 100 км с локализацией зон максимальной электрической проводимости в подкоровой области. Наиболее вероятным источником высокой проводимости там могут быть расплавы или частичное плавление горных пород при температурах выше точки Кюри. Нет никаких сведений о тепловом потоке или гидротермальной активности недр в этом районе кроме косвенных, обсуждавшихся выше. В то же время представленные в Чаунской складчатой зоне полиметаллические месторождения, приуроченные к ультракалиевым гранитоидам, контролируемым Чаунской депрессией, вынуждают предполагать существование литосферной мантийной интрузии во время их образования в этом районе [Ефремов, 2009]. Положение этой мантийной интрузии, в выше цитируемой работе, связывается с зоной отрицательных гравитационных аномалий под Чаунской складчатой областью [Гравиметри-ческая …, 2004], объясняемой разуплотнением в нижней коре и верхней мантии, вызываемым генерацией магм. Но в этом случае она должна обладать высокой электрической проводимостью, что неизбежно отразилось бы на поведении типперов в пунктах PBK и VLK и привело бы к уменьшению их значений. Так как этого не наблюдается, то либо зона разуплотнения не является электрически проводящей и выполнена гранитоидами, либо ее интегральная проводимость существенно меньше по сравнению с интегральной проводимостью блоков C1–C3 в модели. Иначе говоря, все проводники в ЗК и верхней мантии (ВМ) региона должны находиться западнее восточного побережья Чаунской губы, как это получено в результирующей модели, и по системам трещин и глубинных разломов могут быть связаны с Чаунской складчатой зоной. В этом случае расплавы могли поставляться в складчатую область по системе локальных рукавов от глубинной проводящей аномалии под Чаунской губой.
ВЫВОДЫ
Используя записи геомагнитных вариаций, полученные в районе Чаунской губы, были оценены величины типперов, ориентации реальных и мнимых индукционных стрелок в этом районе. На основе их анализа оценена локализация глубинных проводящих неоднородностей, располагающихся западнее и севернее Чаунской складчатой зоны.
Для получения каких-либо количественных данных о конфигурации этих проводящих неоднородностей и их электрических свойствах была выполнена 3D-инверсия типперов с использованием программы ModEM, что позволило построить, хотя и оценочную, ввиду использования всего двух пунктов измерения вариаций, геоэлектрическую модель изучаемого района. На этой основе было произведено сравнение, полученной модели с ранее полученным геоэлектрическим разрезом вдоль профиля 2-ДВ-А по данным МТЗ. Сравнение выявило как сходные черты, так и противоречия в результатах этих двух исследований. Их разрешение будет предметом дальнейших МТ и МВ исследований в этой области, которые в минимальном объеме должны включать выполнение измерений вдоль широтного профиля в восточном направлении, начинающегося от пункта PBK, и меридионального профиля в южном направлении, начинающегося от пункта VLK.
Проведенные 3D-инверсии экспериментальных типперов и их расчеты для конкретных моделей среды с последующей инверсией показали возможность выделения глубинных проводящих блоков при МВ исследованиях.
При интерпретации результатов инверсии отмечается корреляция между положением глубинных проводящих неоднородностей в горизонтальных разрезах и положительными аномалиями в гравитационном поле по спутниковым и наземным данным, опоясывающими Чаунскую складчатую зону с запада и севера.
В результате выполненных работ была построена пилотная модель геоэлектрического разреза района Чаунской губы с использованием пока что имеющимися измерениями магнитных вариаций только в двух пунктах.
Список литературы
Бердичевский М.Н., Дмитриев В.И., Голубцова И.С., Мерщикова Н.А., Пушкарев П.Ю. Магнитовариационные зондирования: новые возможности // Физика Земли. 2003. № 9. С. 3–30.
Бердичевский М.Н., Дмитриев В.И. Модели и методы магнитотеллурики. М.: Научный мир. 2009. 680 с.
Ватрушкина Е.В., Тучкова М.И., Соколов С.Д. Позднеюрский-раннемеловой налсубдукционный вулканизм Чукотского террейна (Арктический регион, Россия) // Геотектоника. 2019. № 6. С. 78–91.
Геологическая карта СССР. Масштаб 1 : 200 000. Лист R-XXI, XXII, XV, XVI. Серия Анюйско-Чаунская. Объяснительная записка. Магадан: ФГБУ “ВСЕГЕИ”. 1979. 107 с.
Государственная геологическая карта Российской Федерации. Масштаб 1 : 2 000 000. Лист R-59-ХХХI, ХХХII. Серия Анюйско-Чаунская. Объяснительная записка. М.: Московский филиал ФГБУ “ВСЕГЕИ”. 2016. 102 с.
Гравиметрическая карта России масштаба 1 : 5 000 000. Дальневосточный федеральный округ / Петров О.В., Морозов А.Ф., Липилин А.В., Литвинова Т.П. и др. (ред.). СПб.: ВСЕГЕИ. 2004. https://www.vsegei.ru/ru/info/gisatlas/dvfo/okrug/gravika.jpg
Глебовский В.Ю., Черных А.А., Каминский В.Д., Васильев В.В., Корнева М.С., Суханова А.В., Редько А.Г., Яковенко И.В. Основные итоги и планы дальнейших магнитометрических и гравиметрических исследований в Северном Ледовитом океане. 70 лет в Арктике, Антарктике и Мировом океане. Сборник научных трудов / В.Д. Каминский, Г.П. Аветисов, В.Л. Иванов (ред.). СПб.: ВНИИОкеангеология. 2018. 554 с
Ефремов С.В. Геохимия и генезис ультракалиевых и каливыех магматитов восточного побережья Чаунской губы (Чукотка), их роль в металлогенической специализации оловоносных гранитоидов // Тихоокеанская геология. 2009. Т. 28. № 1. С. 84-95.
Заварзина Г.А., Мурзин Р.Р., Захарова О.А., Степанова В.C. Результаты комплексного анализа аэрогравимагнитных и сейсморазведочных данных восточной части Восточно-Сибирского моря // Геофизика. 2017. № 4. С. 69–75.
Карта рельефа подошвы литосферы России / В.В. Соловьев (ред.). Масштаб: 1 : 10 000 000. Серия: обзорные карты Российской Федерации масштаба 1 : 10 000 000. ФГБУ “ВСЕГЕИ”. 1995. URL: http://www.geokniga.org/maps/1229
Лаверов Н.П., Лобковский Л.И., Кононов М.В., Добрецов Н.Л., Верниковский В.А., Соколов С.Д., Шипилов Э.В. Геодинамическая модель развития арктического бассейна и примыкающих территорий для мезозоя и кайнозоя и внешняя граница континентального шельфа России // Геотектоника. 2013. № 1. С. 3–35.
Рекант П.В., Петров О.В., Прищепенко Д.В. Формирование складчато-надвиговой структуры южной части шельфа Восточно-Сибирского моря по результатам структурного анализа сейсмических материалов // Региональная геология и металлогения. 2020. № 82. С. 35–59.
Середкина А.И., Филиппов С.В. Глубины залегания магнитных источников в Арктике и их связь с параметрами литосферы // Геология и геофизика. 2021. № 7. С. 902–916. https://doi.org/10.15372/GiG2020162
Соловьев В.М., Селезнев В.С., Сальников А.С., Шибаев С.В., Тимофеев В.Ю., Лисейкин А.В., Шенмайер А.Е. Особенности сейсмического строения области сочленения евразийской и охотоморской плит на востоке (в створе опорного профиля 3ДВ) // Геология и геофизика. 2016. Т. 57. № 11. С. 2044–2058.
Старжинский С.С., Никифоров В.М., Йошикава А. Опыт магнитовариационного зондирования в Арктике в Лаптевоморском регионе // Физика Земли. 2020. № 2. С. 89–102. https://doi.org/10.31857/S0002333720020106
Старжинский С.С. Йошикава А., Хомутов С.Ю. Особенности геоэлектрического разреза прибрежной области Чукотского моря вблизи обсерватории “мыс Шмидта” // Геология и геофизика. 2022. Т. 63. № 12. С. 1754–1770. https://doi.org/10.15372/GiG2021139
Яковлев А.В., Бушенкова Н.А., Кулаков И.Ю., Добрецов Н.Л. Структура верхней мантии арктического региона по данным региональной сейсмотомографии // Геология и геофизика. 2012. Т. 53. № 10. С. 1261–1272.
Antashchuk K., Atakov A., Mazurkevich K., Petrov O. Tectonic structure and metallogeny of the Western Chukotka: insights from comprehensive geophysical dataset interpretation. EGU General Assembly 2020. Online, 4–8 May 2020. EGU2020-11192. https://doi.org/10.5194/egusphere-egu2020-11192
Campanya J., Ogaya X., Jones A.G., Rath V., Vozar J., Meqbel N. The advantages of complementing MT profiles in 3-D environments with geomagnetic transfer function and interstation horizontal magnetic transfer function data: results from a synthetic case study // Geophys. J. Int., 2016. V. 207. P. 1818–1836.
Dyment J., Choi Y., Hamoudi M., Lesur V., Thebault E. Global equivalent magnetization of the oceanic lithosphere // Earth Planet. Sci. Lett. 2015. V. 430. P. 54–65. https://doi.org/10.1016/j.epsl.2015.08.002
Efremov S.V., Travin A.V Isotopic age and paleogeodynamic position of ultrapotassic magmatism of Central Chukotka // Geodynamics & Tectonophysics. 2021. V. 12. № 1. P. 76–83. https://doi.org/10.5800/GT-2021-12-1-0513
Egbert G.D., Kelbert A. Computational recipes for electromagnetics inverse problems // Geophys. J. Int. 2012. V. 189. P. 251–267. https://doi.org/10.1111/j.1365-246X.2011.05347.x
Flechtner F., Reigber C.,· Rummel R., Balmino G. Satellite Gravimetry: A Review of Its Realization // Surveys in Geophysics. 2021. V. 42. № 5. P. 1029–1074.
Förste C., Bruinsma S.L., Abrikosov O., Lemoine J.-M., Marty J.C., Flechtner F., Balmino G., Barthelmes F., Biancale R. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. 2014. GFZ Data Services: Potsdam. Germany. https://doi.org/10.5880/icgem.2015.1
Gaina C., Medvedev S., Torsvik T.H., Koulakov I., Werner S.C., 4D Arctic: A Glimpse into the Structure and Evolution of the Arctic in the Light of New Geophysical Maps, Plate Tectonics and Tomographic Models // Surv. Geophys. 2014. V. 35. P. 1095–1122, https://doi.org/10.1007/s10712-013-9254-y
Gaina C., Werner S.C., Saltus R., Maus S. and the CAMP-GM group. Circum-Arctic Mapping Project: New Magnetic and Gravity Anomaly Maps of the Arctic / A. M. Spencer, D. Gautier, A. Stoupakova, A. Embry, K. Sørensen (eds). Arctic Petroleum Geology. Geol. Soc. Memoir. 2011. V. 35. P. 39–48. https://doi.org/10.1144/M35.3
Jorgensen M.R., Cuma M., Zhdanov M. S. 3D Joint Inversion of Magnetotelluric and Magnetovariational Data to Image Conductive Anomalies in Southern Alberta, Canada. Paper presented at the 2015 SEG Annual Meeting, New Orleans, Louisiana, October 2015. URL: http://www.cemi.utah.edu/seg15/3.pdf (дата обращения: 31.03.2022).
Kelbert A., Meqbel N.M., Egbert G.D., Tandon K. ModEM: A modular system for inversion of electromagnetic geophysical data // Comp. Geosci. 2014. V. 66. P. 40–53. URL: https://doi.org/10.1016/j.cageo.2014.01.010
Laundal K.M., Richmond A.D. Magnetic Coordinate Systems // Space Sci Rev. 2017. V. 206. № 1–4. P. 27–59. URL: https://doi.org/10.1007/s11214-016-0275-y
Li C.-F., Lu Y., Wang J. A global reference model of Curie-point depths based on EMAG2 // Sci. Rep. 2017. V. 7(1). 45129. https://doi.org/10.1038/srep45129
Lu Y., Li C.-F., Wang J., Wan X. Arctic geothermal structures inferred from Curie-point depths and their geodynamic implications // Tectonophysics. 2022. V. 822. Article 229158. URL: https://doi.org/10.1016/j.tecto/2021.229158
Luchitskaya M.V., Tikhomirov P.L, Shats A.L. U-Pb ages and tectonic setting of mid-Cretaceous magmatism in Chukotka (NE Russia). ICAM VI: Proceedings of the International Conference on Arctic Margins VI. Fairbanks. Alaska. May 2011. SPb.: Press VSEGEI. 2014. 332 p. Chapter 6. P. 157–169. UDC: 005.745(100(98)). https://vsegei.ru/ru/public/icam/cam-all_VVS.pdf (дата обращения: 08.02.2022).
Meyer В., Saltus R., Chulliat A. EMAG2v3: Earth Magnetic Anomaly Grid (2-arc-minute resolution). 2017. Version 3. NOAA National Centers for Environmental Information.https://doi.org/10.7289/V5H70CVX (дата обращения: 28.03.2022)
Miller E.L., Verzhbitsky V.E. Structural studies near Pevek, Russia: implications for formation of the East Siberian Shelf and Makarov Basin of the Arctic Ocean // Stephan Mueller Spec. Publ. Ser. 2009. V. 4. P. 223–241. URL: https://doi.org/10.5194/smsps-4-223-2009
Pace F., Martí A., Queralt P., Santilano A., Manzella A., Ledo J., Godio A. Three-Dimensional Magnetotelluric Characterization of the Travale Geothermal Field (Italy) // Remote Sens. 2022. V. 14. № 3. 542. https://doi.org/10.3390/rs14030542
Petrov O., Morozov A., Shokalsky S., Kashubin S., Artemieva I.M., Sobolev N., Petrov E., Ernst R.E., Sergeev S., Smelror M. Crustal structure and tectonic model of the Arctic region // Earth-Science Reviews. 2016. V. 154. P. 29–71.
Sandwell D., Garcia E., Soofi K., Wessel P., Chandler M., Smith W.H.F. Toward 1-mGal accuracy in global marine gravity from CryoSat-2, Envisat, and Jason-1, Special Section: Gravity and Potential Fields. The Leading Edge. 2013. P. 892–899. https://doi.org/10.1190/tle32080892.1
Sidorov R.V., Kaban M.K., Soloviev A.A., Petrunin A.G., Gvishiani A.D., Oshchenko A.A., Popov A.B., Krasnoperov R.I. Sedimentary basins of the eastern Asia Arctic zone: new details on their structure revealed by decompensative gravity anomalies // Solid Earth. 2021. V. 12. P. 2773–2788. https://doi.org/10.5194/se-12-2773-2021
Sinmyo R., Keppler H. Electrical conductivity of NaCl-bearing aqueous fluids to 600°C and 1 GPa // Contrib. Mineral. Petrol. 2017. V. 172. №4. https://doi.org/10.1007/s00410-016-1323-z
Sims W.E., Bostick F.X. Discussion on “The magnetotelluric method in the exploration of sedimentary basins” by Keeva Vozoff (Geophysics, February 1972. P. 98–114) // Geophysics. 1976. V. 41. № 2. P. 325–328.
Sokolov S.D., Ledneva G.V., Tuchkova M.I., Luchitskaya M.V., Ganelin A.V., Verzhbitsky V.E. Chukchi arctic continental margins: tectonic evolution, link to the opening of the Amerasia Basin. ICAM VI: Proceedings of the International Conference on Arctic Margins VI / David B. Stone, Garrik E. Grikurov, James G. Clough, Gordon N. Oakey, Dennis K. Thurston (eds.). Fairbanks. Alaska. 2014. P. 93–113.
Tietze K., Ritter O., Egbert G.D. 3-D inversion of the magnetotelluric phase tensor and vertical magnetic transfer function // Geophys. J. Int. 2015. V. 203. № 2. P. 11281148.
Tikhomirov P.L., Luchitskaya M.V., Kravchenko-Berezhnoy I.R. Comparison of Cretaceous granitoids of the Chaun tectonic zone to those of the Taigonos Peninsula, NE Asia: rock chemistry, composition of rock forming minerals, and conditions of formation // Stephan Mueller Spec. Publ. Ser. 2009. V. 4. P. 289–311. https://doi.org/10.5194/smsps-4-289-2009
Дополнительные материалы отсутствуют.


