Генетика, 2020, T. 56, № 6, стр. 714-725
Возникновение сложных режимов динамики численности в ходе эволюции структурированной лимитированной популяции
Г. П. Неверова 1, *, О. Л. Жданова 1, Е. Я. Фрисман 2, **
1 Институт автоматики и процессов управления Дальневосточного отделения
Российской академии наук
690041 Владивосток, Россия
2 Институт комплексного анализа региональных проблем
679016 Биробиджан, Россия
* E-mail: galina.nev@gmail.com
** E-mail: frisman@mail.ru
Поступила в редакцию 21.05.2019
После доработки 25.06.2019
Принята к публикации 09.07.2019
Аннотация
В работе рассматривается модель микроэволюции двухвозрастной экологически лимитированной популяции под действием естественного отбора, регулирующего выживаемость младшей возрастной группы. Проводится аналитическое и численное исследование модели; определяются параметрические области ее различного динамического поведения. Показано, что появление новых аллелей (например, в результате мутаций), обеспечивающих больший репродуктивный потенциал особей, приводит к естественному отбору этих аллелей и закономерному эволюционному росту среднего значения репродуктивного потенциала в популяции. Однако это увеличение среднего значения репродуктивного потенциала при плотностной регуляции рождаемости приводит к дестабилизации динамики численности возрастных групп. Сценарии изменений режимов динамики могут быть различны и зависят от параметров модели, но основной результат всегда одинаков: динамика становится все более сложной и, как правило, все более хаотической.
В основополагающих работах по теоретической популяционной генетике [1, 2] достаточно подробно изучено действие естественного отбора, которое связано только с генетическими различиями между морфами и не зависит ни от каких других (негенетических) факторов. Эти результаты относятся к серии исследований математических моделей динамики генетической структуры свободно размножающихся популяций, развивающихся в неизменной внешней среде в условиях неограниченности жизненных ресурсов, что позволяло считать фишеровские приспособленности генотипических групп постоянными [3, 4].
Эколого-генетическое направление моделирования, рассматривающее взаимосвязанные изменения численности и генетической структуры популяции, появилось в 60-е гг. прошлого столетия. В это время формировались представления о плотностно- и частотно-зависимых составляющих в действии естественного отбора [5, 6], а также о плотностно-независимых формах естественного отбора, действие которых в условиях экологического лимитирования способно вызвать изменение характера динамики численности популяций [7–11]. Работы в этой области позволили охарактеризовать действие эволюционных факторов, в первую очередь естественного отбора, на изменение генетической структуры, а соответственно и изменений характера динамики популяций, которые сталкиваются с естественным ограничением экологических ресурсов (т.е. находящихся под действием лимитирующих факторов окружающей среды) [12–17].
Даже простейшие модели лимитированных популяций, построенные на классических для математической биологии уравнениях Рикера, Смита, Мэя–Хассела, демонстрируют удивительно сложную динамику [18, 19]. При этом важно учитывать, что большинство биологических популяций имеют ярко выраженную неоднородность, представленную возрастной или стадийной структурой. В популяционной экологии для описания динамики структурированных популяций широко используются матричные модели Лесли–Лефковича [20–23]. Все эффекты, связанные с плотностно-зависимой регуляцией роста популяции и наблюдающиеся в одномерных моделях неструктурированных популяций, отмечаются и в системах динамики структурированных популяций. Наиболее исследованными моделями, демонстрирующими разнообразные типы динамического поведения, являются двумерные системы рекуррентных уравнений или двумерные отображения, преимущественно описывающие динамику двухвозрастной популяции [24]. Такая структура характерна для организмов с небольшим временем жизни, включающим два–три периода размножения. Примерами могут служить мелкие млекопитающие (мышевидные грызуны, беличьи и т.п.), быстросозревающие рыбы (такие как корюшка, навага и др.), многие насекомые, двух- и трехлетние растения [25–28]. Именно мышевидные грызуны, быстросозревающие виды рыб и насекомые обладают сложной флюктуирующей динамикой и являются наиболее частыми объектами исследований в экспериментальной и яркими примерами в теоретической популяционной биологии.
В теоретических исследованиях двухвозрастных популяций неоднократно было показано, что увеличение репродуктивного потенциала и параметров, характеризующих выживаемость особей, проводит к усложнению динамики численности от стабильных режимов до нерегулярных колебаний [29–31]. Однако механизмы роста репродуктивного потенциала, как правило, не рассматривались. Вместе с тем можно предположить, что рост потенциальной плодовитости особей в природных популяциях происходит в процессе их эволюции под действием естественного отбора. Если это так, то в процессе естественной эволюции природной популяции с выраженной сезонностью жизненного цикла должен происходить закономерный переход от равновесных режимов динамики численности к колебаниям и хаосу (псевдостохастическому поведению).
Данная работа посвящена исследованию возможности такого эволюционного перехода. В работе рассматривается простейшая модель эволюции двухвозрастной популяции, в которой плотностно-зависимые факторы лимитируют интенсивность рождаемости, но при этом репродуктивный потенциал определяется генетически и подвержен действию естественного отбора.
МОДЕЛЬ ДИНАМИКИ СТРУКТУРИРОВАННОЙ ПОПУЛЯЦИИ С УЧЕТОМ ПЛОТНОСТНО-ЗАВИСИМОЙ РЕГУЛЯЦИИ РОСТА И ЕСТЕСТВЕННОГО ОТБОРА ПО ВЕЛИЧИНЕ РЕПРОДУКТИВНОГО ПОТЕНЦИАЛА
Рассматривается ситуация, когда популяция может быть представлена к началу очередного сезона размножения совокупностью двух возрастных классов: младшего, включающего неполовозрелых особей, и старшего, состоящего из особей, участвующих в размножении. Предполагается, что времени, протекающего между двумя последовательными периодами размножения, достаточно для развития особей младшего возраста до половозрелого состояния, а новорожденных особей – до состояния младшего возраста. Выживаемость и репродуктивная способность половозрелых особей не зависят от возраста, т.е. отсутствуют возрастные различия у взрослых особей [26, 28]. Предполагается, что регуляция численности популяции осуществляется путем плотностно-зависимого лимитирования рождаемости. Подобный тип саморегуляции наблюдается у достаточно многих животных, особенно мелких млекопитающих, когда рождаемость заметно снижается по мере увеличения численности популяции. Основным проявлением плотностно-зависимой регуляции рождаемости является стресс-синдром, приводящий к снижению половой активности и уменьшению плодовитости особей, вплоть до рассасывания части заложенных эмбрионов. В частности, это характерно для видов, подверженных сильным колебаниям численности, например леммингов, полевок и др. [25].
Уравнения динамики численности двухвозрастной лимитированной популяции с учетом описанных особенностей жизненного цикла имеют вид:
(1)
$\left\{ \begin{gathered} {{X}_{{n + 1}}} = A({{X}_{n}},{{Y}_{n}}){{Y}_{n}}, \hfill \\ {{Y}_{{n + 1}}} = s{{X}_{n}} + v{{Y}_{n}}, \hfill \\ \end{gathered} \right.$Функция A(X, Y) выбрана по аналогии с моделью Рикера:
где а – репродуктивный потенциал; α и β – коэффициенты, характеризующие интенсивности воздействия особей неполовозрелого и половозрелого возрастных классов на уменьшение рождаемости. В работах [29, 30] проведено детальное исследование динамики численности двухвозрастной популяции, описываемой моделью (1) с функцией рождаемости (2), где показано, что падение рождаемости с ростом численности взрослых особей оказывается эффективным механизмом регуляции роста численности, но при увеличении потенциальных репродуктивных возможностей и выживаемости особей может привести к возникновению колебаний численности, имеющих весьма сложную временную организацию. Именно этот механизм является, по-видимому, определяющим в поведении численности мелких млекопитающих, таких как лемминги и некоторые полевки [32].Таким образом, с ростом репродуктивного потенциала (a) и параметров, характеризующих выживаемость особей, происходит усложнение динамики численности от стабилизации до нерегулярных колебаний. В свою очередь естественно предположить, что рост потенциальной плодовитости особей в природных популяциях происходит в процессе их эволюции под действием естественного отбора. Это означает, что в процессе естественной эволюции природной популяции с выраженной сезонностью жизненного цикла должен происходить закономерный переход от устойчивых режимов динамики численности к колебаниям и хаосу (псевдостохастическому поведению), т.е. переход от равновесных режимов динамики к неравновесным.
Проиллюстрируем механизм закономерного эволюционного усложнения динамики численности структурированной популяции, рассмотрев действие естественного отбора на примере одной из самых простых модельных ситуаций, когда репродуктивный потенциал (а) – максимально возможная плодовитость особей – является адаптивным признаком, который определяется одним аутосомным диаллельным локусом с аллеломорфами А и а. В соответствии с выбранной моделью предполагается, что в популяции существуют три генотипические группы АА, Аа и аа с различающимися репродуктивными потенциалами. Обозначим репродуктивные потенциалы этих генотипов аАА, аАа и ааа соответственно.
Модель (1) с функцией рождаемости (2) принимает в этом случае следующий вид:
(3)
$\left\{ \begin{gathered} {{X}_{{n + 1}}} = {{{\bar {a}}}_{n}}{{Y}_{n}}\exp ( - \alpha {{X}_{n}} - \beta {{Y}_{n}}) \hfill \\ {{Y}_{{n + 1}}} = s{{X}_{n}} + v{{Y}_{n}} \hfill \\ {{q}_{{n + 1}}} = \frac{{{{p}_{n}}\left( {{{a}_{{AA}}}{{p}_{n}} + {{a}_{{Aa}}}(1 - {{p}_{n}})} \right)}}{{{{{\bar {a}}}_{n}}}} \hfill \\ {{p}_{{n + 1}}} = \frac{{s{{q}_{n}}{{X}_{n}} + v{{p}_{n}}{{Y}_{n}}}}{{s{{X}_{n}} + v{{Y}_{n}}}} \hfill \\ \end{gathered} \right.,$Первые два уравнения системы (3) описывают динамику численности возрастных классов популяции. Они отличаются от исходной модели (1) только тем, что вместо постоянного параметра а (постоянного репродуктивного потенциала) стоит значение $\bar {a} = {{a}_{{AA}}}p_{n}^{2}$ + $2{{a}_{{Aa}}}{{p}_{n}}(1 - {{p}_{n}})$ + ${{a}_{{aa}}}{{(1 - {{p}_{n}})}^{2}}$, которое меняется в процессе микроэволюции. Два последних уравнения системы (3) описывают динамику частот генов, определяющих репродуктивный потенциал, т.е. описывают сам процесс микроэволюции.
Подробный вывод уравнений модели (3) представлен в Приложении 1 .
СТАЦИОНАРНЫЕ ТОЧКИ МОДЕЛИ И ИХ УСТОЙЧИВОСТЬ
При переходе к безразмерным переменным – относительным численностям sβX → x и βY → y модель (3) сводится к виду:
(4)
$\left\{ \begin{gathered} {{x}_{{n + 1}}} = {{{\bar {r}}}_{n}}{{y}_{n}}\exp ( - \rho {{x}_{n}} - {{y}_{n}}) \hfill \\ {{y}_{{n + 1}}} = {{x}_{n}} + v{{y}_{n}} \hfill \\ {{q}_{{n + 1}}} = \frac{{{{p}_{n}}\left( {{{r}_{{AA}}}{{p}_{n}} + {{r}_{{Aa}}}(1 - {{p}_{n}})} \right)}}{{{{{\bar {r}}}_{n}}}} \hfill \\ {{p}_{{n + 1}}} = \frac{{{{q}_{n}}{{x}_{n}} + v{{p}_{n}}{{y}_{n}}}}{{{{x}_{n}} + v{{y}_{n}}}} \hfill \\ \end{gathered} \right.,$Параметры rАА, rАа и rаа в этом случае характеризуют репродуктивные потенциалы генотипов АА, Аа и аа старшего возрастного класса с учетом выживаемости потомков до взрослого возрастного класса, $\bar {r}$ – средний репродуктивный потенциал, параметр ρ – относительный вклад младшей возрастной группы в лимитирование процесса воспроизводства.
Кроме тривиальной $\left( {\begin{array}{*{20}{c}} {\bar {x} = 0,}&{\bar {y} = 0} \end{array}} \right)$, модель (4) имеет две мономорфные ненулевые по численности стационарные точки:
(5)
$\begin{gathered} \bar {q} = 0,\,\,\,\,\bar {p} = 0,\,\,\,\,\bar {x} = \frac{{1 - v}}{{1 + \rho (1 - v)}}\ln \frac{{{{r}_{{aa}}}}}{{1 - v}}, \\ \bar {y} = \frac{1}{{1 + \rho (1 - v)}}\ln \frac{{{{r}_{{aa}}}}}{{1 - v}} \\ \end{gathered} $(6)
$\begin{gathered} \bar {q} = 1,\,\,\,\bar {p} = 1,\,\,\,\bar {x} = \frac{{1 - v}}{{1 + \rho (1 - v)}}\ln \frac{{{{r}_{{AA}}}}}{{1 - v}}, \\ \bar {y} = \frac{1}{{1 + \rho (1 - v)}}\ln \frac{{{{r}_{{AA}}}}}{{1 - v}} \\ \end{gathered} $(7)
$\begin{gathered} \bar {q} = \frac{{{{r}_{{Aa}}} - {{r}_{{aa}}}}}{{2{{r}_{{Aa}}} - {{r}_{{AA}}} - {{r}_{{aa}}}}},\,\,\,\,\bar {p} = \frac{{{{r}_{{Aa}}} - {{r}_{{aa}}}}}{{2{{r}_{{Aa}}} - {{r}_{{AA}}} - {{r}_{{aa}}}}}, \\ \bar {x} = \frac{{1 - v}}{{1 + \rho (1 - v)}}\ln \frac{{r_{{Aa}}^{2} - {{r}_{{AA}}}{{r}_{{aa}}}}}{{(1 - v)\left( {2{{r}_{{Aa}}} - {{r}_{{AA}}} - {{r}_{{aa}}}} \right)}}, \\ \bar {y} = \frac{1}{{1 + \rho (1 - v)}}\ln \frac{{r_{{Aa}}^{2} - {{r}_{{AA}}}{{r}_{{aa}}}}}{{(1 - v)\left( {2{{r}_{{Aa}}} - {{r}_{{AA}}} - {{r}_{{aa}}}} \right)}}, \\ \end{gathered} $Используя границы областей устойчивости решений модели (4) (приведенные в Приложении 2 ), нетрудно показать, что область устойчивости мономорфного равновесия (5) в плоскости параметров (rAa, raa) имеет вид трапеций, представленных на рис. 1.
Рис. 1.
Область устойчивости мономорфного решения (5). λ = 1 соответствует транскритической бифуркации, λ = –1 – бифуркация удвоения периода, λ = e±iθ – бифуркация Неймарка–Сакера.
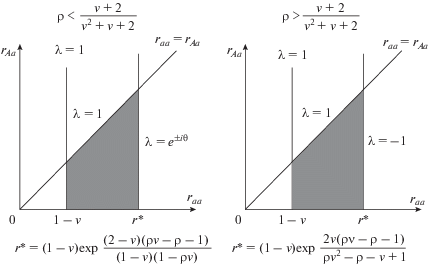
При raa < 1 – v положительного равновесия, мономорфного по аа, не существует. Если raa > 1 – v, raa < r* и raa > rAa, то положительное равновесие, мономорфное по аа, существует и устойчиво. При переходе через границу raa = rAa (но при raa >1 – v и raa < r*) это равновесие теряет устойчивость и устойчивыми оказываются либо полиморфное равновесие, либо другой аттрактор. Если raa > rAa и ρ < (2 + v)/(v2 + v + 2), то при переходе через границу raa = r* = (1 – v)exp((2 – v)(ρv – ρ – 1)/(1 – ‒ v)/(1 – ρv)) потеря устойчивости происходит при комплексно-сопряженных корнях характеристического уравнения, причем генетический мономорфизм аа сохраняется, но возникают колебания численности, сопровождающиеся появлением предельных инвариантных кривых, которые при дальнейшем удалении параметра raa от границы устойчивости разрушаются с образованием весьма сложных предельных структур вплоть до появления генетически мономорфного хаотического аттрактора. Если raa > rAa и ρ > (2 + v)/(v2 + v + 2), то при переходе через границу raa = r* = (1 – ‒ v)exp(2v(ρv – ρ – 1)/(1 – v)/(1 – ρ(v + 1))) потеря устойчивости происходит по сценарию Фейгенбаума и численность популяции начинает демонстрировать двухгодичные колебания [33], а затем при удалении параметра raa от границы каскад бифуркаций удвоения периода колебаний вплоть до хаотического аттрактора при сохранении генетического мономорфизма аа. Отметим, что в случае, когда ρ = (2 + v)/(v2 + v + 2), наблюдается бифуркация коразмерности два – бифуркация flip-NS [34], по сути это множество точек пересечения поверхностей, соответствующих бифуркациям удвоения периода и Неймарка–Сакера.
Для неподвижной точки (6) картина динамического поведения аналогичная, поскольку оба мономорфных решения симметричны относительно rAA и raa. Следовательно, условия устойчивости обеих мономорфных стационарных точек можно представить в виде табл. 1.
Таблица 1.
Условия устойчивости мономорфных стационарных точек
| $\bar {q} = 0,\,\,\,\,\bar {p} = 0$ | $\begin{gathered} 1 - v < {{r}_{{aa}}} < r{\text{*}} \\ {{r}_{{aa}}} > {{r}_{{Aa}}} \\ \end{gathered} $ | $r* = \left\{ \begin{gathered} (1 - v)\exp \frac{{(2 - v)(\rho v - \rho + 1)}}{{(1 - v)(1 - \rho v)}},\,\,\,\,\rho < \frac{{2 + v}}{{{{v}^{2}} + v + 2}} \hfill \\ (1 - v)\exp \frac{{2v(\rho v - \rho + 1)}}{{\rho {{v}^{2}} - \rho - v + 1}},\,\,\,\rho > \frac{{2 + v}}{{{{v}^{2}} + v + 2}} \hfill \\ \end{gathered} \right.$ |
| $\bar {q} = 1,\,\,\,\,\bar {p} = 1$ | $\begin{gathered} 1 - v < {{r}_{{AA}}} < r{\text{*}} \\ {{r}_{{AA}}} > {{r}_{{Aa}}} \\ \end{gathered} $ |
Рассмотрим теперь полиморфное состояние (7). Важно отметить, что для существования и устойчивости этого равновесия необходимо, чтобы репродуктивный потенциал гетерозиготы был больше репродуктивных потенциалов каждой из гомозигот, т.е. rAa > raa, rAa > rAA и при этом rAa > 1 – v. Вместе с тем если 1 – v < rAa < 2(1 – v), то существует возможность вырождения популяции в случае нарушения условий ${{r}_{{AA}}} > \frac{{r_{{Aa}}^{2} - (2{{r}_{{Aa}}} - {{r}_{{aa}}})(1 - v)}}{{{{r}_{{aa}}} + v - 1}}$ или ${{r}_{{aa}}} > \frac{{r_{{Aa}}^{2} - (2{{r}_{{Aa}}} - {{r}_{{AA}}})(1 - v)}}{{{{r}_{{AA}}} + v - 1}}.$
Отметим далее, что при выполнении rAa > raa, rAa > rAA и rAa > 1 – v дополнительным условием устойчивости полиморфного равновесия является неравенство rАa < r*, где r* сложно зависит от параметров v и ρ. Переход значений репродуктивного потенциала гетерозигот через границу rАa = r* приведет к потере устойчивости полиморфного равновесия. Как и для мономорфных равновесий такая потеря устойчивости и дальнейшая эволюция динамики численности происходит по одному из двух описанных сценариев (в зависимости от соотношения параметров v и ρ), при этом возникновение квазипериодических колебаний наблюдается только при ${{r}_{{Aa}}} > (1 - v)\exp \frac{{2 - v}}{{1 - v}}$, и всегда в популяции сохраняется генетический полиморфизм, т.е. присутствуют три генотипа.
В случае, когда репродуктивный потенциал гетерозиготы оказывается меньше репродуктивных потенциалов каждой из гомозигот, т.е. rAa < raa и rAa < rAA, полиморфная стационарная точка может существовать, но она оказывается неустойчивой. Как показывает проведенный нами анализ, в этом случае в рамках модели (4) возникает бистабильность мономорфных решений, т.е. существуют два устойчивых мономорфных аттрактора (при 1 – v < rАА < r* и 1 – v < rаa < r* это две устойчивые мономорфные стационарные точки), каждый из которых имеет во множестве начальных значений переменных свою область (бассейн) притяжения. Какая из гомозигот окажется фиксированной в процессе эволюции определяется начальным соотношением численностей и частот аллелей, а характер асимптотической динамики численности зависит от репродуктивного потенциала этой гомозиготы.
ДИНАМИКА ПОПУЛЯЦИИ
Описанные условия существования и устойчивости стационарных точек модели (4) позволяют в общих чертах охарактеризовать ее динамическое поведение в зависимости от значений популяционных параметров. Далее, чтобы не загромождать описание динамического поведения модели (4), будем рассматривать ситуацию, когда raa < rAA, поскольку симметричная ей ситуация raa > rAA полностью аналогична рассматриваемой, и ее изучение не добавляет качественно новых результатов. В зависимости от поведения траекторий модели (4) можно выделить следующие случаи:
I. raa, rAA < 1 – v. При этих условиях мономорфных равновесий не существует. Если дополнительно и rAa < 1 – v, то полиморфного равновесия также не существует, а существует единственное устойчивое тривиальное равновесие и, соответственно, такая популяция вымирает.
II. raa < 1 – v < rAA (при rAa < 1 – v) или raa < rAa < rAA (при rAa ≥ 1 – v). Эти условия задают в параметрическом пространстве (raa, rAA) полосу, в которой существует мономорфное равновесие ($\bar {q} = 1$, $\bar {p} = 1$); достигая его, популяция теряет свое генетическое разнообразие. С ростом rAA решение ($\bar {q} = 1$, $\bar {p} = 1$) теряет устойчивость, и траектории модели переходят в колебательный режим динамики, при этом характер возникающих колебаний определяется соотношением параметров v и ρ.
III. rAa > raa, rAA. В случае, когда репродуктивный потенциал гетерозиготы больше репродуктивного потенциала каждой из гомозигот и при этом выполняются соотношения rAa ≥ 2(1 – v) (или rAa > 1 – v и дополнительно ${{r}_{{AA}}} > \frac{{r_{{Aa}}^{2} - (2{{r}_{{Aa}}} - {{r}_{{aa}}})(1 - v)}}{{{{r}_{{aa}}} + v - 1}}$ или ${{r}_{{аа}}} > \frac{{r_{{Aa}}^{2} - (2{{r}_{{Aa}}} - {{r}_{{АА}}})(1 - v)}}{{{{r}_{{АА}}} + v - 1}}$), то существует нетривиальное полиморфное равновесие. При небольших значениях репродуктивного потенциала гетерозиготы rAa это равновесие устойчиво, а при больших значениях rAa около него возникают колебания различной сложности, но во всех этих случаях популяция оказывается генетически полиморфной.
IV. rAa < 1 – v < rAA, raa или 1 – v < rAa < rAA, raa. В этом случае репродуктивный потенциал гетерозиготы меньше репродуктивного потенциала каждой из гомозигот и существуют оба мономорфных равновесия: ($\bar {q} = 1$, $\bar {p} = 1$) и ($\bar {q} = 0$, $\bar {p} = 0$), а при rAa > 1 – v еще и полиморфное равновесие, которое всегда неустойчиво. В зависимости от начальных условий популяция “сваливается” либо в одно мономорфное состояние ($\bar {q} = 1$, $\bar {p} = 1$), когда происходит вытеснение аллеля а, либо в другое ($\bar {q} = 0$, $\bar {p} = 0$), когда происходит вытеснение аллеля А, т.е. в любом случае популяция теряет свое генетическое разнообразие. При этом численность популяции либо стремится к соответствующему мономорфному равновесию, либо флуктуирует около этого равновесия.
Деление фазового пространства модели сосуществующими мономорфными равновесиями представлено на рис. 2. Как видно, тип достигаемого равновесия зависит от начальных значений переменных q и p. При одинаковых репродуктивных потенциалах гомозигот (rAA = raa) области притяжения разных мономорфных равновесий в пространстве {q0; p0} равны и симметрично расположены. При разных репродуктивных потенциалах гомозигот область притяжения мономорфного равновесия для гомозиготы с большим репродуктивным потенциалом больше, чем для гомозиготы с меньшим репродуктивным потенциалом (рис. 2,а). Отметим, что рост репродуктивного потенциала гетерозиготы не приводит к видимым изменениям бассейнов притяжения гомозигот. В свою очередь увеличение относительного вклада младшей возрастной группы в лимитирование процесса воспроизводства, а также выживаемости зрелых особей приводит к расширению бассейна притяжения гомозиготы с меньшим репродуктивным потенциалом в пространстве частот аллеля А (рис. 2,б, в).
Рис. 2.
Бассейны притяжения (а–г) мономорфных равновесий в области бистабильности. Белые области соответствуют областям притяжения мономорфного решения $\bar {q} = 0$, $\bar {p} = 0$, а черные – $\bar {q} = 1$, $\bar {p} = 1$. См. текст.
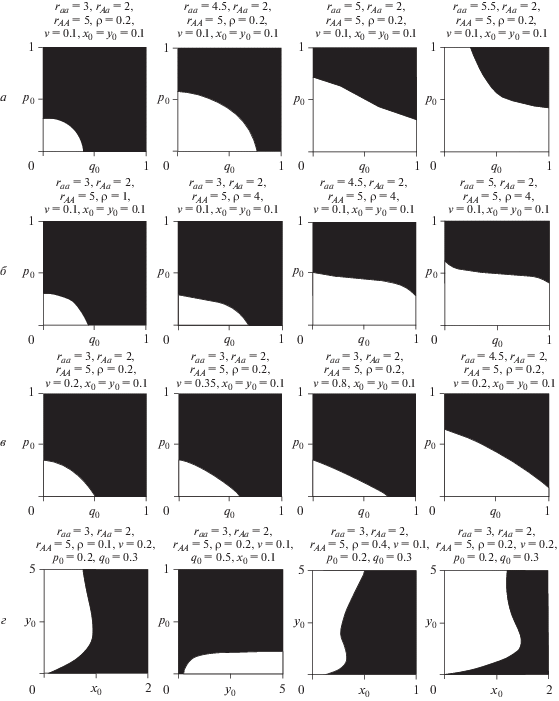
Начальные численности возрастных классов популяции также оказывают влияние на тип достигаемого мономорфного состояния (рис. 2,г). Действительно, возможна ситуация, когда генетический состав популяции будет постоянным, при этом изменение численностей возрастных групп может привести к тому, что начнет преобладать другая гомозигота. В пространстве начальных численностей рост относительного вклада младшей возрастной группы в лимитирование процесса воспроизводства сужает бассейн притяжения гомозиготы с меньшим репродуктивным потенциалом, а увеличение выживаемости старших особей наоборот – расширяет (рис. 2,г).
Изучим более подробно каким образом появление аллелей, обладающих большим репродуктивным потенциалом (например, в результате мутаций), оказывает влияние на динамику генетического состава популяции и численности возрастных классов (рис. 3–5).
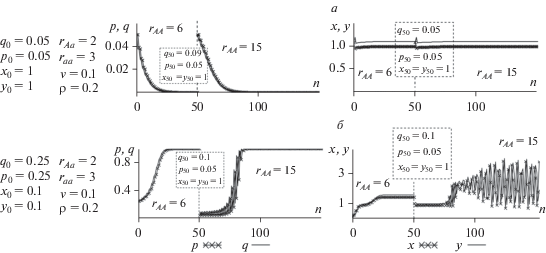
Рис. 3.
Динамика частот гена А и численностей возрастных классов при rAА ≥ rAa ≥ rаa, v = 0.1, ρ = 0.2 и начальных условиях q0 = p0 = 0.05, x0 = y0 = 1. См. текст.
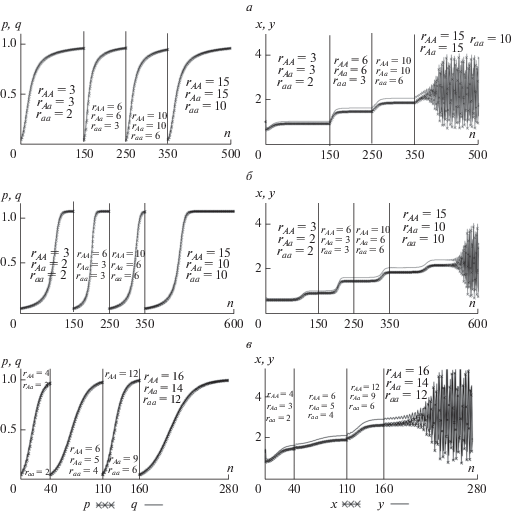
Рис. 4.
Динамика системы (4) в случае сверхдоминирования при различном репродуктивном потенциале гетерозиготы.
Рассмотрим “естественную” ситуацию, когда в равновесной популяции практически установился мономорфизм по aa (например, при raa = 2) и появляется новый аллель А с бóльшим rAA, частота встречаемости которого в возрастных классах популяции составляет, например, q0 = p0 = 0.05. Для того, чтобы оставаться в двухаллельной ситуации, каждый просчет необходимо вести практически до мономорфизма, когда p = 0.95. Затем предполагается, что “хороший” аллель почти зафиксирован (и в этом случае обозначим его через а), но появился новый (обозначим его А), еще лучше, и тогда мы опять оказываемся в двухаллельной ситуации с новыми генотипами и текущими численностями возрастных классов. При этом всегда будет двухаллельный (трехгенотипный) переходящий полиморфизм, “стремящийся” к мономорфизму.
На рис. 3,а представлен случай, когда аллель А, обеспечивающий больший репродуктивный потенциал, является доминантным: rAа = rAA, на рис. 3,б – рецессивным: rAа = rаа и на рис. 3,в – неполное доминирование rаa < rAa < rAA. Как видно, постепенно закрепляются генотипы с все большим репродуктивным потенциалом, а динамика численности сначала стремится к более высокому по значению равновесию, а потом испытывает колебания, которые с ростом rAA становятся все более и более сложными. Скорости процессов с доминантными и рецессивными аллелями существенно различаются (рис. 3,а, б). В случае, когда аллель А, обеспечивающий больший репродуктивный потенциал, является рецессивным rAа = rаа, наблюдается резкая смена одного равновесия другим с некоторым запаздыванием (рис. 3,б). Если же наблюдается промежуточное доминирование, когда на всех этапах rаa < rAa < rAA, то происходит постепенное увеличение численности обоих возрастных классов с последующей стабилизацией, при этом скорость смены одного генотипа другим существенно выше, чем в случаях доминантного наследования. В целом следует отметить, что характер изменения генетического состава в зависимости от вида доминирования аллеля А сказывается на динамике численности возрастных классов, что обусловлено его влиянием на средний репродуктивный потенциал старшего возрастного класса с учетом выживаемости потомков.
В случае появления новых аллелей, обладающих свойством сверхдоминирования, т.е. повышенным потенциалом гетерозиготы (rAa > rAA и rAa > rаa), популяция всегда сохраняет полиморфизм и стремится к все большему среднему значению r, а численность сначала стремится к более высокому значению равновесия, а потом начинает колебаться (рис. 4).
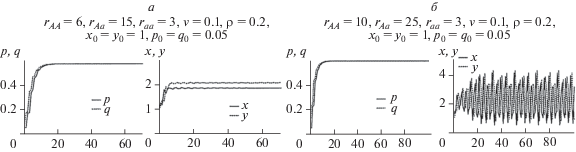
Теперь рассмотрим ситуацию с пониженным репродуктивным потенциалом гетерозиготы. Итак, пусть у нас есть почти мономорфная и почти равновесная популяция (raa = 3), и появляется новый аллель А с бóльшим rAA = 6, но с сильно пониженным репродуктивным потенциалом гетерозигот rAа = 2 (рис. 5,а). В этом случае, несмотря на большой репродуктивный потенциал генотипа AA, аллель А будет вытеснен, популяция окажется мономорфной (аа) и установятся стационарные значения численностей обоих возрастных классов (рис. 5,а). Дело в том, что при низких значениях репродуктивного потенциала гетерозиготы популяция оказывается в состоянии потенциальной бистабильности, когда существуют два устойчивых мономорфных состояния. Однако в силу того, что на начальном этапе развития генетическое разнообразие (текущие значения частот) оказалось в бассейне притяжения равновесия $\bar {q} = 0$, $\bar {p} = 0$, то даже большое значение rAA не способно привести к смещению частот и численностей в бассейн притяжения другого решения. Как результат изменение режима динамики численности не происходит и популяция устойчива и мономорфна по генотипу с низким репродуктивным потенциалом. Принципиально ничего не меняется даже в том случае, если появляется новый аллель с очень большим репродуктивным потенциалом гомозиготы АА (рис. 5,а, при n > 50). При малой начальной концентрации этого гена он неизбежно будет потерян, поскольку популяция по-прежнему находится в бассейне притяжения равновесия $\bar {q} = 0$, $\bar {p} = 0$.
Описанный эффект можно назвать “ловушкой бистабильности”. Этот эффект возникает только в случае, когда репродуктивный потенциал гетерозиготы меньше репродуктивного потенциала каждой из гомозигот, и заключается в том, что более перспективная форма не может естественным образом вытеснить явно более слабого по репродуктивным показателям генетического конкурента.
Для выхода из описанной ловушки необходимо внешнее воздействие на популяцию. Падение численности популяции и связанные с этим случайные процессы (известные как “прохождение через бутылочное горлышко”) могут привести к изменениям генетического состава и “перескоку” популяции из одного бассейна притяжения в другой. На рис. 5,б видно, что если параллельно с появлением аллеля, который обеспечивает бóльший репродуктивный потенциал гомозиготы АА, происходит катастрофическое уменьшение численности (х0 = у0 = 0.1) и связанное с этим случайное изменение генетической структуры, приводящее к росту начальной частоты гена А (q0 = p0 = 0.25), то популяция может попасть в бассейн притяжения нового устойчивого мономорфного равновесия АА: $\bar {q} = 1$, $\bar {p} = 1$ (рис. 5,б). При этом видно, что при rAA = 6 монотонный рост частоты гена А приводит к монотонному росту численности. Последующее достижение генетически мономорфного равновесия АА стабилизирует численность популяции. Появление нового гена, обеспечивающего еще бóльший репродуктивный потенциал (но не меняющего потенциал геторозиготы), не будет играть эволюционной роли до нового внешнего воздействия и нового прохождения “бутылочного горлышка”. Однако теперь достаточно существенно меньшего воздействия, чем требовалось первоначально. На рис. 5,б показано, что если при n = 50 происходит даже сравнительно небольшое случайное снижение численности, приводящее к весьма небольшому случайному росту частоты нового аллеля с rAA = 15, то этого оказывается достаточным для “переброски” популяции в бассейн притяжения мономорфного равновесия этого нового аллеля. Дальнейшая эволюция популяции сводится к переходному процессу (переходящему полиморфизму) к новому мономорфному состоянию. При этом частоты генов испытывают колебания, которые со временем затухают и приводят в итоге к установлению стабильной мономорфной генетической структуры и фиксации гена, обеспечивающего высокий репродуктивный потенциал гомозиготы. Параллельно с этим возникают выраженные нерегулярные колебания численностей возрастных классов популяции, в данном случае квазипериодические.
ЗАКЛЮЧЕНИЕ
В работе проведено аналитическое и численное исследование эволюционной модели естественного отбора в двухвозрастной экологически лимитированной популяции. Предполагается, что рождаемость задается функцией $A(x,y) = a{{e}^{{ - \alpha x - \beta y}}}$, где х и у – численности возрастных групп, а – значение репродуктивного потенциала, контролируемое одним диаллельным геном. Найдены генетически мономорфные и полиморфная стационарные точки, определены условия их существования. Для стационарных точек найдены условия их устойчивости. В соответствии с результатами анализа стационарных точек системы проведено численное исследование модели в различных параметрических областях. Проведена классификация областей различного динамического поведения численности и генетического состава популяции.
Далее выполнено численное исследование модели, которое показало, что появление (например, в результате мутаций) новых аллелей, обеспечивающих больший репродуктивный потенциал особей, приводит к естественному отбору этих аллелей и закономерному эволюционному росту среднего значения репродуктивного потенциала в популяции. Однако это увеличение среднего значения репродуктивного потенциала при плотностной регуляции рождаемости приводит к дестабилизации динамики численности возрастных групп. Сценарии изменений режимов динамики могут быть различны и зависят от параметров модели, но основной результат всегда одинаков: динамика становится все более сложной и, как правило, все более хаотической. Здесь мы наблюдаем один из основных парадоксов эволюционной экологии – медленный прогрессивный эволюционный рост приспособленности приводит в итоге к нарушению стабильности “быстрых” процессов динамики численности популяции.
Итоговый генетический состав популяции, а именно будет ли она устойчиво полиморфной во многом определяется взаимным расположением значений репродуктивных потенциалов гетерозигот и гомозигот. При повышенном репродуктивном потенциале гетерозигот модель естественно предсказывает устойчивый полиморфизм, при промежуточном доминировании – переходящий полиморфизм до мономорфизма или новой мутации. Но в любом случае прогрессивный рост репродуктивного потенциала приводит в итоге к возникновению флуктуаций численности.
Вместе с тем обнаружено, что в рассмотренной модели в случае пониженного репродуктивного потенциала гетерозигот в популяции возникает явление бистабильности. Бистабильность проявляется в том, что устойчивыми являются оба мономорфных состояния равновесия и начальные соотношения численностей возрастных классов и частот аллелей определяют тот генотип, который останется в популяции. В частности, показано, что возможен такой эффект как “ловушка бистабильности”, когда более перспективная форма не может естественным образом вытеснить явно более слабого по репродуктивным показателям генетического конкурента. Однако падение численности популяции, вызванное внешними причинами, и связанные с этим случайные процессы (известные как “прохождение через бутылочное горлышко”) могут привести к случайной флуктуации генетического состава и “перескоку” популяции в состояние, обеспечивающее транзит от одного мономорфного состояния к другому, адаптивно более выигрышному, но ведущему к дестабилизации динамики численности.
Работа выполнена в рамках государственных заданий Института автоматики и процессов управления ДВО РАН, Института комплексного анализа региональных проблем ДВО РАН, а также при частичной финансовой поддержке РФФИ (проект 18-04-00073 а) и Программы фундаментальных исследований РАН “Приоритетные научные исследования в интересах комплексного развития Дальневосточного отделения РАН” (проект 18-5-013).
Настоящая статья не содержит каких-либо исследований с использованием в качестве объекта животных.
Настоящая статья не содержит каких-либо исследований с участием в качестве объекта людей.
Авторы заявляют, что у них нет конфликта интересов.
Список литературы
Haldane J.B.S. A mathematical theory of natural and artificial selection. Part 1 // Trans. Cambr. Philos. Soc. 1924. V. 23. P. 19‒41. https://doi.org/10.1017/S0305004100015644
Fisher R.A. The Genetical Theory of Natural Selection. Oxford: Clarendon Press, 1930. 356 p.
Ратнер В.А. Математическая теория эволюции менделевских популяций // Проблемы эволюции. Т. 3. Новосибирск: Наука, Сиб. отд., 1973. С. 151‒213.
Свирежев Ю.М., Пасеков В.П. Основы математической генетики. М.: Наука, 1982. 512 с.
Birch L.C. Selection in Drosophila pseudoobscura in relation to crowding // Evolution. 1955. V. 9. № 4. P. 160–165. https://doi.org/10.2307/2405474
Charlesworth B. Selection in density-regulated populations // Ecology. 1971. V. 52. P. 469–474. https://doi.org/10.2307/1937629
Gottlieb L.D. Genetic stability in a peripheral isolate of Stephanomeria exigua spp. coronaria that fluctuates in population size // Genetics. 1974. V. 76. № 3. P. 551–556.
Graines M.S., McClenaghay L.R., Rose R.R. Temporal patterns of allozymic variation in fluctuating populations in Microtus ochrogaster // Evolution. 1978. V. 32. № 4. P.723–739. https://doi.org/10.2307/2407488
Фрисман Е.Я. Первичная генетическая дивергенция (теоретический анализ и моделирование). Владивосток: ДВНЦ АН СССР, 1986. 160 с.
Фрисман Е.Я. Изменение характера динамики численности популяции: механизмы перехода к хаосу // Вестн. ДВО РАН. 1995. № 4. С. 97–106.
Axenovich T.I., Zorkoltseva I.V., Akberdin I.R. et al. Inheritance of litter size at birth in farmed arctic foxes (Alopex lagopus, Canidae, Carnivora) // Heredity. 2007. V. 98. P. 99–105.
Hanski I. Metapopulation Ecology. N.Y.: Oxford Univ. Press, 1999. 328 p.
Евсиков В.И., Назарова Г.Г., Рогов В.Г. Популяционная экология водяной полевки (Aricola terrestris L.) в Западной Сибири. Сообщ. I. Репродуктивная способность самок, полиморфных по окраске шерстного покрова, на разных фазах динамики численности популяции // Сиб. экол. журн. 1999. Т. 1. С. 59–68.
Гречаный Г.В., Никитин А.Я., Корзун В.М. и др. Эколого-генетическая детерминация динамики численности популяций. Иркутский гос. ун-т, 2004. 302 с.
Артамонова B.С., Махров А.А. Неконтролируемые генетические процессы в искусственно поддерживаемых популяциях: доказательство ведущей роли отбора в эволюции // Генетика. 2006. Т. 42. № 3. С. 310–324.
Dieckmann U., Metz J.A.J. Surprising evolutionary predictions from enhanced ecological realism // Theor. Popul. Biol. 2006. V. 69. № 3. P. 263–281. https://doi.org/10.1016/j.tpb.2005.12.001
Traykov M., Trenchev I. Mathematical models in genetics // Russ. J. Genetics. 2016. V. 52. № 9. P. 985–992.
Шапиро А.П. К вопросу о циклах в возвратных последовательностях // Управление и информация. 1972. Вып. 3. С. 96–118.
May R.M. Biological population obeying difference equations: stable points, stable cycles, and chaos // J. Theor. Biol. 1975. V. 51. № 2. P. 511–524.
Leslie P.H. On the use of matrices in certain population mathematics // Biometrika. 1945. V. 33. № 3. P. 183–212. https://doi.org/10.2307/2332297
Leslie P.H. Some futher notes on the use of matrices in population mathematics // Biometrica. 1948. V. 35. № 3/4. P. 213–245. https://doi.org/10.2307/2332342
Lefkovitch L.P. The study of population growth in organisms grouped by stages // Biometrics. 1965. V. 21. № 1. P. 1–18. https://doi.org/10.2307/2528348
Caswell H. Matrix Population Models: Construction, Analysis, and Interpretation. 2nd edn. Sin. Ass. Inc., Sunderland, MA, 2001. 722 p.
Фрисман Е.Я., Кулаков М.П., Ревуцкая О.Л. и др. Основные направления и обзор современного состояния исследований динамики структурированных и взаимодействующих популяций // Компьютерные исследования и моделирование. 2019. Т. 11. № 1. С. 119–151. https://doi.org/10.20537/2076-7633-2019-11-1-119-151
Дажо Р. Основы экологии. М.: Прогресс, 1975. 416 с.
Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.: Наука, 1978. 352 с.
Фрисман Е.Я., Луппов С.П., Скокова И.Н., Тузинкевич А.В. Сложные режимы динамики численности популяции, представленной двумя возрастными классами // Математические исследования в популяционной экологии. Владивосток: ДВО АН СССР, 1988. С. 4–18.
Фрисман Е.Я., Скалецкая Е.И. Странные аттракторы в простейших моделях динамики численности биологических популяций // Обозр. прикл. и промышл. математики. 1994. Т. 1. № 6. С. 988–1008.
Фрисман Е.Я., Неверова Г.П., Ревуцкая О.Л., Кулаков М.П. Режимы динамики модели двухвозрастной популяции // Изв. вузов “Прикладная нелинейная динамика”. 2010. Т. 18. № 2. С. 111–130.
Frisman E.Ya., Neverova G.P., Revutskaya O.L. Complex dynamics of the population with a simple age structure // Ecol. Modelling. 2011. V. 222. P. 1943–1950. https://doi.org/10.1016/j.ecolmodel.2011.03.043
Фрисман Е.Я., Жданова О.Л. Эволюционный переход к сложным режимам динамики численности двухвозрастной популяции // Генетика. 2009. Т. 45. № 9. С. 1277–1286.
Чернявский Ф.Б., Лазуткин А.Н. Циклы леммингов и полевок на Севере. Магадан: ИБПС ДВО РАН, 2004. 150 с.
Кузнецов С.П. Динамический хаос. М.: Физматлит, 2001. 296 с.
Кузнецов А.П., Седова Ю.В. Бифуркации трехмерных и четырехмерных отображений: Универсальные свойства // Изв. вузов. “Прикладная нелинейная динамика”. 2012. Т. 20. № 5. С. 26–43.
Дополнительные материалы
- скачать ESM.doc
- Приложение 1. Вывод уравнений динамики.
Приложение 2. Об устойчивости стационарных точек