Геомагнетизм и аэрономия, 2020, T. 60, № 3, стр. 275-280
Структура областей высыпания электронов высокой энергии, инжектируемых точечным источником в геомагнитное поле, представленное первыми гармониками ряда Гаусса
Е. К. Колесников 1, *, Г. Н. Клюшников 2, **
1 Санкт-Петербургский государственный университет
г. Санкт-Петербург, Россия
2 Петербургский институт ядерной физики им. Б.П. Константинова
Национального исследовательского центра ''Курчатовский институт'' (ПИЯФ)
г. Гатчина, Россия
* E-mail: kolesnikov@spbu.ru
** E-mail: g.klyushnikov@spbu.ru
Поступила в редакцию 16.09.2019
После доработки 20.09.2019
Принята к публикации 23.01.2020
Аннотация
Построены области “высыпания” на Землю высокоэнергетических электронов, инжектируемых в ОКП из точечного источника на геостационарной орбите. Геомагнитное поле моделируется суперпозицией первых четырех сферических гармоник ряда Гаусса. Проведено сравнение указанных областей с областями высыпания, построенными ранее для дипольной модели геомагнитного поля. Рассмотрен вопрос о возможном влиянии на конфигурацию областей высыпания поля, создаваемого магнитосферными токами.
1. ВВЕДЕНИЕ
В последние годы в связи с проблемой радиационного загрязнения ближнего космоса заряженными частицами высоких энергий техногенного происхождения большое значение приобрели задачи динамики в геомагнитном поле заряженных частиц высокой энергии, инжектируемых в околоземное космическое пространство (ОКП) на конечном расстоянии от Земли. Источниками указанных частиц, могут являться, в частности, вторичные частицы высоких энергий, генерируемые в материале активных и пассивных орбитальных объектов частицами первичного космического излучения. Потенциальными внутренними источниками частиц высокой энергии являются и космические ускорители высоких энергий, концепции которых разрабатывались как в нашей стране [Панасюк, 1995], так и за рубежом [Varley et al., 1990].
В настоящей работе продолжены исследования конфигурации “областей высыпания” на поверхность Земли электронов высоких энергий, инжектируемых в околоземное космическое пространство (ОКП) точечным источником, начатые в работе [Колесников, 2002]. В отличие от работы [Колесников, 2002], в которой для описания движения электронов в ОКП использовалась простейшая дипольная модель геомагнитного поля, в настоящей работе при построении областей высыпания геомагнитное поле моделируется первыми четырьмя гармониками ряда Гаусса.
2. ПОСТАНОВКА ЗАДАЧИ. АЛГОРИТМ ЧИСЛЕННОГО РЕШЕНИЯ
Рассмотрим точечный источник высокоэнергетических электронов, положение которого задается геоцентрическим расстоянием $r,$ дополнением до широты $\theta $ и долготой $\varphi $ в сферической системе координат с началом в центре Земли и полярной осью, совпадающей с географической осью Земли. Как и в [Колесников, 2002], будем определять направления инжекции j, для которых соответствующая траектория электрона пересекает поверхность Земли, а также “области высыпания”, образованные точками пересечения указанных траекторий электронов с поверхностью Земли. Высотой плотных слоев атмосферы, где становится существенным взаимодействие высокоэнергетических электронов с ядрами атомов атмосферы, будем пренебрегать.
Для решения поставленной задачи нам потребуется уравнение динамики одиночного электрона в магнитном поле Земли. Запишем это уравнение в виде
(1)
$\frac{{{{d}^{2}}{\mathbf{r}}}}{{d{{t}^{2}}}} = - \frac{e}{{{{m}_{0}}\gamma c}}{\mathbf{v}} \times \nabla V,$Представим потенциал геомагнитного поля V в виде ряда Гаусса:
(2)
$\begin{gathered} V = {{R}_{E}}\sum\limits_{n = 1}^\infty {{{{\left( {\frac{{{{R}_{E}}}}{r}} \right)}}^{{n + 1}}}} \times \\ \times \,\,\sum\limits_{m = 0}^n {\left( {g_{n}^{m}\cos m\varphi + h_{n}^{m}\sin m\varphi } \right)} P_{n}^{m}\left( {\cos \theta } \right), \\ \end{gathered} $Таблица 1.
Значения коэффициентов $g_{n}^{m}$ и $h_{n}^{m}$
| n | m | $g_{n}^{m},{\text{ }}{{10}^{{ - 4}}}\,\,{\text{Гс}}$ | $h_{n}^{m},{\text{ }}{{10}^{{ - 4}}}\,\,{\text{Гс}}$ |
|---|---|---|---|
| 1 | 0 | –2944.2 | 0 |
| 1 | –150.1 | 479.7 | |
| 2 | 0 | –244.5 | 0 |
| 1 | 301.3 | –284.6 | |
| 2 | 167.7 | –64.2 | |
| 3 | 0 | 135.1 | 0 |
| 1 | –235.2 | –11.5 | |
| 2 | 122.6 | 24.5 | |
| 3 | 58.2 | –53.8 | |
| 4 | 0 | 90.8 | 0 |
| 1 | 81.4 | 28.3 | |
| 2 | 12.0 | –18.9 | |
| 3 | –33.5 | 18.1 | |
| 4 | 7.0 | –33.0 |
Многочлены Шмидта $P_{n}^{m}$ выражаются, в свою очередь, через присоединенные многочлены Лежандра ${{P}_{{n,m}}}$ (см. табл. 2):
Таблица 2.
Многочлены Лежандра ${{P}_{{nm}}}$ и их производные $P_{{nm}}^{'}$
| n | m | ${{P}_{{nm}}}\left( {\cos \theta } \right)$ | $P_{{nm}}^{{\text{'}}}\left( {\cos \theta } \right)$ |
|---|---|---|---|
| 1 | 0 | $\cos \theta $ | $ - {\kern 1pt} \sin \theta $ |
| 1 | 1 | $\sin \theta $ | $\cos \theta $ |
| 2 | 0 | $\frac{{3\cos 2\theta + 1}}{4}$ | $ - \frac{{3\sin 2\theta }}{2}$ |
| 2 | 1 | $\frac{{3\sin 2\theta }}{2}$ | $3\cos 2\theta $ |
| 2 | 2 | $\frac{{3\left( {1 - \cos 2\theta } \right)}}{2}$ | $3\sin 2\theta $ |
| 3 | 0 | $\frac{{5\cos 3\theta + 3\cos \theta }}{8}$ | $\frac{{ - 3\left( {5\sin 3\theta + \sin \theta } \right)}}{8}$ |
| 3 | 1 | $\frac{{3\left( {\sin \theta + 5\sin 3\theta } \right)}}{8}$ | $\frac{{3\left( {\cos \theta + 15\cos 3\theta } \right)}}{8}$ |
| 3 | 2 | $\frac{{15\left( {\cos \theta - \cos 3\theta } \right)}}{4}$ | $\frac{{15\left( {3\sin 3\theta - \sin \theta } \right)}}{4}$ |
| 3 | 3 | $\frac{{15\left( {3\sin \theta - \sin 3\theta } \right)}}{4}$ | $\frac{{45\left( {\cos \theta - \cos 3\theta } \right)}}{4}$ |
| 4 | 0 | $\frac{{35\cos 4\theta + 20\cos 2\theta + 9}}{{64}}$ | $\frac{{ - 5\left( {7\sin 4\theta + 2\sin 2\theta } \right)}}{{16}}$ |
| 4 | 1 | $\frac{{5\left( {2\sin 2\theta + 7\sin 4\theta } \right)}}{{16}}$ | $\frac{{5\left( {\cos 2\theta + 7\cos 4\theta } \right)}}{4}$ |
| 4 | 2 | $\frac{{15\left( {3 + 4\cos 2\theta - 7\cos 4\theta } \right)}}{{16}}$ | $\frac{{15\left( {7\sin 4\theta - 2\sin 2\theta } \right)}}{4}$ |
| 4 | 3 | $\frac{{105\left( {2\sin 2\theta - \sin 4\theta } \right)}}{8}$ | $\frac{{105\left( {\cos 2\theta - \cos 4\theta } \right)}}{2}$ |
| 4 | 4 | $\frac{{105\left( {3 - 4\cos 2\theta + \cos 4\theta } \right)}}{8}$ | $\frac{{105\left( {2\sin 2\theta - \sin 4\theta } \right)}}{2}$ |
Система (1) сводится к системе обыкновенных дифференциальных уравнений первого порядка
(4)
$\begin{gathered} {{B}_{r}} = - {{R}_{E}}{{\sum\limits_{n = 1}^\infty {\left( {\frac{{{{R}_{E}}}}{r}} \right)} }^{{n + 2}}} \times \\ \times \,\,\sum\limits_{m = 0}^n {\left( {g_{n}^{m}\cos m\varphi + h_{n}^{m}\sin m\varphi } \right)} P_{n}^{m}\left( {\cos \theta } \right), \\ {{B}_{\theta }} = - {{R}_{E}}{{\sum\limits_{n = 1}^\infty {\left( {\frac{{{{R}_{E}}}}{r}} \right)} }^{{n + 2}}} \times \\ \times \,\,\sum\limits_{m = 0}^n {\left( {g_{n}^{m}\cos m\varphi + h_{n}^{m}\sin m\varphi } \right)} \frac{{dP_{n}^{m}\left( {\cos \theta } \right)}}{{d\theta }}, \\ {{B}_{\varphi }} = {{R}_{E}}{{\sum\limits_{n = 1}^\infty {\left( {\frac{{{{R}_{E}}}}{r}} \right)} }^{{n + 2}}} \times \\ \times \,\,\sum\limits_{m = 0}^n {\left( {mg_{n}^{m}\sin m\varphi - mh_{n}^{m}\cos m\varphi } \right)} \frac{{P_{n}^{m}\left( {\cos \theta } \right)}}{{\sin \theta }}. \\ \end{gathered} $Систему (3) удобно представить в следующем удобном для численного интегрирования виде:
(5)
$\left\{ \begin{gathered} \frac{{dr}}{{dt}} = {{{v}}_{r}}, \hfill \\ \frac{{d\theta }}{{dt}} = \frac{{{{{v}}_{\theta }}}}{r}, \hfill \\ \frac{{d\varphi }}{{dt}} = \frac{{{{{v}}_{\varphi }}}}{{r\sin \theta }}, \hfill \\ \frac{{d{{{v}}_{r}}}}{{dt}} = \frac{{e{{\omega }_{r}}}}{{mc}} + \frac{{{v}_{\theta }^{2} + {v}_{\varphi }^{2}}}{r}, \hfill \\ \frac{{d{{{v}}_{\theta }}}}{{dt}} = \frac{{e{{\omega }_{\theta }}}}{{mc}} - \frac{{{{{v}}_{r}}{{{v}}_{\theta }}}}{r} + \frac{{{v}_{\varphi }^{2}{\text{ctg}}\theta }}{r}, \hfill \\ \frac{{d{{{v}}_{\varphi }}}}{{dt}} = \frac{{e{{\omega }_{\varphi }}}}{{mc}} - \frac{{{{{v}}_{r}}{{{v}}_{\varphi }}}}{r} + \frac{{{{{v}}_{\varphi }}{{{v}}_{\theta }}{\text{ctg}}\theta }}{r}, \hfill \\ \end{gathered} \right.$Положим ${{B}_{0}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {M \mathord{\left/ {\vphantom {M {R_{E}^{3}}}} \right. \kern-0em} {R_{E}^{3}}}$ (M = $\sqrt {{{{(g_{1}^{0})}}^{2}}{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} {{{(g_{1}^{1})}}^{2}}{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} {{{(h_{{{\kern 1pt} 1}}^{1})}}^{2}}} R_{E}^{3}{\kern 1pt} {\kern 1pt} - $ модуль магнитного момента Земли). Перейдем в (5) к безразмерным переменным
(6)
$\begin{gathered} {{b}_{r}} = \frac{{{{B}_{r}}}}{{{{B}_{0}}}},\,\,\,\,{{b}_{\theta }} = \frac{{{{B}_{\theta }}}}{{{{B}_{0}}}},\,\,\,\,{{b}_{\varphi }} = \frac{{{{B}_{\varphi }}}}{{{{B}_{0}}}},\,\,\,\,{{u}_{r}} = \frac{{{{{v}}_{r}}}}{c}, \\ {{u}_{\theta }} = \frac{{{{{v}}_{\theta }}}}{c},\,\,\,\,{{u}_{\varphi }} = \frac{{{{{v}}_{\varphi }}}}{c},\,\,\,\,\rho = \frac{r}{{{{R}_{E}}}},\,\,\,\,\tau = \frac{{ct}}{{{{R}_{E}}}}. \\ \end{gathered} $В переменных (6) система (5) принимает вид
(7)
$\left\{ \begin{gathered} \frac{{d\rho }}{{d\tau }} = {{u}_{r}}, \hfill \\ \frac{{d\theta }}{{d\tau }} = \frac{{{{u}_{\theta }}}}{\rho }, \hfill \\ \frac{{d\varphi }}{{d\tau }} = \frac{{{{u}_{\varphi }}}}{{\rho \sin \theta }}, \hfill \\ \frac{{d{{u}_{r}}}}{{d\tau }} = K{{\Omega }_{r}} + \frac{{u_{\theta }^{2} + u_{\varphi }^{2}}}{\rho }, \hfill \\ \frac{{d{{u}_{\theta }}}}{{d\tau }} = K{{\Omega }_{\theta }} - \frac{{{{u}_{r}}{{u}_{\theta }}}}{\rho } + \frac{{u_{\varphi }^{2}{\text{ctg}}\theta }}{\rho }, \hfill \\ \frac{{d{{u}_{\varphi }}}}{{d\tau }} = K{{\Omega }_{\varphi }} - \frac{{{{u}_{r}}{{u}_{\varphi }}}}{\rho } + \frac{{{{u}_{\varphi }}{{u}_{\theta }}{\text{ctg}}\theta }}{\rho }. \hfill \\ \end{gathered} \right.$Пусть электроны, инжектируемые в околоземное космическое пространство из точечного источника, имеют фиксированное значение кинетической энергии Ek. Направление инжекции j задается углом i с направлением местной вертикали и углом q между проекцией j на плоскость местного горизонта и местным азимутальным направлением. Выбор углов i и q осуществляется случайным образом в серии из 100 000 испытаний с равномерным законом распределения в заданных промежутках [imin, imax], [qmin, qmax]. Для каждого варианта выборки начальных значений углов i и q производится численное интегрирование уравнений движения (7) разностным методом Рунге-Кутты-Мерсона четвертого порядка с автоматическим выбором длины шага. Расчет траектории проводится до тех пор, пока не оказывается выполненным одно из следующих условий:
1) траектория электрона пересекает сферу радиусом RE в точке с географическими координатами θ и φ, генерируя на поверхности Земли соответствующую точку области высыпания;
2) полная длина расчетного отрезка траектории превышает установленное предельное значение ${{L}_{{\max }}} = 20{{R}_{E}};$ 3) электрон удаляется на геоцентрическое расстояние, превышающее критическое значение r * = 10RE, с достижением которого дальнейшее движение электрона сопровождается неограниченным монотонным ростом его радиальной координаты.
3. ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАСЧЕТОВ
С использованием описанного алгоритма были построены области высыпания на земную поверхность электронов с энергиями 15, 30 и 60 ГэВ в случае нахождения инжектора на геостационарной орбите в точке с нулевой географической широтой и географической долготой 21°. Расчеты проведены для случаев представления геомагнитного поля первой (дипольной) гармоникой и первыми четырьмя гармониками ряда Гаусса. Результаты расчетов представлены на рис. 1–3.
Рис. 1.
Области высыпания электронов с энергией 15 ГэВ: (а) ‒ вид областей для n = 4, (б) ‒ вид областей для n = 1.
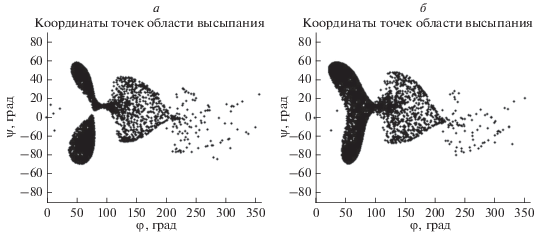
Рис. 2.
Области высыпания электронов с энергией 30 ГэВ: (а) ‒ вид областей для n = 4, (б) ‒ вид областей для n = 1.
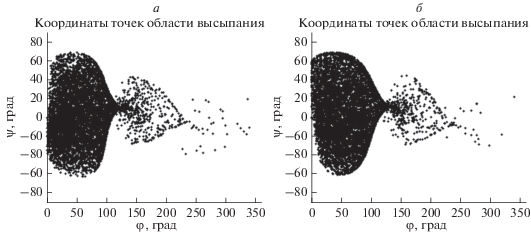
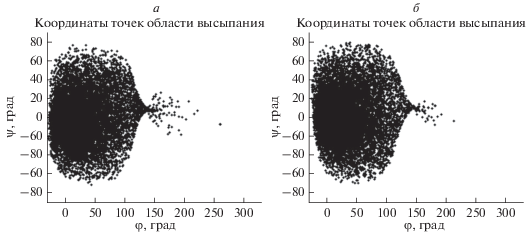
Рис. 3.
Области высыпания электронов с энергией 60 ГэВ: (а) ‒ вид областей для n = 4, (б) ‒ вид областей для n = 1.
На рисунке 1 показаны области высыпания электронов с энергией Ek = 15 ГэВ для n = 1 (рис. 1а) и n = 4 (рис. 1б). Как видно на рис. 1а, область высыпания для n = 1 представляет собой участок земной поверхности, локализованный в диапазоне широт $\lambda \in [ - 49^\circ ,59^\circ ]$ и долгот $\varphi \in [18^\circ ,360^\circ ]$. В случае аппроксимации геомагнитного поля первыми четырьмя гармониками ряда Гаусса (рис. 1б), области высыпания локализованы в диапазоне широт $\lambda \in [ - 53^\circ ,57^\circ ]$ и долгот $\varphi \in [33^\circ ,349^\circ ].$
На рисунке 2 представлены области высыпания для Ek = 30 ГэВ. Как видно на рис. 2а, при n = 1 для электронов рассматриваемой энергии область высыпания оказывается локализованной в диапазонах широт $[ - 61^\circ ,67^\circ ]$ и долгот $[ - 6^\circ ,350^\circ ].$ При аппроксимации геомагнитного поля первыми четырьмя сферическими гармониками область высыпания локализована в близких диапазонах широт $[ - 67^\circ ,79^\circ ]$ и долгот $[ - 6^\circ ,346^\circ ]$ (рис. 2б).
На рисунке 3 представлены области высыпания для Ek = 60 ГэВ. Для n = 1 (рис. 3а) область высыпания локализована в диапазонах широт $[ - 72^\circ ,79^\circ ]$ и долгот $[ - 20^\circ ,203^\circ ].$ В случае же n = 4 область высыпания находится на широтах $\lambda \in $ $ \in [ - 67^\circ ,76^\circ ],$ и долготах $\varphi \in $ $[ - 20^\circ ,232^\circ ].$
На рисунках 1–3 видно, что конфигурации областей высыпания электронов при n = 1 и n = 4 качественно являются весьма близкими. Основные отличия указанных областей состоят в следующем. С переходом от случая n = 1 к случаю n = 4 происходит незначительное изменение формы областейвысыпания, а также поворот на малый угол против часовой стрелки. При n = 4 в строении областей высыпания прослеживается четко выраженная асимметрия (отделение “верхней” компоненты при Ek = 15 ГэВ, увеличение “нижней” части области при Ek = 30 ГэВ).
Имея ввиду, что на высоте инжекции существенный вклад в геомагнитное поле может давать поле магнитосферных токов, для выяснения влияния этого поля на конфигурацию областей высыпания мы провели расчеты областей высыпания в поле, аппроксимируемом эмпирической моделью Цыганенко-87 для эпохи 1965 г. [Цыганенко и др., 1987], учитывающей вклад в геомагнитное поле поля внешних источников для различных значений глобального планетарного индекса геомагнитной активности Kp. Результаты расчетов показали, что даже при максимальном значении геомагнитного индекса Kp = 5 учет поля внешних источников в рассматриваемой задаче не оказывает существенного влияния на конфигурацию областей высыпания электронов с рассматриваемыми высокими значениями энергии 15–60 ГэВ. Физическое объяснение этому явлению состоит в том, что на больших расстояниях от Земли (порядка радиуса геостационарной орбиты), на которых существенным является вклад в геомагнитное поле поля внешних источников, полное геомагнитное поле является слабым и практически не оказывает влияния на траектории инжектируемых электронов высокой энергии. На этих расстояниях, как показывают данные численного моделирования, траектории являются практически прямолинейными. Заметное воздействие геомагнитного поля на траектории начинается с расстояний, значительно меньших радиуса геостационарной орбиты (порядка 2–3 радиусов Земли), на которых основной вклад в геомагнитное поле дает поле внутренних источников.
4. ЗАКЛЮЧЕНИЕ
Установлено, что конфигурации областей высыпания на поверхность Земли электронов высокой энергии, инжектируемых в геомагнитное поле из точечного источника, расположенного на геостационарной орбите, для дипольной модели геомагнитного поля и для геомагнитного поля, представленного суммой первых четырех сферических гармоник ряда Гаусса, являются близкими. Эффект высших гармоник проявляется в определенном изменении формы областейвысыпания, а также в усилении их асимметрии относительно экватора, связанном, в частности, с их поворотомнамалый угол против часовой стрелки. Кроме того, переход от дипольной моделигеомагнитного поля к его аппроксимации первыми гармониками ряда Гаусса приводит к определенному изменению диапазонов широт и долгот, в которых локализованы области высыпания.
С использованием эмпирической модели геомагнитного поля Цыганенко-87 [Цыганенко и др., 1987], учитывающей вклад в геомагнитное поле поля внешних источников, показано, что поле внешних источников в рассматриваемой задаче не оказывает существенного влияния на конфигурацию областей высыпания электронов с рассматриваемыми высокими значениями энергии 15–60 ГэВ.
Список литературы
Акасофу С.И., Чепмен С. Солнечно-земная физика. Ч. 1. М.: Мир, 382 с. 1974.
Колесников Е.К. Структура областей высыпания электронов высокой энергии, инжектируемых в дипольное магнитное поле Земли точечным источником // Геомагнетизм и аэрономия. Т. 42. № 5. С. 624–630. 2002.
Колесников Е.К. Влияние авроральных потоков электронов на динамику техногенных микрочастиц в полярной ионосфере // Геомагнетизм и аэрономия. Т. 41. № 2. С. 238–242. 2001.
Панасюк В.С. Ускорители заряженных частиц из “тролль-проекта” – возможные инструменты для космических исследований // Космич. исслед. Т. 33. № 5. С. 468–473. 1995.
Сергеев В.А., Цыганенко Н.А. Магнитосфера Земли. М.: Наука. 174 с. 1980.
Цыганенко Н.А., Усманов А.В., Папиташвили В.О. и др. Пакет программ для расчётов геомагнитного поля и связанных с ним координатных систем. М.: Межведомственный Геофизический Комитет при Президиуме АН СССР. 58 с. 1987.
Lemaitre G., Vallatra M.S. On Compton’s latitude effect of cosmic radiation // Phys. Rev. V. 43. № 2. P. 87‒91. 1933.
Stormer C. The Polar Aurora. London-New-York: Oxford University press. 437 p. 1955.
Vallatra M.S. On the allowed cone of cosmic radiation // Phys. Rev. V. 50. № 6. P. 493–504. 1936.
Varley R., Hohlfeld R.G., Sansri G., Lovelace G., Cercignani C. Particle accelerators in high earth orbit // Nuovo Cim. B. V. 105. № 1. P. 23–29. 1990.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия


