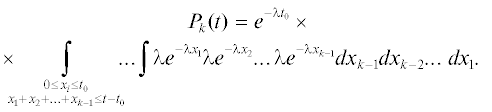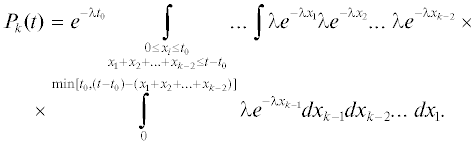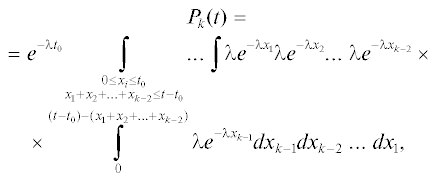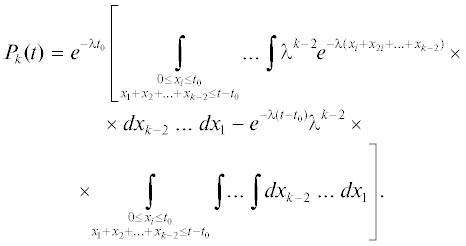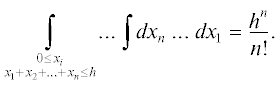Геоэкология. Инженерная геология, гидрогеология, геокриология, 2022, № 4, стр. 65-74
ПРИМЕНЕНИЕ ДИСТАНЦИОННЫХ МЕТОДОВ ПРИ ВЕРОЯТНОСТНОЙ ОЦЕНКЕ ПОРАЖЕНИЯ ЛИНЕЙНОГО СООРУЖЕНИЯ
А. С. Викторов 1, *, М. В. Архипова 1
1 Институт геоэкологии им. Е.М. Сергеева РАН
101000 Москва, Уланский пер., 13, стр. 2, Россия
* E-mail: vic_as@mail.ru
Поступила в редакцию 31.03.2022
После доработки 08.04.2022
Принята к публикации 08.04.2022
- EDN: FCRXKO
- DOI: 10.31857/S0869780922030080
Аннотация
Цель настоящего исследования – разработка метода использования материалов дистанционных съемок для оценки вероятности поражения линейного сооружения на примере боковой речной эрозии. В основу предлагаемого подхода вероятностной оценки поражения инженерного сооружения боковой эрозией положено то, что процесс боковой эрозии, изгибания и спрямления излучин является одновременно главным фактором формирования морфологической структуры ландшафта аллювиальных равнин. Основание решения – математическая модель морфологической структуры аллювиальных равнин. Проведена значительная проверка модели по материалам космических съемок участков долин, находящихся в различных физико-географических условиях. Общей закономерностью строения ландшафтного рисунка аллювиальных равнин в различных физико-географических условиях является экспоненциальное распределение стрелок пакетов и времени развития излучины, что подтверждается большим экспериментальным материалом. На основе модели морфологической структуры аллювиальных равнин получено в ограниченных условиях решение задачи количественной оценки вероятности поражения линейного сооружения речной эрозией; необходимые параметры могут быть оценены по материалам повторных космических съемок.
Многие исследования посвящены оценке вероятности поражения линейных сооружений опасными экзогенными процессами, в частности боковой эрозией рек [4, 5, 11, 12, 14]. Достаточно широкое применение нашло и использование материалов дистанционных съемок при изучении речной эрозии [9, 10]. В различных работах исследовалось воздействие различных факторов на исследуемый процесс и риск поражения сооружения [8, 9, 15–19], однако задача не может считаться до конца решенной. Особую сложность данной задаче придает цикличность процесса, связанная с изгибанием и последующим спрямлением излучин, которое затрудняет оценку риска поражения сооружения даже при известной скорости размыва.
Цель настоящего исследования – разработка метода использования материалов дистанционных съемок для оценки вероятности поражения линейного сооружения на примере боковой речной эрозии.
МЕТОДИКА
В основу предлагаемого подхода вероятностной оценки поражения инженерного сооружения боковой эрозией положено то, что процесс боковой эрозии, изгибания и спрямления излучин является одновременно главным фактором формирования морфологической структуры ландшафта аллювиальных равнин. В силу этого в основу решения поставленной задачи могут быть положены подходы, используемые в математической морфологии ландшафта [1, 3]. Их преимущество заключается в возможности использования материалов космических съемок вместо трудно получаемой контактной информации на основе стационарных наблюдений.
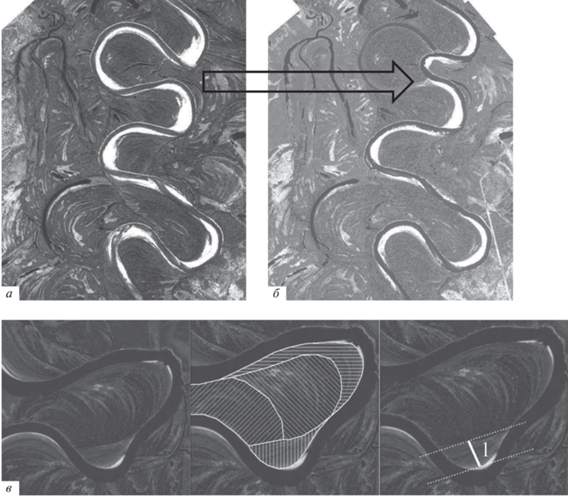
Рассматриваемые аллювиальные равнины представляют собой гривистую поверхность с сочетанием гидроморфных и ксероморфных растительных сообществ, пересеченную руслами меандрирующих рек (рис. 1).
Рис. 1.
Изображения аллювиальных равнин на материалах космической съемки: р. Хейгияха: а – 1964 г. (проект Corona); б – 2017 г., стрелкой показано место спрямления излучины; в – излучины р. Юган с пакетами разного возраста: старые – косая штриховка, современные формирующиеся – вертикальная и горизонтальная штриховка. 1 – стрелка в молодом пакете.
Главнейшими элементами аллювиальных равнин являются:
• старичные (древнестаричные) понижения,
• бывшие прирусловые повышения.
Понижения заняты озерами, болотами и другими гидроморфными комплексами и имеют дугообразную форму, наследуемую от бывших излучин. Повышения, также представляющие собой дуги, заняты более ксероморфными природно-территориальными комплексами в соответствии с зональными, климатическими и геолого-геоморфологическими условиями. Повышения и понижения, прилегая друг к другу, образуют согласованные по форме и ориентировке пакеты дуг (сегменты) (см. рис. 1в). Пакеты разных генераций без видимого порядка и с угловым несогласием прилегают друг к другу, порой “съедая” части друг друга, создавая “рисунок футбольного мяча”, и образуют, таким образом, ландшафтный рисунок аллювиальных равнин.
Один из основных процессов развития аллювиальных равнин – размыв излучин, сопровождающийся их изгибом и завершающийся спрямлением и формированием пакета (см. рис. 1а, б). Затем начинается новый цикл изгибания и формирования следующего пакета. Хордой излучины в рамках настоящей статьи мы называем отрезок, соединяющий соседние точки перегиба (с нулевой кривизной), которые являются границей излучины; стрелками пакета по аналогии со стрелкой дуги мы называем размер пакета в направлении, перпендикулярном хорде основания (см. рис. 1в). Интервал времени от спрямления до следующего спрямления назовем циклом развития излучины. Длительность цикла развития излучины регулируется случайными факторами: погодными условиями, локальными особенностями грунтов и др., и может рассматриваться как случайная величина.
Методика исследования включала:
• формирование модели развития процесса и получение результатов ее анализа;
• эмпирическую проверку модели, включающую:
− выбор ключевых участков,
− измерение необходимых параметров по материалам космической съемки;
• проверку результатов анализа модели на основе использования статистических критериев;
• аналитическое решение оценки вероятности поражения линейного сооружения боковой эрозией на основе сформированной модели.
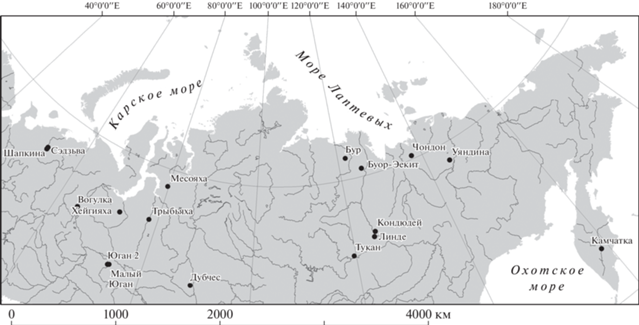
Выбор ключевых участков базировался на соответствии критериям заявленной модели – выбирались участки рек со свободным меандрированием, также учитывалась морфологическая однородность рисунка аллювиальных равнин на материалах космической съемки. Участки выбирались с захватом пойменной зоны, они были вытянуты вдоль течения реки, длина участков составляла от 10 до 30 км. Участки расположены в различных зонально-климатических и физико-географических условиях (рис. 2).
Для изучения были выбраны космические снимки:
− архивные снимки Corona (3–7 м/пикс, 1964–1980 гг.);
− современные высокодетальные снимки 0.5–0.7 м/пикс (Pleiades, Worldview 2, 2011–2018 гг.).
Все снимки были координатно привязаны в программном пакете ArcGIS.
РЕЗУЛЬТАТЫ
Первый этап решения поставленной задачи – формирование модели развития процесса и получение результатов ее анализа.
В более ранних исследованиях [7, 3, 6 ] была создана модель развития морфологической структуры аллювиальных равнин. Из допущений модели для решения поставленной задачи необходимы только следующие:
1) вероятность спрямления излучины за интервал времени $\Delta t$ зависит от величины этого интервала и не зависит от поведения других излучин, при этом вероятность более чем одного спрямления в малый интервал времени много меньше, чем вероятность одного спрямления:
где $\mu $ – параметр (среднее число спрямлений излучин за единицу времени);2) рост ширины пакета за счет формирования грив и межгривных понижений происходит с постоянной скоростью $\varepsilon $.
Предполагается также отсутствие существенного изменения климатических условий, что проявилось бы в непостоянстве значений параметров.
В итоге математического анализа допущений получены выражения, описывающие развитие морфологической структуры аллювиальных равнин в однородных условиях для случая постоянства климатических условий, в частности [7, 3, 6 ]:
• спрямление излучин может быть описано вероятностным процессом – процессом Пуассона, т.е. вероятность $k$ спрямлений за временной интервал $t$ равна:
• время развития излучины и текущее время развития излучины (от последнего спрямления до момента рассмотрения) подчиняются экспоненциальному распределению:
Этот результат, который является опорным для дальнейших построений, нуждается в более репрезентативной эмпирической проверке.
Поскольку скорость роста пакета является постоянной, и если время развития излучины подчиняется экспоненциальному распределению, то и длина стрелки пакета, которая пропорциональна времени развития излучины, должна подчиняться экспоненциальному распределению, но с отличным значением параметра:
Однако эмпирическую проверку модели нельзя напрямую основывать на этой закономерности, так как в процессе развития аллювиальной равнины пакеты частично или полностью стираются. Рассмотрение этой ситуации было проведено ранее при анализе возрастной дифференциации аллювиальных равнин [2]. Было показано, что, несмотря на стирание сформировавшихся (“старых”) пакетов, длины стрелок их сохранившихся фрагментов должны иметь то же самое экспоненциальное распределение. Это может быть одной из основ эмпирической проверки.
С другой стороны, проведенный с использованием теории специального класса случайных процессов (процессов восстановления) анализ позволил показать, что длины стрелок еще формирующихся (“молодых”) пакетов также должны подчиняться экспоненциальному распределению [2]. Это может быть использовано как вторая основа эмпирической проверки.
Таким образом, проверка состояла в оценке согласия эмпирических распределений длин стрелок пакетов и (отдельно) молодых пакетов экспоненциальному распределению:
где λ – параметр.Для проверки полученных выводов по модели аллювиальных равнин была предпринята обработка материалов дистанционных съемок на участках аллювиальных равнин ряда рек Западной и Восточной Сибири и Камчатки (см. рис. 2) (первичное эмпирическое обоснование содержится в более ранних работах [1–3, 7]).
Для каждого космического снимка в пределах однородного участка долины были выделены все возможные стрелки фрагментов пакетов количеством не менее 80 (выборка стрелок в “молодых” пакетах включала не менее 50 измерений), и определен их линейный размер. Стрелки в молодых развивающихся пакетах проводились как перпендикуляр между основанием пакета (хордой) и параллельной ей касательной к вершине пакета. Стрелки в фрагментах старых пакетов проводились как перпендикуляр между касательной в вершине дуги основания фрагмента и параллельной ей касательной к вершине дуги, ограничивающей фрагмент пакета с внешней стороны. В ряде случаев возникали трудности, связанные со стиранием боковой части фрагментов из-за смещения русла, однако в целом, несмотря на указанную неопределенность, в подавляющем большинстве случаев стрелки удавалось провести. Прилегающие фрагменты пакетов отделялись друг от друга на основе угловых несогласий.
Полученные выборки сравнивались с экспоненциальными распределениями со сдвигом. Использование экспоненциальных распределений со сдвигом связано с тем, что на снимках при анализе выделяются фрагменты пакетов, состоящих как минимум из двух грив и одного межгривного понижения, а из одной гривы не выделяются, это и определяет сдвиг. В выборках оценивался сдвиг как минимальное значение выборки, и осуществлялся переход к промежуточной выборке путем вычитания сдвига. Полученная выборка проверялась на согласие с экспоненциальным распределением на основе критерия Пирсона (хи-квадрат) с помощью программы Statistica.
Эмпирическая проверка для модели аллювиальных равнин дала следующие основные результаты.
Для 21 выборки из 22 (13 участков из 14) распределение стрелок всех пакетов отвечает экспоненциальному распределению со сдвигом (табл. 1, рис. 3), как это следует из модели.
Таблица 1.
Соответствие эмпирических распределений стрелок аллювиальных пакетов экспоненциальному распределению со сдвигом
| Номер | Местоположение | Год съемки | Объем выборки | Сдвиг, м | Параметр λ, 1/м | хи-квадрат | хи-квадрат (0.95) |
|---|---|---|---|---|---|---|---|
| 1 | Долина р. Шапкина (Коми) | 1976 | 84 | 32 | 0.002877 | 2.944 | 11.070 |
| 2 | Долина р. Шапкина (Коми) | 2017 | 84 | 37 | 0.003039 | 3.119 | 11.070 |
| 3 | Долина р. Вогулка (Западная Сибирь) | 2013 | 89 | 47 | 0.003824 | 23.231 | 15.507 |
| 4 | Долина р. Хейгияха (Западная Сибирь) | 1964 | 76 | 67 | 0.002967 | 6.217 | 11.070 |
| 5 | Долина р. Хейгияха (Западная Сибирь) | 2017 | 75 | 54 | 0.002873 | 4.682 | 11.070 |
| 6 | Долина р. Юган (Западная Сибирь) | 1970 | 83 | 59 | 0.004571 | 1.430 | 9.488 |
| 7 | Долина р. Юган (Западная Сибирь) | 2012 | 83 | 59 | 0.004607 | 1.917 | 9.488 |
| 8 | Долина р. Трыбьяха (Западная Сибирь) | 2013 | 73 | 22 | 0.005939 | 8.382 | 11.070 |
| 9 | Долина р. Мудуйяха (Западная Сибирь) | 2013 | 141 | 97 | 0.002052 | 9.496 | 11.070 |
| 10 | Долина р. Дубчек (Западная Сибирь) | 2017 | 86 | 79 | 0.002512 | 8.78 | 14.067 |
| 11 | Долина р. Бур (Средняя Сибирь) | 2018 | 86 | 57 | 0.002043 | 5.835 | 9.488 |
| 12 | Долина р. Буор-Эекит (Средняя Сибирь) | 1968 | 77 | 50 | 0.005536 | 2.656 | 7.815 |
| 13 | Долина р. Буор-Эекит (Средняя Сибирь) | 2018 | 79 | 44 | 0.005425 | 8.531 | 12.592 |
| 14 | Долина р. Тукан (Средняя Сибирь) | 2017 | 80 | 19 | 0.004828 | 6.787 | 14.067 |
| 15 | Долина р. Кондюдей (Средняя Сибирь) | 1980 | 89 | 17 | 0.004121 | 2.298 | 9.488 |
| 16 | Долина р. Кондюдей (Средняя Сибирь) | 2017 | 89 | 39 | 0.004421 | 0.852 | 9.488 |
| 17 | Долина р. Чондон (Восточная Сибирь) | 1965 | 109 | 18 | 0.004201 | 1.5688 | 11.070 |
| 18 | Долина р. Чондон (Восточная Сибирь) | 2018 | 111 | 18 | 0.004148 | 2.470 | 11.070 |
| 19 | Долина р. Уяндина (Восточная Сибирь) | 1975 | 101 | 56 | 0.001887 | 2.360 | 11.070 |
| 20 | Долина р. Уяндина (Восточная Сибирь) | 2018 | 104 | 100 | 0.002022 | 3.536 | 11.070 |
| 21 | Долина р. Камчатка (Камчатка) | 1975 | 88 | 55 | 0.003108 | 8.155 | 11.070 |
| 22 | Долина р. Камчатка (Камчатка) | 2017 | 116 | 36 | 0.003501 | 9.179 | 12.592 |
Рис. 3.
Графики эмпирического и теоретического распределения длин стрелок пакетов для: а – р. Шапкина (2017), б – р. Хейгияха (2017), в – р. Буор-Эекит (2018), г – р. Чондон (2018), д – р. Уяндина (2018), е – р. Камчатка (2017). Штриховыми линиями показаны теоретические распределения, сплошными – эмпирические распределения длин стрелок пакетов; серым цветом показаны распределения для всей совокупности стрелок, черным – распределения для молодых (формирующихся) стрелок.
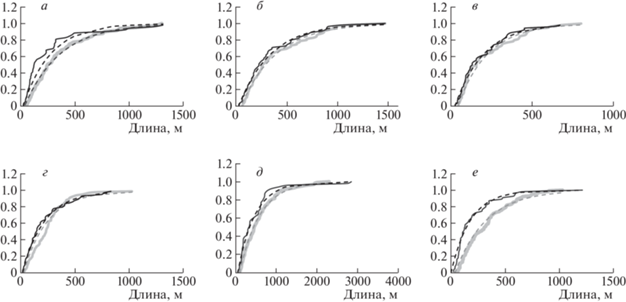
Для “молодых” стрелок проверка проводилась отдельно. Проведенный анализ показал, что для 22 выборок (11 участков) распределение стрелок для всех пакетов отвечает экспоненциальному распределению со сдвигом (табл. 2, рис. 3), как это и следует из модели.
Таблица 2.
Соответствие эмпирических распределений длин стрелок “молодых” аллювиальных пакетов экспоненциальному распределению со сдвигом
| Номер | Местоположение | Год съемки | Объем выборки | Сдвиг, м. | Параметр λ, 1/м | хи-квадрат | хи-квадрат (0.95) |
|---|---|---|---|---|---|---|---|
| 1 | Пойма р. Шапкина | 1976 | 53 | 25 | 0.004645 | 1.899 | 7.815 |
| 2 | Пойма р. Шапкина | 2017 | 53 | 25 | 0.003961 | 7.506 | 7.815 |
| 3 | Пойма р. Сэдьзва | 1976 | 53 | 21 | 0.006619 | 1.188 | 9.488 |
| 4 | Пойма р. Сэдьзва | 2017 | 50 | 21 | 0.006571 | 4.867 | 9.488 |
| 5 | Пойма р. Хейгияха | 2017 | 56 | 32 | 0.003123 | 5.760 | 9.488 |
| 6 | Пойма р. Хейгияха | 1964 | 56 | 31 | 0.003153 | 4.160 | 9.488 |
| 7 | Пойма р. Юган | 2012 | 52 | 27 | 0.004163 | 0.606 | 7.815 |
| 8 | Пойма р. Юган | 1970 | 51 | 43 | 0.004579 | 1.816 | 7.815 |
| 9 | Пойма р. Малый Юган | 2012 | 61 | 17 | 0.005762 | 0.856 | 5.99 |
| 10 | Пойма р. Малый Юган | 1970 | 57 | 13 | 0.00594 | 4.544 | 11.07 |
| 11 | Пойма р. Буор-Эекит | 2018 | 55 | 47 | 0.002343 | 5.430 | 5.99 |
| 12 | Пойма р. Буор-Эекит | 1968 | 60 | 34 | 0.004938 | 2.010 | 7.815 |
| 13 | Пойма р. Линде | 2017 | 55 | 27 | 0.003436 | 5.370 | 9.488 |
| 14 | Пойма р. Линде | 1980 | 55 | 32 | 0.003289 | 8.186 | 9.488 |
| 15 | Пойма р. Кондюдей | 2017 | 68 | 19 | 0.006955 | 1.110 | 9.488 |
| 16 | Пойма р. Кондюдей | 1980 | 68 | 19 | 0.007304 | 0.617 | 9.488 |
| 17 | Пойма р. Уяндина | 2018 | 53 | 74 | 0.002383 | 1.101 | 5.99 |
| 18 | Пойма р. Уяндина | 1975 | 56 | 54 | 0.002374 | 5.214 | 5.99 |
| 19 | Пойма р. Чондон | 1965 | 57 | 18 | 0.00568 | 1.793 | 9.488 |
| 20 | Пойма р. Чондон | 2018 | 52 | 18 | 0.004934 | 4.072 | 11.07 |
| 21 | Пойма р. Камчатка | 2017 | 58 | 22 | 0.005626 | 1.807 | 5.99 |
| 22 | Пойма р. Камчатка | 1975 | 57 | 35 | 0.003619 | 4.322 | 9.488 |
Таким образом, проведенная экспериментальная проверка показала, что сформированная модель (точнее ее фрагмент [6, 7]) согласуется с эмпирическими данными и может быть использована для решения поставленной задачи.
Обоснованная выше модель дает возможность оценить вероятность поражения линейного сооружения речной эрозией.
Расчет значений вероятности поражения линейного сооружения за заданное время функционирования должен учесть повторение циклов развития излучины и последующих спрямлений, а значит и повторение циклов размыва, и возможность поражения сооружения не в первый цикл, а в последующие.
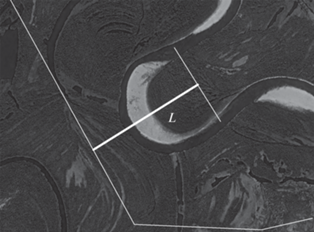
Рассмотрим излучину и линейное сооружение, отстоящее на расстояние L от хорды излучины (рис. 4). Примем упрощение, состоящее в том, что линейное сооружение параллельно хорде излучины.
Рис. 4.
Схема к выводу выражения вероятности поражения линейного сооружения боковой эрозией: тонкими белыми линиями показаны линейное сооружение и хорда излучины, L показана утолщенной белой линией; пояснение в тексте.
Найдем вероятность поражения линейного сооружения за время $t$, при этом ограничимся рассмотрением интервала времен $t \leqslant 2{{t}_{0}}$, где ${{t}_{0}}$ – время достижения излучиной линейного сооружения при непрерывном размыве (от момента спрямления):
Поражение линейного сооружения боковой эрозией на k-ом цикле отвечает выполнению условия:
где ${{\tau }_{k}}$ – длительность k-го цикла развития излучины.Поражение линейного сооружения боковой эрозией на k-ом цикле в первый раз (без поражения на предыдущих циклах) отвечает выполнению условий:
Учитывая независимость циклов и экспоненциальное распределение их длительности, вероятноcть поражения линейного сооружения боковой эрозией в первый раз на k-ом цикле можно записать выражением:
Интегрируя по последней переменной, получаем:
Так как $t \leqslant 2{{t}_{0}}$ и, следовательно, $(t - {{t}_{0}})$ – – $({{x}_{1}} + {{x}_{2}}... + {{x}_{{k - 2}}}) \leqslant {{t}_{0}}$, а значит
Для второго интеграла можно использовать формулу для объема n-мерного симплекса [13]:
В этом случае получаем:
Соответственно, суммируя по k, в итоге получаем общую вероятность поражения линейного сооружения боковой эрозией за время $t$ при $t \leqslant 2{{t}_{0}}$:
Частичная (k-я) сумма этого ряда может быть представлена как:
Учитывая, что первый член, как можно показать, стремится к нулю, а ряд можно представить, как сумму двух сходящихся рядов, после упрощения получаем выражение:
Необходимые для расчета вероятности поражения линейного сооружения параметры вытекают из выражений для расчета вероятности поражения линейного сооружения за заданное время функционирования и включают:
• природные параметры развития процессов:
− среднее число спрямлений излучины за единицу времени,
− скорость размыва борта излучины в точке максимального размыва;
• задаваемые параметры:
− отстояние линейного сооружения от хорды излучины,
− расчетное время функционирования.
Природные параметры развития процессов должны определяться на основе разработанной модели по материалам космических съемок. Среднее число спрямлений – величина обратная средней длительности цикла развития излучины, а средняя скорость размыва излучины в точке максимального размыва определяется по двум повторным снимкам как отношение величины размыва $\Delta r$ к интервалу между съемками ($\Delta t$):
Таким образом, использование разработанной модели морфологической структуры аллювиальных равнин позволяет получить метод количественной оценки вероятности поражения линейного сооружения боковой эрозией. От части принятых упрощений можно отказаться. Так, например, чуть видоизменив (1), нетрудно учесть ситуацию, когда линейное сооружение непараллельно хорде излучины.
ВЫВОДЫ
Выполненное исследование позволяет сделать следующие выводы.
• Дистанционные методы могут быть использованы при оценке вероятности поражения линейных сооружений.
• Перспективной основой решения задачи оценки вероятности поражения линейных сооружений является использование моделей математической морфологии ландшафта.
• Общей закономерностью строения ландшафтного рисунка аллювиальных равнин в различных физико-географических условиях является экспоненциальное распределение стрелок пакетов и времени развития излучины, что подтверждается большим экспериментальным материалом.
• На основе подходов математической морфологии ландшафта получено в ограниченных условиях решение задачи количественной оценки вероятности поражения линейного сооружения речной эрозией; необходимые параметры могут быть оценены по материалам повторных космических съемок.
Статья подготовлена в рамках выполнения государственного задания ИГЭ РАН по теме НИР № 122022400105-9 “Прогноз, моделирование и мониторинг эндогенных и экзогенных геологических процессов для снижения уровня их негативных последствий”.
Список литературы
Викторов А.С. Математическая морфология ландшафта. М.: Тратек, 1998. 180 с.
Викторов А.С. Модель возрастной дифференциации аллювиальных равнин // Геоэкология. 2007. № 4. С. 302–309.
Викторов А.С. Основные проблемы математической морфологии ландшафта. М.: Наука, 2006. 252 с.
Викторов А.С., Архипова М.В., Капралова В.Н., Орлов Т.В. Математическая модель риска поражения инженерных сооружений инициированными термокарстовыми процессами // Геоэкология. 2020. № 3. С. 82–90. https://doi.org/10.31857/S086978092003010
Викторов А.С., Березин П.В., Капралова В.Н. Разработка программного пакета оценки природных рисков на основе материалов повторных дистанционных съемок // Исследование Земли из космоса. 2017. № 5. С. 57–65. https://doi.org/10.7868/S0205961417050062
Викторов А.С., Капралова В.Н., Орлов Т.В., Трапезникова О.Н. и др. Математическая морфология ландшафтов криолитозоны. М.: РУДН, 2016. 232 с.
Викторов А.С., Трапезникова О.Н. Математическая модель морфологической структуры аллювиальных равнин как одна из основ дешифрирования материалов космических съемок // Исследование Земли из космоса. 1997. № 2. С. 44.
Ларионов Г.А., Литвин Л.Ф., Краснов С.Ф., Кирюхина З.П., Добровольская Н.Г. Экспериментальные исследования размыва береговых обрывов и откосов // Геоморфология. 2016. № 2. С. 51–58. https://doi.org/10.15356/0435-4281-2016-2-51-58
Падалко Ю.А., Чибилев А.А. Проблемы развития русловых процессов в бассейне р. Урал // ДАН. 2017. Т. 475. № 6. С. 702–705. https://doi.org/10.7868/S0869565217240215
Панин А., Сидорчук А., Чернов А. Основные этапы формирования пойм равнинных рек Северной Евразии // Геоморфология. 2011. № 3. С. 20–31.
Скапинцев А.Е., Потапов А.Д, Лаврусевич А.А. Инженерная защита трубопроводов от эрозионных процессов // Вестник МГСУ. 2013. № 7. С. 140–151.
Строкова Л.А., Ермолаева А.В. Природные особенности строительства магистрального газопровода “Сила Сибири” на участке Чаяндинское нефтегазоконденсатное месторождение – Ленск // Известия Томского политехнического университета. Инжиниринг георесурсов. 2015. Т. 326. № 4. С. 41–55.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 3. М.: Физматлит, 2003. 662 с.
Чигир В.Г., Власов. С.В., Горбатов В.А., Раух М.В. и др. Использование материалов дистанционных съемок для повышения надежности газопроводов в криолитозоне // Газовая промышленность. 2014. № 7 (709). С. 48–55.
Экология эрозионно-русловых систем России / Р.С. Чалов (ред.) М.: Географический ф-т МГУ, 2002. 163 с.
Roslan Zainal Abidin, Mohd Sofiyan Sulaiman, Naimah Yusoff. Erosion risk assessment: A case study of the Langat River bank in Malaysia // International Soil and Water Conservation Research. 2017. V. 5. Is. 1. P. 26–35. https://doi.org/10.1016/j.iswcr.2017.01.002
Joung R.W. The patterns of some meandering valleys in New South Wales // Austral. Geogr. 1970. V. 11. № 3. P. 269–277.
Lotsari E., Hackney C., Salmela J., Kasvi E., et al. Sub-arctic river bank dynamics and driving processes during the open-channel flow period // Earth Surface Processes and Landforms. 2019. https://doi.org/10.1002/esp.4796
Xiaorong Li, James R. Cooper, Andrew J. Plater. Quantifying erosion hazards and economic damage to critical infrastructure in river catchments: Impact of a warming climate // Climate Risk Management. V. 32. 2021. https://doi.org/10.1016/j.crm.2021.100287
Дополнительные материалы отсутствуют.
Инструменты
Геоэкология. Инженерная геология, гидрогеология, геокриология