Геохимия, 2023, T. 68, № 1, стр. 27-47
Влияние сульфидной серы на кристаллизацию магм нормальной щелочности (пролегомены)
Г. С. Николаев *
Институт геохимии и аналитической химии им. В.И. Вернадского РАН
119991 Москва, ул. Косыгина, 19, Россия
* E-mail: gsnikolaev@rambler.ru
Поступила в редакцию 17.02.2022
После доработки 15.07.2022
Принята к публикации 02.08.2022
- EDN: IANEAM
- DOI: 10.31857/S0016752523010041
Аннотация
Рассмотрено влияние сульфидной серы на кристаллизационную дифференциацию ультраосновных-основных-средних магматических систем с целью оценить его масштабы и направленность при кристаллизации породообразующих фаз. В рамках исследования проведен теоретический анализ влияния серы на активности компонентов силикатного расплава согласно принципу кислотно-оснóвного взаимодействия Коржинского. Для проверки теоретических построений был проведен систематический поиск опубликованных экспериментальных данных допускающих прямое сопоставление серонасыщенных и свободных от серы опытов. Несмотря на очень ограниченное количество таких экспериментов, все они хорошо укладываются в теоретически предсказанные тренды. Установлено, что добавление в систему серы умеренно снижает температуру ликвидуса породообразующих минералов в пределах 20–30°С, и значимо влияет на их состав. В случае хромшпинелида происходит его обогащение хромом на 10–12 мол. % и комплементарное обеднение алюминием. Состав плагиоклаза обогащается анортитовой компонентой: 3 мол. % в дацитах, 8 мол. % в андезитах, в базальтах этот эффект установить не удалось, но можно ожидать его усиления. Оливин и ортопироксен претерпевают незначительное увеличение магнезиальности, но в пользу ортопироксена существенно сокращается поле их совместного сосуществования, что неизбежно должно повлечь изменение их котектических и перитектических пропорций. Для ряда природных объектов из публикаций почерпнуты наблюдения, которые можно интерпретировать как результат проявления влияния серы. Полученные результаты приводят к выводу, что влияние серы на кристаллизацию силикатных магм значимо. А это, как минимум, требует большой осторожности при использовании для серосодержащих систем петрологических зависимостей, калиброванных на свободных от серы экспериментах.
ВВЕДЕНИЕ
Накопление экспериментальных данных по серосодержащим природным магматическим системам привело к разработке модельных зависимостей (Baker, Moretti, 2011; Коптев–Дворников и др., 2012; Ariskin et al., 2013), описывающих термо-композиционные параметры насыщения расплавов сульфидной фазой (SCSS), что в свою очередь, дало возможность моделировать ликвацию сульфидного расплава. Интеграция такой зависимости в программный комплекс для расчета кристаллизации магм COMAGMAT (Ariskin et al., 2018) открыла новое направление в магматической петрологии – численное моделирование эволюции серосодержащих систем и связанных с ними процессов рудогенеза.
Однако, вне рассмотрения оказалась проблема влияния серы на кристаллизацию силикатных систем. Характерно, что ни один из геотермометров минерал-расплав, используемых для описания ликвидусов породообразующих силикатных и оксидных фаз, в ведущих петрологических моделях для расчета кристаллизации магм COMAGMAT, MELTS (Ghiorso, Sack, 1995), PETROLOG (Danyushevsky, Plechov, 2011) не использует концентрацию серы в расплаве в качестве предиктора. Это делает подобные геотермометры нечувствительными к содержанию серы в системе. Двухвалентное железо – единственный макроэлемент состава расплава, концентрация которого изменяется в результате ликвации сульфидной фазы и входит в качестве параметра в геотермометры породообразующих минералов. В силу низкой растворимости сульфидов в силикатных расплавах, их фракционирование сопровождается крайне незначительным понижением содержания железа в остаточном расплаве, что оказывает пренебрежимое влияние на модельные параметры ликвидуса кристаллизующихся фаз. Напротив, теоретический анализ, экспериментальные данные и природные наблюдения дают основания предполагать существенное влияние серы на кристаллизацию силикатных систем.
Целью данной работы является определение масштаба влияния серы на кристаллизацию породобразующих фаз, что, возможно, в будущем послужит стимулом для перекалибровки геотермометров, с включением в них в качестве независимого параметра содержание серы в расплаве. В магматических расплавах сера может находиться в формах разной степени окисления (S2–, S4+, S6+), причем их пропорции зависят от окислительного потенциала системы (Jugo et al., 2005). В качестве первого приближения, настоящее исследование ограничено рассмотрением влияния только сульфидной формы, пренебрегая неизбежным влиянием сульфатной составляющей, которое должно нарастать с ростом ее доли в общем балансе серы в системе.
В начале статьи рассмотрено теоретическое обоснование влияния сульфидной серы на активности компонентов силикатного расплава, которые в свою очередь влияют на параметры ликвидуса кристаллизующихся фаз. Затем приведены экспериментальные свидетельства такого влияния, которые удалось обнаружить в литературе. В заключении представлены найденные в публикациях природные наблюдения, которые можно интерпретировать как проявления влияния серы.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ВЛИЯНИЯ СЕРЫ С ПОЗИЦИЙ ПРИНЦИПА КИСЛОТНО-ОСНОВНОГО ВЗАИМОДЕЙСТВИЯ КОРЖИНСКОГО
Взаимное влияние термодинамических компонентов магмы при ее кристаллизации будет проявляться в их межфазовом распределении, которое, прежде всего, будет зависеть от их активности в расплаве.
Множество моделей силикатного расплава, используемых для оценки кислотно-оснóвного взаимодействия его компонентов, можно разделить на четыре группы в зависимости от представлений о его структурно-химическом строении: молекулярно-оксидную, ионно-молекулярную, ионную и полимерную.
(i) Первая группа моделей описывает расплав с помощью электронейтральных компонентов – молекул оксидов и их соединений. Для получения характеристик расплава, каждому из оксидов приписываются эмпирические коэффициенты, характеризующие его вклад в суммарную основность (кислотность).
(ii) Ионно-молекулярные модели исследуют реакции диссоциации компонентов-оксидов. В качестве меры кислотно-оснóвных свойств расплава может быть использована активность О2–, так как кислород является общей составляющей всех компонентов.
(iii) В основании группы ионных моделей лежит предположение о том, что расплав состоит только из ионов, в нем сохраняется ближний порядок, т.е. вокруг отрицательных ионов ближайшими соседями являются положительные ионы и наоборот, а состав образующихся их сочетаний зависит от энергии взаимодействия. Поскольку силикатные расплавы в большинстве случаев обладают знакопеременными отклонениями от идеальности, калибровка моделей связана с получением полуэмпирических формул для определения активностей.
(iv) В группу полимерных концепций объединены наиболее сложные и максимально приближенные к реальности модели. В настоящее время установлено, что силикатные расплавы представляют ансамбли полимерных преимущественно кремне-кислородных макромолекул-анионов различных размеров и сложности. Они находятся в состоянии динамического равновесия, зависящего от природы сосуществующих катионов. Существующие на сегодня модели сложны и реализованы в большинстве случаев для бинарных систем. При переходе к тройным, четверным и тем более сложным системам алгоритмы расчета становятся чрезмерно трудоемкими даже для современных ЭВМ.
В предлежащем исследовании для теоретического анализа используется принцип кислотно-оснóвного взаимодействия Д.С. Коржинского, который следует отнести к группе ионно-молекулярных теорий взаимодействия. Благодаря методическим разработкам А.А. Маракушева (Маракушев, 1979), ранее являвшийся качественным этот метод теоретического анализа получил возможность численных оценок. Его приблизительно-оценочный характер вполне компенсируется простотой интерпретации и реалистичностью прогноза.
С гносеологической точки зрения принцип кислотно-оснóвного взаимодействия Д.С. Коржинского (Коржинский, 1959) является термодинамической формализацией и адаптацией к преимущественно алюмо-кремне-кислородным растворам природных систем обобщенной теории кислот и оснований М.И. Усановича (Усанович, 1939, 1970). Она объединила в качестве частных случаев теории Й.Н. Брёнстеда, Г.Н. Льюиса и сольвосистем. По Усановичу, “кислота – это частица, которая может отщеплять катионы, включая протон, или присоединять анионы, включая электрон. Основание – частица, которая может присоединять протон и другие катионы или отдавать электрон и другие анионы” (Usanovic, 1964; Усанович, 1970). Важно, что эта теория распространила представления о кислотно-оснóвном взаимодействии на окислительно-восстановительные реакции. Интересно, что к выводу об отсутствии термодинамических оснований для выделения окислительно-восстановительных реакций в отдельную группу пришел также В.П. Древинг: “При всякой химической реакции имеет место перегруппировка электронов” (Древинг, Калашников, 1964).
Принцип кислотно-оснóвного взаимодействия Коржинского утверждает, что при повышении кислотности системы валовые коэффициенты активности оснóвных компонентов понижаются, а кислотных – повышаются в соответствии со степенью их диссоциации. При этом эти изменения будут тем больше, чем более кислотным или оснóвным является компонент. Для магматических систем этот принцип был формализован в виде двух уравнений:
${{\partial \ln {{\gamma }_{{{\text{MeO}}}}}} \mathord{\left/ {\vphantom {{\partial \ln {{\gamma }_{{{\text{MeO}}}}}} {\partial \ln {{a}_{{{{{\text{O}}}^{{2 - }}}}}}}}} \right. \kern-0em} {\partial \ln {{a}_{{{{{\text{O}}}^{{2 - }}}}}}}} = \alpha ,\,\,\,\,{{\partial \ln {{\gamma }_{{{\text{Si}}{{{\text{O}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{\partial \ln {{\gamma }_{{{\text{Si}}{{{\text{O}}}_{{\text{2}}}}}}}} {\partial \ln {{a}_{{{{{\text{O}}}^{{2 - }}}}}}}}} \right. \kern-0em} {\partial \ln {{a}_{{{{{\text{O}}}^{{2 - }}}}}}}} = - \beta .$
Первое записано для оснóвного оксида с обобщенной формулой MeO, диссоциирующего в соответствии с реакцией ${\text{MeO}} = {\text{M}}{{{\text{e}}}^{{2 + }}} + {{{\text{O}}}^{{2 - }}}$ со степенью диссоциации α на кислотный катион и оснóвный анион кислорода. Второе уравнение соответствует реакции ассоциации со степенью диссоциации –β: ${\text{Si}}{{{\text{O}}}_{2}} + {{{\text{O}}}^{{2 - }}} = {\text{SiO}}_{3}^{{2 - }},$ в которой кислотный оксид (например, SiO2) и оснóвный анион кислорода образуют основание. В приведенных формулах γ – валовые коэффициенты активности соответствующих компонентов и ${{a}_{{{{{\text{O}}}^{{2 - }}}}}}$ – активность аниона кислорода, которая характеризует основность силикатного расплава. Эти уравнения могут быть выведены, используя закон действующих масс для указанных реакций диссоциации/ассоциации (Коржинский, 1959), или путем перекрестного дифференцирования выражения термодинамического потенциала системы с вполне подвижными компонентами, которая имеет химический потенциал аниона кислорода в качестве фактора равновесия (Коржинский, 1965а).
Оценка компонентов по параметру кислотность–основность
Для оценки кислотно-оснóвных свойств химических элементов в магмах и определения их места в ряду кислотности–щелочности Д.С. Коржинским использовался потенциал ионизации атомов (Коржинский, 1965б). А.А. Маракушев, логично предполагая, что во всех природных системах в той или иной степени присутствует вода, распространил формалистику описания кислотно-оснóвного взаимодействия в водных растворах на магматические системы. Он предложил в качестве унифицированной шкалы использовать сродство к протону (протонный эквивалент), т.е. свободную энергию реакции гидратации компонента $\Delta G_{Т}^{^\circ }$ в пересчете на один протон (Маракушев, 1976а).
При оценке основности оксидов общий вид этих реакций может быть представлен выражением:
${\raise0.7ex\hbox{$n$} \!\mathord{\left/ {\vphantom {n 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$mMe(2m/n)+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2O = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$mMenOm + H+.
В основе характеристики основности бескислородных соединений лежит реакция типа:
${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2S + OH– = H2O + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$S2–.
Для расчетов привлекались стандартные термодинамические справочные данные (Наумов и др., 1971). Отсутствующие данные по величинам свободной энергии образования высокозарядных простых катионов в водных растворах (Si4+, Ti4+, P5+) были получены путем экстраполяции данных по гидратным ионам ${\text{M(OH}})_{m}^{{n \pm }}$ (Маракушев, 1976а).
Для линейной экстраполяции величины $\Delta G_{Т}^{^\circ }$ в область высоких температур использовалось уравнение (Маракушев, 1978):
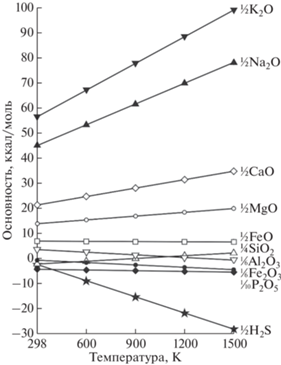
Результаты расчетов, приведенные в табл. 1 и на рис. 1, позволяют выстроить компоненты расплава в ряд по мере увеличения оснóвных свойств при температуре 1200°С: H2S → P2O5 → Fe2O3 → → Al2O3 → SiO2 → TiO2 → Cr2O3 → FeO → MgO → → MnO → CaO → Na2O → K2O. Полученные величины образуют единую шкалу кислотности-основности для заданной температуры, в которой за ноль принята $\Delta G_{T}^{^\circ }$ формальной реакции гидратации протона (Маракушев, 1976б):
Таблица 1.
Свободные энергии $\left( {\Delta G_{T}^{^\circ }} \right)$ и энтальпии $\left( {\Delta H_{{298}}^{^\circ }} \right)$ реакций гидратации, характеризующие кислотно-оснóвные свойства петрогенных компонентов
| Реакция | $\Delta H_{{298}}^{^\circ }$, ккал/моль | $\Delta G_{T}^{^\circ }$, ккал/моль | |
|---|---|---|---|
| 298 K | 1500 K | ||
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Si4+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$SiO2 + H+ | –3.360 | –2.277 | 2.1 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Ti4+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$TiO2 + H+ | –3.192 | –2.097 | 2.3 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}$Al3+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Al2O3 + H+ | 4.365 | 3.325 | –0.9 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$Fe2+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$FeO + H+ | 6.798 | 6.697 | 6.3 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}$Fe3+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Fe2O3 + H+ | 0.058 | –0.881 | –4.7 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$Mn2+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$MnO + H+ | 9.183 | 11.558 | 21.1 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$Mg2+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$MgO + H+ | 12.178 | 13.679 | 19.7 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$Ca2+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$CaO + H+ | 17.853 | 21.192 | 34.7 |
| Na+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$Na2O + H+ | 36.667 | 44.909 | 78.1 |
| K+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$K2O + H+ | 45.801 | 56.388 | 99.1 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 5}}\right.\kern-0em} \!\lower0.7ex\hbox{$5$}}$P5+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {10}}}\right.\kern-0em} \!\lower0.7ex\hbox{${10}$}}$P2O5 + H+ | –4.260 | –4.537 | –5.7 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}$Cr3+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Cr2O3 + H+ | 0.315 | 1.364 | 5.6 |
| ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Sgas + OH– = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$S2– + H2Ogas | 3.589 | –2.780 | –28.5 |
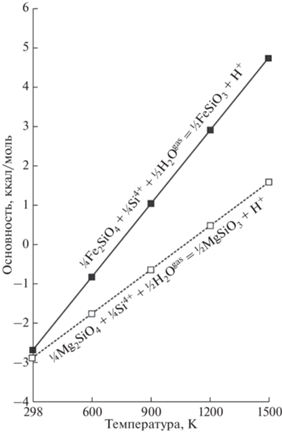
Рис. 1.
Вариации показателя сродства к протону петрогенных компонентов в зависимости от температуры. См. Примечания к табл. 1.
H+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2O = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2O + H+.
Таким образом, сера (H2S) является наиболее кислотным компонентом и ее вклад в эффекты, связанные с кислотно-оснóвным взаимодействием, должен быть максимальным.
Выражение, демонстрирующее влияние сульфидной серы на показатель основности расплава проще всего можно вывести из уравнения смещенного равновесия Коржинского (Коржинский, 1973):
Его анализ показывает, что при постоянном количестве анионов кислорода, увеличение в системе количества сульфидной серы, вызовет увеличение ee активности, т.к. ${{a}_{{{{{\text{S}}}^{{2 - }}}}}} = f\left( {T,P,{{n}_{{{{{\text{S}}}^{{2 - }}}}}}} \right).$ Это, в свою очередь, повлечет понижение активности аниона кислорода, которое отразится на изменении активностей инертных компонентов.
Для оценки основности миналов породообразующих минералов рассчитывались их реакции гидратации, которые получались путем сложения в необходимой пропорции реакций гидратации составляющих ионов, например, реакция для форстерита:
Расчеты для других миналов проводились аналогично, и их результаты приведены в табл. 2 и рис. 2. Размах вариаций показателей кислотности-основности у миналов на порядок ниже, чем у породообразующих оксидов. Это наглядное проявление эффекта кислотно-оснóвного взаимодействия оксидов в процессе образования более сложных соединений, который тем значительнее, чем больше различие окислов по основности.
Таблица 2.
Свободные энергии $\left( {\Delta G_{T}^{^\circ }} \right)$ и энтальпии $\left( {\Delta H_{{298}}^{^\circ }} \right)$ реакций гидратации миналов, и перитектических реакций относительно протонного эквивалента, отражающие их степень основности
| Минал | Реакция | $\Delta H_{{298}}^{^\circ }$, ккал/моль | $\Delta G_{T}^{^\circ }$, ккал/моль | |
|---|---|---|---|---|
| 298 K | 1500 K | |||
| Fo | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Mg2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Si4+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Mg2SiO4 + H+ | 2.740 | 4.153 | 9.9 |
| Fa | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Fe2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Fe2SiO4 + H+ | 1.362 | 2.598 | 7.6 |
| Lb | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Ni2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Ni2SiO4 + H+ | 0.463 | 1.446 | 5.4 |
| Lr | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Ca2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Ca2SiO4 + H+ | 3.539 | 5.811 | 15.0 |
| En | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Mg2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$MgSiO3 + H+ | 0.371 | 1.599 | 6.5 |
| Fs | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Fe2+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$FeSiO3 + H+ | –0.862 | 0.170 | 4.3 |
| Wo | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Ca2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$CaSiO3 + H+ | 0.178 | 2.002 | 9.4 |
| Di | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}$Ca2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}$Mg2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}$CaMgSi2O6 + H+ | –0.277 | 1.290 | 7.6 |
| Hd | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}$Ca2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}$Fe2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}$CaFeSi2O6 + H+ | –0.460 | 0.866 | 6.2 |
| An | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$Ca2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Al3++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$CaAl2Si2O8 + H+ | 0.869 | 1.324 | 3.2 |
| Ab | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$Na+ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$Al3++ ${\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$NaAlSi3O8 + H+ | –1.529 | –0.490 | 3.7 |
| Or | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$K+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$Al3++ ${\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}$KAlSi3O8 + H+ | –1.803 | –0.703 | 3.7 |
| Sp | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Mg2+ + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Al3++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$MgAl2O4 + H+ | 5.281 | 4.883 | 3.3 |
| Hc | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Fe2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Al3++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$FeAl2O4 + H+ | 4.407 | 3.916 | 1.9 |
| Ch | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Fe2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Cr3++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$FeCr2O4 + H+ | 0.887 | 1.848 | 5.7 |
| Mt | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Fe2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Fe3++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$FeFe2O4 + H+ | 1.327 | 0.803 | –1.3 |
| Mf | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$Mg2++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Fe3++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}$MgFe2O4 + H+ | 3.086 | 2.627 | 0.8 |
| Fo → En | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Mg2SiO4 + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$MgSiO3 + H+ | –3.925 | –2.828 | 1.6 |
| Fa → Fs | ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Fe2SiO4 + ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}$Si4++ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$H2Ogas = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}$FeSiO3 + H+ | –4.562 | –2.707 | 4.8 |
Примечания. Fo – форстерит, Fa – фаялит, Lb – либенбергит, Lr – ларнит, En – энстатит, Fs – ферросилит, Wo – волластонит, Di – диопсид, Hd – геденбергит, An – анортит, Ab – альбит, Or – ортоклаз, Sp – шпинель, Hc – герцинит, Ch – хромит, Mt – магнетит, Fo → En и Fa → Fs – соответствующие перитектические реакции.
Рис. 2.
Вариации показателя сродства к протону миналов петрогенных минералов в зависимости от температуры: а – ортосиликаты (сплошная линия), шпинелиды (штриховая линия); б – метасиликаты (сплошная линия), алюмосиликаты (штриховая линия). Обозначения миналов аналогичны табл. 2.
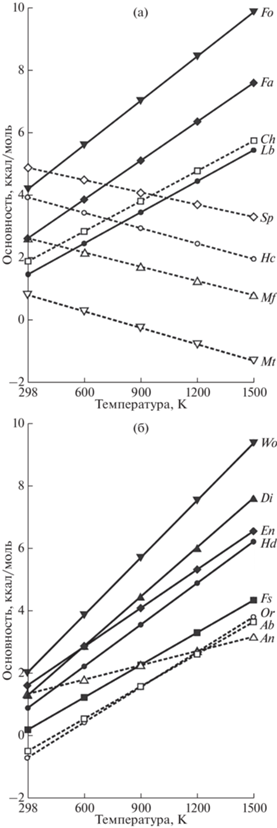
Важно обратить внимание на изменения относительной основности миналов в твердых растворах шпинелида и плагиоклаза, которые происходят с ростом температуры. Является ли это артефактами, обусловленными погрешностью расчетов, или они отражают реальные свойства оценить трудно. Но если эти оценки соответствуют действительности, такие изменения могут быть причиной появления зональности этих минералов при понижении температуры, о чем ниже.
Оценка основности перитектической реакции оливин–ортопироксен. В силу того, что оливин и ортопироксен представляют собой Fe–Mg растворы, то перитектическая реакция может быть описана двумя сопряженными реакциями с участием магнезиальных и железистых миналов. Их формальная запись получается путем вычитания реакции гидратации ортопироксенового минала из реакции гидратации оливинового с соответствующими коэффициентами. Так, для магнезиальных миналов может быть записано:
Соответствующие расчеты приведены в табл. 2 и показаны на рис. 3. Они демонстрируют, что при повышении кислотности системы магнезиальная часть перитектической реакции между оливином и ортопироксеном, как более кислотная, будет иметь энергетическое преимущество, что будет приводить к увеличению магнезиальности вновь образуемого ортопироксена и сдвигу железо-магнезиальных пропорций перитектической реакции в целом.
Влияние увеличения кислотности на ликвидус минералов твердых растворов
Изменение кислотно-оснóвных свойств магматической системы сказывается на параметрах ликвидуса кристаллизующихся фаз (Коржинский, 1960). Это вытекает из преобразования уравнения Шредера (Жариков, 2005):
В силу того, что при кристаллизации энтальпийный эффект всегда положительный, в случае минералов постоянного состава понижение активности компонента вызовет понижение температуры ликвидуса, слагаемой им фазы. Для минералов, представляющих собой твердые растворы, понижение активности его миналов, вызванное увеличением кислотности, приводит к парадоксальному на первый взгляд эффекту: при постоянных температуре и составе системы будет наблюдаться обогащение более оснóвным миналом как кристаллов, так и расплава. Эти изменения состава фаз будут компенсироваться сменой их пропорций, то есть степенью закристаллизованности системы. Правомочность вышесказанного демонстрирует рис. 4а, который изображает идеализированную схему диаграммы состояния системы типа форстерит–фаялит. Сплошной линией на диаграмме показаны фазовые взаимоотношения чистой форстерит–фаялитовой системы, пунктиром – случай с добавлением в систему кислотного компонента, например, серы.
Рис. 4.
Схематическое изображение диаграмм состояния и влияние увеличения кислотности системы на ход кристаллизации: (а) система фаялит–форстерит; (б) гипотетическая ситуация, когда раскисление системы будет происходить компонентом, имеющим промежуточную кислотность; (в) схематическое изображение диаграммы состояния форстерит–кварц и реакции системы на изменения ее кислотности. Сплошной линией на диаграммах показаны фазовые взаимоотношения чистой системы, пунктиром – случай с добавлением в систему кислотного компонента.
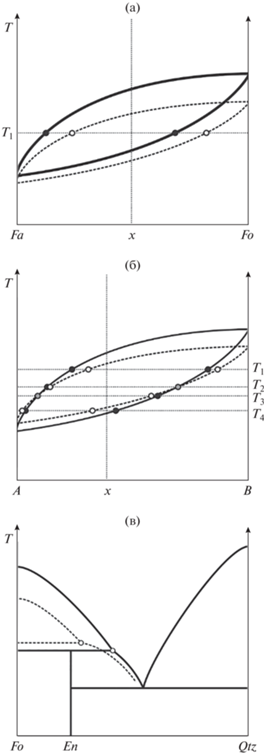
В качестве более сложного случая можно рассмотреть гипотетический вариант, когда твердый раствор сложен основным и кислотным миналами и увеличение кислотности системы оказывает на них разнонаправленное воздействие. Этот случай показан на рис. 4б. При высоких температурах (>T2), как и в первом варианте по сравнению с идеальной схемой происходит обогащение фаз основным компонентом, а при низких (<T3) – должно происходить обогащение кислотным миналом. Относительно идеальной схемы на начальных стадиях кристаллизации соотношение расплав/кристаллы должно быть сдвинуто в пользу расплава, а на конечных – в сторону твердой фазы.
Тройные твердые растворы (как и растворы с бóльшим количеством миналов) на увеличение кислотности должны ответить увеличением доли самого оснóвного компонента и уменьшением доли самого кислотного. Компоненты, обладающие промежуточными значениями этого показателя будут реагировать в соответствии с их степенью близости к крайним членам.
Влияние увеличения кислотности на кристаллизацию в системах с перитектикой
Влияние изменения кислотности – основности на кристаллизацию системы с инконгруентно плавящимся соединением можно продемонстрировать на упрощенной схеме классической диаграммы плавкости Fo–Qtz (рис. 4в). Увеличение кислотности системы приведет к уменьшению активности форстерита и энстатита и понижению их температур ликвидуса. В силу разной основности этих фаз, подавление активности (и соответствующее понижение ликвидусной температуры) форстерита будет более сильным, чем для энстатита. Именно это различие приводит к смещению точки перитектики в более магнезиальную и более высокотемпературную область системы. Увеличение щелочности будет приводить к обратному эффекту.
Влияние увеличения кислотности на Fe3+/Fe2+ в базальтовом расплаве
Еще один важный параметр силикатного расплава, влияющий на кристаллизацию Fe–Mg минералов, – степень окисления железа. Теоретический анализ влияния основности расплава на редокс-состояние железа был проведен Д.С. Коржинским, который пришел к выводу о значительности этого эффекта (Коржинский, 1978). Увеличение кислотности системы приводит к уменьшению активности аниона кислорода:
При этом константа реакции выразится выражением:
Для сохранения величины константы уменьшение активности аниона кислорода повлечет за собой активность электрона, который представляет восстановительный потенциал системы. Это в свою очередь сдвинет влево сопряженную реакцию окисления железа:
Окислительно-восстановительный потенциал свободной от серы базальтовой системы обычно связывается с фугитивностью кислорода, а в качестве его меры используется отклонение фугитивности системы от буферных твердофазовых кислородных реакций (чаще всего используется буфер QFM). Для расчета фугитивности кислорода используются различные по сложности применения оксибарометры (O’Neill, Wall, 1987; Wood et al., 1990; Ballhaus et al., 1991; Николаев и др., 2016), калиброванные на свободных от серы экспериментах.
В случае серосодержащих систем, присутствие иона S2– в расплаве приведет к сдвигу равновесия реакции рекомбинации ионов O2– в сторону элементарного кислорода и повышению количества электронов. Другими словами, должна реализовываться ситуация роста фугитивности кислорода и одновременного увеличения восстановительного потенциала системы и уменьшения кислотности. Это вызовет понижение степени окисления железа как в расплаве, так и в равновесных с ним фазах.
Важно обратить внимание, что такой же эффект S2– должен наблюдаться как для оксибарометров, расчитывающих фугитивность кислорода в зависимости от Fe3+/Fe2+ в расплаве (Николаев и др., 1996а), так и для зависимостей, предназначенных для разделения железа в магматических жидкостях (Sack et al., 1980; Kress, Carmichael, 1991; Николаев и др., 1996б).
Ожидаемые эффекты влияния серы на состав кристаллизующихся фаз
Таким образом, следуя положениям концепции кислотно-основного взвимодействия Коржинского, можно качественно указать направления температурно-композиционных сдвигов для главных породообразующих минералов, которые будут происходить в серонасыщенной системе относительно ее аналога, не содержащего серы. Причем, ярче влияние сульфидной серы должно проявляться в наиболее оснóвных ультрамафитовых расплавах, чем в более кислых дифференциатах. Оливин при увеличении кислотности системы должен обогащаться форстеритовым миналом и обедняться либенбергитовым (табл. 2, рис. 2а). В случае сульфидсодержащей системы на поведение никеля, обусловленное кислотно-основным взаимодействием, будет накладываться его переход в сульфидную фазу. Ортопироксен также должен иметь более магнезиальный состав. Перитектическая реакция между оливином и ортопироксеном должна происходить при более высокой температуре, с участием менее кремнеземистого расплава со сдвигом пропорций реакции в сторону увеличения количества расплава. Причем, из двух сопряженных частей перитектической реакции магнезиальная должна иметь энергетическое преимущественно относительно железистой. Это должно сдвинуть направление тренда суммарной реакции. Для клинопироксена в случае серосодержащей системы можно ожидать увеличения в его составе диопсид-геденбергитовых миналов и уменьшения ферросилитового. Плагиоклаз, в случае реальности вышеприведенных экстраполяционных оценок показателя основности (табл. 2, рис. 2б), в серосодержащих системах при низкой температуре должен демонстрировать увеличение кальциевости, а в высокотемпературных условиях влияние серы может вызывать обратный эффект. Состав кристаллизующегося шпинелида на присутствие сульфидной серы ответит увеличением содержаний хромитового, а также уменьшением – магнетитового и шпинелевого миналов. С переходом серосодержащей системы в более низкотемпературную область относительное обогащение шпинелида хромом возможно может смениться на обогащение глиноземом.
В случае сильных различий по кислотности миналов твердого раствора можно предположить возможность реализации обсуждавшегося выше гипотетического случая диаграммы состояния (рис. 4б). Этот эффект, наверное, следует искать при кристаллизации шпинелида в случае раскисления ультраосновного расплава полевым шпатом.
ВЛИЯНИЕ СЕРЫ НА КРИСТАЛЛИЗАЦИЮ ПОРОДООБРАЗУЮЩИХ МИНЕРАЛОВ ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ
Для проверки теоретических рассуждений на экспериментальном материале и предварительной оценки масштаба исследуемого явления необходимы экспериментальные данные по серосодержащим и свободным от серы системам, пригодные для сопоставления. Для поиска этой информации использовались базы экспериментальных данных MELT (Гирнис, 2003), которая на данный момент содержит информацию о более 40 000 экспериментов, проведенных в рамках более 1900 исследований и INFOREX (Арискин и др., 1997; Ariskin et al., 1996; Арискин, Бармина, 2000; Ariskin, Barmina, 2004), на сегодня включающую в себя данные 464 публикаций (более 15 000 опытов).
Из массива в 3352 серосодержащих эксперимента были отобраны 1285 серонасыщенных опыта, силикатный расплав которых сосуществовал с серосодержащими фазами (сульфиды, ангидрит), как имеющие максимальную концентрацию серы в расплаве. Поскольку большинство этих экспериментальных исследований были направлены на решение других петрологических задач (проблемы растворимости серы в силикатных расплавах, определение формы нахождения серы в силикатных расплавах, определение коэффициентов распределения элементов между сульфидным и силикатным расплавами, исследование смачиваемости сульфидным расплавом и т.д.), то большая часть экспериментов была проведена либо при температурах превышающих температуры кристаллизации силикатных фаз, либо их авторы не приводили информацию о их составе, как не имеющую значения для проводимого ими исследования. Из всего массива данных удалось найти 495 экспериментов из 22 публикаций, содержащих информацию о равновесиях минерал–силикатный расплав для главных породобразующих фаз (оливин, пироксены, плагиоклаз, шпинелид). Эксперименты охватывают широкий спектр природных составов и модельных гаплосистем нормальной и повышенной щелочности (от хондритов и базальтов до дацитов) и проведены в широком диапазоне температур, давлений и состава флюида. Информация о них в обобщенном виде приведена в табл. 3.
Таблица 3.
Экспериментальные исследования, содержащие информацию о равновесии породообразующих минералов с серосодержащим расплавом
| Эксперимен-тальная система | T, °C | P, kb | log(${{f}_{{{{{\text{O}}}_{2}}}}}$) | Летучие компоненты | Состав серосодерж. фазы |
Другие равновесные фазы |
Кол-во опытов | Цель эксперимент. исследования |
Источ-ник |
|---|---|---|---|---|---|---|---|---|---|
| Щелочной оливиновый базальт | 1050, 1160 | 0.001 | ND | Dry | (Fe,Ni)S | LQ, OL | 11 | Определение коэффициента распределения Ni между оливином и сульфидом | [1] |
| Трахиандезит, базальт | 800–1000 | 1–4 | QFM, NNO, MH, MMO | H2O | Po, Anh | LQ, OL, OP, CP, PL, HB, MI, MT | 76 | Растворимость серы в силикатных расплавах, формы ее нахождения в зависимости от ${{f}_{{{{{\text{O}}}_{2}}}}}$ | [2] |
| Гаплобазальт, коматиит | 1350 | 0.001 | –7.9…–10.6 | CO2, CO, SO2 | SL | LQ, OL, OP, SP | 22 | Оценка влияния ${{f}_{{{{{\text{O}}}_{2}}}}}$ и ${{f}_{{{{{\text{S}}}_{2}}}}}$ на коэффициенты ряда сидерофильных металлов между сульфидным, силикатным расплавами и оливином | [3] |
| Дацит | 750–900 | 2.2–3.9 | NNO–NNO+2.7 | H2O | Po, Anh | LQ, PL, HB, OP, CP, MT, IL, MI | 57 | Экспериментальная реконструкция предэруптивных параметров петрогенеза | [4] |
| Базальт | 1370–1410 | 15 | ND | Dry | FeS | LQ, OL, OP, CP | 8 | Исследовано смачивание оливина сульфидным расплавом | [5] |
| Андезит, базальт, щел. базальт, синтетич. аналоги, гаплосоставы | 1300–1600 | 9–27 | IW-1.0–IW-2.1 | Dry | FeS | LQ, OL, OP, CP | 30 | Изучалась растворимость S в силикатных расплавах | [6] |
| Базальт | 1330 | 10 | –8.9…–9.5 | Dry | (Fe,Ni)S | LQ, SP | 5 | Определения коэффициентов распределения ЭПГ между хромитом, сульфидным и силикатным расплавами | [7] |
| Дацит | 800–900 | 2 | NNO+1.2–NNO+4 | H2O | Po, Anh | LQ, HB, PL, MI, MT | 13 | Экспериментальная реконструкция предэруптивных параметров петрогенеза | [8] |
| Базальт | 1300–1355 | 10–16 | NNO–MMO | Dry | SL, Anh | LQ, OL, CP, SP | 18 | Исследовались формы серы в базальтовых расплавах в зависимости от ${{f}_{{{{{\text{O}}}_{2}}}}}$ | [9] |
| Хондрит | 950–1300 | 0.001 | IW–3, COC | Dry | FeS | LQ, OL, OP, SP, ME | 2 | Mоделирование плавления метеоритного вещества | [10] |
| Андезит | 850–950 | 3.8-4.2 | NNO+0.4–NNO+1.2 | H2O, CO2 | Po, Anh | LQ, OP, CP, HB, PL, MT, IL, AP | 17 | Экспериментальная реконструкция предэруптивных параметров петрогенеза | [11] |
| Хондрит | 1200–1700 | 10 | IW-1.2–IW-4.8 | Dry | FeS | LQ, OL, OP, QU, ME | 14 | Моделирование ранней планетарной дифференциации | [12] |
| Дацит | 1000 | 4 | NNO-1 | H2O | Po | LQ, CP | 1 | Растворимость золота в силикатных расплавах | [13] |
| Базальт | 1050–1250 | 2 | QFM–QFM+2.2 | H2O, Cl |
Po, Anh | LQ, OL | 11 | Исследование растворимости сульфидов и сульфатов в базальте | [14] |
| Дацит | 1000 | 4 | NNO-1.2–NNO+3.6 | H2O | Po, Anh | LQ, CP, MT | 21 | Растворимость золота в силикатных расплавах | [15] |
| Хондрит | 1250 | 0.001 | IW-1–IW+1 | Dry | (Fe,Ni)S | LQ, OL, OP, SP, ME | 5 | Моделирование образования брахинита путем частичного плавления хондрита | [16] |
| Базальт | 800–1050 | 20–30 | NNO, CCO | H2O | Po | LQ, CP, GR, HB, MI | 18 | Растворимость серы в водосодержащих базальтовых расплавах | [17] |
| Трахиандезит | 840–950 | 5–15 | CCO–MH | H2O | Po, Anh | LQ, HB, PL, CP, MT, GR | 22 | Исследование влияния ${{f}_{{{{{\text{O}}}_{2}}}}}$ на форму серы при высоких давлениях | [18] |
| Синтетические трахиандезито-базальт, базальт | 1310–1850 | 1–30 | IW-4.6–IW-6.2 | Dry | SL | LQ, OL, OP | 29 | Исследование фазовых равновесий моделирующих образование лав Меркурия | [19] |
| Гаплотрахиандези-базальт, -базальт, хондрит | 1200–1750 | 0.001–40 | IW-1.5–IW-9.4 | Dry | FeS, (Mg, Ca, Fe)S | LQ, OL, OP, QU, ME | 100 | Исследование растворимости серы в модельных породах Меркурия | [20] |
| Трахиандезито-базальт | 1100–1850 | 5.7–50 | IW-5–IW-7 | Cl | FeS | LQ, OL, OP, CP, ME | 11 | Исследование фазовых равновесий моделирующих образование лав на Меркурии | [21] |
| Базальт | 1200 | 10, 15 | QFM-1.8–QFM+1.1 | H2O | SL, MSS, Anh | LQ, OL | 4 | Исследование распределения Re и Mo между сульфидами и силикатным расплавом | [22] |
Примечания. Обозначения буферных равновесий: QFM – SiO2–Fe2SiO4–Fe3O4, MH – Fe3O4–Fe2O3, IW – Fe–FeO, COC – C–CO, MMO – MnO–Mn2O3, NNO – Ni–NiO, CCO – Co–CoO, ND – не определено; Режим летучих компонентов: Dry – номинально “сухие опыты”, т.е. проведенные без добавления летучих; Обозначения серосодержащих фаз: Po – пирротин, Anh – ангидрид SL – сульфидный расплав, MSS – моносульфидный твердый раствор; Обозначения других равновесных фаз: LQ – силикатный расплав, OL – оливин, OP – ортопироксен, CP – клинопироксен, PL – плагиоклаз, HB – роговая обманка, MI – слюда, MT – магнетит, IL – ильменит, SP – шпинелид, AP – апатит, QU – кварц, GR – гранат, ME – металл; Источники: [1] – (Fleet et al., 1977); [2] – (Luhr, 1990); [3] – (Gaetani, Grove, 1997); [4] – (Scaillet, Evans, 1999); [5] – (Holzheid et al.,2000); [6] – (Holzheid, Grove, 2002); [7] – (Sattari et al., 2002); [8] – (Costa et al., 2004); [9] – (Jugo et al., 2005); [10] – (Ford et al., 2008); [11] – (Parat et al., 2008); [12] – (Berthet et al., 2009); [13] – (Jégo et al., 2010); [14] – (Beermann et al., 2011); [15] – (Jégo, Pichavant, 2012); [16] – (Gardner-Vandy et al., 2013); [17] – (Jégo, Dasgupta, 2013); [18] – (Matjuschkin et al., 2016); [19] – (Namur et al., 2016a); [20] – (Namur et al., 2016b); [21] – (Vander-Kaaden, McCubbin, 2016); [22] – (Feng, Li, 2019).
Для вычленения эффекта серы на кристаллизацию силикатного расплава, сопоставляемые эксперименты должны проводиться над идентичными составами и в близких условиях. Это возможно либо в случае исследований, в которых серонасыщенные и свободные от нее эксперименты проводятся параллельно, либо при исследовании серосодержащих систем, в которых в качестве основы для стартовых смесей были взяты уже ранее изучавшиеся свободные от серы составы. Кроме того, важно, чтобы образование в системе равновесных серосодержащих фаз не влияло на состав расплава. Например, появлении среди продуктов опыта ангидрита может уменьшать содержание кальция в расплаве, что в свою очередь приведет к понижению кальциевости плагиоклаза. В тоже время образование пирротина может сдвинуть железо-магниевое отношение силикатных фаз. Это особенно актуально при внесении серы в стартовую шихту в элементарном виде. Столь жесткие требования к экспериментам привели к тому, что их количество очень ограничено. Это – буквально единичные пары опытов для оливина (ортопироксена), плагиоклаза и шпинели.
Влияние сульфидной серы на кристаллизацию оливина и ортопироксена
Г. Гаэтани и Т. Гроув провели экспериментальное исследование, направленное на определение коэффициентов распределения между оливином, силикатным и сульфидным расплавами некоторых сидерофильных элементов (Gaetani, Grove, 1997). В экспериментах в качестве стартового был взят уже экспериментально изученный гаплобазальтовый состав “Fo86” (Ehlers et al., 1992), моделирующий хондритовое вещество. Благодаря этому можно напрямую сравнить кристаллизацию оливина в S-насыщенной и свободной от серы системах. Дополнительно к базовому составу добавлялись 1.5 мас. % синтетического FeS. Эксперименты проводили в той же лаборатории в соответствии с методами, описанными (Ehlers et al., 1992), также при давлении 1 атм и температуре 1350°С. Эксперименты проводились в контролируемых условиях как фугитивности кислорода (от QFM-1 до IQF), так и фугитивности серы (–1.0 ≤ lg(${{f}_{{{{{\text{S}}}_{2}}}}}$) ≤ –2.5). По результатам экспериментов они пришли к выводу, что уменьшение отношения ${{{{f}_{{{{{\text{O}}}_{2}}}}}} \mathord{\left/ {\vphantom {{{{f}_{{{{{\text{O}}}_{2}}}}}} {{{f}_{{{{{\text{S}}}_{2}}}}}}}} \right. \kern-0em} {{{f}_{{{{{\text{S}}}_{2}}}}}}}$ приводит к уменьшению общего количества кристаллов и к увеличению содержания растворенной S. Это в свою очередь ведет к уменьшению содержания FeO, NiO в расплаве, и соответствующему увеличению концентрации остальных петрогенных элементов. Такое изменение состава расплава приводит к насыщению низко-Ca пироксеном в экспериментах, проведенных в условиях низкого отношения ${{{{f}_{{{{{\text{O}}}_{2}}}}}} \mathord{\left/ {\vphantom {{{{f}_{{{{{\text{O}}}_{2}}}}}} {{{f}_{{{{{\text{S}}}_{2}}}}}}}} \right. \kern-0em} {{{f}_{{{{{\text{S}}}_{2}}}}}}}$.
При детальном сравнительном анализе результатов двух обсуждаемых экспериментальных серий бросается в глаза малые потери натрия в серии сульфидонасыщенных экспериментов, которые не превышают 20 отн. %. Тогда как в не содержащих серу опытах (Ehlers et al., 1992), фиксируются от половины до практически полной потери первоначального стартового количества натрия в 3.19 мас. %. Систематический характер этого явления демонстрирует рис. 5а. Потери Na из расплава – давняя проблема экспериментальной петрологии, особенно ярко проявляющаяся в опытах, проводимых методом петли в токе газов, определяющих редокс-условия. Наблюдаемые систематические различия этих серий позволяют высказать предположение, что сера как кислотный компонент подавляет испарение Na из расплава. Такая интерпретация хорошо согласуется с выводами, полученными при исследовании кислотно-оснóвного взаимодействия в процессе испарения щелочных компонентов из расплавов хондр (Яковлев, Шорников, 2022). В силу этого, для дальнейшего сравнения серий (на рис. 5б–5д) составы расплава были пересчитаны на безнатровый базис.
Рис. 5.
Влияние сульфидной серы на равновесие оливин-расплав на примере экспериментального исследования гаплобазальтового состава “Fo86” при 1 атм Эксперименты свободные от серы (Ehlers et al., 1992) – белое; серонасыщенные опыты (Gaetani, Grove, 1997) – черное. а – вариации натрия в экспериментальных стеклах относительно их магнезиальности, отражающие его потери в процессе эксперимента. Пунктирная линия отвечает содержанию натрия в стартовом составе; б–д – вариации результатов экспериментов в зависимости от фугитивности кислорода: б – вариации общего железа в экспериментальных стеклах. Пунктирная линия отвечает содержанию железа в стартовом составе; в – вариации магния в экспериментальных стеклах; г – вариации состава оливина; д – вариации коэффициента сокристаллизации Mg и Fe между оливином и расплавом. На врезке те же данные в форме гистограммы; е – отклонения расчетных температур ликвидуса Ol, полученных с помощью геотермометра (Ford et al., 1983), от экспериментальной температуры в 1350°С.
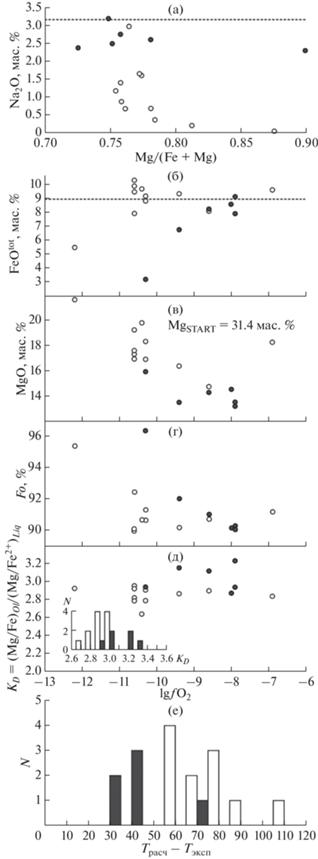
В процессе уравновешивания экспериментальных загрузок в разных окислительно-восстановительных условиях могло происходить изменение состава экспериментального расплава за счет образования новых фаз (оливин, следовые количества пироксена, металлическое железо), что требует анализа для корректности последующих выводов. Однако, отсутствие значимых потерь железа в расплавах для большинства опытов обеих серий (рис. 5б) свидетельствует что образование металлического железа происходило только в самых восстановленных экспериментах. Для серонасыщенной серии характерны расплавы с систематически более низким содержанием Mg (рис. 5в), что соответствует более магнезиальному составу равновесного оливина. Действительно, на диаграмме lg(${{f}_{{{{{\text{O}}}_{2}}}}}$)–Fo (рис. 5г) фигуративные точки разных серий образуют обособленные тренды. Эксперименты проведенные в рамках свободной от серы системы демонстрируют тренд, имеющий нисходящую (lg(${{f}_{{{{{\text{O}}}_{2}}}}}$) < –10) и восходящую (lg(${{f}_{{{{{\text{O}}}_{2}}}}}$) > –10) ветви. Восходящая ветвь тренда образована экспериментами в которых отсутствует металлическое железо и повышенная магнезиальность оливина обеспечивается частичным переходом железа в трехвалентное состояние, не входящее в состав оливина. Серонасыщенные эксперименты проявляют только нисходящий тренд, смещенный в более окисленную область диаграммы. В восстановительной области это соответствует увеличению содержания Fo на 2–5 мол. %, с тенденцией уменьшения этого эффекта по мере увеличения окисленности системы. Ожидаемо систематический сдвиг наблюдается и для коэффициента сокристаллизации Mg и Fe между оливином и расплавом ${{K}_{D}} = {{X_{{{\text{Mg}}}}^{{Ol}}X_{{{\text{F}}{{{\text{e}}}^{{2 + }}}}}^{{Liq}}} \mathord{\left/ {\vphantom {{X_{{{\text{Mg}}}}^{{Ol}}X_{{{\text{F}}{{{\text{e}}}^{{2 + }}}}}^{{Liq}}} {X_{{{\text{Fe}}}}^{{Ol}}X_{{{\text{Mg}}}}^{{Liq}}}}} \right. \kern-0em} {X_{{{\text{Fe}}}}^{{Ol}}X_{{{\text{Mg}}}}^{{Liq}}}}$ (рис. 5д), который в среднем составляет 2.850 ± 0.089 для расплавов свободных от серы и 3.043 ± 0.145 для сульфидонасыщенных систем. Средние значения коэффициента сокристаллизации, выраженного обратной величиной будут составлять 0.351 ± 0.011 и 0.329 ± 0.016, соответственно. Такое различие коэффициентов сокристаллизации обуславливает в серонасыщенной системе сдвиг состава оливина в магнезиальную сторону до 1.7 номера по форстериту относительно Fo86 системы, не содержащей серу.
Для оценки влияния сульфидной серы на температуру кристаллизации оливина был использован геотермометр минерал–расплав (Ford et al., 1983). Результаты расчетов приведены на рис. 5е в виде гистограммы отклонений (ΔТ = Трасч – Тэксп) от единой для обеих серий экспериментальной температуры в 1350°С. Среднее отклонение для экспериментов свободных от серы составляет 70.9 ± 16.7°С, тогда как серонасыщенные эксперименты демонстрируют среднее отклонение в 46.6 ± 17.2°С. Это позволяет полагать, что насыщение базальтового расплава серой будет приводить к понижению ликвидуса оливина на 20–25°С.
Таким образом, наблюдаемые в серонасыщенных опытах систематические сдвиги состава оливина и его ликвидусной температуры, хоть и невелики по абсолютному значению, но полностью соответствуют теоретически предсказанному тренду. Это делает неприемлемой практику использования зависимости (Roeder, Emslie, 1970), калиброванной на свободных от серы экспериментах, в качестве критерия равновесности серосодержащих опытов (Jugo et al., 2005).
О. Намюр с соавторами (Namur et al., 2016a) исследовали влияние серы на кристаллизацию двух модельных составов аппроксимирующих базальты Меркурия. Для каждого состава проводились две серии опытов: как в серонасышенных, так и в не содержащих серы условиях. Эксперименты проводились при номинально сухих условиях субликвидусных температур в широком интервале давлений (1–30 кбар) и сильно восстановительных условиях, впоследствии теоретически оцененных в 5–8 лог. ед. ниже буферного равновесия IW. В силу очень низкой фугитивности кислорода практически все железо находилось в виде металлической или сульфидной фаз, а силикатные минералы представлены почти чистыми форстеритом и энстатитом. В результате этих экспериментов было установлено сильное влияние серы. В системах без серы Р–Т параметры точки оливин-пироксенового ликвидусного равновесия в зависимости от исследованного валового состава составляют 13 кбар – 1450°С и 17 кбар – 1560°С. При добавлении в систему серы (в виде смеси 0.25FeO, 0.5FeS и 0.25S) эти параметры понижаются до 7.5 кбар – 1385°С и 8 кбар – 1480°С, соответственно. При этом температура ликвидуса как оливина, так и пироксена в серонасыщенных условиях понижаются на 15–20°С. Это хорошо согласуется с меньшей степенью закристаллизованности сульфидонасыщенных опытов при 1–5 кбар относительно их не содержащих серу аналогов. Проведенная Намюром с соавторами (2016a) реконструкция фазовых диаграмм показывает, что при давлениях более 7–8 кбар сера вызывает существенное сокращение поля совместной кристаллизации оливина и ортопироксена, а это неизбежно должно повлечь изменения котектических пропорций. Несмотря на то, что при более низких давлениях их эксперименты были ограничены только полем кристаллизации оливина, можно с уверенностью полагать существование соответствующих изменений конфигурации поля перитектических взаимоотношений оливина и ортопироксена, а, следовательно, и их пропорций.
Влияние сульфидной серы на кристаллизацию плагиоклаза
Эксперименты, пригодные для прямого сопоставления были найдены только в двух публикациях (Parat et al., 2008; Scaillet, Evans, 1999). Эти исследования были нацелены на решение частных петрологических проблем – экспериментальной реконструкции предэруптивных физико-химических параметров серонасыщенных магм среднего состава конкретных вулканогенных комплексов.
Исследование Ф. Пара с соавторами (2008) основано на экспериментах с андезитовой системой, моделирующей одну из туфовых свит Колорадо. Две пары опытов (RUN#2–RUN#45 и RUN#20–RUN#36) проводились при давлении 4 кбар, при температуре 900 и 850°С в присутствии флюида H2O и CO2, при фугитивности кислорода NNO + 1. Для проведения серонасыщенных экспериментов в контейнер добавлялась элементарная сера в количестве 1 мас. %. Серосодержащая фаза в продуктах экспериментов представлена каплями пирротинового расплава.
Б. Скайлет и Б. Эванс (1999) проводили кристаллизационные эксперименты на дацитовом составе вулкана Пинатубо (Филиппины). Две пары экспериментов (RUN#16–RUN#17 и RUN#18–RUN#19) проведены при давлении 2.2 кбар и температуре 776°С, в водонасыщенных условиях и фугитивности кислорода соответствующей NNO и NNO + 1. Как и в предыдущем случае сера в экспериментальный реактор добавлялась в элементарном виде (чуть более 1 мас. %), которая при установлении равновесия переходила в пирротин.
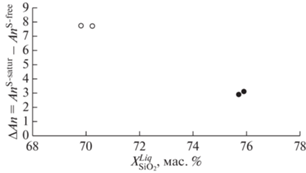
При сравнении результатов параллельных экспериментов можно сделать вывод о том, что добавление серы в андезитовый расплав приводит к увеличению кальциевости плагиоклаза (an#) на 7.7–7.8 номера, его количество в расплаве уменьшается на 40–60 отн. %, что приводит к уменьшению закристаллизованности породы на 9.4–18.4 мас. %, и уменьшению ее цветного индекса (Pl/(Hb + Pl) c 0.62 до 0.42 на фоне слабых изменений количества роговой обманки. При добавлении серы в расплав дацита показатель an# увеличивается на 2.9–3.1 мол. %, а изменение закристаллизованности системы, количества плагиоклаза и цветное число демонстрируют небольшие, иногда противонаправленные вариации, находящиеся, по-видимому, на уровне погрешности их определения. Уменьшение влияния серы с ростом общей кислотности системы (рис. 6) хорошо укладывается в представления о кислотно-оснóвном взаимодействии: его энергетический эффект понижается по мере выравнивания показателей основности реагентов. Руководствуясь этой логикой можно полагать, что в ультрабазит-базитовых системах, как более основных, влияние серы на кристаллизацию плагиоклаза будет еще больше.
Влияние сульфидной серы на кристаллизацию шпинелида
Представление о влиянии серы на кристаллизацию шпинелида можно получить благодаря экспериментальной работе Саттари с соавт. (Sattari et al., 2002). Целью этого исследования было определение коэффициентов распределения платиноидов между шпинелидом, силикатным и сульфидным расплавами при температуре 1330°С и давлении 10 кбар. Были представлены результаты 5 номинально сухих опытов в которых единственной кристаллической фазой был хромшпинелид.
В качестве стартового состава был принят ранее хорошо экспериментально изученный базальт 401 (Roeder, Reynolds, 1991), на примере которого исследовалось влияние на равновесие хромшпинелид – расплав вариаций фугитивности кислорода и содержания хрома в системе при температуре 1200–1300°С и давлении в 1 атм и 10кбар. Сопоставление результатов этих исследований позволяет провести сравнение кристаллизации шпинелида из идентичного расплава как в свободной от серы, так и в сульфидонасыщенной системах. Из выборки 26 опытов (24 при 1 атм и 2 при 10 кбар) при дальнейшем сравнительном анализе были исключены 3 сильно окисленных 1‑атм эксперимента (${{f}_{{{{{\text{O}}}_{2}}}}}$ > NNO) и один высокобарный опыт продолжительностью менее 24 часов, как возможно неравновесный.
В силу того, что опыты проводились при различных температурах, широком диапазоне ${{f}_{{{{{\text{O}}}_{2}}}}}$ и различными содержаниями хрома, которые являются мощными факторами, влияющими на состав хромшпинелида, непосредственно сравнивать между собой результаты экспериментов невозможно. Для сравнительного анализа использовались расчеты проведенные по модели равновесия шпинелид–расплав SPINMELT-2 (Николаев и др., 2018аб), которая была откалибрована на экспериментах, свободных от серы. Моделировались равновесные температура и состав шпинелида соответствующие составу расплава и условиям каждого опыта. В качестве меры для сравнения была выбрана величина отклонения расчетных параметров от экспериментальных (Δ = расч – эксп).
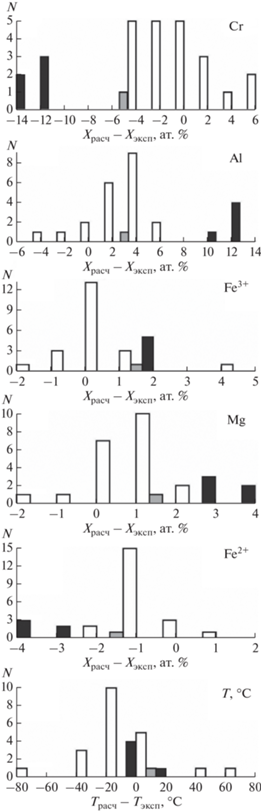
Результаты расчетов приведены на рис. 7 в виде серии гистограмм. Эксперименты, не содержащие серу, воспроизводятся моделью с практически симметричным разбросом, который незначительно превосходит ее заявленную точность (23°С по температуре, для Cr и Al – 3 ат. %, для Mg, Fe2+ и Fe3+ – 0.8 ат. %). Напротив, опыты с серонасыщенными расплавами демонстрируют систематические отклонения, которые следует интерпретировать как результат направленного влияния сульфидной серы. Для части параметров эти отклонения не велики и находятся на грани точности расчета, но для части компонентов они значительны: ΔT = 18.4 ± 3.6°C, ΔCr = –12.0 ± 0.8, ΔAl = 11.1 ± 0.8, ΔFe3+ = 1.0 ± 0.04, ΔFe2+ = –3.2 ± 0.2, ΔMg = 3.1 ± ± 0.3 ат. %. Таким образом, можно утверждать, что появление сульфидной серы в системе понижает ликвидусную температуру шпинелида, и в его составе понижает содержания Al, Fe3+ и Mg, но повышает содержания Cr и Fe2+. Установленные эффекты находятся в согласии с проведенным выше теоретическим анализом: появление серы влечет увеличение содержания наиболее основного минала (в данном случае хромита) и обеднение твердого раствора кислотными миналами, пропорционально их содержанию и степени близости к самому кислотному.
Рис. 7.
Влияние сульфидонасышенных условий на кристаллизацию шпинелида на примере экспериментального исследования базальта 401. Эксперименты свободные от серы (Roeder, Reynolds, 1991): белое – эксперименты при 1 атм, серое – при 10 кбар; серонасыщенные опыты (Sattari et al., 2002) при 10 кбар – черное. Гистограммы демонстрируют систематические различия экспериментальных и расчетных параметров шпинелида, полученных при моделировании равновесия шпинелид-расплав с помощью программы SPINMELT-2.1.
О влиянии серы на кристаллизацию биотита
Ф. Коста, Б. Скайлет и М. Пичаван провели экспериментальное исследование (Costa et al., 2004) дацитовой лавы влк. Сан-Педро (Чилийские Анды). В дополнение к основному массиву экспериментов, не содержащих серу, было выполнено некоторое количество серосодержащих опытов. Вся экспериментальная серия (800–950°С, 2 кбар, 4.5–5.5 мас. % воды) проведена в окислительных условиях между NNO и NNO+3.5, поэтому главной серосодержащей фазой являлся ангидрит и только в наиболее восстановленных опытах (NNO+1.2–NNO+1.4) наблюдалось совместное существование ангидрита и пирротина. Авторы исследования установили, что во всех экспериментах, допускающих прямое сопоставление (например, #94–#89s, #94–#95s, #133–#137s), устойчива базовая минеральная ассоциация дацита (роговая обманка + ортопироксен + + плагиоклаз), тогда как биотит стабилен только в экспериментах с добавлением >0.1 мас. % S. То есть, увеличение содержания серы расширяет поле стабильности биотита.
Таким образом, сопоставление экспериментальных данных, несмотря на их ограниченное количество, приводит к выводу, что наблюдаемые эффекты хорошо укладываются в теоретически предсказанные тренды. Это позволяет признать перспективной постановку задачи учета влияния серы на кристаллизацию породообразующих минералов на всем имеющемся массиве серосодержащих экспериментов (3352 опыта) методами многомерной статистики.
ПРИМЕРЫ ВЛИЯНИЯ СУЛЬФИДНОЙ СЕРЫ НА КРИСТАЛЛИЗАЦИЮ ПРИРОДНЫХ МАГМАТИЧЕСКИХ СИСТЕМ
В данном разделе приведены природные наблюдения, почерпнутые в литературе, которые могут быть рассмотрены с точки зрения влияния сульфидной серы на кристаллизацию силикатной системы. Сложность поиска таких примеров связана: во-первых, с необходимостью иметь достаточно детальное геолого-геохимическое описание объектов, позволяющее не только вычленить эффект серы, но и в случае необходимости переинтерпретировать имеющейся фактический материал; во-вторых, с редко встречающейся в природе ситуацией, когда можно сравнивать породы непосредственно, то есть когда условия их образования отличаются только влиянием серы. Облегчало задачу поиска выявленные выше теоретические и экспериментальные представления о направленности этого процесса.
Хондрит Вигарано
Влияние серы на пропорции кристаллизации оливина и ортопироксена может быть продемонстрировано на материале детального минералогического и петроструктурного исследования порфировых хондр метеорита Вигарано (CV3), проведенного И. Маррокки и Г. Либурелем (Marrocchi, Libourel, 2013). Количественный петроструктурный анализ 25 хондр I типа проводился с помощью обработки EDX-карт по Mg, Si, Fe, Ni и S, который позволил установить модальные содержания силикатных фаз (оливин, пироксен, мезостазис) и сульфидов. Весь комплекс полученной в обсуждаемом исследовании петрологической информации показывает, что сульфиды генетически связаны с низкокальциевым пироксеном процессами высокотемпературного формирования хондр, и не могут быть образованы в результате термального, ударного или гидротермального метаморфизма во время охлаждения хондр или родительского тела. Было установлено, что капли троилита в основном расположены во внешней зоне кристаллов низкокальциевого пироксена. Кроме того, отмечено, что количество капель троилита увеличивается с ростом содержания низкокальциевого пироксена (рис. 8).
Рис. 8.
Модальная доля энстатита в сравнении с модальным содержанием сульфидов для 25 хондр типа I хондрита CV3 Вигарано по данным (Marrocchi, Libourel, 2013); РО, РОР и РР – оливин-порфировые, оливин-пироксен-порфировые и пироксен-порфировые хондры, соответственно.
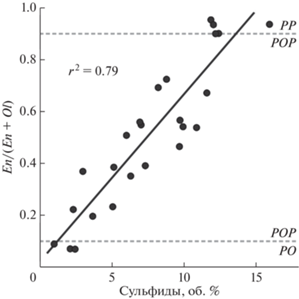
Интерпретируя наблюдаемую картину, И. Маррокки и Г. Либурель предположили, что эволюция расплавов хондр (или их зон) в сторону более кремниевого состава, от оливин-порфировых к пироксен-порфировым, происходит из-за высокого парциального давления SiO в окружающем небулярном газе. Это вызывает насыщение FeS в пироксен-порфировых хондрах при гораздо более низком содержании S, чем в оливин-порфировых, что приводит к сокристаллизации сульфида железа и низкокальциевого пироксена.
Учитывая все вышесказанное, можно предложить альтернативное объяснение: появление в системе серы смещает пропорции кристаллизации расплава хондр в сторону энстатита, и тем большему, чем больше серы оказывается в системе. Такой подход кажется более реалистичным, так как с физико-химической точки зрения трудно представить силикатный расплав, содержащий 10–15% растворенного сульфида.
Cu–Ni–PGE месторождение Сакатти
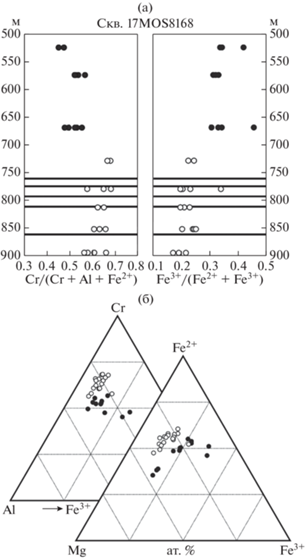
Влияние серы на кристаллизацию шпинелида можно продемонстрировать на примере крупного Cu–Ni–PGE месторождения Сакатти (Brownscombe et al., 2015), обнаруженного в пределах Центрально-Лапландского зеленокаменного пояса, в его центральной структуре Колари–Киттиля–Соданкюля (Сев. Финляндия), среди метапелитов и кварцитов палеопротерозойского возраста. Оно представляет собой месторождение магматических сульфидов, приуроченное к слабо дифференцированному перидотитовому массиву, который погружается на СЗ с подтвержденной протяженностью погружения более 1100 м и максимальной мощностью свыше 400 м. Интрузивное тело сложено орто-мезо-адкумулятами, представленными дунитами и гарцбургитами. Рудная минерализация приурочена к нижней части тела и представлена как вкрапленными сульфидами, так и несколькими массивными сульфидными линзами, мощность которых может достигать 25 м. Верхняя часть тела сложена неминерализованными гарцбургитами. Вариации состава хромшпинелида по разрезу интрузива по данным (Silventoinen, 2020), основанным на образцах керна скв. 17MOS8168 показаны на рис. 9. Хромшпинелиды нижней части разреза, содержащей сульфидную минерализацию, обладают более высокими значениями хромистости и меньшей окисленностью железа относительно шпинелидов верхней не минерализованной части разреза (рис. 9а). Широкие вариации Mg/Fe2+ шпинелидов, в целом, и приуроченность наиболее магнезиальных индивидов к верхней не минерализованной части разреза, говорят о потере первичномагматических значений при близсолидусном переуравновешивании (рис. 9б). Однако, различия двух групп составов в соответствии с теоретическими прогнозами и экспериментальными данными достаточно показательны.
Рис. 9.
Вариации состава хромита на Cu–Ni–PGE месторождении Сакатти (Финляндия) в керне скв. 17MOS8168 по данным (Silventoinen, 2020): (а) по разрезу, вскрытому скважиной; черными жирными линиями отмечены горизонты массивных сульфидных руд (вне масштаба); (б) те же составы на тройных диаграммах состава Al–Cr–Fe3+ и Mg–Fe2+–Fe3+; белые кружки – хромиты из разреза, содержащего сульфидную минерализацию, черные – хромиты неминерализованной части разреза.
Йоко-Довыренский расслоенный интрузив
Влияние сульфидной серы на окислительно-восстановительный режим магматического процесса можно рассмотреть на примере позднерифейского Йоко-Довыренского ультрамафит-мафитового расслоенного плутона Сев. Прибайкалья (Ariskin et al., 2018). Интрузив сформировался в составе Сыннырской рифтогенной ассоциации на ЮЗ замыкании Олокитского прогиба среди терригенных, известняково-доломитовых и паралических пиритоносных углеродистых пород рифея. Площадь эрозионного среза плутона составляет 26 × 3.5 км. Вертикальный разрез центральной части интрузива включает придонный приконтактовый горизонт плагиоперидотитов (150–200 м), который сменяется последовательностью кумулятивных пород расслоенной серии (снизу вверх): примерно 1/3 разреза сложена бронзит-эндиопсид-плагиоклаз содержащими дунитами и лерцолитами, 1/3 – троктолитами от мелано- до лейкоразностей, верхняя часть разреза представлена габброидами эволюционирующими от оливиновых габбро, через оливиновые и безоливиновые габбронориты, к пижонит-содержащим габбро в прикровельной части. На флангах интрузива контрастность расслоенной серии снижается: дуниты выклиниваются, в разрезе преобладают меланотроктолиты и лейкогабброиды. В придонной части плутона среди перидотитов установлены протяженные линзовидные и гнездовые проявления малосульфидной, иногда сидеронитовой минерализации. В северо-восточном замыкании разведано забалансовое Байкальское месторождение сульфидных Cu–Ni–Fe руд.
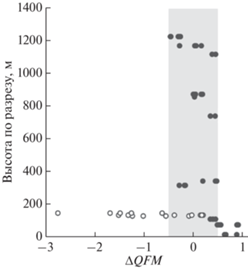
Для оценки окислительно-восстановительных условий кристаллизации магм Йоко-Довыренского расслоенного интрузива использовался Ol-Sp ${{f}_{{{{{\text{O}}}_{2}}}}}$-барометр (Николаев и др., 2016). В основе оксибарометрических расчетов (Фомин и др., 2012) лежат данные по составам включений хромшпинелида в зёрнах кумулусного оливина из пород ЮЗ части плутона (нижняя часть разреза “Йоко” (Ariskin et al., 2017)). Полученные оценки фугитивности кислорода показаны на рис. 10 и демонстрируют вариации, соответствующие интервалу QFM ± 0.5, что соответствует точности оксибарометра. Однако в нижней части (~130 м от нижнего контакта) для трех перидотитов установлена значительно более низкая фугитивность кислорода – на 2–3 лог. ед. ниже буфера QFM. Этот сдвиг коррелирует с накоплением в этих породах сульфидной фазы троилитового состава.
Рис. 10.
Оценка фугитивности кислорода по оксибарометру (Николаев и др., 2016) в породах нижней и средней части разреза Йоко-Довыренского расслоенного интрузива (Сев. Прибайкалье) по данным (Фомин и др., 2012). Белыми точками показаны оценки для образцов, содержащих троилитовую минерализацию.
Весьма маловероятно, чтобы на момент образования пород, в соседних горизонтах кумулятивной толщи, режим кислорода отличался на два порядка. Очевидно, что калиброванный на свободных от серы экспериментах оксибарометр показывает фиктивные заниженные значения. Окислительно-восстановительный потенциал (активность электрона) в этой ситуации зависит не только от фугитивности кислорода, но и от активности серы, которая в простых термодинамических системах является функцией температуры, давления и содержания серы.
Еще один аспект пород Йоко-Довыренского интрузива следует упомянуть в связи с затронутой в данной статье проблематикой: пространственной связи сульфидов и флогопита в породах плутона. В породах нижней приконтактовой зоны массива, содержащих сульфидную минерализацию, часто наблюдаются выделения флогопита (Кислов, 1998). Появление флогопита в породах возможно связано не только с наличием повышенных количеств воды при образовании приконтактовых пород массива, но и с расширением поля стабильности слюды под влиянием серы, которое наблюдалось в экспериментах (Costa et al., 2004).
ВЫВОДЫ
Таким образом, проведен предварительный анализ влияния сульфидной серы на кристаллизацию магматических систем ультраосновного, основного и среднего состава нормальной щелочности. На основе принципа кислотно-оснóвного взаимодействия Коржинского показана направленность этого эффекта при кристаллизации породообразующих фаз.
Для проверки теоретических построений был проведен систематический поиск опубликованных экспериментальных данных допускающих прямое сопоставление сульфидонасыщенных и свободных от серы опытов. Несмотря на очень ограниченное количество таких экспериментов, их результаты хорошо укладываются в теоретически предсказанные тренды. Анализ экспериментальных данных позволил в общем оценить масштабы явления – для некоторых минералов понижение температуры ликвидуса достигает 20–30°С, сдвиг состава до 10–12 ат. % и значимо измененяются пропорции кристаллизации.
Для ряда природных объектов из литературы почерпнуты наблюдения, которые следует интерпретировать как проявления влияния серы, что дает дополнительное подтверждение реальности этого эффекта.
Полученные результаты приводят к выводу, что влияние серы на кристаллизацию силикатных магм значимо. А это, как минимум, требует большой осторожности при использовании для серосодержащих систем петрологических зависимостей, калиброванных на свободных от серы экспериментах.
Автор выражает благодарность к. г.-м. н. О.И. Яковлеву (ГЕОХИ РАН) за в высшей степени полезные обсуждения и консультации по затронутой в данной статье проблематике, д. г.-м. н. А.В. Гирнису (ИГЕМ РАН) за предоставленную свежую версию базы экспериментальных данных MELT и д. г.-м. н. О.А. Луканину (ГЕОХИ РАН) за детальные редакционные комментарии, позволившие улучшить текст рукописи.
Работа выполнена в рамках госзадания ГЕОХИ им. В.И. Вернадского РАН.
Список литературы
Арискин А.А., Бармина Г.С. (2000) Моделирование фазовых равновесий при кристаллизации базальтовых магм (ред. И.Д. Рябчиков). М.: Наука, 363 с.
Арискин А.А., Мешалкин С.С., Альмеев Р.Р., Бармина Г.С., Николаев Г.С. (1997) Информационно-поисковая система ИНФОРЭКС: анализ и обработка экспериментальных данных по фазовым равновесиям изверженных пород. Петрология. 5(1), 32-41.
Арискин А.А., Фомин И.С., Жаркова Е.В, Кадик А.А., Николаев Г.С. (2017) Окислительно-восстановительный режим формирования ультрамафитов и габброидов Йоко-Довыренского массива (по результатам измерений собственной летучести кислорода в оливине). Геохимия. (7), 579-593.
Ariskin A.A., Fomin I.S., Zharkova E.V., Kadik A.A., Nikolaev G.S. (2017) Redox Conditions During Crystallization of Ultramafic and Gabbroic Rocks of the Yoko–Dovyren Massif (Based on the Results of Measurements of Intrinsic Oxygen Fugacity of Olivine). Geochem. Int. 55(7), 595-607.
Гирнис А.В. (2003) Равновесие оливин-ортопироксен-расплав как термобарометр для мантийных магм. Петрология. 11(2), 115-127.
Древинг В.П., Калашников Я.А. (1964) Правило фаз с изложением основ термодинамики. М.: Изд-во Моск. ун-та, 455 с.
Жариков В.А. (2005) Основы физической геохимии. М.: Изд-во Моск. ун-та / Наука, 654 с.
Кислов Е.В. (1998) Йоко-Довыренский расслоенный массив. Улан-Удэ: Изд-во БНЦ СО РАН, 265 с.
Коптев-Дворников Е.В., Арьяева Н.С., Бычков Д.А. (2012) Уравнение термобарометра для описания сульфид-силикатной ликвации в базитовых системах. Петрология. 20(5), 1-18.
Коржинский Д.С. (1959) Кислотно-основное взаимодействие компонентов в силикатных расплавах и направление котектических линий. ДАН СССР. 128(2), 383-386.
Коржинский Д.С. (1960) Кислотность – щелочность как главнейший фактор магматических и послемагматических процессов. в кн. Магматизм и связь с ним полезных ископаемых. М.: Изд-во АН СССР, 21-30
Коржинский Д.С. (1965а) Вывод термодинамических потенциалов открытых систем с внешне задаваемыми кислотностью и восстановленностью. Проблемы геохимии. М.: Наука, 128-136.
Коржинский Д.С. (1965б) Кислотно-основное взаимодействие компонентов в расплавах. Исследование природного и технического минералообразования. М.: Наука, 5-9.
Коржинский Д.С. (1973) Теоретические основы анализа парагенезисов минералов. М.: Наука, 288 с.
Коржинский Д.С. (1978) Зависимость степени окисления железа в магме от щелочности. ДАН СССР. 238(4), 948-950.
Маракушев А.А. (1976а) Кислотно-щелочные свойства безводных силикатов и алюмосиликатов. Записки Всероссийского Минералогического Общества Сер. 2. 105(5), 562-579.
Маракушев А.А. (1976б) Метод термодинамического расчета показателей основности горных пород и минералов. Бюллетень Моск. Общества Испытателей Природы, Отд. Геологический. LI(1), 5-25.
Маракушев А.А. (1978) Термодинамический расчет показателей основности химических элементов и простых окислов // В кн. Очерки физико-химической петрологии, вып. VII, (отв. ред.: Жариков В.А., Федькин В.В.), М.: Наука, 41-82.
Маракушев А.А. (1979) Петрогенезис и рудообразование (геохимические аспекты). М.: Наука, 261 с.
Наумов Г.Б., Рыженко Б.Н., Ходаковский И.Л. (1971) Справочник термодинамических величин (для геологов). М.: Атомиздат, 240 с.
Николаев Г.С., Арискин А.А., Бармина Г.С. (2018а) SPINMELT-2.0: Численное моделирование равновесия шпинелид–расплав в базальтовых системах при давлениях до 15 кбар. I. Формулировка, калибровка и тестирование модели. Геохимия. (1), 28-49.
Nikolaev G.S., Ariskin A.A., Barmina G.S. (2018a) SPINMELT-2.0: Simulation of Spinel–Melt Equilibrium in Basaltic Systems under Pressures up to 15 Kbar: I. Model Formulation, Calibration, and Tests. Geochem. Int. 56(1), 24-45.
Николаев Г.С., Арискин А.А., Бармина Г.С. (2018б) SPINMELT-2.0: Численное моделирование равновесия шпинелид–расплав в базальтовых системах при давлениях до 15 кбар. II. Описание программы, топология модельной системы хромшпинелид-расплав и её петрологические приложения. Геохимия. (2), 135-146.
Nikolaev G.S., Ariskin A.A., Barmina G.S. (2018b) SPINMELT-2.0: Simulation of Spinel–Melt Equilibrium in Basaltic Systems under Pressures up to 15 Kbar: II. Description of the Program Package, the Topology of the Cr-spinel–Melt Model System, and Petrological Implications. Geochem. Int. 56(2), 125-135.
Николаев Г.С., Борисов А.А., Арискин А.А. (1996а) Новые ${{f}_{{{{{\text{O}}}_{2}}}}}$ – барометры для закалочньіх стекол различных петрохимических серий. Геохимия. (9), 836-839.
Nikolaev G.S., Borisov A.A., Ariskin A.A. (1996a) New ${{f}_{{{{{\text{O}}}_{2}}}}}$-Barometers for Quenched Glasses of Various Petrochemical Series. Geochem. Int. 34(9), 753-756.
Николаев Г.С., Борисов А.А., Арискин А.А. (1996б) Расчет соотношения Fe3+/Fe2+ в магматических расплавах: Тестирование и дополнительная калибровка эмпирических уравнений для различных петрохимических серий. Геохимия. (8), 713-722.
Nikolaev G.S., Borisov A.A., Ariskin A.A. (1996b) Calculation of the Ferric–Ferrous Ratio in Magmatic Melts: Testing and Additional Calibration of Empirical Equations for Various Magmatic Series. Geochem. Int. 34(8), 641-649.
Николаев Г.С., Арискин А.А., Бармина Г.С., Назаров М.А., Альмеев Р.Р. (2016) Тестирование Ol–Opx–Sp оксибарометра Балльхауса–Берри–Грина и калибровка нового уравнения для оценки окислительного состояния расплавов, насыщенных оливином и шпинелидом. Геохимия. (4), 323-343
Nikolaev G.S., Ariskin A.A., Barmina G.S., Nazarov M.A., Almeev R.R. (2016) Test of the Ballhaus–Berry–Green Ol–Opx–Sp Oxybarometer and Calibration of a New Equation for Estimating the Redox State of Melts Saturated with Olivine and Spinel. Geochem. Int. 54(4), 301-320.
Усанович М.И. (1939) О кислотах и основаниях. Журн. Общей Химии. 9(2), 182-192.
Усанович М.И. (1970) Исследования в области теории растворов и теории кислот и оснований. Избранные труды. Алма-Ата: Наука, 363 с.
Фомин И.С., Николаев Г.С., Арискин А.А., Жаркова Е.В. (2012) Сопоставление методик оценки окислительно-восстановительных условий и температур закрытия систем оливин-хромшпинелид для пород Йоко-Довыренского расслоенного интрузива. Материалы Второй научной молодежной школы “Новое в познании процессов рудообразования” 11–13 декабря 2012. М.: ИГЕМ РАН, 196-198.
Яковлев О.И., Шорников С.И. (2022) Эффект кислотно-основного взаимодействия при испарении щелочных компонентов из расплавов хондр. Геохимия. 67(5), 403-412.
Yakovlev O.I., Shornikov S.I. (2022) Effect of Acid−Base Interaction at the Evaporation of Alkaline Components from Chondrule Melts. Geochem. Int. 60(5), 401-410.
Ariskin A.A., Barmina G.S. (2004) COMAGMAT: Development of a magma crystallization model and its petrologic applications. Geochem. Int. 42 (Supplementary 1), S1-S157.
Ariskin A.A., Barmina G.S., Meshalkin S.S., Nikolaev G.S., Almeev R.R. (1996) INFOREX-3.0: A database on experimental studies of phase equilibria in igneous rocks and synthetic systems: II. Data description and petrological applications. Computers & Geosciences. 22(10), 1073-1082.
Ariskin A.A., Danyushevsky L.V., Bychkov K.A., McNeill A.W., Barmina G.S., Nikolaev G.S. (2013) Modeling Solubility of Fe-Ni Sulfides in Basaltic Magmas: The Effect of Nickel. Economic Geology. 108, 1983-2003.
Ariskin A.A., Bychkov K.A., Nikolaev G.S., Barmina G.S. (2018) The COMAGMAT-5: Modeling the Effect of Fe–Ni Sulfide Immiscibility in Crystallizing Magmas and Cumulates. J. Petrol. 59(2), 283-298.
Ariskin A., Danyushevsky L., Nikolaev G., Kislov E., Fiorentini M., McNeill A., Kostitsyn Yu., Goemann K., Feig S.T., Malyshev A. (2018) The Dovyren Intrusive Complex (Southern Siberia, Russia): Insights into dynamics of an open magma chamber with implications for parental magma origin, composition, and Cu–Ni–PGE fertility. Lithos. 302–303, 242-262.
Baker D.R., Moretti R. (2011) Modeling the solubility of sulfur in magmas: A 50-year old geochemical challenge: Reviews in Mineralogy and Geochemistry. 73, 167-213.
Ballhaus C., Berry R.F., Green D.H. (1991) High pressure experimental calibration of the olivine-orthopyroxene-spinel oxygen geobarometer: implications for the oxidation state of the upper mantle. Contrib. Mineral. Petrol. 107(1), 27-40; Erratum: (1994) Contrib. Mineral. Petrol. 118(1), 109.
Beermann O., Botcharnikov R.E., Holtz F., Diedrich O., Nowak M. (2011) Temperature dependence of sulfide and sulfate solubility in olivine-saturated basaltic magmas. Geochim. Cosmochim. Acta. 75, 7612-7631.
Berthet S., Malavergne V., Righter K. (2009) Melting of the Indarch meteorite (EH4 chondrite) at 1 GPa and variable oxygen fugacity: Implications for early planetary differentiation processes. Geochim. Cosmochim. Acta. 73, 6402-6420.
Brownscombe W., Ihlenfeld C., Coppard J., Hartshorne C., Klatt S., Siikaluoma J.K., Herrington R.J. (2015) The Sakatti Cu–Ni–PGE sulfide deposit in Northern Finland. In Mineral deposits of Finland, (Eds. Maier W., Lahtinen R., O’Brien H.). Amsterdam: Elsevier, 211-252.
Costa F., Scaillet B., Pichavant M. (2004) Petrological and Experimental Constraints on the Pre-eruption Conditions of Holocene Dacite from Volcán San Pedro (36° S, Chilean Andes) and the Importance of Sulphur in Silicic Subduction-related Magmas. J. Petrology. 45(4), 855-881.
Danyushevsky L.V., Plechov P. (2011), Petrolog3: Integrated software for modeling crystallization processes, Geochem. Geophys. Geosyst. 12, Q07021.https://doi.org/10.1029/2011GC003516
Ehlers K., Grove T.L., Sisson T.W., Recca S.L., Zervas D.A. (1992) The effect of oxygen fugacity on the partitioning of nickel and cobalt between olivine, silicate melt, and metal. Geochim. Cosmochim. Acta. 56, 3733-3743.
Feng Lu, Li Yuan (2019) Comparative partitioning of Re and Mo between sulfide phases and silicate melt and implications for the behavior of Re during magmatic. EPSL. 517, 14-25.
Fleet M.E., MacRae N.D., Herzberg C.T. (1977) Partition of Nickel Between Olivine and Sulfide: A Test for Immiscible Sulfide Liquids. Contrib. Mineral. Petrol. 65, 191-197
Ford C.E., Russell D.G., Craven J.A., Fisk M.R. (1983) Olivine-liquid equilibria: temperature, pressure and composition dependence of the crystal/liquid cation partition coefficients for Mg, Fe2+, Ca and Mn. J. Petrology. 24, 256-265.
Ford R.L., Benedix G.K., McCoy T.J., Rushmer T. (2008) Partial melting of H6 ordinary chondrite Kernouvé: Constraints on the effects of reducing conditions on oxidized compositions. Meteoritics Planet Sci. 43(8), 1399-1414.
Gaetani G.A., Grove T.L. (1997) Partitioning of moderately siderophile elements among olivine, silicate melt, and sulfide melt: Constraints on core formation in the Earth and Mars. Geochim. Cosmochim. Acta. 61(9), 1829-1846.
Gardner-Vandy K.G., Lauretta D.S., McCoy T.J. (2013) A petrologic, thermodynamic and experimental study of brachinites: Partial melt residues of an R chondrite-like precursor. Geochim. Cosmochim. Acta. 122, 36-57.
Ghiorso M.S., Sack R.O. (1995) Chemical mass transfer in magmatic processes IV. A revised and internally consistent thermodynamic model for the interpolation and extrapolation of liquid-solid equilibria in magmatic systems at elevated temperatures and pressures. Contrib. Mineral. Petrol. 119, 197-212.
Holzheid A., Grove T.L. (2002) Sulfur saturation limits in silicate melts and their implications for core formation scenarios for terrestrial planets. Amer.Miner. 87, 227-237.
Holzheid A., Schmitz M.D., Grove T.L. (2000) Textural equilibria of iron sulfide liquids in partly molten silicate aggregates and their relevance to core formation scenarios. J. Geophys. Res. 105(B6), 13 555-13 567.
Jégo S., Dasgupta R. (2013) Fluid-present melting of sulfide-bearing ocean-crust: Experimental constraints on the transport of sulfur from subducting slab to mantle wedge. Geochim. Cosmochim. Acta. 110, 106-134.
Jégo S., Pichavant M. (2012) Gold solubility in arc magmas: Experimental determination of the effect of sulfur at 1000°C and 0.4 GPa. Geochim. Cosmochim. Acta. 84, 560-592.
Jégo S., Pichavant M., Mavrogenes J.A. (2010) Controls on gold solubility in arc magmas: An experimental study at 1000°C and 4 kbar, Geochim. Cosmochim. Acta. 74, 2165-2189.
Jugo P.J., Luth R.W., Richards J.P. (2005) An Experimental Study of the Sulfur Content in Basaltic Melts Saturated with Immiscible Sulfide or Sulfate Liquids at 1300°C and 1.0 GPa. J. Petrol. 46(4), 783-798.
Kress V.C., Carmichael I.S.E. (1991) The compressibility of silicate liquids containing Fe2O3 and the effect of composition, temperature, oxygen fugacity and pressure on their redox states. Contribs. Mineral. Petrol. 108, 82-92.
Luhr J.F. (1990) Experimental Phase Relations of Water- and Sulfur-Saturated Arc Magmas and the 1982 Eruptions of El Chichón Volcano. J. Petrol. 31(5), 1071-1114.
Matjuschkin V., Blundy J.D., Brooker R.A. (2016) The effect of pressure on sulphur speciation in mid‑ to deep‑crustal arc magmas and implications for the formation of porphyry copper deposits. Contrib Mineral Petrol. 171, 66.
Marrocchi Y., Libourel G. (2013) Sulfur and Sulfides in CV Chondrules. Geochim. Cosmochim. Acta. 119, 117-136.
Namur O., Charlier B., Holtz F., Cartier C., McCammon C. (2016b) Sulfur solubility in reduced mafic silicate melts: Implications for the speciation and distribution of sulfur on Mercury. EPSL. 448, 102-114.
Namur O., Collinet M., Charlier B., Grove T.L., Holtz F., McCammon C. (2016a) Melting processes and mantle sources of lavas on Mercury. EPSL. 439, 117-128.
O’Neill H.St.C., Wall V.J. (1987) The Olivine-Orthopyroxene-Spinel Oxygen Geobarometer, the Nickel Precipitation Curve, and the Oxygen Fugacity of the Earth’s Upper Mantle. J. Petrol. 28(6), 1169-1191.
Parat F., Holtz F., Feig S. (2008) Pre-eruptive Conditions of the Huerto Andesite (Fish Canyon System, San Juan Volcanic Field, Colorado): Influence of Volatiles (C–O–H–S) on Phase Equilibria and Mineral Composition. J. Petrol. 49(5), 911-935.
Roeder P.L., Emslie R.F. (1970) Olivine – liquid equilibrium. Contrib. Mineral. Petrol. 29, 275-289.
Roeder P.L., Reynolds I. (1991) Crystallization of Chromite and Chromium Solubility in Basaltic Melts. J. Petrol. 32(5), 909-934.
Sack R.O., Carmichael I.S.E., Rivers M., Ghiorso M.S. (1980) Ferric-ferrous equilibria in natural silicate liquids at 1 Bar. Contrib. Mineral. Petrol. 75, 369-376.
Sattari P., Brenan J.M., Horn I., McDonough W.F. (2002) Experimental Constraints on the Sulfide- and Chromite-Silicate Melt Partitioning Behavior of Rhenium and Platinum-Group Elements. Econ. Geol. 97, 385-398.
Scaillet B., Evans B.W. (1999) The 15 June 1991 Eruption of Mount Pinatubo. I. Phase Equilibria and Pre-eruption P–T–${{f}_{{{{{\text{O}}}_{2}}}}}$–${{f}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ Conditions of the Dacite Magma. J. Petrol. 40(3), 381-411.
Silventoinen S. (2020) Composition of chromite in the Sakatti Cu-Ni-PGE deposit, Central Lapland Greenstone Belt, Finland. Master`s thesis. University of Helsinki, Faculty of Science, Department of Geosciences and Geography, 95 p.
Usanovic M.I. (1964) Moderne Theorien über Säuren und Basen. Wissenschaft und Fortschritt 14, 499-526.
Vander-Kaaden K.E., McCubbin F.M. (2016) The origin of boninites on Mercury: An experimental study of the northern volcanic plains lavas. Geochim. Cosmochim. Acta. 173, 246-263.
Wood B.I., Bryndzia L.T., Johnson K.E. (1990) Mantle oxidation state and its relationship to tectonic environment and fluid speciation. Science. 248(4), 337-345.
Дополнительные материалы отсутствуют.