Известия РАН. Энергетика, 2019, № 1, стр. 140-158
Оценки показателей циркуляционной системы добычи геотермальной энергии в случае маломощного пласта
М. Г. Алишаев *
Институт проблем геотермии Дагестанского научного центра РАН
Махачкала, Россия
* E-mail: alishaev@rambler.ru
Поступила в редакцию 12.12.2017
Аннотация
Рассматриваются вопросы, связанные с планированием циркуляционной системы извлечения тепловой энергии Тарумовского гидротермального месторождения и определением параметров ее эксплуатации. Предлагаются наиболее простые формулы оценки естественного прогрева закачиваемой отработанной воды по стволу нагнетательной скважины и попутного извлечения тепла горных пород. Распространение температурных возмущений в горной породе и отбор тепла с накрывающих тонкий пласт горных пород рассматривается в рамках “схемы Ловерье” для горных пород и “схемы сосредоточенной емкости” для маломощного пласта. Исследуются параметры истощения теплового потенциала тонкого пласта и подпитки его кровлей и подошвой в течение длительного времени. Рассматриваются также потери тепла по стволу добычной скважины. Применительно к глубоким пластам Тарумовского месторождения термальных вод просчитаны эксплуатационные параметры извлечения теплоты и рекомендовано опытно-промышленное строительство ГеоЭС малой мощности (5 МВт). Срок ее эксплуатации составит более 50 лет. Строительство возможно лишь при условии, что будут найдены и внедрены эффективные способы предотвращения карбонатных отложений в скважинах, а также средства борьбы с фенолами в случае добычи минеральных ресурсов термальных вод.
1. ОБ ИЗВЛЕКАЕМОЙ ТЕПЛОВОЙ ЭНЕРГИИ ГИДРОТЕРМАЛЬНОГО МЕСТОРОЖДЕНИЯ
Добыча термальных вод в Дагестане получило широкое распространение в целях отопления, бальнеологии и парникового хозяйства [1]. Однако, строительство ГеоЭС требует более высоких температур (180°С и выше). Оно должно быть окупаемо и рассчитано на стабильную работу в течение 100 лет. При этом темпы добычи должны соответствовать возобновлению тепловых запасов за счет притока законтурных вод, кондуктивного теплообмена с кровлей и подошвой залежи. Если запасы законтурных вод достаточно велики, то строительство возможно за счет тепловой энергии не только рассматриваемой площади, но и резерва законтурных вод. Пластовое давление может надолго стабилизироваться за счет подпитки вод из-за контура, добыча горячей воды будет достаточно длительной, и можно говорить о возобновляемости запасов термальной энергии даже при небольших мощностях пластов, по которым ведется добыча. Целью обратной закачки в таких случаях является лишь захоронение отработанных вод.
В случае замкнутости залежи (или ее плохой связи с законтурными водами) извлечение геотермальной энергии непременно приведет к снижению пластового давления и дебитов скважин. Схемой разработки таких гидротермальных месторождений предусматривается частичная или полная обратная закачка отработанной воды для поддержания пластового давления в залежи и обеспечения стабильной работы скважин. Цикл: “добыча термальной воды – съем тепла (с возможным извлечением ценных компонент) – закачка в пласт отработанной воды” зачастую может стать необходимостью [1, 2].
Тарумовское месторождение глубинных термальных вод [3], применительно к которому будет идти речь, изучено бурением 7 скважин, из которых 3 были аварийными. Они расположены на небольшой площади, менее 6 км2, и на глубине порядка 5500 м. Эффективная мощность продуктивного пласта по разбуренной части площади в Дагестане мала, порядка 3–4 м. Пластовое давление велико, около 70 МПа и более. Дебиты скважин от 1000 до 6800 м3 воды в сут. Строительство на этой площади ГеоЭС под большим вопросом, как и извлечение ценных минералов, так как со снижением давления откладываются карбонаты на стенке скважины и снижаются дебиты вплоть до закупорки. Кроме того, высокое пластовое давление может быть обусловлено замкнутостью данной площади, и, если не будет реализована система циркуляции, то пластовое давление может снизиться из-за недостаточности притока законтурных вод.
Реализация ГЦС позволит снять тепло не только пласта, но и накрывающих и подстилающих пород частично, что должно продлить функционирование добычи еще на десятки лет. Пластовая температура воды и пород выше 190°С, можно снять более 100°С в наземном теплообменном цикле. Добыче воды 1000 м3/сут соответствует тепловая мощность в 4.2 × 100 × 1000/86 400 = 4.86 МВт, что при КПД = 14% обеспечит выработку электроэнергии 0.68 МВт. На разбуренной части Тарумовской площади для получения 1 МВт электроэнергии нужно добывать примерно 1500 кубометров воды в сутки. Реальная добыча (со скважин № 2 и № 4 по 1100 кубов в сут, со скважины № 6 около 6800 кубов) позволяет надеяться на более или менее длительную эксплуатацию их с общим дебитом 5000 кубов в сут. Мощность станции для опытной эксплуатации можно планировать в 5 МВт, что даст возможность обеспечить электрической энергией крупный поселок. Что касается части залежи месторождения в Ставропольском крае, то ее мощность существенно выше, залежь приподнята и площадь значительно больше. Это увеличивает перспективы освоения Тарумовского глубинного месторождения термальных вод для добычи ценных минералов и строительства ГеоЭС. Основная причина консервации пробуренных скважин – отложение карбонатных отложений вблизи устья из-за выпадения солей из термальных вод со снижением давления в жидкости. Средства защиты разрабатываются [4], надежда на освоение еще не потеряна. Наличие фенолов в термальной воде, однако, усложняет ситуацию.
В данной статье обсуждаются энергетические возможности циркуляционной системы “нагнетательная скважина–пласт–добывающая скважина–съем тепла” более подробно с тем, чтобы оценить реальные возможности извлечения тепла не столько хорошо проницаемого маломощного пласта, сколько с кровли и подошвы, т.е. подстилающих и накрывающих пласт горных пород. Для сведения читателей и подтверждения расчетов привлечены промысловые данные по исследованию нагнетательных и добычных скважин залежи фундамента месторождения Белый Тигр на шельфе Вьетнама, где пробурены скважины на нефть глубиной до 5000 м и автор проработал долгие годы.
2. ПРОГРЕВ ЗАКАЧИВАЕМОЙ ВОДЫ ПО СТВОЛУ НАГНЕТАТЕЛЬНОЙ СКВАЖИНЫ
Нагнетание воды для вытеснения нефти и поддержания фонтанного способа добычи получило широкое применение в мировой практике добычи углеводородов. Обычно закачивают морскую или речную воду с ее естественной температурой, которая значительно ниже пластовой температуры. При небольшой приемистости из-за обмена тепла с горными породами происходит естественный прогрев нагнетаемой воды. Такой прогрев, очевидно, зависит от глубины расположения залежи, теплопроводности пород и геотермического градиента. При больших темпах нагнетания эффект прогрева воды при движении ее по стволу скважины мал. Но для глубоко расположенных забоев эффект попутного прогрева нагнетаемой воды по скважине может стать практически значимым и при немалых расходах. При малых темпах нагнетания попутный прогрев желательно учитывать, он сказывается и для средних глубин [5–8].
Приведем замеренные промысловые данные о прогреве вод, закачиваемых в залежь фундамента месторождения Белый Тигр [8], которое расположено на шельфе Южно-Китайского моря во Вьетнаме (табл. 1). Водозабор производился с глубины моря 15–20 м, температура воды на устье скважины 20°С, закачивалась вода на глубину 4000 м и более. Температуры воды на забое, в зависимости от объемов нагнетания Q м3/сут, для ряда нагнетательных скважин залежи фундамента представлены выше. Исследования были проведены после долгих дискуссий во “Вьетсовпетро” и для анализа последствий нагнетания поверхностно-активных веществ на большие глубины.
Таблица 1.
Промысловые термометрические исследования нагнетательных скважин залежи фундамента месторождения Белый Тигр на шельфе Вьетнама
| Скв. 914. Дата 10–12.05.02. Приемистость 1000 м3/сут. Глубина 4000 м. Тпл = 146°С | |||||||
|---|---|---|---|---|---|---|---|
| Q, м3/сут | 960 | 0 | 228 | 347 | 492 | 655 | 844 |
| Tзаб, °С | 45.1 | 87.3 | 61 | 53.4 | 47.9 | 43.1 | 41.2 |
| Скв. 911. Дата 11–22.06.02; Приемистость 1000 м3/сут; Глубина 4150 м; Тпл = 150°С | |||||||
| Q, м3/сут | 984 | 0 | 912 | 1193 | 1483 | 1676 | 1897 |
| Tзаб, °С | 44.3 | 59.4 | 44.6 | 44.5 | 44.5 | 44.5 | 44.5 |
| Скв. 424. Дата 06–10.09.03; Приемистость 2000 м3/сут; Глубина 3930 м; Тпл = 144°С | |||||||
| Q, м3/сут | 2004 | 0 | 1047 | 1523 | 2003 | ||
| Tзаб, °С | 43.2 | 45.8 | 43.7 | 43.4 | 43.3 | ||
| Скв. 485. Дата 03–08.09.03; Приемистость 900 м3/сут; Глубина 4100 м; Тпл = 149°С | |||||||
| Q, м3/сут | 902 | 0 | 500 | 697 | 900 | ||
| Tзаб, °С | 52.1 | 93.7 | 69.4 | 59.2 | 54.3 | ||
Температура в первом столбце соответствует установившемуся режиму с заданным темпом закачки, второй столбец показывает восстановленную за 2–3 сут температуру в скважине при отсутствии закачки, остальные столбцы соответствуют указанным темпам расхода, причем режимы нагнетания менялись через каждые сутки. Приведенные результаты свидетельствуют, что учет попутного прогрева воды может заметно повлиять на термический режим пласта. Пройдя 4 км вглубь за счет теплообмена с горными породами, нагнетаемая вода прогревается ~ на 25°С. Данные свидетельствуют также, что за 2–3 сут температура на забое не восстанавливается до пластовых их значений, после простоя они еще далеки от Тпл. На примере скв. 424 видно, что температура на забое вообще не выросла за 2–3 сут, это из-за ее долговременной работы под нагнетанием.
В случае закачки отработанной термальной воды, она на устье имеет более высокую температуру (40°С и более). Вблизи устья вода будет дополнительно охлаждаться от горной породы, и только с глубин порядка 1–2 км она начнет нагреваться. Применим к новому случаю приближенный расчет, следуя методике [6, 7], и найдем изменение температуры по стволу нагнетательной скважины.
3. ИЗМЕНЕНИЕ ТЕМПЕРАТУРЫ ЗАКАЧИВАЕМОЙ В СКВАЖИНУ ВОДЫ ОТ УСТЬЯ ДО ЗАБОЯ
Введем следующие обозначения: z – вертикальная координата, направлена вниз, z > 0; r – радиальная координата, расстояние до оси скважины в метрах, r > Rс; Rс – радиус скважины в метрах; RТ – радиус температурного влияния скважины в метрах; L – глубина забоя скважины, в метрах; Γ – геотермальный градиент, около 3°С на 100 метров; λ – теплопроводность горной породы, около 1–3 Вт/м °С; Tо – температура закачиваемой в пласт отработанной воды на устье, около 40–60°С; Tв – температура закачиваемой воды на забое скважины, при входе в пласт; Tпл – пластовая температура, равная температуре горной породы на глубине забоя; Tг(z) – температура горной породы вдали от скважины, ее значения: 0 ≤ z ≤ L; Tг(0) = Tн; Tг(L) = Tпл; Tг(z) = Tн+ Γz; Γ = (Tпл– Tн)/L; Tн – температура нейтрального слоя, равная среднегодовой температуре земной поверхности; Tc(z) – усредненная по сечению температура воды в нагнетательной скважине вместе с металлической колонной.
По истечению нескольких недель после пуска в работу нагнетательной скважины термический режим приобретает квазиустановившийся характер, температура вдоль колонны во времени меняется слабо. Профиль температуры по радиальному направлению в горной породе принимаем логарифмически распределенным, а радиус температурного фронта меняющимся от времени по закону квадратного корня [5, 6]
(3.1)
$T(r,z) = {{T}_{{\text{c}}}}(z) + [{{T}_{{\text{г }}}}(z) - {{T}_{{\text{c}}}}(z)]\frac{{\ln ({r \mathord{\left/ {\vphantom {r {{{R}_{{\text{c}}}}}}} \right. \kern-0em} {{{R}_{{\text{c}}}}}})}}{{\ln ({{{{R}_{{\text{Т }}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{Т }}}}} {{{R}_{{\text{с }}}}}}} \right. \kern-0em} {{{R}_{{\text{с }}}}}})}}.$Как показано в [7], для больших времен, в асимптотическом приближении при вычислении притока тепла в скважину радиус температурного фронта следует брать согласно ${{R}_{{\text{T}}}} = 1.56\sqrt {at} ,$ где a есть температуропроводность горных пород. Ее значения вычислялись как отношение теплопроводности к объемной теплоемкости по справочным данным [9–11] и выражались в м2/год [1]. Теплопроводность λ пород горных пород в основном укладывается в интервал λ = 1–3 Вт/м °С (выше для кварцитов λ = 3–7 Вт/(м K), чуть ниже 1 Вт/(м K) для глинистых песчаников) [9, 10]. Объемная теплоемкость основных горных пород близка к 3 МДж/(м3 K) [11]. Для температуропроводности $a = {\lambda \mathord{\left/ {\vphantom {\lambda c}} \right. \kern-0em} c}$ получается основной интервал значений a = 10–30 м2/год.
Воспользуемся представлением температуры (3.1) и определим поток тепла из горной породы в колонну скважины. Для единицы длины колонны в единицу времени имеем поток тепла согласно закону Фурье
(3.2)
${{q}_{{\text{T}}}} = - 2\pi {{R}_{{\text{c}}}}\lambda \frac{{\partial T}}{{\partial r}} = 2\pi \lambda \frac{{{{T}_{{\text{г }}}}(z) - {{T}_{{\text{c}}}}(z)}}{{ln({{{{R}_{{\text{T}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{T}}}}} {{{R}_{{\text{C}}}}}}} \right. \kern-0em} {{{R}_{{\text{C}}}}}})}}.$Прирост температуры вдоль колонны вниз для элемента dz в единицу времени в стационарном режиме определяется радиальным обменом тепла с горными породами
где cв – удельная объемная теплоемкость воды.Введем безразмерный параметр теплообмена α
(3.4)
$\alpha = \frac{{2\pi \lambda L}}{{{{c}_{{\text{в }}}}Qln{\text{(}}{{R}_{T}}{\text{/}}{{R}_{{\text{c}}}}{\text{) }}}},\,\,\,\,{{R}_{{\text{T}}}} \approx 1.56\sqrt {at} .$Подставив (3.2) в (3.3) и произведя некоторые упрощения, для профиля средней температуры воды вдоль колонны скважины будем иметь уравнение с принятым начальным условием нагнетания воды на устье с температурой обратной закачки Tо, т.е.
(3.5)
$T_{{\text{c}}}^{'}(z) + \frac{\alpha }{L}{\kern 1pt} {{T}_{{\text{c}}}}(z) = \frac{\alpha }{L}{\kern 1pt} {{T}_{{\text{г }}}}(z),\,\,\,\,{{T}_{{\text{г }}}}(z) = {{T}_{{\text{н }}}} + \Gamma z,\,\,\,\,{{T}_{{\text{c}}}}(0) = {{T}_{{\text{о }}}}.$Решение задачи (3.5) элементарно и можно представить в виде
(3.6)
${{T}_{{\text{c}}}}(z) = \left( {{{T}_{{\text{н }}}} - \frac{{\Gamma L}}{\alpha } + \Gamma z} \right) + \left( {{{T}_{{\text{о }}}} - {{T}_{{\text{н }}}} + \frac{{\Gamma L}}{\alpha }} \right){{e}^{{ - \frac{\alpha }{L}z}}},$что дает зависимость температуры воды по стволу нагнетательной скважины. Придадим (3.6) более удобный для расчетов вид, заменив геотермальный градиент его средним значением – разностью температуры пласта и нейтральной поверхности, поделенной на длину вертикальной скважины. Тогда вместо (3.6) получим
(3.7)
${{T}_{{\text{c}}}}(z) = \left( {{{T}_{{\text{E}}}} - \frac{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{н }}}}}}{\alpha } + \left( {{{T}_{{{\text{п л }}}}} - {{T}_{{\text{н }}}}} \right)\frac{z}{L}} \right) + \left( {{{T}_{{\text{о }}}} - {{T}_{{\text{н }}}} + \frac{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{н }}}}}}{\alpha }} \right){{e}^{{ - \alpha \frac{z}{L}}}}.$Для изображения профилей температур вертикальной скважины приведем это выражение к безразмерному виду. Введем обозначения: вертикальной координаты ζ; для разности температур обратно закачиваемой воды и нейтрального слоя θо, для изменения средней температуры воды в скважине – Δθс. Время участвует неявно, оно входит в параметр α, определяющий интенсивность теплообмена воды и горной породы.
(3.8)
$\zeta = \frac{z}{L},\,\,\,\,{{\theta }_{{\text{о }}}} = \frac{{{{T}_{{\text{о }}}} - {{T}_{{\text{н }}}}}}{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{н }}}}}},\,\,\,\,\Delta {{\theta }_{{\text{с }}}}\left( \zeta \right) = \frac{{{{T}_{{\text{с }}}}\left( z \right) - {{Т }_{{\text{о }}}}}}{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{н }}}}}}.$Тогда профили изменения температуры вдоль колонны представятся в виде
(3.9)
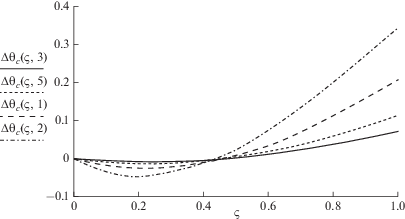
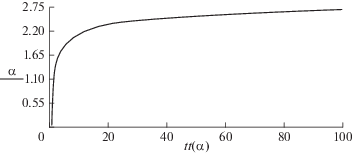
$\Delta {{\theta }_{{\text{с }}}}\left( \zeta \right) = \zeta - \left( {{{\theta }_{{\text{о }}}} + \frac{1}{\alpha }} \right)\left( {1 - {{e}^{{ - \alpha \zeta }}}} \right).$Некоторые параметры задачи применительно к скважинам Тарумовки будем считать постоянными: Rс ≈ 0.1 м; L ≈ 5500 м; λ ≈ 2.5 Вт/м K; св ≈ 4.2 МДж/м3 K. Темпы закачек в скважины примем равными Q = 1000; 2000 и 4000 м3/сут. При а = 20 м2/год и для времен 1 г., 5 и 25 лет значения $\ln \left( {{{{{R}_{{\text{T}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{T}}}}} {{{R}_{{\text{с }}}}}}} \right. \kern-0em} {{{R}_{{\text{с }}}}}}} \right)$ составляют 4.25; 5.05 и 5.85 м. Соответственно и параметр α будет уменьшаться в таком же слабом темпе, оставаясь почти постоянной величиной. Например, для L = 5500 м, λ = 2.5 Вт/м К, Q = 1000 м3/сут формула (3.4) дает α = 0.418; 0.352 и 0.308 соответственно на времена 1 г.; 5 и 25 лет. При малых дебитах, например, для 100 м3/сут, значения параметра были бы больше: α = 4.18; 3.52 и 3.08. На рис. 1 приведены графики для α = 0.3; 0.5; 1 и 2 при θо = 0.25.
Графики показывают, что повышение температур на забое имеет место для малых темпов нагнетания, т.е. при значениях α > 1. Также видно, что до глубин 0.4L ≈ 2 км в случае температуры обратной закачки отработанной воды Тарумовки $0.25\left( {{{T}_{{{\text{п л }}}}}--{{T}_{{\text{н }}}}} \right) + {{T}_{{\text{н }}}}$ = 60°С идет процесс остывания, ниже разогрев. Видно, что при больших темпах нагнетания, более 1000 м3/сут, прирост температуры по стволу составит менее десятой доли от разности температур пластовой и нейтрального слоя, т.е. менее 18°С для Тарумовки.
Температуру воды на забое скважины Тc(L) обозначим Тв. В согласии с (3.8), для нее имеем Δθв = Δθс (1)
(3.10)
$\Delta {{\theta }_{{\text{в }}}} = \left( {1 - \frac{1}{\alpha }} \right) + \left( {{{\theta }_{0}} + \frac{1}{\alpha }} \right)\exp ( - \alpha ).$Формулы (3.9) и (3.10) удобны для расчета температуры воды на забое скважины при заданной приемистости Q. На рис. 2 приведены графики зависимости от параметра α для некоторых выбранных значений ${{\theta }_{{\text{о }}}} = {{\left( {{{T}_{{\text{о }}}}--{{T}_{{\text{н }}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{{\text{о }}}}--{{T}_{{\text{н }}}}} \right)} {\left( {{{T}_{{{\text{п л }}}}}--{{T}_{{\text{н }}}}} \right)}}} \right. \kern-0em} {\left( {{{T}_{{{\text{п л }}}}}--{{T}_{{\text{н }}}}} \right)}}.$
Рис. 2.
Приращение температуры в нагнетательной скважине от устья до забоя, в долях от разности (Tпл– Tн), как функция параметра α для некоторых θо = 0.01; 0.05; 0.1; 0.2 и 0.3.
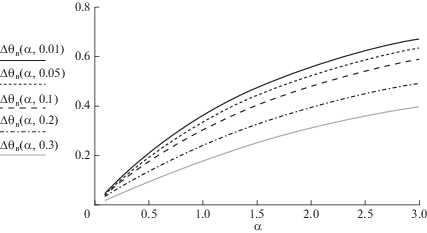
Графики показывают, что при малых расходах в нагнетательных скважинах можно достичь значительного разогрева нагнетаемых вод за счет ее естественного теплообмена. Это обстоятельство находит применение при заводнении нефтяных пластов холодной водой. Если закачка производится в слоистый пласт высоко парафинистой нефти и есть опасения кристаллизации парафина и ухудшении коллекторских свойств, то на начальных этапах рекомендуется воду закачивать малыми темпами, чтобы до забоя скважины она прогрелась. Этот прогрев можно сосчитать по формуле (3.10) или увидеть по графикам на рис. 2. Для всех α > 0.5, прогрев составляет более 10% от разности температур пласта и нейтрального слоя.
4. СЪЕМ ТЕПЛА ГОРНОЙ ПОРОДЫ МАЛОМОЩНЫМ ПЛАСТОМ
Пласт толщиной до 10 м считается маломощным, тонким. Для таких пластов существенным становится приток тепла с кровли и подошвы при циркуляции в пласте более “холодной” воды. Приток тепла с накрывающих и подстилающих пород заметно влияет на температурный фронт нагнетаемой в пласт воды, окружающие породы прогревает воду и могут существенно продлить жизнь циркуляционной системы. Температуропроводность горных пород и время, прошедшее после прохождения по пласту холодного фронта, отражаются на притоке тепла, поступающей с кровли и подошвы.
Хорошо известно решение задачи извлечения тепла из полубесконечного массива горных пород z > 0 с постоянной температурой Tп, омываемой при z = 0 холодной водой с температурой Tв < Tп. Это решение для температуры горной породы может быть представлено в виде, разрешенном относительно температурного снижения [2, 10]:
(4.1)
$\frac{{{{Т }_{{\text{п }}}} - Т \left( {z,t} \right)}}{{{{Т }_{{\text{п }}}} - {{Т }_{{\text{в }}}}}} = erfc\frac{z}{{2\sqrt {at} }},\,\,\,\,a = \frac{\lambda }{c}.$Здесь a есть температуропроводность горной породы по напластованию, c – объемная теплоемкость горной породы, λ – ее теплопроводность. Из формулы (4.1) видно, что распространение изотерм в горной породе происходит пропорционально квадратному корню произведения температуропроводности на время. Например, для изменения температуры на половину своего предельного значения, по таблицам erfc(η) = 0.5 находим значение аргумента η = 0.477. Это значит, что изотерма половинного понижения перепада температур движется по закону $z = 0.954\sqrt {at} .$ За год такая изотерма пройдет от 3 до 6 м в зависимости от теплофизических свойств пород. А за 25 лет изотерма углубится на 15–30 м. Накрывающая кровля за это время может отдать тепловую энергию с мощности двух десятков метров в эксплуатируемый гидротермальный пласт.
Широкую известность для расчета динамики температуры тонкого пласта при нагнетании воды с постоянной интенсивностью получила формула Ловерье [12, 13], первоначально предложенная нефтяниками для вытеснения горячей водой нефти. При выводе этой формулы по поперечному сечению пласта вводят усредненную температуру и пренебрегают кондуктивным членом в направлении движения по сравнению с конвективным переносом. Более того, вводят схему сосредоточенной емкости, при котором толщина пласта принимается равной нулю при сохранении ее теплоемкости и расхода. В горной же породе распространение температуры учитывается лишь в поперечном напластованию направлении. Формула Ловерье определяет как температуру пласта (при z = 0), так и температуру в любой точке кровли (при z > 0), где температура первоначально равнялась пластовой. В одномерном случае галереи она имеет вид [12, 1, 13]
(4.2)
$\frac{{Т - {{Т }_{{{\text{п л }}}}}}}{{{{Т }_{{\text{в }}}} - {{Т }_{{{\text{п л }}}}}}} = erfc\frac{{z + {{2\lambda {\kern 1pt} x} \mathord{\left/ {\vphantom {{2\lambda {\kern 1pt} x} {{{c}_{{\text{в }}}}uh}}} \right. \kern-0em} {{{c}_{{\text{в }}}}uh}}}}{{2\sqrt {a\left( {t - {{{{c}_{{{\text{п л }}}}}x} \mathord{\left/ {\vphantom {{{{c}_{{{\text{п л }}}}}x} {{{c}_{{\text{в }}}}u}}} \right. \kern-0em} {{{c}_{{\text{в }}}}u}}} \right)} }},\,\,\,\,a = \frac{\lambda }{c}.$Здесь: Тпл – начальная температура пласта и пород, Тв – температура воды на входе в галерею, λ и с – теплопроводность и объемная теплоемкость окружающих горных пород, св и спл – объемные теплоемкости воды и пласта, h – мощность пласта, u – скорость фильтрации. Температура остается равной первоначальной пластовой, если подкоренное выражение получается отрицательным или нулем. Фронт температурных возмущений движется от галереи согласно закону ${{x}_{{\text{T}}}}\left( t \right) = \left( {{{{{с }_{{\text{в }}}}} \mathord{\left/ {\vphantom {{{{с }_{{\text{в }}}}} {{{с }_{{{\text{п л }}}}}}}} \right. \kern-0em} {{{с }_{{{\text{п л }}}}}}}} \right)ut,$ и отстает от фронта закачиваемой воды ${{x}_{{\text{в }}}}\left( t \right) = {{ut} \mathord{\left/ {\vphantom {{ut} m}} \right. \kern-0em} m},$ где m – вытесняемая часть пористости. Отношение положения фронта вытеснения к фронту тепла составляет ${{{{x}_{{\text{в }}}}} \mathord{\left/ {\vphantom {{{{x}_{{\text{в }}}}} {{{x}_{{\text{T}}}}}}} \right. \kern-0em} {{{x}_{{\text{T}}}}}} = {{{{c}_{{{\text{п л }}}}}} \mathord{\left/ {\vphantom {{{{c}_{{{\text{п л }}}}}} {(m{{c}_{{\text{в }}}})}}} \right. \kern-0em} {(m{{c}_{{\text{в }}}})}}.$ При значениях: спл = 2.7; св = 4.2 МДж/м3, m = 0.15 это отношение равно 4.3. Фронт тепла отстает от фронта воды более 4-х раз. Когда вытесняемая вода поступит в добычную галерею, фронт тепла пройдет только четверть расстояния до галереи.
Примем в качестве характерного масштаба времени циркуляционной системы время подхода температурного возмущения к галерее и обозначим его через t1. Из (4.2) видно, что время подхода фронта температур к выходу из галереи определяется формулой
(4.3)
${{t}_{1}} = \frac{{{{c}_{{{\text{п л }}}}}l}}{{{{c}_{{\text{в }}}}u}} = \frac{{{{c}_{{{\text{п л }}}}}lbh}}{{{{c}_{{\text{в }}}}Q}},$Проследим за снижением температуры добываемой воды во времени. Пользуясь формулой (4.2) для z = 0, получим температурное распределение в пласте. При x = l найдем температуру Тд в добычной галерее. Вводя еще обозначение (4.3) и производя ряд манипуляций, для снижения температуры продукции на забое ΔТ = Тпл– Тд имеем
(4.4)
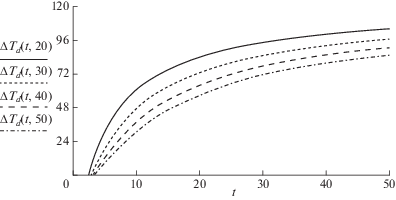
$\frac{{\Delta Т }}{{{{Т }_{{{\text{п л }}}}} - {{Т }_{{\text{в }}}}}} = erfc\frac{{\lambda {\kern 1pt} l}}{{{{c}_{{\text{в }}}}hu\sqrt {a\left( {t - {{t}_{1}}} \right)} }} = erfc\frac{{\lambda {\kern 1pt} {\kern 1pt} {{t}_{1}}}}{{h{{c}_{{{\text{п л }}}}}\sqrt {a\left( {t - {{t}_{1}}} \right)} }} = erfc\frac{{c{\kern 1pt} \sqrt {a{{t}_{1}}} {\kern 1pt} }}{{{{c}_{{{\text{п л }}}}}h\sqrt {{t \mathord{\left/ {\vphantom {t {{{t}_{1}}}}} \right. \kern-0em} {{{t}_{1}}}} - 1} }}.$На рисунке 3 показано снижение температуры жидкости на забое добычной галереи во времени для вышеуказанных параметров: c = 0.8cпл; h = 4 м; t1 = 1.76 лет; а = 20, 30, 40 и 50 м2/год при эксплуатации ГЦС на протяжении 50 лет. При подборе параметров ГЦС удобнее задаваться желаемым значением времени t1 и по нему подбирать соответствующие значения расстояний между скважинами при возможных дебитах скважин.
5. ОХВАТ ПЛАСТА НАГНЕТАЕМОЙ ВОДОЙ И ТЕМПЕРАТУРНЫМ ВОЗДЕЙСТВИЕМ
Прежде чем дать обобщение формулы Ловерье для циркуляционной системы пары скважин, необходимо привести способы расчета времени движения фронта нагнетаемой воды вдоль линий тока для стационарной плоской фильтрации.
Пусть в однородном и бесконечном пласте мощности h нагнетательная скважина расположена в точке $\left( {--a,0} \right),$ а добычная – в точке $\left( {a,0} \right),$ приемистость и дебит скважин одинаковы по объему и фильтрационное движение в пласте установившееся, поле скоростей стационарное. Комплексный потенциал течения запишется в виде суммы потенциалов источника и стока, с разными знаками, т.е. в виде [1, 14, 15]:
(5.1)
$W(z) = \frac{Q}{{2\pi h}}\ln \frac{{z + a}}{{z - a}} = \varphi \left( {x,y} \right) + i\psi \left( {x,y} \right),\,\,\,\,q = \frac{Q}{h}.$Для поля скоростей, дифференцированием (5.1), имеем:
(5.2)
$u - i\text{v} = \frac{{qa}}{{\pi z\left( {a - z} \right)}} = \frac{{qa}}{\pi }\left\{ {\frac{{x\left( {a - x} \right) + {{y}^{2}}}}{{\left( {{{x}^{2}} + {{y}^{2}}} \right)\left[ {{{{\left( {a - x} \right)}}^{2}} + {{y}^{2}}} \right]}} - i\frac{{\left( {a - 2x} \right)y}}{{\left( {{{x}^{2}} + {{y}^{2}}} \right)\left[ {{{{\left( {a - x} \right)}}^{2}} + {{y}^{2}}} \right]}}} \right\}.$Модуль скорости фильтрации, который и определяет движение отмеченной частицы вдоль линии тока (дуги окружности), получим из (5.2) как
(5.3)
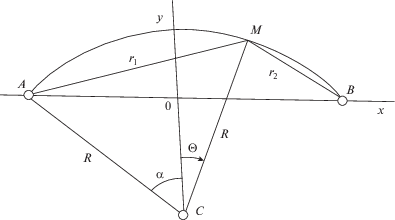
$\sqrt {{{u}^{2}} + {{\text{v}}^{2}}} = \upsilon \left( {x,y} \right) = \frac{{aq}}{\pi }\frac{1}{{\sqrt {{{{\left( {{{a}^{2}} - {{x}^{2}} + {{y}^{2}}} \right)}}^{2}} + 4{{x}^{2}}{{y}^{2}}} }}.$Как видно из формул (5.2–5.3), в декартовых координатах они громоздкие. В полярных координатах чуть проще, но остаются неудобными. Выкладки значительно упрощаются при введении новых геометрических величин R, α, θ, показанных ниже на рис. 4.
На рис. 4 нагнетательная скважина расположена в точке А, добывающая в точке В, расстояние АВ = l = 2а, линия тока АМВ есть дуга окружности с центром в точке С. Вводим центральный угол 2α, опирающийся на дугу АМВ, и радиус окружности R, соответствующий выделенной линии тока, касательная к которой в точке А наклонена к оси абсцисс Ox под углом α. Вводим угол θ, отсчитываемый по часовой стрелке от вертикали CO. Радиус R и угол θ есть новые переменные. Вдоль каждой линии тока радиус не меняется, меняется лишь угол θ, $--\alpha < \theta < \alpha .$ Вводим временно обозначения отрезков: АО = ОВ = а; ОС = h. Тогда имеем очевидные формулы:
(5.4)
$\begin{gathered} \alpha = \arcsin \frac{a}{R},\,\,\,\,\theta = \arcsin \frac{x}{R},\,\,\,\,{{R}^{2}} = {{a}^{2}} + {{h}^{2}},\,\,\,\, \pm OC = \pm h = \frac{{{{x}^{2}} + {{y}^{2}} - {{a}^{2}}}}{{2y}}, \\ {{r}_{1}} = \sqrt {{{{\left( {x + a} \right)}}^{2}} + {{y}^{2}}} = 2R\sin \frac{{\alpha + \theta }}{2},\,\,\,\,{{r}_{2}} = \sqrt {{{{\left( {x - a} \right)}}^{2}} + {{y}^{2}}} = 2R\sin \frac{{\alpha - \theta }}{2}. \\ \end{gathered} $Фронт воды вдоль линии тока проходит со скоростью большей, чем модуль скорости фильтрации (5.3), в 1/m раз, где m есть пористость. Но время, затрачиваемое ею вдоль линии тока до добычной скважины меньше соответственно, чем для фильтрационного движения. Вместо формулы (5.3) можно использовать производную по дуговой координате потенциала скорости φ, выраженной в переменных R и θ, и тогда для движения фронта воды (отмеченной жидкой частицы М) получим задачу:
(5.5)
$\frac{{ds}}{{dt}} = \frac{1}{m}\frac{{\partial \varphi }}{{\partial s}},\,\,\,\,\varphi (x,y) = \frac{q}{{2\pi }}\ln \frac{{{{r}_{1}}}}{{{{r}_{2}}}} = \frac{q}{{2\pi }}\ln \frac{{\sin \frac{{\alpha + \theta }}{2}}}{{\sin \frac{{\alpha - \theta }}{2}}},\,\,\,\,s = \left( {\alpha + \theta } \right)R,\,\,\,\,s(0) = 0.$После подстановок и алгебраических выкладок, задача для угла θ приобретает вид:
(5.6)
$\left( {\cos \theta - \cos \alpha } \right)\frac{{d\theta }}{{dt}} = \frac{{q\sin \alpha }}{{2\pi m{{R}^{2}}}},\,\,\,\,\theta \left( 0 \right) = - \alpha .$Интегрирование с учетом начального условия дает связь угла θ со временем:
(5.7)
$\sin \alpha + \sin \theta - \left( {\alpha + \theta } \right)\cos \alpha = \frac{{q{{{\sin }}^{3}}\alpha }}{{2\pi m{{a}^{2}}}}t.$Времена прихода по разным линиям тока отмеченных частиц из точки А в точку В получим из (5.7), положив θ = α:
(5.8)
$t = \frac{{4\pi m{{a}^{2}}}}{{q{{{\sin }}^{3}}\alpha }}\left( {\sin \alpha - \alpha \cos \alpha } \right).$Переходя к пределу при $\alpha \to 0,$ получим время прихода жидкой частицы ${{t}_{0}}$ по главной линии тока $\psi = 0,$ являющейся отрезком прямой АВ:
(5.9)
${{t}_{0}} = \frac{{4\pi m{{a}^{2}}}}{{3q}},\,\,\,\,\tau \left( \alpha \right) = \frac{t}{{{{t}_{0}}}} = 3\frac{{\sin \alpha - \alpha \cos \alpha }}{{{{{\sin }}^{3}}\alpha }}.$К примеру, для параметров: $m = 0.22;$ $a = 200\quad\,\,{\text{м }};\quad$ $q = 50{{{{{\text{м }}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м }}}^{{\text{2}}}}} {{\text{с у т }}}}} \right. \kern-0em} {{\text{с у т }}}},$ время движения фронта по главной линии тока t0 составляет 737 сут, т.е. около 2-х лет. Для углов α = 30°, 60°, 90°, 120° и 150° значения τ(α) составили 1.117; 1.582; 3; 8.84 и 66.4 соответственно согласно формуле (5.9). Времена же эти будут равны 2.26; 3.19; 6.06; 17.85 и 134 года. На рисунке 5 изображена кривая “обводнения” – доля (угловая мера) пришедших отмеченных частиц в зависимости от безразмерного времени τ. В момент времени τ в добычную скважину приходят частицы воды, вышедшие под углом α к главной линии тока.
Рис. 5.
Кривая “обводнения” добычной скважины дублета в неограниченном однородном пласте. “Водный период” длится бесконечно долго. Она определяет степень охвата площади пласта нагнетаемой водой.
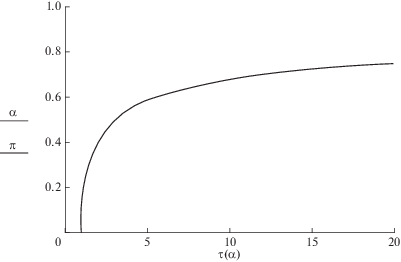
Формулу (5.7) можно использовать для изображения последовательных положений отмеченных частиц жидкости, закачанных в нагнетательную скважину. При проведении расчетов времени достижения данной точки (x, y) линией отмеченных частиц некоторые сложности возникают вблизи скважин и на главной линии тока, где η обращается в нуль. Для определения времени выражаем в безразмерных декартовых координатах ξ и η углы α и θ с помощью легко проверяемых формул:
(5.10)
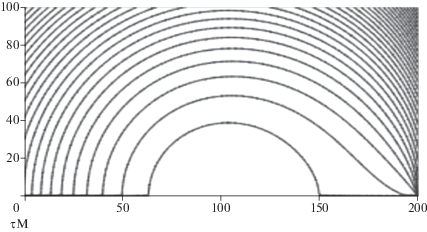
$\begin{gathered} \alpha \left( {\xi ,\eta } \right) = {\text{arcctg}}\frac{{1 - {{\xi }^{2}} - {{\eta }^{2}}}}{{2\eta }},\,\,\,\,\theta \left( {\xi ,\eta } \right) = \arcsin \left( {\xi \sin \alpha \left( {\xi ,\eta } \right)} \right), \\ \tau \left( {\xi ,\eta } \right) = \frac{3}{2}\frac{{\sin \alpha + \sin \theta - \left( {\alpha + \theta } \right)\cos \alpha }}{{{{{\sin }}^{3}}\alpha }},\,\,\,\,\tau = \frac{t}{{{{t}_{0}}}},\,\,\,\,\xi = \frac{x}{a},\,\,\,\,\eta = \frac{y}{a}. \\ \end{gathered} $На рис. 6 приведены последовательные положения контура отмеченных частиц (фронта вытеснения термальной воды нагнетаемой водой) для дублета на полуплоскости через равные промежутки времени. Нагнетательная скважина располагается на оси абсцисс с меткой 100. Добычная скважина с тем же дебитом располагается на оси абсцисс с меткой 200. Контуры ограничивают закачанную воду от пластовой воды. Температурный фронт кратно отстает от фронта вытеснения.
Отношение расстояний вдоль линий тока sT и sв, пройденных температурным фронтом и нагнетаемой в пласт водой, найдется из условия мгновенного выравнивания температуры скелета породы с температурой воды [5]. Скорость фронта воды выражается отношением модуля скорости фильтрации v к пористости m, а скорость фронта температур определяют по характеристическим линиям уравнения переноса тепла:
(5.11)
${{c}_{{{\text{п л }}}}}\frac{{\partial T}}{{\partial t}} + {{c}_{{\text{в }}}}\text{v}\frac{{\partial T}}{{\partial s}} = 0.$Из (5.11) получим для скорости распространения температурных возмущений и отношение путей, проходимых температурным фронтом и фронтом воды:
(5.12)
$\frac{{d{{s}_{{\text{T}}}}}}{{dt}} = \frac{{{{c}_{{\text{в }}}}\text{v}}}{{{{с }_{{{\text{п л }}}}}}},\,\,\,\,{{s}_{Т }}\left( t \right) = \frac{{{{c}_{{\text{в }}}}\text{v}t}}{{{{с }_{{{\text{п л }}}}}}},\,\,\,\,{{s}_{{\text{в }}}}\left( t \right) = \frac{{\text{v}t}}{m},\,\,\,\,\frac{{{{s}_{{\text{Т }}}}\left( t \right)}}{{{{s}_{{\text{в }}}}\left( t \right)}} = \frac{{m{{c}_{{\text{в }}}}}}{{{{c}_{{{\text{п л }}}}}}}.$Отставание температурного фронта определяется в основном параметром m, который имеет порядок около 0.2 для песчаных пластов, и порядок 0.02 для трещиноватых известняков. Объемная теплоемкость воды cв при 20°С равна 4.18 МДж/(м3 К), а для водонасыщенного пласта зависит от ее пористости и материала скелета породы. Как видно из рисунков для кернов Ярегского месторождения работы [11], водонасыщенный керн имеет удельную теплоемкость ≈3 МДж/(м3 К). Для песчаников Узени принимали [17] для заводненной области ${{c}_{{{\text{п л }}}}} = 2.7$ МДж/(м3 К). Если удельные теплоемкости принимать за постоянные величины, то для оценки отставания фронта температур имеем ${{s}_{{\text{T}}}} \approx 1.5m{{s}_{{\text{в }}}}.$ Когда фронт вытеснения пройдет 100 м, тогда фронт температур пройдет в песчаных пластах около 30 м, а в трещинных породах объемом пор 2% – всего 3 м.
Приведенные выкладки могут быть обобщены на случаи радиально цилиндрического и сферического поршневого вытеснений. В цилиндрическом случае радиус фронта вытеснения определяется площадью заводненного круга, в сферическом случае – объемом заводненного шара. Соответственно для температурных фронтов получим:
(5.13)
$\frac{{{{r}_{{\text{T}}}}\left( t \right)}}{{{{r}_{{\text{в }}}}\left( t \right)}} = \sqrt {\frac{{m{{c}_{{\text{в }}}}}}{{{{c}_{{{\text{п л }}}}}}}} ,\,\,\,\,\frac{{{{r}_{{\text{T}}}}\left( t \right)}}{{{{r}_{{\text{в }}}}\left( t \right)}} = \sqrt[3]{{\frac{{m{{c}_{{\text{в }}}}}}{{{{c}_{{{\text{п л }}}}}}}}}.$Подсчеты показывают, что отставание температурного фронта становится в многомерном случае чуть слабее. Для приведенных выше значений теплоемкостей cпл и cв положение температурного фронта находится: в радиальном случае как ${{r}_{{\text{T}}}} \approx \sqrt {1.5m} {{r}_{{\text{в }}}},$ а в сферическом случае как ${{r}_{{\text{T}}}} \approx \sqrt[3]{{1.5m}}{{r}_{{\text{в }}}}.$ При $m \approx 0.2$ для песчаников получим связь ${{r}_{{\text{T}}}} \approx 0.548{{r}_{{\text{в }}}},$ в плоском случае и ${{r}_{{\text{T}}}} \approx 0.669{{r}_{{\text{в }}}}$ в сферическом случае. Для трещиноватых пород малой пористости m $ \approx 0.02$ получим ${{r}_{{\text{T}}}} \approx 0.173{{r}_{{\text{в }}}}$ в цилиндрическом и ${{r}_{T}} \approx 0.311{{r}_{{\text{в }}}},$ в сферическом случае. Следовательно, температурный фронт существенно отстает от фронта вытеснения. Но температурные возмущения идут синхронно с фронтом вытеснения пластовой воды закачиваемой водой. Область распространения температур подобна области вытеснения, линия фронта распространения тепла подобны линиям фронта вытеснения ушедшего времени. Для теплоизолированного пласта контуры отмеченных частиц на рис. 5 могут быть рассматриваемы и как последовательные границы во времени температуры нагнетаемой в пласт воды.
6. ТЕМПЕРАТУРНЫЙ РЕЖИМ ТОНКОГО ПЛАСТА ДЛЯ ПАРЫ СКВАЖИН – ДУБЛЕТА
В работах [14–17] предложены аналоги формулы Ловерье при двумерной установившейся фильтрации в маломощном однородном пласте, в частности для дублета и сдвоенного дублета. При этом кондуктивным переносом тепла в пласте пренебрегается и используется “схема сосредоточенной емкости”. Температурное взаимодействие горного массива и тонкого пласта учитывается лишь теплопроводностью вдоль вертикальной координаты, горизонтальной теплопроводностью пород пренебрегается. Уравнение теплопереноса в пласте по существу служит граничным условием, оно пишется без учета кондуктивной теплопроводности пласта, как вдоль линий тока, так и поперек линий тока. Оно учитывает лишь конвективный перенос тепла вместе с жидкостью и теплообмен с кровлей и подошвой. Пренебрежение кондуктивной теплопроводностью поперек линий тока не внесет значительных погрешностей. Итак, ставится задача:
(6.1)
$c\frac{{\partial T}}{{\partial t}} = \lambda \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}},\,\,\,\,z > 0,\,\,\,\,{{c}_{{{\text{п л }}}}}\frac{{\partial T}}{{\partial t}} + {{c}_{{\text{в }}}}\left( {u\frac{{\partial T}}{{\partial x}} + \text{v}\frac{{\partial T}}{{\partial y}}} \right) = \frac{{2\lambda }}{h}\frac{{\partial T}}{{\partial z}},\,\,\,\,z = 0,$Здесь обозначения те же, что и выше: c, cпл и cв – объемные теплоемкости горной породы, пласта и воды; λ – теплопроводность горной породы, принимаемая одинаковой для кровли и подошвы; u и $\text{v}$ – компоненты скорости фильтрации воды, зависящие от (x, y).
Сформулированная задача имеет точное аналитическое решение [1], которое может быть получено преобразованием Лапласа по времени, переходом к решению линейного уравнения переноса изображения температуры и обращением изображения:
(6.2)
$\frac{{{{T}_{{{\text{п л }}}}} - T}}{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{в }}}}}} = erfc\left( {\frac{{z + \frac{{2\lambda \tau }}{{{{c}_{{{\text{п л }}}}}h}}}}{{2\sqrt {a\left( {t - \tau } \right)} }}} \right),\,\,\,\,a = \frac{\lambda }{c}.$Выкладки не приводим. В [17] дан детальный разбор схем Ловерье для разных задач. Здесь τ обозначено время, в течение которого температурное возмущение доходит от контура нагнетания до данной точки (x, y). Правая часть в (6.2) равна нулю до прихода температурного возмущения в рассматриваемую точку, т.е. при условии $t \leqslant \tau .$ В ряде случаев течений время τ может быть заранее определено в декартовых или полярных координатах. Например, в случае фильтрационного поля, образованного парой равно-дебитных скважин (дублетом), из которых нагнетательная и добычная расположены на расстоянии АВ = l = 2a друг от друга на оси абсцисс (рис. 4), время прихода теплового возмущения вдоль линии тока, выходящего под углом α от начала нагнетания в добычную скважину составит
(6.3)
${{t}_{{AB}}}\left( \alpha \right) = \frac{{\pi {{c}_{{{\text{п л }}}}}{{l}^{2}}h}}{{{{c}_{{\text{в }}}}Q}}\frac{{\sin \alpha - \alpha \cos \alpha }}{{{{{\sin }}^{3}}\alpha }},\,\,\,\,{{t}_{{AB}}}\left( 0 \right) = \frac{{\pi {{c}_{{{\text{п л }}}}}{{l}^{2}}h}}{{3{{c}_{{\text{в }}}}Q}} = {{t}_{1}}.$Снижение температуры начнется после прихода температурных возмущений по главной линии тока и будет более медленным, чем в случае галереи. Для времени прихода температурного возмущения в добычную скважину по главной линии тока α = 0 вторая из формул (6.3) получена предельным переходом при α → 0. Для параметров: спл = 2.7; св = 4.2 МДж/м3; Q = 1000 м3/сут; l = 500 м; h = 4 м; время t1 получается равным 673 сут или 1.84 г. По разным линиям тока (дугам окружностей) температурное снижение будет приходить все с большим запозданием. Вдоль разных линий тока в добычную скважину приходит температурный фронт в разное время. После перемешивания на забое скважины вода примет усредненное по всем линиям тока значение температуры.
В силу симметрии можно ограничиться значениями углов 0 < α < π, причем на части сектора 0 < α < α0 забоя добычи температура остается равной первоначальному пластовому значению ΔT = Tпл– T = 0. Формулы для нахождения относительного снижения температуры добываемой воды на забое примут вид:
(6.4)
$\frac{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{д }}}}}}{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{в }}}}}} = \frac{1}{\pi }\int\limits_0^{{{\alpha }_{0}}} {erfc\left( {\frac{{\sqrt {\lambda c} {{t}_{{AB}}}\left( \alpha \right)}}{{{{c}_{{{\text{п л }}}}}h\sqrt {t - {{t}_{{AB}}}\left( \alpha \right)} }}} \right)} d\alpha ,\,\,\,\,3\frac{{\sin {{\alpha }_{0}} - {{\alpha }_{0}}\cos {{\alpha }_{0}}}}{{{{{\sin }}^{3}}{{\alpha }_{0}}}} = \frac{t}{{{{t}_{1}}}} = {{\tau }_{{AB}}}.$Подсчитаем для безразмерного времени t/t1 > 1 нарастание значений угла α0 со сниженной температурой. На рис. 7 изображен этот график для α0, подсчитанный по (6.4).
Для проведения расчетов снижения температуры добычной скважины удобнее ввести безразмерное время τAB = t/t1. Тогда, после замен в (6.4), формула примет вид:
(6.5)
$\frac{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{д }}}}}}{{{{T}_{{{\text{п л }}}}} - {{T}_{{\text{в }}}}}} = \frac{1}{\pi }\int\limits_0^{{{\alpha }_{0}}} {erfc\left( {\frac{{c\sqrt {a{{t}_{1}}} {{\tau }_{{AB}}}\left( \alpha \right)}}{{{{c}_{{{\text{п л }}}}}h\sqrt {{{\tau }_{{AB}}}\left( {{{\alpha }_{0}}} \right) - {{\tau }_{{AB}}}\left( \alpha \right)} }}} \right)} d\alpha ,\,\,\,\,{{\tau }_{{AB}}}\left( \alpha \right) = 3\frac{{\sin \alpha - \alpha \cos \alpha }}{{{{{\sin }}^{3}}\alpha }}.$Отношение объемных теплоемкостей горной породы и пласта термальных вод меняется в небольших пределах, от 0.8 до 0.9. Объемная теплоемкость сухих горных пород c ≈ 2.2 МДж/(м3 K), тогда как в пластах поры заполнены водой, и объемная теплоемкость возрастает за счет большего значения теплоемкости воды ${{c}_{{{\text{п л }}}}} = \left( {1--m} \right)c + m{{c}_{{\text{в }}}},$ где ${{c}_{{\text{в }}}} \approx 4.2$ МДж/(м3 K). Отношение ${{{{c}_{{{\text{п л }}}}}} \mathord{\left/ {\vphantom {{{{c}_{{{\text{п л }}}}}} c}} \right. \kern-0em} c} \approx 1 + m.$ При пористости от 0.14 до 0.22 можно брать ${{{{c}_{{{\text{п л }}}}}} \mathord{\left/ {\vphantom {{{{c}_{{{\text{п л }}}}}} c}} \right. \kern-0em} c} \approx 1.2.$ Видно, что на долговечности работы циркуляционной системы отражается в основном мощность пласта и температуропроводность горных пород.
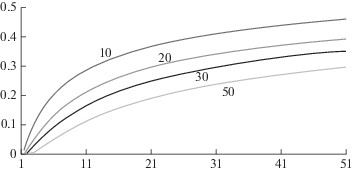
На рисунке 8 даны графики для условий: c/cпл = 0.8; Q = 1000 м3/сут; l = 500 м; h = 4 м. Вдоль оси абсцисс отложено время, отсчитываемое после достижения температурным фронтом добычной скважины. По этим графикам хорошо видно, как отражается температуропроводность горных пород на снижении температуры добычной скважины.
Рис. 8.
Снижение температуры на забое добычной скважины дублета. По оси отложено время в масштабе t1. По оси ординат отложено доля снижения от разности пластовой температуры и температуры нагнетаемой в пласт воды. На кривых показаны температуропроводности, м2/год.
В другом случае, когда фильтрационное поле образовано линейным рядом чередующихся нагнетательных и добычных скважин равной интенсивности, расположенных вдоль оси абсцисс в точках nl, для времени прихода фильтрационной частицы от нагнетательной скважины в точке (0, 0) до точки (х, у), 0 < x < l, y > 0 получится формула:
(6.6)
$t\left( {x,y} \right) = \frac{{4{{l}^{2}}h}}{{\pi {\kern 1pt} Q}}\frac{{{{\theta }_{0}} - \arcsin (\sin {{\theta }_{0}}\cos (\pi x{\text{/}}l))}}{{\sin 2{{\theta }_{0}}}},\,\,\,\,{\text{tg}}{{\theta }_{0}} = \frac{{\operatorname{sh} (\pi y{\text{/}}l)}}{{\sin (\pi x{\text{/}}l)}}.$(6.7)
$t\left( {x,0} \right) = \frac{{2{{l}^{2}}h}}{{\pi {\kern 1pt} Q}}\left( {1 - \cos \frac{{\pi {\kern 1pt} x}}{l}} \right),\,\,\,\,t\left( {l,0} \right) = \frac{{4{{l}^{2}}h}}{{\pi {\kern 1pt} Q}}.$Время движения фильтрационной “частицы” вдоль главной линии тока составляет $t\left( {l,0} \right) = 4{{l}^{2}}h{\text{/}}\pi Q,$ время достижения температурного возмущения в добычную скважину составит t1 = 4l2hспл/πmсвQ. При расстоянии между скважинами l = 0.5 км, дебите Q = 1000 м3/сут, h = 4 м, и объемных теплоемкостях спл= 2.7 и св = 4.2 МДж/(м3 °С) получаем t1 = 819 сут или 2.24 г.
Интерес представляют и другие циркуляционные системы, в которых число нагнетательных скважин кратно больше числа добычных. Можно расписать и дать анализ ГЦС с тремя нагнетательными скважинами, расположенными по вершинам равностороннего треугольника и одной добычной скважины с трехкратным дебитом в центре этого треугольника. В этой задаче также выписывается точное аналитическое решение для тепло и массопереноса в рамках схемы Ловерье для тонкого пласта. Выгода в том, что при больших дебитах добычной скважины относительные потери тепла по стволу меньше.
7. ТЕМПЕРАТУРНЫЕ ПОТЕРИ ВВЕРХ ПО СТВОЛУ ДОБЫВАЮЩЕЙ СКВАЖИНЫ
Подъем воды по стволу добычной скважины связан также с потерями тепла, так как через колонну скважины горячая вода или нефть отдают часть тепла в горную породу. На глубинах разность температур между колонной скважины и горной породой мала, поэтому малы и потери тепла. В верхней части ствола разность температур значительна и потери будут заметными. Может показаться, что в теплообмене нагнетательной и добывающей скважин нет разницы. Однако в добывающей скважине со снижением давления может выделяться растворенный газ, объем расширяется. С этим и связана разница – из-за выделения газа в стволе добычной скважины и его адиабатического расширения может наступить снижение температуры. Причем такой эффект для нефтяной скважины должен проявляться сильнее, так как газа здесь выделяется много больше, нежели при добыче термальной воды. В табл. 2 приведены фактические данные по замеренным значениям температур на забое и на устье для ряда добычных нефтяных скважин залежи фундамента месторождения Белый Тигр.
Таблица 2.
Температуры на забое и устье фонтанирующих нефтяных скважин
| NN | Pаботающий | Дебит | Текущ. | Текущ. | ГДИ | T | T | T | ΔT | |
|---|---|---|---|---|---|---|---|---|---|---|
| скв. | интервал | нефти | обвод. | газфакт | скважин | устье | забой | пласт | потери | |
| от | до | т/сут | % | м3/т | даты | °С | °С | °С | °С | |
| 1 | 3043 | 3103 | 36 | 0.5 | 370 | 08.11.03 | 38 | 133.3 | 132.2 | 95 |
| 2 | 3193 | 3259 | 1160 | 0 | 188 | 03.06.04 | 104 | 138.9 | 137.8 | 35 |
| 66 | 3627 | 3926 | 65 | 12.4 | 108 | 13.04.02 | 29 | 133.3 | 133.3 | 104 |
| 81 | 3575 | 3925 | 215 | 0.4 | 178 | 15.02.04 | 78 | 146.1 | 142.4 | 68 |
| 102 | 3541 | 3602 | 35 | 19.8 | 320 | 15.04.99 | 34 | 126 | 118 | 92 |
| 121 | 3981 | 4022 | 98 | 2.3 | 100 | 02.10.03 | 52 | 140 | 139.5 | 88 |
| 401 | 3070 | 3139 | 710 | 0 | 305 | 17.05.04 | 97 | 134.4 | 132.2 | 37 |
| 402 | 3227 | 3650 | 890 | 0 | 198 | 06.06.04 | 98 | 132.7 | 129.0 | 35 |
| 403 | 3145 | 3217 | 755 | 0 | 210 | 06.11.03 | 96 | 136.1 | 133.3 | 40 |
| 404 | 3200 | 3485 | 580 | 0 | 186 | 23.03.04 | 96 | 135.7 | 135.1 | 40 |
| 407 | 3348 | 3586 | 636 | 0 | 194 | 09.01.04 | 104 | 137.9 | 136.7 | 34 |
| 409 | 3171 | 3331 | 664 | 0 | 200 | 12.06.04 | 95 | 135.7 | 133.4 | 41 |
| 411 | 3375 | 3433 | 770 | 0 | 198 | 05.01.04 | 107 | 132.9 | 132.4 | 26 |
| 426 | 3470 | 3714 | 650 | 0 | 185 | 03.02.04 | 96 | 130 | 130 | 34 |
| 456 | 3496 | 3695 | 830 | 7.8 | 170 | 02.06.04 | 100 | 131 | 131.1 | 31 |
| 478 | 3387 | 4462 | 190 | 0 | 300 | 09.02.04 | 66 | 126.8 | 126.0 | 61 |
| 491 | 3177 | 3398 | 1160 | 0 | 180 | 24.12.03 | 100 | 129.5 | 128.3 | 30 |
| 821 | 3704 | 3968 | 125 | 0.6 | 180 | 22.04.04 | 62 | 157.8 | 155.6 | 96 |
| 910 | 3346 | 3550 | 545 | 0 | 164 | 11.03.04 | 90 | 140.4 | 140.1 | 50 |
| 918 | 3374 | 3662 | 570 | 0 | 160 | 11.09.03 | 90 | 132 | 134 | 42 |
| 1116 | 3153 | 3229 | 750 | 0 | 190 | 18.02.03 | 85 | 127.5 | 121.6 | 42 |
| 7001 | 3346 | 3465 | 1450 | 0 | 177 | 01.08.03 | 102 | 132.9 | 129.7 | 31 |
| 7002 | 3281 | 3511 | 1430 | 0 | 184 | 06.01.04 | 95 | 131.3 | 129.0 | 36 |
Из таблицы видно, что при малых дебитах температурные потери велики (до 100°С), тогда как при высоких дебитах и глубинах 3500–4000 м они порядка 30°С. Потери температуры в добычных скважинах зависят не только от дебита. Наблюдается корреляция потерь температуры с насыщенностью газом пластовой нефти. Влияет также обводнение скважины, время эксплуатации и параметры конструкции скважин.
Для термальных вод перепад температуры от забоя до устья ниже, чем для пластовой нефти. Растворенного газа в нефти значительно больше, и потери температуры вызываются адиабатическим расширением с уменьшением статического давления. В термальных водах растворенного газа мало (около 3–4 м3/т) и потери из-за его выделения в свободную фазу незначительны. Судя по табл. 2, можно полагать, что для геотермальной скважины с высокими дебитами порядка 1000 т/сут и с учетом более высокой теплоемкости воды, средний температурный перепад составит порядка 20°С для глубин 5500 м.
Приведем расчет профиля температуры добычной скважины, пренебрегая эффектами выделения и адиабатического расширения растворенного газа. Поместим начало координат на забое и направим ось Oz вертикально вверх по стволу скважины, 0 < z < L. По аналогии с нагнетательной скважиной – формулами (3.1–3.5) получим уравнение:
(7.1)
$T_{{\text{c}}}^{'}(z) + \frac{\alpha }{L}{\kern 1pt} {{T}_{{\text{c}}}}(z) = \frac{\alpha }{L}{\kern 1pt} {{T}_{{\text{г }}}}(z),\,\,\,\,{{T}_{{\text{г }}}}(z) = {{T}_{{{\text{п л }}}}} - \Gamma z,\,\,\,\,{{T}_{{\text{c}}}}(0) = {{T}_{{\text{д }}}}.$Это уравнение то же, что и (3.5), отличие в начальном условии и профиле температуры окружающих скважину горных пород. Профиль температуры в добычной скважине:
(7.2)
${{T}_{{\text{c}}}}(z) = {{T}_{{{\text{п л }}}}} - \Gamma z + \frac{{\Gamma L}}{\alpha }\left( {1 - {{e}^{{ - \alpha \frac{z}{L}}}}} \right) - ({{T}_{{{\text{п л }}}}} - {{T}_{{\text{д }}}}){{e}^{{ - \alpha \frac{z}{L}}}},$На рисунке 9 приведены профили температур по стволу. Значения t = 2; 5; 10; 25 и 100 лет соответствуют α = 0.364; 0.332; 0.312; 0.289 и 0.260. Из рисунка 9 видно, что первые годы эксплуатации потери температур вдоль добычной скважины будут заметными, в нашем примере они составили более 20°С, но со снижением температуры на забое потери снижаются. Температура на устье составит
(7.3)
${{T}_{{\text{у }}}} = {{T}_{{\text{н }}}} + \left( {{{T}_{{{\text{п л }}}}} - {{T}_{{\text{н }}}}} \right)\frac{{1 - {{e}^{{ - \alpha }}}}}{\alpha } - \left( {{{T}_{{{\text{п л }}}}} - {{T}_{{\text{д }}}}} \right){{e}^{{ - \alpha }}}.$Рис. 9.
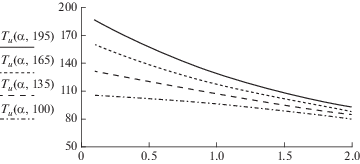
Профили температур добычной скважины от забоя до устья на разных этапах добычи применительно к условиям Тарумовки для температур на забое 195, 165, 135 и 100°С.
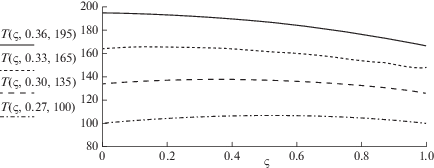
На рисунке 10 представлены устьевые температуры как функции параметра α. По графикам на рис. 10 можно видеть, что для малых α перепад температур от забоя до устья мал, для α = 0.3 он составляет 25, 17, 9 и 1°С при температурах на забое 195, 165, 135 и 105°С соответственно. При высоких дебитах Q параметр α становится меньше в обратной дебиту пропорции, и температурные потери соответственно будут меньше по стволу добычной скважины. Для скв. № 6 (Тарумовское геотермальное месторождение) дебит оценивался 6800 м3/сут и, по истечению первого месяца стабильной работы можно принять по (3.4) значение α = 0.079, температура на устье составит, согласно (6.3), Tу = 188°С, тогда как на забое оно равно Tд = 195°С. Перепад температур составит около 7°С.
Выше нами представлен возможный подход к оценке показателей работы в случае создания циркуляционной системы извлечения геотермальной энергии на длительный период с нагнетанием отработанной воды в тот же пласт. По другим работам [18–20] читатель может ознакомиться с более широким кругом вопросов освоения геотермальной энергии, а также проведением инженерных расчетов ее извлечения.
ЗАКЛЮЧЕНИЕ
В статье дан анализ показателей циркуляционной системы извлечения геотермальной энергии, с нагнетанием отработанной воды обратно в тот же пласт, применительно к Тарумовскому гидротермальному месторождению в Дагестане. Изложены аналитические подходы и получены формулы, позволяющие оценить показатели добычи термальных вод при освоении гидротермальной энергии тонкого пласта совместно с извлечением тепловой энергии накрывающих и подстилающих пласт горных пород.
Рассмотрена проблема изменения температуры закачиваемых обратно в пласт вод по стволу нагнетательной скважины от устья до забоя из-за контакта с горными породами. Скважина эксплуатируется с металлической колонной, температура воды по сечению трубы и металлической колонне усредняются, цементная часть колонны отнесена к горной породе. Радиус колонны считается неизменным по высоте, учитывается геотермальный градиент в горной породе. Теплообмен с горной породой от вертикальной скважины учитывается только в горизонтальном направлении. Предложены удобные для использования аналитические формулы. Приведены промысловые результаты по температурным замерам на забое и устье нагнетательных скважин, позволяющие контролировать предложенные формулы.
Рассмотрена задача конвективного переноса тепла по тонкому пласту с целью прогноза процесса снижения температуры на забое добываемой воды при длительной эксплуатации циркуляционной системы. Найдены формулы для времени начала снижения температуры на забое добычной скважины и последующей динамики падения температуры поступающей на забой воды. Предложенные формулы могут быть успешно использованы для выбора расстановки и определения долговечности эксплуатации циркуляционной системы. Показано, что в реальных условиях Тарумовского месторождения возможна добыча горячей воды и энергии в течение 50 лет и более.
Также рассмотрена задача о возможных потерях тепловой энергии в добычной скважине от забоя скважины до устья в тех же приближениях, что и для нагнетательной скважины. Найдены достаточно удобные формулы для определения температурных потерь. Для контроля приведены промысловые замеры падений температур в нефтяных фонтанных скважинах. Построены расчетные профили температуры добываемой воды во времени для длительной эксплуатации в условиях Тарумовского месторождения.
Список литературы
Гаджиев А.Г., Курбанов М.К., Суетнов В.В., Каспаров С.А., Гайдаров Г.М., Омаров М.О., Алишаев М.Г., Султанов Ю.И. Проблемы геотермальной энергетики Дагестана // М.: Недра, 1980. 208 с.
Геотермальная энергия (ресурсы, использование, разработка). М.: Мир, 1975. 354 с.
Саидов А.М., Джабраилов М.О., Рамазанов Ю.М., Курбанов М.К., Гайдаров Г.М., Китайгородский Н.С. Предварительные результаты гидродинамических исследований глубоких геотермальных скважин Тарумовской площади // В сб. научных трудов “Ресурсы термальных вод Дагестана и оптимизация схем их комплексного освоения” Института проблем геотермии Дагфилиала АН СССР, в. 4. Махачкала, 1985. С. 5–19.
Ахмедов Г.Я. Защита геотермальных систем от карбонатных отложений. М.: Научный мир, 2012. 330 с.
Чекалюк Э.Б. Термодинамика нефтяного пласта. М.: Недра, 1965. 238 с.
Проселков Ю.М. Теплопередача в скважинах. М.: Недра, 1986. 252 с.
Алишаев М.Г. Уточнение потерь тепла для геотермальной скважины. Известия АН. Энергетика. № 1. 2010. С. 36–47.
Шейнман А.Б., Малофеев Г.Е., Сергеев А.И. Воздействие на пласт теплом при добыче нефти. М.: Недра, 1969. 275 с.
Яковлев Б.А. Решение задач нефтяной геологии методами термометрии. М.: Недра, 1979. 138 с.
Пехович А.И., Жидких В.М. Расчеты теплового режима твердых тел. Л.: Энергия, 1976. 352 с.
Чехонин Е., Паршин А., Писаренко Д. и др. Теплофизические свойства пород-коллекторов. М.: Нефтегазовое обозрение. Том 22. № 3. 22 с.
Lauwerier H.A. The transport of heat in an oil layer caused by the injection of hot fluid. ‘Appl. Scientific Res.’ Sec. A., V. 5. № 2–3. 1955. P. 145–160.
Алишаев М.Г., Розенберг М.Д., Теслюк Е.В. Неизотермическая фильтрация при разработке нефтяных месторождений. М.: Недра, 1985. 273 с.
Алишаев М.Г. Предельные мощности извлечения тепла сухих горячих горных пород. Известия РАН. Энергетика. № 4. М.: 2012. С. 71–85.
Алишаев М.Г. Моделирование и расчет в прикладной механике и добыче нефти. Спецкурс для магистров. Махачкала: АЛЕФ, 2015. 288 с.
Алишаев М.Г. Расчет температурного поля пласта при инжекции жидкости для плоского фильтрационного течения // Известия АН СССР, МЖГ, 1980. № 1. С. 67–75.
Алишаев М.Г. Гидродинамические основы разработки нефтяных месторождений со структурно – механическими свойствами нефтей в пластовых условиях // Диссертация на соискание ученой степени доктора технических наук. М.: ВНИИ, 1975. 331 с.
Алхасов А.Б. Геотермальная энергетика: проблемы, ресурсы, технологии. М.: ФИЗМАТЛИТ, 2008. 376 с.
Череменский Г.А. Геотермия. Л.: Недра, 1972. 272 с.
Щербань А.Н., Цирульников А.С., Мерзляков Э.И., Рыженко И.А. Системы извлечения тепла земной коры и методы их расчета // Киев, Наукова думка, 1986. 248 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика