Известия РАН. Энергетика, 2019, № 1, стр. 37-49

Вероятностно-аналитический метод расчета показателей балансовой надежности ОЭС

В. П. Обоскалов^{1, 2, *}, Р. Т. Валиев²

¹ УрО РАН
Екатеринбург, Россия

² Уральский федеральный университет
Екатеринбург, Россия

^* E-mail: vpo1704@mail.ru

Поступила в редакцию 06.08.2018

DOI: 10.1134/S0002331019010096

Полный текст (PDF)

Аннотация

В рамках задачи оценки балансовой надежности (БН) объединенных электроэнергетических систем (ОЭС) рассматриваются аналитические процедуры, основанные на применении математического аппарата теории вероятностей. В качестве основной принята стратегия распределения генерирующей мощности пропорционально нагрузкам узлов. Распределение перетоков мощности по межсистемным связям осуществляется пропорционально разности углов векторов напряжений в узлах электрической сети. Рассмотрена проблема учета потерь мощности в межсистемных связях ОЭС. Показано, что учет потерь значимо влияет на результирующие показатели БН реальных ОЭС и поэтому их учет должен стать неотъемлемой процедурой при оценке БН ОЭС. Рассмотренные математические модели и алгоритмы апробированы на тестовой схеме. В качестве эталонного при оценке результатов принят метод статистического моделирования (Монте-Карло). Сравнение результирующих показателей показывает высокую эффективность и приемлемую точность предлагаемого вероятностно-аналитического метода.

Ключевые слова: электроэнергетические системы, балансовая надежность, показатели надежности, небаланс мощности, статистическое моделирование

ВВЕДЕНИЕ

Основным методом при определении показателей балансовой надежности (ПБН) вплоть до настоящего времени остается статистическое моделирование вероятностных состояний объединенных электроэнергетических систем (ОЭС) [1–5]. Это объясняется тем, что здесь при каждой статистической выборке частные проблемы балансовой надежности (БН) решаются в условиях детерминированности параметров, что позволяет использовать достаточно развитый математический аппарат и в полной мере учесть специфику электроэнергетических систем (ЭЭС).

Наиболее значимым блоком при определении ПБН на этапе анализа вероятностного состояния ОЭС является выбор управляющих воздействий, направленных на обеспечение баланса мощности и энергии при соблюдении технологических и режимных ограничений, за счет частичного локального ограничения нагрузки и (или) генерации. При детерминированности параметров ОЭС на данном этапе успешно реализуются процедуры линейного [6] и нелинейного программирования [7, 8], позволяющие в полной мере или частично учесть стратегии распределения дефицита или избытка мощности, законы Ома и Кирхгофа, ограничения по пропускной способности межсистемных связей (МСС), и простые ограничения по минимуму и максимуму рассматриваемых переменных.

Известны основные недостатки МСМ – достаточно большие временные затраты на получение решения с приемлемой точностью. Для задач перспективного развития энергосистем, где ПБН наиболее востребованы, длительность расчетов не является критичной. Именно это предопределило жизнеспособность МСМ для упомянутого класса задач. Однако использование рыночных механизмов в электроэнергетике, все большее использование генераторов электрической энергии, работающих на возобновляемых источниках энергии и общее усложнение структуры энергосистемы, привели к необходимости учета дополнительных факторов при оценке балансовой надежности энергосистемы [9–11]. Это, в свою очередь, приводит к усложнению моделей, используемых при расчетах ПБН и, как следствие, увеличению времени, требуемого для расчетов показателей. Временные затраты становятся велики даже по меркам задач долгосрочного планирования [9], что побуждает развитие теории балансовой надежности энергосистем в направлении вероятностных моделей без применения МСМ. Однако и в этом случае МСМ является необходимым, как эталонный при отладке тех или иных аналитических процедур.

Одной из специфических особенностей БН ОЭС является неучет закона Ома и второго закона Кирхгофа при большой неопределенности электрических параметров в задачах перспективного развития ЭЭС. Это позволяет исключить математический аппарат решения систем нелинейных уравнений установившихся режимов энергосистем и ограничиться линейным программированием и потоковыми моделями (Форда-Фалкерсона и др.). В основном, это объясняется тем, что БН в большей степени ориентирована на ОЭС, где каждая из составных энергосистем представляется концентрированным узлом, внутри которого нет ограничений по пропускной способности связей. Вся нагрузка и генерация такой концентрированной энергосистемы имеет вероятностный характер и сосредоточена в одном узле. Однако значимыми являются МСС и их ограниченная пропускная способность, которая не позволяет произвольно перераспределять потоки мощности и энергии, в результате чего возможны локальные дефициты мощности при суммарном избытке генерации.

При существующей структуре ОЭС потери мощности и энергии в МСС сопоставимы с математическим ожиданием (МО) недоотпуска электроэнергии потребителя. Их неучет приводит к существенной погрешности результирующих ПБН [5, 7, 8]. Известно, что потери мощности квадратично зависят от тока по МСС. Распределение токов, в свою очередь, определяется законами Ома и Кирхгофа. В результате область учитываемых факторов при расчете ПБН расширяется за счет включения новых ограничений.

К числу таких ограничений относится учет распределения потоков реактивной мощности, определяющих токи по МСС, а следовательно, и потери мощности в электрической сети. При этом распределение потоков активной мощности преимущественно определяется углами, а реактивной мощности – модулями векторов напряжений узлов ОЭС. В результате возникает необходимость оценки (в условиях задачи БН ЭЭС) параметров установившихся режимов ЭЭС в условиях вероятностного характера нагрузок и генерации. Данная задача известна как задача вероятностного потокораспределения (Probabilistic Power Flow), или (если решается оптимизационная задача) оптимального вероятностного потокораспределения (Probabilistic Optimal Power Flow) [12–16]. В рамках данной статьи предлагается вероятностно-аналитический метод (ВАМ) расчета показателей БН, учитывающий потери мощности в ЭЭС и зависимость распределения перетоков активной мощности от фазовых углов напряжений по концам передачи.

ПОСТАНОВКА ЗАДАЧИ

Задача. В рамках БН ОЭС необходимо с учетом вероятностного характера нагрузок и генерации, а также потерь мощности в межсистемных связях, по критерию распределения суммарного небаланса мощности ОЭС пропорционально мощности нагрузок узлов, выполнить распределение располагаемой генерации ОЭС между входящими в состав объединения концентрированными ЭЭС и определить интегральные показатели БН ОЭС.

Дополнительное условие. Потоки мощности по связям распределяются пропорционально разности фазовых углов напряжений инцидентных узлов.

Допущения. В рассматриваемой постановке не учитываются: балансы реактивной мощности, а также вероятностный характер структуры и пропускной способности МСС. Нагрузки и располагаемые генерации (независимые случайные величины) узлов описываются нормальными вероятностными распределениями; модули напряжений неизменны и равны номинальному напряжению сети.

Исходные данные: топология ЭЭС (матрица инциденций); проводимости связей; математические ожидания и дисперсии нагрузок и располагаемой генерации; пропускные способности МСС.

Результирующие данные: вероятность и математическое ожидание суммарного по ОЭС дефицита мощности, вероятности превышения перетоков мощности МСС предельно допустимых величин.

РАСПРЕДЕЛЕНИЕ ПЕРЕТОКОВ МОЩНОСТИ ПО МСС

Согласно критерию пропорционального распределения небалансов активной мощности, без учета потерь мощности в электрической сети,

(1)

$\bar {G} + \Delta \bar {G} = \mu \bar {L},$

где $\bar {L}$ – вектор мощностей узловых нагрузок; $\bar {G}$ – вектор располагаемых узловых генераций; $\Delta \bar {G}$ – вектор инъекций мощности из электрической сети, $\mu {\;}$ – коэффициент избыточности генерации:

(2)

$\mu = {{G}_{\Sigma }}/{{I}_{\Sigma }} = {{\left( {\sum {{{G}_{i}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum {{{G}_{i}}} } \right)} {\left( {\sum {{{I}_{i}}} } \right)}}} \right. \kern-0em} {\left( {\sum {{{I}_{i}}} } \right)}},$

где $\left\{ {{{G}_{i}},{{L}_{i}},i = 1, \ldots n} \right\}$ – компоненты векторов $\bar {G},\bar {L}.$

При этом вектор дополнительной генерации (инъекции) $\Delta \bar {G},$ направленной на выполнение заданного критерия (пропорциональное распределение суммарного НМ),

(3)

$\Delta \bar {G} = \mu \bar {L} - \bar {G}.$

Уравнения узловых напряжений, представляющие баланс активной мощности в узлах ЭЭС при представлении всех электрических величин в относительных единицах, неучете активной составляющей проводимостей связей и допущении неизменности и равенстве модулей напряжений имеют вид [17, 18]:

(4)

$B\bar {\delta } = \Delta \bar {G} = \mu \bar {L} - \bar {G},$

где B – мнимая составляющая матрицы узловых проводимостей; $\bar {\delta }$ – вектор углов напряжений. Из (4) определяются углы векторов напряжений:

(5)

$\bar {\delta } = {{B}^{{ - 1}}}\left( {\mu \bar {L} - \bar {G}} \right).$

При этом обеспечивающий выполнение двух критериев (пропорционального распределения небаланса мощности и распределения активной мощности по разности фазовых углов напряжений) вектор перетоков мощности по МСС:

(6)

$\bar {X} = {{D}_{{{{B}_{{br}}}}}}{{\hat {M}}^{T}}\bar {\delta } = A\left( {\mu \bar {L} - \bar {G}} \right),$

где (с учетом (5)) A = ${{D}_{{{{B}_{{br}}}}}}{{\hat {M}}^{T}}{{B}^{{ - 1}}},$ dim(A) = k(n – 1), dim(M) = nk; ${{D}_{{{{B}_{{br}}}}}}$ – диагональная матрица из реактивных проводимостей ветвей (dim(B_br) = k ×1); $\hat {M}$ – сокращенная на одну строку первая матрица инциденций (узлы-связи).

МО ПЕРЕТОКОВ МОЩНОСТИ

Считая располагаемую генерацию и нагрузки узлов независимыми величинами, и принимая во внимание, что МО произведения независимых случайных величин равно произведению их МО, согласно (6) можно записать:

(7)

${{\bar {m}}_{X}} = - A\left[ {{{m}_{{{{G}_{\Sigma }}}}}E\left( {\frac{{\bar {L}}}{{{{L}_{\Sigma }}}}} \right) - {{{\bar {m}}}_{G}}} \right],$

где ${{m}_{{{{L}_{\Sigma }}}}} = \sum\nolimits_{i = 1}^n {{{m}_{{{{L}_{i}}}}}} ,{{m}_{{{{G}_{\Sigma }}}}} = \sum\nolimits_{i = 1}^n {{{m}_{{{{G}_{i}}}}}} $ – суммарные по ОЭС МО нагрузки и генерации.

В выражении (7) фигурирует МО частного $E\left( {\bar {L}/{{L}_{\Sigma }}} \right)$, где числитель и знаменатель являются зависимыми случайными величинами, что требует дополнительного вероятностного анализа. С этой целью рассмотрим входящую в формулу (7) функцию:

$\bar {\psi }\left( {\bar {L}} \right) = \frac{{\bar {L}}}{{{{L}_{\Sigma }}}};\,\,\,\left\{ {{{\psi }_{i}} = \left( {\frac{{{{L}_{i}}}}{{{{L}_{\Sigma }}}}} \right),\,\,i = 1, \ldots ,n} \right\}.$

Квадратичная аппроксимация данной функции в точке, соответствующей МО нагрузок:

(8)

${{\psi }_{i}} = {{\psi }_{i}}\left( {{{{\bar {m}}}_{L}}} \right) + \sum\limits_{j = 1}^n {\frac{{\partial {{\psi }_{i}}\left( {{{{\bar {m}}}_{L}}} \right)}}{{\partial {{L}_{j}}}}{{{\tilde {L}}}_{j}} + \frac{1}{2}\sum\limits_{j = 1}^n {\sum\limits_{s = 1}^n {\frac{{{{\partial }^{2}}{{\psi }_{i}}\left( {{{{\bar {m}}}_{L}}} \right)}}{{\partial {{L}_{j}}\partial {{L}_{s}}}}{{{\tilde {L}}}_{j}}{{{\tilde {L}}}_{s}}} ,\,\,\,\,i = 1, \ldots ,n,} } $

где ${{\tilde {L}}_{i}} = {{L}_{i}} - E\left( {{{L}_{i}}} \right),$ $i = 1, \ldots ,n$ – центрированные случайные величины.

Выполняя элементарные математические преобразования, нетрудно получить квадратичную составляющую в выражении (8):

$\frac{1}{2}\sum\limits_{j = 1}^n {\sum\limits_{s = 1}^n {\frac{{{{\partial }^{2}}{{\psi }_{i}}\left( {{{{\bar {m}}}_{L}}} \right)}}{{\partial {{L}_{j}}\partial {{L}_{s}}}}{{{\tilde {L}}}_{j}}{{{\tilde {L}}}_{s}}} = - \frac{1}{{m_{{{{L}_{\Sigma }}}}^{2}}}{{{\tilde {L}}}_{i}}{{{\tilde {L}}}_{\Sigma }} + \frac{{{{m}_{{{{L}_{i}}}}}}}{{m_{{{{L}_{\Sigma }}}}^{3}}}} {{\tilde {L}}_{\Sigma }}{{\tilde {L}}_{\Sigma }},$

а следовательно, и в целом представление функции (8):

${{\psi }_{i}} = \frac{{{{m}_{{{{L}_{i}}}}}}}{{{{m}_{{{{L}_{\Sigma }}}}}}} + \frac{1}{{{{m}_{{{{L}_{\Sigma }}}}}}}{{\tilde {L}}_{i}} - \frac{{{{m}_{{{{L}_{i}}}}}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}{{\tilde {L}}_{\Sigma }} - \frac{1}{{m_{{{{L}_{\Sigma }}}}^{2}}}{{\tilde {L}}_{i}}{{\tilde {L}}_{\Sigma }} + \frac{{{{m}_{{{{L}_{i}}}}}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}{{\tilde {L}}_{\Sigma }}{{\tilde {L}}_{\Sigma }},\,\,\,i = 1, \ldots ,n.$

МО данной функции:

$E\left( {{{\psi }_{i}}} \right) = \frac{{{{m}_{{{{L}_{i}}}}}}}{{{{m}_{{{{L}_{\Sigma }}}}}}} + \frac{{{{m}_{{{{L}_{i}}}}}}}{{m_{{{{L}_{\Sigma }}}}^{3}}}{{D}_{{{{L}_{\Sigma }}}}} - \frac{1}{{m_{{{{L}_{\Sigma }}}}^{2}}}\operatorname{cov} \left( {{{L}_{i}}{{L}_{\Sigma }}} \right).$

В то же время корреляционный момент нагрузок L_i, L_Σ:

$\operatorname{cov} \left( {{{L}_{i}},{{L}_{\Sigma }}} \right) = \operatorname{cov} \left( {{{L}_{i}},\sum\limits_{j = 1}^n {{{L}_{j}}} } \right) = {{D}_{{{{L}_{i}}}}},$

где ${{D}_{{{{L}_{i}}}}}$ дисперсия нагрузки узла i. Отсюда

$E\left( {{{\psi }_{i}}} \right) = \frac{1}{{{{m}_{{{{L}_{\Sigma }}}}}}}\left( {1 + \frac{{{{D}_{{{{L}_{\Sigma }}}}}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}} \right){{m}_{{{{L}_{i}}}}} - \frac{1}{{m_{{{{L}_{\Sigma }}}}^{2}}}{{D}_{{{{L}_{i}}}}},\,\,\,\,i = 1, \ldots ,n$

или, в векторном представлении:

$E\left( {\bar {\psi }} \right) = \frac{1}{{{{m}_{{{{L}_{\Sigma }}}}}}}\left( {1 + \frac{{{{D}_{{{{L}_{\Sigma }}}}}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}} \right){{\bar {m}}_{L}} - \frac{1}{{m_{{{{L}_{\Sigma }}}}^{2}}}{{\bar {D}}_{L}}.$

Используя полученную формулу и выражение (7), МО перетоков мощности можно представить в виде:

${{\bar {m}}_{X}} = - A\frac{{{{m}_{{{{G}_{\Sigma }}}}}}}{{{{m}_{{{{L}_{\Sigma }}}}}}}\left[ {\left( {1 + \frac{{\sigma _{{{{L}_{\Sigma }}}}^{2}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}} \right){{{\bar {m}}}_{L}} - \frac{1}{{{{m}_{{{{L}_{\Sigma }}}}}}}{{{\bar {D}}}_{L}}} \right] - A{{\bar {m}}_{G}}.$

КОРРЕЛЯЦИОННАЯ МАТРИЦА ПЕРЕТОКОВ МОЩНОСТИ

Принудительное (по фазовым углам напряжений) распределение небаланса мощности между узлами предопределяет наличие зависимости между перетоками мощности по МСС, что приводит к их корреляции. С целью вычисления корреляционной матрицы в качестве анализируемой вектор-функции рассмотрим дополнительную инъекцию мощности в узлы электрической сети:

$\Delta \bar {G} = \bar {\varphi }\left( {\bar {L},\bar {G}} \right) = \frac{{{{G}_{\Sigma }}}}{{{{L}_{\Sigma }}}}\bar {L} - \bar {G}.$

Согласно (6) и свойствам корреляционной матрицы искомая корреляционная матрица K_X = AK_φA^T. В свою очередь, матрица ${{K}_{\varphi }}$ может быть определена через корреляционные матрицы нагрузок и генераций узлов при линейной аппроксимации вектор-функции $\bar {\varphi }\left( {\bar {L},\bar {G}} \right)$ в области МО узловых нагрузок и генераций

(9)

$\varphi \left( {\bar {L},\bar {G}} \right) = \varphi \left( {{{m}_{{\bar {L}}}},{{m}_{{\bar {G}}}}} \right) + {{J}_{L}}\tilde {L} + {{J}_{G}}\tilde {G} = \varphi \left( {{{m}_{{\bar {L}}}},{{m}_{{\bar {G}}}}} \right) + \left( {\begin{array}{*{20}{c}} {{{J}_{L}}}&{{{J}_{G}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\tilde {L}} \\ {\tilde {G}} \end{array}} \right).$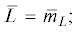

где J_L, J_G – матрицы Якоби, определенные при

$\bar {G} = {{\bar {m}}_{G}}$

(10)

${{J}_{L}} = \left[ {\frac{{\partial {{\varphi }_{i}}}}{{\partial {{L}_{j}}}}} \right] = {{m}_{\mu }}R;\,\,\,\,{{J}_{G}} = \left[ {\frac{{\partial {{\varphi }_{i}}}}{{\partial {{G}_{j}}}}} \right] = - R;$

$\frac{{\partial {{\varphi }_{i}}}}{{\partial {{L}_{i}}}} = {{\mu }_{m}}\left( {1 - \frac{{{{L}_{i}}}}{{{{L}_{\Sigma }}}}} \right);\,\,\,\frac{{\partial {{\varphi }_{i}}}}{{\partial {{L}_{j}}}} = - {{\mu }_{m}}\frac{{{{L}_{i}}}}{{{{L}_{\Sigma }}}},\,\,\,j \ne i;\,\,\,\frac{{\partial {{\varphi }_{i}}}}{{\partial {{G}_{j}}}} = \frac{{{{L}_{i}}}}{{{{L}_{\Sigma }}}} - 1;\,\,\,\frac{{\partial {{\varphi }_{i}}}}{{\partial {{G}_{j}}}} = \frac{{{{L}_{i}}}}{{{{L}_{\Sigma }}}},\,\,\,j \ne i;$

${{\mu }_{m}} = {{m}_{{{{G}_{\Sigma }}}}}/{{m}_{{{{L}_{\Sigma }}}}};\,\,\,R = \left[ {{{R}_{{ii}}} = 1 - \frac{{{{m}_{{{{L}_{i}}}}}}}{{{{m}_{{{{L}_{\Sigma }}}}}}};\,\,\,{{R}_{{ij}}} = - \frac{{{{m}_{{{{L}_{i}}}}}}}{{{{m}_{{{{L}_{\Sigma }}}}}}},\,\,\,j \ne i} \right],$

или, в матричном виде:

$R = I - \frac{1}{{{{m}_{{{{L}_{\Sigma }}}}}}}{\text{diag}}\left( {{{m}_{L}}} \right){{\left[ 1 \right]}_{{n,n}}};$

где I – единичная матрица; diag(m_L) – диагональная матрица из МО нагрузок; ${{\left[ 1 \right]}_{{n,n}}}$ – квадратная матрица n-го порядка, состоящая из единиц.

Согласно (9) матрица корреляционных моментов узловых инъекций:

${{K}_{\varphi }} = \left( {\begin{array}{*{20}{c}} {{{J}_{L}}}&{{{J}_{G}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{K}_{L}}}&0 \\ 0&{{{K}_{G}}} \end{array}} \right){{\left( {\begin{array}{*{20}{c}} {{{J}_{L}}}&{{{J}_{G}}} \end{array}} \right)}^{T}} = {{J}_{L}}{{K}_{L}}J_{L}^{T} + {{J}_{G}}{{K}_{G}}J_{G}^{T},$

где K_L, K_G – соответственно (диагональные при независимости нагрузок и генераций) ковариационные матрицы нагрузки и генерации.

Подставляя матрицы Якоби J_L, J_G (10) в (9), получаем:

${{K}_{\varphi }} = \left( {\begin{array}{*{20}{c}} {{{\mu }_{m}}R}&{ - R} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{K}_{L}}}&0 \\ 0&{{{K}_{G}}} \end{array}} \right){{\left( {\begin{array}{*{20}{c}} {{{\mu }_{m}}R}&{ - R} \end{array}} \right)}^{T}} = \mu _{m}^{2}R{{K}_{L}}{{R}^{T}} + R{{K}_{G}}{{R}^{T}} = R{{K}_{N}}{{R}^{T}},$

где диагональная матрица дисперсий расчетных НМ:

${{K}_{N}} = \mu _{m}^{2}{{K}_{L}} + {{K}_{G}}.$

Используя соотношение (6) нетрудно получить матрицу корреляционных моментов перетоков мощности по МСС:

${{K}_{X}} = A{{K}_{\varphi }}{{A}^{T}} = \left( {AR} \right){{K}_{N}}{{\left( {AR} \right)}^{T}}.$

ПОТЕРИ МОЩНОСТИ

Одним из путей решения проблемы учета потерь мощности в задаче БН является их учет через коэффициент потерь [1–8]. В частности для электрических сетей сверхвысокого напряжения ($U \geqslant 500{\;к В }$) потери мощности составляют ${{k}_{\pi }} = \left( {0.5--1} \right){\% \;}$ от выдачи мощности в электрическую сеть [19]. При использовании коэффициента потерь ключевым моментом является величина выдачи мощности в электрическую сеть, которую в рассматриваемой постановке можно определить как сумму положительных инъекций мощности (3). Отсюда суммарные потери мощности в электрической сети:

${{\pi }_{\Sigma }} = {{k}_{\pi }}\sum\limits_{i = 1}^n {\left( {\Sigma {{G}_{i}} > 0} \right)} .$

Принимая допущение о нормальном распределении узловых инъекций, можно получить математическое ожидание E(π_Σ) и дисперсию D(π_Σ) суммарных потерь мощности через МО $M\left( {a,b,m,D} \right)$ и дисперсию $D\left( {a,b,m,D} \right)$ редуцированного нормального распределения [20]:

$\begin{gathered} E\left( {{{\pi }_{\Sigma }}} \right) = {{k}_{\pi }}\sum\limits_{i = 1}^n {E\left( {\Delta {{G}_{i}} > 0} \right)} = {{k}_{\pi }}\sum\limits_{i = 1}^n {M\left( {0,\infty ,{{m}_{{\Delta {{G}_{i}}}}},{{D}_{{\Delta {{G}_{i}}}}}} \right);} \\ D\left( {{{\pi }_{\Sigma }}} \right) = k_{\pi }^{2}\sum\limits_{i = 1}^n {D\left( {\Delta {{G}_{i}} > 0} \right)} = k_{\pi }^{2}\sum\limits_{i = 1}^n {D\left( {0,\infty ,{{m}_{{\Delta {{G}_{i}}}}},{{D}_{{\Delta {{G}_{i}}}}}} \right),} \\ \end{gathered} $

где

(11)

$M(a,b,m,D) = aF\left( a \right) + b\left[ {1 - F(b)} \right] + m\left[ {F(b) - F(a)} \right] + D\left[ {f(a) - f(b)} \right];$

(12)

$\begin{gathered} D(a,b,m,D) = {{a}^{2}}F\left( a \right) + {{b}^{2}}\left[ {1 - F(b)} \right] + {{m}^{2}}\left[ {F(b) - F(a)} \right] + 2mD\left[ {f(a) - f(b)} \right] + \\ + \,\,D\left[ {\left( {m + a} \right)f\left( a \right) - \left( {m + b} \right)f\left( b \right)} \right] - m_{p}^{2}; \\ \end{gathered} $

$F\left( x \right),$ $f\left( x \right)$ – соответственно интегральная и дифференциальная функции нормального распределения.

Однако величина коэффициента потерь имеет большую неопределенность, поскольку она не привязывается к конкретной структуре электрической сети. Даже в упомянутом диапазоне $\left( {0.5{\kern 1pt} --{\kern 1pt} 1{\% \;}} \right)$ минимальная и максимальная оценки отличаются вдвое. В то же время, потери мощности существенно влияют на МО недоотпуска электроэнергии потребителям. Отсюда следует необходимость более точного расчета потерь мощности.

Известно, что потери активной мощности в МСС являются квадратичной функцией активной${\;}\left\{ {{{P}_{j}}} \right\}$ и реактивной $\left\{ {{{Q}_{j}}} \right\}$ мощностей по связям $j = 1, \ldots ,k{\text{:}}$

(13)

${{\pi }_{\Sigma }} = \sum\limits_{j = 1}^k {{{R}_{j}}\frac{{P_{{j(s)}}^{2} + Q_{{j(s)}}^{2}}}{{U_{s}^{2}}}} ,$

где s – номер одного из инцидентных узлов связи j.

В задаче БН ОЭС распределение реактивной мощности, как и решение уравнений установившихся режимов, не производится в силу большой неопределенности структуры и параметров электрической сети и, кроме того, акцент здесь ставится на обеспеченности потребителей активной энергией. В то же время в качестве исходных данных дополнительно могут быть заданы коэффициенты мощности концентрированных узлов нагрузки $\left\{ {{\text{tg}}{{\varphi }_{i}},\,\,\,\,i = 1, \ldots ,n} \right\},$ которые определяют реактивные мощности концентрированных ЭЭС. В ОЭС разнородность электропотребления концентрированных ЭЭС не очень велика, поэтому при расчете потерь мощности ${\text{tg}}\varphi $ можно считать одинаковым (например, средневзвешенный коэффициент мощности). В этом случае распределение потоков реактивной мощности по МСС будет пропорциональным распределению активной мощности с тем же ${\text{tg}}\varphi .$ В результате, согласно (13), при $U = 1{\;о }.{\text{е }}.$

(14)

${{\pi }_{\Sigma }} = \left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)\sum\limits_{j = 1}^k {{{R}_{j}}x_{j}^{2},} $

где ${{x}_{j}}$ – поток активной мощности по связи $j.$

Принимая во внимание, что:

$x_{j}^{2} = {{\left( {{{{\tilde {x}}}_{j}} + {{m}_{{{{x}_{j}}}}}} \right)}^{2}} = \tilde {x}_{j}^{2} + 2{{\tilde {x}}_{j}}{{m}_{{{{x}_{j}}}}} + m_{{{{x}_{j}}}}^{2},$

выражение (13) можно записать в виде:

${{\pi }_{\Sigma }} = \left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)\left( {\pi \left( {{{m}_{{\bar {X}}}}} \right) + 2\sum\limits_{j = 1}^k {{{R}_{j}}{{m}_{{{{x}_{j}}}}}{{{\tilde {x}}}_{j}}} + \sum\limits_{j = 1}^k {{{R}_{j}}\tilde {x}_{j}^{2}} } \right).$

Согласно этому выражению вектор потерь мощности в связях:

(15)

$\bar {\pi } = \left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)\left( {\bar {\pi }\left( {{{m}_{{\bar {X}}}}} \right) + 2\left[ {{{R}_{i}}{{m}_{{{{X}_{i}}}}}} \right]\tilde {X} + {{R}_{D}}{\text{diag}}\left( {\tilde {X}{{{\tilde {X}}}^{T}}} \right)} \right),$

где $\left[ {{{R}_{i}}} \right]$ – диагональная матрица из элементов $\bar {R},$ ${\text{diag}}\left( A \right)$ – вектор из диагональных элементов матрицы A.

Согласно (15) МО потерь мощности в связях:

$\bar {\pi } = \left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)\left( {\bar {\pi }\left( {{{m}_{{\bar {X}}}}} \right) + \left[ {{{R}_{i}}} \right]{\text{diag}}\left( K \right)} \right),$

где ${\text{diag}}\left( K \right)$ вектор из диагональных элементов матрицы корреляционных моментов перетоков мощности (дисперсии потоков мощности).

Матрица корреляционных моментов потерь мощности в МСС может быть определена при ограничении (15) линейной составляющей:

$\operatorname{cov} \left( {\bar {\pi }} \right) = \left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)\left[ {{{R}_{i}}{{m}_{{{{X}_{i}}}}}} \right]{{K}_{X}}{{\left[ {{{R}_{i}}{{m}_{{{{X}_{i}}}}}} \right]}^{T}}.$

МО суммарных потерь мощности в связях:

$E\left( \pi \right) = \left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)\left( {\pi \left( {{{m}_{{\bar {X}}}}} \right) + \sum\limits_{j = 1}^k {{{R}_{j}}\sigma _{j}^{2}} } \right).$

Оценка дисперсии суммарных потерь мощности может быть получена при представлении (14) в виде квадратичной формы:

${{\pi }_{\Sigma }} = \left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right){{\bar {X}}^{T}}\left[ {{{R}_{i}}} \right]\bar {X}.$

Если принять допущение о нормальном распределении потоков по МСС (приемлемое для БН ОЭС допущение), то дисперсия суммарных потерь определяется формулой [21]:

$\operatorname{var} \left( {{{\pi }_{\Sigma }}} \right) = {{\left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)}^{2}}\left[ {2{\text{tr}}\left( {{{{\left( {\left[ {{{R}_{i}}} \right]{{K}_{X}}} \right)}}^{2}}} \right) + 4\bar {m}_{X}^{T}\left[ {{{R}_{i}}} \right]{{K}_{X}}\left[ {{{R}_{i}}} \right]{{{\bar {m}}}_{X}}} \right],$

где ${\text{tr}}\left( . \right)$ – след матрицы.

Полученные оценки МО и дисперсии потерь мощности позволяют уточнить описанную выше расчетную процедуру за счет учета потерь мощности. Действительно, потери мощности представляют дополнительную нагрузку для ОЭС. В результате корректируется коэффициент избыточности (2):

$\mu = {{G}_{\Sigma }}/\left( {{{L}_{\Sigma }} + {{\pi }_{\Sigma }}} \right) = {{\left( {\sum {{{G}_{i}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum {{{G}_{i}}} } \right)} {\left( {{{\pi }_{\Sigma }} + \sum {{{L}_{i}}} } \right).}}} \right. \kern-0em} {\left( {{{\pi }_{\Sigma }} + \sum {{{L}_{i}}} } \right).}}$

Поскольку в качестве критериальной принята стратегия пропорционального распределения небалансов мощности, то потери также могут быть разнесены по узлам пропорционального их нагрузкам. Это может рассматриваться как простое увеличение нагрузок узлов. В результате описанная выше методика расчета перетоков мощности остается правомерной при поправке коэффициента избыточности.

В общем случае процесс уточнения потерь мощности является итерационным (новые потери – новое потокораспределение). Однако практические расчеты показывают, что здесь можно ограничиться одной итерацией.

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ ДЕФИЦИТА МОЩНОСТИ В ОЭС

Вероятностные параметры коэффициента избыточности. Используемый в стратегии пропорционального распределения небаланса мощности и определяемый отношением суммарной генерации к суммарной нагрузке объединенной ЭЭС коэффициент избыточности (2) может служить основанием при определении вероятности, МО и дисперсии дефицита мощности в ОЭС, а при пропорциональности распределения небаланса мощности и в каждой ЭЭС в отдельности. Действительно, дефицит мощности соответствует $\mu \left( {{{G}_{\Sigma }},{{L}_{\Sigma }}} \right) < 1.$ Отсюда зная характер функции распределения и вероятностные параметры коэффициента избыточности можно определить интересующие нас характеристики дефицитности.

Принимая во внимание, что:

$\frac{{\partial \mu }}{{\partial {{L}_{i}}}} = - \frac{{{{G}_{\Sigma }}}}{{L_{\Sigma }^{2}}};\,\,\,\frac{{\partial \mu }}{{\partial {{G}_{i}}}} = \frac{1}{{{{L}_{\Sigma }}}};\,\,\,\frac{{{{\partial }^{2}}\mu }}{{\partial L_{i}^{2}}} = \frac{{2{{G}_{\Sigma }}}}{{L_{\Sigma }^{3}}};\,\,\,\frac{{{{\partial }^{2}}\mu }}{{\partial {{L}_{i}}\partial {{G}_{i}}}} = \frac{{{{\partial }^{2}}\mu }}{{\partial {{G}_{i}}\partial {{L}_{i}}}} = - \frac{1}{{L_{\Sigma }^{2}}};\,\,\,\frac{{{{\partial }^{2}}\mu }}{{\partial G_{i}^{2}}} = 0,$

и выполняя квадратичную аппроксимацию (2), коэффициент избыточности можно представить в виде

(16)

$\mu \left( {{{G}_{\Sigma }},{{L}_{\Sigma }}} \right) = \frac{{{{m}_{{{{G}_{\Sigma }}}}}}}{{{{m}_{{{{L}_{\Sigma }}}}}}} - \frac{{{{m}_{{{{G}_{\Sigma }}}}}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}{{\tilde {L}}_{\Sigma }} + \frac{1}{{{{m}_{{{{L}_{\Sigma }}}}}}}{{\tilde {G}}_{\Sigma }} - \frac{1}{{m_{{{{L}_{\Sigma }}}}^{2}}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{{\tilde {L}}}_{i}}{{{\tilde {G}}}_{i}}} + \frac{{{{m}_{{{{G}_{\Sigma }}}}}}}{{m_{{{{L}_{\Sigma }}}}^{3}}}} \sum\limits_{i = 1}^n {\tilde {L}_{i}^{2}.} $

Согласно этому математическое ожидание (${{G}_{\Sigma }},{{L}_{\Sigma }}$ – независимые случайные величины)

${{m}_{\mu }} = \frac{{{{m}_{{{{G}_{\Sigma }}}}}}}{{{{m}_{{{{L}_{\Sigma }}}}}}}\left( {1 + \frac{{\sigma _{{{{L}_{\Sigma }}}}^{2}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}} \right).$

Ограничиваясь в (16) только линейной составляющей, достаточно просто можно получить дисперсию коэффициента избыточности:

$\sigma _{\mu }^{2} = \frac{1}{{m_{{{{L}_{\Sigma }}}}^{2}}}\left( {\frac{{m_{{{{G}_{\Sigma }}}}^{2}}}{{m_{{{{L}_{\Sigma }}}}^{2}}}\sigma _{{{{L}_{\Sigma }}}}^{2} + m_{{{{G}_{\Sigma }}}}^{2}} \right).$

Представленные параметры коэффициента избыточности позволяют определить вероятность, МО и дисперсию дефицита мощности. В частности, вероятность дефицита мощности:

$P\left( {\mu < 1} \right) = {{F}_{\mu }}\left( {1,{{m}_{\mu }},{{\sigma }_{\mu }}} \right).$

Используя формулы (11), (12) МО и дисперсии редуцированного интервалом (a, b) распределения нетрудно определить МО и дисперсию дефицита мощности в ОЭС:

(17)

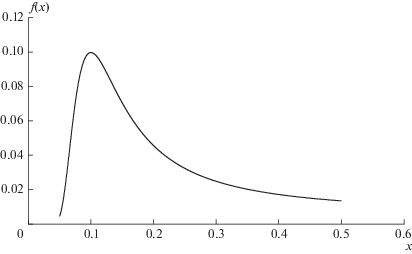
$\begin{gathered} E\left( {def} \right) = {{m}_{{{{L}_{\Sigma }}}}}\left( {1 - M(0;1;{{m}_{\mu }};{{D}_{\mu }})} \right); \\ D\left( {def} \right) = m_{{{{L}_{\Sigma }}}}^{2}D(0;1;{{m}_{\mu }};{{D}_{\mu }}). \\ \end{gathered} $

Следует отметить, что данные формулы выведены для процедуры редуцирования нормального распределения. В то же время, частное двух нормально распределенных случайных величин имеет несимметричное распределение в силу того, что несимметричное распределение имеет гипербола $1{\text{/}}x$ (рис. 1). Отсюда следует, что использование формул (17) связано с погрешностью расчетов. Более точное значение получается при применении гамма-распределения. Расчеты показывают, что ошибка находится в пределах практической допустимости и формулы (17) для нормального распределения могут быть использованы в реальных расчетах.

Рис. 1.

Плотность распределения $z = {1 \mathord{\left/ {\vphantom {1 x}} \right. \kern-0em} x}$ при ${{m}_{x}} = 10,$ ${{\sigma }_{x}} = 4.$

Взаимосвязь дефицита мощности в ОЭС с коэффициентом избыточности позволяет распространить математический аппарат на соотношение между суммарной нагрузкой ${{L}_{\Sigma }}$ и суммарной генерацией ${{G}_{\Sigma }}{\;}$ ОЭС, а следовательно, и на суммарной небаланс мощности ${{N}_{\Sigma }} = {{L}_{\Sigma }} - {{G}_{\Sigma }}{\;}$ в ОЭС. Здесь допущение о нормальном распределении ${{N}_{\Sigma }}$ является более убедительным. При этом МО и дисперсия дефицита мощности:

$E\left( {def} \right) = M\left( {0,\infty ,{{m}_{N}},{{D}_{N}}} \right);\,\,\,\,D\left( {def} \right) = D\left( {0,\infty ,{{m}_{N}},{{D}_{N}}} \right).$

Следует заметить, что расчеты по данным формулам несколько (несущественно для практических расчетов) отличаются от аналогичных показателей, полученных по методу Монте-Карло. Последнему есть логическое объяснение. Действительно, в области положительных дефицитов мощности варьирование НМ осуществляется за счет варьирования только нагрузки, в то время как НМ включает в себя и генерирующую составляющую. Более точными являются расчеты путем численного интегрирования плотности распределения или по формулам редуцированных распределений, но при дисперсиях нагрузок.

$E\left( {def} \right) = M\left( {0,\infty ,{{m}_{N}},{{D}_{L}}} \right);\,\,\,\,D\left( {def} \right) = D\left( {0,\infty ,{{m}_{N}},{{D}_{L}}} \right).$

ТЕСТОВЫЕ РАСЧЕТЫ

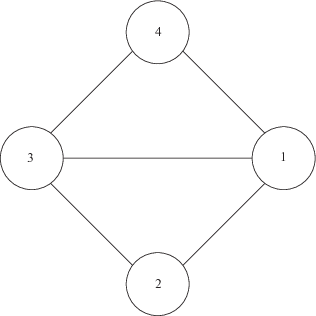
Для проверки предлагаемой вероятностной модели расчета показателей БН рассмотрена структура ОЭС (рис. 2) и исходные данные, представленные в табл. 1 (данные по узлам) и табл. 2 (данные по связям). Для линий электропередачи кроме инцидентных узлов (Fr, To) заданы активные (для расчета потерь мощности) и реактивные (для расчета потокораспределения) сопротивления ($R,X$), а также одинаковые в обоих направлениях пропускные способности (ПС) МСС.

Таблица 1.

Параметры нагрузки и генерации в узлах ОЭС

Узел	${{m}_{L}},$ МВт	${{\sigma }_{L}},$ МВт	${{m}_{G}},$ МВт	${{\sigma }_{G}},$ МВт
1	1000	100	1500	225
2	2000	200	4000	600
3	500	50	1200	180
4	5000	500	4000	600
ОЭС	8500	550	10 700	896

Таблица 2.

Параметры связей электрической сети

							МК			ВАМ
№	Fr	To	R, Ом	X, Ом	B, См	ПС, МВт	MP_ij, МВт	Mπ_ij, МВт	Pr over	MP_ij, МВт	Mπ_ij, МВт	Pr over
1	1	2	1	10	0.1	500	–329	4.31	0.112	–327	4.3	0.107
2	1	3	5	50	0.02	500	101	0.2	0	101	0.2	0.000
3	1	4	5	50	0.02	500	465	4.3	0.409	463	4.3	0.401
4	2	3	3	33	0.03	1500	1151	15.9	0.198	1145	15.7	0.193
5	3	4	1	10	0.1	2000	1816	13.2	0.34	1813	13.1	0.334
							Сумма	37.9		Сумма	37.6
							СКО	22.2		СКО	22

Рис. 2.

Тестовая схема.

В качестве эталонного был принят метод Монте-Карло (выборка – 100000 испытаний). В табл. 2 представлены расчеты МО потокораспределения ($M{{P}_{{ij}}}$), потерь мощности ($M{{\pi }_{{ij}}}$) и вероятностей превышения потока мощности предельно допустимого уровня (PR over) соответственно методами Монте-Карло (МК) и вероятностно-аналитическим (ВАМ). Нетрудно видеть, что при несопоставимо меньших временных затратах ВАМ (в среде MatLab 0.08 с. по сравнению с 11.8 c. при расчетах по методу Монте-Карло) результаты практически совпадают, что свидетельствуют о приемлемости и эффективности предлагаемых вычислительных процедур.

Результирующие показатели БН по ОЭС в целом представлены в табл. 3, где для сравнения обозначены три разновидностей расчетов: без учета потерь; с учетом потерь при ${\text{tg}}\varphi = 0$ (неучет реактивной мощности) и при ${\text{tg}}\varphi = 1$ (учет реактивной мощности с заданным ${\text{tg}}\varphi $). Анализ таблицы показывает, что и здесь результаты, полученные вероятностно-аналитическим методом практически совпадают с аналогичными величинами, полученными методом статистического моделирования.

Таблица 3.

Результирующие показатели ОЭС

Учет потерь	Метод	$P\left( {{\text{def}}} \right)$	MDP, МВт	m_μ,	σ_μ,	m_π, МВт	σ_π, МВт
Неучет потерь	МК	0.0179	6.93	1.264	0.135	0	0
Неучет потерь	ВАМ	0.0182	6.95	1.264	0.133	0	0
${\text{tg}}\varphi = 0$	МК	0.0196	7.54	1.255	0.133	42.2	23.1
${\text{tg}}\varphi = 0$	ВАМ	0.0203	7.83	1.257	0.132	41.8	22.9
${\text{tg}}\varphi = 1$	МК-100 000	0.0217	8.4	1.251	0.132	84.2	46.4
	МК-1000	0.019	7.29	1.26	0.13	81.9	45.7
	МВЭ	0.0223	8.72	1.25	0.131	83.7	45.8

Нетрудно видеть, что потери мощности (mπ, σπ) заметно влияют на результирующие вероятность $P\left( {{\text{def}}} \right)$ системного дефицита мощности и величину недоотпуска электроэнергии ${{M}_{{DP}}},$ хотя приращение недоотпуска электроэнергии существенно меньше приращения потерь. Следует заметить, что расчете потерь мощности недостаточно ограничиваться только активной составляющей потока мощности по МСС (второй режим, ${\text{tg}}\varphi = 0$). Потоки реактивной мощности (третий режим, ${\text{tg}}\varphi \ne 0$) оказывают не менее значимое воздействие на суммарные по ОЭС потери мощности.

С целью оценки разброса результирующих показателей, вычисленных методом Монте-Карло, была выполнена серия расчетов с разным по величине числом испытаний. При 100 000 испытаниях разброс параметров составил около 0.5%, в то время как при 1000 испытаниях наблюдался разброс около 3.4%. При этом результаты по ВАМ оказались внутри интервала неопределенности показателей надежности по методу МК, что позволяет при числе испытаний менее 100 000 считать ВАМ более точным методом. В табл. 3 для режима ${\text{tg}}\varphi = 1$ приведены результаты расчета по методу МК при числе испытаний 100 000 (МК-100 000) и 1000 (МК-100 0).

ЗАКЛЮЧЕНИЕ

Принципы распределения потоков мощности в электрической сети предопределяют величину потерь мощности в ОЭС и риски превышения потоков мощности в межсистемных связях предельно допустимых величин. Специфика оценки балансовой надежности ОЭС состоит в большой неопределенности исходных данных и, как результат, – большое число допущений и ограничений. В частности, здесь не применимы в полной мере процедуры расчета установившихся режимов ЭЭС, например, система уравнений узловых напряжений. Однако вполне обоснованной при решении задач БН ОЭС является тенденция более полного учета электрических свойств ОЭС.

Одним из электрических свойств ЭЭС является распределение потоков активных мощностей по межсистемным связям пропорционально разностям углов, а реактивных мощностей – модулям векторов напряжений в узлах. Первый из этих принципов положен в основу предлагаемого в данной работе метода вероятностного эквивалентирования. Линейная зависимость углов и узловых мощностей позволяют получать вероятностные характеристики углов и перетоков мощности по МСС.

В работе показано, что неучет потерь в межсистемных связях значимо завышает результирующие показатели надежности. Отсюда их учет должен стать неотъемлемой процедурой при оценке БН ОЭС. Проверочные расчеты показали высокую эффективности предложенного вероятностно-аналитического метода определения показателей балансовой надежности ОЭС, что дает основание рекомендовать его для практического использования.

Список литературы

Руденко Ю.Н., Чельцов М.Б. Надежность и резервирование в энергосистемах. Новосибирск: Наука, 1974.
Billinton R., Wenyan L. Reliability assessment of electric power systems using Monte Carlo methods. 1st ed. New York: Springer, 1994. 361 c.
Надежность систем энергетики и их оборудования. Спр. 4 т. / Под общей ред. Ю. Н. Руденко. Т. 2. Надежность электроэнергетических систем. Справочник / Под ред. М. Н. Розанова. М.: Энергоатомиздат, 2000. 568 с.
Чукреев Ю.Я., Чукреев М.Ю. Модели оценки показателей балансовой надежности при управлении развитием электроэнергетических систем. Сыктывкар: Коми научный центр УрО РАН, 2014. 207 с.
Ковалев Г.Ф., Лебедева Л.М. Надежность систем электроэнерегтики. Новосибирск: Сибирская издательская фирма “Наука” Академиздатцентра “Наука,” 2015.
Чукреев Ю.Я. Модели обеспечения надежности электроэнергетических систем. Сыктывкар: Изд-во Коми НЦ УрО РАН, 1995.
Зоркальцев В.И., Ковалев Г.Ф., Лебедева Л.М., Пержабинский С.М. Минимизация дефицита мощности в ЭЭС с учетом потерь мощности в линиях электропередачи // Электричество. 2010. № 9. С. 56–60.
Зоркальцев В.И. Пержабинский С.М. Модели оценки дефицита мощности электроэнергетической системы // Сибирский журн. индустриальной математики, 2012. Том XV. № 1 (49).
Mid-term adequacy forecas. ENTSO-E, 2016. 144 p.
CIGRE Technical brochure on review of the current status of tools and techniques for risk-based and probabilistic planning in power systems. Working group 601 of study committee C4. International conference on large high voltage electric systems. March 2010.
Hary N. The electricity generation adequacy problem: Assessing dynamic effects of capacity remuneration mechanism / N. Hary, V. Rious, M. Saguan // Energy Policy. 2016. issue 91. P. 113–127.
Манусов В.З. Вероятностные задача в электроэнергетике // Новосибирск: НЭТИ, 1981. 119 с.
Borkouska B. Probabilitic load flow. IEEE Paper No, T73 485-0 presented at the summer Meeting, Vancouver. February, 1973.
Allan R.N., Late da Silva A.-M., Burchett R.C. Evaluations methods and accuracy in probabilistic load flow solutions. IEEE Transactions on Power Apparatus and Systems. PAS-100(5): 2539–2546, May 1981.
Leite da Siva A.M., Arienti V.L., Allan R.N. Probabilistic load flow considering dependence between input nodal powers. IEEE Transactions on Power Apparatus and Systems, PAS-10s(6): 2539–2546, June 1981.
Schilling M.Th., Leite da Silva A.M., Billinton R., El-Kafy M.A. Bibliography on power system probabilistic analysis (1962–1988). IEEE Transactions on Power Systems, 5(1): 1–11, February 1990.
Аюев Б.И., Давыдов В.В., Ерохин П.М., Неуймин В.Г. Вычислительные модели потокораспределения в электрических сетях. М.: Флинта : Наука, 2008. 256 с.
Weedy B.M., Cory B.J. Electric Power Systems. John Wiley & Sons Ltd. 1998. 545 p.
Справочник по проектировнию электрических сетей / под ред. Д.Л. Файбисовича // Москва: ЭНАС, 2012. 376 с.
Обоскалов В.П. Надежность обеспечения баланса мощности электроэнергетических систем. Екатеринбург: УГТУ. 2002. 217 с.
Себер Дж. Линейный регрессионный анализ. М.: Мир, 1980. 456 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал