Известия РАН. Энергетика, 2019, № 1, стр. 109-122

Моделирование переходных процессов в катушке-конденсаторе при импульсном воздействии

П. А. Бутырин^1, *, Г. Г. Гусев¹, Д. В. Михеев¹, А. А. Кваснюк¹, М. В. Карпунина¹, Ф. Н. Шакирзянов¹

¹ Национальный Исследовательский Университет “МЭИ”
Москва, Россия

Поступила в редакцию 03.12.2018

DOI: 10.1134/S000233101901014X

Аннотация

В работе рассматриваются вопросы исследования переходных процессов в катушке-конденсаторе (катконе) при различных условиях: режиме холостого хода, короткого замыкания, согласованной и произвольной резистивной нагрузки. Для анализа переходных процессов предлагаются синтезированные по входному сопротивлению схемы замещения каткона с потерями и без потерь, приводятся выражения для нахождения корней характеристического уравнения для каждого из условий и определения добротности колебательного процесса. Приведены результаты экспериментального исследования переходных процессов при импульсном воздействии, подтверждающие корректность предложенных математических моделей.

Ключевые слова: катушка-конденсатор, каткон, переходные процессы, импульсное воздействие, добротность

ВВЕДЕНИЕ

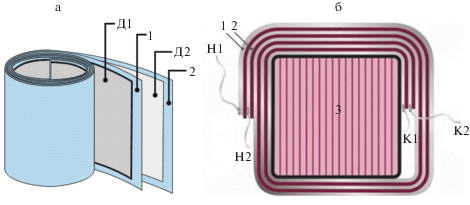
Катушка-конденсатор (каткон) – пассивный элемент электрической цепи, представляющий собой четырехполюсник и сочетающий одновременно свойства индуктивной катушки и конденсатора [1]. В простейшем случае каткон состоит из двух сложенных вместе изолированных друг от друга проводников, скрученных как показано на рис. 1а (1 и 2 – проводники в виде алюминиевой фольги, Д₁ и Д₂ – пленки диэлектрика). Для повышения надежности и удобства конструктивного исполнения, а также обеспечения необходимых регулировочных свойств его располагают на металлическом или неметаллическом сердечнике 3, а каждый из проводников 1 и 2 имеет в начале и конце пару выводов – Н₁, К₁ и Н₂, К₂ (рис. 1б). Данные выводы могут быть соединены по-разному, что позволяет использовать каткон для самых различных инженерных задач.

Рис. 1.

(а) Секция каткона, выполненная в виде спирально скрученных листов алюминиевой фольги 1 и 2, разделенных пленками диэлектрика Д₁ и Д₂. (б) Принцип построения каткона с сердечником (вид сверху).

Идея создания электротехнических устройств на основе данного элемента не нова – он может использоваться для осветительных приборов [2], электротермических устройств [3, 4], индуктивно-емкостных преобразователей [5–7], зарядных устройств [8], фильтров [9–11] и других целей. Авторы настоящей работы уже много лет изучают возможность создания многофункционального устройства на базе кактона и его использования в электроэнергетике и электротехнике для ряда энергетических задач, в частности, для компенсации реактивной мощности, снижения гармонических составляющих напряжения и ограничения токов короткого замыкания в электрических сетях. Сочетание в одном таком устройстве функций индуктивной катушки и конденсатора позволяет уменьшать его массогабаритные и стоимостные показатели и увеличивать надежность изделия в целом.

Авторами для обоснования этих выводов использовались результаты аналитических, физических и расчетно-экспериментальных исследований [12–14] применительно к установившемся режимам работа каткона. Поскольку для практики достаточно характерны переходные процессы, связанные с различными коммутациями, “сбросами” и “набросами” нагрузки и т.д., то для полноценного исследования возможности создания на базе каткона фильтрокомпенсирующих и токоограничивающих устройств требуется изучение поведения каткона и в таких режимах, чему и посвящена настоящая работа.

СИНТЕЗ СХЕМ ЗАМЕЩЕНИЯ КАТКОНА

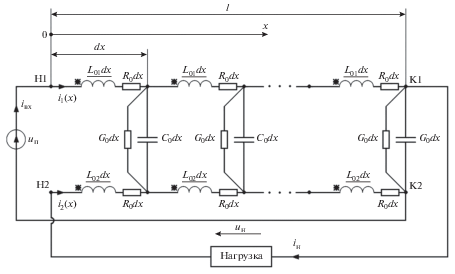
В общем случае схему каткона можно представить в виде линейной или нелинейной цепи с распределенными параметрами (рис. 2), если положить, что [1]:

Рис. 2.

Схема замещения каткона как цепи с распределенными параметрами:

u_п, В – напряжение источника питания

i_вх, i₁(х), i₂(х), А – входной ток, токи в первом и втором проводниках (i_вх = i₁(x) + i₂(x) = const)

R₀₁ = R₀₂ = R₀, Ом/м – сопротивление проводов каткона на единицу длины

L₀₁ = L₀₂ = L₀, Гн/м – индуктивность каткона на единицу длины

C₀, Ф/м – емкость между проводами на единицу длины

G₀, См/м – проводимость на единицу длины, учитывающая потери в изоляции между проводами.

• параметры каждого из проводов идентичны, т.е. индуктивность и активное сопротивление проводов равны между собой L₀₁(i₁) = L₀₂(i₂), R₀₁ = R₀₂ = R₀, и исполнение их такое, что емкость между ними на единицу длины C₀ много больше межвитковой емкости и емкости на землю;

• количество витков в первом и втором проводах равны: w₁ = w₂ = w;

• коэффициенты связи между отдельными витками равны единице, что обусловлено сильной магнитной связью;

• потоки в отдельных витках равны (Ф₁ = Ф₂ = Ф), и не зависят от координаты х, т.е. Ф₁ = Ф₂ = Ф = wMl(i₁ + i₂) = wMli_вх = const;

• входной ток каткона не зависит от координаты x, причем (i₁+ i₂) = i_вх = const;

• распределение токов i₁(x) и i₂(x) носит линейный характер при малых значениях величины $\left| {pl} \right| = \left| {\sqrt {2{{R}_{0}}\left( {j\omega {{C}_{0}} + {{C}_{0}}} \right)} l} \right|,$ учитывающей потери;

• нелинейность кривой намагничивания магнитопровода может быть учтена в эквивалентной схеме замещения, приведенной относительно входа каткона, в виде элемента L_0экl согласно [12] на основе методов гармонической линеаризации и усреднения.

Представленная на рис. 2 схема замещения каткона описывается системами волновых уравнений, которые представлены в табл. 1 для двух случаев: с учетом потерь (R₀ ≠ 0, G₀≠ 0) и без учета потерь (R₀ = 0, G₀ = 0) в катконе.

Таблица 1

С учетом потерь:	Без учета потерь:
$\left. \begin{gathered} - \frac{{\partial {{u}_{1}}}}{{\partial х }} = w\frac{{\partial {{{\text{Ф }}}_{1}}({{i}_{1}})}}{{\partial t}} + {{R}_{0}}{{i}_{1}} \hfill \\ - \frac{{\partial {{и }_{{\text{2}}}}}}{{\partial х }} = w\frac{{\partial {{{\text{Ф }}}_{2}}({{i}_{2}})}}{{\partial t}} + {{R}_{0}}{{i}_{2}} \hfill \\ \frac{{\partial {{i}_{1}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{1}} - {{u}_{2}})}}{{\partial t}} - ({{u}_{1}} - {{u}_{2}}){{G}_{0}} \hfill \\ \frac{{\partial {{i}_{2}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{2}} - {{u}_{1}})}}{{\partial t}} - ({{u}_{2}} - {{u}_{1}}){{G}_{0}} \hfill \\ \end{gathered} \right\}\,\,\,\,(1)$	$\left. \begin{gathered} - \frac{{\partial {{u}_{1}}}}{{\partial х }} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} \hfill \\ - \frac{{\partial {{и }_{{\text{2}}}}}}{{\partial х }} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} \hfill \\ \frac{{\partial {{i}_{1}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{1}} - {{u}_{2}})}}{{\partial t}} \hfill \\ \frac{{\partial {{i}_{2}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{2}} - {{u}_{1}})}}{{\partial t}} \hfill \\ \end{gathered} \right\}\,\,\,\,(2)$

С учетом потерь:

Без учета потерь:

$\left. \begin{gathered} - \frac{{\partial {{u}_{1}}}}{{\partial х }} = w\frac{{\partial {{{\text{Ф }}}_{1}}({{i}_{1}})}}{{\partial t}} + {{R}_{0}}{{i}_{1}} \hfill \\ - \frac{{\partial {{и }_{{\text{2}}}}}}{{\partial х }} = w\frac{{\partial {{{\text{Ф }}}_{2}}({{i}_{2}})}}{{\partial t}} + {{R}_{0}}{{i}_{2}} \hfill \\ \frac{{\partial {{i}_{1}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{1}} - {{u}_{2}})}}{{\partial t}} - ({{u}_{1}} - {{u}_{2}}){{G}_{0}} \hfill \\ \frac{{\partial {{i}_{2}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{2}} - {{u}_{1}})}}{{\partial t}} - ({{u}_{2}} - {{u}_{1}}){{G}_{0}} \hfill \\ \end{gathered} \right\}\,\,\,\,(1)$

$\left. \begin{gathered} - \frac{{\partial {{u}_{1}}}}{{\partial х }} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} \hfill \\ - \frac{{\partial {{и }_{{\text{2}}}}}}{{\partial х }} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} \hfill \\ \frac{{\partial {{i}_{1}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{1}} - {{u}_{2}})}}{{\partial t}} \hfill \\ \frac{{\partial {{i}_{2}}}}{{\partial х }} = - {{C}_{0}}\frac{{\partial ({{u}_{2}} - {{u}_{1}})}}{{\partial t}} \hfill \\ \end{gathered} \right\}\,\,\,\,(2)$

При этом применение системы (1) используется при рассмотрении режимов холостого хода и короткого замыкания (ХХ и КЗ) в катконе (выходные зажимы К₁ и Н₂ разомкнуты и замкнуты соответственно), а системы (2) – при рассмотрении режима работы каткона с произвольной (Z_н = var) и резистивной (R_н = var) нагрузкой, что обусловлено существенной трудностью аналитического решения системы (1) для данного случая. Для решения систем (1) и (2) используются граничные условия, представленные в табл. 2.

Таблица 2

Режим работы каткона	Граничные условия (для схемы на рис. 1)	№
Режим ХХ (Z_н → ∞)	i₂(0) = i₁(l) = 0; i₁(0) = i₂(l) = i_вх(t); u₁(0) = u_п(t); u₂(l) = 0.	(3)
Режим КЗ (Z_н = 0)	i₂(0) = i₁(l) ≠ 0; i₁(0) = i₂(l) = i_вх(t); u₁(0) = u_п(t); u₂(0) = u₁(l); u₂(l) = 0.	(4)
Режим произвольной нагрузки (Z_н = var)	i₁(0) = i₂(l) ≠ 0; i₁(l) = i₂(0) = i_вх(t); u₁(0) = u₂(l)–u_н(t); u₁(l) = 0; u₂(0) = u_п(l)–u_н(t).	(5)

Решая системы (1) и (2) (табл. 1) с учетом граничных условий (3)–(5) (табл. 2) для гармонического режима получены в явном виде выражения входных сопротивлений Z_вх относительно зажимов Н₁ и К₂ (с учетом ограничения слагаемыми первого порядка малости разложения в ряд Маклорена, т.е. cth(pl/2) ~ (2/pl + pl/6) [1]), которые приведены в табл. 3.

Таблица 3

Режим работы каткона		Выражения для входного сопротивления	№
Режим ХХ (Z_н → ∞)	С потерями	${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z} }_{{{\text{в х Х Х }}}}} = \frac{2}{3}{{R}_{0}}l + j{\omega }{{L}_{0}}l + \frac{1}{{j{\omega }{{C}_{0}}l + {{G}_{0}}l}}{\text{,}}\,\,\,\,{\text{О м }}{\text{.}}$	(6)
Режим ХХ (Z_н → ∞)	Без потерь	$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z} _{{{\text{в х Х Х }}}}^{'} = j{\omega }{{L}_{0}}l + \frac{1}{{j{\omega }{{C}_{0}}l}}{\text{,}}\,\,\,\,{\text{О м }}{\text{.}}$	(7)
Режим КЗ (Z_н = 0)	С потерями	${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z} }_{{{\text{в х К З }}}}} = \frac{{(2{{R}_{0}}l + 4j{\omega }{{L}_{0}}l)\left( {\frac{2}{3}{{R}_{0}}l + \frac{4}{{j{\omega }{{C}_{0}}l + {{G}_{0}}l}}} \right)}}{{2\frac{2}{3}{{R}_{0}}l + 4j{\omega }{{L}_{0}}l + \frac{4}{{j{\omega }{{C}_{0}}l + {{G}_{0}}l}}}}{\text{,}}\,\,\,\,{\text{О м }}{\text{.}}$	(8)
Режим КЗ (Z_н = 0)	Без потерь	$\underline Z _{{{\text{в х К З }}}}^{'} = \frac{1}{{j\frac{1}{{4{\omega }{{L}_{0}}l}} + \frac{{j{\omega }{{C}_{0}}l}}{4}}}{\text{,}}\,\,\,\,{\text{О м }}{\text{.}}$	(9)
Режим произвольной нагрузки (Z_н = var)		${{\underline Z }_{{{\text{в х }}}}} = \frac{1}{{{{{\underline Z }}_{{\text{н }}}}\frac{{{{C}_{0}}}}{{4{{L}_{0}}}} + j{\omega }\frac{{{{C}_{0}}}}{4}l + \frac{1}{{j{\omega }4{{L}_{0}}l}}}} + \frac{1}{{\frac{1}{{\frac{1}{{j{\omega }{{C}_{0}}l}} + j{\omega }{{L}_{0}}l}} + \frac{1}{{{{{\underline Z }}_{{\text{н }}}}}}}}{\text{,}}\,\,\,\,{\text{О м }}{\text{.}}$	(10)
Режим резистивной нагрузки (R_н = var)		${{\underline Z }_{{{\text{в х }}}}} = \frac{1}{{{{R}_{{\text{н }}}}\frac{{{{C}_{0}}}}{{4{{L}_{0}}}} + j{\omega }\frac{{{{C}_{0}}}}{4}l + \frac{1}{{j{\omega }4{{L}_{0}}l}}}} + \frac{1}{{\frac{1}{{\frac{1}{{j{\omega }{{C}_{0}}l}} + j{\omega }{{L}_{0}}l}} + \frac{1}{{{{R}_{{\text{н }}}}}}}}{\text{,}}\,\,\,\,{\text{О м }}{\text{.}}$	(11)
Режим согласованной нагрузки (R_н = 2√(L₀/C₀) = 2ρ)		${{\underline Z }_{{{\text{в х }}}}} = \frac{1}{{{{R}_{{\text{н }}}}\frac{{{{C}_{0}}}}{{4{{L}_{0}}}}}} = \frac{{4{{{\rho }}^{2}}}}{{{{R}_{{\text{н }}}}}}{\text{,}}\,\,\,\,{\text{О м }}{\text{.}}$	(12)

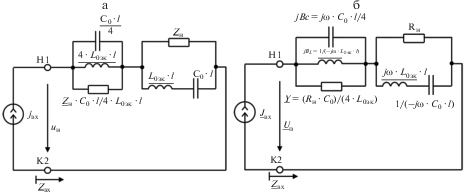
При исследовании режимов работы каткона математическое описание цепи с распределенными параметрами оказывается весьма сложное, поэтому для различных граничных условий были предложены простые эквивалентные электрические схемы замещения с сосредоточенными эквивалентными параметрами (рис. 3а и 3б, рис. 4а и 4б), синтезированные относительно входного сопротивления Z_вх (табл. 3). Выражения (7) и (9) могут быть получены из схем, представленных на рис. 3а и 3б (при пренебрежении первичными параметрами: R₀ ≈ 0 и G₀ ≈ 0), так и из схемы, представленной на рис. 4а (при Z_н → ∞ и Z_н = 0 соответственно).

Рис. 3.

Схема замещения каткона с эквивалентными сосредоточенными параметрами относительно зажимов Н₁ и К₂ при разомкнутых зажимах К₁ и Н₂ в режимах ХХ (а) и КЗ (б).

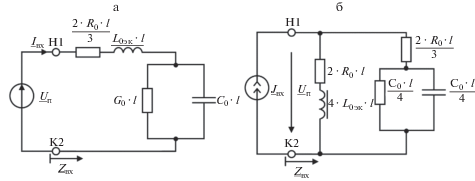
Рис. 4.

Схема замещения каткона с эквивалентными сосредоточенными параметрами относительно зажимов Н₁ и К₂ при подключении произвольной нагрузки к зажимам К₁ и Н₂ для мгновенных (а) и (б) комплексных значений.

Для синтезированных схем замещения каткона при различных граничных условиях могут быть получены выражения для нахождения резонансных частот, приведенные в табл. 4.

Таблица 4

Режим работы каткона		Выражения для резонансной частоты	№
Режим ХХ (Z_н → ∞)	С потерями	${{f}_{{{\text{0Х Х }}}}} = \frac{1}{{2{\pi }}}\sqrt {\frac{1}{{{{L}_{0}}{{C}_{0}}{{l}^{2}} - \frac{{G_{0}^{2}}}{{C_{0}^{2}}}}}} {\text{,}}\,\,\,\,{\text{Г ц }}{\text{.}}$	(13)
Режим ХХ (Z_н → ∞)	Без потерь	$f_{{{\text{0Х Х }}}}^{'} = \frac{1}{{2{\pi }}}\sqrt {\frac{1}{{{{L}_{0}}{{C}_{0}}{{l}^{2}}}}} {\text{,}}\,\,\,\,{\text{Г ц }}{\text{.}}$	(14)
Режим КЗ (Z_н = 0)	С потерями	${{f}_{{{\text{0К З }}}}} = \frac{1}{{2{\pi }}}\sqrt {\frac{1}{{{{L}_{0}}{{C}_{0}}{{l}^{2}} - \frac{{{{L}_{0}}{{C}_{0}}{{R}_{0}}{{G}_{0}}{{l}^{4}}}}{6}}}} {\text{,}}\,\,\,\,{\text{Г ц }}{\text{.}}$	(15)
Режим КЗ (Z_н = 0)	Без потерь	$f_{{{\text{0К З }}}}^{'} = \frac{1}{{2{\pi }}}\sqrt {\frac{1}{{{{L}_{0}}{{C}_{0}}{{l}^{2}}}}} {\text{,}}\,\,\,\,{\text{Г ц }}{\text{.}}$	(16)
Режим резистивной нагрузки (R_н = var)		${{f}_{{{\text{0н }}}}} = \frac{1}{{2{\pi }}}\sqrt {\frac{1}{{{{L}_{0}}{{C}_{0}}{{l}^{2}}}}} {\text{,}}\,\,\,\,{\text{Г ц }}{\text{.}}$ R_н > 2ρ: режим резонанса напряжений R_н < 2ρ: режим резонанса токов	(17)
Режим согласованной нагрузки (R_н = 2√L₀/C₀ = 2ρ)		Режим безразличного резонанса	–

ОПРЕДЕЛЕНИЕ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ

В соответствии с предложенными эквивалентными схемами замещения (рис. 3а и 3б, рис. 4а и 4б) определим корни характеристического уравнения для каждой из схем (Z_вх(p) = 0). Для этого используем уравнения (6)–(12), а результаты расчетов представим в табл. 5.

Таблица 5

Режим работы каткона		Корни характеристического уравнения	№
Режим ХХ (Z_н → ∞)	С потерями	${{p}_{{1,2}}}\, = - \frac{{ - \left( {\frac{{\frac{2}{3}{{R}_{0}}{{C}_{0}}\, + \,{{G}_{0}}{{L}_{0}}}}{{{{L}_{0}}{{C}_{0}}}}} \right)\, \pm \,\sqrt {{{{\left( {\frac{{\frac{2}{3}{{R}_{0}}{{C}_{0}}\, + \,{{G}_{0}}{{L}_{0}}}}{{{{L}_{0}}{{C}_{0}}}}} \right)}}^{2}}\, - \,\frac{{\frac{8}{3}{{R}_{0}}{{G}_{0}}{{l}^{2}}\, + \,4}}{{{{L}_{0}}{{C}_{0}}{{l}^{2}}}}} }}{2}$$p \ne - \frac{{{{G}_{0}}}}{{{{C}_{0}}}}$	(19)
Режим ХХ (Z_н → ∞)	Без потерь	$p = - \frac{1}{{\sqrt {{{L}_{0}}{{C}_{0}}{{l}^{2}}} }};\,\,\,\,p \ne 0$	(20)
Режим КЗ (Z_н = 0)	С потерями	$\begin{gathered} {{p}_{{1,2}}} = - \frac{{R_{0}^{2}{{C}_{0}}{{l}^{3}} + 2{{R}_{0}}{{L}_{0}}{{G}_{0}}{{l}^{3}} + 12{{L}_{0}}l}}{{4{{R}_{0}}{{L}_{0}}{{C}_{0}}{{l}^{3}}}} \pm \\ \pm \,\,\frac{{\sqrt {{{{\left( {\frac{{R_{0}^{2}{{C}_{0}}{{l}^{3}} + 2{{R}_{0}}{{L}_{0}}{{G}_{0}}{{l}^{3}} + 12{{L}_{0}}l}}{{2{{R}_{0}}{{L}_{0}}{{C}_{0}}{{l}^{3}}}}} \right)}}^{2}} - \frac{{R_{0}^{2}{{G}_{0}}{{l}^{3}} + 6{{R}_{0}}l}}{{2{{R}_{0}}{{L}_{0}}{{C}_{0}}{{l}^{3}}}}} }}{2} \\ \end{gathered} $ $\begin{gathered} p \ne - \frac{{\frac{2}{3}{{R}_{0}}{{C}_{0}}{{l}^{2}} + {{G}_{0}}{{L}_{0}}{{l}^{2}}}}{{2{{L}_{0}}{{C}_{0}}{{l}^{2}}}} \pm \\ \pm \,\,\frac{{\sqrt {{{{\left( {\frac{{\frac{2}{3}{{R}_{0}}{{C}_{0}}{{l}^{2}} + {{G}_{0}}{{L}_{0}}{{l}^{2}}}}{{{{C}_{0}}{{L}_{0}}{{l}^{2}}}}} \right)}}^{2}} - \frac{{\frac{8}{3}{{R}_{0}}{{G}_{0}}{{l}^{2}} + 4}}{{{{C}_{0}}{{L}_{0}}{{l}^{2}}}}} }}{2} \\ \end{gathered} $	(21)
Режим КЗ (Z_н = 0)	Без потерь	$p = 0;\,\,\,\,p \ne - \frac{1}{{\sqrt {{{L}_{0}}{{C}_{0}}{{l}^{2}}} }}$	(22)
Режим резистивной нагрузки (R_н = var)		${{p}_{{1,2}}} = - \frac{2}{{{{C}_{0}}{{R}_{{\text{н }}}}l}} \pm \sqrt {\frac{{4{{L}_{0}}}}{{C_{0}^{2}{{L}_{0}}R_{{\text{н }}}^{2}{{l}^{2}}}} - \frac{{R_{{\text{н }}}^{2}}}{{C_{0}^{2}{{L}_{0}}R_{{\text{н }}}^{2}{{l}^{2}}}}} $ $p \ne \frac{{ - \frac{{{{R}_{{\text{н }}}}}}{{{{L}_{0}}l}} \pm \sqrt {\frac{{R_{{\text{н }}}^{2}}}{{L_{0}^{2}{{l}^{2}}}} - \frac{4}{{{{L}_{0}}{{C}_{0}}{{l}^{2}}}}} }}{2}$	(23)
Режим согласованной нагрузки (R_н = 2√L₀/C₀ = 2ρ)		При решении (18) имеем, что корни для числителя и знаменателя совпадают, что свидетельствует об отсутствии переходного процесса:	(24)
Режим согласованной нагрузки (R_н = 2√L₀/C₀ = 2ρ)		${{p}_{1}} = {{p}_{2}} = - \frac{1}{{\sqrt {{{L}_{0}}{{C}_{0}}{{l}^{2}}} }}$	(24)

Выражение (11) с учетом арифметических преобразований и при замене jω оператором p примет следующий вид:

(18)

${{Z}_{{{\text{в х }}}}}(p) = \frac{{p \times 4{{L}_{0}}l + \left( {1 + {{p}^{2}}{{C}_{0}}{{L}_{0}}{{l}^{2}}} \right){{R}_{{\text{н }}}}}}{{p{{C}_{0}}{{R}_{{\text{н }}}}l + {{p}^{2}}{{C}_{0}}{{L}_{0}}{{l}^{2}} + 1}} = 0.$

Решения уравнения (18) позволяет найти корни характеристического уравнения при резистивной и согласованной нагрузке (табл. 5).

Из табл. 5 очевидно, что в зависимости от подключаемого к выходным зажимам сопротивления каткона могут наблюдаться колебательный, предельно-апериодический и апериодический характеры переходных процессов, либо переходной процесс может отсутствовать вовсе (см. (24)), что вытекает из соотношения первичных параметров каткона.

При подключении к выходным зажимам каткона К₁ и Н₂ резистора с произвольным сопротивлением получаем:

R_н > 2ρ: наблюдается колебательный переходной процесс;

R_н = 2ρ: наблюдается отсутствие переходного процесса;

0 ≤ R_н < 2ρ: наблюдается апериодический переходной процесс.

ФИЗИЧЕСКАЯ МОДЕЛЬ КАТКОНА

Конфигурация каткона, состоящего из двух секций С₁ и С₂ (с обозначением соответствующих выводов Н₁, К₁, Н₂, К₂), соединенных между собой согласно последовательно, и двух П-образных участков магнитопровода М₁ и М₂ с регулируемыми по длине немагнитными зазорами НЗ, представлена на рис. 5а, фотография макета каткона – на рис. 5б.

Рис. 5.

Принципиальная схема физической модели каткона с магнитопроводом (а) и фотография двухсекционной физической модели каткона (б).

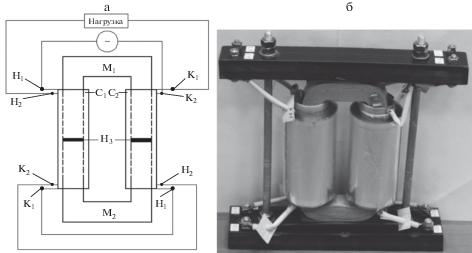
Секции С₁ и С₂ выполнены из двух одинаковых проводов в виде алюминиевой фольги (число витков каждой секции – 150, толщина фольги – 7 мкм, ширина – 84 мм), которые изолированы друг от друга двумя листами полипропилена (толщина – 10 мкм, ширина – 95 мм). Секции намотаны на П-образные участки М₁ и М₂ магнитопровода (аморфная сталь марки 71 КНСР, сечение 20 × 20 мм²). Участки М₁ и М₂ отделены друг от друга одинаковыми по длине двумя немагнитными зазорами НЗ (длина каждого зазора – 0.6 мм, общая длина – 1,2 мм). Использование немагнитных зазоров и изменение их длины обеспечивает снижение нелинейности каткона, обусловленной наличием ферромагнитного сердечника с нелинейной характеристикой, и позволяет осуществлять подбор эквивалентных параметров каткона для решения конкретных задач (например, достижения режима резонанса) [12].

Соединение секций С₁ и С₂ между собой выполнено последовательно согласно, источник напряжения подключается к выводу Н₁ секции С₁ и выводу К₂ секции С₂, нагрузка – к выводу К₁ секции С₂ и выводу Н₂ секции С₁. Эквивалентные параметры синтезированной относительно входного сопротивления схемы замещения каткона были определены в соответствии с алгоритмом, предложенным в [15]: R_L = 2/3G₀l = = 4.483 Ом, L = L₀l = 44.6 × 10^–3 Гн, C = C₀l = 7.46 × 10^–6 Ф, G_C = G₀l = 1 × 10^–5 См.

ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В КАТКОНЕ

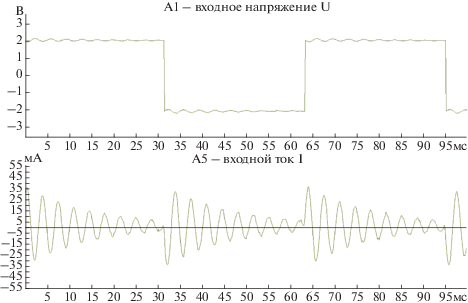
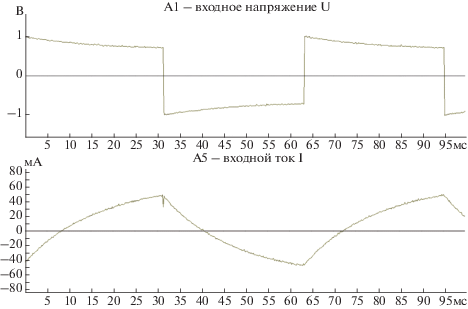
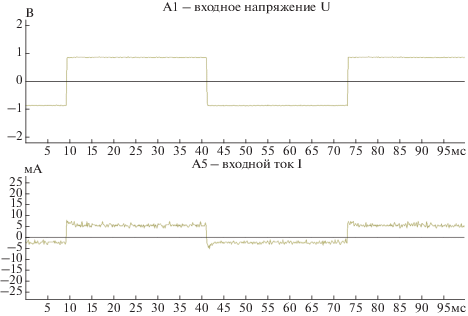
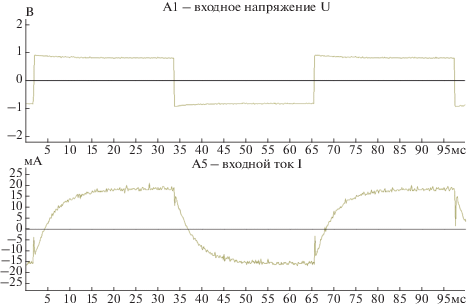
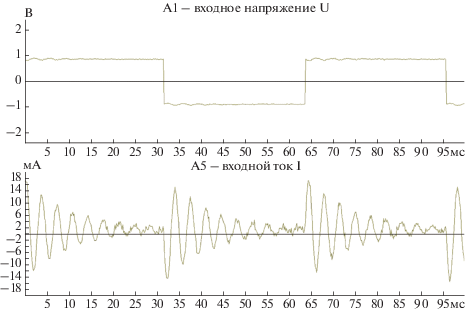
При решении задачи исследования переходных процессов к входу устройства между зажимами Н₁ и К₂ (рис. 5а и 5б) был подключен источник напряжения с импульсным сигналом (меандром) с частотой 15.5 Гц и амплитудным значением напряжения U_m = 1 В. Для значений сопротивлений R_н → ∞, R_н = 0 Ом, R_н = 2ρ = 155 Ом, R_н = 50 Ом, R_н = 9550 Ом были получены осциллограммы входного напряжения и тока с использованием программно-технического комплекса DeltaProfi [16], представленные на рис. 6–10 .

Рис. 6.

Осциллограммы переходного процесса в катконе при R_н → ∞.

Рис. 7.

Осциллограммы переходного процесса в катконе при R_н = 0.

Рис. 8.

Осциллограммы переходного процесса в катконе при R_н = 2ρ = 155 Ом.

Рис. 9.

Осциллограммы переходного процесса в катконе при R_н = 50 Ом.

Рис. 10.

Осциллограммы переходного процесса в катконе при R_н = 9550 Ом.

Таким образом, анализ осциллограмм, представленных на рис. 6–10 , свидетельствует о том, что для полученных эквивалентных параметров физической модели каткона и уравнений (19)–(24):

• при R_н → ∞ > 2ρ и R_н = 9550 Ом > 2ρ – в цепи наблюдается колебательный переходной процесс;

• при R_н = 2ρ = 155 Ом – в цепи переходной процесс практически не наблюдается;

• при R_н = 0 Ом < 2ρ и R_н = 50 Ом < 2ρ – в цепи наблюдается апериодический переходной процесс.

ОПРЕДЕЛЕНИЕ ДОБРОТНОСТИ КОЛЕБАТЕЛЬНОГО КОНТУРА

Для определения добротности колебательного контура рассмотрим эквивалентную схему замещения каткона для режима ХХ с учетом пренебрежения погонной проводимостью (рис. 3а при G₀ = 0). Тогда при нахождении корней характеристического уравнения для данной схемы в случае колебательного процесса получим:

${{p}_{{1,2}}} = {\alpha } \pm j{{{\omega }}_{{{\text{с в }}}}} = - \frac{R}{{2L}} \pm \sqrt {\frac{1}{{LC}} - \frac{{{{R}^{2}}}}{{4{{L}^{2}}}}} .$

Следовательно, постоянная времени τ = 1/|α| = 2L/R, с.

Выражение для входного тока при воздействии источника постоянного напряжения для рассматриваемой схемы будет иметь вид:

(25)

$i(t) = {{i}_{{{\text{с в }}}}}\left( t \right) = {{A}_{0}}{{e}^{{ - \frac{R}{{2L}}t}}}\sin ({{{\omega }}_{{{\text{с в }}}}}t + {\varphi }) = {{i}_{0}}(t)\sin ({{{\omega }}_{{{\text{с в }}}}}t + {\varphi }), {\text{А }}{\text{.}}$

Известно, что в установившемся режиме при резонансе напряжений в R–L–C цепи добротность контура определяется как отношение характеристического сопротивления ρ к сопротивлению резистора R (для схемы на рис. 3а примем, что R = 2/3R₀l), то есть при рассмотрении каткона как линейной цепи:

$Q = \frac{{\rho }}{R} = \frac{{\sqrt {\frac{L}{C}} }}{R} = \frac{1}{{R\sqrt {\frac{C}{L}} }}\quad,$

где C = C₀l (Ф), L = L_0эквl (Гн).

Резонансная частота f_р находится по формуле Томпсона в соответствии с (14):

${{f}_{{\text{р }}}} = \frac{1}{{2{\pi }\sqrt {LC} }}\quad{\text{,}}\,\,\,\,{\text{Г ц }}{\text{.}}$

С другой стороны, если значение резонансной частоты близко к частоте свободных колебаний (f_р ≈ f_св = 1/T_св; T_св = 2π√(LC)), то добротность может быть определена через постоянную времени τ с учетом предшествующих выражений:

(26)

$Q = \frac{1}{{\frac{{2L}}{{\tau }}\sqrt {\frac{C}{L}} }} = \frac{{\tau }}{{2\sqrt {LC} }} = \frac{{\tau }}{{2\frac{{{{T}_{{{\text{с в }}}}}}}{{2{\pi }}}}} = \frac{{\pi {\tau }}}{{{{T}_{{{\text{с в }}}}}}}.$

Таким образом, полученное выражение (26) позволяет определять добротность колебательного контура по осциллограммам колебательных переходных процессов.

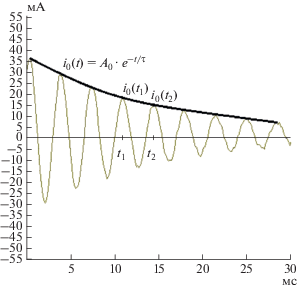
Определим добротность колебательного контура по осциллограмме входного тока для переходного процесса в режиме ХХ (рис. 6). Для этого обозначим на данной осциллограмме значения токов i₀ (см. формулу (25)), изменяющихся по экспоненциальному закону, в момент времени t₁ и t₂ (рис. 11), найдем соотношения данных токов и выразим через них τ в общем виде:

$\left\{ {\begin{array}{*{20}{c}} {{{i}_{0}}\left( {{{t}_{1}}} \right) = {{A}_{0}}{{e}^{{ - \frac{{{{t}_{1}}}}{\tau }}}}} \\ {{{i}_{0}}\left( {{{t}_{2}}} \right) = {{A}_{0}}{{e}^{{ - \frac{{{{t}_{2}}}}{\tau }}}}} \end{array}} \right.,$

$\frac{{{{i}_{0}}\left( {{{t}_{1}}} \right)}}{{{{i}_{0}}\left( {{{t}_{2}}} \right)}} = \frac{{{{e}^{{ - \frac{{{{t}_{1}}}}{{\tau }}}}}}}{{{{e}^{{ - \frac{{{{t}_{2}}}}{\tau }}}}}} = {{e}^{{\frac{{{{t}_{2}} - {{t}_{1}}}}{{\tau }}}}} \to \frac{{{{t}_{2}} - {{t}_{1}}}}{{\tau }} = \ln \frac{{{{i}_{0}}\left( {{{t}_{1}}} \right)}}{{{{i}_{0}}\left( {{{t}_{2}}} \right)}} \to {\tau } = \frac{{{{t}_{2}} - {{t}_{1}}}}{{\ln \frac{{{{i}_{0}}\left( {{{t}_{1}}} \right)}}{{{{i}_{0}}\left( {{{t}_{2}}} \right)}}}},\,\,\,\, {\text{с }}{\text{.}}$

Рис. 11.

Осциллограмма входного тока в катконе при R_н → ∞ (переходной процесс).

С учетом масштабных коэффициентов для рассматриваемой осциллограммы тока (рис. 11) определим τ' и Q':

${\tau '} = \frac{{{{t}_{2}} - {{t}_{1}}}}{{\ln \frac{{{{i}_{0}}\left( {{{t}_{1}}} \right)}}{{{{i}_{0}}\left( {{{t}_{2}}} \right)}}}} = \frac{{3.23}}{{\ln \frac{{18}}{{15}}}} = 17.72\quad {\text{м с }}{\text{.}}$

$Q' = \frac{{{\pi \tau }}}{{{{T}_{{{\text{с в }}}}}}} = \frac{{{\pi } \times 17.72}}{{3.23}} = 17.23.$

При исследовании частотных характеристик физической модели каткона (рис. 5б) в установившимся режиме (при питании от синусоидального источника напряжения) значение резонансной частоты при разомкнутых зажимах К₁ и Н₂ составило f_р = 276 Гц, значения граничных частот – f_р1 = 268 Гц и f_р2 = 284 Гц (полоса пропуская Δf_р = 16 Гц), соответственно, добротность Q" = f_р/Δf_р = 17.25, что практически соответствует значению добротности Q'.

ЗАКЛЮЧЕНИЕ

Впервые проведено физическое и математическое моделирование каткона в переходных процессах. Для этого для различных граничных условий предложены синтезированные относительно входных зажимов каткона эквивалентные схемы замещения (с потерями и без потерь). Для этих схем определены корни характеристических уравнений, что позволило произвести расчет переходных процессов.

Получены осциллограммы колебательного (R_н → ∞ > 2ρ и R_н = 9550 Ом > 2ρ) и апериодического (R_н = 0 Ом < 2ρ и R_н = 50 Ом < 2ρ) переходных процессов, а также осциллограмма режима согласованной нагрузки (R_н = 2ρ), при котором переходной процесс практически не наблюдается.

Получены выражения для определения добротности колебательного контура на основе анализа осциллограммы входного тока при переходном процессе в катконе. Значения добротностей в установившемся режиме и при переходном процессе практически совпадают, что свидетельствует о корректности предлагаемой математической модели.

Полученные результаты исследования поведения каткона в переходных процессах подтверждает вывод о возможности его применения в качестве фильтрокомпенсирующего и токоограничивающего устройств.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-08-00730 А.

Статья рекомендована к публикации по решению Программного комитета XXVI Международной конференции “Электромагнитное поле и материалы (фундаментальные физические исследования)”.

Список литературы

Демирчян К.С., Гусев Г.Г. Синтез схем замещения катушки индуктивности с самокомпенсацией реактивной мощности // Известия АН СССР. Энергетика и транспорт. 1987. № 2. С. 3–10.
Reeves R. Choke-capacitor hybrid as a fluorescent-lamp ballast. Proceedings of the Institution of Electrical Engineers. 1975. V. 122. № 10. P. 1151–1152.
Кувалдин А.Б., Андрюшин Н.Ф., Захаров И.В. Расчет электрических и энергетических параметров многослойного индуктора с самокомпенсацией реактивной мощности // Электричество. 1995. № 7. С. 47–53.
Захаров И.В. Развитие теории, разработка методов и средств повышения эффективности индукторов с самокомпенсацией реактивной мощности: автореферат дисс. … докт. техн. наук: 05.09.10. Алматы, 2007. 41 с.
Волков И.В., Закревский С.И. Преобразователь с распределенными параметрами для стабилизации тока в переменной нагрузке // Электричество. 1984. № 10. С. 40–43.
Ehsani M., Stielau O.H., van Wyk J.D. Integrated reactive components in power electronic circuits. 1993. IEEE Trans. Power Electron. V. 8. P. 208–215.
Konesev S.G., Khazieva R.T., Kirillov R.V. The research of stabilization properties of inductive-capacitive converters based on the two-sections hybrid electromagnetic elements // 2016 Dynamics of Systems, Mechanisms and Machines (Dynamics). 2016. P. 1–7.
Конесев С.Г., Хлюпин П.А., Кириллов Р.В., Хазиева Р.Т. Компьютерная модель системы заряда емкостного накопителя на основе индуктивно-емкостного преобразователя // Нефтегазовое дело. Электронный научный журн. 2015. № 4. С. 374–390. URL: http://ogbus.ru/issues/4_2015/ogbus_4_2015_p374-390_KonesevSG_ru.pdf
Phinney J.W., Perreault D.J. Filters with Active Tuning for Power Applications. IEEE Trans. Power Electron. 2003. V. 18. № 2. P. 636–647.
Neugebauer T.C., Phinney J.W., Perreault D.J. Filters and Components With Inductance Cancellation. IEEE Trans. on Ind. Applicat. 2004. V. 40. № 2. P. 483–491.
Coulibaly S., Loum G., Diby K.A. Design of Integrated LC Filter Using Multilayer Flexible Ferrite Sheets. IOSR Journal of Electrical and Electronics Engineering (IOSR-JEEE). 2015. V. 10. № 6. P. 35–43.
Бутырин П.А., Гусев Г.Г., Кужман В.В., Михеев Д.В., Шакирзянов Ф.Н. Математическая модель фильтрокомпенсирующих устройств на основе гармонической линеаризации характеристики магнитопровода каткона // Вестник МЭИ. 2015. № 5. С. 79–84.
Бутырин П.А., Гусев Г.Г., Михеев Д.В., Шакирзянов Ф.Н. Физическое моделирование поличастотного фильтрокомпенсирующего устройства на основе каткона // Известия РАН. Энергетика. 2017. № 5. С. 67–74.
Butyrin P.A., Gusev G.G., Mikheev D.V., Shakirzianov F.N. Coil-Capacitor As A Basis For Creating Efficient Devices For Distribution Power Networks // Conference on Sustainable Energy Supply and Energy Storage Systems – NEIS 2018. September 20–21, 2018, Hamburg, Germany. P. 173–178.
Бутырин П.А., Гусев Г.Г., Михеев Д.В., Шакирзянов Ф.Н. Идентификация математической модели фильтрокомпенсирующего устройства на основе каткона с учетом нелинейной характеристики магнитопровода // Электричество. 2017. № 10. С. 55–60.
Alexeychik L.V., Zhokhova M.P., Mikheev D.V., Karpunina M.V. Electrotechnical laboratory: from physical experiment to virtual scenario // IV International Conference on Information Technologies in Engineering Education (Inforino 2018). October 23–26, 2018, Moscow, Russia. P. 387–390.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал