Известия РАН. Энергетика, 2019, № 2, стр. 127-134

Рандомизированное вычисление инвариантных нулей модели электроэнергетической системы, заданной в дескрипторной форме

М. Г. Гаджиев¹, Н. Е. Василенко¹, М. Ш. Мисриханов¹, В. Н. Рябченко^1, *

¹ Национальный исследовательский университет “МЭИ” (НИУ “МЭИ”)
Москва, Россия

Поступила в редакцию 24.12.2018
После доработки 08.04.2019
Принята к публикации 25.04.2019

DOI: 10.1134/S0002331019020079

Аннотация

Предложен рандомизированный алгоритм вычисления инвариантных нулей модели электроэнергетической системы как динамической системы с многими входами и многими выходами, заданной в линейной дескрипторной форме. Определения инвариантных нулей осуществляется путем рандомизированного квадрирования представления исходной системы. Рандомизация позволяет сформировать достаточное по мощности семейство обобщенных матриц Розенброка (обобщенных пучков матриц), пересечение множеств конечных собственных значений которых совпадает с инвариантными нулями модели электроэнергетической системы. Таким образом, вычисление инвариантных нулей сводится к обобщенной задаче на собственные значения обобщенного пучка матриц. Применение алгоритма проиллюстрировано на примере вычисления инвариантных нулей линейной дескрипторной модели объединенной энергосистемы, дифференциальные и алгебраические уравнения которой формируется в предположении ограниченного числа синхронизированных векторных измерителей.

Ключевые слова: инвариантные нули, рандомизированный алгоритм, электроэнергетическая система, дескрипторная форма, обобщенная задача на собственные значения

ВВЕДЕНИЕ

В современной теории управления многомерными динамическими системами проблема инвариантных нулей занимает одно из центральных мест [1–4]. Она напрямую связана с понятиями управляемости и наблюдаемости, а также с принципиальной возможностью синтеза и реализации динамических законов управления. Так, если у динамической системы инвариантные нули расположены в начале комплексной плоскости, то оказывается невозможным реализовать законы пропорционально-интегрального (ПИ), пропорционально-дифференциального (ПД) и пропорционально-интегрально-дифференциального (ПИД) управления, а также законы серворегулирования [5–7].

Инвариантные нули моделей ЭЭС рассматривались в многочисленных работах зарубежных авторов в основном применительно к математическим моделям “один вход – один выход” [8–10]. В настоящее время данная проблематика актуализируется в связи c широким внедрением новых технологий, в том числе, синхронизированных векторных измерений, а также использованием многомерных динамических моделей ЭЭС с многими входами и многими выходами [11–15].

В качестве основного объекта практических расчетов в данном случае выступает линеаризация нелинейной дескрипторной математической модели, т.е. модели, имеющей дифференциальные и алгебраические уравнения. Так для нелинейной динамической системы рассматриваются уравнения [16]

(1)

$\dot {x} = f(x,z,u),$

(2)

$0 = g(x,z,u),$

(3)

$y = h(x,z),$

где $x \in {{\mathbb{R}}^{{{{n}_{x}}}}}$ – вектор переменных состояния; $z \in {{\mathbb{R}}^{{{{n}_{z}}}}}$ – вектор параметров; $u \in {{\mathbb{R}}^{r}}$ – вектор входных воздействий; $y \in {{\mathbb{R}}^{m}}$ – вектор выходных сигналов. Вид векторных функций f, g и h определяется математическими моделями элементов системы, измерительными и исполнительными устройствами.

Стандартный подход к линеаризации (1), (2) связан с процедурой разложения в ряд Тейлора векторных функций f и g в малой окрестности установившегося процесса с координатами ${{x}_{0}},{{z}_{0}},{{u}_{0}}$

(4)

$f\left( {x,z,u} \right) \approx f\left( {{{x}_{0}},{{z}_{0}},{{u}_{0}}} \right) + {{\left( {\frac{{\partial f}}{{\partial x}}} \right)}_{0}}\Delta x + {{\left( {\frac{{\partial f}}{{\partial z}}} \right)}_{0}}\Delta z + {{\left( {\frac{{\partial f}}{{\partial u}}} \right)}_{0}}\Delta u,$

(5)

$g\left( {x,z,u} \right) \approx g\left( {{{x}_{0}},{{z}_{0}},{{u}_{0}}} \right) + {{\left( {\frac{{\partial g}}{{\partial x}}} \right)}_{0}}\Delta x + {{\left( {\frac{{\partial g}}{{\partial z}}} \right)}_{0}}\Delta z + {{\left( {\frac{{\partial g}}{{\partial u}}} \right)}_{0}}\Delta u,$

(6)

$h\left( {x,z} \right) \approx h\left( {{{x}_{0}},{{z}_{0}}} \right) + {{\left( {\frac{{\partial h}}{{\partial x}}} \right)}_{0}}\Delta x + {{\left( {\frac{{\partial h}}{{\partial z}}} \right)}_{0}}\Delta z,$

где $\Delta x = x - {{x}_{0}} \doteq x{\text{'}} \in {{\mathbb{R}}^{{{{n}_{x}}}}},$ $\Delta z = z - {{z}_{0}} \doteq x'' \in {{\mathbb{R}}^{{{{n}_{z}}}}},$ $\Delta u = u - {{u}_{0}} \doteq u \in {{\mathbb{R}}^{r}}$ – отклонения соответствующих векторов; ${{\left( * \right)}_{0}}$ – соответствующие частные производные, вычисленные в указанных ранее координатах.

Линеаризация уравнений (1)–(3) в точке установившегося движения дают линейные дескрипторные (алгебро-дифференциальные) уравнения

(7)

$\dot {x}{\text{'}} = {{\left( {\frac{{\partial f}}{{\partial x}}} \right)}_{0}}x{\text{'}} + {{\left( {\frac{{\partial f}}{{\partial z}}} \right)}_{0}}x{\text{''}} + {{\left( {\frac{{\partial f}}{{\partial u}}} \right)}_{0}}u,$

(8)

$0 = {{\left( {\frac{{\partial g}}{{\partial x}}} \right)}_{0}}x{\text{'}} + {{\left( {\frac{{\partial g}}{{\partial z}}} \right)}_{0}}x{\text{''}} + {{\left( {\frac{{\partial g}}{{\partial u}}} \right)}_{0}}u,$

(9)

$y = {{\left( {\frac{{\partial h}}{{\partial x}}} \right)}_{0}}x{\text{'}} + {{\left( {\frac{{\partial h}}{{\partial z}}} \right)}_{0}}x{\text{''}}{\text{.}}$

В дальнейшем с целью упрощения записи уравнений индекс “0” у частных производных будем опускать.

При обратимой матрице Якоби ${{\partial g} \mathord{\left/ {\vphantom {{\partial g} {\partial z}}} \right. \kern-0em} {\partial z}}$ уравнения (7), (8) могут быть преобразованы к форме пространства состояний

(10)

$\begin{gathered} \dot {x}{\text{'}} = \left( {\frac{{\partial f}}{{\partial x}} - \frac{{\partial f}}{{\partial z}}{{{\left( {\frac{{\partial g}}{{\partial z}}} \right)}}^{{ - 1}}}\frac{{\partial g}}{{\partial x}}} \right)x{\text{'}} + \left( {\frac{{\partial f}}{{\partial u}} - \frac{{\partial f}}{{\partial z}}{{{\left( {\frac{{\partial g}}{{\partial z}}} \right)}}^{{ - 1}}}\frac{{\partial g}}{{\partial u}}} \right)u, \\ y = \left( {\frac{{\partial h}}{{\partial x}} - \frac{{\partial h}}{{\partial z}}{{{\left( {\frac{{\partial g}}{{\partial z}}} \right)}}^{{ - 1}}}\frac{{\partial g}}{{\partial x}}} \right)x{\text{'}} - \frac{{\partial h}}{{\partial z}}{{\left( {\frac{{\partial g}}{{\partial z}}} \right)}^{{ - 1}}}\frac{{\partial g}}{{\partial u}}u. \\ \end{gathered} $

Если матрица Якоби ${{\partial g} \mathord{\left/ {\vphantom {{\partial g} {\partial z}}} \right. \kern-0em} {\partial z}}$ вырождена, тогда преобразования к уравнениям (10) не существует. Однако даже в случае обратимости ${{\partial g} \mathord{\left/ {\vphantom {{\partial g} {\partial z}}} \right. \kern-0em} {\partial z}}$ в практических расчетах возникает проблема обусловленности этой матрицы. При числе обусловленности

(11)

${\text{cond}}\left( {\frac{{\partial g}}{{\partial z}}} \right) \gg 1$

матрица Якоби ${{\partial g} \mathord{\left/ {\vphantom {{\partial g} {\partial z}}} \right. \kern-0em} {\partial z}}$ близка к вырожденной и математическая модель (10) становится “жесткой” по отношению малым ошибкам вычислений и вариациям параметров. Другими словами, математическая модель (10) в случае справедливости неравенства (11) является некорректной по А.Н. Тихонову [1, 16].

Если не принимать дополнительных мер, то все вычисления с использованием модели (10), включая анализ управляемости и наблюдаемости, будут приводить к серьезным ошибкам. В качестве одной из таких мер можно рассматривать процедуру предобусловливания (переобусловливания) матрицы. Однако в общем случае данный метод наталкивается на ряд существенных трудностей. Нестрого говоря, улучшение обусловленности матрицы ${{\partial g} \mathord{\left/ {\vphantom {{\partial g} {\partial z}}} \right. \kern-0em} {\partial z}}$ может сопровождаться ухудшением обусловленности матриц в (10) [17]. Альтернативой этому является использование в расчетах исходной линеаризованной дескрипторной модели (7), (8).

Понятие инвариантных нулей

Введем следующие обозначения блочных вектора и матриц:

$\begin{gathered} x = \left( {\begin{array}{*{20}{c}} {x{\text{'}}} \\ \hline {x{\text{''}}} \end{array}} \right) \in {{\mathbb{R}}^{n}},\,\,\,\,{\mathbf{E}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{E}}}_{{{{n}_{x}}}}}}&\vline & 0 \\ \hline 0&\vline & 0 \end{array}} \right) \in {{\mathbb{R}}^{{n \times n}}}, \\ {\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial x}}}&\vline & {\frac{{\partial f}}{{\partial z}}} \\ \hline {\frac{{\partial g}}{{\partial x}}}&\vline & {\frac{{\partial g}}{{\partial z}}} \end{array}} \right) \in {{\mathbb{R}}^{{n \times n}}},\,\,\,\,{\mathbf{B}} = \left( {\begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial u}}} \\ \hline {\frac{{\partial g}}{{\partial u}}} \end{array}} \right) \in {{\mathbb{R}}^{{n \times r}}},\,\,\,\,{\mathbf{C}} = \left( {\begin{array}{*{20}{c}} {\frac{{\partial h}}{{\partial x}}}&\vline & {\frac{{\partial h}}{{\partial z}}} \end{array}} \right) \in {{\mathbb{R}}^{{m \times n}}}, \\ \end{gathered} $

где ${{{\mathbf{E}}}_{{{{n}_{x}}}}}$ – единичная матрица размера ${{n}_{x}} \times {{n}_{x}};$ $n = {{n}_{x}} + {{n}_{z}}.$ Тогда дескрипторную систему (7)–(8) можно переписать в более общем виде

(12)

${\mathbf{E}}\dot {x}(t) = {\mathbf{A}}x(t) + {\mathbf{B}}u(t),\,\,\,\,y(t) = {\mathbf{C}}x(t),$

где $x(t) \in {{\mathbb{R}}^{n}}$ – вектор состояния, $u(t) \in {{\mathbb{R}}^{r}}$ – вектор входа, $y(t) \in {{\mathbb{R}}^{m}}$ – вектор выхода.

Введем определение.

Определение [1]. Комплексная частота $\lambda = \alpha *,$ при которой ранг по столбцам матрицы

(13)

$\left( {\begin{array}{*{20}{c}} {{\mathbf{A}} - \alpha {\text{*}}{\mathbf{E}}}&\vline & {\mathbf{B}} \\ \hline {\mathbf{C}}&\vline & 0 \end{array}} \right)$

уменьшается, называется инвариантным нулем.

В (13) $\lambda \in \mathbb{C}$ – комплексная переменная; 0 – нулевая матрица размера $m \times r.$

Инвариантные нули определяются из условия [19]

(14)

$\left( {\begin{array}{*{20}{c}} {{\mathbf{A}} - \alpha {\text{*}}{\mathbf{E}}}&\vline & {\mathbf{B}} \\ \hline {\mathbf{C}}&\vline & 0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{x}_{0}}} \\ \hline {{{u}_{0}}} \end{array}} \right) = 0$

полного “блокирования” передачи сигнала как собственной, так и вынужденной составляющей движения динамической системы, т.е. при $\lambda = \alpha {\text{*}}$ существуют такие векторы ${{u}_{0}}$ и ${{x}_{0}},$ что реакция выхода системы равна нулю. Таким образом, задача определения инвариантных нулей системы (12) сводится к обобщенной задаче на собственные значения в общем случае прямоугольного пучка матриц

(15)

$\left( {\begin{array}{*{20}{c}} {{\mathbf{A}} - \lambda {\mathbf{E}}}&\vline & {\mathbf{B}} \\ \hline {\mathbf{C}}&\vline & 0 \end{array}} \right).$

Поиск инвариантных нулей для больших динамических систем ($n \gg 1$) наталкивается на серьезные трудности вычислительного характера. Ключевую роль здесь играют ошибки вычисления и проблемы вычисления нулей обобщенных пучков матриц [20]. Поэтому необходимы новые подходы к построению вычислительных алгоритмов.

Рандомизированное квадрирование

Практический способ вычисления инвариантных нулей дескрипторной системы (12) связан с так называемым квадрированием динамической системы¹ ¹.

Пусть $m > r$ (число выходов динамической системы больше числа входов). Введем в рассмотрение дескрипторную систему

(16)

${\mathbf{E}}\dot {x}(t) = {\mathbf{A}}x(t) + {\mathbf{B}}u(t),\,\,\,\,y{\text{*}}(t) = {{{\mathbf{T}}}_{C}}{\mathbf{C}}x(t),\,\,\,\,x(0) = {{x}_{0}},$

где ${{{\mathbf{T}}}_{C}} \in {{\mathbb{R}}^{{r \times m}}}$ – матрица полного ранга по строкам.

Справедливо утверждение, полученное на основе рассуждений, сходных с приведенными в [18] на стр. 65–67.

Теорема 1. Множество инвариантных нулей дескрипторной системы (12) всегда является подмножеством множества инвариантных нулей квадрированной дескрипторной системы (16), но не наоборот.

Пусть далее $r > m$ (число входов системы больше числа выходов). Рассмотрим дескрипторную систему

(17)

${\mathbf{E}}\dot {x}(t) = {\mathbf{A}}x(t) + {\mathbf{B}}{{{\mathbf{T}}}_{B}}u{\text{*}}(t),\,\,\,\,y(t) = {\mathbf{C}}x(t),\,\,\,\,x(0) = {{x}_{0}},$

где ${{{\mathbf{T}}}_{B}} \in {{\mathbb{R}}^{{r \times m}}}$ – матрица полного ранга по столбцам.

Справедливо двойственная теореме 1 утверждение.

Теорема 2. Множество инвариантных нулей дескрипторной системы (12) всегда является подмножеством множества инвариантных нулей квадрированной дескрипторной системы (17), но не наоборот.

Из лемм 1 и 2 следует, что операция квадрирования в общем случае вводит в систему новые нули. Это необходимо учитывать при выборе матриц ${{{\mathbf{T}}}_{C}}$ и ${{{\mathbf{T}}}_{B}}.$ В качестве одного из способа решения задачи выбора матриц ${{{\mathbf{T}}}_{C}}$ и ${{{\mathbf{T}}}_{B}}$ является предлагаемая авторами процедура рандомизации.

Введем в рассмотрение оператор рандомизации $Ran{{d}_{{r \times m}}},$ генерирующий матрицы полного ранга размера $r \times m$ с элементами, распределенными по нормальному закону. Пусть также $Ort{{h}_{{r \times m}}}$ – оператор ортогонализации матрицы полного ранга размера $r \times m.$ Тогда

(18)

$Ort{{h}_{{r \times m}}}\left( {Ran{{d}_{{r \times m}}}} \right)$

– композиция операторов, результатом действия которой является рандомизированная ортогональная матрица полного ранга.

Обозначим $\Omega $ – множество инвариантных нулей системы (12), $\Omega {\kern 1pt} {\text{*}}$ – множество инвариантных нулей квадрированной дескрипторной системы. Для определенности далее будем считать, что $m > r$ и квадрированная система имеет вид (16).

Пусть $\Omega _{i}^{*},$ $i = 1,\,\,2,\,\,...$ – множества инвариантных нулей квадрированных дескрипторных систем, где

(19)

${\mathbf{T}}_{C}^{{(i)}} = {\text{Ort}}{{{\text{h}}}_{{r \times m}}}\left( {{\text{Ran}}{{{\text{d}}}_{{r \times m}}}} \right).$

По аналогии с [21] можно доказать, что в этом выполняется условие $ \cap _{i}^{k}\Omega _{i}^{*} = \Omega .$

Вычисление инвариантных нулей модели объединенной энергосистемы

Вычислим инвариантные нули модели объединенной энергосистемы, состоящей из 25 электрических станций. Математическая модель в фазовых координатах “фазный угол – скольжение генератора” данной ЭЭС в форме (12) имеет матрицы следующих размеров:

(20)

${\mathbf{A}} \in {{\mathbb{R}}^{{50 \times 50}}},\,\,\,\,{\mathbf{B}} \in {{\mathbb{R}}^{{50 \times 25}}},\,\,\,\,{\mathbf{C}} \in {{\mathbb{R}}^{{20 \times 50}}},\,\,\,\,{\mathbf{E}} \in {{\mathbb{R}}^{{50 \times 50}}}.$

В рассматриваемой ЭЭС на каждой из 25 электрических станций имеются соответствующие регулирующие устройства. Измерение фазовых координат осуществляется в режиме “on-line” только на 20 электрических станциях с помощью синхронизированных векторных измерителей, входящих в систему мониторинга параметров режима ЭЭС. Таким образом, пучок матриц (15), описывающий в данном случае динамику энергосистемы в условиях малых колебаний, имеет размеры 70 × 75 и является прямоугольным.

Используя операторы рандомизации и ортогонализации (18), сгенерируем множество матриц

(21)

$\left\{ {{{{\mathbf{T}}}_{i}},\,\,i = \overline {1,k} } \right\} = Ort{{h}_{{25 \times 20}}}\left( {Ran{{d}_{{25 \times 20}}}} \right),$

а затем построим k квадратных пучков матриц

(22)

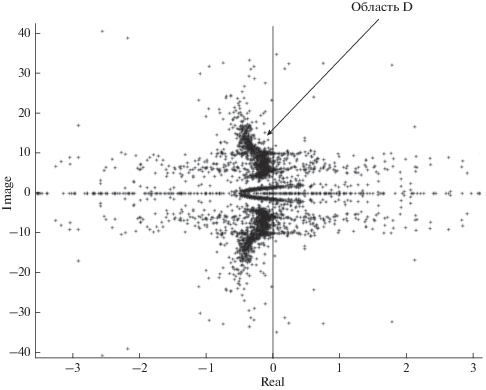
$\left( {\begin{array}{*{20}{c}} {{\mathbf{A}} - \lambda {{{\mathbf{E}}}_{{50}}}}&\vline & {{\mathbf{B}}{{{\mathbf{T}}}_{i}}} \\ \hline {\mathbf{C}}&\vline & {{{0}_{{20 \times 20}}}} \end{array}} \right),\,\,\,\,i = \overline {1,k} .$

Результаты вычислений собственных значений пучков матриц (22) при $k = 500$ (т.е. вычисления 15 000 собственных значений) в виде их обобщенного портрета представлены на рис. 1.

Рис. 1.

Собственные значения матриц (22).

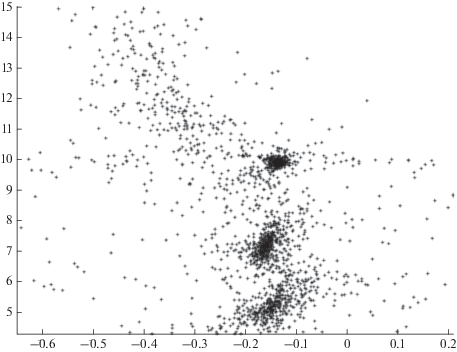
Исследования обобщенного портрета показывают, что в указанной на рис. 1 области D существуют три группы плотных скоплений, которые можно охарактеризовать как претендентов на инвариантные нули. Центры этих скоплений соответствуют комплексным частотам, на которых матрица (15) рассматриваемой модели ЭЭС имеет близкие к нулю минимальные сингулярные значения, то есть данная матрица близка к потере ранга. Это является практическим “индикатором” инвариантного нуля $\alpha {\text{*}}$ [6]. Таким образом, указанные комплексные частоты можно принять за инвариантные нули ЭЭС (20).

Рис. 2.

Собственные значения матриц (22) в области D.

С физической точки зрения вычисленные инвариантные нули соответствуют модальным формам (модам) колебаний, на которых происходит “запирание” анализируемой ЭЭС. Это выражается, во-первых, в практической невозможности восстановить по информации от синхронизированных векторных измерителей, установленных, как указано ранее на 20 электрических станциях, состояние оставшихся 5 электрических станций. А во-вторых, резкую потерю эффективности применяемых системных стабилизаторов, построенных на основе ПИ и ПИД-регуляторов и использующих данные сигналы системы векторных измерений.

ЗАКЛЮЧЕНИЕ

Инвариантные нули непосредственно связаны с управляемостью и наблюдаемостью динамических систем, в том числе, принципиальной возможностью синтеза и реализации законов ПИ, ПД, ПИД-управления, а также серворегулирования. Анализ инвариантных нулей для больших динамических систем, к которым относятся современные ЭЭС, наталкивается на серьезные трудности вычислительного характера, где ключевую роль здесь играют ошибки вычисления и определения нулей обобщенных пучков матриц. Поэтому необходимы новые подходы к построению вычислительных алгоритмов.

В работе предложен алгоритм рандомизированного квадрирования математической модели ЭЭС, заданной в дескрипторной форме, позволяющий эффективно определять все множество инвариантных нулей.

Инвариантные нули непосредственно связаны с частотами входных, выходных сигналов и модами собственных колебаний системы, передача и преобразование которых “блокируется” системой. Это выражается в невозможности восстановления по сигналам синхронизированных векторных измерителей элементов состояния ЭЭС (потерю полной наблюдаемости), а также резкую потерю эффективности ПИ и ПИД-регуляторов, использующих эти сигналы для стабилизации ЭЭС (практическую потерю полной управляемости).

Список литературы

Brockett R.W. Poles, zeros and feedback: State-space interpretation. IEEE Trans. Automat. Control, 1965, AC-10, pp. 129–135.
Rosenbrock H.H. State space and multivariable theory. New York: Wiley, 1970. 257 p.
Zhou K. Essentials of Robust Control. Prentice Hall, 1998. 411 p.
Зубов Н.Е., Микрин Е.А., Рябченко В.Н. Матричные методы в теории и практике систем автоматического управления летательных аппаратов. М.: Изд-во МГТУ имени Н.Э. Баумана, 2016. 666 с.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Условия разрешимости задачи пропорционально-интегрального управления линейной MIMO-системой // Известия РАН. Теория и системы управления. 2018. № 5. С. 141–151.
Мисриханов М.Ш., Рябченко В.Н. Редукция матрицы Розенброка при анализе инвариантных нулей линейной MIMO-системы // Автоматика и Телемеханика. 2008. № 10. С. 31–47.
Смагина Е.М. Вычисление и задание нулей линейной многомерной системы // Автоматика и Телемеханика. 1987. № 12. С. 165–173.
Schrader C.B., Sain M.K. Research on system zeros: a survey // International Journal of control. 1989. Vol. 50. No. 4. P. 1407–1433.
Martins N., Pinto H., Lima L. Efficient methods for finding transfer function zeros of power systems // IEEE Transactions on Power Systems. 1992. Vol. 7. No. 3. P. 1350–1361.
Martins N., Pellanda P.C., Rommes J. Computation of transfer function dominant zeros with applications to oscillation damping control of large power systems // IEEE Transactions on Power Systems. 2007. Vol. 22. No. 4. P. 1218–1226.
Phadke A.G., Thorp J.S. Synchronized Phasor Measurements and Their Applications. – Springer, 2008. 254 p.
Terzija V., Valverde G., Deyu C., Regulski P., Madani V., Fitch J., Skok S., Begovic M.M., Phadke A. Wide-area monitoring, protection, and control of future electric power networks // Proc. IEEE. – 2011. Vol. 99. No. 1. P. 80–93.
Гаджиев М.Г., Гулевич Е.А., Рябченко В.Н., Шаров Ю.В. Идентификация математической модели режима энергосистемы с помощью синхронизированных векторных измерений // Электричество. 2018. № 5. С. 4–10.
Gadzhiev M., Gulevich E., Korobka V., Ryabchenko V.N., Sharov Yu. On the placing of synchronized vector measurement in network 110–330 kV for identification of the Kaliningrad region power system // Rudenko International Conference “Methodological problems in reliability study of large energy system” (RSES 2018). E3S Web of Conference. Vol. 58.
Гаджиев М.Г., Гулевич Е.А., Шаров Ю.В. Идентификация линейной модели электроэнергетической системы в пространстве состояний // Электричество. 2017. № 7. С. 30–38.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Критерии управляемости и наблюдаемости дескрипторной MIMO-системы в форме линейных матричных неравенств // Известия РАН. Теория и системы управления. 2018. № 1. С. 20–26.
Гаджиев М.Г., Шаров Ю.В. Псевдомодальное оценивание запасов статической устойчивости электроэнергетических систем // Электричество. 2017. № 9. С. 14–21.
Macfarlane A.G.J., Kareanias N. Pole and zeros of linear multivariable systems: a survey of the algebraic, geometric and complex variable theory. Int. J. Control, 1976, 24(1). pp. 33–74.
Смагина Е.М. Вопросы анализа линейных многомерных объектов с использованием понятия нуля системы. Томск: Изд-во Том. ун-та, 1990. 160 с.
Мисриханов М.Ш., Рябченко В.Н. Квадратическая проблема собственных значений в электроэнергетических системах // Автоматика и Телемеханика. 2006. № 5. С. 24–47.
Граничин О.Н., Поляк Б.Т. Рандомизированные алгоритмы оценивания и оптимизации при почти произвольных помехах. М.: Наука, 2003. 291 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал