Известия РАН. Энергетика, 2019, № 2, стр. 43-51

Анализ процесса “самопогружения” тепловыделяющего шара под действием силы тяжести

О. О. Корчагина^1, *, А. Р. Аветисян¹

¹ Институт проблем безопасного развития атомной энергетики РАН
Москва, Россия

Поступила в редакцию 22.02.2019
После доработки 10.04.2019
Принята к публикации 17.04.2019

DOI: 10.1134/S0002331019020080

Аннотация

Данная работа посвящена одной из наиболее важных задач атомной энергетики – изоляции радиоактивных отходов. В настоящее время существуют разные способы изоляции РАО и ОЯТ. В настоящей работе рассматривается один из таких способов – метод “самопогружения”. Обобщены квазиодномерные модели процесса “самопогружения” тепловыделяющего шара, представленные в [1] и [2], путем учета мощности источника тепловыделения, а также пористости и трещиноватости окружающих пород. Была получена модель, достаточно точно описывающая процесс “самопогружения” тепловыделяющего шара. А также, были учтены пористость и трещиноватость окружающей породы. Данный анализ может быть использован как для оценки скорости “самопогружения” капсулы с РАО, так и для выбора геологических пород, в которых может быть реализован вышеописанный метод изоляции РАО.

Ключевые слова: процесс “самопогружения”, радиоактивные отходы (РАО), отработавшее ядерное топливо (ОЯТ), тепловыделение, обобщение, квазиодномерные модели, пористость, трещиноватость

ВВЕДЕНИЕ

Одной из наиболее важных задач, от решения которой зависят перспективы развития атомной энергетики, является обращение с долгоживущими компонентами радиоактивных отходов (РАО), в первую очередь, с трансурановыми радионуклидами. В настоящее время рассматриваются несколько вариантов решения этой проблемы. Создание долговременных подземных контролируемых хранилищ на основе принципа “мультибарьерной защиты” рассматривается как наиболее перспективный вариант окончательной изоляции всей совокупности РАО (в том числе и трансурановых элементов) [3], и именно ему уделяется основное внимание разработчиков. Другие варианты основаны на выжигании актиноидов трансмутацией. Они связаны с будущим развитием реакторов нового поколения на быстрых нейтронах и замкнутого ядерного топливного цикла. А также, ввиду того, что количество нарабатываемых актиноидов сравнительно невелико, не исключается возможность удаления их за пределы атмосферы – в космос.

При изоляции РАО в подземных хранилищах считается, что надежность захоронений будет обеспечена совместным использованием как инженерных конструкций (контейнеры, консервирующая матрица, бентонитовые слои и т.д.), имеющих, вообще говоря, ограниченный срок действия порядка 1000 лет, так и естественных геологических барьеров, характеристики которых определяются свойствами вмещающих пород. При решении проблемы захоронения долгоживущих миноров необходимо учитывать, что речь идет о временах от десяти тысяч лет и более, так что велика вероятность, что основную роль по предотвращению выхода радиотоксичных нуклидов в экосистему будут играть геологические барьеры. Поэтому подземные хранилища планируется располагать на глубине от нескольких сотен метров до полукилометра, что должно обеспечить надежное удержание радионуклидов от выхода на поверхность. Отметим, что устройство и эксплуатация таких хранилищ требует значительных затрат, а в случае использования их для изоляции долгоживущих РАО контроль в определенной степени должен осуществляться на протяжении всего времени, пока радиологическая активность остается значимой.

Поскольку к настоящему моменту окончательный выбор в пользу долговременных подземных хранилищ РАО еще не сделан, представляет интерес рассмотреть альтернативные варианты захоронения. В связи с этим для решения проблемы окончательной изоляции долгоживущих трансурановых радионуклидов рассматривается их захоронение методом самопогружения в геологических средах, который ранее предлагался для захоронения всей совокупности РАО, накапливающихся в активной зоне ядерных реакторов [4–6]. Идея метода довольно проста. В предварительно подготовленную скважину опускаются капсулы с РАО. В результате тепловыделения капсулы будут разогревать и расплавлять окружающую породу, и под действием собственного веса опускаться вглубь, вытесняя образующийся расплав.

Приближенная математическая модель процесса “самопогружения” впервые была предложена в работе [1], где решается задача Стокса с плавлением. Были получены аналитические выражения для толщины расплава $\delta $ и скорости погружения шара $U$ при малых числах Стефана ${\text{Ste}} \ll 1.$ В работе [2] была развита эта модель без учета мощности тепловыделения внутри шара.

В данной работе представлена обобщенная квазиодномерная модель погружения тепловыделяющего шара с распределенным источником тепла под действием силы тяжести с учетом мощности тепловыделения. Также в рамках представленной модели производится учет трещиноватости окружающей геологической породы.

Целью настоящей работы является получение обобщенной модели “самопогружения” тепловыделяющего шара учетом мощности тепловыделения и трещиноватости окружающей породы.

Все численные расчеты, описанные в данной работе, производились по программе, реализующей полученную модель, написанной на языке программирования Python.

Постановка задачи

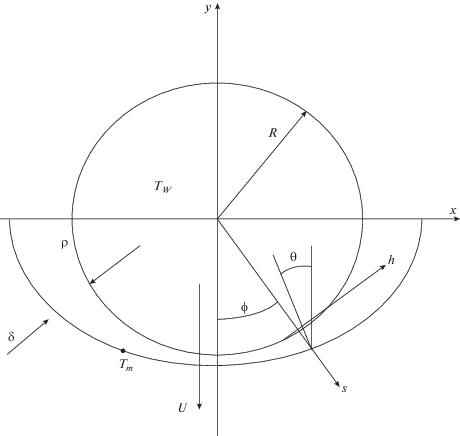
Рассматривается сферически-симметричная капсула, помещенная в среду с теплопроводностью $\lambda .$ Капсула представляет собой шар, заполненный ОЯТ и РАО, в котором за счет радиоактивного распада выделяется тепло достаточное для проплавления окружающей геологической породы. Разность плотностей между шаром и расплавом предполагается достаточно большой, чтобы обеспечить непрерывное погружение шара под действием силы тяжести. При погружении капсулы расплавленная порода вытесняется вверх через узкий слой (рис. 1).

Рис. 1.

Физическая модель.

Ранее эта задача аналитически была решена в работе [1], но ее решение было справедливо только в окрестности фронтовой точки, а при $\phi $ стремящимся к $\frac{\pi }{2},$ толщина расплава $\delta $ устремлялась к бесконечности, что не является физичным. Позже в работе [2] физичность результата удалось добиться за счет введения угла $\theta ,$ который учитывает реальный угол поверхности расплава. Геометрическая связь между углами $\varphi ,$ $\theta $ и толщиной расплава $\delta $ выражается следующим образом:

(1)

$\frac{{d\delta }}{{d\phi }} = (R + \delta ){\text{tg}}(\phi - \theta ).$

Результаты, полученные согласно работе [2], не совсем точно характеризуют процесс “самопогружения”, так как в них не была учтена зависимость температуры поверхности капсулы ${{T}_{W}}$ от каких-либо физических параметров.

Данное исследование посвящено объединению работ [1] и [2], с целью получения квазиодномерной модели процесса “самопогружения” тепловыделяющего шара адекватно описывающей зависимость скорости погружения тепловыделяющей капсулы от режимных и конструктивных параметров, мощности тепловыделения H и радиуса шара R.

РЕШЕНИЕ БЕЗ УЧЕТА ТЕПЛОВЫДЕЛЕНИЯ

В работе [2] было предложено следующее решение без учета тепловыделения, описывающее процесс “самопогружения” тепловыделяющего шара.

Предполагается, что толщина расплава очень мала $\delta \ll R$ и вязкая сила такая, что $\frac{{{{\partial }^{2}}}}{{\partial {{h}^{2}}}} \ll \frac{{{{\partial }^{2}}}}{{\partial {{s}^{2}}}}$ (приближение теории смазки), перенос тепла путем конвективного потока пренебрежимо мал по сравнению с теплопроводностью в квазиустойчивом слое расплава. Тогда поток расплава определяется следующим уравнением Навье-Стокса:

(2)

$\mu \frac{{{{\partial }^{2}}u}}{{\partial {{s}^{2}}}} = \frac{{dp}}{{dh}}$

граничные условия u(s = 0) = 0 и u(s = δ) = 0, где $u$ – тангенциальная скорость, $\mu $ – динамическая вязкость расплава, $s$ – нормаль к шару, $p$ – давление внутри расплава, $h$ – касательная к шару (рис. 1).

Дважды интегрируя (2) получаем:

(3)

$u = \frac{1}{{2\mu }}\frac{{dp}}{{dh}}(s - \delta )s.$

Уравнение баланса массы в расплаве:

(4)

$2\pi R\sin \phi \int\limits_0^\delta {uds} = 2\pi RU\int\limits_0^h {\sin \phi \cos \theta dh} ,$

где $\phi $ – нормальный угол к поверхности шара, $\theta $ – нормальный угол к поверхности раздела фаз. Подставляем уравнение (3) в (4), получаем:

(5)

$\frac{{dp}}{{d\phi }} = - \left( {\frac{{12\mu U{{R}^{2}}}}{{{{\delta }^{3}}\sin \phi }}\int\limits_0^\phi {\sin \phi \cos \theta d\phi } } \right).$

Закон сохранения энергии в расплаве:

(6)

$ - \lambda {{\left( {\frac{{\partial T}}{{\partial s}}} \right)}_{{s = \delta }}}\cos \left( {\phi - \theta } \right) = \rho {{L}_{m}}U\cos \theta ,$

где L_m = L + c_p(T₀ – T_m), $\lambda $ – коэффициент теплопроводности, $\rho $ – плотность расплава, $L$ – скрытая теплота плавления, ${{c}_{p}}$ – удельная теплоемкость среды.

Согласно [1] температура в расплаве аппроксимируется квадратичным полиномом по s, толщина расплава находится из уравнения (6):

(7)

$\delta = \alpha {\kern 1pt} f({\text{Ste}})\frac{{\cos (\phi - \theta )}}{{U\cos \theta }},$

где ${\text{Ste}} = \frac{{{{c}_{p}}\left( {{{T}_{W}} - {{T}_{m}}} \right)}}{{{{L}_{m}}}},$ $\alpha $ – температуропроводность среды. Так как f (Ste) = = ${{(\sqrt {9{\text{St}}{{{\text{e}}}^{2}} + 280{\text{Ste}} + 400} - 3{\text{Ste}} - 20)} \mathord{\left/ {\vphantom {{(\sqrt {9{\text{St}}{{{\text{e}}}^{2}} + 280{\text{Ste}} + 400} - 3{\text{Ste}} - 20)} 4}} \right. \kern-0em} 4},$ при ${\text{Ste}} \ll 1$ f (Ste) можно заменить на ${\text{Ste,}}$ тогда из (7):

(8)

$\delta = \alpha {\text{Ste}}\frac{{\cos \left( {\phi - \theta } \right)}}{{U\cos \theta }}.$

Действующая на шар сила давления выражается следующим образом:

(9)

$F = 2\pi {{R}^{2}}\int\limits_0^\phi {p\sin \phi \cos \phi d\phi } .$

Если на шар не действуют внешние силы, то F эквивалентна $F = \frac{{4\pi {{R}^{3}}\left( {{{\rho }_{H}} - \rho } \right)g}}{3},$ где ${{\rho }_{H}}$ – плотность шара.

Безразмерные параметры определяются как: $\delta * = \frac{\delta }{R};$ $p* = \frac{{p{{R}^{2}}}}{{\mu \alpha }};$ $U* = \frac{{UR}}{\alpha };$ $F* = \frac{F}{{\mu \alpha }}.$

Тогда из уравнений (1), (5), (7) и (9) получается безразмерная система уравнений, описывающая плавление вокруг тепловыделяющего шара, где плавление вызвано разностью температур между поверхностью шара и окружающей породой.

(10)

$\frac{{dp{\text{*}}}}{{d\phi }} = - \frac{{12U{\text{*}}\int\limits_0^\phi {\sin \phi \cos \theta d\phi } }}{{{{\delta }^{{*3}}}\sin \phi }},$

(11)

$\delta * = \frac{{f({\text{Ste}})\cos (\phi - \theta )}}{{U{\text{*}}\cos \theta }},$

(12)

$F* = 2\pi \int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {p{\text{*}}\sin \phi \cos \phi d\phi } ,$

(13)

$\frac{{d\delta {\text{*}}}}{{d\phi }} = \left( {R + \delta {\text{*}}} \right){\text{tg}}(\phi - \theta ).$

Система (10)–(13) имеет четыре неизвестных $\delta *,$ $p{\text{*,}}$ $\theta $ и $U{\text{*}}{\text{.}}$ Эта система аналитически неразрешима. При $\phi = \theta $ получается решение [1]. В работе [2] описан алгоритм решения системы (10)–(13), основанный на итерационном методе. Критерий сходимости данного метода заключается в следующем: если для заданной скорости сила трения и плавучести уравновешивают друг друга, то скорость задана верно.

Решение с учетом тепловыделения

Для обобщения квазиодномерных моделей процесса “самопогружения” тепловыделяющего шара в алгоритме [2] температура поверхности шара заменяется на свою зависимость от радиуса и мощности источника тепловыделения согласно [1].

Суммарная потеря тепла из шара выражается следующим образом:

(14)

$Q = - 2\pi {{R}^{2}}\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\lambda \frac{{\partial T}}{{\partial s}}} \left( {s = 0} \right)\sin \phi d\phi .$

Температурный профиль представляется квадратичным полиномом по s:

(15)

$T = {{T}_{W}} + s\left[ {\frac{{ - 2\left( {{{T}_{W}} - {{T}_{m}}} \right)}}{\delta }} \right] + {{s}^{2}}\left[ {\frac{{{{T}_{W}} - {{T}_{m}}}}{{{{\delta }^{2}}}} - \frac{{\rho U{{L}_{m}}}}{{\lambda \delta }}\cos \phi } \right],$

где ${{T}_{W}}$ – температура поверхности шара, ${{T}_{m}}$ – температура плавления среды, $\rho $ – плотность расплава.

Толщина расплавленного слоя выражается [1]:

(16)

$\delta = \frac{{\alpha {\text{Ste}}}}{{U\cos \phi }}.$

Подставляем (16) и (15) в (14):

(17)

$Q = \pi {{R}^{2}}\lambda U\left[ {\frac{{2\left( {{{T}_{W}} - {{T}_{m}}} \right)}}{{\alpha {\kern 1pt} f({\text{Ste}})}} - \frac{{\rho {{L}_{m}}}}{\lambda }} \right].$

С другой стороны, общее количество тепла связано с мощностью тепловыделения:

(18)

$Q = \frac{4}{3}\pi {{R}^{3}}{{\rho }_{H}}H.$

Из уравнения баланса энергии выражение для скорости погружения:

(19)

$U = \frac{{\left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}} \right)\left( {{{R{{\rho }_{H}}H} \mathord{\left/ {\vphantom {{R{{\rho }_{H}}H} \lambda }} \right. \kern-0em} \lambda }} \right)}}{{\left[ {{{2({{T}_{W}} - {{T}_{m}})} \mathord{\left/ {\vphantom {{2({{T}_{W}} - {{T}_{m}})} {\alpha {\kern 1pt} f({\text{Ste}})}}} \right. \kern-0em} {\alpha {\kern 1pt} f({\text{Ste}})}}} \right] - \left( {{{\rho {{L}_{m}}} \mathord{\left/ {\vphantom {{\rho {{L}_{m}}} \lambda }} \right. \kern-0em} \lambda }} \right)}}.$

Из уравнения баланса силы плавучести $F = \frac{{4\pi {{R}^{3}}\left( {{{\rho }_{H}} - \rho } \right)g}}{3}$ и силы трения [1] ${{F}_{d}} = \frac{{\pi \mu {{R}^{4}}{{U}^{4}}}}{{2{{\alpha }^{3}}{{f}^{3}}({\text{Ste}})}}$ еще одно выражение для скорости:

(20)

$U = {{\left[ {\frac{{8g\Delta \rho {{\alpha }^{3}}{{f}^{3}}({\text{Ste}})}}{{3\mu R}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$

где $\Delta \rho = {{\rho }_{H}} - \rho .$

Система уравнений для нахождения установившейся скорости погружения $U$ и температуры поверхности шара T_W при известном радиусе R и мощности тепловыделения $H$ представляет собой уравнения (19)–(20).

При малом ${\text{Ste,}}$ из равенства силы плавучести и силы трения можно получить следующее выражение для температуры поверхности шара:

(21)

${{T}_{W}} = {{T}_{m}} + \frac{{{{L}_{m}}}}{{\alpha {{c}_{p}}}}{{\left( {\frac{{3R\mu {{U}^{4}}}}{{8g\Delta \rho }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$

Подставляя (19) в (21):

(22)

${{T}_{W}} = {{T}_{m}} + \frac{4}{3}\frac{1}{{\alpha {{c}_{p}}}}{{\left( {\frac{{\mu \rho _{H}^{4}{{H}^{4}}{{R}^{5}}}}{{2g\Delta \rho {{L}_{m}}{{\rho }^{4}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$

Таким образом, выражая температуру поверхности шара согласно (22), удалось учесть зависимость скорости погружения тепловыделяющего шара от режимных и конструктивных параметров, то есть от мощности тепловыделения и радиуса шара.

Некоторые расчеты по обобщенному алгоритму

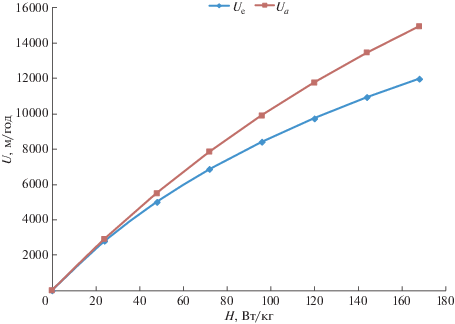
Чтобы проверить работу обобщенного алгоритма, были построены зависимости скорости погружения шара от мощности источника тепловыделения, полученные по алгоритму ${{U}_{a}}(H)$ и согласно уравнениям [1] ${{U}_{1}}(H)$ (рис. 2).

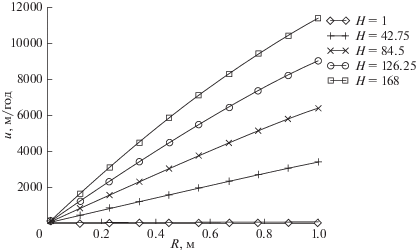
Влиять на процесс “самопогружения” можно за счет выбора конструктивных и режимных параметров. В данной постановке задачи это радиус $R$ и мощность тепловыделения $H.$ Для оценки влияния конструктивных и режимных параметров на процесс “самопогружения” тепловыделяющего шара были построены зависимости $U$ от $R$ для разной $H$ (рис. 3).

Учет пористости-трещиноватости

На скорость погружения тепловыделяющего шара также влияет пористость породы. Логично рассматривать процесс “самопогружения” тепловыделяющего шара именно в гранитную породу. Гранит – глубинная горная порода сложная по своему составу, и пористость является одной из важнейших качественных характеристик камня. В настоящей работе анализируется влияние пористости на скорость “самопогружения” тепловыделяющего шара.

Закон сохранения массы для жидкой и твердой фазы:

(23)

${{V}_{s}}{{\rho }_{s}} = {{V}_{l}}{{\rho }_{l}}.$

Объем расплава, который образуется в единицу времени:

(24)

${{\dot {V}}_{l}} = {{\dot {V}}_{s}}\frac{{{{\rho }_{s}}}}{{{{\rho }_{l}}}} = {{\dot {V}}_{l}}q\frac{{{{\rho }_{s}}}}{{{{\rho }_{l}}}},$

где q = 1 – $\frac{{{{V}_{{{\text{cr}}}}}}}{{{{V}_{t}}}},$ ${{V}_{{{\text{cr}}}}}$ – объем, занимаемый порами, ${{V}_{t}}$ – полный объем, в данном случае объем цилиндра с радиусом R' и высотою ${{U}_{{ph\_b}}}\Delta t,$ ${{U}_{{ph\_b}}}$ – скорость шара или скорость границы раздела фаз, отсюда ${{\dot {V}}_{t}}$ = $\pi {{U}_{{ph\_b}}}R{{{\text{'}}}^{2}},$ где $R{\text{'}}$ – радиус окружности, которую образует поверхность раздела фаз.

С другой стороны, объем расплава, генерирующийся в единицу времени:

(25)

${{\dot {V}}_{l}} = {{u}_{l}}\pi R{{{\text{'}}}^{2}},$

где u_l скорость расплава.

Теперь из (24) и (25) получается следующая связь между скорости погружения шара скорость расплава и пористостью породы.

(26)

${{U}_{{ph\_b}}} = U = {{u}_{l}}\frac{{{{\rho }_{l}}}}{{{{\rho }_{s}}}}\frac{1}{q}.$

Скорость расплава считается из алгоритма, плотность и пористость – характеристики среды, подставляя эти величины в (26) получаем скорость погружения шара с учетом пористости породы.

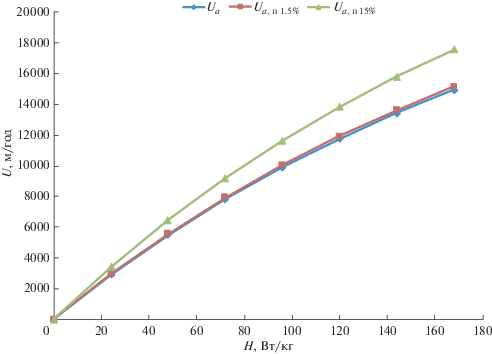
Теперь можно построить зависимость скорости погружения шара от мощности источника тепловыделения для разной пористости.

Графики построены для пористости 0, 1.5 и 15%. Чем больше пористость, тем больше скорость погружения шара.

Рис. 2.

Зависимости скорости погружения шара от мощности источника тепловыделения.

Рис. 3.

Зависимости $U$ от $R$ для разной $H.$

Рис. 4.

Зависимости скорости погружения шара от мощности источника тепловыделения для разной пористости среды.

Выводы

Были получены следующие результаты:

$ - $ обобщены квазиодномерные модели “самопогружения” шара, учитывающие мощность теплового источника;

$ - $ проведены расчеты, описывающие зависимость скорости погружения от радиуса шара и мощности источника тепловыделения;

$ - $ учтены пористость и трещиноватость окружающей среды.

Разработана обобщенная модель, описывающая процесс “самопогружения” тепловыделяющего шара. Получена зависимость скорости погружения от режимных и конструктивных параметров. А также, были учтены пористость и трещиноватость окружающей породы. Установлена зависимость скорости погружения от пористости и трещиноватости. Данный анализ может быть использован как для оценки скорости “самопогружения” тепловыделяющего шара, так и для выбора геологических пород, в которых может быть реализован вышеописанный метод изоляции РАО.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 17-08-01491).

Список литературы

Emerman S.E., Turcotte D.L. Stoke’s problem with melting // Heat Mass Transfer. 1983. V. 26. № 11. P. 1625–1630.
Chen W., Zhu B., Chen Z., Li H., Sun F. New analysis of contact melting of phase change material around a hot sphere // Heat Mass Transfer. 2008. № 44. P. 281–286.
National Research Council (NRC), The Disposal of Radioactive Waste on Land, National Academy Press, Washington, D.C., 1957.
Cohen, J.J., Schwartz L.L., Tewes H.A. Economic and environmental evaluation of nuclear waste disposal by underground in situ melting. – Transactions of the American Nuclear Society, 1974. V. 18. P. 194–195.
Logan S.E. Deep self-burial of radioactive wastes by rock-melting capsules. – Nuclear Technology, 1974. V. 21. P. 111–124.
Авторское свидетельство СССР, N 826 875, кл. G 21,9124, 21.04.1980.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал