Известия РАН. Энергетика, 2019, № 2, стр. 135-156
Модельные представления теплового удара
Э. М. Карташов 1, *, **, Е. В. Ненахов 2
1 Московский технологический университет (МИТХТ)
Москва, Россия
2 Московский авиационный институт (НИУ МАИ)
Москва, Россия
* E-mail: kartashov@mitht.ru
** E-mail: newnew94@mail.ru
Поступила в редакцию 22.04.2019
После доработки 07.05.2019
Принята к публикации 14.05.2019
Аннотация
Статья посвящена математическим моделям теплового удара в терминах динамической термоупругости и их приложению к конкретным условиям интенсивного нагрева и охлаждения твердых тел. Предложена схема вывода уравнения совместности в напряжениях для динамических задач, обобщающее известное соотношение Бельтрами–Митчелла для квазистатических случаев. Предложенное соотношение может быть использовано для рассмотрения многочисленных частных случаев в теории теплового удара в декартовых координатах как для ограниченных тел канонической формы, так и для частично ограниченных. В качестве подробного исследования рассмотрен последний случай в условиях резкого температурного нагрева и охлаждения, теплового нагрева и охлаждения, нагрева и охлаждения средой. Проведены численные эксперименты и описан волновой характер распространения термоупругих волн. Описан малоизученный в термомеханике эффект релаксации границы твердого тела на внезапный нагрев и внезапное охлаждение. Установлено влияние указанного эффекта на максимум внутренних температурных напряжений, зависящих от параметров, характеризующих упругие и теплофизические свойства материалов, а также время нагрева и время охлаждения. Предложено “уравнение совместности” в перемещениях для исследования проблемы теплового удара в цилиндрической и сферической системах координат в телах при радиальном потоке теплоты и центральной симметрии. Сформулирована постановка обобщенной задачи в теории теплового удара, что представляет практический и теоретический интересы для многих направлений науки и техники.
ВВЕДЕНИЕ
Проблема термического удара – одна из центральных в термомеханике в связи с созданием мощных излучателей энергии и их использованием в различных технологических операциях. Ее исследования на основе моделей динамической и квазистатической термоупругости получили широкое развитие: изучены физические закономерности термонапряженного состояния в изотропных и анизотропных упругих телах на основе классических феноменологий Фурье [1–4] и Максвелла–Каттанео–Лыкова о конечной скорости распространения теплоты в твердых телах [5–7]; развита обобщенная теория сопряжения термомеханических полей с полями различной физической природы (электрических, магнитных) [8, 9]; сформулированы определяющие соотношения линеаризованной теории с учетом тепловой памяти [10]; установлена связь макроскопического поведения сплошной среды с внутренними параметрами состояния среды и скоростью их изменения во времени [11]. Интенсификация тепловых воздействий на элементы конструкций, создание новых технологических процессов, основанных на использовании высокоинтенсивных импульсных потоков энергии, стимулирует разработку соответствующих модельных представлений для описания термической реакции конструкционных материалов, применяемых на практике. Систематизация результатов, накопленных в этой области термомеханики, дана в обзорах [12–15] и книге [1].
ОПРЕДЕЛЯЮЩИЕ СООТНОШЕНИЯ ДИНАМИЧЕСКОЙ ТЕРМОУПРУГОСТИ
Пусть $D$ – конечная или частично ограниченная выпуклая область пространства $M\left( {x,y,z} \right),$ описывающая реальное твердое тело и находящаяся в условиях термонапряженного состояния; $S$ – кусочно-гладкая поверхность, ограничивающая область D, $\vec {n} = \left( {{{n}_{1}},{{n}_{2}},{{n}_{3}}} \right)$ – внешняя нормаль к $S$, вектор, непрерывный на $S$,$T\left( {M,t} \right)$ – распределение температуры в области $D$ при $t > 0$; ${{T}_{0}}$ – начальная температура, при которой область находится в недеформированном и напряженном состоянии. Пусть ${{\sigma }_{{ij}}}(M,t),$ ${{\varepsilon }_{{ij}}}(M,t),$ ${{U}_{i}}(M,t)$ – соответственно компоненты тензоров напряжения, деформации и вектора перемещения, удовлетворяющие основным уравнениям (несвязанной) термоупругости (в индексных обозначениях):
(2)
${{\varepsilon }_{{ij}}}(M,t) = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})\left[ {{{U}_{{i,j}}}(M,t) + {{U}_{{j,i}}}(M,t)} \right];$(3)
$\begin{gathered} {{\sigma }_{{ij}}}(M,t) = 2\mu {{\varepsilon }_{{ij}}}(M,t) + \\ + \,\,\left[ {\lambda {{\varepsilon }_{{ii}}}(M,t) - \left( {3\lambda + 2\mu } \right){{\alpha }_{T}}\left( {T\left( {M,t} \right) - {{T}_{0}}} \right)} \right]{{\delta }_{{ij}}}, \\ M > D,\,\,\,\,t > 0, \\ \end{gathered} $(4)
$\bar {e}\left( {M,t} \right) = \quad\,\,\frac{{1 - 2\upsilon }}{E}\bar {\sigma }\left( {M,t} \right) + \,\,\quad3{{\alpha }_{T}}\left[ {T\left( {M,t} \right) - {{T}_{0}}} \right].$Исключая в (2) компоненты вектора перемещения, приходим к известному уравнению совместности деформаций в виде ${{\gamma }_{{pmj}}}{{\gamma }_{{qni}}}{{\varepsilon }_{{ij,mn}}}\left( {M,t} \right) = 0,$ где ${{\gamma }_{{ijk}}}$ – альтернативный (антисимметричный) тензор $\left( {p,q,m,n = x,y,z} \right).$ Это уравнение можно расписать подробнее:
(5)
${{\varepsilon }_{{ij,mn}}} - {{\varepsilon }_{{im,jn}}} - {{\varepsilon }_{{nj,mi}}} + {{\varepsilon }_{{mn,ji}}} = 0.$Выразим из (3) деформации через напряжения
(6)
${{\varepsilon }_{{ij}}}\left( {M,t} \right) = \frac{{1 + \upsilon }}{E}\quad{{\sigma }_{{ij}}}\left( {M,t} \right) - \frac{\upsilon }{E}{{\sigma }_{{nn}}}\left( {M,t} \right){{\delta }_{{ij}}} + {{\alpha }_{T}}\left[ {T\left( {M,t} \right) - {{T}_{0}}} \right]{{\delta }_{{ij}}},$Свернем в (5) в тензоры по индексам $m = n\,:{{\varepsilon }_{{ij,nn}}} - {{\varepsilon }_{{in,jn}}} - {{\varepsilon }_{{nj,ni}}} + {{\varepsilon }_{{nn,ji}}} = 0$ и подставим правые части соотношения (6). Произведя преобразования с использованием (1), (2) и свойств тензорной алгебры, найдем следующее основное уравнение динамической термоупругости в напряжениях:
(7)
$\begin{gathered} \left( {1 + \upsilon } \right){{\sigma }_{{ij,nn}}}\left( {M,t} \right) + {{\sigma }_{{nn,ji}}}\left( {M,t} \right) + \frac{{\upsilon \left( {1 + \upsilon } \right)}}{{\left( {1 - \upsilon } \right)}}{{F}_{{n,n}}}\left( {M,t} \right){{\delta }_{{ij}}} + \\ + \,\,\left( {1 + \upsilon } \right)\left[ {{{F}_{{i,j}}}\left( {M,t} \right) + {{F}_{{j,i}}}\left( {M,t} \right)} \right] + \quad \\ + \,\,E{{\alpha }_{T}}\left[ {\frac{{1 + \upsilon }}{{1 - \upsilon }}{{{\left( {T\left( {M,t} \right) - {{T}_{0}}} \right)}}_{{,nn}}}{{\sigma }_{{ij}}} + {{{\left( {T\left( {M,t} \right) - {{T}_{0}}} \right)}}_{{,ij}}}} \right] = \\ = \frac{{\left( {1 + \upsilon } \right)\rho }}{{2G}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left[ {2{{\sigma }_{{ij}}}\left( {M,t} \right) - \frac{\upsilon }{{1 - {{\upsilon }^{2}}}}{{\sigma }_{{nn}}}\left( {M,t} \right){{\delta }_{{ij}}} + \frac{{2G\left( {2 + \upsilon } \right)}}{{1 - \upsilon }}\quad{{\alpha }_{T}}\left( {T\left( {M,t} \right) - {{T}_{0}}} \right){{\delta }_{{ij}}}} \right], \\ M \in D,\,\,\,\,t > 0, \\ \end{gathered} $(8)
$\begin{gathered} \left( {1 + \upsilon } \right)\Delta {{\sigma }_{{ij}}}\left( {M,t} \right) + {{\sigma }_{{,ij}}}\left( {M,t} \right) + \frac{{\upsilon \left( {1 + \upsilon } \right)}}{{1 - \upsilon }}{\text{div}}\vec {F}\left( {M,t} \right){{\delta }_{{ij}}} + \\ + \,\,\left( {1 + \upsilon } \right)\left[ {{{F}_{{i,j}}}\left( {M,t} \right) + {{F}_{{j,i}}}\left( {M,t} \right)} \right] + \\ + \,\,{{\alpha }_{T}}E\left[ {\frac{{1 + \upsilon }}{{1 - \upsilon }}\Delta T\left( {M,t} \right){{\delta }_{{ij}}} + {{{\left( {T\left( {M,t} \right) - {{T}_{0}}} \right)}}_{{,ij}}}} \right] = \\ = \frac{{\left( {1 + \upsilon } \right)\rho }}{{2G}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left[ {2{{\sigma }_{{ij}}}\left( {M,t} \right) - \frac{\upsilon }{{1 - {{\upsilon }^{2}}}}\sigma \left( {M,t} \right){{\delta }_{{ij}}} + \frac{{2G\left( {2 + \upsilon } \right)}}{{1 - \upsilon }}{{\alpha }_{T}}\left( {T\left( {M,t} \right) - {{T}_{0}}} \right){{\sigma }_{{ij}}}} \right], \\ \left( {M \in D;\,\,\,\,t > 0;\,\,\,\,i,j = 1,2,3} \right), \\ \end{gathered} $Выражение (7) является обобщением уравнений Бельтрами–Митчелла на динамические задачи. Этот случай впервые рассмотрел В. Новацкий, используя уравнения эластокинетики в напряжениях [16], однако конечный результат имеет форму, отличную от (7) и менее удобную для практических приложений. В этом смысле уравнение (7) представляет самостоятельный интерес для термомеханики. Впрочем, для полноты изложения рассмотрим этот вопрос. В [16] предложено уравнение совместности в напряжениях для динамических задач в виде:
(9)
$\begin{gathered} \Xi _{2}^{2}{{\sigma }_{{ij}}} + \frac{{2\left( {\lambda + \mu } \right)}}{{3\lambda + 2\mu }}{{\sigma }_{{nn,ij}}} + \left( {\frac{1}{{c_{2}^{2}}} - \frac{1}{{c_{1}^{2}}}} \right)\frac{{\lambda {{\sigma }_{{ij}}}}}{{3\lambda + 2\mu }}{{{\ddot {\sigma }}}_{{nn}}} + 2\mu {{\alpha }_{T}}\left( {{{\Theta }_{{,ij}}} + \frac{{3\lambda + 2\mu }}{{\lambda + 2\mu }}{{\Theta }_{{,nn}}}{{\delta }_{{ij}}}} \right) - \\ - \,\,\frac{{5\lambda + 4\mu }}{{\lambda + 2\mu }}{{\alpha }_{T}}\rho {{\delta }_{{ij}}}\ddot {\Theta } + {{\zeta }_{{ij}}} = 0 \\ \end{gathered} $(10)
$\left. \begin{gathered} \Xi _{2}^{2} = \left( {{{\nabla }^{2}} - \frac{1}{{с _{2}^{2}}}\partial _{1}^{2}} \right)\,\,{\text{О п е р а т о р }}\,\,{\text{Д а л а м б е р а }};\,\,\,с _{1}^{2} = \frac{{\lambda + 2\mu }}{\rho };\,\,\,c_{2}^{2} = \frac{\mu }{\rho };\,\,\,\Theta = T - {{T}_{0}}; \hfill \\ {{\zeta }_{{ij}}} = {{X}_{{i,j}}} + {{X}_{{j,i}}} + \frac{{\lambda {{\delta }_{{ij}}}}}{{\lambda + 2\mu }}{{X}_{{r,r}}} \hfill \\ \end{gathered} \right\}.$Соотношение (9) менее удобно для практического использования и его можно свести к выражению (7). Для этого перепишем уравнение, используя обозначения [1]:
(11)
$\begin{gathered} {{\sigma }_{{ij,nn}}} + \frac{{2\left( {\lambda + \mu } \right)}}{{3\lambda + 2\mu }}{{\sigma }_{{nn,ij}}} + \frac{\lambda }{{\lambda + 2\mu }}{{F}_{{n,n}}}{{\delta }_{{ij}}} + {{F}_{{i,j}}} + {{F}_{{j,i}}} + \\ + \,\,2\mu {{\alpha }_{T}}\left[ {\frac{{3\lambda + 2\mu }}{{\lambda + 2\mu }}{{{\left( {T - {{T}_{0}}} \right)}}_{{,nn}}}{{\delta }_{{ij}}} + {{{\left( {T - {{T}_{0}}} \right)}}_{{,ij}}}} \right] = \\ = \frac{1}{{2c_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left[ {2{{\sigma }_{{ij}}} - 2c_{2}^{2}\left( {\frac{1}{{c_{2}^{2}}} - \frac{1}{{c_{1}^{2}}}} \right)\frac{\lambda }{{3\lambda + 2\mu }}{{\sigma }_{{nn}}}{{\delta }_{{ij}}} + 2c_{2}^{2}\frac{{5\lambda + 4\mu }}{{\lambda + 2\mu }}\rho {{\alpha }_{T}}\left( {T - {{T}_{0}}} \right){{\delta }_{{ij}}}} \right], \\ \end{gathered} $(12)
${{\zeta }_{{ij}}} = {{X}_{{i,j}}} + {{X}_{{j,i}}}\frac{\lambda }{{\lambda + 2\mu }}{{X}_{{r,r}}}{{\delta }_{{ij}}} = {{F}_{{i,j}}} + {{F}_{{j,i}}} + \frac{\lambda }{{\lambda + 2\mu }}{{F}_{{n,n}}}{{\delta }_{{ij}}}.$Учтем связь постоянных $\lambda ,\,\mu $ и скоростей ${{c}_{1}},\,{{c}_{2}}$ с техническими постоянными $E,G,\upsilon \,:$
Используя эти соотношения в (11), приходим к предложенному нами выражению (7):
(13)
$\begin{gathered} {{\sigma }_{{ij,nn}}} + \frac{1}{{1 + \upsilon }}{{\sigma }_{{nn,ij}}} + \frac{\upsilon }{{1 - \upsilon }}{{F}_{{n,n}}}{{\delta }_{{ij}}} + {{F}_{{i,j}}} + {{F}_{{j,i}}} + \\ + \,\,\frac{E}{{1 + \upsilon }}{{\alpha }_{T}}\left[ {\frac{{1 + \upsilon }}{{1 - \upsilon }}{{{\left( {T - {{T}_{0}}} \right)}}_{{,nn}}}{{\delta }_{{ij}}} + {{{\left( {T - {{T}_{0}}} \right)}}_{{,ij}}}} \right] = \\ = \frac{\rho }{{2G}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left[ {2{{\sigma }_{{ij}}} - \frac{\upsilon }{{1 - {{\upsilon }^{2}}}}{{\sigma }_{{nn}}}{{\delta }_{{ij}}} + 2G\frac{{2 + \upsilon }}{{1 - \upsilon }}{{\alpha }_{T}}\left( {T - {{T}_{0}}} \right){{\delta }_{{ij}}}} \right]. \\ \end{gathered} $Термонапряженное состояние области $D$ при $t > 0$ может возникать при различных режимах теплового воздействия на границу S, создающих термический удар. К ним можно отнести наиболее распространенные на практике случаи [17, 18]: температурный нагрев $T\left( {M,t} \right) = {{T}_{c}}\left( t \right),$ $M \in S,$ $t > 0,$ $\left( {{{T}_{c}}\left( t \right) > {{T}_{0}},\,\,\,t \geqslant 0} \right);$ тепловой нагрев ${{\partial T\left( {M,t} \right)} \mathord{\left/ {\vphantom {{\partial T\left( {M,t} \right)} {\partial n = - \left( {{1 \mathord{\left/ {\vphantom {1 {{{\lambda }_{T}}}}} \right. \kern-0em} {{{\lambda }_{T}}}}} \right){{q}_{0}}\left( t \right)}}} \right. \kern-0em} {\partial n = - \left( {{1 \mathord{\left/ {\vphantom {1 {{{\lambda }_{T}}}}} \right. \kern-0em} {{{\lambda }_{T}}}}} \right){{q}_{0}}\left( t \right)}},$ $M \in S,$ $t > 0$ (${{\lambda }_{T}}$ – теплопроводность материала, ${{q}_{0}}\left( t \right)$ – величина теплового потока); нагрев средой ${{\partial T\left( {M,t} \right)} \mathord{\left/ {\vphantom {{\partial T\left( {M,t} \right)} {\partial n = - h\left[ {T\left( {M,t} \right) - {{T}_{c}}} \right]}}} \right. \kern-0em} {\partial n = - h\left[ {T\left( {M,t} \right) - {{T}_{c}}} \right]}},$ $M \in S,$ $t > 0$ ($h$ – относительный коэффициент теплообмена; ${{T}_{c}}$ – температура окружающей среды $\left( {{{T}_{c}} > {{T}_{0}}} \right)$), а также от действия внутренних источников теплоты. В равной мере могут быть рассмотрены и случаи охлаждения твердого тела.
Уравнение (8), в принципе, справедливо в любой ортогональной системе координат, однако наиболее удобное приложение соотношения (8) для частных случаев реализуется в декартовой системе координат для тел канонической формы (бесконечная пластина; пространство, ограниченное изнутри плоской поверхностью и др.).
В качестве применения соотношения (8) рассмотрим случай, имеющий важное значение для многих практических приложений. Можно выделить класс задач, в которых сочетание теплофизических свойств материала, геометрических размеров конструкций и интересующая исследователя термическая реакция тела касается приповерхностных слоев, в которых происходит резкое (или достаточно интенсивное) изменение температуры и в которых сосредоточено основное количество теплоты, поглощенной во времена близкие к началу нагрева, и, так как толщина приповерхностного слоя мала по сравнению с размерами тела, то в этих случаях твердое тело можно моделировать полуограниченной областью – упругим полупространством $z \geqslant 0,$ что позволяет получить более наглядные и удобные с точки зрения практического использования аналитические представления решений задач теории теплового удара. В этих условиях при одномерном движении величины ${{U}_{x}} = {{U}_{y}} = 0;$ ${{U}_{z}} = {{U}_{z}}\left( {z,t} \right);$ ${{\varepsilon }_{{zx}}} = {{\varepsilon }_{{zy}}} = {{\varepsilon }_{{xx}}} = {{\varepsilon }_{{yy}}} = {{\varepsilon }_{{xy}}} = 0,$ ${{\varepsilon }_{{zz}}} = {{\varepsilon }_{{zz}}}\left( {z,t} \right);$ напряжения ${{\sigma }_{{ij}}} = 0$ для $i \ne j$ и ${{\sigma }_{{ij}}} = {{\sigma }_{{ij}}}\left( {z,t} \right)$ для $i = j,$ температурная функция $T = T\left( {z,t} \right)$ и уравнение (8) при отсутствии объемных сил приводится к следующему виду
(14)
$\frac{{{{\partial }^{2}}{{\sigma }_{{zz}}}}}{{\partial {{z}^{2}}}} - \frac{1}{{\upsilon _{p}^{2}}}\frac{{{{\partial }^{2}}{{\sigma }_{{zz}}}}}{{\partial {{t}^{2}}}} = \frac{{\left( {1 + \upsilon } \right)}}{{\left( {1 - \upsilon } \right)}}{{\alpha }_{T}}\rho \frac{{{{\partial }^{2}}T\left( {z,t} \right)}}{{\partial {{t}^{2}}}},\quad\,\,\,\,z > 0,\,\,\,\,t > 0,$(15)
${{v}_{p}} = \sqrt {\frac{{2G\left( {1 - \upsilon } \right)}}{{\rho \left( {1 - 2\upsilon } \right)}}} = \sqrt {{{\left( {\lambda + 2\mu } \right)} \mathord{\left/ {\vphantom {{\left( {\lambda + 2\mu } \right)} \rho }} \right. \kern-0em} \rho }} ,$(16)
${{\sigma }_{{xx}}}\left( {z,t} \right) = {{\sigma }_{{yy}}}\left( {z,t} \right) = \frac{\upsilon }{{1 - \upsilon }}{{\sigma }_{{zz}}}\left( {z,t} \right) - \frac{{E{{\alpha }_{T}}\left[ {T\left( {z,t} \right) - {{T}_{0}}} \right]}}{{1 - \upsilon }},$(17)
${{\varepsilon }_{{zz}}}\left( {z,t} \right) = \frac{{1 - 2\upsilon }}{{2G\left( {1 - \upsilon } \right)}}{{\sigma }_{{zz}}}\left( {z,t} \right) + \frac{{\left( {1 + \upsilon } \right)}}{{\left( {1 - \upsilon } \right)}}{{\alpha }_{T}}\left[ {T\left( {z,t} \right) - {{T}_{0}}} \right],$Уравнение (14) впервые получила Даниловская [19] непосредственно из соотношений (1)–(3) и независимо от нее Т. Мура, [20] который, по-видимому, не знал о ранней и более общей работе Даниловской.
Как отмечалось, уравнение (8) на практике реализуется в декартовых координатах. Что касается цилиндрической и сферической системы координат, то рассмотрим далее базовое уравнение в теории теплового удара в этих системах координат. Здесь более удобной математической моделью динамической термоупругости является “уравнение совместности” в перемещениях. Подставляя правые части (3) в (1) (в отсутствии объемных сил ${{F}_{i}}\left( {M,t} \right)$) и используя далее (2), (4) после ряда длительных преобразований приходим к соотношению
(18)
$\Delta \vec {U}\left( {M,t} \right) - \frac{1}{{v_{\rho }^{2}}}\frac{{{{\partial }^{2}}\vec {U}\left( {M,t} \right)}}{{\partial {{t}^{2}}}} = \frac{{\left( {1 + \upsilon } \right)}}{{\left( {1 - \upsilon } \right)}}{{\alpha }_{T}}{\text{grad}}\left[ {T\left( {M,t} \right) - {{T}_{0}}} \right],\,\,\,\,\,M \in D,\,\,\,\,\,t > 0.$На основе соотношения (18) рассматриваются математические модели динамической термоупругости в случае радиального потока теплоты в телах цилиндрической формы и центральной симметрии в телах сферической формы. Впрочем, это соотношение может быть использовано и в декартовых координатах при одномерном движении. Рассмотрим практические случаи динамической термоупругости на основе соотношения (18). В первом случае в декартовых координатах (x, y, z) рассматривается область $z > R,$ $t > 0,$ температурное состояние которой описывается функцией ${{T}_{1}} = {{T}_{1}}\left( {z,t} \right),$ при этом ${{U}_{x}} = {{U}_{y}} = 0,$ ${{U}_{z}} = {{U}_{z}}\left( {z,t} \right)$ и соотношение (18) будет
(19)
$\frac{{{{\partial }^{2}}{{U}_{z}}\left( {z,t} \right)}}{{\partial {{z}^{2}}}} - \frac{1}{{{{\upsilon }^{2}}}}\frac{{{{\partial }^{2}}{{U}_{z}}\left( {z,t} \right)}}{{\partial {{t}^{2}}}} = \frac{{1 + \upsilon }}{{1 - \upsilon }}{{\alpha }_{T}}\frac{{\partial {{T}_{1}}\left( {z,t} \right)}}{{\partial z}},\,\,\,\,z > R,\,\,\,\,t > 0.$Во втором случае в сферических координатах $\left( {\rho ,\,\varphi ,\,\theta } \right)$ рассматривается область $\rho > R,$ $t > 0$ при нагреве в условиях центральной симметрии ${{T}_{2}} = {{T}_{2}}\left( {\rho ,t} \right),$ так что ${{U}_{\varphi }} = {{U}_{\theta }} = 0,$ ${{U}_{\rho }} = {{U}_{\rho }}\left( {\rho ,t} \right)$ и (18) записывается в виде
(20)
$\begin{gathered} \frac{{{{\partial }^{2}}{{U}_{\rho }}\left( {\rho ,t} \right)}}{{\partial {{\rho }^{2}}}} + \frac{2}{\rho }\frac{{\partial {{U}_{\rho }}\left( {\rho ,t} \right)}}{{\partial \rho }} - \frac{2}{{{{\rho }^{2}}}}{{U}_{\rho }}\left( {\rho ,t} \right) - \frac{1}{{{{\upsilon }^{2}}}}\frac{{{{\partial }^{2}}{{U}_{\rho }}\left( {\rho ,t} \right)}}{{\partial {{t}^{2}}}} = \frac{{1 + \upsilon }}{{1 - \upsilon }}{{\alpha }_{T}}\frac{{\partial {{T}_{2}}\left( {\rho ,t} \right)}}{{\partial \rho }}, \\ \rho > R,\,\,\,\,t > 0. \\ \end{gathered} $В третьем случае в цилиндрических координатах $\left( {r,\,\varphi ,\,z} \right)$ рассматривается область $r > R,$ $t > 0,$ в условии нагрева радиальным потоком теплоты ${{T}_{3}} = {{T}_{3}}\left( {r,t} \right),$ так что ${{U}_{\varphi }} = {{U}_{z}} = 0,$ ${{U}_{r}} = {{U}_{r}}\left( {r,t} \right)$ и соотношение (18) будет
(21)
$\begin{gathered} \frac{{{{\partial }^{2}}{{U}_{r}}\left( {r,t} \right)}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{U}_{r}}\left( {r,t} \right)}}{{\partial r}} - \frac{1}{{{{r}^{2}}}}{{U}_{r}}\left( {r,t} \right) - \frac{1}{{{{\upsilon }^{2}}}}\frac{{{{\partial }^{2}}{{U}_{r}}\left( {r,t} \right)}}{{\partial {{t}^{2}}}} = \frac{{1 + \upsilon }}{{1 - \upsilon }}{{\alpha }_{T}}\frac{{\partial {{T}_{3}}\left( {r,t} \right)}}{{\partial r}}, \\ r > R,\,\,\,\,t > 0. \\ \end{gathered} $Будем считать, что во всех трех случаях тепловой удар создается внезапным нагревом граничной поверхности до температуры ${{T}_{c}} > {{T}_{0}}\,\left( {{{T}_{c}} = {\text{const}}} \right)$, что приводит к условия симметрии и необходимости учитывать инерционные члены в (1). Последнее означает рассмотрение как раз динамической задачи (и именно) в перемещениях.
Представляет интерес охватить одновременно все три случая (19)–(21) в рамках обобщенной модели. Во избежание излишней громоздкости введем следующие безразмерные переменные:
В области $z > R,\,\,\,\,t > 0\,:$
(22)
$\begin{gathered} \xi = \frac{{{{\upsilon }_{p}}z}}{a};\,\,\,\,\tau = \frac{{\upsilon _{p}^{2}t}}{a};\,\,\,\,{{W}_{1}}\left( {\xi ,\tau } \right) = \frac{{{{T}_{1}}\left( {z,t} \right) - {{T}_{0}}}}{{{{T}_{c}} - {{T}_{0}}}},\,\,\,\,\gamma = \frac{{{{\upsilon }_{p}}R}}{a},\,\,\,\,\sigma _{{\xi \xi }}^{{(1)}}\left( {\xi ,\tau } \right) = \frac{{{{\sigma }_{{zz}}}\left( {z,t} \right)}}{{{{S}_{T}}\left( {{{T}_{c}} - {{T}_{0}}} \right)}}, \\ {{U}_{1}}\left( {\xi ,\tau } \right) = \frac{{\left( {1 - \upsilon } \right){{U}_{z}}\left( {z,t} \right)}}{{\left( {1 + \upsilon } \right){{\alpha }_{T}}\left( {{{T}_{c}} - {{T}_{0}}} \right)\left( {{a \mathord{\left/ {\vphantom {a {{{\upsilon }_{p}}}}} \right. \kern-0em} {{{\upsilon }_{p}}}}} \right)}},\,\,\,\,{{S}_{T}} = \frac{{E{{\alpha }_{T}}}}{{1 - 2\upsilon }} = \frac{{2G\left( {1 + \upsilon } \right){{\alpha }_{T}}}}{{1 - 2\upsilon }}. \\ \end{gathered} $В области $\rho > R,\,\,\,\,t > 0\,:$
(23)
$\begin{gathered} \xi = \frac{{{{\upsilon }_{p}}R}}{a};\,\,\,\,\tau = \frac{{\upsilon _{p}^{2}t}}{a};\,\,\,\,{{W}_{2}}\left( {\xi ,\tau } \right) = \frac{{{{T}_{2}}\left( {\rho ,t} \right) - {{T}_{0}}}}{{{{T}_{c}} - {{T}_{0}}}}, \\ {{U}_{2}}\left( {\xi ,\tau } \right) = \frac{{\left( {1 - \upsilon } \right){{U}_{\rho }}\left( {\rho ,t} \right)}}{{\left( {1 + \upsilon } \right){{\alpha }_{T}}\left( {{{T}_{c}} - {{T}_{0}}} \right)\left( {{a \mathord{\left/ {\vphantom {a {{{\upsilon }_{p}}}}} \right. \kern-0em} {{{\upsilon }_{p}}}}} \right)}},\,\,\,\,\sigma _{{\xi \xi }}^{{(2)}}\left( {\xi ,\tau } \right) = \frac{{{{\sigma }_{{\rho \rho }}}\left( {\rho ,t} \right)}}{{{{S}_{T}}\left( {{{T}_{c}} - {{T}_{0}}} \right)}}. \\ \end{gathered} $В области $r > R,\,\,\,\,t > 0\,:$
(24)
$\begin{gathered} \xi = \frac{{{{\upsilon }_{p}}r}}{a};\,\,\,\,\tau = \frac{{\upsilon _{p}^{2}t}}{a};\,\,\,\,{{W}_{3}}\left( {\xi ,\tau } \right) = \frac{{{{T}_{3}}\left( {r,t} \right) - {{T}_{0}}}}{{{{T}_{c}} - {{T}_{0}}}}, \\ {{U}_{3}}\left( {\xi ,\tau } \right) = \frac{{\left( {1 - \upsilon } \right){{U}_{r}}\left( {r,t} \right)}}{{\left( {1 + \upsilon } \right){{\alpha }_{T}}\left( {{{T}_{c}} - {{T}_{0}}} \right)\left( {{a \mathord{\left/ {\vphantom {a {{{\upsilon }_{p}}}}} \right. \kern-0em} {{{\upsilon }_{p}}}}} \right)}},\,\,\,\,\sigma _{{\xi \xi }}^{{(3)}}\left( {\xi ,\tau } \right) = \frac{{{{\sigma }_{{rr}}}\left( {r,t} \right)}}{{{{S}_{T}}\left( {{{T}_{c}} - {{T}_{0}}} \right)}}. \\ \end{gathered} $Теперь можно записать обобщенную модель задачи, предполагая границы областей свободными от напряжений.
(25)
$\frac{{{{\partial }^{2}}{{U}_{i}}\left( {\xi ,\tau } \right)}}{{\partial {{\xi }^{2}}}} + \frac{{2m + 1}}{\xi }\left[ {\frac{{\partial {{U}_{i}}\left( {\xi ,\tau } \right)}}{{\partial \xi }} - \frac{{{{U}_{i}}\left( {\xi ,\tau } \right)}}{\xi }} \right] - \frac{{{{\partial }^{2}}{{U}_{i}}\left( {\xi ,\tau } \right)}}{{\partial {{\tau }^{2}}}} = \frac{{\partial {{W}_{i}}\left( {\xi ,\tau } \right)}}{{\partial \xi }},\,\,\,\,\xi > \gamma ,\,\,\,\,\tau > 0,$(26)
${{\left. {{{U}_{i}}\left( {\xi ,\tau } \right)} \right|}_{{\tau = 0}}} = {{\left. {\frac{{\partial {{U}_{i}}\left( {\xi ,\tau } \right)}}{{\partial \tau }}} \right|}_{{\tau = 0}}} = 0,\,\,\,\,\xi \geqslant \gamma ,$(27)
${{\left[ {\frac{{\partial {{U}_{i}}\left( {\xi ,\tau } \right)}}{{\partial \xi }} + \frac{{\left( {2m + 1} \right)\upsilon }}{{1 - \upsilon }}\frac{1}{\xi }{{U}_{i}}\left( {\xi ,\tau } \right)} \right]}_{{\xi = \gamma }}} = {{\left. {{{W}_{i}}\left( {\xi ,\tau } \right)} \right|}_{{\xi = \gamma }}},$(28)
$\left| {{{U}_{i}}\left( {\xi ,\tau } \right)} \right| < \infty ,\,\,\,\,\xi \geqslant \gamma ,\,\,\,\,\tau \geqslant 0,$(29)
$\frac{{\partial {{W}_{i}}\left( {\xi ,\tau } \right)}}{{\partial \tau }} = \frac{{{{\partial }^{2}}{{W}_{i}}\left( {\xi ,\tau } \right)}}{{\partial {{\xi }^{2}}}} + \frac{{2m + 1}}{\xi }\frac{{\partial {{W}_{i}}\left( {\xi ,\tau } \right)}}{{\partial \xi }},\,\,\,\,\xi > \gamma ,\,\,\,\,\tau > 0,$(30)
${{\left. {{{W}_{i}}\left( {\xi ,\tau } \right)} \right|}_{{\tau = 0}}} = 0,\,\,\,\,\xi \geqslant \gamma ,\,\,\,\,{{\left. {{{W}_{i}}\left( {\xi ,\tau } \right)} \right|}_{{\xi = \gamma }}} = 1,\,\,\,\,\,\tau > 0,$(31)
$\left| {{{W}_{i}}\left( {\xi ,\tau } \right)} \right| < \infty ,\,\,\,\,\xi \geqslant \gamma ,\,\,\,\,\tau \geqslant 0.$Здесь: $i = 1$ при $m = - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2};\,\,\,\,i = 2$ при $m = {1 \mathord{\left/ {\vphantom {1 {2;\,\,\,\,i = 3}}} \right. \kern-0em} {2;\,\,\,\,i = 3}}$ при $m = 0.$ Решение обобщенной задачи (25)–(31) с целью изучения влияния геометрии области на кинетику соответствующих термоупругих напряжений – пока открытая проблема динамической термоупругости. Ее решение автор предполагает опубликовать в последующем времени.
МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ
Рассмотрим последовательно несколько моделей термической реакции области $\left( {z \geqslant 0,\,\,\,\,t \geqslant 0} \right)$ на нагрев и охлаждение, представляющих значительный практический интерес для многих приложений, отмеченных в [14, 15]. В первом случае рассматривается интенсивный нагрев (охлаждение) поверхности области: например, поверхностный диэлектрический нагрев; расчет термических напряжений в стенках цилиндров паровых машин и двигателей внутреннего сгорания; в теории автоматических систем регулировки температуры; при исследовании области звуковых частот металлов при высоких или очень низких температурах поверхности; многочисленные случаи резкой смены температуры поверхности космических, авиационных объектов, в машиностроительной отрасли и др.
Во втором случае рассматривается нагрев (охлаждение) границы области постоянным тепловым потоком. Последнее встречается при генерировании теплоты в результате пропускания электрического тока через плоский нагревательный элемент; при выделении теплоты в следствии трения; в условиях высокочастотного индукционного нагрева; в ранних фазах нагрева печи ли помещения; при нагреве поверхности земли в ясный безветренный день (знание термонапряженного состояния внутри земли существенно для понимания многих геофизических явлений, например, для понимания магнитного поля земли, пластических свойств вещества земли, а также для выяснения происхождения и причин вулканизма и тектонических движений); при изучении нагрева тела сантиметровыми волнами и др.
В третьем случае тепловой поток с поверхности области является линейной функцией разности температуры между этой поверхностью и окружающей ее средой. Последнее имеет место при излучении черного тела; при теплопередаче через тонкую пленку на поверхности тела; при исследовании утечки теплоты в подводных кабелях; при индукционном нагреве поверхности металлов; при определении потерь теплоты через газовую оболочку (или жидкую среду), окружающую твердое тело; в многочисленных технологических процессах, требующих предварительной тепловой обработки изделия в тепловой камере и др.
Соответствующая модель динамической термоупругости для свободной от напряжений границы области $z \geqslant 0,\,\,\,\,t \geqslant 0$ имеет вид:
(32)
$\frac{{{{\partial }^{2}}{{\sigma }_{{zz}}}}}{{\partial {{z}^{2}}}} - \frac{1}{{\upsilon _{p}^{2}}}\frac{{{{\partial }^{2}}{{\sigma }_{{zz}}}}}{{\partial {{t}^{2}}}} = \frac{{\left( {1 + \upsilon } \right)}}{{\left( {1 - \upsilon } \right)}}{{\alpha }_{T}}\rho \frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}},\,\,\,\,z > 0,\,\,\,\,t > 0,$(33)
${{\left. {{{\sigma }_{{zz}}}\left( {z,t} \right)} \right|}_{{t = 0}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{\sigma }_{{zz}}}\left( {z,t} \right)}}{{\partial t}}} \right|}_{{t = 0}}} = 0,\,\,\,\,z \geqslant 0,$(34)
${{\left. {{{\sigma }_{{zz}}}\left( {z,t} \right)} \right|}_{{z = 0}}} = {{\left. {{{\sigma }_{{zz}}}\left( {z,t} \right)} \right|}_{{z = \infty }}} = 0,\,\,\,\,t \geqslant 0.$При постановке краевой задачи для температурной функции $T\left( {z,t} \right),$ входящей в (32), объединим режимы нагревания и охлаждения и все три вида граничных условий. Следует отметить, что режимы резкого охлаждения в литературе практически не исследованы.
Имеем для $T\left( {z,t} \right)\,:$
(35)
$\frac{{\partial T}}{{\partial t}} = a\frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}},\,\,\,\,z > 0,\,\,\,\,t > 0,$(37)
${{\left. {T\left( {z,t} \right)} \right|}_{{z = 0}}} = {{T}_{c}},\,\,\,\,t > 0\,\,\,({{T}_{c}} > {{T}_{0}} - {\text{н а г р е в }},\,\,\,\,{{T}_{c}} < {{T}_{0}} - {\text{о х л а ж д е н и е }}),$(38)
${{\left. {\frac{{\partial T\left( {z,t} \right)}}{{\partial z}}} \right|}_{{z = 0}}} = \left\{ \begin{gathered} - \frac{1}{{{{\lambda }_{T}}}}{{q}_{0}} - {\text{н а г р е в }} \hfill \\ \frac{1}{{{{\lambda }_{T}}}}{{q}_{0}} - {\text{о х л а ж д е н и е }}, \hfill \\ \end{gathered} \right.$(39)
$\begin{gathered} {{\left. {\frac{{\partial T\left( {z,t} \right)}}{{\partial z}}} \right|}_{{z = 0}}} = h\left[ {{{{\left. {T\left( {z,t} \right)} \right|}}_{{z = 0}}} - {{T}_{c}}} \right], \\ t > 0\,\,\,\,({{T}_{c}} > {{T}_{0}} - {\text{н а г р е в ,}}\,\,\,\,{{T}_{c}} < {{T}_{0}} - {\text{о х л а ж д е н и е }}), \\ \end{gathered} $В (32)–(40) перейдем к безразмерным переменным:
${{\gamma }_{1}} = 0$ – нагрев, ${{\gamma }_{1}} = 1$ – охлаждение,
${{\gamma }_{2}} = - 1$ – нагрев, ${{\gamma }_{2}} = 1$ – охлаждение.
Соотношения (32)–(40) теперь будут:
(41)
$\frac{{{{\partial }^{2}}{{\sigma }_{{zz}}}}}{{\partial {{\xi }^{2}}}} - \frac{{{{\partial }^{2}}{{\sigma }_{{zz}}}}}{{\partial {{\tau }^{2}}}} = \frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}},\,\,\,\,\xi > 0,\,\,\,\,\tau > 0,$(42)
${{\left. {{{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)} \right|}_{{\tau = 0}}} = {{\left. {\frac{{\partial {{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)}}{{\partial \tau }}} \right|}_{{\tau = 0}}} = 0,\,\,\,\,\xi \geqslant 0,$(43)
${{\left. {{{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)} \right|}_{{\xi = 0}}} = {{\left. {{{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)} \right|}_{{\xi = \infty }}} = 0,\,\,\,\,\tau \geqslant 0,$(44)
$\frac{{\partial W}}{{\partial \tau }} = \frac{{{{\partial }^{2}}W}}{{\partial {{\xi }^{2}}}},\,\,\,\,\xi > 0,\,\,\,\,\tau > 0,$(45)
${{\left. {W\left( {\xi ,\tau } \right)} \right|}_{{\tau = 0}}} = {{\gamma }_{1}},\,\,\,\,\xi \geqslant 0,$(46)
${{\left. {W\left( {\xi ,\tau } \right)} \right|}_{{\xi = 0}}} = \left( {1 - {{\gamma }_{1}}} \right),\,\,\,\,\tau > 0,$(47)
${{\left. {\frac{{\partial W\left( {\xi ,\tau } \right)}}{{\partial \xi }}} \right|}_{{\xi = 0}}} = {{\gamma }_{2}},\,\,\,\,\tau > 0,$(48)
${{\left. {\frac{{\partial W\left( {\xi ,\tau } \right)}}{{\partial \xi }}} \right|}_{{\xi = 0}}} = Bi{\text{*}}\left[ {{{{\left. {W\left( {\xi ,\tau } \right)} \right|}}_{{\xi = 0}}} - \left( {1 - {{\gamma }_{1}}} \right)} \right],\,\,\,\,\tau > 0,$(49)
$\left| {W\left( {\xi ,\tau } \right)} \right| < \infty ,\,\,\,\,\xi \geqslant 0,\,\,\,\,\tau \geqslant 0.$В пространстве изображений по Лапласу
(50)
$\left. \begin{gathered} \bar {W}\left( {\xi ,p} \right) = \int\limits_0^\infty {\exp \left( { - p\tau } \right)W\left( {\xi ,\tau } \right)d\tau } \hfill \\ {{{\bar {\sigma }}}_{{\xi \xi }}}\left( {\xi ,p} \right) = \int\limits_0^\infty {\exp \left( { - p\tau } \right){{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)d\tau } \hfill \\ \end{gathered} \right\}$(51)
$\bar {W}\left( {\xi ,p} \right) = - {{\gamma }_{2}}\frac{{\bar {\varphi }\left( p \right)}}{p}\exp \left( { - \xi \sqrt p } \right) + {{{{\gamma }_{1}}} \mathord{\left/ {\vphantom {{{{\gamma }_{1}}} p}} \right. \kern-0em} p},$(52)
$\bar {\varphi }\left( p \right) = \left\{ \begin{gathered} 1 - 1{\text{ - я }}\,\,{\text{к р а е в а я }}\,\,{\text{з а д а ч а ,}} \hfill \\ {1 \mathord{\left/ {\vphantom {1 {\sqrt p - 2{\text{ - я }}\,\,{\text{к р а е в а я }}\,\,{\text{з а д а ч а }},}}} \right. \kern-0em} {\sqrt p - 2{\text{ - я }}\,\,{\text{к р а е в а я }}\,\,{\text{з а д а ч а }},}} \hfill \\ {{Bi{\kern 1pt} {\text{*}}} \mathord{\left/ {\vphantom {{Bi{\kern 1pt} {\text{*}}} {\left( {Bi{\kern 1pt} {\text{*}} + \sqrt p } \right) - 3{\text{ - я }}\,\,{\text{к р а е в а я }}\,\,{\text{з а д а ч а ,}}}}} \right. \kern-0em} {\left( {Bi{\kern 1pt} {\text{*}} + \sqrt p } \right) - 3{\text{ - я }}\,\,{\text{к р а е в а я }}\,\,{\text{з а д а ч а ,}}}} \hfill \\ \end{gathered} \right.$(53)
${{\bar {\sigma }}_{{\xi \xi }}}\left( {\xi ,p} \right) = \frac{{{{\gamma }_{2}}\bar {\varphi }\left( p \right)}}{{p - 1}}\left[ {\exp \left( { - \xi \sqrt p } \right) - \exp \left( { - \xi p} \right)} \right],$где $\bar {\varphi }\left( p \right)$ – соотношения (52).
Переходя к оригиналам в (53), находим искомое решение задачи о тепловом ударе одновременно для режимов интенсивного нагрева и охлаждения:
(54)
${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = \sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) + \left\{ \begin{gathered} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tau > \xi \left( {t < \frac{z}{{{{\upsilon }_{p}}}}} \right), \hfill \\ \sigma _{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,\tau } \right),\,\,\,\,\tau < \xi \left( {t > \frac{z}{{{{\upsilon }_{p}}}}} \right). \hfill \\ \end{gathered} \right.$Здесь функции $\sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right)$ и $\sigma _{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,\tau } \right)$ имеют следующие значения:
– в случае температурного нагрева или охлаждения (46)
(55)
$\begin{gathered} \sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = \frac{{{{\gamma }_{2}}}}{2}\left[ {\exp \left( {\tau - \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} - \sqrt \tau } \right) + \exp \left( {\tau + \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + \sqrt \tau } \right)} \right], \\ \sigma _{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,\tau } \right) = - {{\gamma }_{2}}\exp \left( {\tau - \xi } \right); \\ \end{gathered} $(56)
$\begin{gathered} \sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = \frac{{{{\gamma }_{2}}}}{2}\left[ {\exp \left( {\tau - \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} - \sqrt \tau } \right) - \exp \left( {\tau + \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + \sqrt \tau } \right)} \right], \\ \sigma _{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,\tau } \right) = - {{\gamma }_{2}}\exp \left( {\tau - \xi } \right)\Phi \left( {\sqrt {\tau - \xi } } \right); \\ \end{gathered} $(57)
$\begin{gathered} \sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = \frac{{{{\gamma }_{2}}}}{2}\left\{ {\left[ {\frac{{Bi{\kern 1pt} {\text{*}}}}{{Bi{\kern 1pt} {\text{*}} + 1}}\exp \left( {\tau - \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} - \sqrt \tau } \right)} \right.} \right. + \\ \left. { + \,\,\frac{{Bi{\kern 1pt} {\text{*}}}}{{Bi{\kern 1pt} {\text{*}} - 1}}\exp \left( {\tau + \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + \sqrt \tau } \right)} \right] + \\ \left. { + \,\,\frac{{B{{i}^{{*{\text{2}}}}}}}{{1 - B{{i}^{{*{\text{2}}}}}}}\exp \left[ {Bi{\kern 1pt} {\text{*}}\left( {\xi + Bi{\kern 1pt} {\text{*}}\tau } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + Bi{\kern 1pt} {\text{*}}\sqrt \tau } \right)} \right]} \right\}, \\ \sigma _{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,\tau } \right) = - {{\gamma }_{2}}\frac{{B{{i}^{{*{\text{2}}}}}}}{{B{{i}^{{*{\text{2}}}}} - 1}} \times \\ \times \,\,\left\{ {\exp \left( {\tau - \xi } \right)\left[ {1 - \frac{1}{{Bi{\kern 1pt} {\text{*}}}}\Phi \left( {\sqrt {\tau - \xi } } \right)} \right] - \exp \left[ {B{{i}^{{*{\text{2}}}}}\left( {\tau - \xi } \right)} \right]\Phi {\text{*}}\left( {Bi{\kern 1pt} {\text{*}}\sqrt {\tau - \xi } } \right)} \right\}. \\ \end{gathered} $Здесь $\Phi {\text{*}}\left( z \right) = 1 - \Phi \left( z \right),\,\,\,\,\Phi \left( z \right) = {2 \mathord{\left/ {\vphantom {2 {\sqrt \pi \int_0^z {\exp \left( { - {{y}^{2}}} \right)dy} }}} \right. \kern-0em} {\sqrt \pi \int_0^z {\exp \left( { - {{y}^{2}}} \right)dy} }}$ – функция Лапласа.
Следует отметить, что значение $Bi{\kern 1pt} * = 1,$ входящее в ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right),$ не является особым. При помощи предельного перехода можно показать, что
Вычисление остальных компонент тензора термоупругих напряжений производится по формуле (16), предварительно записанной в системе координат $\left( {\xi ,\tau } \right).$
ФИЗИЧЕСКИЙ АНАЛИЗ РЕШЕНИЯ
Если в (32) отбросить инерционное слагаемое, то есть положить $\rho = 0$ и учесть при этом граничные условия (34), то напряжение ${{\sigma }_{{zz}}}\left( {z,t} \right)$ вообще будет равно нулю и из (16) находим квазистатическое решение задачи (32)–(40) (в исходной системе координат)
Весьма поучительно сравнить оба полученных решения. Прежде всего, на поверхности $z = 0\,\,\left( {\xi = 0} \right)$ оба решения дают одинаковый результат, заключающийся в том, что на этой поверхности по всем направлениям действуют равные между собой сжимающиеся напряжения
(58)
$\sigma = - \frac{{E{{\alpha }_{T}}\left[ {{{T}_{i}}\left( {0,t} \right) - {{T}_{0}}} \right]}}{{1 - \nu }},$Аналогичные сравнения динамических и соответствующих им квазистатических решений, приведенное в [1] для сплошного цилиндра, шара, бесконечной среды с внутренней шаровой или цилиндрической полостью показывают, что соотношение (58) будет справедливо также и в этих случаях, но только для моментов времени микросекундной длительности, то есть непосредственно после воздействия теплового удара. В последующие моменты времени напряжение на поверхности в динамическом случае может превзойти квазистатическое значение. Иным будет положение внутри области $\xi > 0,$ занятой телом. На рис. (1–2) представлены кривые зависимости напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ от времени в фиксированном сечении $\xi = 1,$ рассчитанные по (55)–(57). Вначале рассмотрим данные на рис. 1. Как следует из (54), вначале в фиксированном сечении возникает только составляющая напряжения $\sigma _{{\xi \xi }}^{{\left( 1 \right)}}$ – продольная упругая волна, фронт которой движется со скоростью ${{\upsilon }_{p}}$ от поверхности внутрь тела; напряжение растет от нуля до некоторого отрицательного значения, оставаясь сжимающим (материал, занимающий область $0 < \xi < 1,$ нагревается сильнее, чем материал, расположенный в области $\xi > 1$ и поэтому при $\xi \leqslant 1$ возникают сжимающие напряжения). В момент времени $\tau = 1$ $\left( {t = {z \mathord{\left/ {\vphantom {z {{{\upsilon }_{p}}}}} \right. \kern-0em} {{{\upsilon }_{p}}}}} \right)$ к этому сечению $\left( {\xi = 1} \right)$ приходит волна напряжения, соответствующая функции $\sigma _{{\xi \xi }}^{{\left( 2 \right)}}$ и напряжение скачкообразно возрастает, при температурном нагреве переходит в область положительных (растягивающих) значений и затем убывает, достигая квазистатических значений. Таким образом, процесс распространения термоупругих напряжений на основе динамической модели не является чисто диффузионным, а связан с распространением термоупругих волн.
Рис. 1.
Изменение напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ со временем в сечении $\xi = 1$: 1 – температурный нагрев; 2 – тепловой нагрев; 3 – нагрев средой $\left( {Bi{\kern 1pt} * = 0.5} \right).$
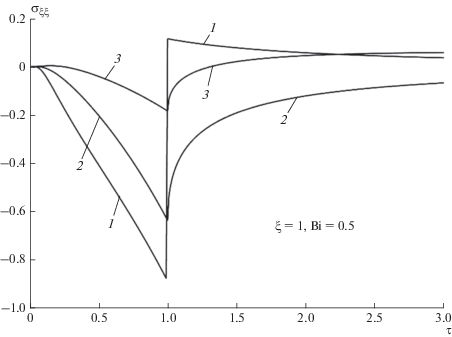
Рис. 2.
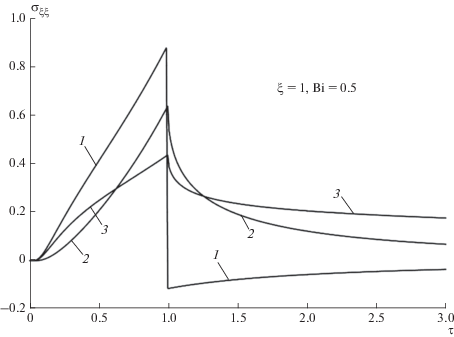
Зависимость напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ от $\tau $ в сечении $\xi = 1$ для температурного охлаждения (1), теплового охлаждения (2), охлаждения средой (3) при $Bi{\kern 1pt} * = 0.5.$
Представляет интерес рассчитать величину скачка напряжений на фронте термоупругой волны, используя теорему запаздывания:
Для вычисления величины $\left| \Delta \right|$ в операционном решении (53) выделим слагаемое $\exp \left( { - \xi p} \right)$ и при $\bar {\varphi }\left( p \right),$ имеющий вид (52), находим:
Таким образом, в случае температурного нагрева в момент времени $\tau = 1$ напряжение имеет скачок на величину $\Delta = 1\,;$ в случае теплового нагрева и нагрева средой напряжение плавно, без скачка изменяется непрерывно, возрастает при прохождении волны расширения, оставаясь практически сжимающими при всех $\tau > 0.$ Из кривых на рис. 1 также следует, что режим (внезапного) температурного нагрева является наиболее опасным при тепловом ударе по сравнению с другими, исследованными выше.
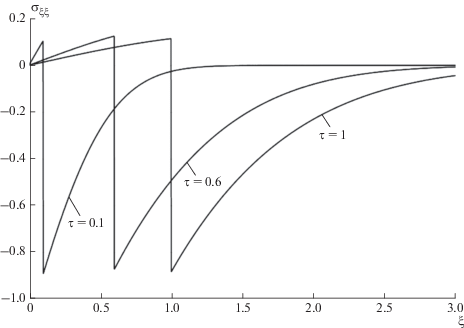
На рис. 3 приведена зависимость напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ по текущей толщине $\xi $ при различных τ. Видно, что в поверхностных слоях напряжения существует в течение незначительного времени и быстро убывают до нуля.
Рис. 3.
Зависимости напряжения от текущей толщины $\xi $ при $\tau = 0.1;0.6;1$ для первой краевой задачи (нагрев).
На рис. 2 приведены зависимости напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ от времени $\tau $ в сечении $\xi = 1$ при различных режимах охлаждения, рассчитанные по соотношениям (54)–(56). Здесь также справедливы все закономерности процесса, описанные выше, с той лишь разницей, что вместо волны расширения в указное сечение приходит волна сжатия. В то же время эти кривые наглядно показывают, что режим охлаждения, создавая растяжения, является более опасным для материала среды, чем режим нагревания, и температурное охлаждение, как и при нагреве, является более разрушительным.
В практических случаях термического нагружения определяющими являются именно начальные (малые) времена микросекундной длительности, когда возникающие в твердых телах кратковременные динамические напряжения приводят к трещинообразованию, растрескиванию поверхностного и приповерхностных слоев. Последнее можно установить, сравнивая максимальные значения напряжения сжатия и растяжения (пересчитанные на величину ${{\sigma }_{{zz}}}\left( {z,t} \right)$) при нагревании и охлаждении с пределом прочности при растяжении и при сжатии (величина последнего приводится в справочниках по физике). Важным моментом в этих исследованиях – прежде всего в условиях температурного нагружения – является скорость тепловой реакции поверхности тела при его нагреве. Рассмотрим этот вопрос, учитывая его практическую значимость.
ЭФФЕКТ ТЕПЛОВОЙ РЕЛАКСАЦИИ ПОВЕРХНОСТИ ОБЛАСТИ
К числу малоисследованных вопросов в теории теплового удара относится эффект релаксации материала на внезапный нагрев. В основном это касается случаев внезапного нагрева границы области до температуры ${{T}_{c}} > {{T}_{0}}$ $\left( {T\left( {0,t} \right) = {{T}_{c}},\,\,\,\,t > 0} \right)$ или внезапного нагрева средой температуры ${{T}_{c}} > {{T}_{0}}$ $\left[ {{{{\left. {\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)} \right|}}_{{z = 0}}} = h\left( {{{{\left. T \right|}}_{{z = 0}}} - {{T}_{c}}} \right),\,\,\,\,t > 0} \right].$ В первом случае скачкообразное изменение температуры поверхности тела от ${{T}_{0}}$ до ${{T}_{c}}$ представляет собой математическую идеализацию, которая практически может осуществиться с некоторым приближением при очень больших Био ($Bi = \left( {{\alpha \mathord{\left/ {\vphantom {\alpha {{{\lambda }_{T}}}}} \right. \kern-0em} {{{\lambda }_{T}}}}} \right)l,$ $l$ – масштабная единица длины). Однако подобное ограничение не исключает из рассмотрения большое количество исследований по тепловому удару при внезапном нагреве границы тела канонической формы (бесконечная пластина; цилиндр; шар; упругое полупространство сплошное и с полостью), отраженных в [1]. Тем не менее, для полноты изучения данной проблемы рассмотрим случай, когда температура поверхности $T\left( {0,t} \right) = \varphi \left( t \right)$ области $z > 0$ возрастает от начальной ${{T}_{0}}$ по линейному закону и достигает значения ${{T}_{c}}$ $\left( {{{T}_{c}} > {{T}_{0}}} \right)$ за малый, но отличный от нуля интервал времени ${{t}_{0}}$:$\varphi \left( t \right) = \left[ {{{\left( {{{T}_{c}} - {{T}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{c}} - {{T}_{0}}} \right)} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}} \right]\left[ {t - \eta (t - {{t}_{0}})(t - {{t}_{0}})} \right] + {{T}_{0}},$ $\eta \left( t \right)$ – функция Хевисайда. В системе координат $\left( {\xi ,\tau } \right)$ граничная функция (при $\xi = 0$) имеет вид:
(59)
$\left\{ \begin{gathered} \varphi \left( \tau \right) = \frac{{\varphi \left( t \right) - {{T}_{0}}}}{{{{T}_{c}} - {{T}_{0}}}} = \frac{\tau }{{{{\tau }_{0}}}} - \eta \left( {\tau - {{\tau }_{0}}} \right)\left( {{\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}} - 1}}} \right. \kern-0em} {{{\tau }_{0}} - 1}}} \right), \hfill \\ {{\tau }_{0}} = {{\upsilon _{p}^{2}{{t}_{0}}} \mathord{\left/ {\vphantom {{\upsilon _{p}^{2}{{t}_{0}}} {a;}}} \right. \kern-0em} {a;}} \hfill \\ \end{gathered} \right.$В пространстве изображений (по Лапласу) находим искомые функции:
(60)
$\left. \begin{gathered} \bar {W}\left( {\xi ,p} \right) = \frac{1}{{{{\tau }_{0}}}}\frac{1}{{{{p}^{2}}}}\left( {{{e}^{{ - \xi \sqrt p }}} - {{e}^{{ - \xi \sqrt p - {{\tau }_{0}}p}}}} \right); \hfill \\ {{{\bar {\sigma }}}_{{\xi \xi }}}\left( {\xi ,p} \right) = - \frac{1}{{{{\tau }_{0}}p\left( {p - 1} \right)}}\left( {{{e}^{{ - \xi \sqrt p }}} - {{e}^{{ - \xi \sqrt p - {{\tau }_{0}}p}}}} \right) + \frac{1}{{{{\tau }_{0}}p\left( {p - 1} \right)}}\left[ {{{e}^{{ - \xi p}}} - {{e}^{{ - \left( {{{\tau }_{0}} + \xi } \right)p}}}} \right], \hfill \\ \end{gathered} \right\}$(61)
$\left. \begin{gathered} W\left( {\xi ,\tau } \right) = \Psi \left( {\xi ,\tau } \right) = \frac{1}{{{{\tau }_{0}}}}\left[ {\left( {\tau + \frac{{{{\xi }^{2}}}}{2}} \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }}} \right) - \xi \sqrt {{\tau \mathord{\left/ {\vphantom {\tau \pi }} \right. \kern-0em} \pi }} \exp \left( {\frac{{ - {{\xi }^{2}}}}{{4\tau }}} \right)} \right];\,\,\,\,\left( {0 \leqslant \tau \leqslant {{\tau }_{0}}} \right) \hfill \\ W\left( {\xi ,\tau } \right) = \Psi \left( {\xi ,\tau } \right) - \Psi \left( {\xi ,\tau - {{\tau }_{0}}} \right);\,\,\,\,\left( {\tau \geqslant {{\tau }_{0}}} \right), \hfill \\ \end{gathered} \right\}$(62)
$\left. \begin{gathered} {{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = F\left( {\xi ,\tau } \right) = \frac{1}{{{{\tau }_{0}}}}\left\{ {\eta \left( {\tau - \xi } \right)\left( {\exp \left( {\tau - \xi } \right) - 1} \right) + \Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }}} \right)} \right\} - \hfill \\ - \,\,\frac{1}{2}\left[ {\exp \left( {\tau - \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} - \sqrt \tau } \right) + \exp \left( {\tau + \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + \sqrt \tau } \right);\,\,\left( {0 \leqslant \tau \leqslant {{\tau }_{0}}} \right)} \right] \hfill \\ {{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = F\left( {\xi ,\tau } \right) - F\left( {\xi ,\tau - {{\tau }_{0}}} \right). \hfill \\ \end{gathered} \right\}$На рис. 4. показаны графики зависимости напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ от времени $\tau $ в точке $\xi = 1$ при различных значениях ${{\tau }_{0}} = {{\upsilon _{p}^{2}{{\tau }_{0}}} \mathord{\left/ {\vphantom {{\upsilon _{p}^{2}{{\tau }_{0}}} a}} \right. \kern-0em} a}.$
Рис. 4.
Изменение напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ со временем в сечении $\xi = 1$ при различных временах релаксации (нагрев).
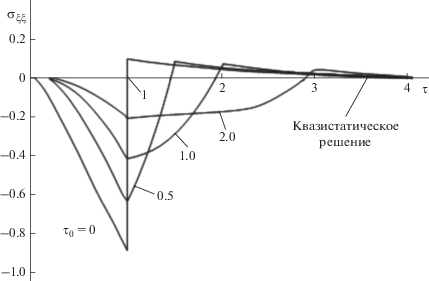
Как можно видеть из графиков, максимум напряжений быстро уменьшается с увеличением ${{\tau }_{0}}.$ При ${{\tau }_{0}} = 3$ этот максимум составляет лишь около 14% от его значения при $\tau = 0$ (мгновенный нагрев). Например, для углеродистой стали ($\nu = 0.3;$ $G = 8 \times {{10}^{9}}$ ${{\text{Н }} \mathord{\left/ {\vphantom {{\text{Н }} {{{{\text{м }}}^{{\text{2}}}}{\text{;}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{2}}}}{\text{;}}}}$ $\rho = 7.85 \times {{10}^{3}}$ ${{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {{{{\text{м }}}^{{\text{3}}}}{\text{;}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{3}}}}{\text{;}}}}$ $a = 13 \times {{10}^{{ - 6}}}$ ${{\text{Н }} \mathord{\left/ {\vphantom {{\text{Н }} {{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{2}}}}}}$) из формулы получаем скорость волны расширения ${{\upsilon }_{p}} = 6 \times {{10}^{3}}\,\,{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}},$ а зависимость между временем $t$ и безразмерной переменной $\tau $ будет иметь вид $t = 3.7 \times {{10}^{{ - 3}}}\tau $ с. При значении ${{\tau }_{0}} = 3$ время нагрева будет ${{\tau }_{0}} = {{10}^{{ - 12}}}$ с.
Для органического стекла ПММА ($\lambda = 2.26 \times {{10}^{9}}\,\,{{\text{Н }} \mathord{\left/ {\vphantom {{\text{Н }} {{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{2}}}}}};$ $\mu = 3.8 \times {{10}^{8}}\,\,{{\text{Н }} \mathord{\left/ {\vphantom {{\text{Н }} {{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{2}}}}}};$ $\rho = 1.2 \times {{10}^{3}}\,\,{{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{3}}}}}};$ $a = 1.13 \times {{10}^{{ - 7}}}\,\,{{{{{\text{м }}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м }}}^{{\text{2}}}}} {\text{c}}}} \right. \kern-0em} {\text{c}}}$) скорость волны расширения ${{\upsilon }_{p}} = 1.6 \times {{10}^{3}}\,\,{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}},$ а зависимость $\tau \left( t \right)$ = $t = 0.44 \times {{10}^{{ - 13}}}\tau $ с. При ${{\tau }_{0}} = 3$ время нагрева составляет ${{\tau }_{0}} = {{10}^{{ - 13}}}$ с.
Эти результаты показывают, что даже при столь малой продолжительности нагрева максимум динамических напряжений снижается по сравнению с его значениями при скачкообразном изменении температуры поверхности тела.
В тоже время для достаточно малых значений величины ${{\tau }_{0}},$ что связано с целым комплексом параметров, входящих в ${{\tau }_{0}},$ идеализация внезапного нагрева границы становится приближенно оправданной. Еще больший интерес представляет режим охлаждения с учетом эффекта релаксации, когда температура поверхности области $z > 0$ убывает от начального значения ${{T}_{0}}$ по линейному закону и достигает конечного значения ${{T}_{c}}$ за время релаксации ${{t}_{0}},$ то есть когда
(63)
$\left\{ \begin{gathered} \varphi \left( \tau \right) = \frac{{\varphi \left( t \right) - {{T}_{c}}}}{{{{T}_{0}} - {{T}_{c}}}} = \frac{\tau }{{{{\tau }_{0}}}} - \eta \left( {\tau - {{\tau }_{0}}} \right)\left( {\frac{\tau }{{{{\tau }_{0}}}} - 1} \right), \hfill \\ {{\tau }_{0}} = {{\upsilon _{p}^{2}{{\tau }_{0}}} \mathord{\left/ {\vphantom {{\upsilon _{p}^{2}{{\tau }_{0}}} {a,}}} \right. \kern-0em} {a,}} \hfill \\ \end{gathered} \right.$(64)
$\left. \begin{gathered} \bar {W}\left( {\xi ,p} \right) = \frac{1}{{{{\tau }_{0}}}}\frac{1}{{{{p}^{2}}}}\left( {\exp \left( { - \xi \sqrt p - {{\tau }_{0}}p} \right) - \exp \left( { - \xi \sqrt p } \right)} \right); \hfill \\ {{{\bar {\sigma }}}_{{\xi \xi }}}\left( {\xi ,p} \right) = - \frac{1}{{{{\tau }_{0}}p\left( {p - 1} \right)}}\left( {\exp \left( { - \xi \sqrt p - {{\tau }_{0}}p} \right) - \exp \left( { - \xi \sqrt p } \right)} \right) + \hfill \\ + \,\,\frac{1}{{{{\tau }_{0}}p\left( {p - 1} \right)}}\left[ {\exp \left( { - \left( {{{\tau }_{0}} + \xi } \right)p} \right) - \exp \left( { - \xi p} \right)} \right]. \hfill \\ \end{gathered} \right\}$Переходя к оригиналам, находим:
(65)
$\begin{gathered} - W\left( {\xi ,\tau } \right) = \Psi \left( {\xi ,\tau } \right) = \frac{1}{{{{\tau }_{0}}}}\left[ {\left( {\tau + \frac{{{{\xi }^{2}}}}{2}} \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }}} \right) - \xi \sqrt {{\tau \mathord{\left/ {\vphantom {\tau \pi }} \right. \kern-0em} \pi }} \exp \left( { - \frac{{{{\xi }^{2}}}}{{4\tau }}} \right)} \right],\,\,\,\,0 \leqslant \tau \leqslant {{\tau }_{0}}, \\ - W\left( {\xi ,\tau } \right) = \Psi \left( {\xi ,\tau } \right) - \Psi \left( {\xi ,\tau - {{\tau }_{0}}} \right),\,\,\,\,\tau \geqslant {{\tau }_{0}}, \\ \end{gathered} $(66)
$\begin{gathered} - {{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = F{\text{*}}\left( {\xi ,\tau } \right) = \frac{1}{{{{\tau }_{0}}}}\left\{ {\eta \left( {\tau - \xi } \right)\left[ {\exp \left( {\tau - \xi } \right) - 1} \right] + \Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }}} \right) - } \right. \\ \left. {\left. { - \,\,\frac{1}{2}\left[ {\exp \left( {\tau - \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} - \sqrt \tau } \right) + \exp \left( {\tau + \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + \sqrt \tau } \right)} \right.} \right]} \right\},\,\,\,\,0 \geqslant \tau \geqslant {{\tau }_{0}}, \\ - {{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = F{\text{*}}\left( {\xi ,\tau } \right) - F{\text{*}}\left( {\xi ,\tau - {{\tau }_{0}}} \right),\,\,\,\,\tau \geqslant {{\tau }_{0}}. \\ \end{gathered} $На рис. 5. показаны графики зависимости напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ от времени в сечении $\xi = 1$ при различных значениях времени релаксации ${{\tau }_{0}}$, характеризующие влияние скорости охлаждения граничной поверхности тела на его термическую реакцию.
Рис. 5.
Изменение напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ со временем в сечении $\xi = 1$ при различных временах релаксации (охлаждение).
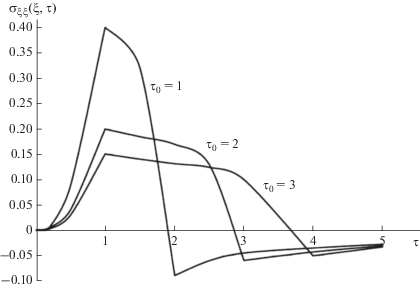
Чем больше время охлаждения, тем меньше максимум напряжений растяжения.
БЕСКОНЕЧНАЯ ПЛАСТИНА И УПРУГОЕ ПОЛУПРОСТРАНСТВО
Переход от бесконечной пластины к упругому полупространству как более удобному объекту исследования с точки зрения модельных представлений в динамической термоупругости практически не рассматривался, если не считать ранней публикации [21], где были высказаны первые соображения по этому вопросу. Изучим эту проблему, представляющую большой практический и теоретический интерес. Рассмотрим упругую однородную изотропную бесконечную пластину $0 \leqslant z \leqslant l,$ $ - \infty < x,\,\,y < + \infty $ конечной толщины l, достаточной для реализации плоского деформированного состояния при свободных от напряжения границах. Напряженное состояние в пластине описывается уравнением (32) с однородными начальными и граничными условиями, температурная функция удовлетворяет уравнению (35). Для уменьшения громоздкости в вычислениях будем считать, что начальное и граничное условия на верхней плоскости симметрии пластины однородные, нижняя плоскость симметрии поддерживается при температуре ${{T}_{0}}.$ В безразмерных переменных $\xi = \frac{{{{\upsilon }_{p}}z}}{a},$ $\tau = \frac{{\upsilon _{p}^{2}t}}{a},$ ${{\xi }_{0}} = \frac{{{{\upsilon }_{p}}l}}{a},$ $W\left( {\xi ,\tau } \right) = \frac{{T\left( {z,t} \right)}}{{{{T}_{0}}}},$ ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = \frac{{{{\sigma }_{{zz}}}\left( {z,t} \right)}}{{{{S}_{T}}{{T}_{0}}}}$ функция ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ удовлетворяет уравнению (41) в области $0 < \xi < {{\xi }_{0}},$ $\tau > 0$ с однородными краевыми условиями, функция $W\left( {\xi ,\tau } \right)$ удовлетворяет уравнению (44) в области $0 < \xi < {{\xi }_{0}},$ $\tau > 0$ с однородными начальным и граничным условиями соответственно при $\tau = 0$ и $\xi = {{\xi }_{0}}$ и граничному условию $W\left( {0,\tau } \right) = 1,$ $\tau > 0.$ Операционное (по Лапласу) решение задачи для ${{\bar {\sigma }}_{{\xi \xi }}}\left( {\xi ,p} \right)$ имеет вид:
(67)
${{\bar {\sigma }}_{{\xi \xi }}}\left( {\xi ,p} \right) = - \frac{{{\text{sh}}\left( {{{\xi }_{0}} - \xi } \right)\sqrt p }}{{\left( {p - 1} \right){\text{sh}}{{\xi }_{0}}\sqrt p }} + \frac{{{\text{sh}}\left( {{{\xi }_{0}} - \xi } \right)p}}{{\left( {p - 1} \right){\text{sh}}{{\xi }_{0}}\sqrt p }} = \bar {\sigma }_{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,p} \right) + \bar {\sigma }_{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,p} \right),$Первое слагаемое в (67) имеет оригинал:
(68)
$\sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = \int\limits_0^\tau {\exp \left( {\tau - \tau {\text{'}}} \right)} \left[ {\frac{\partial }{{\partial \xi }}{{\theta }_{3}}\left( {\frac{\xi }{{2{{\xi }_{0}}}},\frac{{\tau {\text{'}}}}{{\xi _{0}^{2}}}} \right)} \right]d\tau {\text{'}},$Построение оригинала второго слагаемого в (67) требует специального подхода. Изображение $\bar {\sigma }_{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,p} \right)$ запишем в виде:
Таким образом, для малых времен можно записать: для $0 < \tau < {\xi \mathord{\left/ {\vphantom {\xi 2}} \right. \kern-0em} 2}$
(69)
$\begin{gathered} {{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = \left\{ {\exp \left( {\tau - \xi } \right) - \exp \left[ {\xi - \left( {2{{\xi }_{0}} - \xi } \right)} \right] + \exp \left[ {\tau - \left( {2{{\xi }_{0}} + \xi } \right)} \right]} \right\} - \\ - \,\,\frac{1}{2}\left[ {\exp \left( {\tau - \xi } \right)\Phi {\text{*}}\left( {\frac{{{\xi \mathord{\left/ {\vphantom {\xi 2}} \right. \kern-0em} 2} - \tau }}{{\sqrt \tau }}} \right) + \exp \left( {\tau + \xi } \right)\Phi {\text{*}}\left( {\frac{{{\xi \mathord{\left/ {\vphantom {\xi 2}} \right. \kern-0em} 2} + \tau }}{{\sqrt \tau }}} \right)} \right] \\ \end{gathered} $Анализ формулы (69) показывает, что напряжение ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ в некотором фиксированном сечении $\xi = {\text{const}}$ в промежутке времени $0 < \tau < \xi $ изменяется от нуля до некоторого отрицательного значения, которое всегда меньше величины равной 1. В момент времени $\tau = \xi $ напряжение ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ делает скачок на величину равную 1 и переходит в область положительных значений. В момент времени $\tau = 2{{\xi }_{0}} - \xi $ (это то время, которое требуется пройти упругой волне, начавшей двигаться в момент времени $\tau = 0$ от границы $\xi = 0$ до границы $\xi = {{\xi }_{0}},$ отразиться от границы $\xi = {{\xi }_{0}}$ и вернуться в фиксированное сечение $\xi = {\text{const}}$) произойдет разгрузка, напряжение ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ скачком уменьшается на величину $\exp \left[ {\tau - \left( {2{{\xi }_{0}} - \xi } \right)} \right].$ В момент времени $\tau = 2{{\xi }_{0}} + \xi $ напряжение ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ скачком увеличится на величину $\exp \left[ {\tau - \left( {2{{\xi }_{0}} + \xi } \right)} \right]$ и т.д. Причем процесс чрезвычайно быстро затухает. Во времена $\tau = \left( {2{{\xi }_{0}} + \xi } \right)$ динамическое напряжение ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ практически равно нулю. Причем в пластине это затухание протекает значительно быстрее, чем в полупространстве.
Разберем теперь более реальный случай нагрева, а именно, когда нагрев пластины происходит вследствие теплообмена границы $z = 0$ со средой, температура которой равна ${{T}_{0}}$; граница $z = l$ поддерживается при нулевой температуре, начальная температура равна нулю. В системе координат $\left( {\xi ,\tau } \right)$ функция $W\left( {\xi ,\tau } \right)$ удовлетворяет уравнению (44) в области $0 < \xi < {{\xi }_{0}},$ $\tau > 0$ с однородными начальными и граничными условиями при $\tau = 0$ и $\xi = {{\xi }_{0}}$ и граничному условию ${{\left[ {{{\partial W\left( {\xi ,\tau } \right)} \mathord{\left/ {\vphantom {{\partial W\left( {\xi ,\tau } \right)} {\partial \xi }}} \right. \kern-0em} {\partial \xi }}} \right]}_{{\xi = 0}}} = Bi{\kern 1pt} {\text{*}}\left[ {{{{\left. {W\left( {\xi ,\tau } \right)} \right|}}_{{\xi = 0}}} - 1} \right],$ $\tau > 0$, где $Bi{\kern 1pt} * = {{ha} \mathord{\left/ {\vphantom {{ha} {{{\upsilon }_{p}}}}} \right. \kern-0em} {{{\upsilon }_{p}}}}.$ Операционное (по Лапласу) решение задачи для ${{\bar {\sigma }}_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ имеет вид:
(70)
$\begin{gathered} {{{\bar {\sigma }}}_{{\xi \xi }}}\left( {\xi ,p} \right) = \frac{{Bi{\kern 1pt} {\text{*}}}}{{p - 1}} \times \\ \times \,\,\left\{ {\frac{{{\text{sh}}\left( {{{\xi }_{0}}\sqrt p } \right){\text{sh}}\left( {{{\xi }_{0}} - \xi } \right)p}}{{\left[ {Bi{\kern 1pt} *{\text{sh}}\left( {{{\xi }_{0}}\sqrt p } \right) + \sqrt p {\text{ch}}\left( {{{\xi }_{0}}\sqrt p } \right)} \right]{\text{sh}}\left( {{{\xi }_{0}}p} \right)}} - \frac{{{\text{sh}}\left( {{{\xi }_{0}} - \xi } \right)\sqrt p }}{{\left[ {Bi{\kern 1pt} *{\text{sh}}\left( {{{\xi }_{0}}\sqrt p } \right) + \sqrt p {\text{ch}}\left( {{{\xi }_{0}}\sqrt p } \right)} \right]}}} \right\}. \\ \end{gathered} $Поскольку главный интерес составляют времена действия инерционных эффектов (в динамической постановке задачи), то есть малые времена τ, что соответствует в (70) большим $p$, то выделим в (70) основное (главное) слагаемое
(71)
${{\bar {\sigma }}_{{\xi \xi }}}\left( {\xi ,p} \right) = - \frac{{Bi{\kern 1pt} *}}{{\left( {Bi{\kern 1pt} * + \sqrt p } \right)\left( {p - 1} \right)}}\left[ {\exp \left( { - \xi \sqrt p } \right) - \exp \left( { - \xi p} \right)} \right].$В пространстве оригиналов
(72)
${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right) = \sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) + \left\{ \begin{gathered} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tau < \xi , \hfill \\ \sigma _{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,\tau } \right),\,\,\,\,\tau > \xi . \hfill \\ \end{gathered} \right.$Здесь:
(73)
$\begin{gathered} \sigma _{{\xi \xi }}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = - \left\{ {\frac{1}{2}\left[ {\frac{{Bi{\kern 1pt} *}}{{Bi{\kern 1pt} * + 1}}\exp \left( {\tau - \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} - \sqrt \tau } \right) + \frac{{Bi{\kern 1pt} *}}{{Bi{\kern 1pt} * - 1}}\exp \left( {\tau + \xi } \right)\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + \sqrt \tau } \right)} \right] + } \right. \\ \left. { + \,\,\frac{{B{{i}^{{*2}}}}}{{1 - B{{i}^{{*2}}}}}\exp \left[ {Bi{\kern 1pt} *\left( {\xi + Bi{\kern 1pt} *\tau } \right)} \right]\Phi {\text{*}}\left( {\frac{\xi }{{2\sqrt \tau }} + Bi{\kern 1pt} *\sqrt \tau } \right)} \right\}, \\ \end{gathered} $(74)
$\begin{gathered} \sigma _{{\xi \xi }}^{{\left( 2 \right)}}\left( {\xi ,\tau } \right) = \frac{{B{{i}^{{*2}}}}}{{B{{i}^{{*2}}} - 1}} \times \\ \times \,\,\left\{ {\exp \left( {\tau - \xi } \right)\left[ {1 - \frac{1}{{Bi{\kern 1pt} *}}\Phi \left( {\sqrt {\tau - \xi } } \right)} \right] - \exp \left[ {B{{i}^{{*2}}}\left( {\tau - \xi } \right)} \right]\Phi {\text{*}}\left( {Bi{\kern 1pt} *\sqrt {\tau - \xi } } \right)} \right\}. \\ \end{gathered} $Из (73)–(74) следует, что характер изменения напряжения ${{\sigma }_{{\xi \xi }}}\left( {\xi ,\tau } \right)$ с течением времени в каком-либо фиксированном сечении будет зависеть от параметра $Bi{\kern 1pt} *.$ Напряжение для больших значений параметра $Bi{\kern 1pt} *\left( {Bi{\kern 1pt} * \gg 1} \right)$ растет от нуля до некоторого отрицательного значения, затем убывает, переходит в область положительных значений и затем довольно быстро убывает до нуля. Для малых значений параметра $Bi{\kern 1pt} *\left( {Bi{\kern 1pt} * \gg 1} \right)$ напряжение растет в области отрицательных значений, достигает некоторого максимума и затем быстро убывает до нуля (выше показано, что значение $Bi{\kern 1pt} *$ не является особым). Следует обратить внимание, что все явления возникновения динамических температурных напряжений протекает в тонком поверхностном слое и сами напряжения существуют в течении очень незначительных времен. Поэтому с точки зрения динамических температурных напряжений бесконечная пластина при плоскодеформированном состоянии и упругое полупространство ведут себя одинаково.
Дальнейшее обобщение математических моделей теории теплового удара – переход от уравнений параболического типа (35) к уравнениям гиперболического типа с учетом конечной скорости распространения теплоты [22, 23].
ЗАКЛЮЧЕНИЕ
Выделен класс задач, в которых учет геометрических размеров конструкции, исследуемую на термомеханическую реакцию в условиях интенсивного нагрева или охлаждения, касается главным образом приповерхностных слоев. Установлено, что именно эти слои ответственны за тепловую реакцию твердого тела в течение времени близкого к началу нагрева или охлаждения, соответствующего временам микросекундной длительности, в течении которых действуют инерционные эффекты. Исследована термическая реакция массивного тела (упругое полупространство) при различных режимах интенсивного теплового воздействия на его границу. Показано, что процесс распространения термоупругих напряжений на основе динамической модели не является чисто диффузионным, а связан с распространением термоупругих волн. Описан эффект релаксации материала на внезапный нагрев и охлаждение границы области; установлено, что максимум динамических напряжений снижается по сравнению с его значениями при скачкообразном изменении температуры. При этом величина снижения определяется упругими и теплофизическими свойствами материала, а также скоростью нагрева или охлаждения поверхности тела. Показано также, что режим внезапного охлаждения создает напряжения растяжения, более разрушительные по сравнению с режимом нагревания. При этом с увеличением времени охлаждения, максимум напряжений растяжения уменьшается.
Список литературы
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М.: Изд-во URSS, 2012. 970 с.
Паркус Г. Неустановившиеся температурные напряжения. М.: Физматлиз. 1963. 251 с.
Боли Б., Уэйнер Дж. Теория термоупругих напряжений. М.: Мир. 1964. 517 с.
Карташов Э.М. Теория теплового удара на основе обобщенной модели динамической термоупругости. Вестник МИТХТ. 2012. Т. 7. № 1. С. 69–72.
Лыков А.В. Применение методов термодинамики необратимых процессов к исследованию тепло- и массообмена. Инж.-физ. журн. 1984. Т. 9. № 3. С. 287–675.
Шашков А.Г., Бубнов В.А., Яновский С.Ю. Волновые явления теплопроводности. Минск. Наука и техника. 1993. 279 с.
Карташов Э.М., Ненахов Е.В. Динамическая термоупругость в проблеме теплового удара на основе обобщенного уравнения энергии. Тепловые процессы в технике. 2018. Т. 10. № 7–8. С. 334–344.
Подстригач Я.С., Ломакин В.А., Коляно Ю.М. Термоупругость тел неоднородной структуры. М.: Наука. 1984. 368с.
Коляно Ю.М. Методы теплопроводности и термоупругости неоднородного тела. Киев. Наукова думка. 1992. 280с.
Колпащиков В.Л., Яновский С.Ю. Уравнения динамической термоупругости для сред с тепловой памятью. Инж.-физ. журн. 1984. Т. 47. № 4. С. 670–675.
Зарубин В.С., Кувыркин Г.Н. Матем. модели термомеханики. М.: Физматлит 2002. 168 с.
Новацкий В. Обзор работ по динамическим проблемам термоупругости. Механика (сб. переводов). 1966. № 6. С. 101–142.
Коляно Ю.М. Обобщенная термомеханика (обзор). Математические методы и физико-механические поля. Киев. Наукова думка. 1975. Вып. 2. С. 37–42.
Карташов Э.М., Бартенев Г.М. Динамические эффекты в твердых телах в условиях взаимодействия с интенсивными потоками энергии Итоги науки и техники, серия Химия и технология высокомолекулярных соединений. М.: ВИНИТИ, 1988 Т. 25. С. 3–88.
Карташов Э.М., Партон В.З. Динамическая термоупругость и проблемы термического удара. Итоги науки и техники, серия Механика деформируемого твердого тела. М.: ВИНИТИ, 1991 Т. 22. С. 55–127.
Новацкий В. Теория упругости. М.: Мир. 1975. 872 с.
Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука. 1964. 487 с.
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М.: Высш. шк. 2001. 540 с.
Даниловская В.И. Температурные напряжения в упругом полупространстве, возникающие вследствие внезапного нагрева его границы. Прикл. матем. и мех. 1950. Т. 14. Вып. 3. С. 317–318.
Mura T. Dynamical thermal stresses due to thermal shocks. Res. Rep. Fac. Engng., Meiji. Univ. 1956. V. 8. P. 63–73.
Даниловская В.И. Динамические температурные напряжения в бесконечной пластине // Инженерный журнал. 1961. Т. 1. Вып. 4. С. 86–94.
Карташов Э.М., Кудинов В.А. Математические модели теплопроводности и термоупругости. М.: Изд-во МИЭРА. 2018. 1200 с.
Карташов Э.М. Аналитические решения гиперболических моделей нестационарной теплопроводности // Тонкие химические технологии. 2018. Т. 13. № 2. С. 71–80.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика


