Известия РАН. Энергетика, 2019, № 3, стр. 14-25
Применение электроракетной двигательной установки на базе высокочастотного ионного двигателя мощностью до 600 Вт для межпланетных космических аппаратов
Р. В. Ахметжанов 1, *, А. Б. Деркачев 2, Р. А. Ельников 1, В. Г. Петухов 1, Г. А. Попов 1
1 Научно-исследовательский институт прикладной механики и электродинамики федерального
государственного бюджетного образовательного учреждения высшего образования
“Московский авиационный институт (национальный исследовательский университет)”
(НИИ ПМЭ МАИ)
Москва, Россия
2 Акционерное общество “Конструкторское бюро химавтоматики”
Воронеж, Россия
* E-mail: ahmetzhanov1991@mail.ru
Поступила в редакцию 04.04.2019
После доработки 19.04.2019
Принята к публикации 23.04.2019
Аннотация
В статье рассматривается задача проектирования траектории межпланетного космического аппарата (КА), оснащенного электроракетной двигательной установкой (ЭРДУ) на базе нового российского высокочастотного ионного двигателя ВЧИД-11, разработка которого ведется в Научно-исследовательском институте прикладной механики и электродинамики Московского авиационного института. В качестве примера анализируется задача перелета к крупному астероиду 55 Pandora, принадлежащему к спектральному классу E и находящемуся в Главном астероидном поясе, состав которого был подтвержден радарными данными [1]. Средний диаметр данного небесного тела в настоящее время оценивается в 66.7 км. В статье проведена оценка энергетических возможностей КА, оснащенного перспективной ЭРДУ на базе ВЧИД-11, для космической миссии к данному объекту Солнечной системы.
ВВЕДЕНИЕ
В настоящее время внимание большого числа российских и зарубежных ученых, работающих в области астрофизики, космохимии и планетологии, в значительной степени обращено на малые небесные тела Солнечной системы. Свидетельством этому является большое количество реализованных космических миссий, основной задачей которых является исследование таких небесных тел.
В качестве примеров автоматических межпланетных станций (АМС), осуществлявших исследование малых небесных тел Солнечной системы, можно привести следующие АМС: Galileo, NEAR Shoemaker, Deep Space-1, Stardust, Hayabusa и Hayabusa-2, Rosetta, Dawn [2–6].
Это далеко неполный список реализованных космических миссий к малым телам Солнечной системы. Уже само их количество говорит о чрезвычайной актуальности задач по изучению таких небесных тел.
Вместе с тем, проектный анализ подобных космических проектов показывает, что запас рабочего топлива на борту КА, необходимый для осуществления того или иного межпланетного перелета, оказывается очень значительным. Это может приводить к чрезмерному увеличению стартовой массы КА, уменьшению доли комплекса научной аппаратуры.
В связи с этим ЭРДУ, построенные на базе холловских или ионных электроракетных двигателей (ЭРД), находят все большее применение в составе межпланетных КА.
Широко известно, что использование ЭРД в составе маршевых двигательных установок КА позволяет существенно увеличить эффективность космических транспортных операций за счет высокого удельного импульса тяги, которым обладают такие двигатели. Некоторые космические миссии принципиально не могут быть реализованы без применения ЭРД.
В данной работе представлены результаты проектно-баллистического анализа космической миссии малого КА, оснащенного ЭРДУ на базе перспективного высокочастотного ионного двигателя ВЧИД-11, разработка которого ведется в настоящее время. Основные характеристики данного варианта ЭРД представлены в следующем разделе.
ВЫСОКОЧАСТОТНЫЙ ИОННЫЙ ДВИГАТЕЛЬ ВЧИД-11
В 2017–2018 гг. в НИИ ПМЭ МАИ в рамках ФЦП “Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 гг.” был разработан, создан и испытан лабораторный образец высокочастотного ионного двигателя ВЧИД-11. Основные рабочие характеристики данного двигателя на номинальном режиме работы представлены в работе [7]. Помимо номинального режима ВЧИД-11 был испытан на режимах с диапазоном тяг от 1.6 мН до 17 мН.
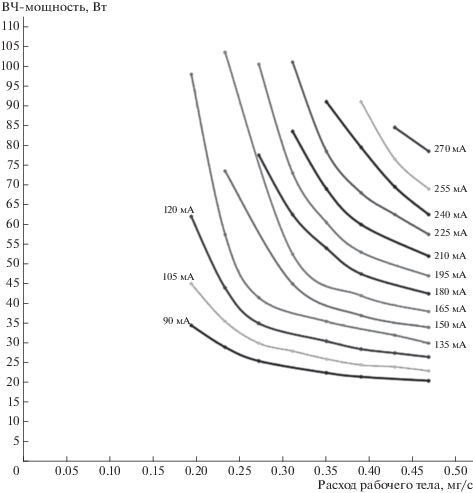
В ходе экспериментальных исследований созданного макета ВЧИД-11 были получены зависимости ВЧ-мощности на входе в индуктор от секундного расхода рабочего тела макета при различных значениях тока ионного пучка. Данные зависимости позволяют выбрать для двигателя оптимальные рабочие точки [8]. Графики зависимостей представлены на рис. 1.
По результатам экспериментальных исследований были выбраны оптимальные режимы работы для различных уровней потребляемой мощности ВЧИД-11. На основе полученных характеристик макета ВЧИД-11 были рассчитаны характеристики ЭРДУ на базе ВЧИД-11 со следующими допущениями:
| Потребляемая мощность катода-нейтрализатора (КН): | 10 Вт |
| Потребляемая мощность системы хранения и подачи рабочего тела (СХПРТ) и блока управления расходом (БУР): | 5 Вт |
| Расход рабочего тела через КН: | 0.05 мг/с |
| КПД системы питания и управления (СПУ): | 85% |
Характеристики ЭРДУ на базе одного ВЧИД-11 представлены в табл. 1.
Таблица 1.
Основные характеристики ЭРДУ на базе ВЧИД-11
| Тяга, мН | Удельный импульс тяги, с | Потребляемая мощность ЭРДУ, Вт | КПД ЭРДУ, % |
|---|---|---|---|
| 1.6 | 682 | 83.2 | 6.4 |
| 5.0 | 2098 | 196.7 | 26.1 |
| 13.2 | 3728 | 493.3 | 48.9 |
| 17.0 | 3615 | 600.9 | 50.1 |
Для решения задачи перелета к астероиду 55 Pandora предлагается использовать ЭРДУ на базе трех двигателей ВЧИД-11 c характеристиками, указанными в табл. 1 для тяги 17 мН.
ПРИМЕНЕНИЕ ЭРДУ НА БАЗЕ ВЧИД-11 ДЛЯ ПЕРЕЛЕТА К АСТЕРОИДУ 55 PANDORA
Для выведения данного межпланетного КА в околоземное космическое пространство рассматривается транспортная система на базе ракеты-носителя (РН) “Союз-2.1б” и разгонного блока (РБ) “Фрегат”. Масса головного блока, выводимого на опорную круговую орбиту высотой 200 км и наклонением 51.8°, принята равной 8200 кг [9]. В некоторой точке опорной орбиты происходит включение маршевой двигательной установки РБ, за счет которой головной блок РН переводится на отлетную гиперболическую траекторию. После выдачи отлетного импульса скорости происходит отделение РБ от КА.
Основные характеристики космической транспортной системы, использованные для расчета, представлены в табл. 2.
Таблица 2.
Основные характеристики космической транспортной системы на базе РН “Союз-2.1б” и химического разгонного блока (РБ) “Фрегат” [9, 10]
| Характеристика | Значение |
|---|---|
| Масса, выводимая РН “Союз-2.1б” на опорную ОИСЗ, кг | 8200 |
| Высота опорной ОИСЗ, км | 200 |
| Наклонение опорной ОИСЗ, градус | 51.8 |
| Удельный импульс тяги маршевой ДУ РБ “Фрегат”, с | 333.2 |
| Конечная масса РБ “Фрегат”, кг | 1050 |
| Масса переходного адаптера РБ-КА, кг | 50 |
Рассматриваемая схема гелиоцентрического перелета к астероиду предполагает наличие одного гравитационного маневра у планеты Марс. Анализ гелиоцентрического участка траектории движения осуществлялся в рамках метода грависфер нулевой протяженности в два этапа.
На первом из них анализ траектории КА осуществлялся в рамках методики, использующей импульсную аппроксимацию активных участков [11, 12]. На этапе перелета Земля–Марс, равно как и на этапе перелета Марс–астероид, предполагается наличие одного импульса скорости в глубоком космосе, а сам гравитационный маневр у Марса может рассматриваться как активный (т.е. также с приложением импульса скорости при его реализации).
Оптимизация траектории движения КА в рамках данной методики [11, 12] сводится к задаче численной минимизации функции следующего вида:
(1)
$\Delta {{V}_{\sum }}(X) = {{V}_{\infty }} + \Delta {{V}_{{DSM1}}} + \Delta {{V}_{{GA}}} + \Delta {{V}_{{DSM2}}} + V_{\infty }^{{A - }},$Данный вектор включает в себя следующие параметры: ${{T}_{0}}$ – момент времени старта от Земли; ${{T}_{{GA}}}$ – момент времени реализации активного гравитационного маневра у Марса; ${{T}_{A}}$ – момент времени подлета к астероиду; ${{t}_{{DSM1}}}$ и ${{t}_{{DSM2}}}$ – моменты времени реализации первого и второго маневра в глубоком космосе; ${{V}_{\infty }}$ – вектор гиперболического избытка скорости отлета от Земли; $V_{\infty }^{{\text{M}}}$ – вектор гиперболического избытка скорости отлета от Марса.
Отметим также, что
Укрупненный алгоритм нахождения функции (1) при заданном векторе $X$ может быть представлен в следующем виде.
1) Используя значение ${{T}_{0}},$ получаем радиус-вектор $\left( {{{r}_{0}}} \right)$ и вектор скорости Земли $\left( {{{V}_{0}}} \right)$ в гелиоцентрической эклиптической системе координат в момент старта.
2) Аналогично, используя значение ${{T}_{{GA}}},$ получаем радиус-вектор $\left( {{{r}_{{\text{M}}}}} \right)$ и вектор скорости Марса $\left( {{{V}_{{\text{M}}}}} \right)$ в момент выполнения гравитационного маневра.
3) Далее, используя значение ${{T}_{A}},$ получаем радиус-вектор $\left( {{{r}_{A}}} \right)$ и вектор скорости астероида $\left( {{{V}_{{\text{A}}}}} \right)$ в момент подлета КА к нему.
Отметим, что для нахождения указанных векторов в данной работе использовалась модель эфемерид DE405 [13].
4) Используя вектор ${{V}_{\infty }},$ находим вектор гелиоцентрической скорости КА в момент выхода из грависферы Земли (в начальной точке гелиоцентрической траектории):
5) Используя известное решение ограниченной задачи двух тел (Солнце-КА), по векторам ${{r}_{0}}$ и ${{V}_{0}}$ определяем кеплеровы элементы первого участка гелиоцентрической траектории (от момента старта ${{T}_{0}}$ до момента реализации первого маневра в глубоком космосе ${{t}_{{DSM1}}}$). По найденным элементам находим гелиоцентрическую скорость $\left( {{{V}_{{1{\text{c}}}}}} \right)$ и радиус-вектор КА $\left( {{{r}_{1}}} \right)$ в момент ${{t}_{{DSM1}}}.$
6) Для участка перелета от точки приложения первого импульса в глубоком космосе (характеризующейся радиусом-вектором ${{r}_{1}}$) до точки гравитационного маневра у Марса (положение которой задано радиусом-вектором ${{r}_{{\text{M}}}}$) решается задача Ламберта. Длительность этого участка перелета может быть легко найдена:
7) Из решения задачи Ламберта может быть найден вектор гелиоцентрической скорости КА в точке приложения импульса в глубоком космосе $\left( {{{V}_{{2{\text{c}}}}}} \right).$ В общем случае эта скорость не равна уже найденному ранее вектору ${{V}_{{1{\text{c}}}}}.$ Тогда первый импульс скорости в глубоком космосе (на участке перелета Земля-Марс) может быть найден следующим образом:
8) Используя вектор гелиоцентрической скорости КА в момент подлета к Марсу $\left( {{{V}_{{{\text{KC1}}}}}} \right),$ который также может быть найден из решения задачи Ламберта, определяем гиперболический избыток скорости подлета КА к Марсу:
9) Далее, используя вектор гиперболического избытка скорости отлета от Марса ($V_{\infty }^{{{\text{M + }}}},$ напомним, что этот вектор входит в состав оптимизируемых параметров), находим гелиоцентрическую скорость КА в момент выхода из грависферы Марса. А за тем, выполняя действия аналогичные п. 4–8, находят для участка перелета Марс–астероид вектор импульса скорости второго маневра в глубоком космосе $\left( {\Delta {{V}_{{{\text{DSM2}}}}}} \right)$ и скорость КА относительно астероида в момент подлета к нему $\left( {V_{\infty }^{{{\text{A}} - }}} \right).$
Здесь необходимо отметить, что гиперболические избытки скорости подлета к Марсу и отлета от него в общем случае могут быть не равны: $V_{\infty }^{{M + }} \ne V_{\infty }^{{M - }},$ а угол между этими векторами может оказаться больше допустимого (из-за ограничений, накладываемых на минимальное расстояние пролета КА от планеты).
В этом случае во время пролета промежуточной планеты должен быть использован дополнительный импульс скорости. В рассматриваемом примере импульс скорости прикладывается на асимптоте подлетной или отлетной ветви гиперболической (относительно Марса) траектории.
Алгоритм расчета активного гравитационного маневра кратко может быть представлен следующим образом.
1) Из скалярного произведения векторов $V_{\infty }^{{{\text{M}} - }}$ и $V_{\infty }^{{{\text{M + }}}}$ определяем угол между векторами гиперболического избытка скорости подлета и отлета от Марса:
2) Далее сравниваем величины векторов $V_{\infty }^{{M - }}$ и $V_{\infty }^{{M + }}$ и выбираем наименьшую из них:
3) Определяем максимальный угол поворота асимптоты гиперболы пролета с гиперболическим избытком скорости $V_{\infty }^{{\min }}.$ Этот угол определяется минимально допустимым расстоянием пролета КА от гравитационного центра планеты ${{R}_{{\min }}}.$
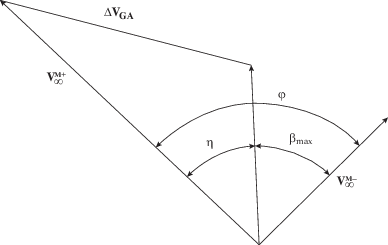
4) Находим требуемый угол поворота гиперболического избытка скорости (см. рис. 2):
5) Определяем требуемый импульс скорости при реализации активного гравитационного маневра:
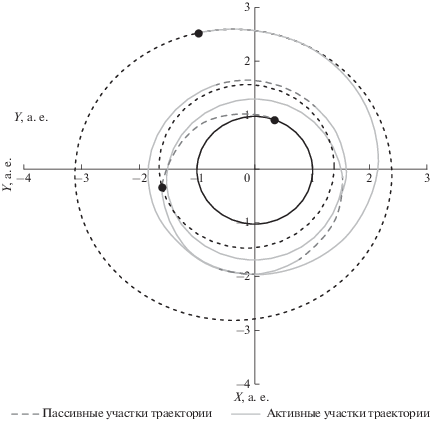
Выполняя численную минимизацию функционала (1) в пространстве выбираемых параметров, было получено локально-оптимальное решение задачи межпланетного перелета в рамках импульсной аппроксимации активных участков движения межпланетного КА. Общий вид полученной траектории представлен на рис. 3.
Рис. 3.
Проекция гелиоцентрической траектории перелета на плоскость эклиптики, по осям отложены астрономические единицы.
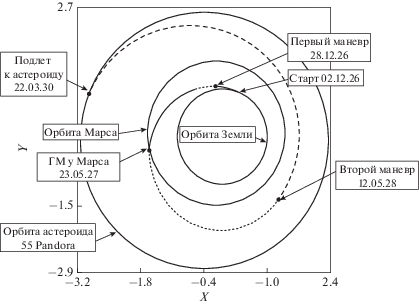
Основные результаты, полученные в результате решения задачи межпланетного перелета, представлены в табл. 3.
Таблица 3.
Основные результаты предварительного анализа перелета к астероиду 55 Pandora
| Характеристика | Значение |
|---|---|
| Момент времени старта от Земли | 02.12.2026 |
| Гиперболический избыток скорости отлета от Земли, км/с | 4.69 км/с |
| Момент времени реализации первого маневра в глубоком космосе | 28.12.2026 |
| Величина импульса скорости при реализации первого маневра, км/с | 1.726 × 10–4 |
| Момент времени реализации гравитационного маневра у Марса | 23.05.2027 |
| Импульс скорости при реализации гравитационного маневра, км/с | 2.144 × 10–4 |
| Момент времени реализации второго маневра в глубоком космосе | 12.05.2028 |
| Величина импульса скорости при реализации второго маневра, км/с | 3.954 |
| Момент времени подлета к астероиду | 22.03.2030 |
| Скорость КА относительно астероида в момент подлета к нему, км/с | 1.589 |
Малая величина импульса скорости при реализации первого маневра в глубоком космосе позволяет сделать вывод о том, что первый участок движения КА (от момента старта до точки гравитационного маневра) может быть реализован полностью пассивно. Сам гравитационный маневр у Марса также может рассматриваться как пассивный.
Второй участок движения КА (от точки гравитационного маневра до точки встречи с астероидом) может быть реализован за счет использования ЭРДУ. В данном случае КА рассматривается как материальная точка, движущаяся в центральном ньютоновском гравитационном поле Солнца под действием силы тяги ЭРДУ. Величина силы тяги и удельного импульса ЭРДУ на активных участках рассматриваются постоянными (сила тяги ЭРДУ принята равной 3 × 17 мН, удельный импульс тяги составляет 3615 с).
Система уравнений, описывающая движение КА на участке перелета Марс–астероид может быть представлена в следующем виде:
(2)
$\begin{gathered} \frac{{d\overline V }}{{dt}} = - \frac{{\mu \cdot r}}{{{{r}^{3}}}} + \delta \frac{P}{{{{m}_{0}} - m}}{{p}_{0}}, \\ \frac{{dr}}{{dt}} = V,\,\,\,\,\frac{{dm}}{{dt}} = \delta \frac{P}{w}, \\ \end{gathered} $Для нахождения законов управления вектором тяги ЭРДУ используется принцип максимума Л.С. Понтрягина [14]. В качестве критерия оптимальности перелета рассматривается величина затрат рабочего тела ЭРДУ, которая минимизируется (при фиксированном времени перелета Марс–астероид). В этом случае функционал задачи оптимального управления примет вид:
где ${{T}_{{GA}}}$ и ${{T}_{{GA}}}$ – начальный и конечный момент времени соответственно (момент времени выполнения гравитационного маневра у Марса и момент времени подлета к астероиду).В рассматриваемой постановке, гамильтониан задачи оптимального управления может быть представлен в следующем виде:
(3)
$H = - \frac{{\delta P}}{w} + \left( {{{\lambda }_{\text{v}}}, - \frac{{\mu \cdot r}}{{{{r}^{3}}}} + \delta \frac{P}{{{{m}_{0}} - m}}{{p}_{0}}} \right) + ({{\lambda }_{r}},V) + {{\lambda }_{m}}\frac{{\delta P}}{w},$Законы оптимального управления вектором тяги (направление вектора тяги и моменты времени включения и отключения ЭРДУ) могут быть найдены из условий максимума функции Гамильтона (3):
(4)
$\begin{array}{*{20}{c}} {{{p}_{0}} = {{{{\lambda }_{\text{v}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{\text{v}}}} {{{\lambda }_{\text{v}}}}}} \right. \kern-0em} {{{\lambda }_{\text{v}}}}};} \\ {\delta = \left\{ {\begin{array}{*{20}{c}} {1,\,\,\psi > 0;} \\ {0,\,\,\psi \leqslant 0,} \end{array}} \right.} \end{array}$Переменные, сопряженные к фазовым, которые входят в соотношения (4) и (5), находятся из системы следующего вида:
Задача нахождения оптимального управления вектором тяги ЭРДУ сводится к численному решению двухточечной краевой задачи. Используя допущения метода грависфер нулевой протяженности, можно записать ее начальные и граничные условия:
(6)
$r({{T}_{{GA}}}) = {{r}_{M}},\,\,\,\,{\mathbf{v}}\left( {{{T}_{{GA}}}} \right) = {{{\mathbf{v}}}_{0}},\,\,\,\,m\left( {{{T}_{{GA}}}} \right) = 0;$(7)
$r\left( {{{T}_{A}}} \right) = {{r}_{A}},\,\,\,\,{\mathbf{v}}\left( {{{T}_{A}}} \right) = {{V}_{A}},\,\,\,\,{{\lambda }_{m}}\left( {{{T}_{A}}} \right) = 0,$Последнее условие, входящее в (7), – есть условие трансверсальности, которое позволяет замкнуть краевую задачу. Оно возникает из-за того, что масса рабочего тела ЭРДУ на правом конце траектории не задана.
Выбираемыми параметрами краевой задачи являются семь сопряженных переменных в начальной точке рассматриваемого сегмента гелиоцентрической траектории: ${{\lambda }_{\text{v}}},$ ${{\lambda }_{r}},$ ${{\lambda }_{m}}.$
Итак, предлагается следующая схема перелета КА к астероиду 55 Pandora. КА вместе с РБ выводится с помощью РН на опорную круговую орбиту высотой 200 км и наклонением 51.8°. В некоторой точке данной орбиты РБ импульсно переводит КА на отлетную гиперболическую траекторию с гиперболическим избытком скорости, равным 4.69 км/с. Используя массовые характеристики космической транспортной системы, представленные в табл. 1, не составляет труда оценить начальную массу КА на отлетной гиперболической траектории. Она составляет 1179.538 кг.
Участок движения Земля–Марс рассматривается полностью пассивным, равно как и сам гравитационный маневр у Марса (см. табл. 3). Второй участок движения от Марса до астероида реализуется с использованием ЭРДУ КА. Управление вектором тяги ЭРДУ осуществляется с использованием формализма принципа максимума. При этом конечный момент времени подлета к астероиду ${{T}_{A}}$ является внешним выбираемым параметром задачи.
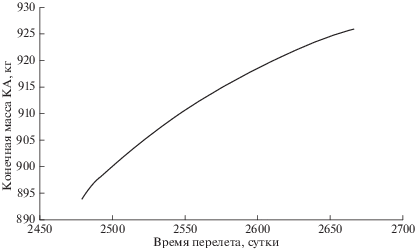
На рис. 4 представлена зависимость конечной массы межпланетного КА от суммарного времени перелета.
Задавшись величиной потребной конечной массы КА, можно определить потребное суммарное время перелета. Например, для конечной массы 920 кг суммарное время перелета составляет 2610.25 сут.
На рисунке 5 представлена проекция перелетной траектории на плоскость эклиптики для данного примера.
Основные результаты проведенного анализа представлены в табл. 4.
Таблица 4.
Основные результаты анализа межпланетного перелета для КА, оснащенного ЭРДУ на базе трех ВЧИД-11
| Характеристика | Значение |
|---|---|
| Момент времени старта от Земли | 02.12.2026 |
| Гиперболический избыток скорости отлета от Земли, км/с | 4.69 км/с |
| Момент времени подлета к астероиду | 24.01.2034 |
| Суммарная длительность перелета, сутки | 2610.25 |
| Стартовая масса КА, кг | 1179.538 |
| Конечная масса КА, кг | 920.024 |
| Потребный запас рабочего тела ЭРДУ (ксенона), кг | 259.514 |
ЗАКЛЮЧЕНИЕ
В данной работе была проведена оценка энергетических затрат КА, оснащенного ЭРДУ на базе ВЧИД-11, работающих на режиме с повышенной мощностью, для перелета к крупному астероиду 55 Pandora из состава Главного пояса астероидов.
Траектория движения КА построена при использовании двух плодотворных идей, позволяющих существенно улучшить массовые характеристики межпланетного КА: идеи использования гравитационного маневра у промежуточного небесного тела (в данном случае – Марса) и идеи использования высокоэффективной двигательной установки на базе перспективного ионного двигателя ВЧИД-11.
В результате проведенного исследования были выявлены основные характеристики рассматриваемого класса перелетных траекторий: определен потребный запас рабочего тела ЭРДУ, конечная масса КА и моторное время ЭРДУ в зависимости от суммарной длительности межпланетного перелета.
Из полученного массива решений было выбрано одно, обеспечивающее доставку в окрестность астероида КА с конечной массой около 920 кг. При этом суммарная длительность межпланетной транспортной операции составляет около семи лет.
Полученное локально-оптимальное решение задачи межпланетного перелета показывает теоретическую возможность реализации рассматриваемой космической миссии при использовании РН среднего класса. Полученные массовые характеристики межпланетного КА (потребный запас рабочего тела ЭРДУ и конечная масса) позволяют сделать вывод о целесообразности применения ЭРДУ на базе ВЧИД-11 для межпланетных КА малой размерности.
Работы выполнены в рамках реализации федеральной целевой программы “Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 гг.” (Соглашение № 14.577.21.0248. Уникальный идентификатор работ (проекта): RFMEFI57717X0248).
Список литературы
Слюта Е.Н. Физико-механические свойства и гравитационная деформация металлических астероидов // Астрономический Вестник. 2013. Т. 47. № 2. С. 122–140.
McCormack M.H., Bell J., Mitton J. Asteroid Rendezvous: NEAR Shoemaker’s Adventures at Eros. // Cambridge, UK. 2002. 130 p.
Rayman M.D., Lehman D.H. Deep Space One: NASA’s First Deep-Space Technology Validation Mission // 48th International Astronautical Congress. Turin, Italy, October 6–10, 1997. IAF-97-Q.5.05.
Nishiyama K., Hosoda S., Ueno K., Kuninaka H. The Ion Engine System for Hayabusa-2 // 32nd International Electric Propulsion Conference, Wiesbaden, Germany. September 11–15, 2011. IEPC-2011-309.
Auster H.U., Richter I., Glassmeier K.H., Berghofer G., Carr C.M., Motschmann U. Magnetic field investigations during Rosetta’s 2867 Šteins flyby. Planetary and Space Science. V. 58. № 9. P. 1124–1128.
Rayman M., Fraschetti T.C., Raymond C.A., Russell C.T. Dawn: A mission in development for exploration of main belt asteroids Vesta and Ceres // Acta Astronautica. V. 58. № 11. P. 605–616.
Ахметжанов Р.В., Богатый А.В., Дьяконов Г.А., Ким В.П., Меркурьев Д.В., Любинская Н.В., Семенихин С.А., Попов Г.А., Якуб П.А. Электрические ракетные двигатели нового поколения для малых космических аппаратов. Известия Российской академии наук. Энергетика. 2019 г.
Антропов Н.Н., Ахметжанов Р.В., Богатый А.В., Гришин Р.А., Кожевников В.В., Плохих А.П., Попов Г.А., Хартов С.А. Экспериментальные исследования высокочастотного ионного двигателя // Известия Российской академии наук. Энергетика. 2016. № 2. С. 4–14.
https://www.samspace.ru/products/launch_vehicles/rn_soyuz_2/ [Дата обращения: 10.01.2019]
Аксюшкин В.А., Викуленков В.П., Ишин С.В. Итоги создания и начальных этапов эксплуатации межорбитальных космических букстров типа “Фрегат” // Вестник НПО им. С.А. Лавочкина. 2014. № 1(22). С. 3–9.
Константинов М.С., Мин Тейн. Анализ сложных схем полета к Сатурну с использованием гравитационных маневров и импульсов скорости в глубоком космосе // Электронный журн. “Труды МАИ”. Вып. № 52 http://trudymai.ru/upload/iblock/8ea/analiz-slozhnykh-skhem-poleta-k-saturnu-s-ispolzovaniem-gravitatsionnykh-manevrov-i-impulsov-skorosti-v-glubokom-kosmose.pdf [Дата обращения: 10.01.2019]
Battin R.H. An Introduction to the Mathematics and Methods of Astrodynamics // AIAA. 1999.
Standish E.M. JPL planetary and lunar ephemerides // DE405/LE405. Interoffice Memorandum, 1998. 312.F-98-048. P. 1–18.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов // М.: Наука, 1976.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика