Известия РАН. Энергетика, 2019, № 3, стр. 140-154
Оптимизация многовитковых траекторий межорбитального перелета с идеально-регулируемым двигателем малой тяги
В. Г. Петухов 1, *, Паинг Сое Ту У 2, **
1 Научно-исследовательский институт прикладной механики и электродинамики МАИ
Москва, Россия
2 Московский авиационный институт
Москва, Россия
* E-mail: vgpetukhov@gmail.com
** E-mail: paingsoethuoo53@gmail.com
Поступила в редакцию 14.05.2019
После доработки 20.05.2019
Принята к публикации 24.05.2019
Аннотация
Рассматривается задача оптимизации многовитковых траекторий межорбитального перелета космического аппарата с идеально-регулируемым двигателем, решение которой необходимо для использования в качестве начального приближения для задачи оптимизации траекторий космических аппаратов с электроракетными двигательными установками. Для математического моделирования движения космического аппарата используются дифференциальные уравнения в равноденственных элементах, а в качестве независимой переменной используется вспомогательная долгота, введенная таким образом, что дифференциальное уравнение для нее совпадает с дифференциальным уравнением для истинной долготы в невозмущенном движении. Для решения задачи оптимизации используется подход, основанный на применении принципа максимума и метода продолжения. Приводится описание математической модели движения космического аппарата, формулировка задачи оптимального управления, соответствующей ей краевой задачи и метода ее решения. На примерах оптимизации типовых межорбитальных перелетов оценивается эффективность и быстродействие разработанного метода.
ВВЕДЕНИЕ
Рассматривается задача оптимизации многовиткового межорбитального перелета космического аппарата (КА) с идеально-регулируемым двигателем малой тяги. Математическая модель идеально-регулируемого двигателя предполагает, что реактивная мощность двигателя (половина произведения тяги на скорость истечения) задана, но в рамках этого ограничения тяга и скорость истечения могут изменяться произвольным образом. Целью оптимизации является минимизация затрат топлива на перелет, а для решения задачи оптимизации траектории применяется подход, основанный на применении принципа максимума [1]. В работе [2] показано, что дифференциальные уравнения оптимального движения КА с идеально-регулируемым двигателем разделяются на динамическую и параметрическую части. Динамическая часть не зависит от массы КА, и в результате ее решения может быть определена оптимальная программа изменения вектора реактивного ускорения. Зная эту программу, зависимость массы КА от времени (включая конечную массу КА и требуемые затраты топлива) можно определить, решая параметрическую задачу, которая сводится к вычислению интеграла от квадрата реактивного ускорения по времени. Возможность разделения задачи оптимизации траектории КА с идеально-регулируемым двигателем на динамическую и параметрическую части следует из существования первого интеграла системы дифференциальных уравнений оптимального движения [3], который имеет вид m2pm = const, где m – масса КА, а pm – сопряженная к ней переменная, и условия трансверсальности вида pm(tf) = 0, где tf – время окончания перелета.
Практическая значимость задачи оптимизации траектории КА с идеально-регулируемым двигателем связана, в первую очередь, с возможностью использования решения этой задачи в качестве начального приближения для оптимизации траекторий КА с электроракетными двигателями ограниченной тяги (однорежимными двигателями с фиксированными значениями тяги и скорости истечения и ограниченно регулируемыми двигателями, тяга и скорость истечения которых являются функциями от потребляемой электрической мощности). Эффективный метод продолжения оптимальной траектории с идеально-регулируемым двигателем в оптимальную траекторию с двигателем ограниченной тяги представлен, например, в [4]. Кроме того, решение задачи оптимизации перелета КА с идеально-регулируемым двигателем позволяет получить нижнюю и верхнюю оценки затрат топлива на перелет с двигателем ограниченной тяги.
На практике задача оптимизации траектории КА с идеально-регулируемым двигателем сводится к задаче оптимального управления вектором реактивного ускорения. Применение принципа максимума позволяет свести эту задачу оптимального управления к краевой задаче для системы дифференциальных уравнений для фазовых и сопряженных переменных. Задача оптимизации траектории КА с идеально-регулируемым двигателем обладает хорошими аналитическими свойствами, что существенно облегчает решение краевой задачи принципа максимума. В работах [3, 5] представлен метод решения этой задачи, основанный на применении принципа максимума и метода продолжения по параметру (метода ньютоновской гомотопии). Представленный в [3, 5] метод сходится с тривиальных (нулевых) начальных приближений для неизвестных начальных значений сопряженных переменных. Более того, в [3, 5] предложен метод продолжения по гравитационному параметру, позволяющий устойчиво вычислять экстремальные траектории с различным числом целых витков вокруг притягивающего центра.
Методы, предложенные в работах [3, 5], имеют ограничение, связанное с практической невозможностью оптимизации траекторий с очень большой угловой дальностью перелета. Практически доступная для рассмотрения угловая дальность составляет десятки витков (максимум – около ста витков), что вполне достаточно для анализа межпланетных траекторий, но мало для проведения оптимизации межорбитальных перелетов, где требуемое число витков может исчисляться сотнями и тысячами. Существуют две причины этого ограничения. Во-первых, в [3, 5] рассматривались дифференциальные уравнения движения КА, записанные в декартовых координатах. Таким образом, все компоненты фазового и сопряженного векторов знакопеременны и имеют периодическую составляющую, равную текущему периоду обращения. Это обстоятельство снижает точность численного интегрирования и затрудняет решение краевой задачи при большом числе витков. Во-вторых, многовитковая задача является многоэкстремальной: для фиксированной длительности перелета существует множество решений с разным числом витков. Для определения оптимального числа витков, обеспечивающего минимальное значение функционала, при применении методов из [3, 5] приходится вычислять последовательность экстремалей с разным числом оборотов. При далеком от оптимального соотношении угловой дальности и длительности перелета экстремальная траектория может проходить вблизи притягивающего центра или удаляться от него на большое расстояние. В обоих случаях скорость сходимости и численная устойчивость типичного численного метода будет хуже, чем на экстремальной траектории с оптимальным числом витков. Разумеется, при наличии некоторого опыта и при малом числе витков найти оптимальное число витков с помощью решения серии задач оптимизации с разной угловой дальностью достаточно легко, но с увеличением требуемого числа витков (и, соответственно, трудоемкости расчета одной экстремальной траектории) сложность задачи оптимизации соотношения угловой дальности и времени перелета существенно увеличивается.
В настоящей статье предлагается метод, позволяющий практически снять ограничение на максимально допустимое число витков. Для достижения этой цели дифференциальные уравнения движения КА записываются в равноденственных переменных, в качестве независимой переменной используется вспомогательная долгота (“невозмущенная” часть истинной долготы), а задача оптимизации межорбитального перелета формулируется как задача с заданной угловой дальностью и свободным временем перелета. Использование равноденственных элементов вместо декартовых координат позволяет избежать знакопеременности большинства орбитальных параметров, повысить точность и увеличить скорость численного интегрирования уравнений движения. Использование вспомогательной долготы в качестве независимой переменной упрощает постановку задачи оптимизации траектории с фиксированной угловой дальностью и свободным временем. В [6] было показано, что для заданного типа экстремалей типичного межорбитального перелета с фиксированной длительностью перелета может существовать множество локальных минимумов функционала по угловой дальности перелета, в то время как для перелета с фиксированной угловой дальностью существует единственный минимум функционала по длительности перелета. Поэтому можно сделать предположение, что для типичной задачи предлагаемый в данной работе метод вычислит траекторию перелета заданной угловой дальности с глобально-оптимальным временем перелета.
1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ
Рассматривается задача оптимизации перелета КА с идеально-регулируемым двигателем в центральном ньютоновском гравитационном поле. Дифференциальные уравнения движения КА под действием сил гравитации и тяги в модифицированных равноденственных элементах p, ex, ey, ix, iy, L [7] имеют вид:
(1)
$\begin{gathered} \frac{{dp}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{{2p}}{q}{{a}_{t}}, \\ \frac{{d{{e}_{x}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \left[ {\sin L{{a}_{r}} + \frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}{{a}_{t}} - \frac{{{{e}_{y}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{e}_{y}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \left[ { - \cos L{{a}_{r}} + \frac{{\left( {q + 1} \right)\sin L + {{e}_{y}}}}{q}{{a}_{t}} + \frac{{{{e}_{x}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{i}_{x}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\cos L{{a}_{n}},\,\,\,\,\frac{{d{{i}_{y}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\sin L{{a}_{n}}, \\ \frac{{dL}}{{dt}} = \sqrt {\mu p} {{\left( {\frac{q}{p}} \right)}^{2}} + \sqrt {\frac{p}{\mu }} \frac{\xi }{q}{{a}_{n}}, \\ \end{gathered} $Введем в рассмотрение вспомогательную долготу K, подчиняющуюся дифференциальному уравнению
и отклонение истинной долготы от вспомогательной LK = L–K, которое, в соответствии с (1) и (2), подчиняется дифференциальному уравнениюЗаменяя в системе (1) шестое уравнение на (2) и (3), получим следующую систему дифференциальных уравнений:
(4)
$\begin{gathered} \frac{{dp}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{{2p}}{q}{{a}_{t}}, \\ \frac{{d{{e}_{x}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \left[ {\sin L{{a}_{r}} + \frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}{{a}_{t}} - \frac{{{{e}_{y}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{e}_{y}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \left[ { - \cos L{{a}_{r}} + \frac{{\left( {q + 1} \right)\sin L + {{e}_{y}}}}{q}{{a}_{t}} + \frac{{{{e}_{x}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{i}_{x}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\cos L{{a}_{n}},\,\,\,\,\frac{{d{{i}_{y}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\sin L{{a}_{n}}, \\ \frac{{d{{L}_{K}}}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{\xi }{q}{{a}_{n}},\,\,\,\,\frac{{dK}}{{dt}} = \sqrt {\mu p} {{\left( {\frac{q}{p}} \right)}^{2}}. \\ \end{gathered} $В системе (4) истинная долгота L во всех уравнениях заменяется на ее выражение через вспомогательную долготу K и отклонение истинной долготы LK: L = K + LK. Если величина реактивного ускорения мала, то уравнения движения (4) сводятся к системе дифференциальных уравнений с 6 медленными переменными p, ex, ey, ix, iy, LK и одной быстрой K.
Правые части системы (4) не зависят явным образом от времени, а правая часть дифференциального уравнения для K положительна для любых значений фазовых координат при p > 0. Таким образом, если исключить случай вырождения оскулирующей орбиты в отрезок прямой линии, можно провести замену независимой переменной t на K с использованием соотношения
(5)
$dK = \frac{{dK}}{{dt}}dt \Rightarrow \frac{d}{{dK}} = \frac{{dt}}{{dK}}\frac{d}{{dt}} = \frac{1}{{\sqrt {\mu p} }}{{\left( {\frac{p}{q}} \right)}^{2}}\frac{d}{{dt}}.$В итоге получим следующую систему дифференциальных уравнений:
(6)
$\begin{gathered} \frac{{dp}}{{dK}} = \frac{{2{{p}^{3}}}}{{\mu {{q}^{3}}}}{{a}_{t}}, \\ \frac{{d{{e}_{x}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{2}}}}\left[ {\sin L{{a}_{r}} + \frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}{{a}_{t}} - \frac{{{{e}_{y}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{e}_{y}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{2}}}}\left[ { - \cos L{{a}_{r}} + \frac{{\left( {q + 1} \right)\sin L + {{e}_{y}}}}{q}{{a}_{t}} + \frac{{{{e}_{x}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{i}_{x}}}}{{dK}} = \frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\cos L{{a}_{n}},\,\,\,\,\frac{{d{{i}_{y}}}}{{dK}} = \frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\sin L{{a}_{n}}, \\ \frac{{d{{L}_{K}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{3}}}}\xi {{a}_{n}}. \\ \end{gathered} $При необходимости система может быть дополнена уравнением для времени
Использование истинной долготы L в качестве независимой переменной в задачах оптимизации траекторий КА рассматривалось ранее в ряде работ [8, 9]. Следует отметить, что производная dL/dt может менять свой знак при достаточно больших значениях бинормальной компоненты реактивного ускорения, поэтому использование истинной долготы в качестве независимой переменной требует контроля знака ее производной и на ряде решений может оказаться некорректным. Вспомогательная долгота K, в отличие от L, имеет положительную производную по времени на всех невырожденных орбитах, поэтому использование K в качестве независимой переменной предпочтительнее, чем использование L. Кроме того, следует отметить, что в [8, 9] дифференциальные уравнения движения с истинной долготой в качестве независимой переменной использовались в процедуре оптимизации траектории, основанной на прямом подходе, в то время как в этой статье рассматривается непрямой подход, основанный на использовании принципа максимума, позволяющий построить чрезвычайно эффективный и быстродействующий метод оптимизации.
Далее в статье ограничимся рассмотрением задачи перелета между двумя заданными точками с фиксированной угловой дальностью ΔK и свободным временем перелета. В этом случае, без потери общности, начальные условия движения задаются для фиксированного значения начальной вспомогательной долготы K0 в виде
(8)
$\begin{gathered} p\left( {{{K}_{0}}} \right) = {{p}_{0}},\,\,\,\,{{e}_{x}}\left( {{{K}_{0}}} \right) = {{e}_{{x0}}},\,\,\,\,{{e}_{y}}\left( {{{K}_{0}}} \right) = {{e}_{{y0}}}, \\ {{i}_{x}}\left( {{{K}_{0}}} \right) = {{i}_{{x0}}},\,\,\,\,{{i}_{y}}\left( {{{K}_{0}}} \right) = {{i}_{{y0}}},\,\,\,\,{{L}_{K}}\left( {{{K}_{0}}} \right) = 0, \\ \end{gathered} $(9)
$\begin{gathered} p\left( {{{K}_{f}}} \right) = {{p}_{f}},\,\,\,\,{{e}_{x}}\left( {{{K}_{f}}} \right) = {{e}_{{xf}}},\,\,\,\,{{e}_{y}}\left( {{{K}_{f}}} \right) = {{e}_{{yf}}}, \\ {{i}_{x}}\left( {{{K}_{f}}} \right) = {{i}_{{xf}}},\,\,\,\,{{i}_{y}}\left( {{{K}_{f}}} \right) = {{i}_{{yf}}},\,\,\,\,{{L}_{K}}\left( {{{K}_{f}}} \right) = 0. \\ \end{gathered} $В рамках модели идеально-регулируемого двигателя ограниченной мощности (ОМ-модель, [3]) величины тяги T и скорости истечения c могут произвольно изменяться при выполнении единственного ограничения, заключающегося в постоянстве реактивной мощности: Pb = Tc/2 = const. Легко показать, что зависимость массы КА от времени t при известной зависимости величины реактивного ускорения от времени $a\left( t \right) = \sqrt {a_{r}^{2}\left( t \right) + a_{t}^{2}\left( t \right) + a_{n}^{2}\left( t \right)} $ вычисляется с помощью соотношения
где m0 = m(t0) – масса КА в начальный момент времени t0, $J\left( t \right) = \frac{1}{2}\int_{{{t}_{0}}}^t {{{a}^{2}}\left( t \right)dt} .$Поэтому задача максимизации массы КА в конечный момент времени tf (или минимизации массы топлива) эквивалентна задаче минимизации функционала $J\left( {{{t}_{f}}} \right) = \frac{1}{2}\int_{{{t}_{0}}}^{{{t}_{f}}} {{{a}^{2}}\left( t \right)dt} .$ В случае, если в качестве независимой переменной используется K вместо t, необходимо заменить переменную в последнем интеграле, таким образом минимизируемый функционал примет вид:
2. ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ С ИДЕАЛЬНО-РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
Рассмотрим задачу оптимизации траектории КА с идеально-регулируемым двигателем ограниченной мощности, то есть задачу минимизации функционала (10) для динамической системы (6), (8), (9).
Функция Понтрягина задачи оптимального управления (6), (8), (9), (10) имеет вид
(11)
$H = - \frac{1}{2}\frac{{{{a}^{2}}}}{{{{q}^{2}}}}\sqrt {\frac{{{{p}^{3}}}}{\mu }} + \frac{{{{p}^{2}}}}{{{{q}^{3}}\mu }}{{{\mathbf{A}}}^{T}}{\mathbf{a}},$(12)
$\begin{gathered} {{A}_{t}} = 2p{{p}_{p}} + \left[ {\left( {q + 1} \right)\cos L + {{e}_{x}}} \right]{{p}_{{ex}}} + \left[ {\left( {q + 1} \right)\sin L + {{e}_{y}}} \right]{{p}_{{ey}}}, \\ {{A}_{r}} = q\left( {\sin L{{p}_{{ex}}} - \cos L{{p}_{{ey}}}} \right), \\ {{A}_{n}} = \xi \left( { - {{e}_{y}}{{p}_{{ex}}} + {{e}_{x}}{{p}_{{ey}}} + {{p}_{{LK}}}} \right) + \frac{{{{s}^{2}}}}{2}\left( {\cos L{{p}_{{ix}}} + \sin L{{p}_{{iy}}}} \right), \\ \end{gathered} $Необходимо сделать следующее замечание по поводу оптимальности времени перелета в рассматриваемой постановке. Правые части системы (6) не зависят явно от времени t. Эту систему можно расширить дифференциальным уравнением для времени (7), правая часть которого также не зависит от времени. Функция Понтрягина для такой расширенной системы примет вид ${{H}_{t}} = H + \frac{1}{{\sqrt {\mu p} }}{{\left( {\frac{p}{q}} \right)}^{2}}{{p}_{t}},$ где pt – сопряженная ко времени переменная. Без потери общности можно положить, что t(K0) = 0. Необходимым условием оптимальности времени перелета будет pt(Kf) = 0. Из независимости функции Понтрягина от времени следует, что dpt/dt ≡ 0. Поэтому из необходимого условия оптимальности по t следует, что pt(K) ≡ 0 и ${{H}_{t}} \equiv H.$ Следовательно, на решении задачи оптимального управления (6), (8), (9), (10) автоматически выполняются необходимые условия оптимальности времени перелета.
Из условия максимума функции Понтрягина (11) по управлению a легко получить выражение для оптимального управления:
подставляя которое в (11) получим выражение для гамильтониана рассматриваемой задачи оптимального управления: где $k = \frac{1}{{2{{q}^{4}}}}\sqrt {\frac{{{{p}^{5}}}}{{{{\mu }^{3}}}}} .$ Очевидно, что уравнения оптимального движения примут вид(15)
$\frac{{d{\mathbf{x}}}}{{dK}} = \frac{{\partial H}}{{\partial {\mathbf{p}}}},\,\,\,\,\frac{{d{\mathbf{p}}}}{{dK}} = - \frac{{\partial H}}{{\partial {\mathbf{x}}}},$Краевая задача (15), (8), (9) решалась методом продолжения по параметру [3, 5, 10–12] с использованием метода комплексного шага [13, 14] для высокоточного вычисления производных от невязок краевой задачи при K = Kf от p0 и с коррекцией решения методом Ньютона после каждого шага численного интегрирования дифференциальных уравнений метода продолжения по параметру.
3. ЧИСЛЕННЫЕ ПРИМЕРЫ
Для оценки эффективности разработанного метода и зависимости скорости вычислений от угловой дальности перелета рассмотрена задача оптимизации довыведения низкоорбитального КА с начальной эллиптической орбиты, имеющей высоту перигея 250 км, высоту апогея 1000 км, наклонение 97.6° и аргумент перигея 0° на круговую орбиту высотой 1200 км с наклонением 98.0° без изменения долготы восходящего узла. Значения начальной истинной и вспомогательной долгот совпадают и равны 150°. В этом и всех последующих примерах высоты приведены относительно среднего радиуса Земли 6371 км, а гравитационный параметр Земли принят равным 398 600.436 км3/с2. Тесты производительности проводились на четырехядерном персональном компьютере с центральными процессорами Intel Core i7, работающими на частоте 2.0 ГГц под управлением операционной системы Microsoft Windows 10. В табл. 1 представлены результаты расчета оптимальных траекторий с угловой дальностью от 1 до 2500 витков. В таблице используются следующие обозначения: Nrev – число витков, Δt – длительность перелета, Vx – характеристическая скорость перелета. Из табл. 1 видно, что время оптимизации траектории изменяется от 0.16 секунд процессорного времени на один виток оптимизируемой траектории при малой угловой дальности до 0.06…0.07 секунд на один виток оптимизируемой траектории при угловой дальности 500…2500 витков.
Таблица 1.
Результаты оптимизации траектории довыведения низкоорбитального КА на целевую орбиту
| Nrev | Процессорное время, с | Δt, сутки | J, м2/с3 | Vx, м/с | ΔtJ, сут м2/с3 |
|---|---|---|---|---|---|
| 1 | 0.16 | 0.073 | 12.40170 | 347.198 | 0.90296 |
| 4 | 0.65 | 0.287 | 3.10764 | 346.331 | 0.89344 |
| 20 | 2.12 | 1.432 | 0.62202 | 346.029 | 0.89086 |
| 100 | 8.84 | 7.156 | 0.12442 | 345.966 | 0.89034 |
| 500 | 32.42 | 35.773 | 0.02489 | 345.953 | 0.89023 |
| 1000 | 63.51 | 71.545 | 0.01244 | 345.951 | 0.89022 |
| 2500 | 185.04 | 178.860 | 0.00498 | 345.950 | 0.89021 |
Оптимальная длительность перелета в рассматриваемом примере практически линейно зависит от угловой дальности Δt [сутки] = 0.0715Nrev + 0.0013, произведение длительности перелета на значение функционала стремится к предельному значению около 0.8902 сут м2/с3 при увеличении угловой дальности перелета, причем уже начиная с угловой дальности 20 витков значение этого произведения в первых трех значащих цифрах не изменяется. Характеристическая скорость перелета также стремится к асимптотическому значению около 345.95 м/с при увеличении числа витков, однако и при угловой дальности в 1 виток значение характеристической скорости больше асимптотического всего на 0.36%.
На рис. 1 представлены зависимости от времени траекторных параметров (большой полуоси, эксцентриситета и наклонения), реактивного ускорения и углов ориентации реактивного ускорения для оптимальной четырехвитковой траектории выведения низкоорбитального КА на целевую орбиту. Под углом тангажа здесь понимается угол между трансверсальным направлением и проекцией вектора реактивного ускорения на плоскость оскулирующей орбиты, а под углом рысканья – угол между этой плоскостью и вектором реактивного ускорения.
Рис. 1.
Зависимости от времени траекторных параметров, реактивного ускорения и углов ориентации реактивного ускорения для оптимальной четырехвитковой траектории выведения низкоорбитального КА на целевую орбиту.
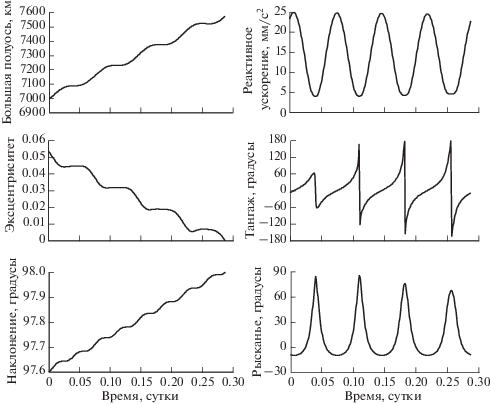
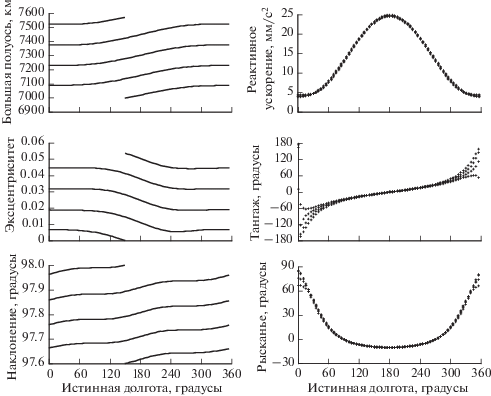
На рис. 1 видно, что большая полуось, эксцентриситет и наклонение на оптимальной траектории перелета имеют практически постоянный вековой уход и подвержены короткопериодическим колебаниям с орбитальным периодом. Программа изменения величины реактивного ускорения близка к гармоническим колебаниям со средним значением 14.4 мм/с2 и с амплитудой около 10.5 мм/с2. Угол тангажа на первом витке колеблется с амплитудой около 60°, а на последующих витках амплитуда его колебаний возрастает до 180°. Угол рысканья достигает максимальных значений (67…85°) в районе перигея и минимальных (около –10°) – в районе апогея. На рис. 2 представлены зависимости от истинной долготы тех же траекторных параметров и параметров управления, что и на рис. 1. Видно, что формы зависимости траекторных параметров от истинной долготы почти точно повторяются на каждом витке, а зависимость величины реактивного ускорения от истинной долготы остается практически постоянной на всех витках оптимальной траектории перелета. Разумеется, такое поведение параметров оптимальной траектории связано с малыми относительными изменениями орбитальных элементов в процессе перелета.
Рис. 2.
Зависимости от истинной долготы траекторных параметров, реактивного ускорения и углов ориентации реактивного ускорения для оптимальной четырехвитковой траектории выведения низкоорбитального КА на целевую орбиту.
Рассмотрим теперь на примере перелета с высокоэллиптической орбиты на геостационарную орбиту (ГСО) задачу оптимизации траектории с большим изменением элементов орбиты. Пусть начальная орбита имеет высоту перигея 10 000 км, высоту апогея 80 000 км, наклонение 63° и нулевые значения аргумента перигея и долготы восходящего узла. Начальные значения истинной и вспомогательной долготы примем равными 100°. Конечная орбита – ГСО – круговая орбита высотой 35 793 км с нулевым наклонением. Зависимости от числа витков процессорного времени решения задачи оптимизации, оптимальной длительности перелета, функционала, характеристической скорости и произведения функционала на время перелета представлены в табл. 2.
Таблица 2.
Результаты оптимизации траектории довыведения КА с высокой эллиптической орбиты на ГСО
| Nrev | Процессорное время, с | Δt, сутки | J, м2/с3 | Vx, м/с | ΔtJ, сут м2/с3 |
|---|---|---|---|---|---|
| 1 | 0.38 | 3.190 | 16.76575 | 2840.944 | 53.48479 |
| 4 | 1.06 | 12.595 | 5.84182 | 3214.116 | 73.57626 |
| 20 | 1.93 | 52.394 | 1.25686 | 3059.728 | 65.85197 |
| 100 | 8.89 | 261.804 | 0.25304 | 3065.137 | 66.24557 |
| 500 | 44.42 | 1310.237 | 0.05066 | 3067.256 | 66.37392 |
| 1000 | 86.95 | 2620.844 | 0.02533 | 3067.544 | 66.39115 |
Из представленных в табл. 2 результатов видно, что ΔtJ стремится к асимптотическому пределу (около 66.4 сут м2/с3) при увеличении угловой длительности перелета, однако, в отличие от предыдущего примера, величина этого произведения изменяется немонотонно. Характеристическая скорость перелета с ростом числа витков асимптотически стремится к предельному значению (около 3067.6 м/с) снизу. Отметим, что оптимальное двухимпульсное решение с первым импульсом в апогее начальной орбиты требует суммарного приращения скорости 2064.73 м/с.
Вид оптимальной 100-витковой траектории перелета на ГСО представлен на рис. 3.
Рис. 3.
Проекции оптимальной 100-витковой траектории перелета на ГСО на координатные плоскости геоцентрической системы координат J2000.
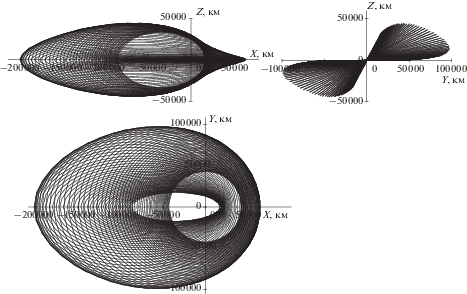
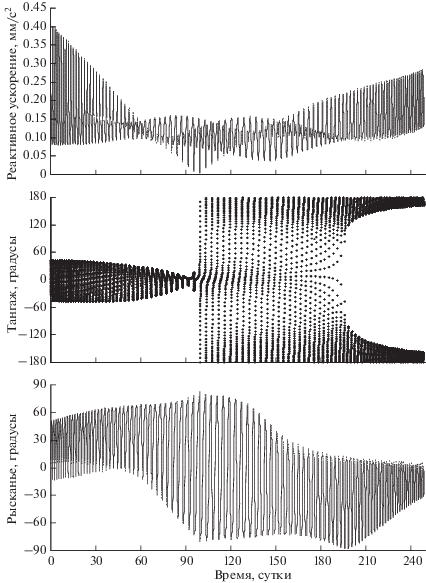
На рис. 4 представлены зависимости траекторных параметров от времени и оптимальная программа управления для 100-витковой траектории выведения КА на ГСО. Видно, что зависимость эксцентриситета от времени имеет максимум, из чего следует, что данная оптимальная траектория, в терминологии [11], принадлежит к классу E‑траекторий. Зависимость большой полуоси от времени также имеет максимум, превышающий 120 тыс. км, а наклонение монотонно уменьшается. Оптимальная программа изменения реактивного ускорения имеет сложный вид и может быть разделена на три участка. На первом участке достигаются максимальные значения реактивного ускорения с колебаниями в диапазоне 0.15…0.5 мм/с2. На втором участке реактивное ускорение изменяется в диапазоне 0…0.15 мм/с2, а на третьем – в диапазоне 0.05…0.3 мм/с2. В начале перелета угол тангажа колеблется около нулевого значения с амплитудой менее 60 градусов, а на следующем участке траектории угол тангажа изменяется от –180 до 180 градусов, обеспечивая торможение в окрестности перигея для уменьшения высоты апогея и разгон в окрестности апогея для увеличения высоты перигея. Угол рысканья на большей части траектории имеет малое абсолютное значение в окрестности перигея и 50…90 градусов в окрестности апогея. В районе смены режима управления по тангажу происходит кратковременное возрастание абсолютного значения угла рысканья в окрестности перигея почти до 90 градусов, а в конце перелета значение угла рысканья в апогее снижается почти до 12 градусов.
Рис. 4.
Зависимости от времени траекторных параметров, реактивного ускорения и углов ориентации реактивного ускорения для оптимальной 100-витковой траектории выведения КА на ГСО.
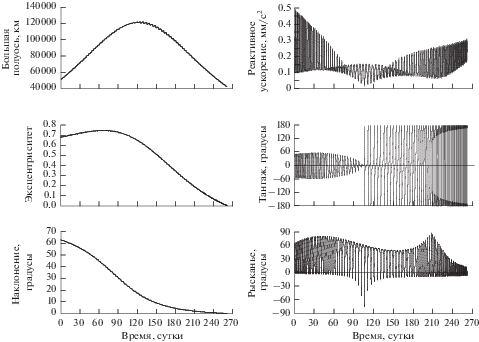
Для демонстрации работоспособности разработанного метода в случае оптимизации межорбитального перелета между двумя эллиптическими орбитами, рассмотрим расчет оптимальной 100-витковой траектории между начальной орбитой с высотой перигея 10 000 км, высотой апогея 80 000 км, аргументом перигея 80°, наклонением 50°, долготой восходящего узла 100° с начальными значениями истинной и вспомогательной долгот 100° на конечную орбиту с высотой перигея 30 000 км, высотой апогея 50 000 км, аргументом перигея 150°, наклонением 63.4° и долготой восходящего узла 90°. Проекции оптимальной траектории на координатные плоскости геоэкваториальной системы координат J2000 представлены на рис. 5, а оптимальная программа управления – на рис. 6. Для рассматриваемого случая характерно отклонение от симметрии в программе угла тангажа и наличие тормозного участка на конечном участке перелета. Программа изменения реактивного ускорения имеет сложный вид. В начале перелета реактивное ускорение может превышать 0.4 мм/с2, а в середине – достигать околонулевого значения.
ЗАКЛЮЧЕНИЕ
В работе рассмотрена задача оптимизации траектории многовиткового межорбитального перелета КА с идеально-регулируемыми двигателем. В математической модели используются дифференциальные уравнения движения КА в равноденственных переменных, а в качестве независимой переменной используется вспомогательная долгота, дифференциальное уравнение для которой совпадает с дифференциальным уравнением для истинной долготы в невозмущенном движении.
Рассмотрена задача оптимизации траектории с фиксированной угловой дальностью и оптимальным временем перелета. Для решения задачи используется подход, основанный на применении принципа максимума для сведения задачи оптимального управления к двухточечной краевой задаче, которая, в свою очередь, редуцируется к задаче Коши с использованием метода продолжения по параметру. Для вычисления матрицы производных от невязок краевой задачи по неизвестным начальным значениям сопряженных переменных используется численное дифференцирование методом комплексного шага, позволяющее вычислять производные с точностью вычисления функций.
Разработанный метод был проверен на задачах оптимизации типичных межорбитальных перелетов: выведение низкоорбитального КА на круговую целевую орбиту, довыведение КА на ГСО и перелет между эллиптическими орбитами. На примере решения этих задач метод продемонстрировал хорошую вычислительную устойчивость и высокое быстродействие. Например, при вычислении траекторий со 100 витками, быстродействие нового метода оказалось на 3 порядка выше, чем при использовании ранее разработанных методов, использующих дифференциальные уравнения движения КА в декартовых координатах. Представленный в статье метод позволяет рассчитывать оптимальные траектории КА с идеально-регулируемым двигателем с любой, представляющей практический интерес, угловой дальностью и снимает ограничение на максимальную угловую дальность в 50…100 витков, достигнутую при использовании методов, основанных на использовании дифференциальных уравнений движения КА в декартовых координатах.
Работа выполнена за счет средств гранта Российского научного фонда (соглашение № 16-19-10429-П).
Список литературы
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1976.
Irving J.H. Low thrust flight: variable exhaust velocity in gravitational fields. (In Seifert H.S. (eds.)): Space Technology, John Wiley and Sons Inc., New York, 1959.
Петухов В.Г. Оптимизация межпланетных траекторий космических аппаратов с идеально-регулируемым двигателем методом продолжения // Космич. исслед. Т. 46. № 3. 2008. С. 224–237. (Cosmic Research. P. 219).
Петухов В.Г. Метод продолжения для оптимизации межпланетных траекторий с малой тягой // Космич. исслед. Т. 50. № 3. 2012. С. 258–270. (Cosmic Research. P. 249).
Petukhov V.G. One Numerical Method to Calculate Optimal PowerLimited Trajectories. IEPC-95-221. Moscow. 1995.
Петухов В.Г. Оптимизация траекторий космических аппаратов с электроракетными двигательными установками методом продолжения // Дисс. на соискание ученой степени д.т.н., М., МАИ, 2013.
Walker M.J.H., Ireland B., Owens J. A Set of Modified Equinoctial Elements, Celestial Mechanics. V. 36 (1985). P. 409–419; V. 38 (1986). P. 391.
Graham K.F., Rao A.V. Minimum-Time Trajectory Optimization of Low-Thrust Earth-Orbit Transfers with Eclipsing // J. Spacecraft and Rockets. V. 53 (2016). № 2. P. 289–303.
Betts J.T. Optimal low-thrust orbit transfers with eclipsing // Optimal Control Applications and Methods. V. 36 (2015). № 2. P. 218–240.
Haberkorn T., Martinon P., Gergaud J. Low thrust minimum-fuel orbital transfer: a homotopic approach // J. Guidance, Control, and Dynamics. V. 27. № 6 (2004). P. 1046–1060
Петухов В.Г. Оптимизация многовитковых перелетов между некомпланарными эллиптическими орбитами // Космич. исслед. Т. 42. № 3. С. 260–279 (Cosmic Research. P. 250).
Иванюхин А.В., Петухов В.Г. Задача минимизации тяги и ее приложения // Космич. исслед. Т. 53. № 4. 2015. С. 320–321. (Cosmic Research. P. 300).
Lyness J.N., Moller C.B. Numerical differentiation of analytic functions // SIAM J. Numer. Anal. 1967. № 4. P. 202–210.
Martins J.R.R.A., Sturdza P., Alonso J.J. The complex-step derivative approximation // ACM Transaction on Mathematical Software. V. 29. № 3 (2003). P. 245–262.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика