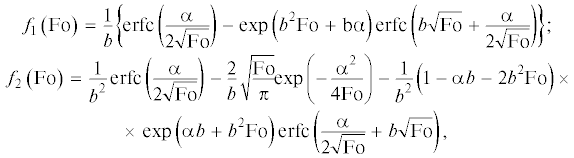Известия РАН. Энергетика, 2019, № 4, стр. 108-118

Температурное поле анизотропного полупространства, обладающего изотропным покрытием, при его локальном нагреве в условиях теплообмена с внешней средой

А. В. Аттетков^1, *, И. К. Волков¹

¹ Московский государственный технический университет им. Н.Э. Баумана (МГТУ им. Н.Э. Баумана)
Москва, Россия

Поступила в редакцию 29.05.2019
После доработки 07.08.2019
Принята к публикации 12.08.2019

DOI: 10.1134/S0002331019040034

Аннотация

Предложена математическая модель процесса формирования температурного поля системы, имитируемой анизотропным полупространством с изотропным покрытием постоянной толщины, при его локальном нагреве в условиях теплообмена с внешней средой. Показано, что температурное поле изучаемой системы представляет собой сумму двух независимых аддитивных составляющих. С применением интегрального преобразования Лапласа найдено аналитическое решение для первой из аддитивных составляющих температурного поля, формируемого за счет различия начальной температуры системы и температуры внешней среды. Идентифицирована вторая независимая аддитивная составляющая температурного поля, формируемого вследствие воздействия нестационарного теплового потока на внешнюю поверхность покрытия при равенстве температуры внешней среды начальной температуре анализируемой системы. С применением методов интегральных преобразований в аналитически замкнутом виде найдено решение соответствующей задачи нестационарной теплопроводности. Полученные результаты подтверждают обнаруженный ранее эффект “сноса” температурного поля в анизотропном материале с анизотропией свойств общего вида.

Ключевые слова: анизотропное полупространство, изотропное покрытие, локальное тепловое воздействие, температурное поле, интегральные преобразования

ВВЕДЕНИЕ

В связи с внедрением композиционных материалов в инженерную практику возрастает значимость исследований, проведенных в “анизотропном разделе” математической теории теплопроводности [1–5]. Специфика математических моделей теплопереноса в областях с анизотропией свойств общего вида [5] и необходимость решения реальных задач стимулируют разработку новых высокопроизводительных и абсолютно устойчивых алгоритмов [6, 7], для их тестирования необходимы решения, полученные аналитическими методами, – тестовые задачи.

В “анизотропном разделе” теории теплопроводности мало задач, для которых известны решения, представленные в аналитически замкнутом виде [5, 8–13]. Поэтому любой новый результат, связанный с решением задач “анизотропной теплопроводности” аналитическими методами, имеет и теоретическое, и конкретное прикладное значение.

Основная цель проведенных исследований – решение задачи об определении процесса формирования температурного поля анизотропного полупространства, граница которого обладает изотропным покрытием конечной толщины, подверженным локальному тепловому воздействию в условиях теплообмена с внешней средой.

ИСХОДНЫЕ ДОПУЩЕНИЯ И МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Для достижения поставленной цели, при построении исходной математической модели процесса формирования температурного поля $T\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}},~t} \right)$ объекта исследований в фиксированной декартовой системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ пространства ${{\mathbb{R}}^{3}},$ предполагалось, что:

1) объект исследований представляет собой анизотропное полупространство

${\Omega } = \left\{ {\left. {\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right] \in {{\mathbb{R}}^{3}}:~\begin{array}{*{20}{c}} { - \infty < {{x}_{1}} < + \infty } \\ {h < {{x}_{2}} < + \infty } \\ { - \infty \leqslant {{x}_{3}} \leqslant + \infty } \end{array}} \right\},} \right.$

граница которого (плоскость ${{x}_{2}} = h,$ $h > 0$) обладает изотропным покрытием толщины $h - {\text{const}};$

2) в системе “анизотропное полупространство – изотропное покрытие” реализуются условия идеального теплового контакта [2, 3];

3) внешняя поверхность изотропного покрытия (плоскость ${{x}_{2}} = 0$) находится как под воздействием внешней среды с температурой ${{T}_{{\text{с}}}} - {\text{const,}}$ отличной от начальной температуры ${{T}_{0}} - {\text{const}}$ объекта исследований, так и теплового потока с плотностью мощности $q\left( {{{x}_{1}},{{x}_{3}},t} \right);$

4) внешний тепловой поток с плотностью мощности $q\left( {{{x}_{1}},{{x}_{3}},t} \right)$ воздействует на поверхность ${{x}_{2}} = 0 - 0$ изотропного покрытия анизотропного полупространства в направлении, противоположном направлению ее внешней нормали;

5) при любом фиксированном значении временного переменного $t \geqslant 0$ функционал $q\left( {{{x}_{1}},{{x}_{3}},t} \right)$ интегрируем с квадратом в ${{\mathbb{R}}^{2}}$ по совокупности пространственных переменных ${{x}_{1}},$ ${{x}_{3}},$ то есть [14]

${{\left. {q\left( {{{x}_{1}},{{x}_{3}},t} \right)} \right|}_{{\left( {t \geqslant 0} \right)}}} \in {{L}^{2}}\left( {{{\mathbb{R}}^{2}}} \right);$

6) при любых фиксированных значениях пространственных переменных ${{x}_{1}},$ ${{x}_{3}},$ представленных вектором ${{\left[ {{{x}_{1}},{{x}_{3}}} \right]}^{{\text{T}}}} \in {{\mathbb{R}}^{2}},$ функционал $q\left( {{{x}_{1}},{{x}_{3}},t} \right)$ интегрируем с квадратом на полуинтервале $\left[ {0, + \infty )} \right.$ по временному переменному t, то есть

${{\left. {q\left( {{{x}_{1}},{{x}_{3}},t} \right)} \right|}_{{\left( {{{{\left[ {{{x}_{1}},{{x}_{3}}} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.{\text{\;}}.$

Согласно исходным допущениям, представленным выше, при использовании следующих обозначений:

$\theta = \frac{{T - {{T}_{0}}}}{{{{T}_{{\text{с}}}} - {{T}_{0}}}};\,\,\,\,~x = \frac{{{{x}_{1}}}}{l},~\,\,\,\,y = \frac{{{{x}_{2}}}}{l},\,\,\,\,z = \frac{{{{x}_{3}}}}{l};$

${\text{Fo}} = \frac{{{{\lambda }_{{\text{п}}}}t}}{{{{c}_{{\text{п}}}}{{\rho }_{{\text{п}}}}{{l}^{2}}}};\,\,\,\,{\text{Bi}} = \frac{{\alpha l}}{{{{\lambda }_{{\text{п}}}}}};\,\,\,\,{{\mu }_{{ij}}} = \frac{{{{\lambda }_{{ij}}}}}{{{{\lambda }_{{22}}}}};\,\,\,\,~\mu = \frac{{{{\lambda }_{{\text{п}}}}}}{{{{\lambda }_{{22}}}}};$

$a = \frac{{c\rho {{\lambda }_{{\text{п}}}}}}{{{{c}_{{\text{п}}}}{{\rho }_{{\text{п}}}}{{\lambda }_{{22}}}}};\,\,\,\,Q = \frac{{ql}}{{{{\lambda }_{{\text{п}}}}\left( {{{T}_{{\text{с}}}} - {{T}_{0}}} \right)}};~\,\,\,\,H = \frac{h}{l},$

где $l$ – используемая единица масштаба пространственных переменных; ${{\lambda }_{{ij}}} \equiv {{\lambda }_{{ji}}}$ – компонента тензора теплопроводности анизотропного материала объекта исследований, $c$ и ρ – его удельная массовая теплоемкость и плотность соответственно, а ${{\lambda }_{{\text{п}}}},$ ${{c}_{{\text{п}}}}$ и ${{\rho }_{{\text{п}}}}$ соответствующие теплофизические характеристики изотропного материала покрытия, функционал $\theta \left( {x,y,z,{\text{Fo}}} \right),$ определяющий процесс формирования искомого температурного поля, должен удовлетворять системе двух линейных дифференциальных уравнений в частных производных второго порядка параболического типа [2–5]:

(1)

$\begin{gathered} \frac{{\partial \theta }}{{\partial {\text{Fo}}}} = \frac{{{{\partial }^{2}}\theta }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\theta }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\theta }}{{\partial {{z}^{2}}}},\,\,\,\,\left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\,0 < y < H,\,\,\,\,{\text{Fo}} > 0; \\ a\frac{{\partial \theta }}{{\partial {\text{Fo}}}} = {{\mu }_{{11}}}\frac{{{{\partial }^{2}}\theta }}{{\partial {{x}^{2}}}} + 2{{\mu }_{{12}}}\frac{{{{\partial }^{2}}\theta }}{{\partial x\partial y}} + 2{{\mu }_{{13}}}\frac{{{{\partial }^{2}}\theta }}{{\partial x\partial z}} + \frac{{{{\partial }^{2}}\theta }}{{\partial {{y}^{2}}}} + 2{{\mu }_{{23}}}\frac{{{{\partial }^{2}}\theta }}{{\partial y\partial z}} + {{\mu }_{{33}}}\frac{{{{\partial }^{2}}\theta }}{{\partial {{z}^{2}}}}, \\ \left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\,y > H,\,\,\,\,~{\text{Fo}} > 0, \\ \end{gathered} $

нулевому начальному условию:

(2)

${{\left. {\theta \left( {x,y,z,{\text{Fo}}} \right)} \right|}_{{{\text{Fo}} = 0}}} = 0,$

неоднородному краевому условию [15]:

(3)

${{\left. { - \frac{{\partial \theta }}{{\partial y}}} \right|}_{{y = 0}}} = {{\left. {{\text{Bi}}\left( {1 - \theta } \right)} \right|}_{{y = 0}}} + Q\left( {x,z,{\text{Fo}}} \right)$

и условиям идеального теплового контакта в системе “анизотропное полупространство–изотропное покрытие”, т.е. граничным условиям четвертого рода [2–5]:

(4)

$\begin{gathered} \theta \left( {x,H - 0,z,{\text{Fo}}} \right) = \theta \left( {x,H + 0,z,{\text{Fo}}} \right); \\ {{\left. {\mu \frac{{\partial \theta }}{{\partial y}}} \right|}_{{y = H - 0}}} = {{\left. {\left[ {{{\mu }_{{12}}}\frac{{\partial \theta }}{{\partial x}} + \frac{{\partial \theta }}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial \theta }}{{\partial z}}} \right]} \right|}_{{y = H + 0}}}. \\ \end{gathered} $

При этом, если предположить наличие у искомого температурного поля аддитивной структуры:

(5)

$\theta \left( {x,y,z,{\text{Fo}}} \right) = {{\theta }_{1}}\left( {y,{\text{Fo}}} \right) + {{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right),$

где функционал ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right)$ являлся решением следующей смешанной задачи для системы уравнений в частных производных второго порядка параболического типа:

(6)

$\begin{gathered} \frac{{\partial {{\theta }_{1}}}}{{\partial {\text{Fo}}}} = \frac{{{{\partial }^{2}}{{\theta }_{1}}}}{{\partial {{y}^{2}}}},\,\,\,\,0 < y < H,\,\,{\text{Fo}} > 0;\,\,\,\,a\frac{{\partial {{\theta }_{1}}}}{{\partial {\text{Fo}}}} = \frac{{{{\partial }^{2}}{{\theta }_{1}}}}{{\partial {{y}^{2}}}},\,\,\,\,y > H,\,\,{\text{Fo}} > 0;\,\,\,\,{{\theta }_{1}}\left( {y,0} \right) = 0; \\ - {{\left. {\frac{{\partial {{\theta }_{1}}}}{{\partial {\text{y}}}}} \right|}_{{y = 0}}} = {{\left. {{\text{Bi}}\left( {1 - {{\theta }_{1}}} \right)} \right|}_{{y = 0}}};\,\,\,\,{{\theta }_{1}}\left( {{\text{H}} - 0,{\text{\;Fo}}} \right) = {{\theta }_{1}}\left( {{\text{H}} + 0,{\text{\;Fo}}} \right); \\ {{\left. {\mu \frac{{\partial {{\theta }_{1}}}}{{\partial y}}} \right|}_{{y = H - 0}}} = {{\left. {\frac{{\partial {{\theta }_{1}}}}{{\partial y}}} \right|}_{{y = H + 0}}};\,\,\,\,{{\left. {{{\theta }_{1}}\left( {y,{\text{Fo}}} \right)} \right|}_{{\left( {{\text{Fo}} \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.;\,\,\,\,{{\left. {{{\theta }_{1}}\left( {y,{\text{Fo}}} \right)} \right|}_{{\left( {y \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right., \\ \end{gathered} $

то согласно исходным допущениям и (1)–(6) функционал ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)$ должен определять процесс формирования температурного поля объекта исследований, внешняя граница которого находится под воздействием теплового потока $Q\left( {x,z,{\text{Fo}}} \right),$ при условии равенства температуры внешней среды его нулевой начальной температуре, то есть

(7)

$\begin{gathered} \frac{{\partial {{\theta }_{2}}}}{{\partial {\text{Fo}}}} = \frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{z}^{2}}}},\,\,\,\,\left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\,0 < y < H,~\,\,{\text{Fo}} > 0; \\ a\frac{{\partial {{\theta }_{2}}}}{{\partial {\text{Fo}}}} = {{\mu }_{{11}}}\frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{x}^{2}}}} + 2{{\mu }_{{12}}}\frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial x\partial y}} + 2{{\mu }_{{13}}}\frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial x\partial z}} + \frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{y}^{2}}}} + 2{{\mu }_{{23}}}\frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial y\partial z}} + {{\mu }_{{33}}}\frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{z}^{2}}}}, \\ \left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\,y > H,\,\,~{\text{Fo}} > 0;\,\,\,\,{{\theta }_{2}}\left( {x,y,z,0} \right) = 0;\,\,\,\,{{\left. {\frac{{\partial {{\theta }_{2}}}}{{\partial y}}} \right|}_{{y = 0}}} = {{\left. {{\text{Bi}}{{\theta }_{2}}} \right|}_{{y = 0}}} - Q\left( {x,z,{\text{Fo}}} \right); \\ {{\theta }_{2}}\left( {x,H - 0,z,{\text{Fo}}} \right) = {{\theta }_{2}}\left( {x,H + 0,z,{\text{Fo}}} \right); \\ {{\left. {\mu \frac{{\partial {{\theta }_{2}}}}{{\partial y}}} \right|}_{{y = H - 0}}} = {{\left. {\left[ {{{\mu }_{{12}}}\frac{{\partial {{\theta }_{2}}}}{{\partial x}} + \frac{{\partial {{\theta }_{2}}}}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial {{\theta }_{2}}}}{{\partial z}}} \right]} \right|}_{{y = H + 0}}};\,\,\,\,{{\left. {Q\left( {x,z,{\text{Fo}}} \right)} \right|}_{{\left( {{\text{Fo}} \geqslant 0} \right)}}} \in {{L}^{2}}\left( {{{\mathbb{R}}^{2}}} \right); \\ {{\left. {Q\left( {x,z,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {x,z} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.{\text{\;}};\,\,\,\,{{\left. {{{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)} \right|}_{{\left( {y \geqslant 0} \right) \wedge \left( {{\text{Fo}} \geqslant 0} \right)}}} \in {{L}^{2}}\left( {{{\mathbb{R}}^{2}}} \right); \\ {{\left. {{{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {x,z} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {{\text{Fo}} \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.;\,\,\,\,{{\left. {{{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {x,z} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {y \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.. \\ \end{gathered} $

ТЕМПЕРАТУРНОЕ ПОЛЕ

Идентификация функционала ${{{\mathbf{\theta }}}_{{\mathbf{1}}}}\left( {y,{\mathbf{Fo}}} \right).$ Математическая модель для определения первой независимой аддитивной составляющей ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right)$ процесса формирования искомого температурного поля представляет собой смешанную задачу (6) для системы уравнений в частных производных второго порядка параболического типа. А так как эта задача является линейной и одномерной, то для ее решения естественным является использование интегрального преобразования Лапласа, задаваемого парой линейных интегральных операторов [2, 16]:

(8)

$L\left[ \cdot \right] \equiv \int\limits_0^\infty { \cdot \,{\text{exp}}\left( { - s{\text{Fo}}} \right)d{\text{Fo}}} ;\,\,\,\,~{{L}^{{ - 1}}}\left[ \cdot \right] \equiv \int\limits_{{\sigma } - i\infty }^{{\sigma } + i\infty } { \cdot \,{\text{exp}}\left( {s{\text{Fo}}} \right)ds} ,$

и применяемого по временному переменному ${\text{Fo}}{\text{.}}$

С использованием математической модели (6) и стандартных свойств линейного оператора $L\left[ \cdot \right]$ [2], определяющего прямое интегральное преобразование Лапласа (8), убеждаемся в том, что изображение:

(9)

${{U}_{1}}\left( {y,s} \right) \triangleq L\left[ {{{\theta }_{1}}\left( {y,{\text{Fo}}} \right)} \right]$

оригинала ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right)$ является решением следующей краевой задачи для системы двух обыкновенных линейных дифференциальных уравнений второго порядка:

$\frac{{{{d}^{2}}{{U}_{1}}}}{{d{{y}^{2}}}} = s{{U}_{1}},\,\,\,\,0 < y < H;$

$\frac{{{{d}^{2}}{{U}_{1}}}}{{d{{y}^{2}}}} = as{{U}_{1}},\,\,\,\,y > H;$

${{\left. {\left[ {\frac{{d{{U}_{1}}}}{{d{\text{y}}}} - {\text{Bi}}{{U}_{1}}} \right]} \right|}_{{y = 0}}} = - \frac{{{\text{Bi}}}}{s};$

${{U}_{1}}\left( {H - 0,s} \right) = {{U}_{1}}\left( {H + 0,s} \right);$

${{\left. {\mu \frac{{\partial {{U}_{1}}}}{{\partial y}}} \right|}_{{y = H - 0}}} = {{\left. {\frac{{\partial {{U}_{1}}}}{{\partial y}}} \right|}_{{y = H + 0}}};$

${{\left. {{{U}_{1}}\left( {y,{\text{s}}} \right)} \right|}_{{\left( {{\text{s}} \in \mathbb{C}} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.,$

которое может быть найдено стандартными методами [17] и представлено в следующем виде

(10)

$\begin{gathered} {{\left. {{{U}_{1}}\left( {y,s} \right)} \right|}_{{\left( {0 \leqslant y \leqslant H} \right)}}} = \left\{ {\left( {\mu + \sqrt a } \right){\text{exp}}\left[ { - \left( {y - H} \right)\sqrt s } \right] + \left( {\mu - \sqrt a } \right){\text{exp}}\left[ {\left( {y - H} \right)\sqrt s } \right]} \right\}{{\left( {2\mu } \right)}^{{ - 1}}}C\left( s \right); \\ {{\left. {{{U}_{1}}\left( {y,s} \right)} \right|}_{{\left( {y \geqslant H} \right)}}} = C\left( s \right){\text{exp}}\left[ { - \left( {y - H} \right)\sqrt {as} } \right]; \\ C\left( s \right) = \frac{{2\mu {\text{Bi}}}}{{s\left\{ {\left( {\mu - \sqrt a } \right)\left( {\sqrt s - {\text{Bi}}} \right){\text{exp}}\left( {H\sqrt s } \right) - \left( {\mu - \sqrt a } \right)\left( {\sqrt s - {\text{Bi}}} \right){\text{exp}}\left( { - H\sqrt s } \right)} \right\}}} = \\ = {\text{Bi}}\sum\limits_{n = 0}^\infty {\frac{{{{{\left( {\mu - a} \right)}}^{n}}}}{{{{{\left( {\mu + a} \right)}}^{{n + 1}}}}}} \sum\limits_{k = 0}^n {C_{n}^{k}{{{\left( { - 1} \right)}}^{{n - k}}}\frac{{{{{\left( {2{\text{Bi}}} \right)}}^{{n - k + 1}}}}}{{s{{{\left( {\sqrt s + {\text{Bi}}} \right)}}^{{n - k + 1}}}}}} {\text{exp}}\left( { - H\left( {2k + 1} \right)\sqrt s } \right). \\ \end{gathered} $

Таким образом, согласно (9) и (10), завершение процедуры идентификации функционала ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right)$ целиком определяется нахождением оригинала

(11)

${{f}_{m}}\left( {{\text{Fo}}} \right) \triangleq {{L}^{{ - 1}}}\left[ {\frac{{{\text{exp}}\left( { - \alpha \sqrt s } \right)}}{{s{{{\left( {\sqrt s + b} \right)}}^{m}}}}} \right].$

При этом, если $m \in \left\{ {1,2} \right\},$ то для нахождения оригинала ${{f}_{m}}\left( {{\text{Fo}}} \right)$ достаточно воспользоваться соответствующими таблицами “изображение–оригинал” [2]:

(12)

где ${\text{erfc}}\left( x \right)$ – дополнительная функция ошибок Гаусса [2]. Если $m > 2,$ то, последовательно применив теорему Эфроса и теорему запаздывания [2] с последующим использованием соответствующих таблиц “изображение–оригинал” [18], получаем:

(13)

$\begin{gathered} {{f}_{m}}\left( {{\text{Fo}}} \right) = \frac{1}{{{{b}^{m}}\sqrt {\pi {\text{Fo}}} }}\int\limits_{\alpha }^\infty {{\text{exp}}\left( { - \frac{{{{\tau }^{2}}}}{{4{\text{Fo}}}}} \right)\left\{ {1 - {\text{exp}}\left[ { - b\left( {\tau - \alpha } \right)} \right]{{e}_{{m - 1}}}\left[ {b\left( {\tau - \alpha } \right)} \right]} \right\}d\tau } ; \\ {{e}_{k}}\left( x \right) \triangleq \sum\limits_{k = 0}^n {\frac{{{{x}^{k}}}}{{k!}}} . \\ \end{gathered} $

Идентификация функционала ${{{\mathbf{\theta }}}_{{\mathbf{2}}}}\left( {x,y,z,{\mathbf{Fo}}} \right).$ Функционал ${{\theta }_{2}}(x,y,z,{\text{Fo}}),$ определяющий вторую независимую аддитивную составляющую процесса формирования искомого температурного поля, полностью определен математической моделью (7), которая, как и предшествующая ей математическая модель (6), представляет собой смешанную задачу для системы линейных уравнений в частных производных второго порядка параболического типа. Но в отличие от (6) смешанная задача (7) является многомерной и отражает анизотропию свойств материала полупространства.

На первом этапе решения смешанной задачи (7), воспользовавшись двухмерным экспоненциальным интегральным преобразованием Фурье, задаваемым парой линейных интегральных операторов [19]:

(14)

${\Phi }\left[ \cdot \right] \equiv \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty { \cdot \,{\text{exp}}\left( { - ipx - irz} \right)dxdz} } ;\,\,\,\,{{{\Phi }}^{{ - 1}}}\left[ \cdot \right] \equiv \frac{1}{{{{{\left( {2\pi } \right)}}^{2}}}}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty { \cdot \,{\text{exp}}\left( {ipx + irz} \right)dpdr} } ,$

где $i$ – “мнимая” единица [2], стандартными свойствами оператора ${\Phi }\left[ \cdot \right]$ [19] и обозначениями:

(15)

${{U}_{2}}\left( {p,y,r,{\text{Fo}}} \right) \triangleq {\Phi }\left[ {{{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)} \right];\,\,\,\,{\Delta }\left( {p,r,{\text{Fo}}} \right) \triangleq {\Phi }\left[ {Q\left( {x,z,{\text{Fo}}} \right)} \right],$

представим ее в пространстве изображений интегрального преобразования (14) в следующем виде:

(16)

$\begin{gathered} \frac{{\partial {{U}_{2}}}}{{\partial {\text{Fo}}}} = \frac{{{{\partial }^{2}}{{U}_{2}}}}{{\partial {{y}^{2}}}} - \left( {{{p}^{2}} + {{r}^{2}}} \right){{U}_{2}},\,\,\,\,0 < y < H,~\,\,{\text{Fo}} > 0; \\ a\frac{{\partial {{U}_{2}}}}{{\partial {\text{Fo}}}} = \frac{{{{\partial }^{2}}{{U}_{2}}}}{{\partial {{y}^{2}}}} + 2i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)\frac{{\partial {{U}_{2}}}}{{\partial y}} - \left( {{{\mu }_{{11}}}{{p}^{2}} + 2{{\mu }_{{13}}}pr + {{\mu }_{{33}}}{{r}^{2}}} \right){{U}_{2}},\,\,\,\,y > H,~\,\,{\text{Fo}} > 0; \\ {{U}_{2}}\left( {p,y,r,0} \right) = 0;\,\,\,\,{{\left. {\frac{{\partial {{U}_{2}}}}{{\partial y}}} \right|}_{{y = 0}}} = {{\left. {{\text{Bi}}{{U}_{2}}} \right|}_{{y = 0}}} - {\Delta }\left( {p,r,{\text{Fo}}} \right); \\ {{U}_{2}}\left( {p,H - 0,r,{\text{Fo}}} \right) = {{U}_{2}}\left( {p,H + 0,r,{\text{Fo}}} \right); \\ {{\left. {\mu \frac{{\partial {{U}_{2}}}}{{\partial y}}} \right|}_{{y = H - 0}}} = {{\left. {\left[ {\frac{{\partial {{U}_{2}}}}{{\partial y}} + i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right){{U}_{2}}} \right]} \right|}_{{y = H + 0}}};\,\,\,\,{{\left. {{\Delta }\left( {p,r,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {p,r} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.; \\ {{\left. {{{U}_{2}}\left( {p,y,r,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {p,r} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {{\text{Fo}} \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.;\,\,\,\,{{\left. {{{U}_{2}}\left( {p,y,r,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {p,r} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {{\text{y}} \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.. \\ \end{gathered} $

При этом, согласно результатам предварительного анализа смешанной задачи (16), кажется очевидной целесообразность ее решения с использованием интегрально преобразования Лапласа (8). Действительно, в пространстве изображений этого интегрального преобразования смешанной задаче (16) соответствует краевая задача для системы двух обыкновенных линейных дифференциальных уравнений второго порядка, решение которой может быть найдено стандартными методами [17], но реализуемость обратного перехода в пространство изображений двухмерного экспоненциального интегрального преобразования Фурье (14) представляется весьма проблематичной. Поэтому обратимся к процедуре построения сингулярного интегрального преобразования по пространственному переменному $y \in \left[ {0, + \infty )} \right.,$ в пространстве изображений которого смешанная задача (16) трансформируется в соответствующую задачу Коши для обыкновенного линейного дифференциального уравнения первого порядка.

Если предположить, что изображение ${{U}_{2}}\left( {p,y,r,{\text{Fo}}} \right)$ двухмерного экспоненциального интегрального преобразования Фурье (14) оригинала ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)$ обладает следующей структурой:

(17)

${{U}_{2}}\left( {p,y,r,{\text{Fo}}} \right) = W\left( {p,y,r,{\text{Fo}}} \right)\left\{ \begin{gathered} 1,\,\,\,\,0 < y < H \hfill \\ {\text{exp}}\left[ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)\left( {y - H} \right)} \right],\,\,\,\,y > H \hfill \\ \end{gathered} \right\},$

то согласно (17) и (16) функционал $W\left( {p,y,r,{\text{Fo}}} \right)$ должен удовлетворять соответствующему аналогу смешанной задачи (16):

(18)

$\begin{gathered} \frac{{\partial W}}{{\partial {\text{Fo}}}} = b\left( y \right)\frac{{{{\partial }^{2}}W}}{{\partial {{y}^{2}}}} - d\left( {y,p,r} \right)W,\,\,\,\,y > 0,\,\,\,\,{\text{Fo}} > 0;\,\,\,\,W\left( {p,y,r,0} \right) = 0; \\ {{\left. {\left[ {\frac{{\partial W}}{{\partial y}} - {\text{Bi}}W} \right]} \right|}_{{y = 0}}} = - {\Delta }\left( {p,r,{\text{Fo}}} \right);\,\,\,\,W\left( {p,H - 0,r,{\text{Fo}}} \right) = W\left( {p,H + 0,r,{\text{Fo}}} \right); \\ {{\left. {\mu \frac{{\partial W}}{{\partial y}}} \right|}_{{y = H - 0}}} = {{\left. {\frac{{\partial W}}{{\partial y}}} \right|}_{{y = H + 0}}};\,\,\,\,{{\left. {{\Delta }\left( {p,r,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {p,r} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.{\text{\;}}; \\ {{\left. {W\left( {p,y,r,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {p,r} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {{\text{Fo}} \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right.;\,\,\,\,{{\left. {W\left( {p,y,r,{\text{Fo}}} \right)} \right|}_{{\left( {{{{\left[ {p,r} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {{\text{y}} \geqslant 0} \right)}}} \in {{L}^{2}}\left[ {0, + \infty )} \right., \\ \end{gathered} $

при записи которого использованы функционалы:

(19)

$\begin{gathered} b\left( y \right) \triangleq \left\{ {\begin{array}{*{20}{c}} {1,}&{0 < y < H} \\ {{{a}^{{ - 1}}},}&{y > H} \end{array}} \right\};\,\,\,\,d\left( {y,p,r} \right) \triangleq \\ \triangleq \left\{ \begin{gathered} \left( {{{p}^{2}} + {{r}^{2}}} \right),\,\,\,\,0 < y < H \hfill \\ {{a}^{{ - 1}}}\left[ {\left( {{{\mu }_{{11}}} - \mu _{{12}}^{2}} \right){{p}^{2}} + 2\left( {{{\mu }_{{13}}} - {{\mu }_{{12}}}{{\mu }_{{23}}}} \right)pr + \left( {{{\mu }_{{33}}} - \mu _{{32}}^{2}} \right){{r}^{2}}} \right],\,\,\,\,y > H \hfill \\ \end{gathered} \right\}. \\ \end{gathered} $

При этом положительная определенность квадратичной формы, определяющей функционал $d\left( {y,p,r} \right)$ при $y > H,$ при переходе к исходным обозначениям проверяется непосредственно с использованием критерия Сильвестра [20] и свойств тензора теплопроводности второго ранга [5].

Воспользовавшись общей теорией интегральных преобразований [14, 16], определяем весовую функцию искомого сингулярного интегрального преобразования, предназначенного для применения к смешанной задаче (18), (19) по пространственному переменному $y \in \left[ {0, + \infty )} \right.{\text{:}}$

(20)

$\rho \left( y \right) \triangleq \left\{ {\begin{array}{*{20}{c}} {1,}&{0 < y < H} \\ {a,}&{y > H} \end{array}} \right\};$

и формулируем задачу Штурма–Лиувилля для нахождения его ядра $K\left( {y,\eta ,p,r} \right){\text{:}}$

(21)

$\begin{gathered} \frac{{{{d}^{2}}K\left( {y,\eta ,p,r} \right)}}{{d{{y}^{2}}}} + {{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)K\left( {y,\eta ,p,r} \right) = 0,\,\,\,\,0 < y < H; \\ \frac{{{{d}^{2}}K\left( {y,\eta ,p,r} \right)}}{{d{{y}^{2}}}} + {{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)K\left( {y,\eta ,p,r} \right) = 0,\,\,\,\,y > H; \\ {{\left. {K\left( {y,\eta ,p,r} \right)} \right|}_{{y = H}}} = 1,\,\,\,\,{{\left. {\frac{{dK\left( {y,\eta ,p,r} \right)}}{{dy}}} \right|}_{{y = 0}}} = {\text{Bi}}; \\ K\left( {H - 0,\eta ,p,r} \right) = \mu K\left( {H + 0,\eta ,p,r} \right);\,\,\,\,{{\left. {\frac{{dK\left( {y,\eta ,p,r} \right)}}{{dy}}} \right|}_{{y = H - 0}}} = {{\left. {\frac{{dK\left( {y,\eta ,p,r} \right)}}{{dy}}} \right|}_{{y = H + 0}}}, \\ \end{gathered} $

где использованы следующие обозначения:

(22)

$\begin{gathered} {{d}_{{\text{о}}}}\left( {\eta ,p,r} \right) \triangleq {{\eta }^{2}} - \left( {{{p}^{2}} + {{r}^{2}}} \right); \\ {{d}_{{\text{н}}}}\left( {\eta ,p,r} \right) \triangleq a{{\eta }^{2}} - \left[ {\left( {{{\mu }_{{11}}} - \mu _{{12}}^{2}} \right){{p}^{2}} + 2\left( {{{\mu }_{{13}}} - {{\mu }_{{12}}}{{\mu }_{{23}}}} \right)pr + \left( {{{\mu }_{{33}}} - \mu _{{32}}^{2}} \right){{r}^{2}}} \right]. \\ \end{gathered} $

Таким образом, согласно (21) и (22) имеем:

(23)

$\begin{gathered} {{\left. {K\left( {y,\eta ,p,r} \right)} \right|}_{{0 \leqslant y \leqslant H}}} = \cos \left[ {y\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right] + \frac{{{\text{Bi}}}}{{\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} }}\sin \left[ {y\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right]; \\ {{\left. {K\left( {y,\eta ,p,r} \right)} \right|}_{{y \geqslant H}}} = {{c}_{1}}\left( {\eta ,p,r} \right)\cos \left[ {\left( {y - H} \right)\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} } \right] + {{c}_{2}}\left( {\eta ,p,r} \right) \times \\ \times \,\,\sin \left[ {\left( {y - H} \right)\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} } \right]; \\ {{c}_{1}}\left( {\eta ,p,r} \right) = {{\mu }^{{ - 1}}}\left\{ {\cos \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right] + \frac{{{\text{Bi}}}}{{\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} }}\sin \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right]} \right\}; \\ {{c}_{2}}\left( {\eta ,p,r} \right) = \frac{1}{{\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} }}\left\{ {{\text{Bi}}\cos \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right] - \sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} \sin \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right]} \right\} \\ \end{gathered} $

и первый из двух линейных операторов:

(24)

$G\left[ \cdot \right] \equiv \int\limits_0^\infty { \cdot ~\,\rho \left( y \right)K\left( {y,\eta ,p,r} \right)dy} ,$

задающих искомое сингулярное интегральное преобразование по пространственному переменному $y$, предназначенное для решения смешанной задачи (18), (19), полностью определен равенствами (24), (20), (23) и (22).

Для определения линейного интегрального оператора ${{G}^{{ - 1}}}\left[ \cdot \right],$ реализующего переход из пространства изображений искомого сингулярного интегрального преобразования в пространство его оригиналов, необходимо знать функцию Вейля–Титчмарша [16]. С этой целью определяем функционал $\chi \left( {y,\eta ,p,r} \right),$ удовлетворяющий задаче Штурма–Лиувилля (21), (22), в которой краевые условия при $y = 0$ заменены на сопряженные им, то есть

(25)

${{\left. {\chi \left( {y,\eta ,p,r} \right)} \right|}_{{y = 0}}} = {\text{Bi}},\,\,\,\,{{\left. {\frac{{d\chi \left( {y,\eta ,p,r} \right)}}{{dy}}} \right|}_{{y = 0}}} = - 1;$

В этом случае, согласно (21), (22) и (25), получаем:

(26)

$\begin{gathered} {{\left. {\chi \left( {y,\eta ,p,r} \right)} \right|}_{{0 \leqslant y \leqslant H}}} = {\text{Bi}}\cos \left[ {y\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right] - \frac{1}{{\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} }}\sin \left[ {y\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right]; \\ {{\left. {\chi \left( {y,\eta ,p,r} \right)} \right|}_{{y \geqslant H}}}\, = \,{{c}_{3}}\left( {\eta ,p,r} \right)\cos {\kern 1pt} \left[ {\left( {y - H} \right)\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} } \right] + {{c}_{4}}\left( {\eta ,p,r} \right)\sin \left[ {\left( {y - H} \right)\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} } \right]; \\ {{c}_{3}}\left( {\eta ,p,r} \right) = {{\mu }^{{ - 1}}}\left\{ {{\text{Bi}}\cos \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right] - \frac{1}{{\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} }}\sin \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right]} \right\}; \\ {{c}_{4}}\left( {\eta ,p,r} \right) = \frac{{ - 1}}{{\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} }}\left\{ {{\text{Bi}}\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} \sin \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right] + \cos \left[ {H\sqrt {{{d}_{{\text{о}}}}\left( {\eta ,p,r} \right)} } \right]} \right\}. \\ \end{gathered} $

Нас интересует решение Вейля, принадлежащее евклидову пространству ${{L}^{2}}\left[ {0, + \infty )} \right.,$ которое с точностью до множителя, зависящего от $\eta ,$ имеет следующий вид [16, 21]:

(27)

${v}\left( {y,\eta ,p,r} \right) = \chi \left( {y,\eta ,p,r} \right) + m\left( {\eta ,p,r} \right)K\left( {y,\eta ,p,r} \right).$

Воспользовавшись равенствами (27), (26), (23) при $y \geqslant H,$ и формулами Эйлера [2] и известным результатом [21]:

${\text{exp}}\left[ {i\left( {y - H} \right)\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} } \right] \in {{L}^{2}}\left[ {H, + \infty )} \right.;$

${\text{exp}}\left[ { - i\left( {y - H} \right)\sqrt {{{d}_{{\text{н}}}}\left( {\eta ,p,r} \right)} } \right] \notin {{L}^{2}}\left[ {H, + \infty } \right),$

приходим к выводу о том, что должно выполняться равенство:

${{c}_{4}}\left( {\eta ,p,r} \right) + i{{c}_{3}}\left( {\eta ,p,r} \right) + m\left( {\eta ,p,r} \right)\left\{ {{{c}_{1}}\left( {\eta ,p,r} \right) + i{{c}_{2}}\left( {\eta ,p,r} \right)} \right\} = 0,$

из которого находим

${\text{Im}}m\left( {\eta ,p,r} \right) = \frac{{{{c}_{2}}\left( {\eta ,p,r} \right){{c}_{3}}\left( {\eta ,p,r} \right) - {{c}_{1}}\left( {\eta ,p,r} \right){{c}_{4}}\left( {\eta ,p,r} \right)}}{{c_{1}^{2}\left( {\eta ,p,r} \right) + c_{2}^{2}\left( {\eta ,p,r} \right)}}$

и согласно общей теории сингулярной задачи Штурма–Лиувилля [16, 21], определяем дифференциал спектральной функции ${{\sigma }_{y}}\left( {\eta ,p,r} \right){\text{:}}$

(28)

$\begin{gathered} d{{\sigma }_{y}}\left( {\eta ,p,r} \right) = \frac{{2\eta \left[ {{{c}_{2}}\left( {\eta ,p,r} \right){{c}_{3}}\left( {\eta ,p,r} \right) - {{c}_{1}}\left( {\eta ,p,r} \right){{c}_{4}}\left( {\eta ,p,r} \right)} \right]}}{{\pi \left( {{\text{B}}{{{\text{i}}}^{2}} + 1} \right)\left[ {c_{1}^{2}\left( {\eta ,p,r} \right) + c_{2}^{2}\left( {\eta ,p,r} \right)} \right]}}d\eta ; \\ \eta > {{\delta }_{y}}\left( {p,r} \right) \equiv \left\{ {\begin{array}{*{20}{c}} {{{\delta }_{{\text{о}}}}\left( {p,r} \right),}&{0 < y < H} \\ {{{\delta }_{{\text{н}}}}\left( {p,r} \right),}&{y > H} \end{array}} \right\}; \\ {{\delta }_{{\text{о}}}}\left( {p,r} \right) \triangleq \sqrt {{{p}^{2}} + {{r}^{2}}} ,\,\,\,\,{{\delta }_{{\text{н}}}}\left( {p,r} \right) \triangleq \left\{ {{{a}^{{ - 1}}}\left[ {\left( {{{\mu }_{{11}}} - \mu _{{12}}^{2}} \right){{p}^{2}} + } \right.} \right. \\ {{\left. {\left. { + \,\,2\left( {{{\mu }_{{13}}} - {{\mu }_{{12}}}{{\mu }_{{23}}}} \right)pr + \left( {{{\mu }_{{33}}} - \mu _{{32}}^{2}} \right){{r}^{2}}} \right]} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}};\,\,\,\,d{{\sigma }_{y}}\left( {\eta ,p,r} \right) \equiv 0,\,\,\,\,\eta < {{\delta }_{y}}\left( {p,r} \right). \\ \end{gathered} $

Таким образом, линейный интегральный оператор

(29)

${{G}^{{ - 1}}}\left[ \cdot \right] \equiv \int\limits_{{{{\delta }}_{y}}\left( {p,r} \right)}^\infty { \cdot \,K\left( {y,\eta ,p,r} \right)d{{\sigma }_{y}}\left( {\eta ,p,r} \right)} $

полностью определен равенствами (23), (22), (28), и процедура идентификации искомого сингулярного интегрального преобразования завершена.

В пространстве изображений сингулярного интегрального преобразования, заданного парой линейных интегральных операторов $G\left[ \cdot \right],$ ${{G}^{{ - 1}}}\left[ \cdot \right],$ определенных равенствами (24), (29), (16), (23), (22), (28), изображение

(30)

$w\left( {p,\eta ,r,{\text{Fo}}} \right) \triangleq G\left[ {W\left( {p,y,r,{\text{Fo}}} \right)} \right]$

функционала $W\left( {p,y,r,{\text{Fo}}} \right),$ являющегося решением смешанной задачи (18), должно удовлетворять соответствующей ей задаче Коши:

(31)

$\frac{{dw\left( {p,\eta ,r,{\text{Fo}}} \right)}}{{d{\text{Fo}}}} = - {{\eta }^{2}}w\left( {p,\eta ,r,{\text{Fo}}} \right) + {\Delta }\left( {p,r,{\text{Fo}}} \right),\,\,\,\,{\text{Fo}} > 0;\,\,\,\,w\left( {p,\eta ,r,0} \right) = 0.$

Решение задачи Коши (31) может быть найдено с использованием стандартных методов [17] и представлено в следующем виде:

(32)

$w\left( {p,\eta ,r,{\text{Fo}}} \right) = \int\limits_0^{{\text{Fo}}} {{\Delta }\left( {p,r,\tau } \right){\text{exp}}\left[ { - {{\eta }^{2}}\left( {{\text{Fo}} - {\tau }} \right)} \right]d\tau } ,$

где согласно (18) функционал ${\Delta }\left( {p,r,\tau } \right)$ – изображение двухмерного экспоненциального интегрального преобразования Фурье (14) функционала $Q\left( {x,z,{\text{Fo}}} \right),$ определяющего плотность мощности внешнего теплового потока.

Таким образом, формально для завершения процедуры идентификации второй аддитивной составляющей процесса формирования искомого температурного поля объекта исследований, представленный функционалом ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right),$ осталось реализовать два следующих действия:

1) согласно (30) к равенству (32) применить линейный интегральный оператор ${{G}^{{ - 1}}}\left[ \cdot \right],$ определенный равенствами (29), (28), (23), (22), и с учетом (17) определить функционал ${{U}_{2}}\left( {p,y,r,{\text{Fo}}} \right);$

2) согласно (15) к равенству, определяющему изображение ${{U}_{2}}(p,y,r,{\text{Fo}}),$ применить оператор ${{{\Phi }}^{{ - 1}}}\left[ \cdot \right]$ обращения двухмерного экспоненциального интегрального преобразования Фурье (14) и определить функционал ${{\theta }_{2}}(x,y,z,{\text{Fo}}).$

ЗАКЛЮЧЕНИЕ

1. Процесс формирования искомого температурного поля полностью определен двумя независимыми аддитивными составляющими, первая из которых представлена функционалом ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right),$ описывающим процесс формирования температурного поля объекта исследований вследствие отличия его начальной температуры от температуры внешней среды, а вторая – функционалом ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right),$ описывающим процесс формирования температурного поля объекта исследований вследствие воздействия внешнего теплового потока при равенстве температуры внешней среды нулевой начальной температуре объекта исследований.

2. Специфика структуры функционала ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)$ в пространстве изображений двухмерного экспоненциального интегрального преобразования Фурье (14), представленной равенством (17), явно указывает на проявление теоретически известного “эффекта сноса температурного поля в анизотропном материале” [22, 23], подтвержденного многочисленными вычислительными экспериментами и уже имеющего реальные приложения [7].

3. Аддитивную композицию (3) краевых условий второго и третьего родов (“нагрев тепловым потоком” и “нагрев средой” соответственно) можно представить как краевое условие третьего рода:

$ - {{\left. {\frac{{\partial \theta }}{{\partial y}}} \right|}_{{y = 0}}} = {\text{Bi}}{{\left. {\left[ {1 + \frac{{Q\left( {x,z,{\text{Fo}}} \right)}}{{{\text{Bi}}}}} \right] - \theta } \right|}_{{y = 0}}},$

из которого следует, что в рассматриваемой ситуации значимость “нагрева тепловым потоком” при фиксированной плотности его мощности убывает с ростом значения ${\text{Bi}}{\text{.}}$

4. При подготовке к проведению вычислительных экспериментов с использованием полученных результатов целесообразно применение теоремы о возможности одновременного приведения к каноническому виду двух квадратичных форм [20], что позволяет реализовать связь, существующую между двухмерным экспоненциальным интегральным преобразованием Фурье и двухмерным интегральным косинус – преобразованием [19, 22].

5. Так как решение смешанной задачи (18) получено с использованием сингулярного интегрального преобразования (24), (29), примененного по пространственному переменному $y \in \left[ {0, + \infty )} \right.,$ а краевое условие при $y = 0$ не является однородным, то при интерпретации результатов вычислительных экспериментов следует помнить о том, что равенство понимается в смысле евклидовой нормы в ${{L}^{2}}\left[ {0, + \infty )} \right..$

Список литературы

Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 448 с.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М.: Высшая школа, 2001. 550 с.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М.: URSS, 2012. 312 с.
Формалëв В.Ф. Теплопроводность анизотропных тел. Аналитические методы решения задач. М.: Физматлит, 2014. 312 с.
Формалëв В.Ф. Теплоперенос в анизотропных твердых телах. Численные методы, тепловые волны, обратные задачи. М.: Физматлит, 2015. 280 с.
Формалëв В.Ф., Колесник С.А. Математическое моделирование аэрогазодинамического нагрева затупленных анизотропных тел. М.: Изд-во МАИ, 2016. 160 с.
Аттетков А.В., Волков И.К. Температурное поле анизотропного полупространства, подвижная граница которого находится под воздействием внешнего теплового потока // Тепловые процессы в технике. 2015. Т. 7. № 2. С. 73–79.
Аттетков А.В., Волков И.К. Температурное поле анизотропного полупространства, подвижная граница которого содержит пленочное покрытие // Изв. РАН. Энергетика. 2015. № 3. С. 39–49.
Аттетков А.В., Волков И.К. Температурное поле анизотропного полупространства с подвижной границей при его нагреве внешней средой // Изв. РАН. Энергетика. 2016. № 6. С. 125–133.
Формалëв В.Ф., Колесник С.А., Кузнецова Е.Л. Нестационарный теплоперенос в анизотропном полупространстве в условиях теплообмена с окружающей средой, имеющей заданную температуру // Теплофизика высоких температур. 2016. Т. 54. № 6. С. 876–882.
Формалëв В.Ф., Колесник С.А., Кузнецова Е.Л., Селин И.А. Аналитическое исследование теплопереноса в теплозащитных композиционных материалах с анизотропией общего вида при произвольном тепловом потоке // Механика композиционных материалов и конструкций. 2017. Т. 23. № 2. С. 168–182.
Аттетков А.В., Волков И.К. Квазистационарное температурное поле анизотропной системы с подвижной границей, нагреваемой средой с осциллирующей температурой // Изв. РАН. Энергетика. 2017. № 5. С. 144–155.
Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. М.: Высшая школа, 1970. 712 с.
Пехович А.И., Жидких В.М. Расчет теплового режима твердых тел. Л.: Энергия, 1968. 304 с.
Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. М.: Изд-во МГТУ им. Н.Э. Баумана, 2015. 228 с.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. 424 с.
Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969. 344 с.
Снеддон И. Преобразования Фурье. М.: Изд-во иностр. лит., 1955. 668 с.
Беллман Р. Введение в теорию матриц. М.: Наука, 1969. 368 с.
Наймарк М.А. Линейные дифференциальные операторы. М.: Наука, 1969. 528 с.
Аттетков А.В., Волков И.К. Температурное поле анизотропной охлаждаемой пластины, находящейся под воздействием импульсно-периодического теплового потока с интенсивностью гауссовского типа // Изв. РАН. Энергетика. 2012. № 5. С. 71–79.
Аттетков А.В., Волков И.К. Температурное поле охлаждаемой изотропной пластины с анизотропным покрытием, находящейся под воздействием внешнего теплового потока // Тепловые процессы в технике. 2013. Т. 5. № 2. С. 50–58.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал