Известия РАН. Энергетика, 2019, № 4, стр. 51-57

Переходные процессы несут информацию о повреждении наблюдаемого энергообъекта; получение и применение такой информации составляет задачу релейной защиты [1]. Переходные процессы в длинных линиях отличаются своеобразием математического описания и физических представлений. Имеются два подхода – волновой и спектральный [2]. Волновой подход приводит к разностным уравнениям (уравнения Бержерона), а в более общем плане – к дифференциально-разностным [3–5]. Спектральный подход приводит к уравнениям длинной линии на спектральных компонентах и к цифровому спектральному анализу наблюдаемых величин [6, 7].

Наибольшую сложность представляет получение информации по результатам наблюдения кратковременного переходного процесса однофазного замыкания на землю в распределительной сети. Замыкание, как физическое явление, представляет собой диссипативный процесс. Модель замыкания – резистивный двухполюсник, в общем случае нелинейный с неопределенной характеристикой. Наблюдателю, не располагающему никакой иной информацией о случившемся повреждении контролируемой сети, надлежит определить место подключения к фидеру неизвестного резистивного элемента. В сети с изолированной нейтралью однофазное замыкание на землю сопровождается кратковременным интенсивным переходным процессом. Токи и напряжения, зафиксированные в это время, наряду с априорной информацией о первичных параметрах фидера, составляют информационную базу наблюдателя – локатора замыкания. Процедура локации связана с математическим оформлением физических предпосылок, т.е. в придании им формы конкретного критерия, отражающего свойства места замыкания. Заметим, что ранее удалось представить в такой форме критерий контроля во времени нелинейного элемента, столь же недоступного наблюдению, как и место замыкания, – ветви намагничивания трансформатора [8].

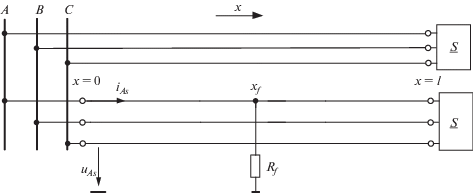
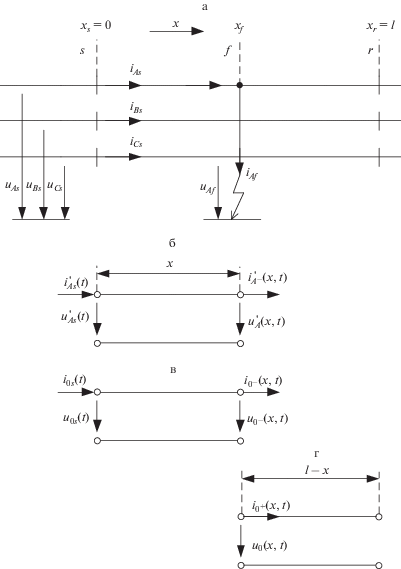
Граничные условия в месте замыкания. На рис. 1а иллюстрируется случай замыкания на землю фазы $A$ в месте с координатой ${{x}_{f}};$ ${{u}_{{Af}}},$ ${{i}_{{Af}}}$ – напряжение и ток замыкания. Кроме них показаны наблюдаемые напряжения и токи ${{u}_{{\nu f}}},$ ${{i}_{{\nu f}}},$ $\nu = A,$ $B,$ $C.$ Наблюдаемая сторона фидера обозначена символом $s,$ ненаблюдаемая – $r.$

В месте замыкания напряжение и ток связаны условием диссипативности

которое говорит о том, что мгновенная мощность замыкания не может быть отрицательной

Имеется еще одна интерпретация условия (1), отличающаяся высокой наглядностью. Образуем двумерный вольт-амперный вектор ${\mathbf{w}}$ с элементами $u,$ $i$

На плоскости $u,$ $i$ или в пространстве с координатами $u,$ $i,$ $t$ вектор ${\mathbf{w}}\left( t \right)$ описывает годограф. Вектор места замыкания ${{{\mathbf{w}}}_{{Af}}}\left( t \right) = {{\left[ {{{u}_{{Af}}}\left( t \right),{{i}_{{Af}}}\left( t \right)} \right]}^{{\text{T}}}}$ на плоскости $u,$ $i$ описывает кривую, которая в соответствии с условием (1) располагается в первом и третьем квадрантах, не заходя во второй и четвертый.

Еще одно граничное условие касается составляющих тока ${{i}_{{Af}}}$ – нулевой ${{i}_{{0f}}}$ и безнулевой $i_{{Af}}^{'} = {{i}_{{Af}}} - {{i}_{{0f}}}.$ В месте замыкания они пропорциональны

Алгоритмическая модель фидера. Любое место фидера с координатой $x$ интерпретируется наблюдателем как предполагаемое место повреждения. Алгоритмическая модель выстраивается для предположительно неповрежденного участка от места наблюдения ${{x}_{s}}$ до точки $x$ (рис. 1б, 1в) и выполняет преобразование величин $u_{{As}}^{'}\left( t \right),$ $i_{{As}}^{'}\left( t \right),$ ${{u}_{{0s}}}\left( t \right),$ ${{i}_{{0s}}}\left( t \right)$ места наблюдения в напряжения $u_{A}^{'}\left( {x,t} \right),$ ${{u}_{0}}\left( {x,t} \right)$ и токи $i_{{A - }}^{'}\left( {x,t} \right),$ ${{i}_{{0 - }}}\left( t \right).$ Знак в индексе носит тот же смысл, что и в обозначениях ${{i}_{{Af - }}},$ ${{i}_{{Af + }}}$ на рис. 1, где знаки отличают продольные токи от поперечного тока ${{i}_{f}}.$

Фидер как длинная линия описывается разностными уравнениями, вид которых зависит от способа учета потерь [3]. Если учесть потери сосредоточенными сопротивлениями по концам участка линии длиной $x$ (рис. 2), то участок получит следующее описание

где ${{a}_{x}} = {{R}_{{\text{В}}}} + {{{{R}^{0}}x} \mathord{\left/ {\vphantom {{{{R}^{0}}x} 2}} \right. \kern-0em} 2},$ ${{b}_{x}} = {{R}_{{\text{В}}}}$ – ${{{{R}^{0}}x} \mathord{\left/ {\vphantom {{{{R}^{0}}x} 2}} \right. \kern-0em} 2};$ ${{R}_{{\text{В}}}} = \sqrt {{{{{L}^{0}}} \mathord{\left/ {\vphantom {{{{L}^{0}}} {{{C}^{0}}}}} \right. \kern-0em} {{{C}^{0}}}}} $ – волновое сопротивление линии, ${{\tau }_{x}} = x\sqrt {{{L}^{0}}{{C}^{0}}} $ – время пробега волны вдоль отрезка линии, ${{R}^{0}},$ ${{L}^{0}},$ ${{C}^{0}}$ – первичные (удельные) параметры линии.

Из основных уравнений (4) следует описание алгоритмической модели [9]

где ${{R}_{{{\text{В1}}}}}$ = $\sqrt {{{L_{1}^{0}} \mathord{\left/ {\vphantom {{L_{1}^{0}} {C_{1}^{0}}}} \right. \kern-0em} {C_{1}^{0}}}} ,$ ${{R}_{{{\text{В0}}}}}$ = $\sqrt {{{L_{0}^{0}} \mathord{\left/ {\vphantom {{L_{0}^{0}} {C_{0}^{0}}}} \right. \kern-0em} {C_{0}^{0}}}} $ и ${{\tau }_{{1x}}}$ = $x\sqrt {L_{1}^{0}C_{1}^{0}} ,$ ${{\tau }_{{0x}}}$ = $x\sqrt {L_{0}^{0}C_{0}^{0}} $ – волновые сопротивления и времена пробега волны вдоль участка $x$ в каналах прямой и нулевой последовательности; ${{a}_{{1x}}} = {{R}_{{{\text{В1}}}}}$ + $R_{1}^{0}{x \mathord{\left/ {\vphantom {x 2}} \right. \kern-0em} 2},$ ${{b}_{{1x}}} = {{R}_{{{\text{В1}}}}}$ – $R_{1}^{0}{x \mathord{\left/ {\vphantom {x 2}} \right. \kern-0em} 2}{{b}_{{1\,x}}}$ = ${{R}_{{В1}}} - {{R_{1}^{0}x} \mathord{\left/ {\vphantom {{R_{1}^{0}x} 2}} \right. \kern-0em} 2},$ ${{a}_{{0x}}} = {{R}_{{{\text{В0}}}}}$ + ${{R_{0}^{0}x} \mathord{\left/ {\vphantom {{R_{0}^{0}x} 2}} \right. \kern-0em} 2},$ ${{b}_{{0x}}} = {{R}_{{{\text{В0}}}}}$ – ${{R_{0}^{0}x} \mathord{\left/ {\vphantom {{R_{0}^{0}x} 2}} \right. \kern-0em} 2};$ $R_{1}^{0},$ $L_{1}^{0},$ $C_{1}^{0}$ и $R_{0}^{0},$ $L_{0}^{0},$ $C_{0}^{0}$ – первичные параметры фидера прямой и нулевой последовательности.

Суммируясь, выходные сигналы каналов по рис. 1б, 1в определяют напряжение и ток в месте предполагаемого повреждения

Что же касается тока предполагаемого места повреждения ${{i}_{A}}\left( {x,t} \right),$ то возможны два варианта его оценки. В первом случае принимается условие

а во втором к произвольному месту $x$ применяется граничное условие (3) что, правда, потребует отдельного определения тока ${{i}_{{0 + }}}\left( {x,t} \right)$ как реакции на напряжение ${{u}_{0}}\left( {x,t} \right).$

Информационные свойства годографа вольт-амперного вектора. Наряду с критерием (1) инструментом распознавания становится двумерный вектор – функция времени и координаты

Годограф, описываемый им во времени на плоскости $u,$ $i$ для фиксированного места $x,$ в общем случае заходит во все квадранты. Если ${{Q}_{{\text{н}}}}$ и ${{Q}_{{\text{ч}}}}$ – обозначения нечетных (первого и третьего) и четных (второго и четвертого) квадрантов, то данное обстоятельство отражается условием

Критерий (1) говорит о том, что в месте замыкания условие (12) обходится без четных квадрантов

Структура алгоритмической модели, формирующей вектор ${{{\mathbf{w}}}_{A}}\left( {x,t} \right),$ составленная для неповрежденного фидера (рис. 1б, 1в, 1г), неизменна при всех значениях $x = 0...l.$ Поврежденному фидеру она адекватна только до неизвестного места ${{x}_{f}},$ т.е. при $x = 0...{{x}_{{f - }}}.$ За этим местом $\left( {x = {{x}_{{f + }}}...l} \right)$ наступает полная неадекватность. В то же время, оценка тока предполагаемого места повреждения согласно допущению (11) несет в себе методическую погрешность. Естественно предположить, что такое положение вещей не может не отразиться на свойствах годографа, описываемого вектором ${{{\mathbf{w}}}_{A}}\left( {x,t} \right),$ однако должны сохраняться принципиальные различия между тем, как ведет себя годограф при $x < {{x}_{f}}$ и при $x > {{x}_{f}}.$ Прежде всего имеется в виду очередность смены одного квадранта другим, иначе говоря, движение вектора по часовой стрелке или против, а кроме того соотношение длительностей пребывания вектора в четных и нечетных квадрантах.

Рассмотрим в качестве примера замыкание в двухфидерной сети 35 кВ (рис. 3). Фидеры длиной $l = 20$ км идентичны. Первичные параметры прямой последовательности $R_{1}^{0} = 0.14$ Ом/км, $C_{1}^{0} = 380$ нФ/км, $L_{1}^{0} = 0.194$ мГн/км, нулевой последовательности $R_{0}^{0} = 0.67$ Ом/км, $C_{0}^{0} = 400$ нФ/км, $L_{0}^{0} = 4.5$ мГн/км. Комплексная мощность нагрузки каждого фидера $\underline S = 300$ кВт + $j186$ кВАр. Имитировалось замыкание фазы $A$ на землю в месте ${{x}_{f}} = 10$ км через переходное сопротивление ${{R}_{f}} = 0...25$ Ом.

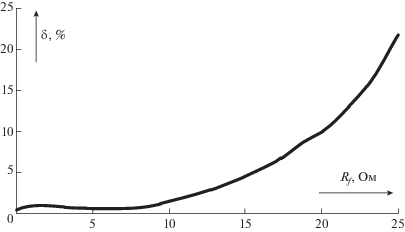
На рис. 4 приведены годографы ${{{\mathbf{w}}}_{A}}\left( {x,t} \right)$ при трех значениях координаты: $x < {{x}_{f}},$ $x = {{x}_{f}}$ и $x > {{x}_{f}},$ если применяется простое условие (11), а на рис. 5 – зависимость погрешности определения значения координаты ${{x}_{f}}$ от величины переходного сопротивления $\delta = \left( {{{{{{\hat {x}}}_{f}}} \mathord{\left/ {\vphantom {{{{{\hat {x}}}_{f}}} {{{x}_{f}}}}} \right. \kern-0em} {{{x}_{f}}}}} \right) - 1,$ где ${{\hat {x}}_{f}}$ – значение $x,$ при переходе через которое изменяется направление вращения вектора ${{{\mathbf{w}}}_{A}}\left( {x,t} \right).$ Наблюдаемые величины подвергались дискретизации с частотой 50 кГц.

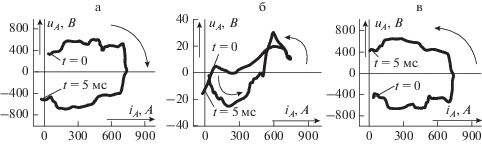
Алгоритм автоматического определения направления движения годографа ${\mathbf{w}}\left( t \right)$ основывается на закономерностях, присущих определенным типам движения. Если движение происходит по часовой стрелке (рис. 4а), то в нем стадия увеличения тока сменяется стадией понижения напряжения, за которой следует стадия снижения тока, а затем стадия повышения напряжения. На рисунке 4а эту четвертую стадию цикла не удается увидеть, она оказалась за пределами окна наблюдения. Если же движение совершается против часовой стрелки (рис. 4в), то на смену стадии увеличения тока приходит стадия повышения напряжения, а на смену стадии снижения тока – стадия понижения напряжения, не попавшая в окно наблюдения на рис. 4в.

Закономерности чередования интервалов совпадения и несовпадения знаков напряжения и тока на выходе алгоритмической модели фидера до и после места замыкания ранее были описаны в [10]. Вольт-амперный вектор реализует критерий распознавания места замыкания в двумерном виде и в этом смысле уравнивает локацию в базисе мгновенных величин с локацией в комплексном базисе синусоидального режима. Можно также заметить, что динамика вольт-амперного вектора интерпретирует метод локации более полно и в более общем виде, чем предыдущие двумерные представления критерия локации линии в базисе мгновенных значений [10, 11]. В информационном аспекте усматривается аналогия между годографом этого вектора и значением комплексной мощности на выходе алгоритмической модели в синусоидальном режиме.