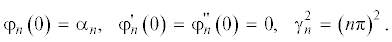Известия РАН. Энергетика, 2019, № 4, стр. 67-74

Новые модельные представления нестационарного теплообмена

Э. М. Карташов^1, *, И. В. Кудинов², В. А. Кудинов²

¹ Московский технологический университет (МИТХТ)
Москва, Россия

² Самарский государственный технический университет
Самара, Россия

^* E-mail: kartashov@mitht.ru

Поступила в редакцию 28.05.2019
После доработки 08.08.2019
Принята к публикации 12.08.2019

DOI: 10.1134/S0002331019040058

Полный текст (PDF)

Аннотация

Рассмотрена серия новых модельных представлений нестационарного теплообмена на основе соотношений Онзагера. Принимая последовательно различные представления термодинамических движущих сил и постоянных феноменологических коэффициентов, соотношения Онзагера дают все более обобщающие законы теплопереноса на уровне элементарных актов и далее с использованием основного уравнения энергии указанные законы приводят к основным дифференциальным уравнениям локально-неравновесного теплопереноса, лежащим в основе соответствующих краевых задач нестационарной теплопроводности. Рассмотрены численные эксперименты по описанию тепловой реакции бесконечной пластины при температурном нагреве в рамках новых модельных представлений нестационарного теплообмена. Описаны особенности полученных аналитических решений.

Ключевые слова: соотношение Онзагера, основные феноменологические законы теплопереноса, дифференциальные уравнения теплопроводности, краевые задачи, аналитические решения

ВВЕДЕНИЕ

Теория переноса в системах $\bar {\Omega } = \left\{ {M\left( {x,y,z} \right) \in \bar {D} = D + S,~t \geqslant 0} \right\},$ не находящихся в состоянии термодинамического равновесия, объединяет такие разнообразные явления, как теплопроводность, диффузию, электропроводность, поглощение звуковых волн и другие. Как показал в [1] А.В. Лыков, для этих явлений термодинамика необратимых процессов основана на обобщенной системе уравнений Онзагера для потоков субстанций ${{\vec {J}}_{i}}\left( {M,t} \right)$ (теплоты, массы и т.д.), имеющей для изотропной среды вид:

(1)

${{\vec {J}}_{i}}\left( {M,t} \right) = L_{i}^{{\left( r \right)}}\frac{{\partial {{{\vec {J}}}_{i}}\left( {M,t} \right)}}{{\partial t}} + \sum\limits_{k = 1}^N {\left[ {{{L}_{{ik}}}{{{\vec {X}}}_{k}}\left( {M,t} \right) + L_{{ik}}^{'}\frac{{\partial {{{\vec {X}}}_{k}}\left( {M,t} \right)}}{{\partial t}}} \right]} ,$

где ${{\vec {X}}_{k}}\left( {M,t} \right)$ – термодинамические движущие силы (градиент температуры, концентрация и т.д.); $L_{i}^{{\left( r \right)}},$ ${{L}_{{ik}}},$ $L_{{ik}}^{'}$ – постоянные феноменологические коэффициенты переноса $\left( {{{L}_{{ik}}} = {{L}_{{ki}}}} \right).$ Соотношение (1) имеет исключительно важное значение для развития модельных представлений в теории нестационарного тепло- и массопереноса. При надлежащем выборе величин в (1) появляется возможность последовательно переходить от более простых к более сложным математическим моделям переноса и развивать математическую теорию соответствующих краевых задач по широкому спектру исследований. Если в (1) пренебречь производной по времени от движущей силы и положить ${{\vec {J}}_{i}}\left( {M,t} \right)$ = $\vec {q}\left( {M,t} \right)$ (вектор плотности теплового потока), ${{\vec {X}}_{k}}\left( {M,t} \right)$ = ${\text{grad}}T\left( {M,t} \right)$ (градиент температуры в области $\bar {\Omega }$), ${{L}_{{ik}}} = - \lambda $ (теплопроводность материала), $L_{i}^{{\left( r \right)}} = 0,$ $L_{{ik}}^{'} = 0,$ то (1) приведет к линейному градиентному соотношению Фурье $\vec {q}\left( {M,t} \right)$ = = $ - \lambda {\text{grad}}T\left( {M,t} \right),$ лежащему в основе наиболее распространенной на практике феноменологической модели теплопроводности в недеформируемых твердых телах. Вместе с уравнением энергии для изотропных твердых тел $с\rho \frac{{\partial T\left( {M,t} \right)}}{{\partial t}}$ = $ - {\text{div}}\vec {q}\left( {M,t} \right) + F\left( {M,t} \right)$ закон Фурье приводит уравнению нестационарной теплопроводности параболического типа:

(2)

$\frac{{\partial T\left( {M,t} \right)}}{{\partial t}} = a\Delta T\left( {M,t} \right) + \frac{{F\left( {M,t} \right)}}{{c\rho }},\,\,\,\,\left( {M,t} \right) \in \Omega .$

Математическая теория краевых задач для уравнения (2) разработана в [2–4]. Полагая в (1) ${{\vec {J}}_{i}}\left( {M,t} \right)$ = $\vec {q}\left( {M,t} \right),$ $L_{i}^{{\left( r \right)}} = - {{\tau }_{r}},$ $~{{L}_{{ik}}} = - \lambda ,$ $~L_{{ik}}^{'} = 0,$ ${{\vec {X}}_{k}}\left( {M,t} \right)$ = ${\text{grad}}T\left( {M,t} \right),$ приходим к обобщенному закону Максвелла–Каттанео–Лыкова:

(3)

$\vec {q}\left( {M,t} \right) = - \lambda {\text{grad}}T\left( {M,t} \right) - {{\tau }_{r}}\frac{{\partial{ \vec {q}}\left( {M,t} \right)}}{{\partial t}}$

учитывающего конечную скорость распространения теплоты. Коэффициент ${{\tau }_{r}}$ в (3) – время релаксации теплового потока, характеризующее свойство тепловой инерции тела (время задержки передачи кванта энергии на микроуровне от элемента объема тела к соседним элементам); величина ${{\tau }_{r}}~$связана со скоростью распространения теплоты ${{\upsilon }_{\tau }}$ соотношением ${{\upsilon }_{{\tau }}} = \sqrt {{a \mathord{\left/ {\vphantom {a {{{\tau }_{r}}}}} \right. \kern-0em} {{{\tau }_{r}}}}} .$ Уравнение энергии и соотношение (3) приводят к уравнению нестационарного теплопереноса гиперболического типа:

(4)

$\frac{{\partial T\left( {M,t} \right)}}{{\partial t}} = a\Delta T\left( {M,t} \right) - {{\tau }_{r}}\frac{{{{\partial }^{2}}T\left( {M,t} \right)}}{{\partial {{t}^{2}}}} + \frac{{{{\tau }_{r}}}}{{с\rho }}\left[ {\frac{{\partial F\left( {M,t} \right)}}{{\partial t}} + \frac{1}{{{{\tau }_{r}}}}F\left( {M,t} \right)} \right],\,\,\,\,\left( {M,t} \right) \in \Omega $

применяемому для изучения высокоинтенсивных нестационарных процессов. Математическая теория краевых задач для уравнения (4) разработана в [5, 6]. Полагая далее в (1) ${{\vec {J}}_{i}}\left( {M,t} \right)$ = $\vec {q}\left( {M,t} \right),$ $L_{i}^{{\left( r \right)}}$ = $ - {{\tau }_{r}},$ $~{{L}_{{ik}}} = - \lambda ,$ $~L_{{ik}}^{'}$ = $ - \lambda {{\tau }_{{\text{Т}}}},$ ${{\vec {X}}_{k}}\left( {M,t} \right)$ = ${\text{grad}}T\left( {M,t} \right),$ приходим к соотношению

(5)

$\vec {q}\left( {M,t} \right) = - \lambda {\text{grad}}T\left( {M,t} \right) - {{\tau }_{r}}\frac{{\partial{ \vec {q}}\left( {M,t} \right)}}{{\partial t}} - \lambda {{\tau }_{{\text{Т}}}}{\text{grad}}\frac{{\partial T\left( {M,t} \right)}}{{\partial t}}~,$

обобщающему закон (4). Соотношение (5) в литературе получило название уравнения двухфазного запаздывания [7] (учитываются как релаксация теплового потока через коэффициент ${{\tau }_{r}},$ так и градиента температуры через коэффициент ${{\tau }_{{\text{Т}}}}).$ Соотношение (5) и уравнение теплового баланса приводят к следующему уравнению нестационарного теплопереноса гиперболического типа

(6)

$\begin{gathered} \frac{{\partial T\left( {M,t} \right)}}{{\partial t}} = a\Delta \left[ {T\left( {M,t} \right) + {{\tau }_{{\text{Т}}}}\frac{{\partial T\left( {M,t} \right)}}{{\partial t}}} \right] - \\ - \,\,{{\tau }_{r}}\frac{{{{\partial }^{2}}T\left( {M,t} \right)}}{{\partial {{t}^{2}}}} + \frac{{{{\tau }_{r}}}}{{с\rho }}\left[ {\frac{{\partial F\left( {M,t} \right)}}{{\partial t}} + \frac{1}{{{{\tau }_{r}}}}F\left( {M,t} \right)} \right],\,\,\,\,\left( {M,t} \right) \in \Omega \\ \end{gathered} $

применяемому для изучения переходного термического процесса в твердом теле при его резком тепловом нагреве и охлаждении [7].

Математическая теория краевых задач для уравнения (6) разработана в [8]. Полагая в (1) $L_{i}^{{\left( r \right)}} = - {{\tau }_{r}},$ $~{{L}_{{ik}}} = - \lambda ,$ $~L_{{ik}}^{'}$ = $ - \lambda {{\tau }_{{\text{Т}}}},$

${{\vec {J}}_{i}}\left( {M,t} \right) = \frac{1}{{{{\tau }_{r}}}}\int\limits_0^t {\left[ {\vec {q}\left( {M,\tau } \right) + {{\tau }_{r}}\frac{{\partial{ \vec {q}}\left( {M,\tau } \right)}}{{\partial \tau }} + {{\tau }_{r}}^{2}\frac{{{{\partial }^{2}}\vec {q}\left( {M,\tau } \right)}}{{\partial {{\tau }^{2}}}}} \right]\exp \left( { - \frac{{t - \tau }}{{{{\tau }_{r}}}}} \right)d\tau } ,$

${{\vec {X}}_{k}}\left( {M,t} \right) = \frac{1}{{{{\tau }_{{\text{T}}}}}}\int\limits_0^t {{\text{grad}}\left[ {T\left( {M,\tau } \right) + {{\tau }_{{\text{T}}}}\frac{{\partial T\left( {M,\tau } \right)}}{{\partial \tau }} + \tau _{\tau }^{2}\frac{{{{\partial }^{2}}T\left( {M,\tau } \right)}}{{\partial {{\tau }^{2}}}}} \right]\exp \left( { - \frac{{t - \tau }}{{{{\tau }_{T}}}}} \right)d\tau } ,$

приходим к следующему обобщенному закону для теплового потока

(7)

$\begin{gathered} \vec {q}\left( {M,t} \right) = - {{\tau }_{r}}\frac{{\partial{ \vec {q}}\left( {M,t} \right)}}{{\partial t}} - \tau _{r}^{2}\frac{{{{\partial }^{2}}\vec {q}\left( {M,t} \right)}}{{\partial {{t}^{2}}}} - \lambda {\text{grad}}T\left( {M,t} \right) - \lambda {{\tau }_{{\text{Т}}}}{\text{grad}}\frac{{\partial T\left( {M,t} \right)}}{{\partial t}} - \\ - \,\,\lambda \tau _{{\text{Т}}}^{2}{\text{grad}}\frac{{{{\partial }^{2}}T\left( {M,t} \right)}}{{\partial {{t}^{2}}}}. \\ \end{gathered} $

В соотношении (7) учитываются релаксация и теплового потока, и градиента температуры, то есть учитывается пространственно-временная нелокальность [9]. Из (7) следует, что тепловой поток и градиент температуры не могут изменяться мгновенно, а лишь с некоторым запаздыванием (ускорением) во времени, оцениваемым коэффициентами релаксации ${{\tau }_{r}}$ и ${{\tau }_{{\text{Т}}}}.$ Следовательно, соотношение (7) представляет собой выражение полного закона сохранения, в котором пространственно-временные изменения теплового потока и температуры взаимно согласованы. Это условие адекватного протекания реальных физических процессов. Соотношение (7) перепишем в виде:

(8)

$\begin{gathered} \vec {q}\left( {M,t} \right) + {{\tau }_{r}}\frac{{\partial{ \vec {q}}\left( {M,t} \right)}}{{\partial t}} + \tau _{r}^{2}\frac{{{{\partial }^{2}}\vec {q}\left( {M,t} \right)}}{{\partial {{t}^{2}}}} = \\ = - \lambda {\text{grad}}\left[ {T\left( {M,t} \right) + {{\tau }_{{\text{Т}}}}\frac{{\partial T\left( {M,t} \right)}}{{\partial t}} + \tau _{{\text{Т}}}^{2}\frac{{{{\partial }^{2}}T\left( {M,t} \right)}}{{\partial {{t}^{2}}}}} \right]. \\ \end{gathered} $

Выражение (8) можно рассматривать как разложение левой и правой частей линейного градиентного соотношения Фурье $\vec {q}\left( {M,t} \right)$ = $ - \lambda {\text{grad}}T\left( {M,t} \right)$ в ряд по временной переменной с соответствующими коэффициентами релаксации [9]. В зависимости от принятого числа членов в разложении (8), которое порождено соотношением Онзагера (1), мы будем получать различного вида уравнения, как основу соответствующих краевых задач локально-неравновесного теплообмена. Первые слагаемые разложения в (8) приводят к локальному классическому уравнению теплопроводности параболического типа (2), поскольку оно выводится без учета временной и пространственной локальной неравновесности. Если ограничиться в (8) первыми двумя слагаемыми слева и первым справа, то придем к формуле для теплового потока Максвелла–Каттанео–Лыкова (3) и далее к уравнению гиперболического типа (4), которое является нелокальным частично так как в нем учитывается лишь временная неравновесность релаксацией теплового потока. Если в (8) ограничиться первыми двумя слагаемыми слева и справа, то придем к уравнению двухфазного запаздывания и далее к уравнению гиперболического типа (4). Последнее учитывает релаксацию как теплового потока, так и градиента температуры, то есть учитывается как временная, так и пространственная нелокальность. Это уравнение описывает более полно локально-неравновесные процессы теплопереноса. Наиболее полное выражение (7) приводит к уравнению

(9)

$\begin{gathered} \frac{{\partial T\left( {M,t} \right)}}{{\partial t}} + {{\tau }_{r}}\frac{{{{\partial }^{2}}T\left( {M,t} \right)}}{{\partial {{t}^{2}}}} + \tau _{r}^{2}\frac{{{{\partial }^{3}}T\left( {M,t} \right)}}{{\partial {{t}^{3}}}} = a\Delta \left[ {T\left( {M,t} \right) + {{\tau }_{{\text{Т}}}}\frac{{\partial T\left( {M,t} \right)}}{{\partial t}} + } \right. \\ + \,\,\tau _{{\text{Т}}}^{2}\frac{{{{\partial }^{2}}T\left( {M,t} \right)}}{{\partial {{t}^{2}}}} + \frac{1}{{с\rho }}\left[ {F\left( {M,t} \right) + {{\tau }_{r}}\frac{{\partial F\left( {M,t} \right)}}{{\partial t}} + \tau _{r}^{2}\frac{{{{\partial }^{2}}F\left( {M,t} \right)}}{{\partial {{t}^{2}}}}} \right],\,\,\,\,~\left( {M,t} \right) \in \Omega \\ \end{gathered} $

лежащему в основе математической модели локально-неравновесного теплопереноса с учетом пространственно-временной нелокальности [9].

Следует подчеркнуть, что феноменологические законы теплопереноса (3), (5), (7) на уровне элементарных актов и соответствующие им дифференциальные уравнения (4), (6), (9) вошли в теплофизику лишь в последние годы. Что касается математической теории постановки краевых задач для указанных уравнений и нахождении аналитических решений такого рода задач, то это направление теплофизики (и одновременно математической физики) находятся в самом начале своего развития.

ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

Исследуем тепловую реакцию бесконечной пластины в условияx температурного нагрева на основе краевой задачи для обобщенного уравнения (9) в области $\bar {\Omega } = \left( {x \in \left[ {0,l} \right]~t \geqslant 0} \right)$ при F = 0; T₀ – начальная температура, Т_с – температура плоскостей симметрии. В безразмерных переменных

(10)

$\xi = \frac{x}{l},\,\,\,\,~{{F}_{0}} = \frac{{at}}{{{{l}^{2}}}},\,\,\,\,{{F}_{0}}_{1} = \frac{{a{{\tau }_{r}}}}{{{{l}^{2}}}},\,\,\,\,F_{{{{0}_{{_{1}}}}}}^{*} = \frac{{a{{\tau }_{T}}}}{{{{l}^{2}}}},\,\,\,\,\Theta \left( {\xi ,{{F}_{0}}} \right) = \frac{{T\left( {x,t} \right) - {{T}_{c}}}}{{{{T}_{0}} - {{T}_{c}}}}.$

Задача принимает вид

(11)

$\frac{{\partial \Theta }}{{\partial {{F}_{0}}}} + ~{{F}_{{{{0}_{1}}}}}\frac{{{{\partial }^{2}}\Theta }}{{\partial F_{0}^{2}}} + ~F_{{{{0}_{1}}}}^{2}\frac{{{{\partial }^{3}}\Theta }}{{\partial F_{0}^{3}}} = \frac{{{{\partial }^{2}}\Theta }}{{\partial {{\xi }^{2}}}} + ~F_{{{{0}_{1}}}}^{*}\frac{{{{\partial }^{3}}\Theta }}{{\partial {{\xi }^{2}}\partial {{F}_{0}}}} + ~F_{{{{0}_{1}}}}^{{*2}}\frac{{{{\partial }^{4}}\Theta }}{{\partial {{\xi }^{2}}\partial {{F}_{0}}^{2}}},\,\,\,\,0 < \xi < {\text{1}},\,\,\,\,{{F}_{0}} > 0,$

(12)

$\Theta \left( {\xi ,0} \right) = 1,\,\,\,\,~\frac{{\partial \Theta \left( {\xi ,0} \right)}}{{\partial {{F}_{0}}}} = \frac{{{{\partial }^{2}}\Theta \left( {\left( {\xi ,0} \right),0} \right)}}{{\partial F_{0}^{2}}} = 0,\,\,\,\,~0 \leqslant \xi \leqslant 1,$

(13)

$\Theta \left( {0,{{F}_{0}}} \right) = \Theta \left( {1,{{F}_{0}}} \right) = 0,\,\,\,\,{{F}_{0}} > 0.$

Аналитическое решение $\Theta \left( {\xi ,{{F}_{0}}} \right)$ запишем в виде

(14)

$\Theta \left( {\xi ,{{F}_{0}}} \right) = \sum\limits_{n = 1}^\infty {{{\varphi }_{n}}({{F}_{0}})\sin n\pi \xi } .$

Из (11)–(14) находим:

(15)

${{\varphi }_{n}}\left( 0 \right) = \frac{{2\left[ {1 - {{{\left( { - 1} \right)}}^{n}}} \right]}}{{n\pi }} = {{\alpha }_{n}},$

(16)

$~F_{{{{0}_{1}}}}^{2}\frac{{{{d}^{3}}{{\varphi }_{n}}}}{{dF_{0}^{3}}} + \left( {~{{F}_{0}}_{1} + \gamma _{n}^{2}~F_{{{{0}_{1}}}}^{{*2}}} \right)\frac{{{{d}^{2}}{{\varphi }_{n}}}}{{dF_{0}^{2}}} + \left( {1 + ~F_{{{{0}_{1}}}}^{*}\gamma _{n}^{2}} \right)\frac{{d{{\varphi }_{n}}}}{{d{{F}_{0}}}} + \gamma _{n}^{2}{{\varphi }_{n}} = 0,\,\,\,\,{{F}_{0}} > 0,$

(17)

В пространстве изображений по Лапласу $\overline {{{\varphi }_{n}}} \left( p \right)$ = $\int_0^\infty {{\text{exp}}\left( { - p{{F}_{0}}} \right){{\varphi }_{n}}\left( {{{F}_{0}}} \right)d{{F}_{0}}} $ решение задачи Коши (16)–(17) запишем в виде:

(18)

$\frac{{\overline {{{\varphi }_{n}}} \left( p \right)}}{{{{\alpha }_{n}}}} = \frac{{{{p}^{2}} + {{\gamma }_{{1n}}}p + {{\gamma }_{{2n}}}}}{{{{p}^{3}} + {{\gamma }_{{1n}}}{{p}^{2}} + {{\gamma }_{{2n}}}p + {{\gamma }_{{3n}}}}}~,$

где введены обозначения

(19)

${{\gamma }_{{1n}}} = \frac{{~{{F}_{{{{0}_{1}}}}} + \gamma _{n}^{2}~F_{{{{0}_{1}}}}^{{*2}}}}{{~F_{{{{0}_{1}}}}^{2}}},\,\,\,\,{{\gamma }_{{2n}}} = \frac{{1 + ~F_{{{{0}_{1}}}}^{*}\gamma _{n}^{2}}}{{~F_{{{{0}_{1}}}}^{2}}},\,\,\,\,{{\gamma }_{{3n}}} = \frac{{\gamma _{n}^{2}}}{{~F_{{{{0}_{1}}}}^{2}}}~.$

Нахождение оригинала для (18) достаточно длительная вычислительная процедура, что предполагается проделать в последующей публикации. В настоящем численном эксперименте рассматривается случай $~{{F}_{{{{0}_{1}}}}} = F_{{{{0}_{1}}}}^{*}.$ Находим из (18)–(19):

(20)

$\frac{{\overline {{{\varphi }_{n}}} \left( p \right)}}{{{{\alpha }_{n}}}} = \frac{{~{{F}_{{{{0}_{1}}}}}\left( {~{{F}_{{{{0}_{1}}}}}p + 1} \right)}}{{~F_{{{{0}_{1}}}}^{2}{{p}^{2}} + {{F}_{{{{0}_{1}}}}}p + 1}} + \frac{1}{{\left( {p + \gamma _{n}^{2}} \right)\left( {~F_{{{{0}_{1}}}}^{2}{{p}^{2}} + {{F}_{{{{0}_{1}}}}}p + 1} \right)}}.$

Находим оригиналы (20) и записываем искомое решение в виде (14):

(21)

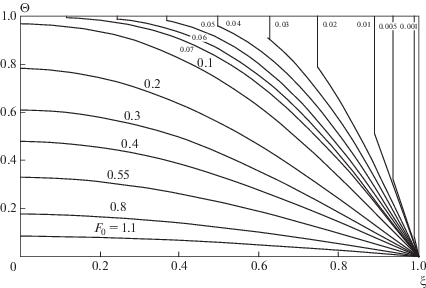
$\begin{gathered} \Theta \left( {\xi ,{{F}_{0}}} \right) = \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{{\left[ {1 - {{{\left( { - 1} \right)}}^{n}}} \right]}}{n}} \sin n\pi z~\left\{ {\frac{2}{{\sqrt 3 }}\sin \left( {\frac{{\sqrt 3 ~{{F}_{0}}}}{{2~{{F}_{{{{0}_{1}}}}}}} + \frac{\pi }{3}} \right){\text{exp}}\left( { - \frac{{~{{F}_{0}}}}{{2~{{F}_{{{{0}_{1}}}}}}}} \right) + } \right. \\ + \left. {\,\,\frac{4}{{{{{\left[ {1 - 2{{{\left( {n\pi } \right)}}^{2}}~{{F}_{{{{0}_{1}}}}}} \right]}}^{2}} + 3}}\left[ {1 - \cos \left( {\frac{{\sqrt 3 ~{{F}_{0}}}}{{2~{{F}_{{{{0}_{1}}}}}}}} \right){\text{exp}}\left( { - \frac{{~{{F}_{0}}}}{{2~{{F}_{{{{0}_{1}}}}}}}} \right) + \frac{1}{{\sqrt 3 }}\sin \left( {\frac{{\sqrt 3 ~{{F}_{0}}}}{{2~{{F}_{{{{0}_{1}}}}}}}} \right){\text{exp}}\left( { - \frac{{~{{F}_{0}}}}{{2~{{F}_{{{{0}_{1}}}}}}}} \right)} \right]} \right\}. \\ \end{gathered} $

На рис. 1 приведены изохромы области 0 < ξ < 1 (температурные кривые по ξ при фиксированном F₀), рассчитанные по решению (21) (рис. 1, 2 ). Из данных рис. 1 следует, что при малом значении $~{{F}_{{{{0}_{1}}}}}$ = 10^–3 и F₀ ≥ 10^–4 полученные кривые совпадают с аналогичными для классической тепловой задачи на основе уравнения Фурье (2) (при F = 0) [2]. В [9] отмечены особенности аналитического решения задачи (11)–(13) для более малых значений $~{{F}_{{{{0}_{1}}}}}$ и $~{{F}_{0}},$ то есть для $~{{F}_{{{{0}_{1}}}}}$ = 10^–10 и F₀ < 10^–6 (что представляет интерес для исследования высокоинтенсивных процессов в диапазоне времен микросекундной длительности). Описаны скачки температуры в окрестности граничных точек (рис. 2) области и установлено, что совпадения кривых с кривыми для параболического уравнения не наблюдается. Наличие указанных скачков температуры на временном участке, близком к начальному, свидетельствует о том, что ввиду теплоинерционности среды температурный нагрев границы не может быть принят мгновенно: плоскости симметрии пластины $x \in \left[ {0,l} \right]$ принимают температуру Т_с лишь за некоторый конечный отрезок времени t₀, что означает, что более физично было бы условие

$T\left( {0,t} \right) = T\left( {l,t} \right) = \frac{{{{T}_{c}} - {{T}_{0}}}}{{{{t}_{0}}}}\left[ {t - \eta \left( {t - {{t}_{0}}} \right)\left( {t - {{t}_{0}}} \right)} \right] + {{T}_{0}},$

где η(z) – единичная функция Хевисайда.

Рис. 1.

Распределение температуры в пластине: $~{{F}_{{{{0}_{1}}}}}$ = 10^–3, n = 10⁴ (n – число членов ряда в (21)).

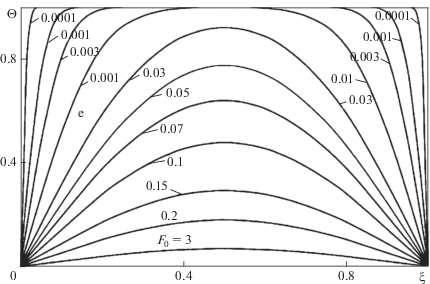
Рис. 2.

Распределение температуры в пластине: $~{{F}_{{{{0}_{1}}}}}$ = 10^–6, n = 10⁵ (n – число членов ряда в (21)).

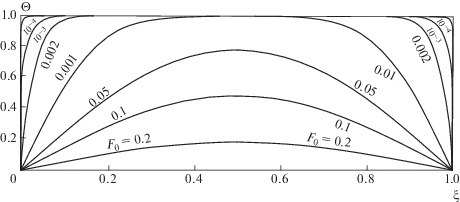
Сравним аналитические решения первой краевой задачи для гиперболических уравнений (9) и(6) (при F = 0). В последнем случае имеем в безразмерных переменных (10) задачу:

(22)

$\frac{{\partial \Theta \left( {\xi ,{{F}_{0}}} \right)}}{{\partial {{F}_{0}}}} + ~{{F}_{{{{0}_{1}}}}}\frac{{{{\partial }^{2}}\Theta \left( {\xi ,{{F}_{0}}} \right)}}{{\partial F_{0}^{2}}} = \frac{{{{\partial }^{2}}\Theta \left( {\xi ,{{F}_{0}}} \right)}}{{\partial {{\xi }^{2}}}},\,\,\,\,0 < \xi < {\text{1}},\,\,\,\,{{F}_{0}} > 0,$

(23)

$\Theta \left( {\xi ,0} \right) = 1,\,\,\,\,~\frac{{\partial \Theta \left( {\xi ,0} \right)}}{{\partial {{F}_{0}}}} = 0,\,\,\,\,0 \leqslant \xi \leqslant 1,$

(24)

$\Theta \left( {0,{{F}_{0}}} \right) = \Theta \left( {1,{{F}_{0}}} \right) = 0,\,\,\,\,{{F}_{0}} > 0,$

Решение $\Theta \left( {\xi ,{{F}_{0}}} \right)$ находится по развитой методике (14)–(20) и записывается в виде:

при $4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}} < 1$

(25)

$\Theta \left( {\xi ,{{F}_{0}}} \right) = \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{{\left[ {1 - {{{\left( { - 1} \right)}}^{n}}} \right]}}{n}\sin n\pi z\left[ {\frac{{{{\alpha }_{n}}~{{F}_{{{{0}_{1}}}}} - 1}}{{{{\alpha }_{n}} - {{\beta }_{n}}}}{\text{exp}}\left( { - {{\alpha }_{n}}~{{F}_{0}}} \right) + } \right.} \left. {\frac{{{{\beta }_{n}}~{{F}_{{{{0}_{1}}}}} + 1}}{{{{\beta }_{n}} - {{\alpha }_{n}}}}{\text{exp}}\left( { - {{\beta }_{n}}~{{F}_{0}}} \right)} \right],$

где

(26)

$\left. {\begin{array}{*{20}{c}} {{{\alpha }_{n}} = {{\left[ {1 - \sqrt {1 - 4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}}} } \right]} \mathord{\left/ {\vphantom {{\left[ {1 - \sqrt {1 - 4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}}} } \right]} {2{{F}_{{{{0}_{1}}}}}}}} \right. \kern-0em} {2{{F}_{{{{0}_{1}}}}}}}~} \\ {\begin{array}{*{20}{c}} {{{\beta }_{n}} = {{\left[ {1 - \sqrt {1 + 4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}}} } \right]} \mathord{\left/ {\vphantom {{\left[ {1 - \sqrt {1 + 4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}}} } \right]} {2{{F}_{{{{0}_{1}}}}}}}} \right. \kern-0em} {2{{F}_{{{{0}_{1}}}}}}}~} \\ {\gamma _{n}^{2} = {{{\left( {n\pi } \right)}}^{2}}} \end{array}} \end{array}} \right\}$

при $4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}} > 1$

(27)

$\begin{gathered} \Theta \left( {\xi ,{{F}_{0}}} \right) = \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{{\left[ {1 - {{{\left( { - 1} \right)}}^{n}}} \right]}}{n}\sin n\pi z} \times \\ \times \,\,\left[ {\cos \left( {{{\sqrt {4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}} - 1} } \mathord{\left/ {\vphantom {{\sqrt {4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}} - 1} } {2~{{F}_{{{{0}_{1}}}}}}}} \right. \kern-0em} {2~{{F}_{{{{0}_{1}}}}}}}} \right) + \frac{{\sin \left( {{{\sqrt {4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}} - 1} } \mathord{\left/ {\vphantom {{\sqrt {4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}} - 1} } {2~{{F}_{{{{0}_{1}}}}}}}} \right. \kern-0em} {2~{{F}_{{{{0}_{1}}}}}}}} \right)}}{{\sqrt {4\gamma _{n}^{2}~{{F}_{{{{0}_{1}}}}} - 1} }}} \right]{\text{exp}}\left( { - \frac{{~{{F}_{0}}}}{{~{{F}_{{{{0}_{1}}}}}}}} \right). \\ \end{gathered} $

Результаты, рассчитанные по формулам (25)–(27) представлены на рис. 3. Анализ кривых показывает, что при малых $~{{F}_{0}}{\text{\;и}}$ $~{{F}_{{{{0}_{1}}}}}$ = 0.15 × 10^–2 на границе теплового возмущения наблюдается скачок температуры, то есть образуется фронт тепловой волны, в пределах которой температура изменяется от ее значения на фронте до начальной. Область среды, находящейся за фронтом теплового возмущения, оказывается невозмущенной и температура здесь равна начальной. При достаточно больших значениях времени $~{{F}_{0}} > 0.02$ ($~{{F}_{{{{0}_{1}}}}}$ = 0.15 × 10^–2) значения температуры совпадают с величинами, полученными из решения параболического уравнения. Более подробный анализ особенностей аналитических решений тепловых задач для уравнения (22) проведен в [9].

Рис. 3.

Распределение температуры в пластине: ${{F}_{{0r}}} = 6.25 \times {{10}^{{ - 3}}},$ n = 10⁵ (n – число членов ряда (25)–(27)).

ВЫВОДЫ

Показано, что соотношение Онзагера, приводящее последовательно все более к обобщающим феноменологическим законам нестационарного теплопереноса на уровне элементарных актов, дает результаты, совпадающие с разложением линейного градиентного закона Фурье для теплового потока в ряд по времени c коэффициентами релаксации теплового потока и градиента температуры. На основе полученных соотношений рассмотрены новые модельные представления нестационарного теплообмена, обобщающие классические феноменологические модели Фурье. Рассмотрена серия краевых задач локально-неравновесного теплопереноса с учетом пространственно-временной нелокальности (и ее частного случая) о температурном нагреве бесконечной пластины. Найдены точные аналитические решения, проведен численный эксперимент и описаны его особенности.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-38-00059 мола.

Список литературы

Лыков А.В. Применение методов термодинамики необратимых процессов к исследованию тепло- и массообмена / Инж.-физич. журн. 1965. Т. 9. № 3. С. 287–304.
Лыков А.В. Теория теплопроводности. М. Высш. школа. 1967. С. 600.
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М. Высш. школа. 2001. С. 540.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М.: URSS. 2012. С. 655.
Карташов Э.М. Аналитические решения гиперболических моделей теплопроводности / Инж.-физич. журн. 2014. Т. 87. № 5. С. 1–10.
Кудинов В.А., Кудинов И.В., Карташов Э.М. (общая редакция). Методы решения параболических и гиперболических уравнений. М.: URSS. 2015. С. 280.
Кирсанов Ю.А., Юдахин А.Е. Переходные термические процессы в твердом теле / Изв. РАН, Энергетика. 2015. № 6. С. 45–51.
Карташов Э.М. Математические модели теплопроводности с двухфазным запаздыванием / Инж.-физич. журн. 2016. Т. 89. № 1. С. 34–35.
Кудинов В.А., Кудинов И.В. Математическая модель локально-неравновесного теплопереноса с учетом пространственно-временной нелокальности / Инж.-физич. журн. 2015. Т. 85. № 2. С. 393–408.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал