Известия РАН. Энергетика, 2019, № 4, стр. 27-41
Оптимизация энергопотребления на основе использования накопителя энергии
Н. В. Коровкин 1, Н. В. Силин 2, *, Ф. М. Рахимов 2
1 Институт энергетики и транспортных систем Санкт-Петербургского политехнического
университета Петра Великого
Санкт-Петербург, Россия
2 Инженерная школа Дальневосточного федерального университета
Владивосток, Россия
* E-mail: silin22@mail.ru
Поступила в редакцию 15.07.2019
После доработки 09.08.2019
Принята к публикации 12.08.2019
Аннотация
Рассмотрены вопросы оптимизации работы малых ГЭС в условиях жесткого дефицита воды, выполняемой за счет подключения к сети накопителя энергии и ветрогенератора, а также оптимального управления нагрузкой. Предполагается, что нагрузкой системы является сосредоточенный автономный энергообъект (ЭО), потребляющий только активную мощность. Графики потребления имеют дневной максимум и различаются по дням недели. Мощность нагрузки допускает разделение на две части: строго заданную и вариативную, изменяемую при оптимизации. К таким ЭО относятся, группа частных домов (поселок), многоквартирный дом, ферма, не крупное промышленное предприятие с преимущественным потреблением активной мощности. В работе получена строгая математическая постановка задачи, решение которой соответствует минимальным затратам на накопитель и ветрогенератор, которые позволят обеспечить бесперебойное снабжение ЭО электроэнергией в условиях дефицита воды, необходимой для работы МГЭС. Используемый математический аппарат – генетический алгоритм и метод минимизации линейной функции при линейных ограничениях в виде равенств и неравенств (симплекс-метод). Рассмотрение проводится применительно к условиям республики Таджикистан.
1. ВВЕДЕНИЕ И АКТУАЛЬНОСТЬ ПРОБЛЕМЫ
В последнее время малой энергетике, использующей возобновляемые источники энергии, уделяется пристальное внимание [1, 2]. Заинтересованность в применении возобновляемых источников энергии (солнца, ветра, речной воды и др.) объяснима отсутствием закупок топлива и возможностью электроснабжения труднодоступных районов. Последнее важно особенно для стран с горным рельефом и малонаселенными районами, где прокладка электросети экономически нецелесообразна. Одновременно для этих стран и районов характерен большой гидроэнергетический потенциал, что привело к ускоренному развитию в них малых и МГЭС (МГЭС). Активное сооружение и эксплуатация этих станций, не имеющих, как правило, водохранилищ, связано и со стремлением избежать экологического ущерба, который наносится водохранилищами крупных ГЭС, а также небольшими затратами на их строительство и скорым возвратом инвестиций (до 5 лет).
Основные задачи развития нетрадиционной энергетики в России определены в постановлении Правительства Российской Федерации № 335 от 28 марта 2019 г., согласно которому в государственную программу Российской Федерации “Энергоэффективность и развитие энергетики” внесены существенные изменения. Государственная программа получила новое наименование “Развитие энергетики”, а срок реализации продлен на период до 2024 г. В программе определены ключевые вопросы развития энергетики, одним из которых является опережающее развитие возобновляемой энергетики (включая гидроэнергетику), направленное на диверсификацию топливно-энергетического баланса страны.
МГЭС (мощность до 100 кВт) можно устанавливать практически в любом месте. Гидроагрегат включает водозаборное устройство, энергоблок и устройство автоматического регулирования. МГЭС применяются в качестве источников электроэнергии для фермерских хозяйств, дачных поселков, хуторов и небольших производств в труднодоступных районах – там, где невыгодно прокладывать сети.
Основным достоинством малой гидроэнергетики является безопасность с экологической точки зрения. В ходе сооружения объектов данной отрасли и дальнейшей их эксплуатации нет вредных воздействий на качество и свойства воды. Современные станции имеют простые конструкции и автоматизированы полностью, т.е. при эксплуатации они не требуют присутствия человека. ЭЭ МГЭС соответствует требованиям нормативных документов по напряжению и частоте, причем станции способны работать автономно. Общий ресурс работы станции более 40 лет (не меньше 5 лет до капремонта).
Применение энергии небольших водотоков при помощи МГЭС – одно из самых эффективных направлений развития возобновляемой энергетики в такой горной стране, как Таджикистан. МГЭС с установленной мощностью оборудования 3 кВт и более широко и эффективно используются для выработки ЭЭ в маломощных автономных энергосистемах. Так в горных районах Таджикистана в настоящее время работает свыше 300 таких станций, снабжающих ЭЭ небольшие поселки [3].
Начало освоения малой энергетики в Таджикистане относится к тридцатым годам прошлого века. Первая малая гидроэлектростанция, Варзобская ГЭС-1, мощностью 7.15 МВт была построена в 1936 г. и успешно функционирует до настоящего времени. В конце 1949 в начале 1950 гг. была разработана “Схема использования гидроэнергетических ресурсов малых водотоков для электрификации сельского хозяйства Таджикской ССР”, целью которой являлась сплошная электрификация всей сельской территории республики [4]. Реализация “Схемы” началась практически одновременно с ее разработкой. К концу 1958 г. в республике действовало уже 53 МГЭС, общей установленной мощностью 12 МВт. В 1978 г. общее количество построенных малых ГЭС достигло 69 при общей суммарной мощности в 32 МВт. Однако, в связи с переориентацией на большую энергетику и строительством крупных ГЭС, программа создания МГЭС была свернута. В итоге к началу 90-х гг. в эксплуатации осталось всего пять станций. Возрождение МГЭС связано с постановлением Правительства Республики Таджикистан № 73 от 2 февраля 2009 г. о “Долгосрочной Программе строительства МГЭС на период 2009–2020 гг.”, согласно которому к 2020 г. должно быть построено 189 малых ГЭС мощностью от 50 до 10 тыс. кВт. В декабре 2015 г. Правительством Республики Таджикистан было принято Постановление № 795 “О Программе освоения возобновляемых источников энергии и строительства МГЭС на 2016–2020 гг.”. Целью этой программы – надежное и эффективное обеспечение электроэнергией населения удаленных и изолированных районов республики, а также малого и среднего бизнеса [5].
В период с 1991 г. по всей Республике Таджикистан введено в эксплуатацию свыше 300 МГЭС [6], большинство из которых построены для электроснабжения удаленных локальных потребителей взамен существующих дизельных электростанций. Основными причинами замены являются дороговизна привозного топлива, а также то, что большая часть станций во время гражданской войны в начале 90-х гг. была разграблена и демонтирована [6].
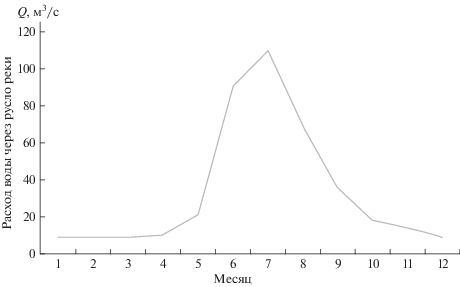
Одним из основных препятствий для широкого внедрения МГЭС является дефицит водных ресурсов в зимний период [7]. На рис. 1 приведен типовой помесячный график расхода воды горной реки на территории Таджикистана. Из графика видно, что режим стока воды колеблется в широких пределах, период половодья соответствует весеннее-летнему периоду, а в остальные месяцы наблюдается резкий дефицит воды [8] и сокращение расхода более чем в 10 раз.
Отсутствие значительного по объему водохранилища, обеспечивающего стабильность расхода воды в течение всего года, приводит к фактической остановке МГЭС, что обуславливает необходимость введения и использования дополнительного источника.
В настоящей статье мы рассмотрим оптимизацию работы системы: МГЭС, накопитель энергии и ветрогенератор в условиях жесткого дефицита воды с целью поддержки стабильного уровня выработки ЭЭ. Оптимизация, рассматриваемая в статье, выполняется также за счет оптимального управления нагрузкой.
Материал в статье излагается в следующем порядке:
– в разделе “Принимаемые допущения и исходные данные” мы подробно рассмотрим необходимые для решения задачи данные и формы их представления;
– в разделе “Формулировка задачи” мы дадим математически строгую формулировку нашей задачи, сведя ее к задаче многоцелевой оптимизации с нелинейными ограничениями;
– в разделе “Вычисление ограничений” мы рассмотрим наиболее сложный этап решения сформулированной в предыдущем разделе задачи – вычисление входящих в нее ограничений; этот раздел имеет подразделы: “Переход к дискретному времени” и “Сведение процедуры вычисления ограничений к задаче линейного программирования”;
– далее коротко приводятся наши предложения по конструкции ветрогенератора – раздел “Использование ветрогенераторов”;
– заключают изложение раздел “Результаты и выводы”.
2. ПРИНИМАЕМЫЕ ДОПУЩЕНИЯ И ИСХОДНЫЕ ДАННЫЕ
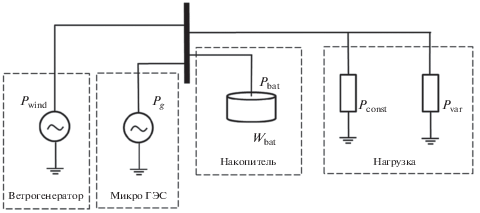
Рассматриваемая в работе автономная энергосистема в упрощенном виде представлена на рис. 2. Выработка ЭЭ производится ветрогенератором и МГЭС, в энергосистеме имеется также накопитель, содержащий собственно накопитель энергии и преобразователь, соединяющий его с сетью. Мы будем, для определенности, полагать, что в роли накопителя выступает батарея аккумуляторов или суперконденсаторов [9], что, однако, не является обязательным в нашем исследовании.
Для сети и нагрузки примем математическую модель, основанную на нижеследующих допущениях:
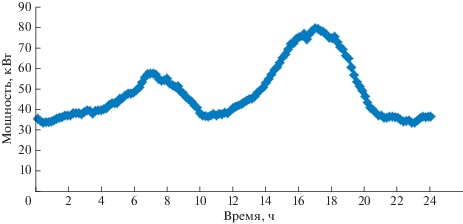
– график потребления ${{P}_{{{\text{load}}}}}(t)$ неоднороден по времени как в течении дня, так и для различных дней интервала Т оптимизации, который принят равным 168 часам – одной неделе, типичный вид зависимости ${{P}_{{{\text{load}}}}}(t)$ в течении суток приведен на рис. 3, где представлена усредненная экспериментальная кривая потребления поселка в зимний период;
Рис. 3.
Экспериментальная зависимость ${{P}_{{{\text{load}}}}}(t)$ потребления поселка в зимний период.
– мощность нагрузки может быть условно представлена как сумма строго заданной ${{P}_{{{\text{const}}}}}(t)$ и вариативной ${{P}_{{{\text{var}}}}}(t)$ частей, из которых только последняя может изменяться при оптимизации, очевидно, что ${{P}_{{{\text{load}}}}}(t)$ = ${{P}_{{{\text{const}}}}}(t)$ + ${{P}_{{{\text{var}}}}}(t);$
– общее количество ЭЭ ${{W}_{{{\text{load}}}}}$ = $\int_0^T {{{P}_{{{\text{load}}}}}(t)dt} ,$ потребленной за интервал Т оптимизации известно, соответственно, известна и средняя мощность потребления ${{P}_{{{\text{ave}}}}}$ = ${{{{W}_{{{\text{load}}}}}} \mathord{\left/ {\vphantom {{{{W}_{{{\text{load}}}}}} T}} \right. \kern-0em} T},$ также задано и значение ${{W}_{{{\text{load}},{\text{var}}}}}$ = $\int_0^T {{{P}_{{{\text{var}}}}}(t)dt} $ – энергия потребленная вариативной частью нагрузки;
– начальная ${{W}_{{{\text{bat}}}}}(0)$ и конечная ${{W}_{{{\text{bat}}}}}(T)$ = ${{W}_{{{\text{bat}}}}}(0)$ + $\int_0^T {{{P}_{{{\text{bat}}}}}(t)dt} $ энергии накопителя одинаковы, откуда следует, что $\int_0^T {{{P}_{{{\text{bat}}}}}(t)dt} = 0;$
– наилучшим режимом выработки ЭЭ для МГЭС является режим, при котором расходуется минимальное количество воды при одновременном отсутствии дефицита мощности в нагрузке;
– мощность поставляемая в сеть ветрогенератором ${{P}_{{{\text{wind}}}}}(t)$ задается исходя из среднестатистических значений для зимнего периода соответствующей местности, определим также среднюю мощность поставляемую в сеть ветрогенератором ${{P}_{{{\text{ave}},{\text{wind}}}}}$ = $\frac{1}{T}\int_0^T {{{P}_{{{\text{wind}}}}}(t)dt} ;$
– потери в элементах рассматриваемой автономной энергосистемы не учитываются
– это упрощающее допущение может быть легко снято и принято здесь, чтобы не перегружать изложение деталями.
3. ФОРМУЛИРОВКА ЗАДАЧИ
Сформулируем далее цель оптимизации нашей локальной энергосистемы. Необходимо таким образом управлять вариативной частью нагрузки – ${{P}_{{{\text{var}}}}}(t)$ и накопителем – ${{P}_{{{\text{bat}}}}}(t),$ чтобы одновременно выполнялись два условия:
1. Режим выработки ЭЭ МГЭС возможно менее изменялся во времени, в предельном наилучшем для нас случае мощность выработки не изменялась во времени, то есть ${{P}_{g}}(t)$ = ${{P}_{{g,0}}} = {\text{const}}$ – именно это условие и учитывает ситуацию зимнего периода, так как ЭЭ в дефиците и потребление выработанной МГЭС ЭЭ всегда максимально возможное, то неравномерность нагрузки означает просто недоиспользование имеющейся воды;
2. При заданном потреблении ${{W}_{{{\text{load}}}}}$ ЭЭ установленные мощности ${{P}_{{{\text{wimd}},\,\max }}}$ ветрогенератора, ${{P}_{{{\text{bat}},\,\max }}}$ преобразователя и емкость ${{W}_{{{\text{bat}},\,\max }}}$ преобразователя должны быть минимальными – это условие обеспечивает минимальную стоимость всей системы.
Сформулированная цель оптимизации может быть записана в следующем виде:
(1)
$\left\{ \begin{gathered} {{P}_{{{\text{wimd}},\,\max }}} \to min, \hfill \\ {{P}_{{{\text{bat}},\,\max }}} \to min, \hfill \\ {{W}_{{{\text{bat}},\,\max }}} \to min, \hfill \\ \Delta = \delta \left( {{{P}_{{g,\,{\text{ave}}}}}} \right), \hfill \\ {{P}_{{{\text{wimd}},\,\max }}} \geqslant 0,\,\,\,\,{{P}_{{{\text{bat}},\,\max }}} \geqslant 0,\,\,\,\,{{W}_{{{\text{bat}},\,\max }}} \geqslant 0. \hfill \\ \end{gathered} \right.$Здесь вариация δ определяется следующим образом:
(2)
$\delta = \mathop {\max }\limits_{t \in \left[ {0,T} \right]} \frac{{\left| {{{P}_{{g,\,{\text{ave}}}}} - {{P}_{g}}(t)} \right|}}{{{{P}_{{g,\,{\text{ave}}}}}}},\,\,\,\,{{P}_{{g,\,{\text{ave}}}}} = \frac{1}{T}\int\limits_0^T {{{P}_{g}}(t)dt} ,$Решение этой нелинейной задачи многоцелевой оптимизации (1) следует выполнять при ограничении $\Delta = \delta \left( {{{P}_{{g,\,{\text{ave}}}}}} \right),$ вычисление которого значительно превосходит по сложности вычисление минимизируемых функций. Поэтому рассмотрим и само это ограничение и способ его вычисления подробнее. Равенство нулю вариации Δ соответствует тому, что МГЭС работает в оптимальном режиме. Однако, при этом величины ${{P}_{{{\text{wimd}},\,\max }}},$ ${{P}_{{{\text{bat}},\,\max }}},$ ${{W}_{{{\text{bat}},\,\max }}}$ могут быть большими, и вся система в целом будет весьма дорогой. Уменьшение установленных мощностей ветрогенератора ${{P}_{{{\text{wimd}},\,\max }}},$ преобразователя ${{P}_{{{\text{bat}},\,\max }}},$ а также и емкости ${{W}_{{{\text{bat}},\,\max }}}$ аккумуляторов удешевляет систему, но все более нагружает МГЭС и, начиная с каких-то значений, приводит к невозможности сохранять выработку ЭЭ ${{P}_{g}}(t)$ на постоянном уровне и, следовательно, появлению ненулевых значений вариации $\delta \left( {{{P}_{{g,\,{\text{ave}}}}}} \right).$
Значительный интерес представляет решение поставленной многоцелевой задачи при различных задаваемых уровнях вариации Δ. Чем больше этот уровень, тем меньше стоимость всей системы, но и одновременно, тем менее эффективно работает МГЭС. Компромисс между этими взаимно противоречащими тенденциями зависит от конкретной ситуации (имеющихся для реализации проекта технических возможностей, перспективных планов развития данной локальной сети, планируемого объема финансирования) у заказчика.
Перейдем к методу вычисления ограничения $\Delta = \delta \left( {{{P}_{{g,\,{\text{ave}}}}}} \right).$ Фактически, нам необходимо указать алгоритм вычисления оптимального ${{P}_{g}}(t).$ Так как при известной ${{P}_{g}}(t)$ вычисление ограничения не представляет труда. Здесь оптимальность ${{P}_{g}}(t)$ понимается в том смысле, что используя все возможности нашей локальной системы, а именно: управление вариативной частью нагрузки ${{P}_{{{\text{var}}}}}(t),$ управление накопителем ЭЭ – ${{P}_{{{\text{bat}}}}}(t)$ и используя энергию, получаемую от ветрогенератора ${{P}_{{{\text{wind}}}}}(t),$ мы должны найти такие ${{P}_{{{\text{var}}}}}(t),$ ${{P}_{{{\text{bat}}}}}(t),$ ${{P}_{g}}(t),$ что ${{P}_{g}}(t)$ возможно меньше уклоняется на временном интервале $\left[ {0,T} \right]$ от своего среднего значения ${{P}_{{g,{\text{ave}}}}}.$
Сложность задачи (1) может быть несколько уменьшена, если известно соотношение стоимости киловатта установленной мощности ветрогенератора Swind и преобразователя энергии Sbat. Пусть ${{{{S}_{{{\text{wind}}}}}} \mathord{\left/ {\vphantom {{{{S}_{{{\text{wind}}}}}} {{{S}_{{{\text{bat}}}}}}}} \right. \kern-0em} {{{S}_{{{\text{bat}}}}}}} = m,$ тогда, в силу того, что ${{P}_{{{\text{wimd}},\,\max }}}$ и ${{P}_{{{\text{bat}},\,\max }}}$ это установленные мощности ветрогенератора и преобразователя соответственно, и смысл задачи (1), найти наиболее дешевую оптимальную конфигурацию локальной энергосистемы, можно прейти к следующей формулировке:
(3)
$\left\{ \begin{gathered} {{P}_{{{\text{wimd,}}\,{\text{max}}}}} + m{{P}_{{{\text{bat,}}\,{\text{max}}}}} \to min, \hfill \\ {{W}_{{{\text{bat,}}\,{\text{max}}}}} \to min, \hfill \\ \delta \left( {{{P}_{{g,\,{\text{ave}}}}}} \right) = \mathop {\max }\limits_{t \in \left[ {0,T} \right]} \left( {{{\left| {{{P}_{{g,\,{\text{ave}}}}} - {{P}_{g}}(t)} \right|} \mathord{\left/ {\vphantom {{\left| {{{P}_{{g,\,{\text{ave}}}}} - {{P}_{g}}(t)} \right|} {{{P}_{{g,\,{\text{ave}}}}}}}} \right. \kern-0em} {{{P}_{{g,\,{\text{ave}}}}}}}} \right) = \Delta , \hfill \\ {{P}_{{{\text{wimd}},\,\max }}} \geqslant 0;\,\,\,\,{{P}_{{{\text{bat}},\,\max }}} \geqslant 0;\,\,\,\,{{W}_{{{\text{bat}},\,\max }}} \geqslant 0. \hfill \\ \end{gathered} \right.$Решением задачи (3) является множество Парето, для построения которого предлагается использование генетического алгоритма [10] и алгоритм недоминирующей сортировки [11] NSGA-II.
4. ВЫЧИСЛЕНИЕ ОГРАНИЧЕНИЙ
Таким образом, “внутри” нелинейной многоцелевой задачи, сформулированной выше, нам необходимо многократное решение более простой задачи: определения оптимального ${{P}_{g}}(t)$ и вычисления по нему $\delta \left( {{{P}_{{g,\,{\text{ave}}}}}} \right).$ Рассмотрим теперь постановку этой “внутренней” задачи.
Исходными данными для поставленной задачи являются:
– зависимости ${{P}_{{{\text{const}}}}}(t)$ и ${{P}_{{{\text{wind}}}}}(t),$ их характерный вид представлен на рис. 2;
– общее количество ЭЭ ${{W}_{{{\text{load}}}}},$ потребленной за время Т, и общее количество энергии ${{W}_{{{\text{load,}}\,{\text{var}}}}}$, которая потребляется вариативной частью нагрузки.
Постановка задачи также включает в себя ограничение на переменные задачи и связи между ними. Баланс мощности [12] рассматриваемой сети выражается соотношением:
(4)
${{\forall }_{{t \in \left[ {0,T} \right]}}}:\,\,\,\,\underbrace {{{P}_{{{\text{const}}}}}(t) + {{P}_{{{\text{var}}}}}(t)}_{{{P}_{{{\text{load}}}}}(t)} = {{P}_{g}}(t) + {{P}_{{{\text{wind}}}}}(t) + {{P}_{{{\text{bat}}}}}(t).$Нагрузка должна потребить за время Т энергию ${{W}_{{{\text{load}}}}}.$ При этом ту часть энергии нагрузки ${{W}_{{{\text{load,}}\,{\text{var}}}}},$ которая потребляется вариативной частью нагрузки в соответствии с принятыми выше допущениями также задана:
(5)
${{W}_{{{\text{load}}}}} = \int\limits_0^T {{{P}_{{{\text{load}}}}}(t)dt} ,\,\,\,\,{{W}_{{{\text{load,}}\,{\text{var}}}}} = \int\limits_0^T {{{P}_{{{\text{var}}}}}(t)dt} .$Для накопителя:
(6)
${{\forall }_{{t \in \left[ {0,T} \right]}}}:\,\,\,\, - {{P}_{{{\text{bat,}}\,{\text{max}}}}} \leqslant {{P}_{{{\text{bat}}}}}(t) \leqslant {{P}_{{{\text{bat,}}\,{\text{max}}}}},$(7)
${{\forall }_{{t \in \left[ {0,T} \right]}}}:\,\,\,\,0 \leqslant {{W}_{{{\text{bat}}}}}(t) \leqslant {{W}_{{{\text{bat,}}\,{\text{max}}}}}.$Последнее неравенство далее будет использоваться и в иной эквивалентной форме:
(8)
${{\forall }_{{t \in \left[ {0,T} \right]}}}:\,\,\,\,0 \leqslant \int\limits_0^t {{{P}_{{{\text{bat}}}}}(t)dt} \leqslant {{W}_{{{\text{bat,}}\,{\text{max}}}}}.$В силу того, что ${{W}_{{{\text{bat}}}}}(T)$ = ${{W}_{{{\text{bat}}}}}(0){\text{:}}$
Вариативная компонента ${{P}_{{{\text{var}}}}}(t)$ мощности нагрузки должна быть неотрицательна, также производимая МГЭС мощность ${{P}_{g}}(t)$ положительна и не может превышать суммарную установленную мощность ${{P}_{{g,\max }}}$ генераторов:
(10)
${{\forall }_{{t \in \left[ {0,T} \right]}}}:\,\,\,\,0 \leqslant {{P}_{{{\text{var}}}}}(t) \leqslant {{P}_{{{\text{var,}}\,{\text{max}}}}},\,\,\,\,0 \leqslant {{P}_{g}}(t) \leqslant {{P}_{{g,\max }}}.$4.1. Переход к дискретному времени
Введем в рассмотрение вектора ${{{\mathbf{P}}}_{{{\text{var}}}}},$ ${{{\mathbf{P}}}_{{{\text{bat}}}}},$ ${{{\mathbf{P}}}_{g}},$ ${{{\mathbf{P}}}_{{{\text{wind}}}}},$ ${{{\mathbf{P}}}_{{{\text{load}}}}},$ ${{{\mathbf{P}}}_{{{\text{const}}}}},$ элементы которых являются значениями соответственно величин ${{P}_{{{\text{var}}}}}(t),$ ${{P}_{{{\text{bat}}}}}(t),$ ${{P}_{{{\text{net}}}}}(t),$ ${{P}_{{{\text{wind}}}}}(t),$ ${{P}_{{{\text{load}}}}}(t),$ ${{P}_{{{\text{const}}}}}(t)$ в дискретные моменты времени ${{t}_{k}}:\{ {{t}_{1}} = 0;{{t}_{k}} = {{t}_{{k - 1}}} + h;{{t}_{N}} = T\} ,$ где h – шаг наблюдения – 10 мин в наших расчетах. Тогда ${{{\mathbf{P}}}_{{{\text{var}}}}},$ ${{{\mathbf{P}}}_{{{\text{bat}}}}}$ и аналогично для всех введенных векторов:
(11)
${{{\mathbf{P}}}_{{{\text{var}}}}} = {{\left[ {{{P}_{{{\text{var}},\,1}}},\,\,{{P}_{{{\text{var}},\,2}}},\,\, \cdots ,\,\,{{P}_{{{\text{var}},\,N}}}} \right]}^{T}},\,\,\,\,{{{\mathbf{P}}}_{{{\text{bat}}}}} = {{\left[ {{{P}_{{{\text{bat,}}\,{\text{1}}}}},\,\,{{P}_{{{\text{bat,}}\,{\text{2}}}}},\,\, \cdots ,\,\,{{P}_{{{\text{bat,}}\,N}}}} \right]}^{T}}.$В (11) “Т” – символ транспонирования, и для краткости записи приняты обозначения ${{P}_{{{\text{var}},\,k}}} = {{P}_{{{\text{var}}}}}({{t}_{k}}),$ ${{P}_{{{\text{bat}},\,k}}} = {{P}_{{{\text{bat}}}}}({{t}_{k}}),$ которые будут далее использоваться для всех векторов.
Неизвестными векторными величинами нашей задачи являются вектора ${{{\mathbf{P}}}_{{{\text{var}}}}},$ ${{{\mathbf{P}}}_{{{\text{bat}}}}},$ ${{{\mathbf{P}}}_{g}}.$ Объединим их в один вектор неизвестных Y:
(12)
${\mathbf{Y}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \\ {{{{\mathbf{P}}}_{g}}} \end{array}} \right].$Запишем теперь, используя введенные вектора, ограничения (4)–(11). Начнем с ограничений типа равенств: (4), (5), (9). Перепишем (4) таким образом, чтобы в правой части находились только известные величины:
(13)
$\left[ {\begin{array}{*{20}{c}} {{\mathbf{E}},}&{{\mathbf{E}},}&{\mathbf{E}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \\ {{{{\mathbf{P}}}_{g}}} \end{array}} \right] = \left[ {{{{\mathbf{P}}}_{{{\text{const}}}}} - {{{\mathbf{P}}}_{{{\text{wind}}}}}} \right],$Заменяя интегралы суммами, для элементов векторов получим следующее уравнение:
Второе равенство в (5) также может быть переписано для элементов векторов в виде:
Для дальнейшего последние соотношения удобно представить в матричной форме:
(14)
$\left[ \begin{gathered} \begin{array}{*{20}{c}} {{\mathbf{1}},}&{{\mathbf{0}},}&{\mathbf{0}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{\mathbf{0}},}&{{\mathbf{1}},}&{\mathbf{1}} \end{array} \hfill \\ \end{gathered} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \\ {{{{\mathbf{P}}}_{g}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {h\sum\limits_{k = 1}^{k = 1008} {{{P}_{{{\text{var}},\,k}}}} } \\ {\frac{{{{W}_{{{\text{load}}}}}}}{h} - \sum\limits_{k = 1}^{k = 1008} {{{P}_{{{\text{wind}},\,k}}}} } \end{array}} \right].$В соотношении (14) h – шаг сетки по времени – 10 мин, соответственно, одна неделя – 168 ч или 1008 десятиминутных интервалов, 0 – матрица строка, содержащая 1008 нулей, 1 – матрица строка, содержащая 1008 единиц. Аналогично (14) уравнение (9) для компонент векторов будет иметь вид:
Или в матричной форме:
(15)
$\left[ {\begin{array}{*{20}{c}} {{\mathbf{0}},}&{{\mathbf{1}},}&{\mathbf{0}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \\ {{{{\mathbf{P}}}_{g}}} \end{array}} \right] = 0.$Перейдем далее к ограничениям типа неравенств (6), (8) и (10). Ограничения (6) и (10) устанавливают границы изменения неизвестных нашей задачи. Соответствующие им неравенства для элементов векторов имеют вид:
(16)
$ - {{P}_{{{\text{bat,}}\,{\text{max}}}}} \leqslant {{P}_{{{\text{bat}},\,k}}} \leqslant {{P}_{{{\text{bat,}}\,{\text{max}}}}},\,\,\,\,k = \overline {1,1008,} $(17)
$0 \leqslant {{P}_{{{\text{var}},\,k}}} \leqslant {{P}_{{{\text{var}},\,\max }}},\,\,\,\,0 \leqslant {{P}_{{g,k}}} \leqslant {{P}_{{g,\,\max }}},\,\,\,\,k = \overline {1,1008} .$Ограничение (8) при переходе к векторам порождает 1008 двойных неравенств:
Матричная форма записи этих неравенств имеет вид:
(18)
$\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\mathbf{N}}&{\mathbf{D}}&{\mathbf{N}} \end{array}} \\ {\begin{array}{*{20}{c}} {\mathbf{N}}&{ - {\mathbf{D}}}&{\mathbf{N}} \end{array}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \\ {{{{\mathbf{P}}}_{g}}} \end{array}} \right] \leqslant \frac{{{{W}_{{{\text{bat,}}\,{\text{max}}}}}}}{h}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{1}}}^{T}}} \\ {{{{\mathbf{0}}}^{T}}} \end{array}} \right],\,\,\,\,{\mathbf{D}} = \underbrace {\left[ {\begin{array}{*{20}{c}} 1&0& \cdots &0 \\ 1&1& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 1&1& \cdots &1 \end{array}} \right]}_{1008}.$В соотношении (18) N – квадратная матрица размера 1008 × 1008, все элементы которой нули.
Таким образом, формирование ограничений типа равенств и неравенств закончено и можно перейти к записи целевой функции. В качестве целевой функции, как было определено в постановке задачи, должен выступать некоторый функционал $F({{{\mathbf{P}}}_{{{\text{var}}}}},{{{\mathbf{P}}}_{{{\text{bat}}}}},{{{\mathbf{P}}}_{g}}),$ характеризующий неоднородность выработки ЭЭ на МГЭС. Мы будем искать минимум этого функционала.
Введем в рассмотрение два вектора А и В, компоненты которых ${{{\alpha }}_{k}}\,{\text{и}}\,{{{\beta }}_{k}}$ неотрицательны:
(19)
${\mathbf{A}} = {{\left[ {{{{\alpha }}_{1}},{{{\alpha }}_{2}}, \cdots ,{{{\alpha }}_{{1008}}},} \right]}^{T}}{\text{,}}\,\,\,\,{\text{B}} = {{\left[ {{{{\beta }}_{1}},{{{\beta }}_{2}}, \cdots ,{{{\beta }}_{{1008}}},} \right]}^{T}},\,\,\,\,{{{\alpha }}_{k}} \geqslant 0,\,\,\,\,{{{\beta }}_{k}} \geqslant 0,\,\,\,\,k = \overline {1,1008} .$Используя ${{P}_{{{\text{ave}}}}} = {{{{W}_{{{\text{load}}}}}} \mathord{\left/ {\vphantom {{{{W}_{{{\text{load}}}}}} T}} \right. \kern-0em} T}$ – среднюю мощность, потребляемую нагрузкой за интервал времени Т, ${{P}_{{{\text{ave,}}\,{\text{wind}}}}}$ = $\frac{1}{T}\int_0^T {{{P}_{{{\text{wind}}}}}(t)dt} $ – среднюю мощность, поставляемую в сеть ветрогенератором, и, учитывая, что $\int_0^T {{{P}_{{{\text{bat}}}}}(t)dt} = 0,$ запишем для потребляемой от сети мощности неравенства:
(20)
$\left[ {\begin{array}{*{20}{c}} {\mathbf{N}}&{\mathbf{N}}&{ - {\mathbf{E}}}&{ - {\mathbf{E}}}&{\mathbf{N}} \\ {\mathbf{N}}&{\mathbf{N}}&{\mathbf{E}}&{\mathbf{N}}&{ - {\mathbf{E}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \end{array}} \\ {{{{\mathbf{P}}}_{g}}} \\ {\mathbf{A}} \\ {\mathbf{B}} \end{array}} \right] \leqslant \left( {{{P}_{{{\text{ave}}}}} - {{P}_{{{\text{ave,}}\,{\text{wind}}}}}} \right) \cdot \left[ {\begin{array}{*{20}{c}} { - {{{\mathbf{1}}}^{T}}} \\ {{{{\mathbf{1}}}^{T}}} \end{array}} \right].$4.2. Сведение процедуры вычисления ограничений к задаче линейного программирования
Таким образом, в качестве минимизируемого функционала может быть взят линейный функционал:
(21)
$F({{{\mathbf{P}}}_{{{\text{var}}}}},{{{\mathbf{P}}}_{{{\text{bat}}}}},{{{\mathbf{P}}}_{g}}) = \sum\limits_{k = 1}^{k = 1008} {({{{\alpha }}_{k}} + {{{\beta }}_{k}})} \xrightarrow[{{{{\mathbf{P}}}_{{{\text{var}}}}},{{{\mathbf{P}}}_{{{\text{bat}}}}},{{{\mathbf{P}}}_{g}}}]{}\min .$Задача (21) минимизации линейного функционала с линейными ограничениями типа равенств и неравенств, полученными выше, классифицируется как задача линейного программирования. Результат этой классификации чрезвычайно важен, так как методы решения этой задачи хорошо изучены и доказано существование ее единственного решения, доставляющего глобальный минимум функционалу F. Приведем задачу к стандартному виду, используемому, например, в пакете MATLAB:
В записи минимизируемого функционала скобки $\left\langle { \cdot , \cdot } \right\rangle $ обозначают скалярное произведение векторов. Вектор X неизвестных и вектор коэффициентов С нашей задачи имеют вид:
Объединим соотношения (13)–(15) в одно матричное равенство и сформируем тем самым матрицу ${{{\mathbf{A}}}_{{{\text{eq}}}}}$ и вектор ${{{\mathbf{b}}}_{{{\text{eq}}}}}{\text{:}}$
(22)
$\underbrace {\left[ {\begin{array}{*{20}{c}} {\mathbf{E}}&{\mathbf{E}}&{\mathbf{E}}&{\mathbf{N}}&{\mathbf{N}} \\ {\mathbf{1}}&{\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}} \\ {\mathbf{0}}&{\mathbf{1}}&{\mathbf{1}}&{\mathbf{0}}&{\mathbf{0}} \\ {\mathbf{0}}&{\mathbf{1}}&{\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}} \end{array}} \right]}_{{{{\mathbf{A}}}_{{{\text{eq}}}}}} \cdot \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \end{array}} \\ {{{{\mathbf{P}}}_{g}}} \\ {\mathbf{A}} \\ {\mathbf{B}} \end{array}} \right] = \underbrace {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{const}}}}} - {{{\mathbf{P}}}_{{{\text{wind}}}}}} \\ {h\sum\limits_{k = 1}^{k = 1008} {{{P}_{{{\text{var}},\,k}}}} } \\ {\frac{{{{W}_{{{\text{load}}}}}}}{h} - \sum\limits_{k = 1}^{k = 1008} {{{P}_{{{\text{wind}},\,k}}}} } \\ 0 \end{array}} \right]}_{{{{\mathbf{b}}}_{{{\text{eq}}}}}}.$Объединим соотношения (18) и (20) в одно матричное неравенство и сформируем тем самым матрицу ${{{\mathbf{A}}}_{{{\text{ineq}}}}}$ и вектор ${{{\mathbf{b}}}_{{{\text{ineq}}}}}{\text{:}}$
(23)
$\underbrace {\left[ {\begin{array}{*{20}{c}} {\mathbf{N}}&{\mathbf{N}}&{ - {\mathbf{E}}}&{ - {\mathbf{E}}}&{\mathbf{N}} \\ {\mathbf{N}}&{\mathbf{N}}&{\mathbf{E}}&{\mathbf{N}}&{ - {\mathbf{E}}} \\ {\mathbf{N}}&{\mathbf{D}}&{\mathbf{N}}&{\mathbf{N}}&{\mathbf{N}} \\ {\mathbf{N}}&{ - {\mathbf{D}}}&{\mathbf{N}}&{\mathbf{N}}&{\mathbf{N}} \end{array}} \right]}_{{{{\mathbf{A}}}_{{{\text{ineq}}}}}} \cdot \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{\mathbf{P}}}_{{{\text{var}}}}}} \\ {{{{\mathbf{P}}}_{{{\text{bat}}}}}} \end{array}} \\ {{{{\mathbf{P}}}_{g}}} \\ {\mathbf{A}} \\ {\mathbf{B}} \end{array}} \right] \leqslant \underbrace {\left[ {\begin{array}{*{20}{c}} { - \left( {{{P}_{{{\text{ave}}}}} - {{P}_{{{\text{ave,}}\,{\text{wind}}}}}} \right) \cdot {{{\mathbf{1}}}^{T}}} \\ {\left( {{{P}_{{{\text{ave}}}}} - {{P}_{{{\text{ave,}}\,{\text{wind}}}}}} \right) \cdot {{{\mathbf{1}}}^{T}}} \\ {\frac{{{{W}_{{{\text{bat,}}\,{\text{max}}}}}}}{h} \cdot {{{\mathbf{1}}}^{T}}} \\ {{{{\mathbf{0}}}^{T}}} \end{array}} \right]}_{{{{\mathbf{b}}}_{{{\text{ineq}}}}}}.$Неравенства (16), (17) и (19) дают возможность сформировать вектора ${{{\mathbf{X}}}_{{\min }}}$ и ${{{\mathbf{X}}}_{{\max }}}{\text{:}}$
(24)
$\begin{gathered} {{{\mathbf{X}}}_{{\min }}} = \left[ {{\mathbf{0}},\,\, - {{P}_{{{\text{bat,}}\,{\text{max}}}}} \cdot {\mathbf{1}},\,\,{\mathbf{0}},\,\,{\mathbf{0}},\,\,{\mathbf{0}}} \right], \\ {{{\mathbf{X}}}_{{\max }}} = [{{P}_{{{\text{var,}}\,{\text{max}}}}} \cdot {\mathbf{1}},\,\,{{P}_{{{\text{bat,}}\,{\text{max}}}}} \cdot {\mathbf{1}},\,\,{{P}_{{g,\,\max }}} \cdot {\mathbf{1}},\,\,\left( {{{P}_{{{\text{ave}}}}} - {{P}_{{{\text{ave,}}\,{\text{wind}}}}}} \right) \cdot {\mathbf{1}}, \\ \left( {{{P}_{{g,\,\max }}} - \left( {{{P}_{{{\text{ave}}}}} - {{P}_{{{\text{ave,}}\,{\text{wind}}}}}} \right)} \right) \cdot {\mathbf{1}}]. \\ \end{gathered} $Таким образом, “внутренняя” задача определения оптимального ${{{\mathbf{P}}}_{g}},$ а, соответственно, и ${{P}_{g}}(t)$ сведена к стандартному для задач линейного программирования виду и задача (1) поставлена полностью.
5. ИСПОЛЬЗОВАНИЕ ВЕТРОГЕНЕРАТОРОВ
В качестве ветрогенераторов можно использовать как горизонтально-осевые, так и вертикально-осевые установки [13]. В настоящее время наибольшее распространение получили ВЭУ с горизонтальной осью [14]. Однако их использование в системе с М-ГЭС ограничено, так как они требуют ориентации относительно воздушных потоков, фундаментов, монтажа высокой конструкции, кроме того, создают значительный уровень шума и опасны для летающей фауны. Здесь необходимо отметить, что к ветровым установкам, предназначенным для размещения в непосредственной близости от среды проживания людей, предъявляются повышенные требования по уровню шумов, вибрации, устойчивости к порывам ветра. Кроме того, необходимо учитывать архитектурно-эстетические ограничения, а также дополнительные требования к системе управления, обеспечения работы в расширенных диапазонах скоростей ветра и т.д.
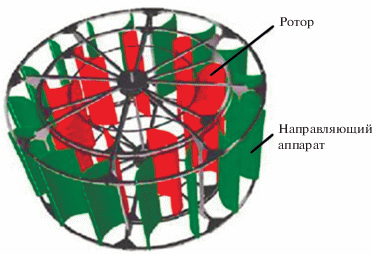
Вертикально-осевые ветротурбины характеризуются простотой изготовления лопастей, независимостью от направления ветра, устойчивой работой при турбулентности ветрового потока, возможностью установки вблизи потребителя, на крыше и углах зданий, устойчивостью к погодным условиями, перепадам температур, возможностью установки генератора на уровне земли [15]. Поэтому производители предлагают широкий спектр ветровых турбин с вертикальной осью. Наиболее известными из них являются установки на основе роторов Дарье, Савониуса, Мак-Гроува [16, 17], ветрогенераторы геликоидного и многолопастного типов. Эксплуатационные характеристики перечисленных вертикально-осевых ветровых установок заметно отличаются друг от друга [18, 19], что обусловлено различиями в принципах взаимодействия лопастей с потоком, а также их конструкционными особенностями. Одной из разновидностей конструкции ВЭУ является вертикально осевая турбина многолопастного типа (рис. 4).
Отличительной особенностью данного типа турбины является то, что конструкция установки состоит из двух рядов “рабочих” лопастей. Рабочее колесо охвачено внешним контуром неподвижных направляющих лопастей (называемых статором), которые принимают набегающий поток воздуха и направляют его на ротор (ветроколесо) под заданным углом. Наличие статора повышает производительность турбины за счет создания вихрей низкого давления, увеличивает поток воздуха через турбину, при порывах ограничивает число оборотов, делает ветрогенератор более безопасным, бесшумным и надежным. Исследования показывают [19, 20], что ветроустановки многолопастного типа могут обеспечить удовлетворительный уровень шума и низкий уровень вибраций за счет наличия внешнего контура.
6. РЕЗУЛЬТАТЫ И ВЫВОДЫ
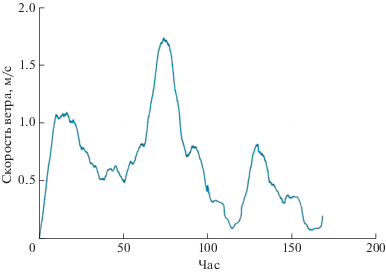
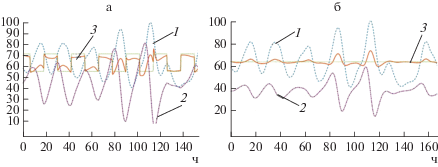
Решение задачи (21), необходимое для вычисления ограничений при решении (3), имеет типичный вид, представленный на рис. 5. Решение получено для усредненного графика ветровой активности, представленного на рис. 6, построенного на основании аппроксимации многомесячных экспериментальных данных в горных районах Таджикистана. На рис. 5 представлены некоторые решения задачи (21), генерируемые в ходе решения (3), при этом решение, представленное на рис. 5а, соответствует относительно большому уровню Δ, а решение, представленное на рис. 5б, соответствует относительно малому уровню Δ.
Рис. 5.
Типичные решения задачи (21). На графиках: 1 – мощность вариативной части нагрузки, 2 – энергия, запасенная в накопителе, 3 – мощность, генерируемая МГЭС.
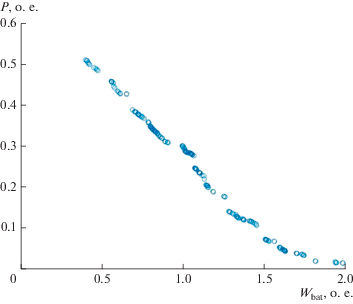
Решение (3) представлено на рис. 7, где по оси ординат в относительных единицах (приведено к ${{P}_{{{\text{ave}}}}}$) отложен первый из минимизируемых функционалов (${{P}_{{{\text{wimd,}}\,{\text{max}}}}} + m{{P}_{{{\text{bat,}}\,{\text{max}}}}},$ для $m = 1$), а по оси абсцисс, также в относительных единицах (приведено к ${{P}_{{{\text{ave}}}}}$) отложен второй минимизируемый функционал $\left( {1080h{{P}_{{{\text{wind,}}\,{\text{ave}}}}}} \right).$ Уровень Δ неравномерности загрузки МГЭС – ~0.1. Множество Парето, представленное на рис. 7, позволяет в широком диапазоне изменения параметров всей системы определять ее состав оптимальным образом.
Список литературы
Фортов В.Е., Попель О.С. Состояние развития возобновляемых источников энергии в мире и в России // Теплоэнергетика. 2014. № 6. С. 4.
Strachan P.A. et al. Promoting community renewable energy in a corporate energy world //Sustainable Development. 2015. T. 23. № 2. C. 96–109.
Абдуллаев Ф.С., Баканин Г.В., Горзон С.М. и др. Гидроэнергетические ресурсы Таджикской ССР. Ленинград: Недра, 1965. 658 с.
Послание Президента Республики Таджикистан от 23.04.2014 г. [Электронный ресурс] http://mmk.tj/ru/president/letter/2014
Постановление Правительства Республики Таджикистан № 795 от 30.12.2015 г. “О Программе освоения возобновляемых источников энергии и строительства малых гидроэлектростанций на 2016–2020”.
Сайт Министерства энергетики и водных ресурсов Республики Таджикистан http://mewr.tj/ ?page_id=549
Киргизов А.К. К вопросу использования малой гидроэнергетики в условиях Таджикистана / А.К. Киргизов. М.Б. Иноятов // Вестник Таджикского технического университета. 2008. № 2(18). С. 38–42.
Тресман А.Г. Кривые обеспеченности и естественная зарегулированность стока рек Таджикистана / А.Г. Тресман. Душанбе: Дониш, 1969. 168 с.
Деньщиков К.К. и др. Cуперконденсатoры в современной энергетике. Известия РАН. Энергетика. 2011. № 5. С. 125–132.
Коровкин Н.В., Потиенко А.А. Использование генетического алгоритма для решения электротехнических задач. Электричество. № 11. 2002.
Deb K., Agrawal S., Pratap A., Meyarivan T. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II. In: Schoenauer M. et al. (eds) Parallel Problem Solving from Nature PPSN VI. PPSN 2000. Lecture Notes in Computer Science, vol. 1917. Springer, Berlin, Heidelberg.
Демирчян К.С. Теоретические основы электротехники / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин // С-Пб.: Питер, 2009. 446 с.
Твайделл Дж. Возобновляемые источники энергии / Твайделл Дж., Уэйр А. // Пер. с англ. М.: Энергоатомиздат, 1990. 392 с.
Kane M. World trends in wind energy. A focus per country. Analysis //Systemes Solaires. Le Journal de l’Eolien. 2016. C. 24–31.
Кирпичникова И.М. Ветроэнергетическая установка с вертикальной осью врещения / И.М. Кирпичникова, Е.В. Соломин // Вестник ЮУрГУ, серия “Энергетика”. 2008. Вып. 10. № 26. С. 32–35.
Де Рензо Д. Ветроэнергетика. / Под ред. Д. де Рензо: Пер. с англ.; под ред. Шефтера Я.И. М.: Энергоатомиздат, 1982. 272 с, ил.
Фатеев Е.М. Ветродвигатели и ветроустановки. М.: Сельхозиздат, 1957. 536 с.
Khoharo H., Kumar L., Jamali M.S. Modeling and Comparative Performance Analysis of Different Bladed Vertical Axis Wind Turbine (VAWT) // 2018 International Conference and Utility Exhibition on Green Energy for Sustainable Development (ICUE). IEEE. 2018. C. 1–7.
Горелов Д.Н., Кузьменко Ю.Н. Экспериментальная оценка предельной мощности ветроколеса с вертикальной осью вращения // Теплофизика и аэромеханика. 2001. Т. 8. № 2. С. 329–334.
Power correlation for vertical axis wind turbines with varying geometries. International Journal of Energy Research 2010. 35 : 423–435. https://doi.org/10.1002/er.1703
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика