Известия РАН. Энергетика, 2019, № 4, стр. 98-107

Математическое моделирование теплопереноса в технологическом водоеме-охладителе

Г. В. Кузнецов¹, В. И. Максимов^1, *

¹ Национальный исследовательский Томский политехнический университет
Томск, Россия

Поступила в редакцию 16.04.2019
После доработки 08.08.2019
Принята к публикации 12.08.2019

DOI: 10.1134/S0002331019040083

Аннотация

Представлены результаты математического моделирования гидродинамики и теплопереноса в технологическом водоеме-охладителе с учетом турбулентного характера течения жидкости. Исследованы режимы смешанной конвекции в открытом водоеме с участками ввода и вывода воды при различных параметрах входного потока. Рассматривалась плоская нестационарная задача в рамках модели Навье-Стокса в безразмерных переменных “вихрь скорости–функция тока–температура” для жидкости и уравнении теплопроводности для стенок. Дополнительно введены в рассмотрение уравнения $k - \varepsilon $ модели с соответствующими краевыми условиями. Система нестационарных уравнений динамики вязкой жидкости решена методом конечных разностей с использованием итерационного алгоритма, разработанного для решения нелинейных задач теплопереноса в условиях интенсивного локального тепловыделения. Использовалась неравномерная разностная сетка. Получены распределения гидродинамических параметров и температур, характеризующие основные закономерности исследуемых процессов. Выделены циркуляционные течения и проведен анализ механизма образования вихрей и распределения температуры в области решения при режимах вынужденной конвекции, числах Рейнольдса (10⁴ ≤ Re ≤ 10⁷) и Грасгофа (Gr ≥ 10¹²). Результаты исследований позволяют сделать вывод о возможности использования уравнений Навье-Стокса в переменных “вихрь скорости–функция тока” для моделирования достаточно сложных по своему характеру течений в режиме турбулентной смешанной конвекции в открытых технологических водоемах-охладителях. Выявлено, что скорость потока оборотной воды на входе в водоем существенно влияет на гидродинамику течения и распределение температуры. Варьирование числа Re в относительно небольшом диапазоне приводит к масштабным изменениям структуры потоков жидкости. Установлено, что, изменяя интенсивность притока оборотной воды, можно управлять тепловым режимом водоема в условиях ввода и отвода массы в режиме смешанной конвекции.

Ключевые слова: водоем-охладитель, математическое моделирование, смешанная конвекция, турбулентность

ВВЕДЕНИЕ

Проблема загрязнения технологических водоемов промышленных предприятий не только сохраняет свою значимость [1–5] в течение последних десятилетий, но с каждым годом становится все более актуальной в связи с общим ухудшением состояния окружающей среды [6]. Одним из важнейших аспектов этой крупной научно-технической проблемы является образование и распространение микроорганизмов, бактерий и водорослей [4, 6–10] в технологических водоемах. Условия и характеристики процессов развития микроорганизмов и водорослей определяются, в основном, тепловым режимом среды, в которой они присутствуют [7, 10]. Поэтому анализ интенсивности загрязнения технологических водоемов наиболее типичными природными загрязнителями возможен только при достоверной оценке температурных полей водоемов. Решение же задачи теплопереноса в рассматриваемых условиях сопряжено с описанием не только процессов теплопроводности, но и конвекции в условиях достаточно интенсивного притока оборотной воды, ее отведения и отвода теплоты в грунт (или подвода) по большей части внешнего контура водоема и охлаждения или нагрева на границе раздела “вода–воздух”.

Предпринимались попытки решения задачи теплопереноса в технологических водоемах тепловых электростанций [4, 5, 7, 11–13]. Но в этих работах рассмотрены диапазоны изменения параметров, соответствующие ламинарным режимам течения жидкости. В реальной же практике перенос массы, импульса и энергии при циркуляции воды в технологических водоемах происходит в условиях развитой турбулентности, обусловленной как локальностью ввода массы, так и большими размерами областей движения воды. Представляет интерес решение задачи теплопереноса в технологическом водоеме с учетом конвекции и теплопроводности, а также турбулентного режима течения жидкости в области с тремя непроницаемыми стенками, одной свободной поверхностью, наличием источников ввода и вывода массы. Также целесообразно сопоставление результатов решения задач в условиях ламинарного и турбулентного режимов течения.

Цель работы – математическое моделирование теплопереноса в технологическом водоеме в рамках модели, отличающейся от известных учетом турбулентного характера течения жидкости.

ФИЗИЧЕСКАЯ МОДЕЛЬ

Проведено моделирование турбулентного течения несжимаемой вязкой жидкости и теплопереноса в прямоугольной области с двумя вертикальными и одной горизонтальной стенками конечной толщины и одной свободной поверхностью (рис. 1). На внешних границах области рассматривались неоднородные условия теплообмена. Неоднородность обусловлена различными теплофизическими характеристиками сред и условиями отвода или подвода теплоты на границах области решения. Испарение воды на свободной поверхности не учитывалось, так как интенсивность этого процесса не настолько велика, чтобы изменить конфигурацию свободной поверхности. Ввод воды с более высокой температурой по сравнению со средней температурой водоема осуществлялся на левой вертикальной границе (в ее нижней части), а отвод в верхней части правой вертикальной границы (рис. 1). Рассматривался нестационарный процесс теплопереноса в связи с необходимостью учета теплоемкости материала твердых стенок (способности аккумулировать тепло) и значимыми перепадами температур между втекающей в водоем жидкостью и начальной температурой среды.

Рис. 1.

Область решения задачи: (1) твердая стенка; (2, 3) участки ввода и вывода жидкости в полость; (4) жидкость; (5) свободная поверхность жидкости; (6) внешние границы твердых стенок.

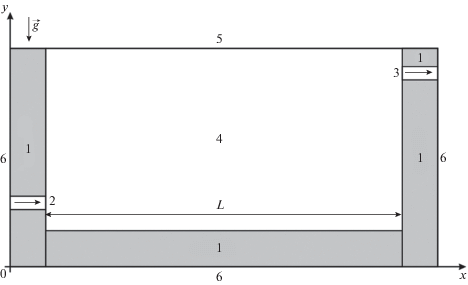
Возможны различные варианты расположения каналов ввода и вывода воды. Выбран наиболее типичный, с одной стороны, вариант (рис. 1), реализация которого, с другой стороны, приводит к формированию достаточно интересных для анализа тепловых режимов структур течения жидкости. При постановке задачи также предполагалось, что теплообмен на границах раздела “жидкость–твердая стенка” можно описать условиями четвертого рода, а на внешних границах области решения интенсивность теплопередачи не зависит от времени [11–13].

Представляет интерес изучение влияния условий теплообмена на внешних границах области решения (рис. 1) на тепловой режим водоема. Эти условия не только определяют интенсивность теплоотвода (или теплопритока), но и могут оказывать существенное влияние на режим течения жидкости. Известно [7–10], что изменение температуры воды на несколько градусов приводит в определенных условиях к росту скорости размножения микроорганизмов в 1.5–1.7 раза. Поэтому локальный теплоотвод (или подвод энергии) могут кардинально изменить условия существования микроорганизмов.

Исходя из анализа различных возможных вариантов реализации рассматриваемой схемы на практике, можно на правой, левой и нижней границах области решения использовать при постановке задачи граничные условия 1–3 или 4-го рода. При этом надо иметь ввиду, что для корректного использования условий четвертого рода при решении уравнения энергии необходимо расширять размеры области анализа путем ввода дополнительных подобластей до значений пространственных координат, при которых фронт прогрева не достигает этих внешних “дополнительных” границ. Такой подход повышает достоверность результатов моделирования, но существенно усложняет алгоритм решение задачи. Использование же наиболее традиционных условий теплоизоляции на внешних границах области (рис. 1) может вносить большие погрешности в решение, так как даже при умеренных градиентах температур всегда возможен значимый (при больших временах) сток тепла во внешнюю среду с этих границ. По выше изложенным причинам для численного моделирования выбраны граничные условия второго рода на внешних границах области [11–13].

Специфика рассматриваемой задачи заключается в процессах, протекающих на свободной поверхности жидкости. Возникает проблема граничных условий, как для уравнения энергии, так и для уравнений движения на этой границе. На практике эти условия не могут быть заданы точно. При математическом моделировании и последующем решении сопряженной задачи возникают практически непреодолимые препятствия в связи с неоднозначностью описания свободноконвективного течения воздушной среды вблизи свободной поверхности, движущейся даже с относительно небольшими скоростями жидкости. По этим причинам область решения ограничивалась свободной поверхностью. Также предполагалось, что на этой границе обоснованно использование граничных условий третьего рода для уравнения энергии. В рамках такого приближения необходима информация по температуре воздуха вблизи открытой поверхности водоема, а также скорости ветра при попытках максимально приблизить результаты математического моделирования к реальной практике. Расчет коэффициента теплоотдачи для рассматриваемых условий возможен в рамках общих рекомендаций.

Моделирование теплоотвода с трех внешних непроницаемых (рис. 1) границ области решения (соответствующих области контакта “вода–грунт”) проводилось с использованием граничных условий второго рода [14–16]. Такой, на первый взгляд, формальный прием, имеет не худший, чем другие варианты, физический смысл. Вследствие большой энергоемкости грунта (или бетонных стенок водоема) сток тепла на этой границе можно считать практически постоянным при известной температуре воды в водоеме. Выбор же значений q всегда может быть проведен с требуемой для практики или для обоснования достоверности результатов теоретического анализа точностью [15–17]. Так, например, такой выбор может быть реализован при решении нелинейной задачи путем расчета на каждой последующей итерации величины q, исходя из полученного на предыдущей итерации градиента температур вблизи границы раздела сред. Кроме этого достаточно точно могут быть установлены значения теплового потока по исходным данным каждой задачи. Последнее создает объективные условия для получения достоверных результатов при моделировании процессов теплоотвода в грунт.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОД РЕШЕНИЯ

Система нестационарных уравнений Навье-Стокса для жидкости и уравнением теплопроводности для твердых стенок, соответствующая принятой физической модели рассматриваемого процесса, в целом незначительно отличается от математической модели [11–13]. Дополнительно введены в рассмотрение уравнения $k - \varepsilon $ модели с соответствующими краевыми условиями. Задача решалась в безразмерной постановке.

Для приведения системы уравнений неразрывности, турбулентного движения и энергии к безразмерному виду использовались следующие соотношения:

$\begin{gathered} X = \frac{x}{L},\,\,\,\,Y = \frac{y}{L},\,\,\,\,\tau = \frac{t}{{{{t}_{0}}}},\,\,\,\,U = \frac{u}{{{{V}_{{in}}}}},\,\,\,\,V = \frac{{v}}{{{{V}_{{in}}}}},\,\,\,\,\Theta = \frac{{T - {{T}_{0}}}}{{\Delta T}},\,\,\,\,\Psi = \frac{\psi }{{{{\psi }_{0}}}}, \\ \Omega = \frac{\omega }{{{{\omega }_{0}}}},\,\,\,\,\Delta T = {{T}_{{in}}} - {{T}_{0}},\,\,\,\,{{\psi }_{0}} = {{V}_{{in}}}L,\,\,\,\,{{\omega }_{0}} = \frac{{{{V}_{{in}}}}}{L},\,\,\,\,K = {k \mathord{\left/ {\vphantom {k {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}},\,\,\,\,E = {\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}, \\ \end{gathered} $

где x, y – размерные координаты; X, Y – безразмерные координаты, соответствующие x, y; L – длина полости по оси x; t₀ – масштаб времени; τ – безразмерное время;

u, v – скорости по осям x, y соответственно; U, V – безразмерные скорости, соответствующие u, v; V_in – масштаб скорости (скорость жидкости на входе); Θ – безразмерная температура; T₀ – температура жидкости и твердого тела в начальный момент времени; T_in – температура жидкости на входе; ψ – функция тока; ψ₀ – масштаб функции тока; Ψ – безразмерный аналог ψ; ω – вихрь скорости; ω₀ – масштаб вектора скорости; Ω – безразмерный аналог ω, k – кинетическая энергия турбулентности; k₀ – масштаб кинетической энергии турбулентности; K – безразмерный аналог кинетической энергии турбулентности; ε – скорость диссипации кинетической энергии турбулентности; ε₀ – масштаб скорости диссипации кинетической энергии турбулентности; E – безразмерный аналог скорости диссипации кинетической энергии турбулентности.

Уравнения Навье-Стокса в приближении Буссинеска в безразмерных переменных “вихрь скорости–функция тока–температура” для воды (режим смешанной конвекции) и уравнение теплопроводности для твердых стенок будут иметь вид [14, 17]:

$\begin{gathered} \frac{{\partial \Omega }}{{\partial \tau }} + U\frac{{\partial \Omega }}{{\partial X}} + V\frac{{\partial \Omega }}{{\partial Y}} = \frac{{{{\partial }^{2}}}}{{\partial {{X}^{2}}}}\left[ {\left( {\frac{1}{{\operatorname{Re} }} + \frac{1}{{{{{\operatorname{Re} }}_{t}}}}} \right)\Omega } \right] + \frac{{{{\partial }^{2}}}}{{\partial {{Y}^{2}}}}\left[ {\left( {\frac{1}{{\operatorname{Re} }} + \frac{1}{{{{{\operatorname{Re} }}_{t}}}}} \right)\Omega } \right] + \frac{{\operatorname{Gr} }}{{{{{\operatorname{Re} }}^{2}}}}\frac{{\partial \Theta }}{{\partial Y}} + \\ + \,\,2\frac{{\partial U}}{{\partial Y}}\frac{{{{\partial }^{2}}}}{{\partial {{X}^{2}}}}\left( {\frac{1}{{{{{\operatorname{Re} }}_{t}}}}} \right) - 2\frac{{\partial V}}{{\partial X}}\frac{{{{\partial }^{2}}}}{{\partial {{Y}^{2}}}}\left( {\frac{1}{{{{{\operatorname{Re} }}_{t}}}}} \right) + 2\left( {\frac{{\partial V}}{{\partial Y}} - \frac{{\partial U}}{{\partial X}}} \right)\frac{{{{\partial }^{2}}}}{{\partial X\partial Y}}\left( {\frac{1}{{{{{\operatorname{Re} }}_{t}}}}} \right), \\ \end{gathered} $$\frac{{\partial \Theta }}{{\partial \tau }} + U\frac{{\partial \Theta }}{{\partial X}} + V\frac{{\partial \Theta }}{{\partial Y}} = \frac{\partial }{{\partial X}}\left[ {\left( {\frac{1}{{\operatorname{PrRe} }} + \frac{1}{{{{{\Pr }}_{t}}{{{\operatorname{Re} }}_{t}}}}} \right)\frac{{\partial \Theta }}{{\partial X}}} \right] + \frac{\partial }{{\partial Y}}\left[ {\left( {\frac{1}{{\operatorname{PrRe} }} + \frac{1}{{{{{\Pr }}_{t}}{{{\operatorname{Re} }}_{t}}}}} \right)\frac{{\partial \Theta }}{{\partial Y}}} \right],$

$\frac{{{{\partial }^{2}}\psi }}{{\partial {{X}^{2}}}} + \frac{{{{\partial }^{2}}\psi }}{{\partial {{Y}^{2}}}} = - \Omega ,$

$\begin{gathered} \frac{{\partial K}}{{\partial \tau }} + U\frac{{\partial K}}{{\partial X}} + V\frac{{\partial K}}{{\partial Y}} = \frac{\partial }{{\partial X}}\left[ {\left( {\frac{1}{{\operatorname{Re} }} + \frac{1}{{{{\sigma }_{k}}{{{\operatorname{Re} }}_{t}}}}} \right)\frac{{\partial K}}{{\partial X}}} \right] + \\ + \,\,\frac{\partial }{{\partial Y}}\left[ {\left( {\frac{1}{{\operatorname{Re} }} + \frac{1}{{{{\sigma }_{k}}{{{\operatorname{Re} }}_{t}}}}} \right)\frac{{\partial K}}{{\partial Y}}} \right] + {{{\tilde {P}}}_{k}} + {{{\tilde {G}}}_{k}} - E, \\ \end{gathered} $

$\frac{1}{{\operatorname{Fo} }}\frac{{\partial \Theta }}{{\partial \tau }} = \frac{{{{\partial }^{2}}\Theta }}{{\partial {{X}^{2}}}} + \frac{{{{\partial }^{2}}\Theta }}{{\partial {{Y}^{2}}}},$

здесь Gr = $\frac{{{\text{g}}\beta {{L}^{{\text{3}}}}\Delta T}}{{{{{v}}^{2}}}}$ – число Грасгофа; ${{\operatorname{Re} }_{t}} = \frac{E}{{{{c}_{{\mu }}}{{K}^{2}}}}$ – турбулентное число Рейнольдса; ${{\tilde {P}}_{k}} = \frac{1}{{{{{\operatorname{Re} }}_{t}}}}\left[ {2{{{\left( {\frac{{\partial U}}{{\partial X}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial V}}{{\partial X}}} \right)}}^{2}}} \right.$ + $\left. {{{{\left( {\frac{{\partial U}}{{\partial X}} + \frac{{\partial V}}{{\partial X}}} \right)}}^{2}}} \right];$ ${{\tilde {G}}_{k}} = - \frac{1}{{{{{\operatorname{Re} }}_{t}}{{{\Pr }}_{t}}}}\frac{{\partial \Theta }}{{\partial Y}};$ $\beta $ – температурный коэффициент объемного расширения; g – ускорение, создаваемое массовыми силами; Re = $\frac{{2VL}}{{v}}$ – число Рейнольдса; Pr = $\frac{\nu }{a}$ – число Прандтля; Fo = $\frac{{a{{t}_{0}}}}{{{{L}^{2}}}}$ – число Фурье; $a$ – коэффициент температуропроводности; $\nu $ – коэффициент кинематической вязкости; с_μ = 0.09; с_1ε = 1.44; с_2ε = 1.92; с_1ε = 0.8; σ_ε = 1, 3; σ_κ = 1.

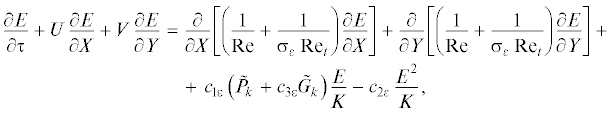
Начальные условия:

$\Psi (X,Y,0) = \Omega (X,Y,0) = \Theta (X,Y,0) = K(X,Y,0) = E(X,Y,0) = 0.$

Граничные условия:

– на внешнем контуре рассматриваемой области (кроме свободной поверхности жидкости) задаются граничные условия второго рода $\frac{{\partial \Theta }}{{\partial n}} = \operatorname{Ki} ;$

– на свободной поверхности жидкости:

$\frac{{{{\partial }^{2}}\Psi }}{{\partial {{Y}^{2}}}} = {{\tau }_{z}},\,\,\,\,\frac{{\partial {{\Theta }_{f}}(X,Y)}}{{\partial Y}} = \operatorname{Bi} {{\Theta }_{w}}(X,Y) + \operatorname{Bi} \frac{{{{T}_{0}} - {{T}_{e}}}}{{{{T}_{{in}}} - {{T}_{0}}}},\,\,\,\,{\text{E}} = {\text{K}} = 0$

– на внутренних границах раздела твердой и жидкой фазы:

$\Psi = 0,\,\,\,\,\frac{{\partial \Psi }}{{\partial (X,Y)}} = 0,$

$\left\{ \begin{gathered} {{\Theta }_{w}} = {{\Theta }_{f}} \hfill \\ \frac{{\partial {{\Theta }_{w}}}}{{\partial X}} = {{\lambda }_{{w,f}}}\frac{{\partial {{\Theta }_{f}}}}{{\partial X}} \hfill \\ \end{gathered} \right.,$

${\text{K = 0;}}$

– участок ввода жидкости:

$\Theta = 1,$

$\frac{{\partial \Psi }}{{\partial Y}} = {{\Psi }_{{in}}};\,\,\,\,\frac{{\partial E}}{{\partial X}} = 0,\,\,{\text{K = }}{{{\text{K}}}_{{in}}};$

– участок оттока жидкости:

$\frac{{\partial \Theta (X,Y)}}{{\partial Y}} = 0,$

$\frac{{\partial \Psi }}{{\partial Y}} = 0,\,\,\,\,\frac{{\partial E}}{{\partial X}} = 0,\,\,\,\,\frac{{\partial K}}{{\partial X}} = 0;$

для κ-ε модели вблизи твердой поверхности принимается

$\frac{{\partial K}}{{\partial n}} = 0;\,\,\,\,E = \frac{{c_{{\mu }}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}{{K}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{k\Delta n}},$

здесь $\operatorname{Ki} = \frac{{qL}}{{{{\lambda }_{w}}({{T}_{{in}}} - {{T}_{0}})}}$ – число Кирпичева; $\operatorname{Bi} = \frac{{{{\alpha }_{k}}L}}{{{{\lambda }_{w}}}}$ – число Био; ${{\tau }_{z}} = \frac{{\tau _{z}^{'}L}}{{{{V}_{{in}}}\mu }}$ – безразмерное касательное напряжение; $\tau _{z}^{'}$ – касательное напряжение на свободной поверхности; μ – динамическая вязкость жидкости; α_k – коэффициент теплообмена между внешней средой и рассматриваемой областью решения; T_e – температура окружающей среды; λ_w и λ_f – коэффициенты теплопроводности твердой и жидкой фаз; λ_w,f = = λ_w/λ_f – относительный коэффициент теплопроводности; q – тепловой поток на внешних границах области решения; Ψ_in и K_in – безразмерные аналоги функции тока и кинетической энергии турбулентности на входе.

Сформулированная выше система нестационарных уравнений динамики вязкой жидкости с соответствующими краевыми условиями решена методом конечных разностей с использованием итерационного алгоритма [14–16], разработанного для решения нелинейных задач теплопереноса в условиях интенсивного локального тепловыделения. Использовалась неравномерная разностная сетка. Выбор шагов по времени проводился аналогично [18] для обеспечения условий сходимости итерационного процесса. В качестве начального приближения использовались стационарные решения, полученные при малых числах Рейнольдса.

АНАЛИЗ РЕЗУЛЬТАТОВ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

В реальной практике параметры, характеризующие условия нагрева и охлаждения воды в технологических водоемах промышленных предприятий, изменяются в достаточно широких диапазонах. Так, например, температура воздуха в зимнее время года опускается до –20°С, а в летнее поднимается до +30°С. Численные исследования были проведены при следующих достаточно типичных значениях безразмерных и размерных величин: Pr = 7.1, 10⁴ ≤ Re ≤ 10⁷, Gr ≥ 10¹², T₀ = 293 K, 293 ≤ T_in ≤ 343 K, 273 ≤ T_e ≤ 297 K. Рассматривался открытый водоем глубиной 5 и длиной 10 м, толщина бетонных стенок 1 м. Ширина входного и выходного канала составляла 0.3 м.

Следует также отметить, что диапазоны изменения безразмерных величин и размерных характеристик выбирались исходя из следующих условий. Первое – соответствие диапазонам изменения параметров в реальных вариантах реализации таких систем “жидкость–твердое тело–газообразная внешняя среда”. Второе – реальные условия режимов как вынужденной, так и естественной конвекции без вырождения какого-либо из этих механизмов теплопереноса. Рассматривались в основном не самые благоприятные для реализации “сопряженного” теплопереноса диапазоны изменения, как размерных величин, так и безразмерных комплексов. Так, например, увеличение начальной температуры оборотной воды на 20–30° могло существенно изменить (при прочих равных условиях) соотношение между характерными временами реализации режимов вынужденной и естественной конвекции.

На рис. 2 приведены типичные результаты решения задачи при различных значениях числа Рейнольдса.

Рис. 2.

Структура течения (левая часть рисунка) и поле температур при: а – Re = 8 × 10⁵, б – Re = 3 × 10⁶, в – Re = 4 × 10⁶, г – Re = 8 × 10⁶. Gr = 4.56 × 10¹³. Размеры приведены в м, температуры – в К.

Линии тока и поля температур (рис. 2а) при Gr = 4.56 × 10¹³, Re = 8 × 10⁵ иллюстрируют образование одного обширного вихря в нижней части полости. “Горячая” жидкость, сливаемая в водоем, за счет сил естественной конвекции поднимается вверх, охлажденная, двигаясь вдоль дна, направляет основной поток к левой стенке и верхней границе полости. Хорошо видно, что распределение температуры в водоеме по глубине существенно неоднородно. Происходит это за счет того, что охлаждаемая жидкость в нижней части водоема практически не смешивается, как показывают результаты численного моделирования, с основным нагретым потоком.

На рис. 2б приведены линии тока и поле температур при Gr = 4.56 × 10¹³, Re = 3 × 10⁶. Хорошо видны две локальные вихревые структуры. Верхняя является следствием работы сил естественной и вынужденной конвекции. Относительно холодная жидкость опускается вдоль левой стенки, отжимая входной поток вниз. Нижний вихрь образован за счет доминирования вынужденной конвекции. В результате интенсивного движения основного потока и естественной конвекции при охлаждении жидкости за счет теплоотвода на правой и нижней границах образуется зона замкнутого циркуляционного течения. Вихрь в нижней части области обширнее своего аналога в верхней части, который ограничивается поднимающимся потоком остывающей, но еще достаточно горячей жидкости. Температурное поле отражает гидродинамику течения. При увеличении числа Re до 4 × 10⁶ поток нагретой и остывающей воды смещается вправо и верхний вихрь заметно расширяется (рис. 2в). При дальнейшем увеличении сил инерции (Re = 8 × 10⁶) в водоеме формируется по существу один обширный вихрь (рис. 2г). При этом вследствие высокой интенсивности вихря остывающая, но еще не холодная, жидкость поднимается вверх только вдоль правой стенки к выходному отверстию.

Анализ полученных результатов показывает, что скорость потока оборотной воды на входе в водоем существенно влияет на гидродинамику течения и распределение температуры. Варьирование числа Re в относительно небольшом диапазоне приводит к масштабным изменениям структуры потоков жидкости. Это позволяет сделать вывод о том, что изменяя интенсивность притока оборотной воды можно управлять тепловым режимом водоема в условиях ввода и отвода массы в режиме смешанной конвекции.

ЗАКЛЮЧЕНИЕ

Решение задачи сопряженного теплопереноса в водоеме-охладителе ТЭС иллюстрирует возможность моделирования существенно неоднородных температурных полей таких водоемов в условиях ввода нагретой до достаточной высоких температур оборотной воды и ее последующего охлаждения за счет конвекции и теплопроводности.

Полученные теоретические следствия дают новую информацию, которая не только характеризует конвективный режим течения оборотной воды в водоеме-охладителе, но и является дополнительной для построения и апробации моделей смешанной конвекции в областях с теплопроводными и аккумулирующими энергию стенками.

Результаты исследований показывают возможность использования уравнений Навье-Стокса в переменных “вихрь скорости – функция тока” для моделирования достаточно сложных по своему характеру течений в режиме турбулентной смешанной конвекции и при неоднородном теплообмене на внешних границах области решения.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-79-10015).

Список литературы

Попов В.М., Рябцев В.И., Рябцев Г.А. О тепловом загрязнении окружающей среды выбросами и сбросами ТЭС и ТЭЦ // Безопасность жизнедеятельности. 2002. № 4. С. 26–28.
Мадоян Аш. Ар., Паламарчук А.В., Мадоян Ар. Аш., Симагин А.С. Повышение эффективности использования охлаждающей воды прудов–охладителей АЭС и ТЭС // Экология промышленного производства. 2005. № 3. С. 49–52.
Горгуленко В.В., Тушкова Г.И. Экотоксикологическая оценка воды реки Ини и Беловского водохранилища (Кемеровская область) // Водные ресурсы. 2013. Т. 40. № 4. С. 367–374.
Kirillin G., Shatwell T., Kasprzak P. Consequences of thermal pollution from a nuclear plant on lake temperature and mixing regime // J. Hydrology. 2013. V. 496. P. 47–56.
Palancar M.C., Aragón J.M., Sánchez F., Gil R. Effects of warm water inflows on the dispersion of pollutants in small reservoirs // J. Environmental Management. 2006. V. 81. Iss. 3. P. 210–222.
Щур Л.А. Фитопланктон как индикатор состояния экосистемы водоема-охладителя березовской ГРЭС-1 (Красноярский край) // Водные ресурсы. 2009. Т. 36. № 5. С. 597–605.
Poornima E.H., Rajadurai M., Rao V.N.R., Narasimhan S.V., Venugopalan V.P. Use of coastal waters as condenser coolant in electric power plants: Impact on phytoplankton and primary productivity // J. Thermal Biology. 2006. V. 31. Iss. 7. P. 556–564.
Калайда М.Л., Новикова Г.В., Синютина Т.П., Шмакова А.А. Борьба с биообрастаниями – важная задача энерго- и ресурсосбережения // Энергетика Татарстана. 2008. № 3. С. 85–92.
Кириллов В.В., Зарубина Е.Ю., Митрофанова Е.Ю., Яныгина Л.В., Крылова Е.Н. Биологическая оценка последствий термического загрязнения водоема–охладителя Беловской ГРЭС // Ползуновский вестник. 2004. № 2. С. 133–141.
Страшкраба М., Гнаук А. Пресноводные экосистемы. Математическое моделирование. М.: Мир, 1989. 376 с.
Кузнецов Г.В., Максимов В.И. Численное исследование влияния условий неоднородного теплообмена на смешанную конвекцию в прямоугольной области с локальными источниками ввода и вывода массы // Известия Российской академии наук. Энергетика. 2008. № 4. С. 112–118.
Kuznetsov G.V., Maksimov V.I. Mathematical modeling of convective–conductive heat transfer in a rectangular domain in a conjugate statement // J. Engineering Thermophysics. 2007. V. 16 № 4. P. 270–275.
Кузнецов Г.В., Максимов В.И. Смешанная конвекция в прямоугольной области с локальными источниками ввода и вывода массы в условиях неоднородного теплообмена // Известия Томского политехнического университета. 2006. Т. 308. № 5. С. 114–118.
Kuznetsov G.V., Sheremet M.A. Numerical simulation of turbulent natural convection in a rectangular enclosure having finite thickness walls // International J. Heat and Mass Transfer. 2010. V. 53. P. 7812–7822.
Kuznetsov G.V., Sheremet M.A. Two-dimensional problem of natural convection in a rectangular domain with local heating and heat-conducting boundaries of finite thickness // Fluid Dynamics. 2006. V. 41. № 6. P. 881–890.
Kuznetsov G.V., Sheremet M.A. Conjugate natural convection in an enclosure with a heat source of constant heat transfer rate // International J. heat and mass transfer. 2011. V. 54. Iss. 1–3. P. 260–268.
Vardar N. Numerical analysis of the transient turbulent flow in a fuel oil storage tank// International J. Heat and Mass Transfer. 2010. V. 46. Iss. 18. P. 3429–3440.
Strakhov V.L., Garashchenko A.N., Kuznetsov G.V., Rudzinskii V.P. Mathematical simulation of thermophysical and thermo chemical processes during combustion of intumescent fire-protective coatings // Combustion, Explosion and Shock Waves. 2001. V. 37. Iss. 2. P. 178–186.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал