Известия РАН. Энергетика, 2019, № 4, стр. 58-66
Сопоставительный анализ выражений по расчету индуктивностей катушек с симметрией вращения
Г. Н. Цицикян 1, *, М. Ю. Антипов 1, **
1 Филиал “ЦНИИ СЭТ” ФГУП “Крыловский государственный научный центр”
Санкт-Петербург, Россия
* E-mail: george.20021940@mail.ru
** E-mail: posich@mail.ru
Поступила в редакцию 25.06.2019
После доработки 07.08.2019
Принята к публикации 12.08.2019
Аннотация
В известном руководстве по расчету индуктивностей П.Л. Калантарова и Л.А. Цейтлина (изд. 3, 1986 г.), содержатся формулы, таблицы и кривые для расчета собственных и взаимных индуктивностей проводов, контуров и катушек различной геометрии. При расчете конструкций, обладающих симметрией вращения, их индуктивности и взаимные индуктивности, как правило, записаны в виде выражений, содержащих величины, значения которых сведены в таблицы или даны в виде рядов в зависимости от отношений, определяемых геометрическими размерами (главы 6 и 7), и число учитываемых членов ряда связано с допускаемой погрешностью. Вместе с тем для получения практических оценок весьма важно наличие аппроксимирующих формул при соблюдении достаточной точности расчета, а тем более готовых замкнутых выражений в пределах общепринятой идеализации. В этом контексте важную роль играют замкнутые выражения для индуктивности катушек прямоугольного сечения и взаимной индуктивности двухслойных соленоидов, основанных на публикации A. Gray “Absolute Measurements in Electricity and Magnetism”, Macmillan and Co. ltd, 1921, но не получившей распространения в отечественной литературе. Этому вопросу посвящена представленная статья, в которой с целью проверки предпринят соответствующий сопоставительный анализ.
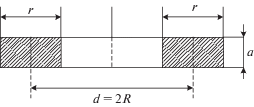
В литературе по расчету индуктивностей катушек с симметрией вращения особое место занимают формулы, представленные в [1, 2], которые практически не встречаются в известной учебной и справочной литературе, и поэтому требуют дополнительной проверки и подтверждения. Учитывая их простоту, [1, формулы приложения 10–12], целесообразно провести сопоставительный анализ с известными рекомендациями, также имеющими свои ограничения, и на этой основе сформулировать соответствующие выводы о возможности или невозможности их применения. В работах [1, 2] даны одни и те же формулы для кругового кольца прямоугольного сечения, а в работе [1] – для индуктивности соленоида и для взаимной индуктивности концентрических соленоидов в общем случае неодинаковой длины. Первая из перечисленных конфигураций показана на рис. 1.
Индуктивность катушки прямоугольного сечения, изображенной на рис.1, на основании формулы (10) приложения [1] определяется выражением в следующей откорректированной форме записи:
(1)
$L = {{\mu }_{0}}R\left( {{\text{ln}}\frac{{8R}}{{{{R}_{1}}}} - 2} \right) = {{\mu }_{0}}R\left( {{\text{ln}}\frac{{8R}}{{{{{\left( {{{r}^{2}} + {{a}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} + \ln \frac{{{{{\left( {{{r}^{2}} + {{a}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{R}_{1}}}} - 2} \right),$Величина ${{R}_{1}}$ в выражении (1) является средним геометрическим расстоянием площади прямоугольника со сторонами $r$ и a.
В результате выражение (1) перезаписывается в виде:
(2)
$\begin{gathered} L = {{\mu }_{0}}R\left( {\ln \frac{{8R}}{{{{{\left( {{{r}^{2}} + {{a}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} + \frac{{{{r}^{2}}}}{{12{{a}^{2}}}}\ln \left( {1 + \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right) + \frac{{{{a}^{2}}}}{{12{{r}^{2}}}}\ln \left( {1 + \frac{{{{r}^{2}}}}{{{{a}^{2}}}}} \right) - } \right. \\ \left. {_{{_{{_{{}}^{{^{{^{{}}}}}}}}^{{}}}}^{{^{{^{{}}}}}} - \,\,\frac{{2r}}{{3a}}{\text{arctg}}\frac{a}{r} - \frac{{2a}}{{3r}}{\text{arctg}}\frac{r}{a} + \frac{1}{{12}}} \right), \\ \end{gathered} $(3)
${{L}_{{r = a}}} = {{\mu }_{0}}R\left( {\ln \frac{{8R}}{a} + \frac{1}{{12}} - \frac{2}{3} + \frac{1}{{12}}} \right) = {{\mu }_{0}}R\left( {\ln \frac{{8R}}{a} - \frac{1}{2}} \right).$Умножая выражение (3) на ${{w}^{2}},$ где $w$ – количество витков, распределенных вдоль $a$ (рис. 1), и заменяя в (3) обозначение $R$ на $\frac{d}{2}$ получим выражение, известное как аппроксимирующая формула Уилера [3]:
(4)
$L = \frac{{{{\mu }_{0}}{{w}^{2}}d}}{2}\left( {\ln \frac{{4d}}{a} - \frac{1}{2}} \right) = \frac{{{{\mu }_{0}}{{w}^{2}}d}}{2}\left( {\ln \left( {\frac{{d\pi }}{a}} \right) - 0.2584} \right).$Так как выражение (2) при перестановке $r$ на $a$ и наоборот, остается неизменным, то при $a \ll r$ (рис. 1) индуктивность (1) оказывается равной
Формула (5) может быть получена из выражений (6–9) и (6–10) справочника [4] при $w = 1,0$ и $\rho = \frac{r}{{2R}} < 0.5,$ если в (6–10) пренебречь всеми членами по порядку малости равными или большими, чем ${{\rho }^{2}},$ и тогда будем иметь:
Теперь можно сопоставить численные значения для $L$ при $r = a,$ т.е. для дисковой катушки квадратного сечения по выражению (2) с численным значением, вытекающим из формул справочника (6–13) и (6–14) при $\alpha = \frac{a}{d} = \frac{a}{{2R}} \leqslant 0.2.$
Тогда из (6–13) и (6–14) получаем следующее приближение $\left( {w = 1,0} \right){\text{:}}$
по которому при $\frac{a}{{2R}} = 0.2$ имеем: $1.8008{{\mu }_{0}}R,$ а в соответствии с выражением (2) при $r = a{\text{:}}$Рассмотрим характерный случай, когда средний диаметр катушки квадратного сечения равен утроенному размеру стороны сечения, т.е. $r = a$ и $2R = d = 3a$ (рис. 1). Тогда согласно выражению (2) получим, что
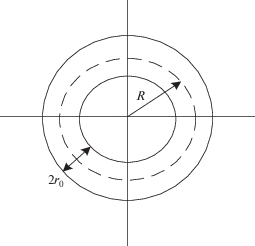
Сопоставим выражения для индуктивности круглого кольца в соответствии с рис. 2. Для индуктивности круглого кольца со средним радиусом $R$ и радиусом ${{r}_{0}}$ сечения кольца в [5, 6] рекомендовано следующее выражение:
(6)
$L \approx {{L}_{{{\text{ВНЕШ}}}}} = {{\mu }_{0}}R\left( {\ln \frac{{8R}}{{{{r}_{0}}}} - 2} \right).$Выражение (6) можно получить на основе представления для взаимной индуктивности двух соосных круговых контуров, расположенных в одной плоскости с радиусами $R$ и $\left( {R - {{r}_{0}}} \right)$ через сферическую функцию Лежандра с полуцелым индексом:
(7)
$M = {{L}_{{{\text{ВНЕШ}}}}} = {{\mu }_{0}}\sqrt {R\left( {R - {{r}_{0}}} \right)} {{Q}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( g \right),$где $g = \frac{{{{R}^{2}} + {{{\left( {R - {{r}_{0}}} \right)}}^{2}}}}{{2R\left( {R - {{r}_{0}}} \right)}}$ = $1 + \frac{{{{{\left( {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R}} \right)}}^{2}}}}{{2\left( {1 - \frac{{{{r}_{0}}}}{R}} \right)}} \cong 1 + \frac{1}{2}{{\left( {\frac{{{{r}_{0}}}}{R}} \right)}^{2}} = 1 + \Delta g,$ и при этом выражение для ${{Q}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(g)$ при $\Delta g \ll 1$ может быть записано в виде [7, формула П.II-4]:
Окончательно
(8)
$\begin{gathered} {{L}_{{{\text{ВНЕШ}}}}} = {{\mu }_{0}}{{\left( {R\left( {R - {{r}_{0}}} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left[ {\ln \frac{{8R}}{{{{r}_{0}}}} - \ln 4 - 0.6137} \right] = \\ = {{\mu }_{0}}{{\left( {R\left( {R - {{r}_{0}}} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left[ {\ln \frac{{8R}}{{{{r}_{0}}}} - 2} \right], \\ \end{gathered} $При ${{r}_{0}} \ll R$ разницей между (6) и (8) можно пренебречь.
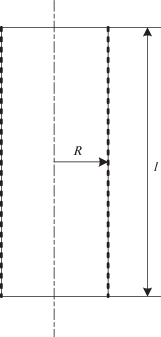
Продолжая сопоставления, заметим, что формула (11) для индуктивности соленоида [1] (рис. 3), записанная в виде
где $K = \frac{2}{3}\left\{ {\frac{{K\left( k \right) + \left( {{\text{t}}{{{\text{g}}}^{2}}\alpha - 1} \right)E\left( k \right)}}{{\sin \alpha }} - {\text{t}}{{{\text{g}}}^{2}}\alpha } \right\},$ проверяется при условии, что $K\left( k \right)$ и $E\left( k \right)$ являются полными эллиптическими интегралами 1-го и 2-го рода от k, а не от k', связанных между собой соотношением ${{k}^{2}} + {{\left( {k{\kern 1pt} '} \right)}^{2}} = 1,$ и при этом ${{\left( {k{\kern 1pt} '} \right)}^{2}} = \frac{{{{l}^{2}}}}{{{{l}^{2}} + {{{\left( {2R} \right)}}^{2}}}}$ и ${\text{ctg}}\alpha = \frac{l}{{2R}}.$ Тогда формула (9) может быть перезаписана в виде [8]:(10)
$L = {{\mu }_{0}}\frac{{8{{R}^{3}}}}{{3{{\varepsilon }^{2}}}}\left\{ { - 1 + {{k}^{{ - 3}}}\left( {1 - {{k}^{2}}} \right)K + {{k}^{{ - 3}}}\left( {2{{k}^{2}} - 1} \right)E} \right\},\,\,\,\,{\text{где}}\,\,\,\,\varepsilon = {l \mathord{\left/ {\vphantom {l w}} \right. \kern-0em} w}.$Следует обратить внимание и на аппроксимирующее выражение для индуктивности соленоида с шагом между витками, обозначенным, как $s$ и диаметром витка d, предложенное в [9] в виде формулы (9), которая при введенных обозначениях имеет вид:
(11)
$L = \frac{{{{\mu }_{0}}\pi {{d}^{2}}{{w}^{2}}}}{{4\sqrt {{{d}^{2}} + {{{\left( {w - 1} \right)}}^{2}}{{s}^{2}}} }} = \frac{{{{\mu }_{0}}\pi {{d}^{2}}{{w}^{2}}}}{{4\sqrt {{{d}^{2}} + {{l}^{2}}} }} = - \frac{{{{\mu }_{0}}\pi {{{{w}^{2}}{{d}^{2}}} \mathord{\left/ {\vphantom {{{{w}^{2}}{{d}^{2}}} l}} \right. \kern-0em} l}}}{{4{{{\left[ {{{{\left( {\frac{d}{l}} \right)}}^{2}} + 1} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}},$Формулу (11) можно сопоставить с формулой Уилера [3]
(12)
$L = \frac{{{{\mu }_{0}}\pi {{w}^{2}}{{{{d}^{2}}} \mathord{\left/ {\vphantom {{{{d}^{2}}} l}} \right. \kern-0em} l}}}{{4\left[ {1 + 0.45\frac{d}{l}} \right]}}.$Из сопоставления (11) и (12) видно, что различия будут проистекать из сравнения $\left( {1 + 0.45\frac{d}{l}} \right)$ с ${{\left[ {{{{\left( {\frac{d}{l}} \right)}}^{2}} + 1} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$
При $d = l$ имеем 1.45 против 1.414; при $d = 0.5l{\text{:}}$ 1.225 и соответственно 1.118, при $d = 1.2l - 1.54$ и $1.562,$ $d = 1.35l - 1.6075$ и $1.68$ т.е. разница в диапазоне изменения $\frac{d}{l}$ от 0.5 до 1.35 оказывается сравнительно небольшой.
В работе [8] приведены кривые по оценке погрешности вычислений индуктивности соленоида для большинства из известных работ, посвященных данному вопросу. В литературе [10] приведена замкнутая формула, пригодная как для длинного, так и для короткого соленоида. Эта формула в принятых обозначениях записывается в виде:
(13)
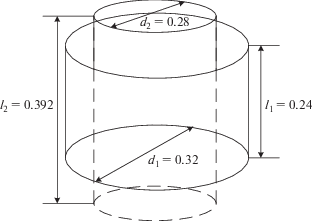
$L = {{\mu }_{0}}{{w}^{2}}\frac{d}{2}\left[ {\ln \left( {1 + \frac{{\pi d}}{{2l}}} \right) + \frac{1}{{2.3004 + 3.437\frac{l}{d} + 1.7636{{{\left( {\frac{l}{d}} \right)}}^{2}} - \frac{{0.47}}{{{{{\left( {0.755 + \frac{d}{l}} \right)}}^{{1.44}}}}}}}} \right].$Для конфигурации двухслойного соленоида, изображенного на рис. 4, результаты расчетов по нижеприведенной формулe (14), заимствованной из [1], а именно:
(14)
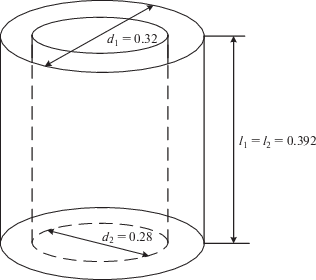
$M = \frac{{{{\mu }_{0}}\pi R_{2}^{2}{{w}_{1}}{{w}_{2}}}}{{2d}}\left[ {1 + \frac{{R_{1}^{2}R_{2}^{2}}}{{8{{d}^{4}}}}\left\{ {3 - \frac{{l_{1}^{2}}}{{R_{2}^{2}}}} \right\}} \right],$Продолжая сравнение сопоставим два выражения для взаимной индуктивности концентрических соленоидов одинаковой длины, вытекающих из выражений 7-2, 7-6 и 7-7 [4] в соответствии с рис. 5, и для двухслойного соленоида по формуле (14) в предположении, что ${{l}_{1}} = {{l}_{2}} = l$ и с радиусами слоев ${{R}_{2}} = \frac{{{{d}_{2}}}}{2}$ и ${{R}_{1}} = \frac{{{{d}_{1}}}}{2}.$
Имеем в соответствии с (14) при ${{l}_{1}} = {{l}_{2}} = l{\text{:}}$
(15)
$\begin{gathered} M = \frac{{{{\mu }_{0}}\pi {{{\left( {\frac{{{{d}_{2}}}}{2}} \right)}}^{2}}{{w}_{1}}{{w}_{2}}}}{{2{{{\left( {\frac{{d_{1}^{2}}}{4} + \frac{{{{l}^{2}}}}{4}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left\{ {1 + \frac{{{{{\left( {\frac{{{{d}_{1}}}}{2}} \right)}}^{2}}{{{\left( {\frac{{{{d}_{2}}}}{2}} \right)}}^{2}}}}{{8{{{\left( {\frac{{d_{1}^{2}}}{4}\, + \,\frac{{{{l}^{2}}}}{4}} \right)}}^{2}}}}\left( {3 - \frac{{4{{l}^{2}}}}{{d_{2}^{2}}}} \right)} \right\} = \\ = \frac{{{{\mu }_{0}}\pi {{{\left( {\frac{{{{d}_{2}}}}{2}} \right)}}^{2}}{{w}_{1}}{{w}_{2}}}}{{{{{\left( {d_{1}^{2} + {{l}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left\{ {1 + \frac{{d_{1}^{2}d_{2}^{2}}}{{8{{{\left( {d_{1}^{2} + {{l}^{2}}} \right)}}^{2}}}}\left( {3 - \frac{{4{{l}^{2}}}}{{d_{2}^{2}}}} \right)} \right\}.~ \\ \end{gathered} $В выражениях 7-2, 7-6 и 7-7 [4] ограничимся двумя членами разложения. Тогда по справочнику [4] можем записать:
(16)
${{M}_{{{\text{СПР}}}}} = \frac{{{{\mu }_{0}}{{w}_{1}}{{w}_{2}}}}{{{{l}^{2}}}}\frac{\pi }{8}~d_{2}^{2}{{d}_{1}}\left[ { - 1 + \frac{{{{{\left( {d_{1}^{2} + 4{{l}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{d}_{1}}}} + \frac{1}{8}{{{\left( {\frac{{{{d}_{2}}}}{{{{d}_{1}}}}} \right)}}^{2}}\left\{ {1 - \frac{{d_{1}^{3}}}{{{{{\left( {d_{1}^{2} + 4{{l}^{2}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right\}} \right].$В частности, при $l = {{d}_{1}}$ из (15) и (16) соответственно находим:
(17)
$M\left( {l = {{d}_{1}}} \right) = \frac{{{{\mu }_{0}}{{w}_{1}}{{w}_{2}}\pi d_{2}^{2}}}{{{{d}_{1}}}}\frac{1}{{4\sqrt 2 }}\left[ {1 + \frac{1}{{32}}{{{\left( {\frac{{{{d}_{2}}}}{{{{d}_{1}}}}} \right)}}^{2}}\left[ {3 - 4{{{\left( {\frac{{{{d}_{1}}}}{{{{d}_{2}}}}} \right)}}^{2}}} \right]} \right],$(18)
${{M}_{{{\text{СПР}}}}}\left( {l = {{d}_{1}}} \right) = \frac{{{{\mu }_{0}}{{w}_{1}}{{w}_{2}}\pi d_{2}^{2}}}{{{{d}_{1}}}}\frac{1}{8}\left[ {1.2361 + 0.1138{{{\left( {\frac{{{{d}_{2}}}}{{{{d}_{1}}}}} \right)}}^{2}}} \right].$Тогда, например, при $\frac{{{{d}_{2}}}}{{{{d}_{1}}}} = 0.8$ получаем, соответственно, $M = 0.1322{{\mu }_{0}}{{w}_{1}}{{w}_{2}}\pi {{d}_{2}},$ а ${{M}_{{{\text{СПР}}}}} = 0.1309{{\mu }_{0}}{{w}_{1}}{{w}_{2}}\pi {{d}_{2}},$ и разница между оценками несущественна.
Для конфигурации двухслойного соленоида, показанного на рис. 5, результаты расчетов по формулам (15) и (16), соответственно, дают: $0.354 \times {{10}^{{ - 3}}}$ Гн и $0.348 \times {{10}^{{ - 3}}}$ Гн, т.е. достаточно близкие величины.
При ${{l}_{1}} = {{l}_{2}} = 0$ и ${{w}_{1}} = {{w}_{2}} = 1$ из (14) и (15) получаем:
(19)
$M = \frac{{{{\mu }_{0}}\pi }}{2}\frac{{R_{2}^{2}}}{{{{R}_{1}}}}\left[ {1 + \frac{3}{8}{{{\left( {\frac{{{{R}_{2}}}}{{{{R}_{1}}}}} \right)}}^{2}}} \right].$Полученное выражение согласуется с формулой (5–22) в [4] для взаимной индуктивности двух концентрических контуров радиусов ${{R}_{1}}$ и ${{R}_{2}},$ расположенных в одной плоскости при ограничении первыми двумя членами разложения.
ВЫВОДЫ
Выражение для индуктивности катушки прямоугольного сечения, приведенное в [1, 2] может быть, с учетом корректировки формы записи, использовано без ограничений для получения численных оценок. Для индуктивности соленоида можно использовать формулы (10) и (13). Для коэффициента взаимной индукции между слоями двухслойного соленоида можно пользоваться формулами (14) и (15), а также формулой (19), для двух контуров, расположенных в одной плоскости.
Список литературы
Miki A., Hosoya T., Okuyama K. A calculation method for impulse voltage distribution and transferred voltage in transformer winding. IEEE Trans on Power Apparatus and Systems. 1978. T-PAS V. 97. № 3. P. 930–939.
Rahimpour E., Christian Y., Feser K., Mohseni H. Transfer Function method to diagnose axial displacement and radial deformation of transformer winding. IEEE Trans. on Power Delivery. 2003. V. 18. № 2. P. 493–505.
Wheeler H.A. Inductance formulas for circular and square coils // Proc. IEEE letters. 1982. V. 70. № 12. P. 1449–1451.
Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей: Справочная книга, 3-изд. Л.: Энергоатомиздат. Ленингр. отд-ние. 1986. 488 с.
Теоретические основы электротехники: в 3-х т. Учебник для вузов. Т. 3 / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.П. Чечурин. СПб.: Питер, 2003. 277 с.
Fields and waves in communication electronics / Simon Ramo, John R. Whinnery, Theodore Van Duzer, 3rd ed. John Wiley & sons, inc. 1994.
Цицикян Г.Н. Векторный потенциал поля медленно движущихся тел в приложении к задачам электродинамической левитации. Известия академии наук. Энергетика. 1994. № 4. С. 130–144.
NASA\TM-2013-217918, Magnetic Field Force and Inductance Computation for an Axially Symmetric Solenoid. http://www.sti.nasa.gov
Robert Weaver. Numerical Methods for inductance calculation. http://electronbunker.ca/eb/CalcMethods.html
D. W.Knight. Solenoid inductance calculation. http://g3ynch/info/zdocs/magnetics
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика