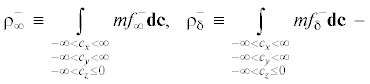Известия РАН. Энергетика, 2019, № 4, стр. 75-97
Кинетический анализ интенсивной конденсации (дозвуковой и сверхзвуковой режимы)
Ю. Б. Зудин 1, *, Д. С. Уртенов 1, В. С. Устинов 1
1 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: yzudin@gmail.com
Поступила в редакцию 20.06.2019
После доработки 08.08.2019
Принята к публикации 12.08.2019
Аннотация
На основе полученного ранее аналитического решения задачи интенсивной конденсации выведена его аппроксимация, пригодная для проведения расчетов для всего диапазона дозвуковой конденсации. Искомой являлась зависимость фактора давления от температурного фактора с числом Маха в качестве параметра. Рассмотрен равновесный изотермический случай, разграничивающий аномальную и нормальную ветви конденсации. Развитая ранее “модель перемешивания” использована для расчета режимов сверхзвуковой конденсации. Исследованы особенности сверхзвуковой конденсации при увеличении числа Маха: инверсия решения; бифуркация решения; переход к двузначным решениям; предельное число Маха, для которого существует решение. Проведена классификация двузначных решений, позволяющая выделять устойчивые ветви. Для всего диапазона изменения интенсивности конденсации построена огибающая семейства максимумов давления. Проведено исследование влияния коэффициента конденсации на уравнения сохранения массы, нормальной компоненты импульса и энергии молекулярных потоков. Рассмотрено явление “запирания конденсации” за счет снижения проницаемости поверхности конденсированной фазы. Проведены расчеты “разрешенных” режимов конденсации.
ВВЕДЕНИЕ
Целью настоящей работы является построение аналитического решения задачи интенсивной конденсации с позиций молекулярно-кинетической теории. Несмотря на “бум” численных исследований, аналитический подход по сей день сохраняет ряд преимуществ: а) замкнутое качественное описание задачи и выявление полного перечня безразмерных определяющих параметров; б) возможность проводить параметрические исследования путем варьирование краевых и начальных условий; в) использование для валидации численных расчетов. Широкий спектр аналитических решений задач теории теплопроводности и термоупругости представлен в известных монографиях Э.М. Карташова [1, 2].
Интенсивные процессы испарения/конденсации играют определяющую роль при воздействии на конденсированную фазу мощного источника энергии. Так, лазерное облучение мишени сопровождается интенсивными процессами испарения и конденсации на поверхности конденсированной фазы (ПКФ), взаимосвязанными с внешним газодинамическим течением [3]. Особенностью интенсивного испарения (интенсивной конденсации) является образование в газовой области вблизи ПКФ неравновесного слоя Кнудсена (СК), в котором утрачивают свой феноменологический смысл статистически осредненные параметры – температура, плотность, давление. В СК внешнее газодинамическое течение, описываемое уравнениями Навье-Стокса, сменяется дискретным молекулярно-кинетическим течением, описываемым уравнением Больцмана. Противоположно направленные молекулярные потоки в СК – эмитируемый ПКФ и падающий на нее из внешней (“навье-стоксовской”) области – имеют существенно различные функции распределения (ФР) молекул по скоростям. Вследствие этого суммарная ФР на поверхности претерпевает разрыв, который сходит на нет на границе СК с навье-стоксовской областью. Макроскопические параметры в СК определяются путем интегрирования ФР с соответствующими весовыми функциями по трехмерному полю молекулярных скоростей с учетом уравнения состояния идеального газа.
Вычислительной проблемой кинетического анализа является отсутствие точных решений нелинейного интегро-дифференциального уравнения Больцмана11. При численном решении возникают трудности, связанные с высокой размерностью уравнения Больцмана и сложной структурой входящего в него интеграла столкновений [4]. Поэтому при численном моделировании уравнения Больцмана его, как правило, заменяют на упрощенные аналоги: релаксационные уравнения, цепочка моментных уравнений и др.
Принципиальная проблема кинетического анализа заключается в избыточности информации, содержащейся в решении уравнения Больцмана. Знание поведения ФР в тонком СК представляет чисто фундаментальный интерес. Для приложений важны газодинамические уравнения в навье-стоксовской области, граничные условия (ГУ) для которых необходимо задавать на ПКФ. Предположим, что нам известны кривые распределений температуры и давления газа в навье-стоксовской области. Экстраполяция этих кривых на ПКФ отсечет на ней некоторые “фиктивные” значения, не равные истинным значениям этих величин. В этом смысле говорят о скачках температуры и давления.
Из вышеизложенного следует актуальность постановки важной прикладной задачи определения экстраполированных ГУ без привлечения уравнения Больцмана. Для этого необходимо – в рамках некоторого упрощенного подхода – корректно учесть взаимосвязь микроскопической задачи для уравнения Больцмана и макроскопической задачи для газодинамических уравнений. Гипотетическое решение микроскопической задачи позволит рассчитать ФР, а затем с ее помощью найти распределения макроскопических параметров в СК. Макроскопическая задача для навье-стоксовской области является стандартной, однако требует задания ГУ на основе решения микроскопической задачи. Точное решение уравнения Больцмана определяет ФР; поэтому уравнения сохранения молекулярных потоков массы, импульса и энергии в СК обращаются в тождества. При поиске экстраполированных ГУ задается ФР со свободными параметрами (одним – для задачи испарения и двумя – для задачи конденсации); поэтому последние должны определяться из решения системы уравнений сохранения.
При анализе интенсивных процессов испарения/конденсации возникает принципиальный вопрос о возможности сверхзвукового течения испаряющегося (конденсирующегося) газа. Как показали Ландау и Лифшиц [5], реализация сверхзвукового испарения в стационарном режиме является физически невозможной. Численные исследования сверхзвуковой конденсации продемонстрировали возможность ее реализации для определенных сочетаний режимных параметров.
Кинетический анализ испарения/конденсации. Предметом кинетического анализа испарения/конденсации является трехмерная ФР молекул по скоростям $f = f\left( {\mathbf{c}} \right),$ которая изменяется от равновесного максвелловского распределения в навье-стоксовской области
(1)
${{f}_{\infty }} = \frac{{{{n}_{\infty }}}}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{v}_{\infty }^{3}}}\exp \left( { - {{{\left( {\frac{{{\mathbf{c}} - {{{\mathbf{u}}}_{\infty }}}}{{{{{v}}_{\infty }}}}} \right)}}^{2}}} \right)$ФР (1) имеет сдвиг по молекулярной скорости, обусловленный воздействием потока испарения (конденсации). Положительная половина ФР на ПКФ задается в виде равновесного полумаксвеллиана при температуре ${{T}_{w}}$
(3)
$f_{w}^{ + } = \frac{{{{n}_{w}}}}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{v}_{w}^{3}}}\exp \left( { - {{{\left( {\frac{{\mathbf{c}}}{{{{{v}}_{w}}}}} \right)}}^{2}}} \right).$В одномерном случае вектор ${{{\mathbf{u}}}_{\infty }}$ вырождается в скалярную скорость испарения (конденсации) ${{u}_{\infty }}.$ Используя (1), можно выразить молекулярные потоки массы, импульса и энергии через параметры течения на бесконечности и записать уравнения сохранения массы
импульса(5)
$\int\limits_{\mathbf{c}} {mc_{z}^{2}f{\mathbf{dc}}} = {{\rho }_{\infty }}u_{\infty }^{2} + {{p}_{\infty }}$(6)
$\int\limits_{\mathbf{c}} {\frac{{m{{c}^{2}}}}{2}{{c}_{z}}f{\mathbf{dc}}} = {{u}_{\infty }}\left( {\frac{{{{\rho }_{\infty }}u_{\infty }^{2}}}{2} + \frac{5}{2}{{p}_{\infty }}} \right).$Интегрирование в левых частях уравнений (4)–(6) осуществляется по всему трехмерному пространству молекулярных скоростей: $ - \infty < {{c}_{x}} < \infty ,$ $ - \infty < {{c}_{y}} < \infty ,$ $ - \infty < {{c}_{z}} < \infty .$ Так как положительная половина ФР известна из условия (3), для выполнения интегрирования требуется найти ее отрицательную половину $ - f_{w}^{ - }.$ Перепишем систему уравнений (4)–(6) в более наглядном виде
(9)
$J_{3}^{ + } - J_{3}^{ - } = \frac{{{{\rho }_{\infty }}u_{\infty }^{3}}}{2} + \frac{5}{2}{{p}_{\infty }}{{u}_{\infty }},$Как видно из уравнений (7)–(9), небаланс молекулярных потоков массы $\left( {i = 1} \right),$ импульса $\left( {i = 2} \right)$ и энергии $\left( {i = 3} \right)$ на ПКФ (левые части уравнений) приводит к появлению в навье-стоксовской области (правые части уравнений) макроскопических потоков испарения (${{u}_{\infty }} > 0$ при $J_{i}^{ + } > J_{i}^{ - }$) или конденсации (${{u}_{\infty }} < 0$ при $J_{i}^{ + } < J_{i}^{ - }$). Величины $J_{i}^{ + }$ рассчитываются известным образом путем подстановки функции $f = f_{w}^{ + }$ из условия (3) в подынтегральные выражения левых частей уравнений (4)–(6) [4]
(10)
$\left. \begin{gathered} J_{1}^{ + } = \frac{1}{{2\sqrt \pi }}{{\rho }_{w}}{{{v}}_{w}}, \hfill \\ J_{2}^{ + } = \frac{1}{4}{{\rho }_{w}}{v}_{w}^{2}, \hfill \\ J_{3}^{ + } = \frac{1}{{2\sqrt \pi }}{{\rho }_{w}}{v}_{w}^{3}. \hfill \\ \end{gathered} \right\}$При известных значениях $J_{i}^{ + }$ кинетический анализ сводится к определению $J_{i}^{ - }.$ В задаче испарения задаются температура ${{T}_{w}}$ на ПКФ и соответствующая ей плотность газа (насыщенного пара) ${{\rho }_{w}}.$ Искомыми являются зависимости температуры ${{T}_{\infty }}$ и плотности ${{\rho }_{\infty }}$ в навье-стоксовской области от числа Маха ${\text{M}} \equiv {{u}_{\infty }}{{\left( {{{5k{{T}_{\infty }}} \mathord{\left/ {\vphantom {{5k{{T}_{\infty }}} {3m}}} \right. \kern-0em} {3m}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$22. Используя уравнение состояния идеального газа, можно перейти от плотности к давлению – $p = {{\rho kT} \mathord{\left/ {\vphantom {{\rho kT} m}} \right. \kern-0em} m}.$ Тогда мы приходим к стандартным искомым зависимостям задачи испарения: $\tilde {p}\left( {\text{M}} \right);$ $\tilde {T}\left( {\text{M}} \right).$ Здесь $\tilde {T} = {{{{T}_{\infty }}} \mathord{\left/ {\vphantom {{{{T}_{\infty }}} {{{T}_{w}}}}} \right. \kern-0em} {{{T}_{w}}}};$ $\tilde {p} = {{{{p}_{\infty }}} \mathord{\left/ {\vphantom {{{{p}_{\infty }}} {{{p}_{w}}}}} \right. \kern-0em} {{{p}_{w}}}}$ – соответствующие безразмерные величины.
В задаче конденсации величина $\tilde {T} = {{{{T}_{\infty }}} \mathord{\left/ {\vphantom {{{{T}_{\infty }}} {{{T}_{w}}}}} \right. \kern-0em} {{{T}_{w}}}}$ задается в качестве дополнительного параметра (“температурного фактора”), а целью анализа является зависимость $\tilde {p}\left( {\tilde {T}} \right)$ при ${\text{M}} = {\text{idem}}{\text{.}}$ В отличие от случая испарения, при конденсации мы фактически имеем две отдельные задачи. Задача “нормальной” конденсации горячего газа на холодной поверхности $\left( {\tilde {T} > 1} \right)$ отвечает феноменологическим представлениям о процессе. Задача “аномальной” конденсации холодного газа на горячей поверхности $\left( {\tilde {T} < 1} \right)$ выглядит абстрактной, однако она описывает реальную физическую ситуацию. Так, при лазерном облучении поверхности (которая может быть как жидкой, так и твердой) происходит интенсивное испарение вещества. После окончания лазерного импульса перегретый пар за счет адиабатического расширения быстро охлаждается. Так как скорость охлаждения конденсированной фазы значительно меньше, то мы будем иметь конденсацию низкотемпературного пара на высокотемпературной поверхности [6].
В дальнейшем при графическом представлении результатов расчета удобнее оперировать с зависимостью $\eta \left( {\tilde {T}} \right),$ где $\eta = {{{{p}_{w}}} \mathord{\left/ {\vphantom {{{{p}_{w}}} {{{p}_{\infty }} = {{{\tilde {p}}}^{{ - 1}}}}}} \right. \kern-0em} {{{p}_{\infty }} = {{{\tilde {p}}}^{{ - 1}}}}}$ – обратное отношение давлений. Во избежание путаницы в терминах мы будем именовать величину η “фактором давлений”.
Модель перемешивания. В рамках модели перемешивания [7] внутри СК вводится промежуточная поверхность “δ–δ” (“поверхность перемешивания”), на которой выставляются следующие условия
• Параметры на поверхности перемешивания (с индексом “δ”) и на бесконечности (с индексом “∝”) связаны линейными соотношениями
(11)
${{\rho }_{{\delta }}} = {{\alpha }_{{\rho }}}{{\rho }_{\infty }},\,\,\,\,{{{v}}_{{\delta }}} = {{\alpha }_{{v}}}{{{v}}_{\infty }},\,\,\,\,{{\tilde {u}}_{{\delta }}} = {{\alpha }_{u}}{{\tilde {u}}_{\infty }}.$• При движении конденсирующегося пара от поверхности “∞–∞” к поверхности “δ–δ” сохраняется отрицательная составляющая молекулярного потока массы
Здесь
отрицательные плотности падающего потока на соответствующих поверхностях, ${{u}_{{\delta }}}$ – газодинамическая скорость на поверхности перемешивания.
• Отрицательная половина ФР на поверхности перемешивания $f_{{\delta }}^{ - }$ определяется соотношением, аналогичным (1)
(14)
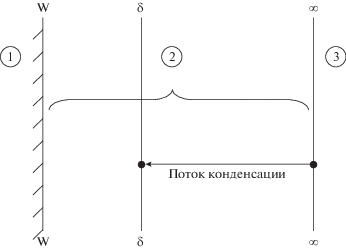
$f_{\delta }^{ - } \equiv {{\left. {{{f}_{\delta }}} \right|}_{{{{c}_{z}} < 0}}} = \frac{{{{n}_{{\delta }}}}}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{v}_{\delta }^{3}}}\exp \left( { - {{{\left( {\frac{{{\mathbf{c}} - {{{\mathbf{u}}}_{\delta }}}}{{{{{v}}_{\delta }}}}} \right)}}^{2}}} \right).$Схема процесса конденсации в рамках модели перемешивания приведена на рис. 1. В результате мы имеем четыре неизвестных $\left( {{{\rho }_{\infty }},{{\alpha }_{{\rho }}},{{\alpha }_{{v}}},{{\alpha }_{u}}} \right)$ для четырех уравнений (7)–(9), (12). Дополнительные связи между термодинамическими параметрами следуют из уравнения состояния идеального газа, записанного для каждой из трех поверхностей “w–w”, “δ–δ”, “∞–∞”
(15)
$\frac{{{{p}_{w}}}}{{{{p}_{\infty }}}} = \frac{{{{\rho }_{w}}}}{{{{\rho }_{\infty }}}}\frac{{{{T}_{w}}}}{{{{T}_{\infty }}}},\,\,\,\,\frac{{{{p}_{\delta }}}}{{{{p}_{\infty }}}} = \frac{{{{\rho }_{\delta }}}}{{{{\rho }_{\infty }}}}\frac{{{{T}_{\delta }}}}{{{{T}_{\infty }}}}.$С учетом соотношений (15) система уравнений (7)–(9), (12) после некоторых преобразований приводится к виду
(16)
$\sqrt {\tilde {T}\eta } - {{\alpha }_{{\rho }}}{{\alpha }_{V}}I_{1}^{ - } = 2\sqrt \pi {{\tilde {u}}_{\infty }},$(18)
$\frac{1}{{\sqrt {\tilde {T}} }}\eta - {{\alpha }_{{\rho }}}\alpha _{V}^{3}I_{3}^{ - } = \sqrt \pi \tilde {u}_{\infty }^{3} + \frac{5}{2}\sqrt \pi {{\tilde {u}}_{\infty }},$(19)
${\text{erfc(}}{{\tilde {u}}_{\infty }}) = {{\alpha }_{{\rho }}}{{\alpha }_{V}}{{\alpha }_{u}}{\text{erfc}}({{\alpha }_{u}}{{\tilde {u}}_{\infty }}).$(20)
$\left. \begin{gathered} I_{1}^{ - } = \exp \left( { - \tilde {u}_{\delta }^{2}} \right) - \sqrt \pi {{{\tilde {u}}}_{\delta }}erfc\left( {{{{\tilde {u}}}_{\delta }}} \right), \hfill \\ I_{2}^{ - } = \frac{{2{{{\tilde {u}}}_{\delta }}}}{{\sqrt \pi }}\exp \left( { - \tilde {u}_{\delta }^{2}} \right) - \left( {1 + 2\tilde {u}_{\delta }^{2}} \right){\text{erfc}}\left( {{{{\tilde {u}}}_{\delta }}} \right), \hfill \\ I_{3}^{ - } = \left( {1 + \frac{{\tilde {u}_{\delta }^{2}}}{2}} \right)\exp \left( { - \tilde {u}_{\delta }^{2}} \right) - \frac{{\sqrt \pi {{{\tilde {u}}}_{\delta }}}}{2}\left( {\frac{5}{2} + \tilde {u}_{\delta }^{2}} \right){\text{erfc}}\left( {{{{\tilde {u}}}_{\delta }}} \right); \hfill \\ \end{gathered} \right\}$Система уравнений (16)–(19) представляет собой замкнутое кинетическое описание задачи интенсивной конденсации. Ее аналитическое решение в параметрическом виде было получено в [7] с помощью программного пакета системы компьютерной алгебры Maple 11.
На рис. 2, 3 приведено сопоставление результатов решения по модели перемешивания [7] с результатами численного исследования [8], выполненного с помощью метода дискретных скоростей. Как видно из рисунков, имеет место удовлетворительное согласование в области аномальной конденсации $\left( {\tilde {T} < 1} \right)$ и хорошее согласование – в области нормальной конденсации $\left( {\tilde {T} > 1} \right).$
Рис. 2.
Зависимость безразмерного обратного давления от температурного фактора для диапазона $0 < \left| {\text{M}} \right| \leqslant 0.5{\text{:}}$: — – расчет по модели перемешивания [7]; ─ ─ ─ – результаты численного решения [8]; 1 – $\left| {\text{M}} \right|$ = 0.1, 2 – 0.2, 3 – 0.3, 4 – 0.4; 5 – 0.5.
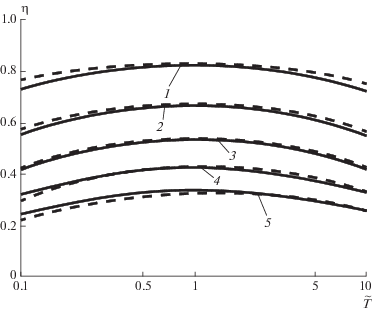
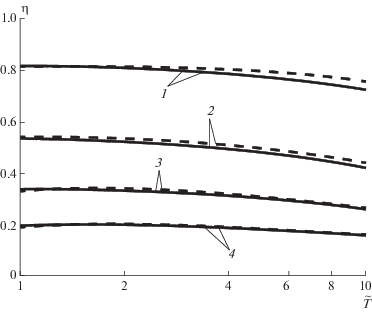
Рис. 3.
Зависимость безразмерного обратного давления от температурного фактора для диапазона $0.5 < \left| {\text{M}} \right| \leqslant 1.0$ (нормальная ветвь конденсации): — – расчет по модели перемешивания [7]; ─ ─ ─ – результаты численного решения [8]; ── ── – результаты приближенного решения [4]; 1 – $\left| {\text{M}} \right|$ = 0.1, 2 – 0.3, 3 – 0.5, 4 – 0.7.
Приближенное решение задачи дозвуковой конденсации. Полученное в [7] аналитическое решение имеет чрезвычайно громоздкий вид и практически не может быть воспроизведено в формульном виде. Поэтому представляет интерес найти аппроксимацию этого решения, удобную для проведения прикладных расчетов. Исследование асимптотик общего решения по температурному фактору позволяет искать аппроксимацию в виде
(21)
$\tilde {T} \to 0:\tilde {p} \equiv {{\tilde {p}}_{0}} = 1 + {{f}_{0}}{{\tilde {T}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$(22)
$\tilde {T} \to \infty :\tilde {p} \equiv {{\tilde {p}}_{\infty }} = 1 + {{f}_{\infty }}{{\tilde {T}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$При построении аппроксимации поставим условие выполнения предельного перехода при |M| → 0 к аналитическому решению в линейном приближении, полученному в [7]
(23)
$\tilde {p} = 1 + (1.01{{\tilde {T}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + 0.929{{\tilde {T}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}})\left| {\text{M}} \right|.$Опуская промежуточные выкладки, запишем приближенное решение для области дозвуковой конденсации $\left( {\left| {\text{M}} \right| < 1} \right)$
(24)
$\left. \begin{gathered} \tilde {p} \approx 1 + {{\left( {{{{\left( {{{{\tilde {p}}}_{0}} - 1} \right)}}^{{\frac{1}{n}}}} + {{{\left( {{{{\tilde {p}}}_{\infty }} - 1} \right)}}^{{\frac{1}{n}}}}} \right)}^{n}}, \hfill \\ n = 1 + {{f}_{n}}. \hfill \\ \end{gathered} \right\}$(25)
$f = {{k}_{1}}\left| {\text{M}} \right| + {{k}_{2}}{{\left| {\text{M}} \right|}^{{\text{2}}}} + {{k}_{3}}{{\left| {\text{M}} \right|}^{{\text{3}}}} + {{k}_{4}}{{\left| {\text{M}} \right|}^{{\text{4}}}} + {{k}_{5}}{{\left| {\text{M}} \right|}^{{\text{5}}}} + {{k}_{6}}{{\left| {\text{M}} \right|}^{{\text{6}}}},$Таблица 1.
Значения коэффициентов полиномов в формуле (25)
| ${{f}_{n}}$ | ${{f}_{0}}$ | ${{f}_{\infty }}$ | |
|---|---|---|---|
| ${{k}_{1}}$ | 1.3 | 0.9293 | 1.011 |
| ${{k}_{2}}$ | 2.8 | 1.028 | –0.002559 |
| ${{k}_{3}}$ | –10.1 | –5.18 | 1.222 |
| ${{k}_{4}}$ | 11.1 | 19.19 | –3.612 |
| ${{k}_{5}}$ | –4.1 | –25.055 | 8.042 |
| ${{k}_{6}}$ | 0 | 13.05 | –4.967 |
При проведении кинетического анализа конденсации полагается, что давление в навье-стоксовской области всегда выше давления насыщения при температуре ПКФ: $\tilde {p} > 1,$ ${{p}_{\infty }} > {{p}_{w}}$ [9, 10]. В то же время отношение плотностей ${{{{\rho }_{\infty }}} \mathord{\left/ {\vphantom {{{{\rho }_{\infty }}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}$ может быть как меньше, так и больше единицы. Зафиксируем теперь температурный фактор $\tilde {T} = \tilde {T}{\text{*}}$ в точке максимума зависимости $\eta \left( {\tilde {T}} \right)$ (т.е. в точке минимума зависимости $\tilde {p}\left( {\tilde {T}} \right)$). Тогда для каждого числа Маха получим минимально возможное значение отношения плотностей: величина ${{{{\rho }_{\infty }}} \mathord{\left/ {\vphantom {{{{\rho }_{\infty }}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}$ будет увеличиваться при отклонении $\tilde {T}$ от $\tilde {T}{\text{*}}$ как в большую, так и в меньшую сторону. Для изотермического случая $\tilde {T}{\text{*}} = 1,$ $T{\text{*}} = {{T}_{w}},$ разграничивающего аномальную и нормальную ветви конденсации, будем иметь: ${{{\text{M}}}_{{\min }}} \approx {\text{0}}{\text{.2437,}}$ ${{\rho }_{{\infty \min }}} \approx 1.647{{\rho }_{w}}.$
Следовательно, в рамках кинетического анализа для установления устойчивой изотермической конденсации требуется в точности задать указанное число Маха и создать в конденсирующемся паре давление, равное ${{p}_{\infty }} \approx 1.647{{p}_{w}}.$ В этом случае число падающих на поверхность молекул окажется в ≈1.647 раз больше, чем число молекул, эмитируемых ПКФ при той же температуре ${{T}_{\infty }} = {{T}_{w}}.$ В то же время при феноменологическом подходе равенство температур ПКФ и пара должно приводить к полному прекращению конденсации44. Рассмотренный пример наглядно иллюстрирует нетривиальную кинетическую картину интенсивной конденсации.
Сверхзвуковая конденсация. В прикладном плане кинетический анализ задачи интенсивной конденсации необходим для постановки ГУ на ПКФ для уравнений течения сжимаемого газа в навье-стоксовской области. Принципиальное различие дозвукового и сверхзвукового режимов конденсации состоит в возможности (или невозможности) распространения против потока возмущений плотности – звуковой волны. При дозвуковой конденсации $\left( {\left| {\text{M}} \right| < 1} \right)$ звуковая волна распространяется в сторону конденсирующегося газа; поэтому один параметр (например, ${{p}_{\infty }}$) должен быть искомым, а два остальных (например, $\left| {\text{M}} \right|,\,{{T}_{\infty }}$) необходимо задавать. При сверхзвуковой конденсации возмущения плотности не проходят против потока. Тогда ПКФ перестает влиять на течение, и все три параметра в навье-стоксовской области – $\left| {\text{M}} \right|,$ ${{T}_{\infty }},$ ${{p}_{\infty }}$ – можно задавать произвольно.
Такая “автономность” внешнего потока ни в коей мере не означает, что сама по себе постановка задачи сверхзвуковой конденсации для уравнения Больцмана является бессмысленной. Наоборот, решение этой задачи необходимо для ответа на вопрос: при каких параметрах натекающего потока и ПКФ сверхзвуковая конденсация возможна, а при каких – невозможна. В первом случае следует считать, что ПКФ воспринимает весь падающий молекулярный поток, не оказывая на него никакого влияния. Во втором случае на поверхности следует задавать граничное условие дозвуковой конденсации. Такая постановка задачи приведет к радикальному изменению течения: газ у ПКФ будет тормозиться до дозвуковой скорости; вверх по натекающему сверхзвуковому потоку будет распространяться ударная волна.55 На основании приведенных рассуждений можно полагать, что при устойчивой сверхзвуковой конденсации происходит слияние СК со стоячей ударной волной. Таким образом, кинетический анализ сверхзвуковой конденсации необходим не для решения “автономных” газодинамических уравнений, а для качественной “диагностики течения”.
Невозможность заранее предсказать область существования решения для сверхзвуковой конденсации приводит к необходимости использования “метода проб и ошибок”: строить конкретное решение, исследовать его устойчивость и только в результате его судить о существовании этого решения. Эта особенность сверхзвуковой конденсации в идейном плане соответствует известной теореме математического анализа: почленное дифференцирование бесконечного функционального ряда возможно после того, как доказана равномерная сходимость ряда, составленного из производных функций [11].
К настоящему времени выполнено ограниченное количество теоретических исследований сверхзвуковой конденсации. Численные расчеты работы [12] показали, что существуют области параметров, в которых стационарная сверхзвуковая конденсация невозможна. Решения задачи сверхзвуковой конденсации с помощью метода Мотт-Смита [9] получены в работе [13]. Эти решения имеют вид ударной волны перед ПКФ, переводящей сверхзвуковое течение в дозвуковое. В численном исследовании [14] получено, что устойчивые стационарные решения существуют здесь только для определенных сочетаний параметров. Авторы [10] с помощью метода прямого статистического моделирования Монте-Карло показали, что при сверхзвуковом режиме для каждого значения $\left| {\text{M}} \right|$ существует некоторая предельная нижняя кривая ${{\tilde {p}}_{{\lim }}}\left( {\tilde {T}} \right)$ (в наших обозначениях – предельная верхняя кривая ${{\eta }_{{\lim }}}\left( {\tilde {T}} \right)$). Эта кривая определяет границу между областью, в которой значения ${{p}_{\infty }},$ ${{T}_{\infty }}$ могут быть произвольными, и областью параметров, для которых сверхзвуковая конденсация невозможна.
Проведем анализ сверхзвуковой конденсации с помощью “модели перемешивания”. Расчеты по системе уравнений (16)–(19) дают следующие результаты. В области $1 \leqslant \left| {\text{M}} \right| \leqslant 1.16$ зависимости $\eta \left( {\tilde {T}} \right)$ имеют тот же вид, что и для дозвуковой конденсации: при увеличении числа Маха кривые смещаются вниз, а точки их максимумов – вправо по оси $\tilde {T}$ (рис. 4а).
Рис. 4.
Сверхзвуковая конденсация. Нормальные (однозначные) режимы а) диапазон $1 \leqslant \left| {\text{M}} \right| \leqslant 1.16{\text{:}}$ 1 – $\left| {\text{M}} \right|$ = 1.0, 2 – 1.05, 3 – 1.1, 4 – 1.16. б) диапазон $1.16 < \left| {\text{M}} \right| \leqslant 1.375{\text{:}}$ 1 – $\left| {\text{M}} \right|$ = 1.25, 2 – 1.30, 3 – 1.35, 4 – 1.375.
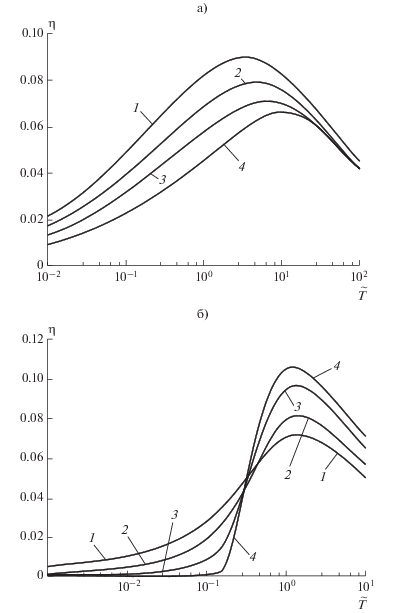
При $\left| {\text{M}} \right| \approx 1.16$ имеет место инверсия зависимости $\eta \left( {\tilde {T}} \right){\text{:}}$ в области $1.16 < \left| {\text{M}} \right| \leqslant 1.375$ аномальная ветвь $\eta \left( {\tilde {T}} \right)$ продолжает опускаться, в то время как нормальная ветвь решения начинает подниматься. При увеличении числа Маха величина максимума зависимости $\eta \left( {\tilde {T}} \right)$ возрастает (рис. 4б); соответственно, величина минимума зависимости $\tilde {p}\left( {\tilde {T}} \right)$ убывает. Указание на существование инверсии зависимости ${{\eta }_{{\max }}}\left( {\tilde {T}{\text{*}}} \right)$ содержится также в работе [15].
В точке $\left| {\text{M}} \right| \approx 1.375$ имеет место бифуркация решения: последнее однозначное решение сменяется первым двузначным (рис. 5).
Рис. 5.
Сверхзвуковая конденсация. Бифуркация зависимости $\eta \left( {\tilde {T}} \right)$ при $\left| {\text{M}} \right|$ = 1.375. 1 – нормальная (однозначная) зависимость; 2 – аномальная (двузначная) зависимость.
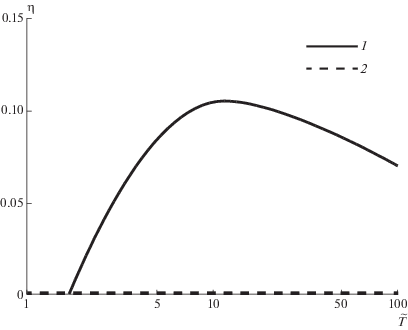
В области $1.375 < \left| {\text{M}} \right| \leqslant 2.24$ реализуются только двузначные решения: каждому значению температурного фактора соответствуют два значения давления в навье-стоксовской области. Ветвь аномальной конденсации $\tilde {T} < 1$ здесь вначале исчезает (|M| = 1.375), а при увеличении числа Маха постепенно “заполняется” двузначной областью.
Область $1.375 < \left| {\text{M}} \right| \leqslant 2.24$ можно, в свою очередь, разбить на две подобласти. В диапазоне 1.375 ≤ |M| ≤ 1.5 ход кривых имеет взаимопересекающийся характер и поэтому труден для интерпретации. В диапазоне 1.5 ≤ |M| ≤ 2.24 двузначные кривые $\eta (\tilde {T})$ становятся упорядоченными. Каждую из этих пар кривых можно разбить на “нижнюю” (меньшие $\eta $, большие $\tilde {p}$) и “верхнюю” (большие η, меньшие $\tilde {p}$). Примем в качестве границы нижней и верхней кривых точку, в которой выполняется условие $\frac{{d\eta }}{{d\tilde {T}}} = \infty .$ Как показывают расчеты, это условие для всего диапазона 1.5 ≤ |M| ≤ 2.24 выполняется приблизительно при одном и том же значении фактора давления: η ≈ 0.06. Как видно из рис. 6а, при увеличении числа Маха обе ветви смещаются влево по оси $\tilde {T}$ и все более раздвигаются.
Рис. 6.
Сверхзвуковая конденсация, область двузначных режимов. а) Зависимость обратного отношения давлений от температурного фактора 1 – |M| = 1.5, 2 – |M| = 1.7, 3 – |M| = 1.9, 4 – |M| = 2.1, 5 – |M| = 2.24. б) Зависимость числа Маха на поверхности перемешивания от температурного фактора. 1 – |M| = 1.5, 2 – |M| = 1.7, 3 – |M| = 1.9, 4 – |M| = 2.1, 5 – |M| = 2.24.
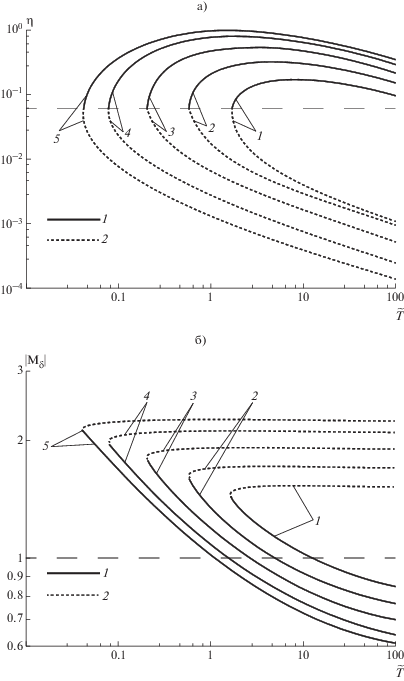
При рассмотрении двузначной области решений возникает принципиальный вопрос, какая из ветвей зависимостей $\eta (\tilde {T})$ реализуется в действительности. Напомним, что в рамках рассматриваемой модели “поверхность перемешивания” физически представляет собой внешнюю сторону ПКФ. Будем полагать, что при фиксированных параметрах $\tilde {T},$ |M| будет реализован режим с меньшим значением числом Маха на поверхности перемешивания. Как видно из рис. 6б, для верхней ветви $\eta (\tilde {T})$ на рис. 6а величина |Mδ| будет всегда меньше, чем для нижней. Физически это означает, что в двузначной области сверхзвуковой конденсации “выбираются” режимы с меньшими давлениями газа. На этом основании будем полагать верхние кривые $\eta (\tilde {T})$ на рис. 6а “устойчивыми”.
При увеличении температурного фактора величина |Mδ| для каждой “устойчивой” кривой уменьшается и при определенных значениях $\tilde {T}$ становится меньшей единицы. Такие режимы можно трактовать как ударную волну, переводящую сверхзвуковое течение в дозвуковое.
При $\left| {\text{M}} \right| \approx 2.24$ в точке максимума зависимости $\eta (\tilde {T})$ достигалась изобарическая конденсация: ${{\eta }_{{\max }}} = {{\tilde {p}}_{{\min }}} = 1.$ В нашем анализе этот случай считался предельным, так как в противном случае приходится допустить существование нефизичных режимов с инверсией давлений на ПКФ и в конденсирующемся газе: ${{\eta }_{{\max }}} > 1,$ ${{\tilde {p}}_{{\min }}} < 1,$ ${{p}_{{\min }}} < {{p}_{w}}.$
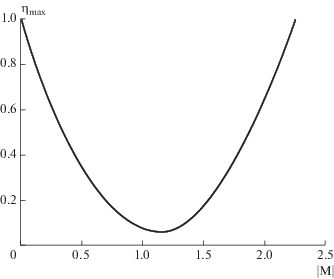
Как показывают расчеты, огибающая семейства максимумов функций фактора давления от числа Маха для всей области существования конденсации $0 < \left| {\text{M}} \right| \leqslant 2.24$ (рис. 7), имеет минимум в точке инверсии $\left| {\text{M}} \right| \approx 1.16.$ При $\left| {\text{M}} \right| \to 0$ достигается изобарический равновесный случай: при нулевом потоке конденсации давление в газе равно давлению насыщения при температуре ПКФ: ${{\eta }_{{\max }}} = {{\tilde {p}}_{{\min }}} = 1.$ Так как при постановке задачи задается фиксированный температурный фактор $\tilde {T} \ne 1,$ то условие изотермичности здесь в общем случае выполняться не будет. Выше было получено, что изобарическая конденсация достигается также на верхней границе существования области сверхзвуковой конденсации $\left| {\text{M}} \right| \approx 2.24,$ т.е. в предельном неравновесном случае.
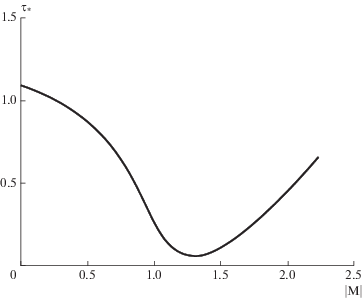
Проследим теперь за координатами максимумов фактора давления. Для этого были проведены расчеты зависимости от числа Маха обратного температурного фактора $\tau * \equiv \tilde {T}_{ * }^{{ - 1}},$ соответствующего огибающей семейства максимумов $\eta \left( {\tilde {T}} \right).$ Как видно из рис. 8, зависимость $\tau {\text{*}}\left( {\left| {\text{M}} \right|} \right)$ имеет минимум при $\left| {\text{M}} \right| \approx 1.29.$ Интересно отметить, что при $\left| {\text{M}} \right| \to 0$ величина τ* стремится не к единице, а к значению ≈1.0886. Этот результат был получен в [7] при исследовании линейной задачи конденсации. В свою очередь, на верхней границе режимов сверхзвуковой конденсации имеем: $\left| {\text{M}} \right| \approx 2.24,$ $\tau * \approx 0.64.$ Таким образом, в отличие от зависимости ${{\eta }_{{\max }}}\left( {\left| {\text{M}} \right|} \right),$ предельная величина ${{\tau }_{ * }}$ на обеих границах области существования конденсации $0 < \left| {\text{M}} \right| \leqslant 2.24$ отлична от единицы.
Рис. 8.
Зависимость координат обратного температурного фактора, соответствующих максимумам обратного давления, от числа Маха.
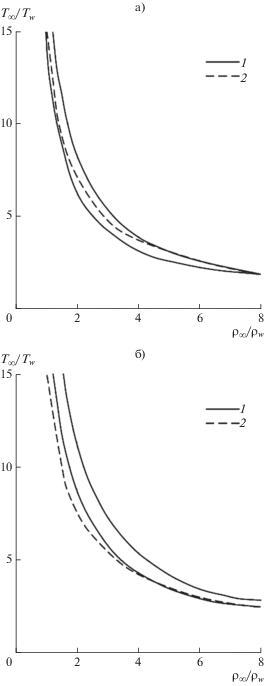
На рис. 9 приведено сопоставление полученных результатов расчета по модели перемешивания с результатами работы [13] для случаев $\left| {\text{M}} \right| = 1.1,$ $\left| {\text{M}} \right| = 1.2,$ представленными в координатах ${{{{T}_{\infty }}} \mathord{\left/ {\vphantom {{{{T}_{\infty }}} {{{T}_{w}}}}} \right. \kern-0em} {{{T}_{w}}}} = f\left( {{{{{\rho }_{\infty }}} \mathord{\left/ {\vphantom {{{{\rho }_{\infty }}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}} \right).$ Как видно из рисунков, расчетные кривые в целом попадают в диапазон, указанный в работе [13] как область существования решений типа ударной волны. Согласование здесь может считаться скорее качественным, однако эти результаты представляют фактически единственную валидацию полученных выше данных.
Рис. 9.
Зависимость температурного фактора от отношения плотностей. 1 – границы диапазона существования режимов сверхзвуковой конденсация согласно [13]; 2 – расчет по модели перемешивания: (а) $\left| {\text{M}} \right| = 1.1;$ (б) $\left| {\text{M}} \right| = 1.2.$
Укажем здесь на ограниченность подхода [13], который основан на методе Мотт-Смита, учитывающем только решения типа ударной волны. Это означает, что постулируется переход сверхзвукового течения газа в навье-стоксовской области в дозвуковое течение на ПКФ. Тем самым из рассмотрения заранее исключаются возможные решения, сохраняющие сверхзвуковой режим течения на ПКФ.
Представленные на рис. 4–6 расчетные кривые представляют собой искомые предельные зависимости ${{\eta }_{{\lim }}}\left( {\tilde {T}} \right).$ Они определяют границу между областью, в которой значения ${{p}_{\infty }},$ ${{T}_{\infty }}$ могут быть произвольными, и областью параметров, для которых стационарная сверхзвуковая конденсация невозможна. Полученные результаты демонстрируют принципиальную применимость модели перемешивания к рассмотренной специфической и малоисследованной проблеме. Достоинством используемого аналитического подхода является его гибкость, а также возможность весьма просто выполнять необходимые расчеты.
Диффузная схема отражения молекул. Предыдущие рассуждения относились к случаю поверхности, которая адсорбирует все падающие на нее из навье-стоксовской области молекулы (“абсолютно проницаемая ПКФ”). В общем случае ПКФ имеет ограниченную проницаемость и пропускает лишь часть проходящего через нее молекулярного потока, которая определяется коэффициентом конденсации β. Величина β отражает состояние поверхности и физическую природу конденсированной фазы и может изменяться в диапазоне 0 < β ≤ 1.
Рассмотрим влияние коэффициента конденсации на уравнения сохранения молекулярных потоков. Будем обозначать через $J_{i}^{ + }$ потоки массы (i = 1), импульса (i = 2) и энергии (i = 3), эмитируемые ПКФ в случае ее абсолютной проницаемости. Пусть теперь поверхность пропускает не весь поток, поступающий из жидкой в газовую фазу, а только его часть $J_{{i{\beta }}}^{ + }$ = $\beta J_{i}^{ + }.$ Со своей стороны, пусть только часть β потока молекул $J_{i}^{ - },$ падающего из навье-стоксовской области на ПКФ, захватывается ею, а оставшаяся часть (1 – β)$J_{i}^{ - }$ – отражается от нее. Тогда отходящий от поверхности суммарный молекулярный поток будет
i = 1, 2, 3.Из (26) можно найти макроскопические потоки ${{J}_{{i\infty }}}$ в навье-стоксовской области, определяемые как разности эмитируемых и падающих молекулярных потоков
(27)
${{J}_{{i\infty }}} = J_{{i\beta }}^{ + } - J_{i}^{ - } = {\text{\;}}\beta \left( {J_{i}^{ + } - J_{i}^{ - }} \right).$Введем “коэффициенты проницаемости” как отношение отходящего от ПКФ потока (случай β < 1) к потоку, эмитируемому абсолютно проницаемой ПКФ (случай β = 1)
Тогда, используя в (28) соотношения (26), (27), получаем
Величины $J_{i}^{ + }$ определяются соотношениями (10); макроскопические потоки в навье-стоксовской области следуют из уравнений (7)–(9)(32)
${{J}_{{3\infty }}} = \frac{1}{2}{{\rho }_{\infty }}u_{\infty }^{3} + \frac{5}{2}{{p}_{\infty }}{{u}_{\infty }}.$Из уравнений (28)–(32) получаем выражения для коэффициентов проницаемости для каждого из трех уравнений сохранения
(33)
${{\psi }_{1}} = 1 - 2\sqrt \pi \frac{{1 - \beta }}{\beta }\frac{{{{{\tilde {u}}}_{\infty }}}}{{\eta \sqrt {\tilde {T}} }},$(34)
${{\psi }_{2}} = 1 - 2\frac{{1 - \beta }}{\beta }\frac{{1 + 2\tilde {u}_{\infty }^{2}}}{\eta },$(35)
${{\psi }_{3}} = 1 - \frac{5}{2}\sqrt \pi \frac{{1 - \beta }}{\beta }\frac{{\sqrt {\tilde {T}} {{{\tilde {u}}}_{\infty }}\left( {1 + 2/5\tilde {u}_{\infty }^{2}} \right)}}{\eta }.$Таким образом, в общем случае β ≤ 1 уравнения сохранения молекулярных потоков (7)–(9) принимают вид
При кинетическом анализе принимается равенство между собой всех трех коэффициентов проницаемости: ψ1 = ψ2 = ψ3. Такая упрощенная схема отражения молекул называется “диффузной”. Она была впервые предложена в работе [16] в рамках линейного приближения, а затем модифицирован авторами [17] для задач случая интенсивного испарения/конденсации. Следует указать на внутреннюю противоречивость диффузной схемы
• В рамках диффузной схемы определяется лишь коэффициент проницаемости потока массы ψ1. Физически это означает, что выполняется только баланс потока массы (i = 1), в то время как потоки нормальной компоненты импульса (i = 2) и энергии (i = 3) через ПКФ остаются несбалансированными. Иными словами, в рамках диффузной схемы используется формула (33) и игнорируются формулы (34), (35).
• Кинетический анализ имеет дело с газовой фазой с заданным граничным условием на поверхности. Однако в рамках диффузной схемы полагается, что ПКФ “отфильтровывает” также молекулы, поступающие со стороны жидкой фазы. Последняя тем самым неявно включается в механизм движения молекулярных потоков, что противоречит исходной картине процесса.
Указанных противоречий лишены исследования, основанные на моделировании процессов испарения/конденсации методом молекулярной динамики [18]. Этот метод, появившийся в середине прошлого века, имеет дело со сравнительно небольшими системами. Основной идеей метода молекулярной динамики является исследование различных свойств веществ путем моделирования движения и взаимодействия отдельных частиц – атомов и молекул. Для описания взаимодействия частиц используются различные потенциалы: потенциал твердых сфер, потенциал Леннарда-Джонса, непрерывные потенциалы и др.
Исследования интенсивного испарения (интенсивной конденсации) методом молекулярной динамики показали важную роль флуктуаций энергии связи в поверхностном слое жидкости. Получено, что значительный вклад в молекулярный поток вносят частицы, кинетическая энергия которых одного порядка со средней тепловой энергией. Была исследована структура переходного слоя между газовой и жидкой фазами, вычислены флуктуации потенциальной энергии и парные корреляционные функции. Отметим, что в рамках метода молекулярной динамики до настоящего времени не были предложены корреляционные зависимости для параметров, пригодные для прикладных расчетов. Поэтому ниже будет использована диффузная схема отражения молекул, апробированная в целом ряде работ.
Перейдем к расчету коэффициента проницаемости ψ1. Согласно (10) имеем
Принимая, что при переходе от общего случая β ≤ 1 к предельному случаю β = 1 температура ПКФ остается неизменной (Tw = idem), из равенств (28), (30) получаем
Таким образом, диффузная схема отражения сводится к замене реальной плотности насыщения пара при температуре поверхности ${{\rho }_{w}}$ на ее модифицированное значение ρwβ
(41)
${{\rho }_{w}} \to {{\rho }_{{w\beta }}} = {{\rho }_{w}}\left( {1 - 2\sqrt \pi \frac{{1 - \beta }}{\beta }\frac{{{{{\tilde {u}}}_{\infty }}}}{{\eta \sqrt {\tilde {T}} }}} \right).$Как уже указывалось, эмитируемый поверхностью молекулярный поток имеет равновесный максвелловский спектр, определяемый соотношением (3). В рамках диффузной схемы предполагается, что отраженный поток после взаимодействия с ПКФ “забывает” свой первоначальный спектр и также приобретает максвелловское распределение.
Общий случай граничных условий. Запишем с учетом (41) систему уравнений сохранения молекулярных потоков (16)–(18) в следующем виде
(42)
$\frac{1}{{2\sqrt \pi }}\left( {{{\rho }_{{w\beta }}}{{{v}}_{w}} - {{\rho }_{\delta }}{{{v}}_{\delta }}I_{1}^{ - }} \right) = 2\sqrt \pi {{\rho }_{\infty }}{{u}_{\infty }},$(43)
$\frac{1}{4}\left( {{{\rho }_{{w\beta }}}{v}_{w}^{2} - {{\rho }_{\delta }}{v}_{\delta }^{2}I_{2}^{ - }} \right) = {{\rho }_{\infty }}u_{\infty }^{2} + {{p}_{\infty }},$(44)
$\frac{1}{{2\sqrt \pi }}\left( {{{\rho }_{{w\beta }}}{v}_{w}^{3} - {{\rho }_{\delta }}{v}_{\delta }^{3}I_{2}^{ - }} \right) = \frac{1}{2}{{\rho }_{\infty }}u_{\infty }^{3} + \frac{5}{2}{{p}_{\infty }}{{u}_{\infty }}.$Мы видим, что при замене ρw на ρwβ вид уравнений не изменяется. Тогда исходную систему уравнений (16)–(19) можно переписать в виде
(45)
$\sqrt {\tilde {T}} {{\eta }_{\beta }} - {{\alpha }_{\rho }}{{\alpha }_{{v}}}I_{1}^{ - } = 2\sqrt \pi {{\tilde {u}}_{\infty }},$(46)
${{\eta }_{\beta }} - {{\alpha }_{\rho }}\alpha _{{v}}^{2}I_{2}^{ - } = 2 + 4\tilde {u}_{\infty }^{2},$(47)
$\frac{1}{{\sqrt {\tilde {T}} }}{{\eta }_{\beta }} - {{\alpha }_{\rho }}\alpha _{{v}}^{3}I_{3}^{ - } = \sqrt \pi \tilde {u}_{\infty }^{3} + \frac{5}{2}\sqrt \pi {{\tilde {u}}_{\infty }},$(48)
${\text{erfc}}\left( {{{{\tilde {u}}}_{\infty }}} \right) = {{\alpha }_{\rho }}{{\alpha }_{{v}}}{{\alpha }_{u}}{\text{erfc}}\left( {{{\alpha }_{u}}{{{\tilde {u}}}_{\infty }}} \right).$(49)
$\eta = {{\eta }_{\beta }} + 2\sqrt \pi \frac{{1 - \beta }}{\beta }\frac{{{{{\tilde {u}}}_{\infty }}}}{{\sqrt {\tilde {T}} }}.$Выразим скоростной фактор через число Маха для одноатомного газа: ${{\tilde {u}}_{\infty }} = \sqrt {{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}} {\text{M}} = - \sqrt {{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}} \left| {\text{M}} \right|$66. Тогда из уравнения (49) найдем искомый фактор давления
Здесь A = $\sqrt {\frac{{10\pi }}{3}} \frac{{1 - \beta }}{\beta }\frac{{\left| {\text{M}} \right|}}{{\sqrt {\tilde {T}} }}$ – обобщенный параметр, описывающий механизм диффузного отражения и включающий коэффициент конденсации, температурный фактор и число Маха.Соотношение (50) является ключевым для расчета влияния величины β на процесс конденсации. Рассмотрим различные варианты изменения параметра A
• Модифицированный фактор давления рассчитывается из системы уравнений (45)–(48) как функция температурного фактора $\tilde {T}$ и числа Маха |M|: ηβ =ηβ($\tilde {T},$ |M|). Предельный случай β = 1 соответствует абсолютно проницаемой поверхности: A = 0, η = ηβ.
• При β < 1 из (50) имеем: A > 0, η < ηβ. Это означает, что при снижении проницаемости поверхности фактор давления уменьшается, т.е. давление в навье-стоксовской области возрастает. При фиксированном β эта тенденция выражается тем сильнее, чем меньше температурный фактор и чем больше число Маха.
• Каждому сочетанию параметров $\tilde {T},$ $\left| {\text{M}} \right|$ отвечает некоторое минимальное значение коэффициента конденсации, определяемое равенством $A = {{\eta }_{\beta }}$
(51)
${{\beta }_{{{\text{min}}}}} = {{\left( {1 + \sqrt {\frac{3}{{10\pi }}} \frac{{{{\eta }_{{\beta }}}\sqrt {\tilde {T}} }}{{\left| {\text{M}} \right|}}} \right)}^{{ - 1}}}.$Отсюда следует, что конденсация возможна только в диапазоне ${{\beta }_{{{\text{min}}}}} < \beta \leqslant 1,$ в то время как область $0 < \beta \leqslant {{\beta }_{{{\text{min}}}}}$ является “запертой” для конденсации.
Влияние коэффициента конденсации. На рис. 10 приведены зависимости фактора давления от коэффициента конденсации с числом Маха в качестве параметра.
Рис. 10.
Зависимость обратного отношения давлений от коэффициента конденсации (а) $\tilde {T} = 10;$ 1 – $\left| {\text{M}} \right| = 1 \times {{10}^{{ - 2}}},$ 2 – $\left| {\text{M}} \right| = 4 \times {{10}^{{ - 2}}},$ 4 – $\left| {\text{M}} \right| = 1 \times {{10}^{{ - 1}}},$ 5 – $\left| {\text{M}} \right| = 2 \times {{10}^{{ - 1}}}.$
(б) $\tilde {T} = 1;$ 1 – $\left| {\text{M}} \right| = 1 \times {{10}^{{ - 2}}},$ 2 – $\left| {\text{M}} \right| = 4 \times {{10}^{{ - 2}}},$ 4 – $\left| {\text{M}} \right| = 1 \times {{10}^{{ - 1}}},$ 5 – $\left| {\text{M}} \right| = 2 \times {{10}^{{ - 1}}}.$ в) $\tilde {T} = 0.1;$ 1 – $\left| {\text{M}} \right| = 1 \times {{10}^{{ - 3}}},$ 2 – $\left| {\text{M}} \right| = 4 \times {{10}^{{ - 3}}},$ 3 – $\left| {\text{M}} \right| = 1 \times {{10}^{{ - 2}}},$ 4 – $\left| {\text{M}} \right| = 2 \times {{10}^{{ - 2}}},$ 5 – $\left| {\text{M}} \right| = 4 \times {{10}^{{ - 2}}},$ 6 – $\left| {\text{M}} \right| = 1 \times {{10}^{{ - 1}}}.$
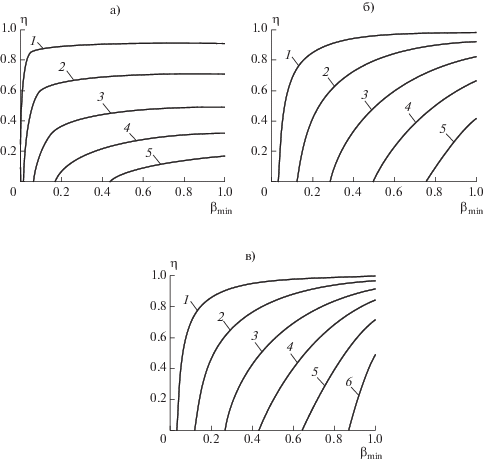
Как видно из рис. 10, при уменьшении $\beta $ от единицы до ${{\beta }_{{{\text{min}}}}}$ фактор давления убывает с некоторого максимального значения до нуля. Это означает, что при уменьшении $\beta $ и фиксированном значении ${{p}_{w}}$ давление в навье-стоксовской области увеличивается, так что при $\beta = {{\beta }_{{{\text{min}}}}}$ имеет место эффект “запирания конденсации”: ${{p}_{\infty }} \to \infty .$ Таким образом, каждая кривая ${\text{M}} = {\text{idem}}$ пересекается с осью абсцисс в точке $\beta = {{\beta }_{{{\text{min}}}}}.$ Область справа от этой точки является для конденсации “разрешенной, слева – "запертой”. Сопоставление рис. 10а, 10б, показывает, что при снижении температурного фактора запирание конденсации происходит при всех меньших числах Маха. Отсюда следует, что диапазон “разрешенных” значений $\beta $ для аномальной области конденсации $\left( {\tilde {T} < 1} \right)$ является значительно более узким, чем для нормальной области $\left( {\tilde {T} > 1} \right).$
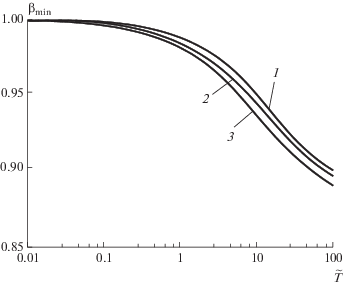
На рисунке 11 приведена зависимость запирающего значения коэффициента конденсации от температурного фактора при $\left| {\text{M}} \right| \leqslant 1.$ Как видно из рисунка, при снижении $\tilde {T}$ порог запирания конденсации монотонно возрастает и при $\tilde {T} \to 0$ достигает единицы, делая конденсацию невозможной. При увеличении числа Маха кривая ${{\beta }_{{{\text{min}}}}}\left( {\tilde {T}} \right)$ все более смещается в сторону единицы, тем самым увеличивая порог запирания и сужая разрешенную область.
Рис. 11.
Зависимость “запирающего” значения коэффициента конденсации от температурного фактора. Дозвуковая конденсация: 1 − |M| = 0.1, 2 − |M| = 0.3, 3 − |M| = 0.5, 4 − |M| = 1.
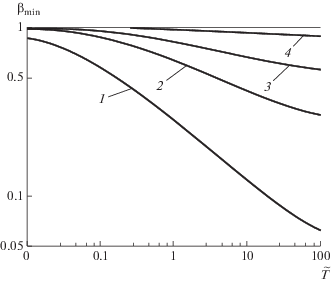
В однозначной области сверхзвуковой конденсации $1 < \left| {\text{M}} \right| \leqslant 1.16$ дозвуковые тенденции решения сохраняются, причем с ростом числа Маха область существования конденсации становится все более узкой (рис. 12). В диапазоне $1.16{\text{\;}} < \left| {\text{M}} \right| \leqslant 1.375$ имеет место инверсия зависимости $~{{\beta }_{{{\text{min}}}}}\left( {\tilde {T}} \right).$ В аномальной области $\left( {\tilde {T} < 1} \right)$ с ростом $\left| {\text{M}} \right|$ эта кривая продолжает подниматься, а в нормальной области $\left( {\tilde {T} > 1} \right)$ – начинает опускаться. В двузначной области сверхзвуковой конденсации неустойчивые ветви практически сливаются с единицей. Последние, таким образом, оказываются физически противоречивыми сразу по двум признакам: а) сверхзвуковые числа Маха на поверхности перемешивания; б) запирание конденсации за счет понижения проницаемости ПКФ. В то же время устойчивые ветви обнаруживают значительно более широкую разрешенную область.
ЗАКЛЮЧЕНИЕ
На основе полученного ранее аналитического решения задачи интенсивной конденсации выведена его аппроксимация, пригодная для проведения расчетов для всего диапазона дозвуковой конденсации. Искомой являлась зависимость фактора давления от температурного фактора с числом Маха в качестве параметра. Рассмотрен равновесный изотермический случай, разграничивающий аномальную и нормальную ветви конденсации. Развитая ранее “модель перемешивания” использована для расчета режимов сверхзвуковой конденсации. Исследованы особенности сверхзвуковой конденсации при увеличении числа Маха: а) инверсия решения; б) бифуркация решения; в) переход к двузначным решениям; г) предельное число Маха, для которого существует решение. Проведена классификация двузначных решений, позволяющая выделять устойчивые ветви. Для всего диапазона изменения интенсивности конденсации построена огибающая семейства максимумов давления. Проведено исследование влияния коэффициента конденсации на уравнения сохранения массы, нормальной компоненты импульса и энергии молекулярных потоков. Рассмотрено явление “запирания конденсации” за счет снижения проницаемости поверхности конденсированной фазы. Проведены расчеты “разрешенных” режимов конденсации.
Список литературы
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М. Высшая школа, 2001. 540 с.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М. URSS, 2012. 653 с.
Анисимов С.И., Имас Я.А., Романов Г.С., Ходыко Ю.В. Действие излучения большой мощности на металлы. М.: Наука, 1970. 272 с.
Коган М.Н. Динамика разреженного газа. М.: Наука, 1967. 440 с.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. Теоретическая физика: Т. VI. М.: Наука, 1986. 736 с.
Gusarov A.V., Smurov I. Target-vapour interaction and atomic collisions in pulsed laser ablation. J. Physics D: Applied Physics. 2001. V. 34. № 8. P. 1147−1156.
Zudin Y. Non-equilibrium Evaporation and Condensation Processes: Analytical Solutions. Heidelberg: Springer, 2018. 217 p.
Gusarov A.V., Smurov I. Gas-dynamic boundary conditions of evaporation and condensation: numerical analysis of the Knudsen layer // Phys. Fluids. 2002. V. 14. P. 4242−4255.
Mott-Smith H.M. The solution of the Boltzmann equation for a shock wave // Phys. Rev. 1951. V. 82. P. 885–892.
Абрамов А.А., Бутковский А.В. Влияние отношения температуры потока к температуре стенки на сильную конденсацию газа // ТВТ. 2008. Т. 46. № 2. С. 257–261.
Смирнов В.И. Курс высшей математики. Т. 1. М.: Наука, 1974. 336 с.
Aoki K., Sone Y., Yamada T. Numerical analysis of gas flows condensing on its plane condensed phase on the basis of kinetic theory // Phys. Fluids A. 1990. V. 2. P. 1867−1878.
Кузнецова И.А., Юшканов A.A., Яламов Ю.И. Сверхзвуковая конденсация одноатомного газа // ТВТ. 1997. Т. 35. № 2. С. 342–346.
Абрамов А.А., Коган М.Н. О режиме сверхзвуковой конденсации газа // Докл. АН СССР. 1984. Т. 278. № 5. С. 1078–1081.
Bardos C., Golse F., Sone Y. Half-Space Problems for the Boltzmann Equation: A Survey // Journal of Statistical Physics. 2006. V. 124. Issue 2–4. P. 275–300.
Муратова Т.М., Лабунцов Д.А. Кинетический анализ процессов испарения и конденсации // ТВТ. 1969. Т. 7. № 5. С. 959–967.
Коган М.Н., Макашев Н.К. О роли слоя Кнудсена в теории гетерогенных реакций и в течениях с реакциями на поверхности // Изв. АН СССР. Механика жидкости и газа. 1971. № 6. С. 3–11.
Nagayama G., Tsuruta T. A general expression for the condensation coefficient based on the transition state theory and molecular dynamics simulation // J. Chem. Phys. 2003. V. 118. P. 1392–1399.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика