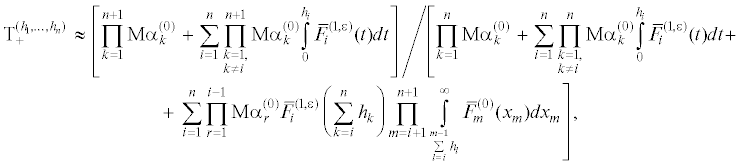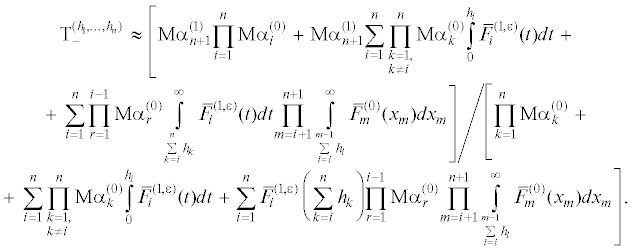Известия РАН. Энергетика, 2019, № 5, стр. 26-32
Полумарковские и скрытые марковские и полумарковские модели систем энергетики
Ю. Е. Обжерин *
Федеральное государственное автономное образовательное учреждение высшего образования
“Севастопольский государственный университет”
Севастополь, Россия
* E-mail: objsev@mail.ru
Поступила в редакцию 10.12.2018
После доработки 21.10.2019
Принята к публикации 23.10.2019
Аннотация
Одной из важных задач теории надежности и эффективности систем энергетики является задача создания информационных систем управления системами энергетики и переход к интеллектуальному управлению и инжинирингу. Решение этой задачи возможно на основе построения математических моделей, касающихся различных аспектов структуры и функционирования этих систем. В работе рассматриваются возможности применения полумарковских процессов с общим фазовым пространством состояний, скрытых марковских и полумарковских моделей для моделирования систем энергетики.
ВВЕДЕНИЕ
Согласно дорожной карте Национальной технологической инициативы EnergyNet одними из основных задач этого проекта являются следующие:
1. “Цифровизация” систем энергетики, создание цифровых сетей, цифровых подстанций.
2. Создание информационных систем управления системами энергетики и переход к интеллектуальному управлению и инжинирингу.
Решение этих задач возможно на основе построения математических моделей, касающихся различных аспектов структуры и функционирования систем энергетики и разработки на их основе алгоритмов и информационных систем поддержки принятия решений при проектировании и эксплуатации систем, а также прогнозирования их состояний. При построении адекватных моделей систем энергетики необходимо использовать существующие возможности современного математического аппарата. В работе рассматриваются возможности применения аппарата теории полумарковских процессов с общим фазовым пространством состояний, скрытых марковских и полумарковских моделей для моделирования систем энергетики.
1. ПОЛУМАРКОВСКИЕ ПРОЦЕССЫ, СКРЫТЫЕ МАРКОВСКИЕ И ПОЛУМАРКОВСКИЕ МОДЕЛИ, ИХ ПРИМЕНЕНИЕ ДЛЯ МОДЕЛИРОВАНИЯ СИСТЕМ ЭНЕРГЕТИКИ
Полумарковские процессы широко используются для построения моделей и анализа систем различного назначения: технических, производственных, энергетических, информационных, экономических, биологических и т.д.
Исследования по этому направлению активно проводятся во Франции, США, Италии, Англии, Китае, Индии, России, Украине, Швеции, Японии и ряде других стран. По результатам исследований опубликовано несколько монографий и большое число статей. Так, ведущие мировые издательства Elsevier, Springer, World Scientific опубликовали за последнее время следующие монографии по данной тематике [1–7].
В большинстве этих работ использовались полумарковские процессы с конечным множеством состояний. При построении моделей конкретных систем предполагалось, что большинство случайных величин, характеризующих систему, имеют экспоненциальное распределение, что существенно сужает возможности применения полученных результатов.
Большой вклад в развитие теории полумарковских процессов и их применение внесли работы ученых стран СНГ В.С. Королюка, А.Ф. Турбина, И.А. Ушакова, А.В. Свищука, В.А. Каштанова, В.М. Шуренкова. В их работах [8–13] разработаны алгоритмы асимптотического и стационарного фазового укрупнения полумарковских процессов, построены модели эволюционных стохастических систем и алгоритмы их усреднения. Эти работы являются актуальными и в настоящее время, они дают большие возможности для моделирования систем различного назначения, в том числе и энергетических.
Эффективным средством построения моделей систем и их анализа является аппарат теории полумарковских процессов с общим фазовым пространством состояний [2, 5, 8, 9, 11]. Использование этого класса случайных процессов позволяет:
– освободиться от ряда ограничений при построении моделей, в частности, от предположения об экспоненциальном законе распределения случайных величин, характеризующих систему;
– получить аналитические выражения для характеристик системы, которые можно использовать для инженерных расчетов;
– построить модели ряда систем энергетики.
Для решения проблемы размерностей моделей можно использовать алгоритмы асимптотического и стационарного фазового укрупнения полумарковских процессов, разработанные В.С. Королюком, А.Ф. Турбиным, А.В. Свищуком [8–11]. Этот подход открывает большие возможности для моделирования систем.
Начиная с 80-х гг., для моделирования и анализа систем широкое применение получили скрытые марковские и полумарковские модели. В этих моделях предполагается, что наблюдаемая последовательность сигналов связана с марковским (полумарковским) процессом с ненаблюдаемыми (скрытыми) состояниями, и ставится задача по наблюдаемой последовательности сигналов оценить структуру и характеристики ненаблюдаемого процесса. Скрытые марковские и полумарковские модели позволяют по результатам наблюдений проводить диагностику системы, прогнозировать ее состояния. Скрытым марковским и полумарковским моделям посвящено большое число работ, в частности, недавно вышедшие монографии [14–16].
Скрытые марковские и полумарковские модели применяются в следующих областях: диагностика и обслуживание оборудования; надежность систем; прогнозирование функционирования систем; оценка производительности сетей; распознавание и синтез речи; машинный перевод; распознавание образов; картографирование мозга с помощью функциональной магнитно-резонансной томографии; раннее определение патологических событий; распознавание деятельности человека; прогнозирование структуры белка; моделирование анализа финансовых временных рядов и некоторых других областях. В литературе отмечается, что данный подход используется более чем в тридцати областях.
Полумарковские процессы с общим фазовым пространством состояний и скрытые марковские и полумарковские модели могут быть эффективно использованы для построения моделей, касающихся различных аспектов структуры и функционирования систем энергетики: надежности, эффективности, контроля, диагностики, технического обслуживания и прогнозирования.
На этой основе могут быть решены следующие задачи:
1. Построены полумарковские и скрытые марковские и полумарковские модели:
– надежности систем энергетики;
– контроля и диагностики систем энергетики;
– технического обслуживания систем энергетики;
– прогнозирования состояний систем энергетики.
2. Нахождение технических и экономических характеристик систем, пригодных для инженерных расчетов.
3. Решение задач нахождения оптимальных значений параметров систем энергетики на основе целевых функций, полученных с помощью моделей.
4. Создание на основе полученных результатов, программного обеспечения для информационных систем оценки надежности, контроля, диагностики, обслуживания систем энергетики и прогнозирования их состояний.
2. ПОЛУМАРКОВСКАЯ МОДЕЛЬ ОДНОПОТОЧНОЙ ЛИНИИ С ПРОМЕЖУТОЧНЫМИ НАКОПИТЕЛЯМИ
В качестве примера использования аппарата теории полумарковских процессов с общим фазовым пространством состояний для моделирования систем энергетики рассматривается многофазная, однопоточная система, состоящая из обслуживающих устройств и промежуточных накопителей, связи между которыми изображены на рис. 1. Системы такого вида играют важную роль в энергетике [17].
На рисунке 1 приняты следующие обозначения: ${{A}_{i}},\;\;i = \overline {1,n + 1} $ – обслуживающие устройства; ${{H}_{i}},\,\,i = \overline {1,n} - 1$ промежуточные накопители. Модель системы строится при следующих предположениях.
1. Возможными состояниями каждого из обслуживающих устройств ${{A}_{i}}$ являются: работоспособное, восстановления и отключения.
2. Время безотказной работы (восстановления) устройства ${{A}_{i}}$ является случайной величиной (СВ) $\alpha _{i}^{{(0)}}(\alpha _{i}^{{(1)}})$ с функцией распределения (ФР) $F_{1}^{{(0)}}(x)\;(F_{i}^{{(1)}}(x)).$ СВ $\alpha _{i}^{{(0)}}(\alpha _{i}^{{(1)}})$ независимы, имеют конечные математические ожидания; у ФР $F_{i}^{{(0)}}(x)\;(F_{i}^{{(1)}}(x))$ существуют плотности $f_{i}^{{(0)}}(x)(f_{i}^{{(1)}}(x)).$
3. Накопители ${{H}_{i}}$ являются абсолютно надежными устройствами, имеющими ограниченные емкости ${{h}_{i}} \geqslant 0$ (емкость накопителя ${{H}_{i}}$ выражается в единицах времени, которое понадобится устройству ${{A}_{{i + 1}}}$ для полного освобождения этого накопителя).
4. Работоспособное устройство ${{A}_{i}}$ отключается, сохраняя работоспособное состояние, при пустом накопителе ${{H}_{{i - 1}}}$ или переполненном накопителе ${{H}_{{i + 1}}}.$
5. Производительность устройства ${{A}_{i}}$ постоянна и равна ${{c}_{i}},$ при этом ${{c}_{i}} \geqslant {{c}_{{i + 1}}}.$
6. Система находится в состоянии отказа, если выходное устройство ${{A}_{{n + 1}}}$ не занято обработкой продукта; восстановление устройств ${{A}_{i}}$ считается неограниченным.
Для описания функционирования системы введем следующее дискретно-непрерывное пространство полумарковских состояний:
Для приближенного нахождения характеристик надежности рассматриваемой системы используем алгоритм фазового укрупнения [11], который состоит в следующем.
Предположим, что стохастическое ядро вложенной цепи Маркова (ВЦМ) $\{ {{\xi }_{n}};n \geqslant 0\} $ полумарковского процесса $\xi (t)$ исходной системы близко к стохастическому ядру ВЦМ $\{ \xi _{n}^{{(0)}};n \geqslant 0\} $ опорной системы S0 с единственным стационарным распределением $\rho (dx).$ Тогда для приближенного нахождения средней стационарной наработки на отказ ${{T}_{ + }},$ среднего стационарного времени восстановления ${{T}_{ - }}$ и стационарного коэффициента готовности ${{К}_{{\text{Г}}}}$ исходной системы S можно использовать следующие приближенные формулы [11]:
(1)
${{T}_{ + }} \approx \frac{{(\rho ,{{{\bar {m}}}_{1}})}}{{(\rho ,{{P}^{{(r)}}}{{{\bar {1}}}_{0}})}},\,\,\,\,{{T}_{ - }} \approx \frac{{(\rho ,{{P}^{{(r)}}}{{{\bar {m}}}_{0}})}}{{(\rho ,{{P}^{{(r)}}}{{{\bar {1}}}_{0}})}},\,\,\,\,{{K}_{{\text{Г}}}} = \frac{{{{Т}_{ + }}}}{{{{Т}_{ + }} + {{Т}_{ - }}}},$Важным моментом применения этого метода является выбор опорной системы ${{S}_{0}}.$ Предположим, что у устройств ${{A}_{i}},\;i = \overline {1,n} $ быстрое восстановление, т.е. их времена восстановления $\alpha _{i}^{{(1)}}$ зависят от малого положительного параметра ε таким образом, что
Используя формулы (1), можно показать, что стационарные характеристики рассматриваемой системы: стационарная наработка на отказ ${\rm T}_{ + }^{{({{h}_{1}},...,{{h}_{n}})}}$ и среднее стационарное время восстановления ${\rm T}_{ - }^{{({{h}_{1}},...,{{h}_{n}})}}$ приближенно вычисляются по формулам:
Зная выражения для ${\rm T}_{ + }^{{({{h}_{1}},...,{{h}_{n}})}}$ и ${\rm T}_{ - }^{{({{h}_{1}},...,{{h}_{n}})}}$ можно найти стационарный коэффициент готовности ${\rm K}_{\Gamma }^{{({{h}_{1}}, \ldots ,{{h}_{n}})}}$ по формуле (1).
В таблице 1 представлены результаты нахождения стационарных характеристик четырехфазной системы с использованием формул (3), (4) и на основе имитационного моделирования.
Таблица 1.
Результаты моделирования четырехфазной системы
| $M\alpha _{1}^{{(0)}} = M\alpha _{2}^{{(0)}} = M\alpha _{3}^{{(0)}} = M\alpha _{4}^{{(0)}} = 17\;{\text{ч}},$$M\alpha _{1}^{{(1)}} = M\alpha _{2}^{{(1)}} = 0.6\;{\text{ч}},$$M\alpha _{3}^{{(1)}} = M\alpha _{3}^{{(1)}} = 0.8\;{\text{ч}},$${{h}_{1}} = {{h}_{2}} = {{h}_{3}} = h,$${\text{время\;}}\,\,{\text{обработки}}--0.2\;{\text{ч}}$ | ||||
|---|---|---|---|---|
| Величина резерва времени, ч | Результаты аналитического моделирования | Результаты имитационного моделирования | ||
| $h$ | ${\rm T}_{ + }^{{({{h}_{1}},{{h}_{2}},{{h}_{3}})}}$, ч | ${\rm T}_{ - }^{{({{h}_{1}},{{h}_{2}}{{h}_{3}})}}$, ч | ${\rm K}_{\Gamma }^{{({{h}_{1}},{{h}_{2}},{{h}_{3}})}}$ | ${\rm K}_{\Gamma }^{{({{h}_{1}},{{h}_{2}},{{h}_{3}})}}$ |
| 0 | 4.250 | 0.700 | 0.859 | 0.879 |
| 0.1 | 6.518 | 0.736 | 0.899 | 0.929 |
| 0.2 | 8.693 | 0.736 | 0.919 | 0.932 |
| 0.3 | 10.507 | 0.780 | 0.931 | 0.923 |
| 0.4 | 11.929 | 0.790 | 0.938 | 0.933 |
| 0.5 | 13.029 | 0.795 | 0.943 | 0.927 |
| 0.6 | 13.885 | 0.797 | 0.946 | 0.937 |
| 0.7 | 14.556 | 0.799 | 0.948 | 0.940 |
| 0.8 | 15.084 | 0.799 | 0.950 | 0.939 |
| 0.9 | 15.501 | 0.800 | 0.951 | 0.935 |
| 1.0 | 15.830 | 0.800 | 0.952 | 0.941 |
| 1.1 | 16.089 | 0.800 | 0.953 | 0.943 |
| 1.2 | 16.292 | 0.800 | 0.953 | 0.945 |
| 1.3 | 16.451 | 0.800 | 0.954 | 0.946 |
| 1.4 | 16.575 | 0.800 | 0.954 | 0.947 |
| 1.5 | 16.671 | 0.800 | 0.954 | 0.945 |
При моделировании предполагалось, что все СВ (времена работы и восстановления устройств и накопителей) распределены по экспоненциальному закону.
ЗАКЛЮЧЕНИЕ
В статье показаны возможности применения полумарковских процессов с общим фазовым пространством состояний и скрытых марковских и полумарковских моделей для построения моделей и анализа функционирования систем энергетики. Для решения проблемы размерности моделей предлагается использовать алгоритмы асимптотического и стационарного фазового укрупнения систем.
Работа выполнена в рамках государственного задания Министерства образования и науки Российской Федерации (№ 1.10513.2018/11.12), при финансовой поддержке Российского фонда фундаментальных исследований (№ 18-01-00392а).
Список литературы
Grabski F. Semi-Markov Processes: Applications in System Reliability and Maintenance. Elsevier, 2015. 255 p.
Obzherin Yu.E., Boyko E.G. Semi-Markov Models: Control of Restorable Systems with Latent Failures. Elsevier, Academic Press, 2015. 212 p.
Janssen J., Manca R. Applied Semi-Markov Processes. Springer Science + Business Media, 2006. 315 p.
Korolyuk V.S., Limnios N. Stochastic Systems in Merging Phase Space. World Scientific, Imperial Coledge Press, 2005. 348 p.
Limnios N., Oprisan G. Semi-Markov Processes and Reliability. Springer Science+Business Media, 2001. 225 p.
Janssen J., Limnios N. (Eds.). Semi-Markov Models and Applications. Kluwer Academic Publishers, 1999. 404 p.
Silvestrov D., Silvestrov S. Nonlinearly Perturbed Semi-Markov Processes. Springer, 2017. 143 p.
Королюк В.С., Турбин А.Ф. Процессы марковского восстановления в задачах надежности систем. К.: Наук. думка, 1982. 236 с.
Королюк В.С. Стохастические модели систем. К.: Наук. думка, 1989. 208 с.
Королюк В.С., Свищук А.В. Эволюционные стохастические системы. Алгоритмы усреднения и диффузионной аппроксимации. Киев: Ин-т математики НАН Украины, 2000. 344 с.
Корлат А.Н., Кузнецов В.Н., Новиков М.М., Турбин А.Ф. Полумарковские модели восстанавливаемых систем и систем массового обслуживания. Кишинев: Штиинца, 1991. 276 с.
Шуренков В.М. Эргодические процессы Маркова. М.: Наука, гл. ред. физ.-мат. лит., 1989. 336 с.
Каштанов В.А., Медведев А.И. Теория надежности сложных систем (теория и практика). М.: Европейский центр по качеству, 2002. 469 с.
Yu Shun-Zheng. Hidden Semi-Markov Models: Theory, Algorithms and Applications. Elsevier, 2015. 208 p.
Barbu V.S., Limnios N. Semi-Markov Chains and Hidden Semi-Markov Models toward Applications: their use in Reliability and DNA Analysis. Springer, 2008. 226 p.
Hoek J., Elliott R.J. Introduction to Hidden Semi-Markov Models. Cambridge University Press, 2018. 185 p.
Руденко Ю.Н., Ушаков И.А. Надежность систем энергетики. Новосибирск: Наука. Сиб. отделение, 1989. 328 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика