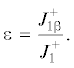Известия РАН. Энергетика, 2020, № 1, стр. 138-158
Анализ сопряженной задачи “испарение–теплопроводность”
Ю. Б. Зудин 1, *, Д. С. Уртенов 1, В. С. Устинов 1
1 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: yzudin@gmail.com
Поступила в редакцию 21.11.2019
После доработки 25.11.2019
Принята к публикации 28.11.2019
Аннотация
Рассмотрена сопряженная задача: “испарение с поверхности конденсированной фазы – теплопроводность в облучаемом теле”. На основе модели перемешивания получены выражения для кинетических скачков температуры и давления газа на поверхности конденсированной фазы. Проведен анализ влияния коэффициента испарения – конденсации на уравнения сохранения массы, импульса и энергии в слое Кнудсена. С помощью концепции фронта теплового возмущения исследована краевая задача теплопроводности в полуограниченном теле. Получено аналитическое решение сопряженной задачи в линейном приближении и выполнен анализ его асимптотик. Показано, что зависимость параметра испарения от времени определяется обобщенным кинетическим параметром, включающим тепловой поток, коэффициент испарения–конденсации, а также комплекс теплофизических свойств. Для случая интенсивного испарения решение выполнялось с помощью программного пакета системы компьютерной алгебры Maple. Полученное решение позволяет рассчитывать период сопряжения, в течение которого формируется мощный поток испаренного вещества через поверхность конденсированной фазы.
ВВЕДЕНИЕ
Настоящая работа посвящена аналитическому исследованию сопряженной задачи, состоящей из двух взаимосвязанных задач: а) молекулярно-кинетической модели интенсивного испарения с поверхности конденсированной фазы (ПКФ); б) модели фронта теплового возмущения (ФТВ) в облучаемом теле.
Как известно, большинство задач гидродинамики и теплообмена описываются дифференциальными уравнениями в частных производных. Так, уравнения Навье–Стокса и уравнение энергии представляют собой квазилинейные дифференциальные уравнения, решение которых, как правило, может быть получено с помощью численных методов. Однако даже в нынешний компьютерный век важную роль продолжают играть аналитические решения задач гидродинамики и теплообмена. По сравнению с численными исследованиями они обладают следующими преимуществами.
• Ценность аналитического подхода заключается в замкнутом качественном описании задачи, выявления определяющих параметров и их классификации по степени важности.
• Общность, присущая аналитическим решениям, позволяет проводить их параметрические исследования путем варьирования начальных и краевых условий задачи.
• Для тестирования численных решений полных уравнений необходимо иметь базовые аналитические решения упрощенных уравнений, полученных в результате оценки и выбрасывания отдельных членов.
• Аналитические решения используются для проверки корректности постановки численных исследований. Укажем в этой связи на аналитические решения задач теории теплопроводности и термоупругости, представленные в работах Карташова [1, 2].
Исследование задачи интенсивного испарения актуально для практических разработок теплообменного оборудования, систем комплексной тепловой защиты летательных аппаратов, вакуумных технологий и др. Перечислим приложения, связанные с процессом интенсивного испарения.
• Моделирование испарения теплоносителя в вакуум при разгерметизации защитной оболочки атомного реактора космического аппарата [3].
• Организация лазерного облучения материалов [4].
• Моделирование обтекания космических объектов при их входе в земную атмосферу [5].
Знание закономерностей интенсивного испарения необходимо также для исследования некоторых фундаментальных проблем.
• При воздействии солнечного излучения на поверхность кометы происходит испарение ее ледяного ядра с образованием атмосферы. В зависимости от расстояния до Солнца интенсивность испарения изменяется в широких пределах и может достигать огромных значений. Переменный во времени процесс испарения оказывает сильное влияние на плотность атмосферы кометы и характер ее движения [6].
• Макроскопические квантово-механические эффекты в сверхтекучем гелии вызывают перенос тепла за счет противотока нормальной и сверхтекучей компонент. Этот уникальный механизм приводит к чрезвычайно высокой эффективности теплопередачи. Как следствие, термическое сопротивление в объеме сверхтекучего гелия является исчезающе малым, и транспорт тепла в нем осуществляется за счет испарения на межфазной границе.
КИНЕТИЧЕСКИЙ АНАЛИЗ ИНТЕНСИВНОГО ИСПАРЕНИЯ
Уравнения сохранения. Проблема интенсивного испарения с поверхности конденсированной фазы (ПКФ) в заполненное газом пространство представляет собой краевую задачу для уравнений газодинамики. Со стороны газовой фазы на ПКФ располагается слой Кнудсена, имеющий толщину порядка длины свободного пробега молекул. В пределах неравновесного слоя Кнудсена непрерывное макроскопическое описание среды теряет свою применимость. Состояние газа подчиняется здесь дискретным микроскопическим закономерностям, описываемым кинетическим уравнением Больцмана [7]. Со своей стороны, в удаленной от ПКФ газовой области справедливы уравнения Н-авье–Стокса (“навьестоксовская область”). Наложение разномасштабных задач – микроскопической и макроскопической – приводит к возникновению на ПКФ кинетических скачков параметров. Вследствие этого температура и давление газа, используемые в качестве граничных условий (ГУ) для уравнений газодинамики в навьестоксовской области, не будут равны своим истинным значениям. Если скорость испарения мала по сравнению со скоростью теплового движения молекул, то реализуется случай “слабого испарения”. Тогда при анализе течения в слое Кнудсена достаточно учитывать только линейные отклонения кинетических параметров от равновесия. Со своей стороны, при истечении пара со скоростью, сравнимой со скоростью звука, говорят об “интенсивном испарении”. При этом кинетические скачки параметров становятся сравнимыми с их абсолютными значениями в навьестоксовской области.
Рассмотрим задачу об испарении с ПКФ в полупространство, заполненное паром – одноатомным идеальным газом. Запишем уравнения сохранения в слое Кнудсена молекулярных потоков массы
импульса и энергии(3)
$J_{3}^{ + } - J_{3}^{ - } = \frac{1}{2}{{\rho }_{\infty }}u_{\infty }^{3} + \frac{5}{2}{{p}_{\infty }}{{u}_{\infty }}.$В правых частях уравнений (1)–(3) стоят макроскопические потоки испаренного вещества. Эмитируемые поверхностью молекулярные потоки $J_{i}^{ + }{\text{\;}}\left( {i = 1,2,3} \right)$ определяются интегрированием равновесной максвелловской функции распределения и записываются в виде [7]:
Здесь $u$ – газодинамическая скорость; $\rho $ – плотность; $p$ – давление; ${v} = \sqrt {2{{R}_{g}}T} $ – тепловая скорость молекул, характеризующая их среднюю кинетическую энергию при температуре ПКФ; $T$ – температура; ${{R}_{g}}$ – индивидуальная газовая постоянная; индексы “$\infty $”, “$w$” обозначают условия соответственно на бесконечности и на ПКФ.Для определения падающих на ПКФ молекулярных потоков $~J_{i}^{ - }$ $\left( {i = 1,2,3} \right)$ был предложен ряд теоретических и полуэмпирических моделей. Их детальный обзор можно найти, в частности, в работах [8–11]. Ниже для расчета $J_{i}^{ - }$ мы будем использовать представленную в монографии [11] “модель перемешивания”. Эта модель, основанная на учете взаимодействия в слое Кнудсена эмитируемого и падающего молекулярных потоков, позволила получить аналитические решения задач интенсивного фазового перехода – испарения и конденсации.
Коэффициент испарения–конденсации. В эталонном варианте молекулярно-кинетической теории рассматривается абсолютно проницаемая ПКФ. Предполагается, что поверхность адсорбирует все молекулы, падающие на нее из газовой области, и эмитирует все молекулы, поступающие к ней из глубины конденсированной фазы. В общем случае межфазная граница является частично проницаемой и пропускает лишь некоторую часть $\beta < 1$ молекулярных потоков, подходящих к ней с обеих сторон. Величина $\beta $ называется “коэффициентом испарения–конденсации” (КИК). Ее значение зависит от состояния поверхности и физической природы конденсированной фазы и может изменяться в диапазоне $0 < \beta \leqslant 1.$
Рассмотрим влияние КИК на уравнение сохранения массы молекулярных потоков. Пусть ПКФ эмитирует в газовую фазу не весь поток $J_{1}^{ + },$ а только его часть $~\beta J_{1}^{ + }.$ Пусть также только часть падающего на ПКФ потока $\beta J_{1}^{ - },$ захватывается ею, а оставшаяся часть – $\left( {1 - \beta } \right)J_{1}^{ - }$ – отражается в газовую область. В результате такой селекции отходящий от ПКФ суммарный молекулярный поток будет содержать две составляющих – эмитируемую и отраженную
Заменяя в уравнении (1) $J_{1}^{ + }$ на $J_{{1{\beta }}}^{ + },$ получаем уравнение сохранения потока массы для случая частично проницаемой ПКФ
Введем “коэффициент проницаемости” $\varepsilon $ как отношение отходящего от ПКФ потока массы (при $\beta < 1$) к потоку, эмитируемому абсолютно проницаемой ПКФ (при $\beta = 1$)
Исключая из уравнений (7), (8) падающий поток $J_{1}^{ - }$ и используя уравнение состояния идеального газа ${{p}_{w}} = 1{\text{/}}2{{\rho }_{w}}{v}_{w}^{2},$ из (9) получаем:
(10)
$\varepsilon = 1 - 2\sqrt \pi \frac{{1 - \beta }}{\beta }\frac{{\tilde {p}s}}{{\sqrt {\tilde {T}} }}.$В вычислительном плане влияние КИК на законы сохранения сводится к замене реальной плотности пара ${{\rho }_{w}}$ на ее эффективное значение ${{\rho }_{{w\beta }}} = \varepsilon {{\rho }_{w}}$ при условии ${{T}_{w}} = {\text{const}}{\text{.}}$ С помощью уравнения состояния эффективной плотности можно поставить в соответствие эффективное давление: ${{p}_{{w{\beta }}}} = 1{\text{/}}2{{\rho }_{{w{\beta }}}}{v}_{w}^{2}.$ Тогда из (10) получаем связь эффективного и истинного давлений
(11)
${{\tilde {p}}^{{ - 1}}} = \tilde {p}_{*}^{{ - 1}} + 2\sqrt \pi \frac{{1 - \beta }}{\beta }\frac{s}{{\sqrt {\tilde {T}} }},$Если интенсивность испарения мала по сравнению с интенсивностью молекулярного перемешивания, то при анализе можно ограничиться линейными по скоростному фактору отклонениями параметров от равновесия: $s \ll 1.$ Этот случай слабого испарения является предметом исследования линейной кинетической теории, разработанной Лабунцовым и Муратовой [12, 13]. Указанными авторами были получены следующие выражения для кинетических скачков температуры
и давления(16)
$\frac{{{{p}_{w}} - {{p}_{\infty }}}}{{{{p}_{w}}}} = 2\sqrt \pi \frac{{1 - 0.4\beta }}{\beta }s.$Для случая интенсивного испарения в монографии [11] на основе модели перемешивания предложены приближенные аппроксимации аналитического решения для температуры
(17)
${{\tilde {T}}^{{ - 1}}} = 1 + {{k}_{{T1}}}{\text{M}} + {{k}_{{T2}}}{{{\text{M}}}^{2}} + {{k}_{{T3}}}{{{\text{M}}}^{3}}$(18)
${{\tilde {p}}^{{ - 1}}} = 1 + {{k}_{{p1}}}{\text{M}} + {{k}_{{p2}}}{{{\text{M}}}^{2}} + {{k}_{{p3}}}{{{\text{M}}}^{3}}.$Значения входящих в формулы (17), (18) числовых коэффициентов приведены в табл. 1.
ЛАЗЕРНОЕ ОБЛУЧЕНИЕ ПОВЕРХНОСТИ
Таблица 1.
Значения числовых коэффициентов в формулах (17), (18)
| ${{k}_{{T1}}}$ | ${{k}_{{T2}}}$ | ${{k}_{{T3}}}$ | ${{k}_{{p1}}}$ | ${{k}_{{p2}}}$ | ${{k}_{{p3}}}$ |
|---|---|---|---|---|---|
| 0.405 | –0.144 | 0.226 | 1.94 | 1.38 | 0.45 |
Лазерная абляция. Создание физических основ лазерной технологии требует детального теоретического исследования воздействия мощного излучения на поверхность конденсированного вещества (“мишени”). Взаимодействие лазерного излучения с мишенью включает цепочку взаимосвязанных процессов: перенос излучения и его поглощение в мишени; перенос тепла в мишени; испарение на поверхности мишени; газовая динамика в навьестоксовской области. Важную роль играет при этом лазерная абляция – совокупность физико-химических процессов, результатом которых является удаление вещества с поверхности раздела фаз. Лазерная абляция приводит к интенсивным процессам испарения и конденсации и, как следствие, к формированию мощного потока вещества через ПКФ.
Так как газодинамические условия испарения на границе пара с ПКФ существенно зависят от ее температуры, то расчет лазерной абляции должен проводиться в рамках сопряжения газодинамической задачи и задачи теплопереноса в мишени. Теоретическое описание сопряженной задачи было впервые предложено автором [14], который нашел связь между температурой мишени и параметрами пара при звуковом испарении $\left( {{\text{M}} = 1} \right)$. Затем появились модели [15–17], обобщающие метод работы [14] на весь диапазон чисел Маха парового потока. В работах [16, 17] была предложена “тепловая модель” лазерной абляции. Рассматривалось уравнение теплопроводности в мишени, связанное с газодинамическими уравнениями с помощью граничных условий (ГУ), следующих из решения задачи интенсивного испарения. Авторы [18] определяли скорость испарения в предположении, что высокотемпературная конденсированная фаза ведет себя как плотный газ. В работе [19] показано, что после окончания лазерного импульса ПКФ охлаждается главным образом за счет теплоотвода вглубь мишени В результате этого давление насыщенного пара, соответствующее температуре ПКФ, становится меньше актуального давления пара, что приводит к его обратной конденсации на мишени.
Здесь важно специально подчеркнуть, что все упомянутые выше работы представляли собой численные исследования. Для обобщения полученных результатов, а также для составления общей физической картины процесса необходимо иметь приближенную аналитическую модель сопряженной задачи “теплопроводность–испарение”. Разработка такой модели и получение на ее основе аналитического решения сопряженной задачи является целью настоящей статьи.
Фронт теплового возмущения. В различных приложениях задача теплопроводности является сопряженной с некоторой внешней задачей: краевой задачей термоупругости, обратной задачей теплопроводности, задачей оптимального управления и др. Предметом нашего анализа является сопряженная задача “теплопроводность в мишени–интенсивное испарение с ПКФ”. При этом рассматривается либо процесс собственно испарения (в случае жидкой мишени), либо процесс сублимации (в случае твердой мишени).
Как известно [1, 2], математическое моделирование включает в качестве составных частей решение комплекса задач [1, 2]. Наиболее важной из них является задача построения модели, в идеале сочетающей простоту с адекватностью исследуемому процессу. Математическое моделирование может строиться на основе как численных, так и аналитических методов. Последние, в свою очередь, могут быть либо точными (классическими), либо разнообразными приближенными:
• Прямые численные методы в ряде случаев оказываются малоэффективными. Так как исследуемая задача, как правило, является многопараметрической, то ее численное решение дает в качестве конечного продукта частное решение, описывающее конкретные условия.
• К классическим аналитическим методам можно отнести: метод разделения переменных, метод источников, метод тепловых потенциалов, интегральные преобразования в конечных и бесконечных пределах и др. Точные аналитические методы могут быть использованы лишь для решения линейных дифференциальных уравнений. Однако и здесь применение классических методов приводит к решениям в виде плохо сходящихся бесконечных рядов.
• К приближенным относятся: вариационные методы, методы взвешенных невязок, интегральные методы и др. Приближенные методы проигрывают численным в точности расчетов, но выигрывают за счет своей универсальности. Однако не все приближенные методы являются эффективными. В частности, они являются непригодными для решения задач теплопроводности при малых значениях времени. Во-первых, при этом для определения собственных чисел краевой задачи необходимо решать алгебраические уравнения высоких степеней. Во-вторых, выполнение начальных условий приводит к системам алгебраических линейных уравнений с плохо обусловленными матрицами коэффициентов. Несмотря на наличие стандартных компьютерных программ, решение таких систем представляет существенные вычислительные трудности.
Эффективный приближенный подход к решению краевых задач теплопроводности основан на концепции фронта теплового возмущения (ФТВ), монотонно продвигающегося от поверхности вглубь тела [20]. Этот подход опирается на интегральный метод теплового баланса (или метод осреднения функциональных поправок). В рамках данного метода дифференциальное уравнение теплопроводности заменяется на интеграл теплового баланса. Поле температур аппроксимируется полиномом, коэффициенты которого находятся из дополнительных ГУ, задаваемых на границах области и на ФТВ. Выполнение этих условий должно быть эквивалентным выполнению их в граничных точках исходного дифференциального уравнения. Использование интегрального метода приводит к простым аналитическим решения, точно удовлетворяющим начальному и граничным условиям и приближенно-исходному дифференциальному уравнению.
Как уже указывалось, ключевым вопросом моделирования интенсивного испарения является задание ГУ на поверхности раздела конденсированной и газовой фаз. Из кинетического анализа следует, что молекулярные потоки, эмитируемые ПКФ и налетающие на нее из пара, обладают существенно различными спектрами. Вследствие этого на ПКФ возникают кинетические скачки температуры и давления, которые могут быть рассчитаны по формулам (17), (18).
Уравнение теплопроводности. Для описания взаимодействия лучистого потока с мишенью необходимо решать сопряженную задачу, включающую систему уравнений сохранения молекулярных потоков в газе и уравнение теплопроводности в нагреваемом теле. Рассмотрим нестационарное одномерное уравнение теплопроводности в полуограниченном теле $0 \leqslant y < \infty $
(19)
$\frac{{\partial \vartheta }}{{\partial t}} = {{a}_{m}}\frac{{{{\partial }^{2}}\vartheta }}{{\partial {{y}^{2}}}}.$Пусть при $t > 0$ температура поверхности ${{T}_{w}}$ изменяется во времени по некоторому закону ${{\vartheta }_{w}} = {{\vartheta }_{w}}\left( t \right).$ Тогда граничное условие будет иметь вид: $\vartheta = {{\vartheta }_{w}}$ при $y = 0~\left( {t > 0} \right),$ где ${{\vartheta }_{w}} = ~{{T}_{w}} - {{T}_{0}}.$ В случае простых однородных ГУ типа ${{T}_{w}} = {\text{const}},$ $q = {\text{const}}$ уравнение (19) после введения автомодельной переменной ${y \mathord{\left/ {\vphantom {y {\sqrt t }}} \right. \kern-0em} {\sqrt t }}$ преобразуется в обыкновенное дифференциальное уравнение. Его решение получается с помощью интеграла Дюамеля [1, 2] и записывается в виде интегралов вероятностей (функций ошибок).
Будем использовать приближенный интегральный метод слоя конечной толщины $\delta ,$ основанный на концепции ФТВ. Введем обобщенную переменную $\eta = y{\text{/}}\delta .$ На внешней поверхности теплового слоя, распространяющегося вглубь тела, задано условие адиабатности: $y = \delta \left( {\eta = 1} \right):\partial \vartheta {\text{/}}\partial y = 0.$ Представим перепад температур через тепловой слой в виде $\vartheta = {{\vartheta }_{w}}f,$ где ${{\vartheta }_{w}} = {{\vartheta }_{w}}\left( t \right),$ $f = f\left( \eta \right).$ Тогда частные производные в (19) можно записать в виде:
Здесь штрих обозначает производную по времени
Граничными условиями (ГУ) для функции $f\left( \eta \right)$ будут: на границе тела
на ФТВПростейшей функцией, удовлетворяющей ГУ (20), (21), является квадратная парабола $f = {{\left( {1 - \eta } \right)}^{2}}.$ В рамках интегрального метода эту функцию следует подставить в исходное уравнение (19) и проинтегрировать последнее по $\eta $ в пределах от $\eta = 0$ до $\eta = 1.$ В результате получаем обыкновенное дифференциальное уравнение, которое удобно записать в следующем компактном виде:
(22)
$\frac{{\delta {\kern 1pt} '}}{\delta } + \frac{{\vartheta _{w}^{'}}}{{{{\vartheta }_{w}}}} = \frac{{6{{a}_{m}}}}{{{{\delta }^{2}}}}.$Уравнение (22) представляет собой линейное неоднородное дифференциальное уравнение первого порядка относительно $\delta \left( t \right).$ Его общее решение имеет вид квадратуры [21]
(23)
${{\delta }^{2}} = \frac{{12{{a}_{m}}}}{{\vartheta _{w}^{2}}}\int\limits_0^t {\vartheta _{w}^{2}dt} .$Будем искать закон продвижения ФТВ вглубь мишени в автомодельном виде, следующем из соображений анализа размерностей: $\delta = m\sqrt {{{a}_{m}}t} ,$ где $m$ – “модуль роста”. Из квадратуры (23), получаем следующее выражение для модуля роста:
(24)
${{m}^{2}} = \frac{{12}}{{\vartheta _{w}^{2}}}\frac{1}{t}\int\limits_0^t {\vartheta _{w}^{2}dt} .$При этом будем иметь следующую связь перепада температур параметров ${{\vartheta }_{w}}$ и теплового потока $q{\text{:}}$
(25)
${{\vartheta }_{w}} = \frac{m}{2}q\sqrt {\frac{t}{{{{\lambda }_{m}}{{c}_{{pm}}}{{\rho }_{m}}}}} .$Здесь ${{\lambda }_{m}},$ ${{c}_{{pm}}},$ ${{\rho }_{m}}$ – соответственно теплопроводность, изобарная теплоемкость и плотность мишени. Использование зависимости (25) в квадратуре (24) дает второе выражение для модуля роста:
Из эквивалентных выражений (24), (26) можно получить предельные варианты решения, удовлетворяющие автомодельному закону продвижения ФТВ. Так, при ${{\vartheta }_{w}} = {\text{const}}$ (ГУ первого рода) из интеграла (24) получаем: $m = 12,$ $\delta = \sqrt {12{{a}_{m}}t} .$ В свою очередь, при $q = {\text{const}}$ (ГУ второго рода) соотношение (26) дает: $m = 6,$ $\delta = \sqrt {6{{a}_{m}}t} .$ Согласно определению коэффициента теплоотдачи имеем: $\frac{q}{{{{\vartheta }_{w}}}} = 2\frac{{{{\lambda }_{m}}}}{\delta } = \gamma \sqrt {\frac{{{{\lambda }_{m}}{{c}_{{pm}}}{{\rho }_{m}}}}{t}} ,$ где $\gamma = 2{\text{/}}m.$ Из полученных выше предельных решений будем иметь: $\gamma = {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }}$ – для ГУ ${{\vartheta }_{w}} = {\text{const;}}$ $\gamma = \sqrt {2{\text{/}}3} $ – для ГУ $q = {\text{const}}{\text{.}}$ Приведем для сравнения точные решения для указанных случаев [21]: $\gamma = {1 \mathord{\left/ {\vphantom {1 {\sqrt \pi }}} \right. \kern-0em} {\sqrt \pi }}$ – для ГУ ${{\vartheta }_{w}} = {\text{const;}}$ $\gamma = {{\sqrt \pi } \mathord{\left/ {\vphantom {{\sqrt \pi } 2}} \right. \kern-0em} 2}$ – для ГУ $q = {\text{const}}{\text{.}}$ Таким образом, соотношение (25) удовлетворительно описывает закон теплоотдачи в полуограниченном теле. Относительные погрешности $\Delta $ приближенных решений можно получить из их сопоставления с точными результатами: $\Delta \approx 2\% $ – для ГУ ${{\vartheta }_{w}} = {\text{const;}}$ $\Delta \approx 5\% $ – для ГУ $q = {\text{const}}{\text{.}}$
СОПРЯЖЕННАЯ ЗАДАЧА
Облучение недогретой жидкости. Перейдем к анализу сопряженной задачи “теплопроводность–испарение”. Рассмотрим процесс облучения постоянным во времени тепловым потоком $q = {\text{const}}$ жидкой мишени с однородным начальным распределением температур ${{T}_{0}} < {{T}_{s}}$ (рис. 1).
Рис. 1.
Схема сопряженной задачи “испарение с поверхности конденсированной фазы–теплопроводность в облучаемом теле”.
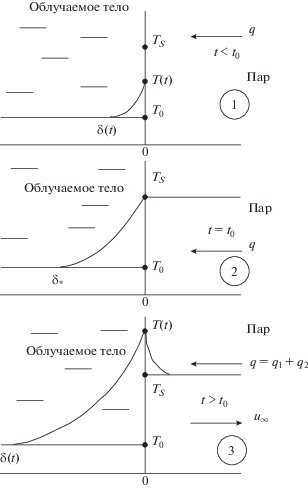
Указанный процесс можно разбить на следующие две стадии.
• Стадия теплопроводности: $t < {{t}_{0}}.$ Перепад температур на поверхности жидкости, недогретой до температуры насыщения, растет во времени по закону
(27)
${{\vartheta }_{w}} \equiv {{T}_{w}} - {{T}_{s}} = q\sqrt {\frac{3}{2}\frac{t}{{{{\lambda }_{m}}{{c}_{{pm}}}{{\rho }_{m}}}}} .$В конце стадии теплопроводности $\left( {t = {{t}_{0}}} \right)$ температура поверхности ${{T}_{w}}\left( t \right)$ становится равной температуре насыщения при давлении в системе ${{T}_{s}} \equiv {{T}_{s}}\left( {{{p}_{\infty }}} \right).$ Толщина теплового слоя достигает значения, равного ${{\delta }_{0}} = \sqrt {6{{a}_{m}}{{t}_{0}}} .$ Время достижения стадии сопряжения составляет
(28)
${{t}_{0}} = {{\lambda }_{m}}{{c}_{{pm}}}{{\rho }_{m}}{{\left( {\frac{{{{\vartheta }_{0}}}}{q}} \right)}^{2}},$• Стадия сопряжения: $t > {{t}_{0}}.$ При $t = {{t}_{0}}$ включается процесс испарения. Падающий на поверхность тепловой поток $q = {\text{const}}$ теперь включает две составляющие
Здесь(30)
${{q}_{1}} = {{2{{\lambda }_{m}}{{\vartheta }_{w}}} \mathord{\left/ {\vphantom {{2{{\lambda }_{m}}{{\vartheta }_{w}}} \delta }} \right. \kern-0em} \delta } - $Для последующего анализа вводятся следующие безразмерные величины:
• толщина теплового слоя $\tilde {\delta } = {\delta \mathord{\left/ {\vphantom {\delta {{{\delta }_{0}}}}} \right. \kern-0em} {{{\delta }_{0}}}},$
• перепад температур, отсчитываемый от температуры насыщения $\theta = {{\left( {{{T}_{{\text{w}}}} - {{T}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{{\text{w}}}} - {{T}_{s}}} \right)} {{{\vartheta }_{0}}}}} \right. \kern-0em} {{{\vartheta }_{0}}}},$
• перепад температур, отсчитываемый от начальной температуры тела $\tilde {\vartheta } \equiv 1 + \theta = $ $ = \,\,{{\left( {{{T}_{{\text{w}}}} - {{T}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{{\text{w}}}} - {{T}_{0}}} \right)} {{{\vartheta }_{0}}}}} \right. \kern-0em} {{{\vartheta }_{0}}}},$
• “параметр испарения” – доля теплового потока, идущего на испарение $\psi = {{{{q}_{2}}} \mathord{\left/ {\vphantom {{{{q}_{2}}} q}} \right. \kern-0em} q},$
• время, отсчитываемое от начала стадии сопряжения $\tau = {{\left( {t - {{t}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {t - {{t}_{0}}} \right)} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}},$
Запишем в безразмерном виде дифференциальное уравнение (22), определяющее продвижение ФТВ
(32)
$\frac{{d\left( {{{{\tilde {\delta }}}^{2}}} \right)}}{{d\tau }} + 2\frac{{d{\text{ln}}\left( {\tilde {\vartheta }} \right)}}{{d\tau }}{{\tilde {\delta }}^{2}} = 1,$Уравнения (32), (33) являются базовыми для последующих расчетов. Для случая, когда функция $\tilde {\vartheta }\left( \tau \right)$ задана в явном виде, решение уравнения (32) записывается в виде квадратуры, следующей из (23):
(34)
${{\tilde {\delta }}^{2}} = 1 + \frac{2}{{{{{\tilde {\vartheta }}}^{2}}}}\int\limits_0^{\tau } {{{{\tilde {\vartheta }}}^{2}}d\tau } .$Процедура решения включает следующую цепочку вычислений.
1. Исходными являются давление ${{p}_{\infty }}$ в газе и температура ${{T}_{w}}$ ПКФ. Из кинетического анализа с учетом уравнения состояния идеального газа определяется условное давление газа ${{p}_{{w\beta }}}$ на поверхности для эталонного случая $\beta = 1.$
2. Находится давление насыщения при температуре ПКФ: ${{p}_{w}} \equiv {{p}_{s}}\left( {{{T}_{w}}} \right).$
3. Определяется связь безразмерного перепада температур $\tilde {\vartheta }$ и параметра испарения $\psi .$
4. Из квадратуры (34) выражается безразмерная толщина теплового слоя $\tilde {\delta }.$
5. Полученные зависимости $\tilde {\vartheta }\left( \tau \right)$ и $\tilde {\delta }\left( \tau \right)$ подставляются в дифференциальное уравнение (32), из решения которого находится итоговая зависимость $\psi \left( \tau \right).$
Слабое испарение. Рассмотрим вначале случай слабого испарения: $s \ll 1.$ В рамках линейной задачи цепочка уравнений существенно упрощается.
• Из соотношения (16) определяется условный скачок давлений $\frac{{{{p}_{{w{\beta }}}} - {{p}_{\infty }}}}{{{{p}_{w}}}}.$
• Из соотношения (11) находится действительный скачок давлений $\frac{{{{p}_{w}} - {{p}_{\infty }}}}{{{{p}_{w}}}}.$
• Определяется связь безразмерного перепада температур $\tilde {\vartheta }$ и параметра испарения $\psi {\text{:}}$
Здесь введен “кинетический параметр”
(36)
$B = 2\sqrt \pi \frac{{1 - 0.4\beta }}{\beta }\frac{{q{{R}_{g}}T_{s}^{2}}}{{{{\vartheta }_{0}}{{\rho }_{w}}{{{\text{v}}}_{w}}{{r}^{2}}}}.$• Из уравнения (33) следует выражение для безразмерной толщины теплового слоя:
• Из квадратуры (34) получаем искомое решение сопряженной задачи $\psi \left( \tau \right)$ в неявном виде:
(38)
$\tau = \frac{1}{2}{{\left( {1 + B} \right)}^{2}}\frac{{\psi \left( {2 - \psi } \right)}}{{{{{\left( {1 - \psi } \right)}}^{2}}}} + {{B}^{2}}{\text{ln}}\left( {1 - \psi } \right).$Здесь важно подчеркнуть, что входящий в решение (38) кинетический параметр $B$ обобщает влияние на процесс испарения ряда факторов: теплового потока $q,$ КИК $\beta ,$ а также температур ПКФ и пара. На рисунке 2 приведены зависимости $\psi \left( \tau \right)$ для различных значений $B.$
Рис. 2.
Линейная задача. Зависимость параметра испарения от времени для различных значений кинетического параметра. $1 - B = 0,$ $2 - B = 0.4,$ $3 - B = 1,$ $4 - B = 2,$ $5 - B = 4.$
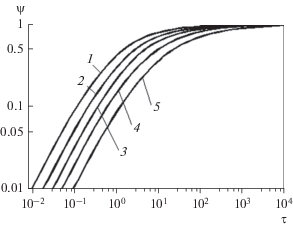
С течением времени параметр испарения монотонно растет. При $\tau \to \infty ~$ наступает асимптотическая стадия “чистого испарения”: $\psi = 1,$ ${{q}_{1}} = 0,$ $q = {{q}_{2}}.$ При этом увеличение кинетического параметра приводит ко все большему “затягиванию” сопряженной стадии процесса, когда одновременно проявляются как нагрев тела, так и испарение.
Рассмотрим асимптотики решения (38). В начальный период доля идущего на испарение теплового потока является пренебрежимо малой
При достаточно больших временах облучение массив тела успевает полностью прогреться, поэтому все подводимое к поверхности тепло расходуется на испарение
При неограниченно большом значении $B$ режим испарения практически не может реализоваться в силу неравенства $\tau \ll B.$ При этом задача формально остается сопряженной, однако для всех значений времени рассматриваемый процесс “зависает” в начальной области $\tau \to 0$
Асимптотики (39)–(41) представляются естественными с физической точки зрения. Принципиально отличной является асимптотика
Из (42) следует, что даже при нулевом значении кинетического параметра задача продолжает сохранять сопряженный характер. Иными словами, по-прежнему происходит перераспределение составляющих теплового баланса с режима прогрева массива при $\tau \to 0$ на режим чистого испарения при $\tau \to \infty .$ Это означает, что случай нагрева мишени при $q = {\text{const}}$, описываемый уравнением (27), не реализуется ни при каком значении времени.
“Парадоксальная” асимптотика (42) в действительности имеет ясное физическое объяснение. Как следует из соотношения (41), предельный случай $B \to 0$ реализуется при стремлении к нулю падающего на мишень теплового потока: $B\sim q \to 0.$ Это, в свою очередь, означает одновременное “выключение” обеих составляющих теплового баланса (29): ${{q}_{1}}\sim {{q}_{2}}\sim 0.$ Последние одновременно стремятся к нулю, поэтому при $B \to 0$ задача всегда остается сопряженной. Принципиально иная ситуация имеет место при нагреве тела постоянным тепловым потоком без испарения. В этом случае при $q \to 0$ происходит только “остановка” повышения температуры ПКФ.
Из изложенного следует, что введение условия (29) в систему уравнений переводит рассматриваемую задачу в качественно новое (сопряженное) состояние. Интересно отметить, что описанный выше физический “парадокс” в математическом плане эквивалентен известному явлению бифуркации решения [22]. Отметим, что обнаружение и исследование подобного специального режима лишний раз подчеркивает преимущества аналитического решения задачи.
Как видно из рис. 2, переход от стадии теплопроводности $\left( {\psi = 0} \right)$ к стадии испарения $\left( {\psi = 1} \right)$ совершается не мгновенно, а за некоторый конечный “период сопряжения”, в течение которого формируется мощный поток испаренного вещества через ПКФ. Проведем оценку характерного времени протекания сопряженной стадии процесса, которая представляет значительный интерес для приложений, связанных с лазерной абляцией. Найдем время $t*,$ в течение которого параметр испарения достигает значения, равного $\psi = 0.95.$ Тогда из (38) получаем:
Интенсивное испарение. При переходе к задаче интенсивного испарения пункты 1–4 кинетической цепочки по-прежнему выполнялся аналитически, однако математические выкладки приобретают весьма громоздкий вид. Расчет квадратуры согласно пункту 5 осуществлялся численно с помощью программного пакета системы компьютерной алгебры Maple. В отличие от линейной задачи, здесь удобно пользоваться размерными параметрами, в частности, – задавать конкретные значения плотности теплового потока.
Результаты расчета параметра испарения для случая задачи интенсивного испарения представлены на рис. 3–6 в виде сплошных кривых. Пунктиром нанесены кривые, соответствующие линейному решению (38). Важно отметить, что, как видно из рис. 3, 4, при уменьшении КИК в диапазоне $0.1{\text{\;}} < \beta \leqslant 1$ величины $\beta $ и $q$ практически не оказывают влияния на зависимость $\psi \left( \tau \right)$.
Рис. 3.
Зависимость параметра испарения от безразмерного времени для $\beta $ = 1, $q = {{10}^{6}}$ W/m2. 1 – интенсивное испарение; 2 – слабое испарение.
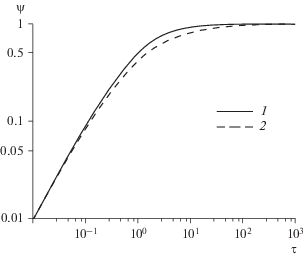
Рис. 4.
Зависимость параметра испарения от безразмерного времени для $\beta = {{10}^{{ - 1}}},$ $q = {{10}^{6}}$ W/m2. 1 – интенсивное испарение; 2 – слабое испарение.
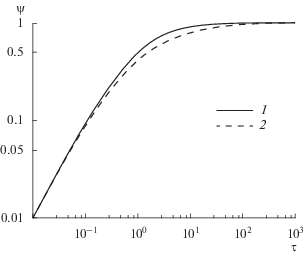
Рис. 5.
Зависимость параметра испарения от безразмерного времени для $\beta = {{10}^{{ - 2}}}.{\text{\;}}$ 1 – интенсивное испарение; 2 – слабое испарение. (а) $q = {{10}^{6}}$ W/m2, (б) $q = 5 \times {{10}^{6}}$ W/m2, (в) $q = {{10}^{7}}$ W/m2.
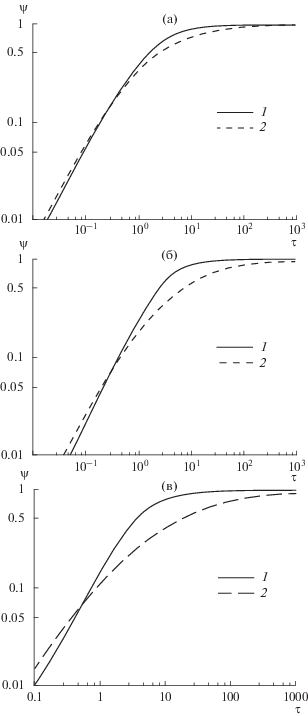
Рис. 6.
Зависимость параметра испарения от безразмерного времени для $\beta = {{10}^{{ - 3}}}.{\text{\;}}$ 1 – интенсивное испарение; 2 – слабое испарение. (a) $q = {{10}^{5}}$ W/m2; (б) $q = 5 \times {{10}^{5}}$ W/m2; (в) $q = {{10}^{6}}$ W/m2.
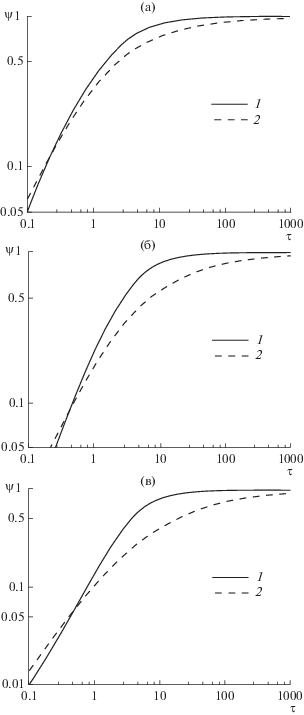
Это означает, что здесь реализуется “парадоксальная” асимптотика (42). В диапазоне меньших значений КИК $\left( {{{{10}}^{{ - 3}}} < \beta \leqslant {{{10}}^{{ - 2}}}} \right),$ наоборот, проявляется сильное влияние $\beta $ и $q$ на характер кривой $\psi \left( \tau \right).$ Как видно из рис. 5, зависимость параметра испарения от времени при увеличении $q$ для каждого фиксированного значения $\beta $ становится все более пологой.
Из рис. 6 следует, что подобная картина наблюдается также и при меньших значениях теплового потока.
Интересно отметить, что установленная расчетная тенденция одновременного воздействия $\beta $ и $q$ соответствует влиянию кинетического параметра на линейное решение (38). Итак, хотя в области интенсивного испарения уже нельзя количественно выделить универсальный параметр $B,$ тем не менее “память” от его влияния на качественном уровне сохраняется. Как показывают оценки, использование линейного решения (38) в диапазоне $0 < B < {{10}^{{ - 2}}}$ приводит к погрешности менее 2%. Так, для случая испарение при атмосферном давлении додекана (одного их предельных углеводородов группы алканов) получаем следующую зависимость (рис. 7)
(44)
${{q}_{{{\text{max}}}}} = {\text{\;}}\frac{{33.5\beta }}{{1 - 0.4\beta }}\,\,\,\,\frac{{{\text{кВт}}}}{{{{{\text{м}}}^{{\text{2}}}}}}.$Рис. 7.
Испарение додекана при атмосферном давлении. Зависимость максимального теплового потока от коэффициента испарения–конденсации, рассчитанная по формуле (43).
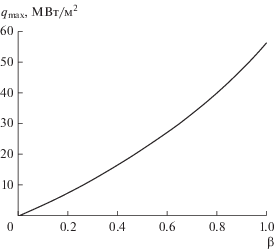
Тогда, задаваясь некоторым значением КИК, из формулы (44) можно определить максимальное значение теплового потока, при котором расчет зависимости $\psi \left( \tau \right)$ еще может проводиться по линейному решению (38).
Полученные результаты показывают нетривиальный характер изменения термодинамического состояния пара в зависимости от КИК. Этот вопрос продолжает быть актуальным при исследовании более сложной физической задачи испарения пара в газовую атмосферу. При этом будет происходить смешение испаренного и атмосферного газов, которое будет влиять на температуру и давление в навьестоксовской области.
Облучение насыщенной жидкости. Предыдущие выкладки относились к общему случаю облучения недогретой жидкости (рис. 1). Рассмотрим теперь частный случай, когда тепловой поток падает на поверхность массива, равномерно нагретого до температуры насыщения: ${{T}_{0}} = {{T}_{s}}.$ Это означает, что время нагрева поверхности тела до насыщения и начальный недогрев жидкости тождественно равны нулю: ${{t}_{0}} = {{\vartheta }_{0}} = 0.$ Согласно (36), при этом кинетический параметр обращается в бесконечность: $B \to \infty .$ При этом уже при $t \geqslant 0$ реализуется стадия сопряжения, минуя стадию теплопроводности.
Для прояснения физической картины процесса облучения насыщенной жидкости рассмотрим случай слабого испарения. Здесь естественным масштабом времени вместо ${{t}_{0}}$ становится величина ${{t}_{{00}}} = {{t}_{0}}{{B}^{2}},$ определяемая из соотношений (28), (36):
(45)
${{t}_{{00}}} = \frac{{8\pi }}{3}{{\left( {\frac{{{{c}_{p}}}}{{{{R}_{g}}}}} \right)}^{2}}{{\left( {\frac{{{{R}_{g}}{{T}_{s}}}}{r}} \right)}^{4}}{{\left( {\frac{{1 - 0.4\beta }}{\beta }} \right)}^{2}}\frac{{{{a}_{w}}}}{{{v}_{w}^{2}}}.$Решение (38) принимает вид:
(46)
$\tilde {t} = \frac{{\psi \left( {2 - \psi } \right)}}{{2{{{\left( {1 - \psi } \right)}}^{2}}}} + {\text{ln}}\left( {1 - \psi } \right),$Как видно из (46), в отличие от параметрического решения вида $\psi \left( {t,~B} \right)$ для случая недогретой жидкости мы имеем универсальное решение вида $\psi \left( t \right).$ Соответствующая соотношению (46) зависимость $\psi \left( {\tilde {t}} \right)$ приведена на рис. 8.
Рис. 8.
Зависимость параметра испарения от безразмерного времени для случая облучения насыщенной жидкости.
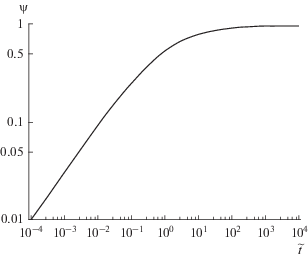
Полученное решение с максимальной погрешностью менее 5% может быть аппроксимировано простым соотношением
Как следует из (47), для случая облучения насыщенной жидкости параметр испарения $\psi $ не зависит от падающего на мишень теплового потока, а определяется температурой пара, его теплофизическими свойствами, а также коэффициентом испарения–конденсации (КИК).
Рассмотрим асимптотики решения (46). Как и в общем случае облучения недогретой жидкости, в начальный период доля теплового потока, идущего на испарение, является пренебрежимо малой
При достаточно больших временах облучение массив тела успевает полностью прогреться до максимально возможной температуры, и все подводимое к поверхности тепло расходуется на испарение
Согласно известному физико-химическому правилу Трутона [13] имеем: ${{R}_{g}}{{T}_{s}}/r \approx {{10}^{{ - 1}}}$. Учитывая соотношение для изобарной теплоемкости одноатомного идеального газа ${{{{c}_{p}}} \mathord{\left/ {\vphantom {{{{c}_{p}}} {{{R}_{g}}}}} \right. \kern-0em} {{{R}_{g}}}} = 5{\text{/}}2,$ согласно (43) получаем для периода сопряжения:
(50)
${{t}_{*}} = 1.64{{\left( {\frac{{1 - 0.4\beta }}{\beta }} \right)}^{2}}\frac{{{{a}_{w}}}}{{{v}_{w}^{2}}}.$Интересно сравнить эту величину с характерным временем межмолекулярных столкновений [23], определяемым соотношением
Из соотношений (50), (51) будем иметь:
(52)
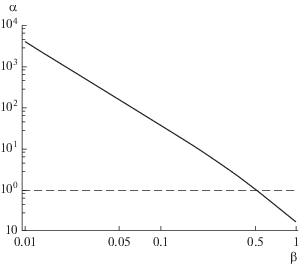
$\alpha \equiv \frac{{t{\text{*}}}}{{{{t}_{{mol}}}}} \approx 0.41{{\left( {\frac{{1 - 0.4\beta }}{\beta }} \right)}^{2}}.$На рис. 9 приведена зависимость параметра $\alpha $ от КИК.
Как видно из рисунка, в эталонном случае $\beta = 1$ период сопряжения почти на порядок меньше времени межмолекулярных столкновений $\left( {\alpha = 0.148} \right).$ Физически это означает, что с началом облучения происходит практически мгновенный переход к состоянию полного испарения. С уменьшением КИК характерные времена обоих процессов сближаются и при $\beta = 0.51$ становятся равными друг другу $\left( {\alpha = 1} \right).$ Наконец, при $\beta = {{10}^{{ - 2}}}$ будем иметь: $\alpha \approx 4 \times {{10}^{3}}.$ Таким образом, уменьшение КИК приводит ко все большему затягиванию стадии сопряжения, причем этот эффект особенно ярко проявляется при $\beta < {{10}^{{ - 1}}}.$
ЗАКЛЮЧЕНИЕ
Рассмотрена сопряженная задача, состоящая из двух взаимосвязанных задач: а) молекулярно-кинетической модели интенсивного испарения с поверхности конденсированной фазы (ПКФ); б) модели фронта теплового возмущения в облучаемом теле (“мишени”). На основе развитой ранее модели перемешивания молекулярных потоков получены выражения для кинетических скачков температуры и давления газа на ПКФ. Проведен анализ влияния коэффициента испарения–конденсации (КИК) на уравнения сохранения молекулярных потоков массы, импульса и энергии в слое Кнудсена. Получено выражение для коэффициента проницаемости поверхности конденсированной фазы. С помощью интегрального метода слоя конечной толщины, основанного на концепции фронта теплового возмущения (ФТВ), проведено решение нестационарного одномерного уравнения теплопроводности в мишени. Выполнен анализ условий сопряжения системы уравнений сохранения молекулярных потоков в навьестоксовской области и уравнения теплопроводности в мишени. Для случая слабого испарения получено аналитическое решение для параметра испарения. Показано, что его зависимость от времени определяется обобщенным кинетическим параметром, включающим тепловой поток, КИК, а также комплекс теплофизических свойств. Рассмотрен частный случай испарения с поверхности мишени, однородно нагретой до температуры насыщения. Показано, что снижение КИК приводит к существенному затягиванию сопряженной стадии процесса испарения. Проведен детальный анализ асимптотик полученного решения. Для случая интенсивного испарения решение выполнялось численно с помощью программного пакета системы компьютерной алгебры Maple. Полученные результаты могут быть использовании при теоретическом анализе процесса лазерной абляции. Они позволяют проводить аналитический расчет “периода сопряжения”, в течение которого одновременно действуют закономерности теплопроводности в мишени и испарения с ее поверхности.
Обозначения:
$a$ – коэффициент температуропроводности; $B$ – кинетический параметр; ${{c}_{p}}$ – изобарная теплоемкость; ${\text{M}}$ – число Маха; $m$ – модуль роста; $r$ – теплота фазового перехода; ${{R}_{g}}$ – индивидуальная газовая постоянная; $T$ – температура; $v$ – тепловая скорость молекул; $u$ – газодинамическая скорость; $s$ – скоростной фактор; $p$ – давление; $y$ – координата, отсчитываемая от поверхность конденсированной фазы; ${\text{Pr}}$ – число Прандтля; $q$ – тепловой поток; $J_{i}^{ + }$ – молекулярные потоки, $~$эмитируемые поверхностью конденсированной фазы; $J_{i}^{ - }$ – молекулярные потоки, $~$падающие на поверхность конденсированной фазы; $\beta $ – коэффициент испарения–конденсации; $\varepsilon $ – коэффициент проницаемости; $\rho $ – плотность; $\vartheta $ – разность температур; $\delta $ – толщины теплового слоя; $\eta $ – обобщенная переменная; $\lambda $ – теплопроводность; $\tau $ – безразмерное время; $\psi $ – параметр испарения; $\nu $ – кинематический коэффициент вязкости.
Нижние индексы:
“$w$” – газ на ПКФ; “$\infty $” – газ на бесконечности; “$m$” – мишень.
Список литературы
Карташов Э.М. Аналитические методы решения краевых задач нестационарной теплопроводности в областях с движущимися границами // Изв. РАН. Энергетика. 1999. № 5. С. 3–34.
Карташов Э.М. Аналитические решения гиперболических моделей нестационарной теплопроводности // Тонкие химические технологии. 2018. Т. 13. № 2. С. 81–90.
Ларина И.Н., Рыков В.А., Шахов Е.М. Испарение с поверхности и истечение пара через плоский канал в вакуум // Изв. РАН. МЖГ. 1996. № 1. С. 150–158.
Мажукин В. И., Носов В.В. Поверхностное испарение алюминиевой мишени в вакууме при воздействии лазерного УФ излучения в условиях образования плазмы // Квантовая электроника. 2005. Т. 35. № 5. С. 454–466.
Холодов А.С. Об эволюции возмущений, вызванных движением метеороидов в атмосфере Земли // Компьютерные исследования и моделирование. 2013. Т. 5. № 6. С. 993–1030.
Захаров В.В., Крифо Ж.Ф., Лукьянов Г.А., Родионов А.В. О моделировании сложных неравновесных течений газа в широком диапазоне чисел Кнудсена на примере внутренней атмосферы комет // Математическое моделирование. 2002. Т. 14. № 8. С. 91−95.
Коган М.Н. Динамика разреженного газа. М.: Наука, 1967. 440 с.
Зудин Ю.Б. Приближенный кинетический анализ интенсивного испарения // Инженерно-физический журн. 2015. Т. 88. № 4. С. 980–986.
Зудин Ю.Б. Линейный кинетический анализ испарения и конденсации // Теплофизика и Аэромеханика. 2016. Т. 23. № 3. С. 437–450.
Зудин Ю.Б. Полуэмпирическая модель интенсивного испарения жидкости // Теплофизика и Аэромеханика. 2017. Т. 24. №4. С. 539–552.
Zudin Yuri B. Non-equilibrium Evaporation and Condensation Processes: Analytical Solutions. Heidelberg: Springer, 2018. 217 p.
Лабунцов Д.А. Анализ процессов испарения и конденсации // Теплофизика высоких температур. 1967. Т. 5. № 4. С. 647−654.
Муратова Т.М., Лабунцов Д.А. Кинетический анализ процессов испарения и конденсации // Теплофизика высоких температур. 1969. Т. 7. № 5. С. 959−967.
Анисимов С.И. Об испарении металла, поглощающего лазерное излучение // Журн. экспериментальной и теоретической физики. 1968. Т. 54. № 1. С. 339–342.
Ytrehus T. Theory and experiments on gas kinetics in evaporation, in: J.L. Potter (Ed.), Rarefied Gas Dynamics N.Y. 1977. V. 51(2). P. 1197−1212.
Khight C.J. Theoretical modeling of rapid surface vaporization with back pressure. AIAA J. 1979. V. 17(5). P. 519–523.
Khight C.J. Transient vaporization from a surface into vacuum. 1982. AIAA J. V. 20(7). P. 950–955.
Ho J.R., Grigoropoulos C.P., Humphrey J.A.C. Computational study of heat transfer and gas dynamics in the pulsed laser evaporation of metals. 1995. J. Appl. Phys. V. 78(6). Р. 4696–4709.
Gusarov A.V., Gnedovets A.G., Smurov I. Gas dynamics of laser ablation: Influence of ambient atmosphere // J. Appl. Phys. 2000. V. 88. P. 4352–4364.
Кудинов И.В., Кудинов В.А., Котова Е.В. Аналитические решения задач теплопроводности на основе определения фронта теплового возмущения // Изв. вузов. Математика. 2016. № 11. С. 27–41.
Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 488 с.
Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: МЦНМО, 2014. 341 с.
Черчиньяни К. Теория и приложения уравнения Больцмана. М.: Мир, 1978. 496 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика