Известия РАН. Энергетика, 2020, № 1, стр. 21-39

Термохимическое моделирование неизоэнтропических процессов в камерах сгорания и соплах ракетных двигателей

Д. М. Борисов^1, *, В. В. Миронов¹, Ю. А. Шураев¹

¹ ГНЦ ФГУП “Исследовательский Центр им. М.В. Келдыша”
Москва, Россия

Поступила в редакцию 26.12.2019
После доработки 13.01.2020
Принята к публикации 14.01.2020

DOI: 10.31857/S0002331020010033

Аннотация

Ключевые слова: неизоэнтропические сдвиговые течения, химическое равновесие продуктов сгорания топлива, массовые скорости образования компонент смеси, камера сгорания и сопло ракетного двигателя

ВВЕДЕНИЕ

Одним из основных направлений развития средств выведения современных ракетно-космических систем является совершенствование энергомассовых характеристик двигательных установок и обеспечение их работоспособности. Рабочие процессы, протекающие в камерах сгорания и соплах ракетных двигателей, характеризуются высокой тепловой напряженностью и химической активностью продуктов сгорания топлива.

Термохимическому и газодинамическому моделированию камер сгорания и сопел ракетных двигателей посвящено большое число теоретических и экспериментальных исследований, по результатам которых созданы отраслевые методики и программные комплексы для определения различных характеристик двигательных установок [1–4] и т.д.

Наибольшее распространение для термодинамического расчета камер сгорания и сопел ракетных двигателей получила модель равновесного течения с замораживанием [4], согласно которой в областях с малой скоростью протекания химических реакций процессы химических превращений не рассматриваются. В качестве критерия для определения областей замороженного течения берется величина статической температуры продуктов сгорания. Для топлив с углеводородным горючим данная величина полагается равной ${{T}_{{{\text{зам}}}}} \leqslant 2000\,\,{\text{K}}.$ В случае топливной пары кислород-водород принимается ${{T}_{{{\text{зам}}}}} \leqslant 1600\, - \,1800\,\,{\text{K}}.$ Однако указанная методика, как и все более ранние, основана на расчете термохимических процессов в идеальном газе [1]. Вместе с тем течение в пристенном пограничном слое двигательной установки не является идеальным вследствие наличия вязкой диссипации кинетической энергии и интенсивного теплообмена продуктов сгорания топлива со стенкой сопла. По указанной причине применение методов расчета химических равновесий [1] для моделирования термохимических процессов в пристенном пограничном слое является приближенным допущением.

В настоящей работе сформулирован подход к решению проблемы термохимического моделирования неизоэнтропических сдвиговых течений. Для расчета химического равновесия продуктов сгорания топлива создана методика определения массовых скоростей образования компонентов смеси в неизоэнтропическом течении. В рамках предложенного подхода, в качестве примера, проведен расчет пограничного слоя на стенке камеры сгорания и сопла кислородно-водородного ракетного двигателя. Выполнено тестирование полученного численного решения и проведены параметрические исследования процессов течения и теплообмена.

ТЕРМОХИМИЧЕСКАЯ МОДЕЛЬ РАБОЧЕГО ПРОЦЕССА В КАМЕРЕ СГОРАНИЯ И СОПЛЕ РАКЕТНОГО ДВИГАТЕЛЯ

За начало отсчета энтальпии принимается состояние вещества при выбранных стандартной температуре и давлении ($T = {{T}^{0}},p = {{p}^{0}}$) и устойчивом агрегатном состоянии, соответствующем данным условиям.

Если завершенная химическая реакция

$\sum\limits_i {{{\nu }_{i}}{{A}_{i}}} = \sum\limits_i {{{\nu }_{i}}{{B}_{i}}} $

протекает при произвольных постоянных температуре и давлении ($T,p$), то уравнение первого начала термодинамики для указанной реакции записывается следующим образом

$\Delta h = \Delta q + \Delta {{q}_{х}},$

$\sum\limits_i {{{\nu }_{i}}\left[ {\int\limits_{{{T}^{0}}}^{{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}} {{{c}_{{{\text{т}}{{{\text{в}}}_{i}}}}}dT + {{q}_{{{\text{п}}{{{\text{л}}}_{i}}}}}\left( {{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}} \right) + \int\limits_{{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}}^{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}} {{{c}_{{{{{\text{ж}}}_{i}}}}}dT} + {{q}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}\left( {{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}} \right) + \int\limits_{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}}^T {{{c}_{{{{p}_{i}}}}}dT} } } \right]} = \Delta q\left( {T,p} \right) - \sum\limits_i {{{\nu }_{i}}{{q}_{{{{х}_{i}}}}}} ,$

или

(1)

$\Delta q\left( {T,p} \right) = \sum\limits_i {{{\nu }_{i}}\left[ {\int\limits_{{{T}^{0}}}^{{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}} {{{c}_{{{\text{т}}{{{\text{в}}}_{i}}}}}dT + {{q}_{{{\text{п}}{{{\text{л}}}_{i}}}}}\left( {{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}} \right) + \int\limits_{{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}}^{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}} {{{c}_{{{{{\text{ж}}}_{i}}}}}dT} + {{q}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}\left( {{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}} \right) + \int\limits_{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}}^T {{{c}_{{{{p}_{i}}}}}dT + {{q}_{{{{х}_{i}}}}}} } } \right]} ,$

где

$\Delta q$ – внешний приток тепла к термодинамической системе, равный по величине тепловому эффекту химической реакции;

$\Delta {{q}_{х}} = - \sum\nolimits_i {{{\nu }_{i}}{{q}_{{{{х}_{i}}}}}} $ – суммарное изменение химической энергии всех участвующих в реакции веществ;

${{q}_{{{{х}_{i}}}}}$ – химическая энергия i-го компонента.

Здесь принято правило суммирования, согласно которого стехиометрические коэффициенты ${{\nu }_{i}},$ вступающих в реакцию веществ (реагентов), считаются отрицательными, а продуктов реакции – положительными.

Пусть все вещества находятся в стандартных условиях ($T = {{T}^{0}},p = {{p}^{0}}$ и устойчивом агрегатном состоянии при данных температуре и давлении). Тогда уравнение первого начала термодинамики (1) принимает вид

(2)

$\sum\limits_i {{{\nu }_{i}}{{q}_{{{{х}_{i}}}}}} = \Delta {{q}^{0}}\left( {{{T}^{0}},{{p}^{0}}} \right).$

Если химическое соединение $i = i{\kern 1pt} * $ образовано простыми веществами (${{q}_{{{{х}_{i}}}}} = 0,\,\,i \ne i{\kern 1pt} * $), находящимися в стандартных условиях, то выполняется равенство

${{q}_{{{{х}_{{i * }}}}}} = {1 \mathord{\left/ {\vphantom {1 {{{\nu }_{{i * }}}}}} \right. \kern-0em} {{{\nu }_{{i * }}}}}\Delta {{q}^{0}}\left( {{{T}^{0}},{{p}^{0}}} \right) = \Delta q_{{i * }}^{0}\left( {{{T}^{0}},{{p}^{0}}} \right),$

где $\Delta q_{{i*}}^{0}\left( {{{T}^{0}},{{p}^{0}}} \right)$ – тепловой эффект химической реакции образования соединения $i = i{\kern 1pt} * $ из простых веществ в стандартном состоянии, отнесенный к одному молю соединения. Указанная величина называется теплотой образования соединения $i = i{\kern 1pt} * ,$ или энтальпией образования. Из чего следует, что химическая энергия вещества ${{q}_{{{{х}_{{i * }}}}}}$ совпадает с его теплотой образования и после определения стандартного состояния является величиной постоянной.

Из последнего соотношения и уравнения (2) следует, что для любой химической реакции между любыми веществами в стандартных условиях справедливо равенство

(3)

$\sum\limits_i {{{\nu }_{i}}\Delta q_{i}^{0}\left( {{{T}^{0}},{{p}^{0}}} \right)} = \Delta {{q}^{0}}\left( {{{T}^{0}},{{p}^{0}}} \right),$

выражающее закон Гесса, согласно которого тепловой эффект произвольной химической реакции между произвольными веществами в стандартном состоянии определяется величинами теплоты образования участвующих в реакции веществ.

Сформулированный в настоящей работе подход к термохимическому моделированию неизоэнтропических процессов в пристенном пограничном слое, в качестве иллюстрации, применяется для расчета течения в камере сгорания и сопле кислородно-водородного ракетного двигателя.

Считается, что равновесный состав продуктов сгорания топлива определяется ш-естью ($m = 6$) компонентами: ${{{\text{H}}}_{{\text{2}}}}{\text{O,}}\,\,{{{\text{O}}}_{{\text{2}}}}{\text{,}}\,\,{{{\text{H}}}_{{\text{2}}}}{\text{,}}\,\,{\text{OH,}}\,\,{\text{O,}}\,\,{\text{H}},$ образованными двумя химическими элементами – атомарным кислородом и водородом ($n = 2$).

Согласно фундаментальному термохимическому правилу в данной смеси могут протекать $m\, - \,n\, = \,4$ независимых химических реакций, в качестве которых выбираются следующие завершенные реакции

(4)

$\begin{gathered} 1)\,\,{{{\text{H}}}_{2}}{\text{O}} = {{{\text{H}}}_{2}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{{\text{O}}}_{2}} + \Delta {{q}_{1}}, \hfill \\ 2)\,\,{{{\text{H}}}_{2}}{\text{O}} = {\text{OH}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{{\text{H}}}_{2}} + \Delta {{q}_{2}}, \hfill \\ 3)\,\,{{{\text{H}}}_{2}} = 2{\text{H}} + \Delta {{q}_{3}}, \hfill \\ 4)\,\,{{{\text{O}}}_{2}} = 2{\text{O}} + \Delta {{q}_{4}}. \hfill \\ \end{gathered} $

Остальные возможные реакции являются следствием выбранных уравнений. Например, одна из возможных реакций

${{{\text{H}}}_{2}}{\text{O}} = {{{\text{H}}}_{2}} + {\text{O}} + \Delta q$

является суммой первого и умноженного на 0.5 четвертого уравнений, а поскольку при алгебраических операциях над термохимическими уравнениями тепловые эффекты реакций складываются, то включать данную реакцию в систему (4) не следует, так как это приведет к линейной зависимости уравнений.

Указанное свойство термохимических уравнений является следствием закона сохранения энергии (2), записанного для каждой из указанных реакций

(5)

$\sum\limits_{i = 1}^m {{{\nu }_{{ji}}}{{q}_{{{{х}_{i}}}}}} = \Delta q_{j}^{0}\left( {{{T}^{0}},{{p}^{0}}} \right),\,\,\,\,j = 1,...,m{\kern 1pt} - {\kern 1pt} n.$

Полученная система из $m{\kern 1pt} - {\kern 1pt} n$ уравнений имеет $m$ неизвестных ${{q}_{{{{х}_{i}}}}}.$ Данная система будет удовлетворяться при назначении любым $n$ неизвестным произвольных значений, в качестве которых выбираются нулевые величины. Компоненты, химическая энергия которых полагается равной нулю, называются простыми веществами.

По соглашению [5] в качестве простых веществ выбираются газообразные H₂, O₂, ${{{\text{N}}}_{{\text{2}}}}{\text{,}}\,\,{\text{C}}{{{\text{l}}}_{{\text{2}}}}$ и др., твердый углерод С и металлы. Следуя принятому соглашению, в качестве простых веществ для рассматриваемой системы принимаются молекулярный кислород ${{{\text{O}}}_{{\text{2}}}}$ и водород ${{{\text{H}}}_{{\text{2}}}}$. После чего величины химической энергии остальных $m{\kern 1pt} - {\kern 1pt} n$ компонентов смеси берутся из справочных данных.

Поскольку уравнения (5) являются линейно независимыми, то величины химической энергии указанных $m{\kern 1pt} - {\kern 1pt} n$ компонентов смеси могут быть определены непосредственно из решения системы и должны совпадать со справочными данными.

В качестве уравнений (4) предпочтительно выбирать реакции диссоциации веществ, поскольку, как будет показано ниже, в таком случае вид соответствующих уравнений для массовых скоростей образования компонентов смеси получается универсальным для любого вида ракетного топлива, состав продуктов сгорания которого содержит указанные вещества.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МНОГОКОМПОНЕНТНОГО ПОГРАНИЧНОГО СЛОЯ НА СТЕНКЕ КАМЕРЫ СГОРАНИЯ И СОПЛА РАКЕТНОГО ДВИГАТЕЛЯ

В случае многоскоростного течения реагирующей газовой смеси рассматриваются m индивидуальных объемов веществ ${{V}_{i}}\left( t \right),$ совпадающих в момент времени t между собой и с индивидуальным объемом смеси $V\left( t \right) \equiv {{V}_{i}}\left( t \right).$

Уравнение неразрывности для i-го компонента имеет вид

(6)

$\frac{d}{{dt}}\oint\limits_{{{V}_{i}}(t)} {{{\rho }_{i}}d{{V}_{i}}} = \oint\limits_{{{V}_{i}}(t)} {{{{\dot {m}}}_{i}}d{{V}_{i}}} ,\,\,\,\,\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + {{\nabla }_{k}}{{\rho }_{i}}v_{i}^{k} = {{\dot {m}}_{i}},$

где ${{\dot {m}}_{i}}$ – массовая скорость образования вещества в результате химических превращений. Здесь индекс i применяется для обозначения химического вещества и не является тензорным.

Из уравнения неразрывности для компонента смеси можно получить формулу дифференцирования элементарной частицы $\delta {{m}_{i}}$ сплошной среды

(7)

${{\left( {\frac{{d\delta {{m}_{i}}}}{{dt}}} \right)}_{i}} = {{\left( {\frac{{d{{\rho }_{i}}\delta {{V}_{i}}}}{{dt}}} \right)}_{i}} = {{\left( {\frac{{d{{\rho }_{i}}}}{{dt}}} \right)}_{i}}\delta {{V}_{i}} + {{\rho }_{i}}{{\left( {\frac{{d\delta {{V}_{i}}}}{{dt}}} \right)}_{i}} = \left[ {\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + \frac{{\partial {{\rho }_{i}}}}{{\partial {{x}^{k}}}}v_{i}^{k}} \right]\delta {{V}_{i}} + {{\rho }_{i}}{{\nabla }_{k}}v_{i}^{k}\delta {{V}_{i}} = {{\dot {m}}_{i}}\delta {{V}_{i}}.$

Здесь использовано выражение [6] для производной элементарного объема по времени ${{\left( {{{d\delta {{V}_{i}}} \mathord{\left/ {\vphantom {{d\delta {{V}_{i}}} {dt}}} \right. \kern-0em} {dt}}} \right)}_{i}} = {{\nabla }_{k}}v_{i}^{k}\delta {{V}_{i}}.$ Индекс i у знака производной показывает, что данная величина относится к индивидуальному бесконечно малому объему $\delta {{V}_{i}}(t),$ движущемуся со скоростью ${{\vec {v}}_{i}}.$

Везде по тексту символ $\delta $ обозначает дифференциал величины массы, объема, числа молей или меры химической реакции в бесконечно малой частице сплошной среды и вводится для удобства чтения формул дифференцирования.

Для массы компонента $\delta {{m}_{i}}$ в объеме $\delta V(t),$ который движется со скоростью $\vec {v},$ можно записать

$\frac{{d\delta {{m}_{i}}}}{{dt}} = \frac{{d{{\rho }_{i}}\delta V}}{{dt}} = \frac{{d{{\rho }_{i}}}}{{dt}}\delta V + {{\rho }_{i}}\frac{{d\delta V}}{{dt}} = \left[ {\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + \frac{{\partial {{\rho }_{i}}}}{{\partial {{x}^{k}}}}{{v}^{k}} + {{\rho }_{i}}{{\nabla }_{k}}{{v}^{k}}} \right]\delta V = \left[ {\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + {{\nabla }_{k}}{{\rho }_{i}}{{v}^{k}}} \right]\delta V,$

где скорость смеси $\vec {v}$ определяется выражением $\rho {{v}^{k}} = \sum\nolimits_i {{{\rho }_{i}}v_{i}^{k}} .$

Если ввести в рассмотрение скорость диффузии $v_{{Di}}^{k} = v_{i}^{k} - {{v}^{k}},$ то производная ${{\left( {{{d\delta {{m}_{i}}} \mathord{\left/ {\vphantom {{d\delta {{m}_{i}}} {dt}}} \right. \kern-0em} {dt}}} \right)}_{i}}\;\;$ записывается следующим образом

${{\left( {\frac{{d\delta {{m}_{i}}}}{{dt}}} \right)}_{i}} = \left[ {\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + {{\nabla }_{k}}{{\rho }_{i}}{{v}^{k}}} \right]\delta {{V}_{i}} + {{\nabla }_{k}}{{\rho }_{i}}v_{{Di}}^{k}\delta {{V}_{i}},$

или с учетом предыдущего равенства

(8)

${{\left( {\frac{{d\delta {{m}_{i}}}}{{dt}}} \right)}_{i}} = \frac{{d\delta {{m}_{i}}}}{{dt}} + {{\nabla }_{k}}{{\rho }_{i}}v_{{Di}}^{k}\delta {{V}_{i}}.$

Последнее слагаемое в правой части представляет дивергенцию диффузионного потока компонента смеси.

Для закона сохранения внутренней энергии индивидуального объема сплошной среды принимается общее уравнение [6]

$\frac{d}{{dt}}\oint\limits_{V(t)} {{{e}^{{{\text{вн}}}}}dV} = \oint\limits_{V(t)} {{{p}^{{ij}}}{{\nabla }_{j}}{{v}_{i}}dV} - \oint\limits_{V(t)} {{{\nabla }_{k}}{{q}^{k}}dV} + \oint\limits_{V(t)} {{{q}_{V}}dV} ,$

где

${{e}^{{{\text{вн}}}}}$ – внутренняя энергия единицы объема среды,

${{p}^{{ij}}}{{\nabla }_{j}}{{v}_{i}}$ – работа внутренних поверхностных сил в единице объема,

$\vec {q}$ – тепловой поток процесса теплопроводности,

${{q}_{V}}$ – мощность объемных источников энергии.

Выражение работы внутренних поверхностных сил преобразуется к виду

$\begin{gathered} {{p}^{{ij}}}{{\nabla }_{j}}{{v}_{i}} = \left( { - p{{g}^{{ij}}} + \lambda {{g}^{{ij}}}{{\nabla }_{k}}{{v}^{k}} + 2\mu {{e}^{{ij}}}} \right){{\nabla }_{j}}{{v}_{i}} = - p{{\nabla }_{k}}{{v}^{k}} + \left( {\lambda {{g}^{{ij}}}{{\nabla }_{k}}{{v}^{k}} + 2\mu {{e}^{{ij}}}} \right){{\nabla }_{j}}{{v}_{i}} = \\ = - \left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial t}}} \right. \kern-0em} {\partial t}} + {{\nabla }_{k}}p{{v}^{k}}} \right) + {{dp} \mathord{\left/ {\vphantom {{dp} {dt}}} \right. \kern-0em} {dt}} + \left( {\lambda {{g}^{{ij}}}{{\nabla }_{k}}{{v}^{k}} + 2\mu {{e}^{{ij}}}} \right){{\nabla }_{j}}{{v}_{i}}. \\ \end{gathered} $

С учетом приведенного равенства для уравнения внутренней энергии получается следующее выражение

$\frac{d}{{dt}}\oint\limits_{V(t)} {hdV} = \oint\limits_{V(t)} {\left[ {{{dp} \mathord{\left/ {\vphantom {{dp} {dt}}} \right. \kern-0em} {dt}} + \left( {\lambda {{g}^{{ij}}}{{\nabla }_{k}}{{v}^{k}} + 2\mu {{e}^{{ij}}}} \right){{\nabla }_{j}}{{v}_{i}}} \right]dV} - \oint\limits_{V(t)} {{{\nabla }_{k}}{{q}^{k}}dV + } \oint\limits_{V(t)} {{{q}_{V}}dV} ,$

здесь $h = {{e}^{{{\text{вн}}}}} + p$ – энтальпия единицы объема среды.

В случае течения химически реагирующей смеси уравнение внутренней энергии принимает вид

$\frac{d}{{dt}}\sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {{{n}_{i}}{{h}_{i}}d{{V}_{i}}} } = \oint\limits_{V(t)} {{{a}_{\tau }}dV} - \oint\limits_{V(t)} {{{\nabla }_{k}}{{q}^{k}}dV} - \frac{d}{{dt}}\sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {{{n}_{i}}{{q}_{{{{x}_{i}}}}}d{{V}_{i}}} } ,$

согласно введенным обозначениям

${{n}_{i}}$ – число молей вещества в единице объема,

${{h}_{i}}$ – энтальпия одного моля вещества,

${{a}_{\tau }} = {{dp} \mathord{\left/ {\vphantom {{dp} {dt}}} \right. \kern-0em} {dt}} + \left( {\lambda {{g}^{{ij}}}{{\nabla }_{k}}{{v}^{k}} + 2\mu {{e}^{{ij}}}} \right){{\nabla }_{j}}{{v}_{i}}$ – работа сил давления и вязких напряжений,

${{q}_{{{{x}_{i}}}}}$ – химическая энергия одного моля вещества,

$\frac{d}{{dt}}\sum\nolimits_i {\oint_{{{V}_{i}}(t)} {{{n}_{i}}{{q}_{{{{x}_{i}}}}}d{{V}_{i}}} } $ – суммарная мощность источников энергии, возникающих в индивидуальных объемах компонент, вследствие химических превращений.

Левая часть уравнения внутренней энергии, с учетом равенства (6), преобразуется следующим образом

$\begin{gathered} \frac{d}{{dt}}\sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {{{n}_{i}}{{h}_{i}}d{{V}_{i}}} } = \frac{d}{{dt}}\sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {{{\rho }_{i}}h_{i}^{ * }d{{V}_{i}}} } = \sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {\left( {\frac{{\partial {{\rho }_{i}}h_{i}^{ * }}}{{\partial t}} + {{\nabla }_{k}}{{\rho }_{i}}h_{i}^{ * }v_{i}^{k}} \right)d{{V}_{i}}} } = \\ = \sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {\left( {h_{i}^{ * }{{{\dot {m}}}_{i}} + {{\rho }_{i}}\frac{{\partial h_{i}^{ * }}}{{\partial t}} + {{\rho }_{i}}v_{i}^{k}{{\nabla }_{k}}h_{i}^{ * }} \right)d{{V}_{i}}.} } \\ \end{gathered} $

Здесь и ниже по тексту индекс “$ * $” применяется для обозначения массовой плотности величины.

Суммарная мощность химических источников энергии записывается в виде

$\frac{d}{{dt}}\sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {{{n}_{i}}{{q}_{{{{x}_{i}}}}}d{{V}_{i}}} } = \sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {\left( {\frac{{\partial {{\rho }_{i}}q_{{{{x}_{i}}}}^{ * }}}{{\partial t}} + {{\nabla }_{k}}{{\rho }_{i}}q_{{{{x}_{i}}}}^{ * }v_{i}^{k}} \right)d{{V}_{i}}} } = \sum\limits_i {\oint\limits_{{{V}_{i}}(t)} {q_{{{{x}_{i}}}}^{ * }{{{\dot {m}}}_{i}}d{{V}_{i}}} } .$

При выводе данного соотношения учтено, что после определения стандартного состояния химическая энергия вещества ${{q}_{{{{x}_{i}}}}}$ является величиной постоянной.

После подстановки полученных соотношений в исходное уравнение и принимая во внимание, что в рассматриваемый момент времени $V\left( t \right) \equiv {{V}_{i}}\left( t \right),$ $i = 1,...,m$ для закона сохранения внутренней энергии окончательно может быть записано следующее выражение

(9)

$\sum\limits_i {{{\rho }_{i}}\frac{{dh_{i}^{ * }}}{{dt}}} = {{a}_{\tau }} - {{\nabla }_{k}}{{q}^{k}} - \sum\limits_i {H_{i}^{ * }} {{\dot {m}}_{i}} - \sum\limits_i {f_{{Di}}^{k}{{\nabla }_{k}}h_{i}^{ * }} ,$

где

$H_{i}^{ * } = h_{i}^{ * } + q_{{{{x}_{i}}}}^{ * }$ – полная энтальпия единицы массы вещества,

$f_{{Di}}^{k} = {{\rho }_{i}}v_{{Di}}^{k}$ – диффузионный поток компонента смеси.

Несложно убедиться в том, что полученное уравнение является инвариантным относительно определения стандартного состояния.

Производная энтальпии может быть представлена в виде

$\begin{gathered} \frac{{dh_{i}^{ * }}}{{dt}} = \frac{d}{{dt}}\left[ {\int\limits_{{{T}^{0}}}^{{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}} {c_{{{\text{т}}{{{\text{в}}}_{i}}}}^{ * }dT + q_{{{\text{п}}{{{\text{л}}}_{i}}}}^{ * }\left( {{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}} \right) + \int\limits_{{{T}_{{{\text{п}}{{{\text{л}}}_{i}}}}}}^{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}} {c_{{{{{\text{ж}}}_{i}}}}^{ * }dT} + q_{{{\text{ис}}{{{\text{п}}}_{i}}}}^{ * }\left( {{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}} \right) + \int\limits_{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}}^T {c_{{{{p}_{i}}}}^{ * }dT} } } \right] = \\ = \frac{d}{{dt}}\int\limits_{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}}^T {c_{{{{p}_{i}}}}^{ * }dT} = \mathop {\lim }\limits_{\Delta t \to 0} \left[ {\int\limits_{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}}^{T + \Delta T} {c_{{{{p}_{i}}}}^{ * }dT - \int\limits_{{{T}_{{{\text{ис}}{{{\text{п}}}_{i}}}}}}^T {c_{{{{p}_{i}}}}^{ * }dT} } } \right]\frac{1}{{\Delta t}} = c_{{{{p}_{i}}}}^{ * }\frac{{dT}}{{dt}}. \\ \end{gathered} $

При выводе данного выражения принято во внимание, что величины энтальпии, теплоты плавления и испарения, а также теплоемкости всех фаз компонентов смеси слабо зависят от давления и являются функциями только температуры.

Тогда для левой части уравнения внутренней энергии является справедливым равенство

$\sum\limits_i {{{\rho }_{i}}\frac{{dh_{i}^{ * }}}{{dt}}} = \sum\limits_i {{{\rho }_{i}}c_{{{{p}_{i}}}}^{ * }\frac{{dT}}{{dt}}} = \rho c_{p}^{ * }\frac{{dT}}{{dt}},\,\,\,\,c_{p}^{ * } = \sum\limits_i {{{c}_{i}}c_{{{{p}_{i}}}}^{ * }} ,$

которое не зависит от выбора стандартного состояния.

Третье слагаемое в правой части, с учетом формулы дифференцирования элементарной частицы сплошной среды (7), преобразуется следующим образом

$\begin{gathered} \sum\limits_i {H_{i}^{ * }} {{{\dot {m}}}_{i}} = \sum\limits_i {H_{i}^{ * }} \frac{1}{{\delta {{V}_{i}}}}{{\left( {\frac{{d\delta {{m}_{i}}}}{{dt}}} \right)}_{i}} = \frac{1}{{\delta V}}\sum\limits_i {{{H}_{i}}} {{\left( {\frac{{d\delta {{n}_{i}}}}{{dt}}} \right)}_{{{\text{хим}}}}} = \frac{1}{{\delta V}}\sum\limits_i {{{H}_{i}}} {{\left( {\frac{{\Delta \delta {{n}_{i}}}}{{\Delta t}}} \right)}_{{{\text{хим}}}}} = \\ = \frac{1}{{\delta V}}\sum\limits_i {\sum\limits_j {{{H}_{i}}{{{\left( {\frac{{\Delta \delta {{n}_{{ij}}}}}{{\Delta t}}} \right)}}_{{{\text{хим}}}}}} } = \frac{1}{{\delta V}}\sum\limits_i {\sum\limits_j {{{\nu }_{{ij}}}{{H}_{i}}{{{\left( {\frac{{\Delta \delta {{n}_{{ij}}}}}{{{{\nu }_{{ij}}}}}\frac{1}{{\Delta t}}} \right)}}_{{{\text{хим}}}}} = } } \frac{1}{{\delta V}}\sum\limits_i {\sum\limits_j {{{\nu }_{{ij}}}{{H}_{i}}{{{\left( {\frac{{\Delta \delta {{\xi }_{j}}}}{{\Delta t}}} \right)}}_{{{\text{хим}}}}}} } = \\ = \frac{1}{{\delta V}}\sum\limits_j {{{{\left( {\frac{{\Delta \delta {{\xi }_{j}}}}{{\Delta t}}} \right)}}_{{{\text{хим}}}}}} \sum\limits_i {{{\nu }_{{ij}}}{{H}_{i}}} = \frac{1}{{\delta V}}\sum\limits_j {\tilde {\Delta }{{H}_{j}}\left( T \right){{{\left( {\frac{{d\delta {{\xi }_{j}}}}{{dt}}} \right)}}_{{{\text{хим}}}}}} , \\ \end{gathered} $

где согласно принятым обозначениям

$\delta {{n}_{i}}$ – число молей i-го компонента в элементарном объеме $\delta {{V}_{i}}\left( t \right),$

$\Delta \delta {{n}_{{ij}}}$ – изменение числа молей i-го компонента в бесконечно малом объеме $\delta {{V}_{i}}\left( t \right)$ вследствие протекания j-ой химической реакции,

$\Delta \delta {{n}_{i}}\; = \;\sum\nolimits_j {\Delta \delta {{n}_{{ij}}}} $ – изменение числа молей i-го компонента в элементарном объеме $\delta {{V}_{i}}\left( t \right)$ вследствие протекания всех, идущих в смеси, химических реакций,

$\tilde {\Delta }{{H}_{j}}\left( T \right) = \sum\nolimits_i {{{\nu }_{{ij}}}{{H}_{i}}\left( T \right)} $ – изменение полной энтальпии в завершенной j-ой химической реакции, идущей при текущем значении температуры T, и равное тепловому эффекту реакции $\tilde {\Delta }{{H}_{j}}\left( T \right) = \Delta {{q}_{j}}\left( T \right),$

${{\left( {{{d\delta {{\xi }_{j}}} \mathord{\left/ {\vphantom {{d\delta {{\xi }_{j}}} {dt}}} \right. \kern-0em} {dt}}} \right)}_{{{\text{хим}}}}}$ – скорость изменения меры j-ой химической реакции в бесконечно малом объеме смеси $\delta V\left( t \right),$ совпадающем в рассматриваемый момент времени с элементарными объемами компонент $\delta V\left( t \right) \equiv \delta {{V}_{i}}\left( t \right).$

Тепловой эффект химической реакции $\Delta {{q}_{j}}\left( T \right)$ и скорость изменения меры химической реакции ${{\left( {{{d\delta {{\xi }_{j}}} \mathord{\left/ {\vphantom {{d\delta {{\xi }_{j}}} {dt}}} \right. \kern-0em} {dt}}} \right)}_{{{\text{хим}}}}}$ не зависят от выбора начала отсчета энтальпии по определению, следовательно, не зависит от выбора стандартных условий и третье слагаемое в правой части уравнения энергии $\sum\nolimits_i {H_{i}^{ * }{{{\dot {m}}}_{i}}} .$

Для диффузионного члена является справедливым инвариантное равенство

$\sum\limits_i {f_{{Di}}^{k}{{\nabla }_{k}}h_{i}^{ * }} = \sum\limits_i {f_{{Di}}^{k}\frac{{dh_{i}^{ * }}}{{dT}}\frac{{\partial T}}{{\partial {{x}^{k}}}}} = \sum\limits_i {f_{{Di}}^{k}c_{{{{p}_{i}}}}^{ * }\frac{{\partial T}}{{\partial {{x}^{k}}}}} ,$

из чего следует, что уравнение (9) является инвариантным к определению стандартного состояния.

С учетом приведенных выше выкладок для закона сохранения энергии может быть получено следующее выражение

$\rho c_{p}^{ * }\frac{{dT}}{{dt}} = \frac{{dp}}{{dt}} + \left( {\lambda {{g}^{{ij}}}{{\nabla }_{k}}{{v}^{k}} + 2\mu {{e}^{{ij}}}} \right){{\nabla }_{j}}{{v}_{i}} - {{\nabla }_{k}}{{q}^{k}} - \sum\limits_i {H_{i}^{ * }} {{\dot {m}}_{i}} - \sum\limits_i {f_{{Di}}^{k}c_{{{{p}_{i}}}}^{ * }\frac{{\partial T}}{{\partial {{x}^{k}}}}} ,$

которое представляет температурную форму уравнения внутренней энергии сплошной среды.

Использование в численных расчетах сдвиговых течений температурной формы уравнения энергии является предпочтительным, поскольку позволяет в достаточно простом виде поставить граничные условия и реализовать алгоритм метода решения задач сопряженного теплообмена [7, 8] на теплопроводящей стенке. Кроме того, наличие в правой части слагаемого с известным продольным градиентом давления оказывает стабилизирующее действие на процесс численного счета.

С учетом полученных соотношений система уравнений модели неизоэнтропического сдвигового течения в камере сгорания и сопле ракетного двигателя в криволинейной системе координат, связанной с линиями кривизны обтекаемой поверхности [9], записывается следующим образом:

уравнение неразрывности

$\frac{1}{{\sqrt {{{g}_{{22}}}} }}\frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho v}}{{\partial y}} + \left[ {\frac{1}{2}\frac{1}{g}\frac{1}{{\sqrt {{{g}_{{22}}}} }}\frac{{\partial g}}{{\partial x}} - \frac{1}{2}\frac{1}{{{{g}_{{22}}}\sqrt {{{g}_{{22}}}} }}\frac{{\partial {{g}_{{22}}}}}{{\partial x}}} \right]\rho u = 0,$

уравнение движения

$\frac{1}{{{{g}_{{22}}}}}\rho u\frac{{\partial u}}{{\partial x}} + \frac{1}{{\sqrt {{{g}_{{22}}}} }}\rho v\frac{{\partial u}}{{\partial y}} = - \frac{1}{{{{g}_{{22}}}}}\frac{{\partial p}}{{\partial x}} + \frac{1}{{\sqrt {{{g}_{{22}}}} }}\mu \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} + \frac{1}{{\sqrt {{{g}_{{22}}}} }}\left[ {2\mu \Gamma _{{23}}^{2} + \frac{{\partial \mu }}{{\partial y}}} \right]\frac{{\partial u}}{{\partial y}},$

уравнения диффузии

(10)

$\frac{1}{{\sqrt {{{g}_{{22}}}} }}\rho u\frac{{\partial {{c}_{i}}}}{{\partial x}} + \rho v\frac{{\partial {{c}_{i}}}}{{\partial y}} = \frac{\partial }{{\partial y}}\left[ {\left( {\frac{{{{\mu }_{m}}}}{{S{{c}_{m}}}} + \frac{{{{\mu }_{t}}}}{{S{{c}_{t}}}}} \right)\frac{{\partial {{c}_{i}}}}{{\partial y}}} \right] + {{\dot {m}}_{i}},\,\,\,\,i = 1,6,$

уравнение энергии

$\begin{gathered} \frac{1}{{\sqrt {{{g}_{{22}}}} }}{{c}_{p}}\rho u\frac{{\partial T}}{{\partial x}} + {{c}_{p}}\rho v\frac{{\partial T}}{{\partial y}} = \frac{1}{{\sqrt {{{g}_{{22}}}} }}u\frac{{\partial p}}{{\partial x}} + \mu {{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^{2}} + \\ + \,\,\frac{1}{{\sqrt g }}\frac{\partial }{{\partial y}}\left[ {\sqrt g \left( {\frac{{{{\mu }_{m}}}}{{{{{\Pr }}_{m}}}} + \frac{{{{\mu }_{t}}}}{{{{{\Pr }}_{t}}}}} \right){{c}_{p}}\frac{{\partial T}}{{\partial y}}} \right] - \sum\limits_i {{{H}_{i}}{{{\dot {m}}}_{i}}} + \sum\limits_i {\left( {\frac{{{{\mu }_{m}}}}{{S{{c}_{m}}}} + \frac{{{{\mu }_{t}}}}{{S{{c}_{t}}}}} \right)} {{c}_{p}}_{i}\frac{{\partial {{c}_{i}}}}{{\partial y}}\frac{{\partial T}}{{\partial y}}, \\ \end{gathered} $

уравнение состояния

$p = \rho RT,$

где согласно принятым обозначениям

$g,{{g}_{{ij}}},\Gamma _{{ij}}^{k}$ – определитель, компоненты метрического тензора и символы Кристоффеля 2-го рода используемой криволинейной системы координат,

$\mu = {{\mu }_{m}} + {{\mu }_{t}}$ – коэффициент эффективной вязкости,

${{\Pr }_{m}},{{\Pr }_{t}},S{{c}_{m}},S{{c}_{t}}$ – молекулярное и турбулентное числа Прандтля и Шмидта.

УРАВНЕНИЯ МАССОВЫХ СКОРОСТЕЙ ОБРАЗОВАНИЯ КОМПОНЕНТОВ СМЕСИ

Приведенная выше система уравнений химически реагирующего пограничного слоя не является замкнутой. Для замыкания полученной модели указанную систему необходимо дополнить шестью ($m = 6$) соотношениями для массовых скоростей образования компонентов смеси ${{\dot {m}}_{i}},$ которые в случае равновесного течения могут быть определены из условий химического равновесия продуктов сгорания топлива в элементарном объеме смеси $\delta V(t),$ совпадающем в рассматриваемый момент времени с элементарными объемами компонентов $\delta V(t) \equiv \delta {{V}_{i}}(t),$ $i = 1, \ldots ,m.$

Следуя выбранной модели горения кислородно-водородного топлива считается, что равновесный состав продуктов сгорания определяется шестью ($m = 6$) компонентами: ${{{\text{H}}}_{{\text{2}}}}{\text{O}}\; - \;{\text{(1),}}\,\,{{{\text{O}}}_{{\text{2}}}}\; - \;{\text{(2),}}\,\,{{{\text{H}}}_{{\text{2}}}}\; - \;{\text{(3),}}\,\,{\text{OH}}\; - \;{\text{(4),}}\,\,{\text{O}}\; - \;{\text{(5),}}\,\,{\text{H}}\; - \;{\text{(6)}},$ образованными двумя химическими элементами – атомарным кислородом и водородом ($n = 2$).

В качестве протекающих в смеси независимых химических реакций выбираются $m\, - \,n\, = \,4$ незавершенных реакции (4).

Выражение для константы равновесия j-ой реакции, записанное для бесконечно малого объема сплошной среды $\delta V,$ имеет вид

${{K}_{{pj}}} = \prod\limits_i {\delta n_{i}^{{{{\nu }_{{ij}}}}}{{{\left( {{{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {\delta n}}} \right. \kern-0em} {\delta n}}} \right)}}^{{\sum\limits_i {{{\nu }_{{ij}}}} }}}} ,$

где

$\delta {{n}_{i}}$ – число молей компонента смеси в элементарном объеме $\delta V$,

$\delta n = \sum\nolimits_i {\delta {{n}_{i}}} $ – суммарное число молей компонентов смеси в бесконечно малом объеме $\delta V,$

$\bar {p}\; = \;{p \mathord{\left/ {\vphantom {p {{{p}^{0}}}}} \right. \kern-0em} {{{p}^{0}}}}$ – давление смеси, отнесенное к величине стандартного давления.

В соответствии с приведенным выражением, для константы равновесия первой химической реакции (j = 1) можно записать

${{\nu }_{{11}}} = - 1,\,\,\,\,{{\nu }_{{31}}} = 1,\,\,\,\,{{\nu }_{{21}}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},\,\,\,\,\sum\limits_i {{{\nu }_{{i1}}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} ,\,\,\,\,{{K}_{{p1}}} = \frac{{\delta {{n}_{3}}\sqrt {\delta {{n}_{2}}} }}{{\delta {{n}_{1}}}}\sqrt {{{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {\sum\limits_i {\delta {{n}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {\delta {{n}_{i}}} }}} .$

Полная производная константы равновесия по времени для бесконечно малого объема сплошной среды $\delta V(t)$, движущегося со скоростью смеси $\vec {v},$ определяется выражением

$\frac{{d{{K}_{{p1}}}}}{{dt}} = \sum\limits_i {\frac{{\partial {{K}_{{p1}}}}}{{\partial \delta {{n}_{i}}}}\frac{{d\delta {{n}_{i}}}}{{dt}} + } \frac{{\partial {{K}_{{p1}}}}}{{\partial p}}\frac{{dp}}{{dt}}.$

Частная производная ${{\partial {{K}_{{p1}}}} \mathord{\left/ {\vphantom {{\partial {{K}_{{p1}}}} {\partial \delta {{n}_{1}}}}} \right. \kern-0em} {\partial \delta {{n}_{1}}}}$ записывается в виде

$\begin{gathered} \frac{{\partial {{K}_{{p1}}}}}{{\partial \delta {{n}_{1}}}} = - \frac{1}{{{{{\left( {\delta {{n}_{1}}} \right)}}^{2}}}}\delta {{n}_{3}}\sqrt {\delta {{n}_{2}}} \sqrt {{{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {\sum\limits_i {\delta {{n}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {\delta {{n}_{i}}} }}} - \frac{{\delta {{n}_{3}}\sqrt {\delta {{n}_{2}}} }}{{\delta {{n}_{1}}}}{{0.5} \mathord{\left/ {\vphantom {{0.5} {\sqrt {{{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {\sum\limits_i {\delta {{n}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {\delta {{n}_{i}}} }}} }}} \right. \kern-0em} {\sqrt {{{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {\sum\limits_i {\delta {{n}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {\delta {{n}_{i}}} }}} }}{{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {{{{\left( {\sum\limits_i {\delta {{n}_{i}}} } \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {\sum\limits_i {\delta {{n}_{i}}} } \right)}}^{2}}}} = \\ = - \frac{{\delta {{n}_{3}}\sqrt {\delta {{n}_{2}}} }}{{\delta {{n}_{1}}}}\sqrt {{{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {\sum\limits_i {\delta {{n}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {\delta {{n}_{i}}} }}} \left( {{1 \mathord{\left/ {\vphantom {1 {\delta {{n}_{1}}}}} \right. \kern-0em} {\delta {{n}_{1}}}} + {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {\delta {{n}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {\delta {{n}_{i}}} }}} \right) = - {{K}_{{p1}}}\left( {{1 \mathord{\left/ {\vphantom {1 {\delta {{n}_{1}}}}} \right. \kern-0em} {\delta {{n}_{1}}}} + {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {\delta {{n}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {\delta {{n}_{i}}} }}} \right) = \\ = - {{K}_{{p1}}}\left( {{{{{M}_{{m1}}}} \mathord{\left/ {\vphantom {{{{M}_{{m1}}}} {\delta {{m}_{1}}}}} \right. \kern-0em} {\delta {{m}_{1}}}} + {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{\delta {{m}_{i}}} \mathord{\left/ {\vphantom {{\delta {{m}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{\delta {{m}_{i}}} \mathord{\left/ {\vphantom {{\delta {{m}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right) = - \frac{{{{K}_{{p1}}}}}{\rho }\left( {{{{{M}_{{m1}}}} \mathord{\left/ {\vphantom {{{{M}_{{m1}}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}} + {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right)\frac{1}{{\delta V}}. \\ \end{gathered} $

Остальные частные производные константы равновесия вычисляются аналогично.

С учетом полученных соотношений и формул дифференцирования элементарной частицы сплошной среды (7, 8), полную производную по времени константы равновесия первой химической реакции можно представить в виде

$\begin{gathered} \frac{{d{{K}_{{p1}}}}}{{dt}} = \sum\limits_i {\frac{{\partial {{K}_{{p1}}}}}{{\partial \delta {{n}_{i}}}}\frac{{d\delta {{n}_{i}}}}{{dt}} + } \frac{{\partial {{K}_{{p1}}}}}{{\partial p}}\frac{{dp}}{{dt}} = \sum\limits_i {\frac{{\partial {{K}_{{p1}}}}}{{\partial \delta {{n}_{i}}}}} \frac{1}{{{{M}_{{mi}}}}}\frac{{d\delta {{m}_{i}}}}{{dt}} + \frac{{\partial {{K}_{{p1}}}}}{{\partial p}}\frac{{dp}}{{dt}} = \\ = \sum\limits_i {\frac{1}{{{{M}_{{mi}}}}}\frac{{\partial {{K}_{{p1}}}}}{{\partial \delta {{n}_{i}}}}} {{{\dot {m}}}_{i}}\delta {{V}_{i}} + \frac{{\partial {{K}_{{p1}}}}}{{\partial p}}\frac{{dp}}{{dt}} = - \frac{1}{{{{M}_{{m1}}}}}\frac{{{{K}_{{p1}}}}}{\rho }\left( {{{{{M}_{{m1}}}} \mathord{\left/ {\vphantom {{{{M}_{{m1}}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}} + {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right){{{\dot {m}}}_{1}} + \\ + \,\,\frac{1}{{{{M}_{{m2}}}}}\frac{1}{2}\frac{{{{K}_{{p1}}}}}{\rho }\left( {{{{{M}_{{m2}}}} \mathord{\left/ {\vphantom {{{{M}_{{m2}}}} {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}} - {1 \mathord{\left/ {\vphantom {1 {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right){{{\dot {m}}}_{2}} + \frac{1}{{{{M}_{{m3}}}}}\frac{{{{K}_{{p1}}}}}{\rho }\left( {{{{{M}_{{m3}}}} \mathord{\left/ {\vphantom {{{{M}_{{m3}}}} {{{c}_{3}}}}} \right. \kern-0em} {{{c}_{3}}}} - {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right){{{\dot {m}}}_{3}} - \\ - \,\,\frac{1}{{{{M}_{{m4}}}}}\frac{1}{2}\frac{{{{K}_{{p1}}}}}{\rho }{1 \mathord{\left/ {\vphantom {1 {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}{{{\dot {m}}}_{4}} - \frac{1}{{{{M}_{{m5}}}}}\frac{1}{2}\frac{{{{K}_{{p1}}}}}{\rho }{1 \mathord{\left/ {\vphantom {1 {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}{{{\dot {m}}}_{5}} - \\ - \,\,\frac{1}{{{{M}_{{m6}}}}}\frac{1}{2}\frac{{{{K}_{{p1}}}}}{\rho }{1 \mathord{\left/ {\vphantom {1 {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{c}_{i}}} \mathord{\left/ {\vphantom {{{{c}_{i}}} {{{M}_{{mi}}}}}} \right. \kern-0em} {{{M}_{{mi}}}}}} }}{{{\dot {m}}}_{6}} + \frac{{{{K}_{{p1}}}}}{{2p}}\frac{{dp}}{{dt}}. \\ \end{gathered} $

С другой стороны, константа равновесия реакции идеального газа является функцией только температуры. Следовательно, является справедливым равенство

$\frac{{d{{K}_{{p1}}}}}{{dt}} = \frac{{d{{K}_{{p1}}}}}{{dT}}\frac{{dT}}{{dt}}.$

После подстановки данного равенства в предыдущее выражение получается первое уравнение для массовых скоростей образования компонентов смеси

$\begin{gathered} - \left( {{1 \mathord{\left/ {\vphantom {1 {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}} + {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{M}_{{m1}}}} \mathord{\left/ {\vphantom {{{{M}_{{m1}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{M}_{{m1}}}} \mathord{\left/ {\vphantom {{{{M}_{{m1}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right){{{\dot {m}}}_{1}} + \frac{1}{2}\left( {{1 \mathord{\left/ {\vphantom {1 {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}} - {1 \mathord{\left/ {\vphantom {1 {\sum\limits_i {{{{{M}_{{m2}}}} \mathord{\left/ {\vphantom {{{{M}_{{m2}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{M}_{{m2}}}} \mathord{\left/ {\vphantom {{{{M}_{{m2}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right){{{\dot {m}}}_{2}} + \\ + \,\,\left( {{1 \mathord{\left/ {\vphantom {1 {{{c}_{3}}}}} \right. \kern-0em} {{{c}_{3}}}} - {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{M}_{{m3}}}} \mathord{\left/ {\vphantom {{{{M}_{{m3}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{M}_{{m3}}}} \mathord{\left/ {\vphantom {{{{M}_{{m3}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right){{{\dot {m}}}_{3}} - {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{M}_{{m4}}}} \mathord{\left/ {\vphantom {{{{M}_{{m4}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{M}_{{m4}}}} \mathord{\left/ {\vphantom {{{{M}_{{m4}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}{{{\dot {m}}}_{4}} - \\ - {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{M}_{{m5}}}} \mathord{\left/ {\vphantom {{{{M}_{{m5}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{M}_{{m5}}}} \mathord{\left/ {\vphantom {{{{M}_{{m5}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}{{{\dot {m}}}_{5}} - {{0.5} \mathord{\left/ {\vphantom {{0.5} {\sum\limits_i {{{{{M}_{{m6}}}} \mathord{\left/ {\vphantom {{{{M}_{{m6}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}} \right. \kern-0em} {\sum\limits_i {{{{{M}_{{m6}}}} \mathord{\left/ {\vphantom {{{{M}_{{m6}}}} {{{M}_{{mi}}}{{c}_{i}}}}} \right. \kern-0em} {{{M}_{{mi}}}{{c}_{i}}}}} }}{{{\dot {m}}}_{6}} = \frac{1}{{{{K}_{{p1}}}}}\frac{{d{{K}_{{p1}}}}}{{dT}}\rho \frac{{dT}}{{dt}} - \frac{\rho }{{2p}}\frac{{dp}}{{dt}}. \\ \end{gathered} $

Стоящая в правой части выражения производная ${{d{{K}_{{p1}}}} \mathord{\left/ {\vphantom {{d{{K}_{{p1}}}} {dT}}} \right. \kern-0em} {dT}}$ является известной величиной и определяется из справочных данных. После чего полученное уравнение может быть решено совместно с системой уравнений пограничного слоя (10).

Повторив все приведенные выше выкладки для каждого из трех оставшихся уравнений химических реакций, можно записать еще три уравнения массовых скоростей образования компонентов.

Недостающие два уравнения для массовых скоростей получаются из условия сохранения вещества каждого атомарного элемента (кислорода и водорода) в бесконечно малой частице сплошной среды, которые в данном случае имеют вид

$\begin{gathered} {{{\dot {m}}}_{1}} + \frac{{{{M}_{{m1}}}}}{{{{M}_{{m3}}}}}{{{\dot {m}}}_{3}} + \frac{1}{2}\frac{{{{M}_{{m1}}}}}{{{{M}_{{m4}}}}}{{{\dot {m}}}_{4}} + \frac{1}{2}\frac{{{{M}_{{m1}}}}}{{{{M}_{{m6}}}}}{{{\dot {m}}}_{6}} = 0, \\ {{{\dot {m}}}_{1}} + 2\frac{{{{M}_{{m1}}}}}{{{{M}_{{m2}}}}}{{{\dot {m}}}_{2}} + \frac{{{{M}_{{m1}}}}}{{{{M}_{{m4}}}}}{{{\dot {m}}}_{4}} + \frac{{{{M}_{{m1}}}}}{{{{M}_{{m5}}}}}{{{\dot {m}}}_{5}} = 0. \\ \end{gathered} $

В результате система уравнений модели неизоэнтропического химически равновесного течения в пограничном слое на стенке камеры сгорания и сопла ракетного двигателя (10) замыкается шестью соотношениями для массовых скоростей образования продуктов сгорания топлива

(11)

$\sum\limits_{i = 1}^6 {{{a}_{{ij}}}{{{\dot {m}}}_{i}}} = {{b}_{j}},\,\,\,\,j = 1, \ldots ,6$

которые решаются совместно.

Уравнения системы (11) получены в предположении малости диффузионного переноса компонентов смеси. В случае, когда диффузионным переносом пренебречь нельзя, полная производная по времени константы равновесия химической реакции для бесконечно малого объема $\delta V(t),$ движущегося со скоростью смеси $\vec {v},$ с учетом формул дифференцирования элементарной частицы сплошной среды (7, 8), записывается в виде

$\begin{gathered} \frac{{d{{K}_{{pj}}}}}{{dt}} = \sum\limits_i {\frac{{\partial {{K}_{{pj}}}}}{{\partial \delta {{n}_{i}}}}\frac{{d\delta {{n}_{i}}}}{{dt}} + } \frac{{\partial {{K}_{{pj}}}}}{{\partial p}}\frac{{dp}}{{dt}} = \sum\limits_i {\frac{{\partial {{K}_{{pj}}}}}{{\partial \delta {{n}_{i}}}}\frac{1}{{{{M}_{{mi}}}}}\frac{{d\delta {{m}_{i}}}}{{dt}} + } \frac{{\partial {{K}_{{pj}}}}}{{\partial p}}\frac{{dp}}{{dt}} = \\ = \sum\limits_i {\frac{1}{{{{M}_{{mi}}}}}\frac{{\partial {{K}_{{pj}}}}}{{\partial \delta {{n}_{i}}}}\left( {{{{\dot {m}}}_{i}} + {{\nabla }_{k}}f_{{Di}}^{k}} \right)\delta {{V}_{i}} + } \frac{{\partial {{K}_{{pj}}}}}{{\partial p}}\frac{{dp}}{{dt}}, \\ \end{gathered} $

где слагаемое с дивергенцией диффузионного потока в приближении пограничного слоя определяется выражением

${{\nabla }_{k}}f_{{Di}}^{k} = \frac{1}{{\sqrt g }}\frac{{\partial \sqrt g f_{{Di}}^{k}}}{{\partial {{x}^{k}}}} \approx \frac{1}{{\sqrt g }}\frac{{\partial \sqrt g f_{{Di}}^{3}}}{{\partial {{x}^{3}}}} = - \frac{\partial }{{\partial {{x}^{3}}}}\left[ {\left( {\frac{{{{\mu }_{m}}}}{{S{{c}_{m}}}} + \frac{{{{\mu }_{t}}}}{{S{{c}_{t}}}}} \right)\frac{{\partial {{c}_{i}}}}{{\partial {{x}^{3}}}}} \right].$

Проделав все выкладки аналогично предыдущему случаю и учитывая, что константа равновесия реакции идеального газа является функцией только температуры, можно получить четыре алгебраических уравнения для массовых скоростей образования компонентов смеси

(12)

$\sum\limits_{i = 1}^6 {{{a}_{{ij}}}{{{\dot {m}}}_{i}}} = {{b}_{j}},\,\,\,\,j = 1, \ldots ,4.$

В случае наличия интенсивного диффузионного переноса получить недостающие два уравнения для массовых скоростей из условия сохранения вещества каждого атомарного элемента (кислорода и водорода) не представляется возможным, поскольку общее число атомов указанных элементов в бесконечно малом объеме смеси $\delta V(t)$ в процессе расширения изменяется и является отличным от исходного.

В данном случае для замыкания термохимической модели в системе уравнений (12) следует перейти от неизвестных массовых скоростей образования продуктов сгорания топлива ${{\dot {m}}_{i}},(i = 1, \ldots ,6),$ к неизвестным скоростям изменения степеней диссоциации веществ ${{d{{\alpha }_{j}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{j}}} {dt}}} \right. \kern-0em} {dt}},(j = 1, \ldots ,4),$ число которых совпадает с числом независимых химических реакций. После чего указанная алгебраическая система может быть решена совместно с уравнениями пограничного слоя.

Неизвестные величины ${{\dot {m}}_{i}}$ выражаются через скорости изменения степеней диссоциации веществ ${{d{{\alpha }_{j}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{j}}} {dt}}} \right. \kern-0em} {dt}}$ следующим образом.

Массовая скорость образования H₂O

Суммарное изменение числа молей первого компонента смеси ${{{\text{H}}}_{{\text{2}}}}{\text{O}}$ в первой и второй химических реакциях в бесконечно малом индивидуальном объеме $\delta {{V}_{1}}(t)$ за время $\Delta t$ определяется равенством

$\Delta \delta {{n}_{1}} = \Delta \delta {{n}_{{11}}} + \Delta \delta {{n}_{{12}}},$

где

$\Delta \delta {{n}_{1}}$ – суммарное изменение числа молей ${{{\text{H}}}_{{\text{2}}}}{\text{O}}$ в первой и второй реакциях,

$\Delta \delta {{n}_{{11}}}$ – изменение числа молей ${{{\text{H}}}_{{\text{2}}}}{\text{O}}$ в первой реакции,

$\Delta \delta {{n}_{{12}}}$ – изменение числа молей ${{{\text{H}}}_{{\text{2}}}}{\text{O}}$ во второй реакции.

Тогда для изменения степеней диссоциации рассматриваемых химических реакций можно записать следующие выражения

$\Delta {{\alpha }_{1}} = {{\Delta \delta {{n}_{{11}}}} \mathord{\left/ {\vphantom {{\Delta \delta {{n}_{{11}}}} {\delta {{n}_{1}}}}} \right. \kern-0em} {\delta {{n}_{1}}}},\,\,\,\,\Delta {{\alpha }_{2}} = {{\Delta \delta {{n}_{{12}}}} \mathord{\left/ {\vphantom {{\Delta \delta {{n}_{{12}}}} {\delta {{n}_{1}}}}} \right. \kern-0em} {\delta {{n}_{1}}}},$

а суммарное изменение числа молей первого вещества выразить в виде

$\Delta \delta {{n}_{1}} = \delta {{n}_{1}}\left( {\Delta {{\alpha }_{1}} + \Delta {{\alpha }_{2}}} \right),$

или

$\Delta \delta {{m}_{1}} = \delta {{m}_{1}}\left( {\Delta {{\alpha }_{1}} + \Delta {{\alpha }_{2}}} \right),\,\,\,\,\delta {{m}_{1}} = {{\rho }_{1}}\delta {{V}_{1}}.$

После деления последнего равенства на $\Delta t$ и перехода к пределу получается соотношение, выражающее производную бесконечно малой частицы сплошной среды движущейся со скоростью компонента смеси ${{\vec {v}}_{1}}$

${{\left( {\frac{{d\delta {{m}_{1}}}}{{dt}}} \right)}_{1}} = \delta {{m}_{1}}\left( {\frac{{d{{\alpha }_{1}}}}{{dt}} + \frac{{d{{\alpha }_{2}}}}{{dt}}} \right).$

Учитывая формулу дифференцирования элементарной частицы сплошной среды (7), приходим к искомому равенству, выражающему массовую скорость образования ${{{\text{H}}}_{{\text{2}}}}{\text{O}}$ через скорости изменения степеней диссоциации

${{\dot {m}}_{1}} = {{\rho }_{1}}\left( {\frac{{d{{\alpha }_{1}}}}{{dt}} + \frac{{d{{\alpha }_{2}}}}{{dt}}} \right).$

Массовая скорость образования O₂

Суммарное изменение числа молей второго компонента смеси ${{{\text{O}}}_{{\text{2}}}}$ в первой и четвертой химических реакциях в бесконечно малом индивидуальном объеме $\delta {{V}_{2}}(t)$ за время $\Delta t$ определяется равенством

$\Delta \delta {{n}_{2}} = \Delta \delta {{n}_{{21}}} + \Delta \delta {{n}_{{24}}},$

где

$\Delta \delta {{n}_{2}}$ – суммарное изменение числа молей ${{{\text{O}}}_{{\text{2}}}}$ в первой и четвертой реакциях,

$\Delta \delta {{n}_{{21}}}$ – изменение числа молей ${{{\text{O}}}_{{\text{2}}}}$ в первой реакции,

$\Delta \delta {{n}_{{24}}}$ – изменение числа молей ${{{\text{O}}}_{{\text{2}}}}$ в четвертой реакции.

Для меры первой химической реакции $\Delta \delta {{\xi }_{1}},$ протекающей за время $\Delta t$ в элементарном объеме $\delta {{V}_{2}}(t),$ справедливо равенство

$\Delta \delta {{\xi }_{1}} = \frac{{\Delta \delta {{n}_{{21}}}}}{{{{\nu }_{{21}}}}} = \frac{{\Delta \delta {{n}_{{11}}}}}{{{{\nu }_{{11}}}}},$

тогда приращение числа молей второго компонента в результате протекания данной реакции за указанный промежуток времени определяется выражением

$\Delta \delta {{n}_{{21}}} = \frac{{{{\nu }_{{21}}}}}{{{{\nu }_{{11}}}}}\Delta \delta {{n}_{{11}}} = \frac{{{{\nu }_{{21}}}}}{{{{\nu }_{{11}}}}}\delta {{n}_{1}}\Delta {{\alpha }_{1}}.$

Изменение степени диссоциации четвертой реакции составляет

$\Delta {{\alpha }_{4}} = {{\Delta \delta {{n}_{{24}}}} \mathord{\left/ {\vphantom {{\Delta \delta {{n}_{{24}}}} {\delta {{n}_{2}}}}} \right. \kern-0em} {\delta {{n}_{2}}}},$

откуда

$\Delta \delta {{n}_{{24}}} = \delta {{n}_{2}}\Delta {{\alpha }_{4}}.$

Тогда суммарное приращение числа молей ${{{\text{O}}}_{{\text{2}}}}$ вследствие протекания первой и четвертой химических реакций определяется равенством

$\Delta \delta {{n}_{2}} = \frac{{{{\nu }_{{21}}}}}{{{{\nu }_{{11}}}}}\delta {{n}_{1}}\Delta {{\alpha }_{1}} + \delta {{n}_{2}}\Delta {{\alpha }_{4}},$

или

$\frac{1}{{{{M}_{{m2}}}}}\Delta \delta {{m}_{2}} = \frac{1}{{{{M}_{{m1}}}}}\frac{{{{\nu }_{{21}}}}}{{{{\nu }_{{11}}}}}\delta {{m}_{1}}\Delta {{\alpha }_{1}} + \frac{1}{{{{M}_{{m2}}}}}\delta {{m}_{2}}\Delta {{\alpha }_{4}}.$

После деления полученного уравнения на $\Delta t$ и перехода к пределу получается соотношение, выражающее производную бесконечно малой частицы сплошной среды движущейся со скоростью компонента смеси ${{\vec {v}}_{2}}$

${{\left( {\frac{{d\delta {{m}_{2}}}}{{dt}}} \right)}_{2}} = \frac{{{{M}_{{m2}}}}}{{{{M}_{{m1}}}}}\frac{{{{\nu }_{{21}}}}}{{{{\nu }_{{11}}}}}\delta {{m}_{1}}\frac{{d{{\alpha }_{1}}}}{{dt}} + \delta {{m}_{2}}\frac{{d{{\alpha }_{4}}}}{{dt}}.$

Учитывая формулу дифференцирования элементарной частицы сплошной среды (7), приходим к искомому равенству, выражающему массовую скорость образования ${{{\text{O}}}_{{\text{2}}}}$ через скорости изменения степеней диссоциации

${{\dot {m}}_{2}} = \frac{{{{M}_{{m2}}}}}{{{{M}_{{m1}}}}}\frac{{{{\nu }_{{21}}}}}{{{{\nu }_{{11}}}}}{{\rho }_{1}}\frac{{d{{\alpha }_{1}}}}{{dt}} + {{\rho }_{2}}\frac{{d{{\alpha }_{4}}}}{{dt}}.$

Аналогично определяются выражения для массовых скоростей образования оставшихся четырех компонентов продуктов сгорания топлива.

После подстановки найденных соотношений в уравнения (12) получается система из четырех алгебраических уравнений относительно четырех неизвестных скоростей изменения степеней диссоциации веществ ${{d{{\alpha }_{j}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{j}}} {dt}}} \right. \kern-0em} {dt}}$

(13)

$\sum\limits_{i = 1}^4 {{{{\hat {a}}}_{{ij}}}\frac{{d{{\alpha }_{i}}}}{{dt}}} = {{\hat {b}}_{j}},\,\,\,\,j = 1, \ldots ,4$

которые решаются совместно с уравнениями пограничного слоя.

КОНЕЧНО-РАЗНОСТНАЯ АППРОКСИМАЦИЯ И ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ ХИМИЧЕСКИ РАВНОВЕСНОГО ПОГРАНИЧНОГО СЛОЯ

Конечно-разностная аппроксимация системы уравнений пограничного слоя (10) выполняется по неявной несимметричной разностной схеме с первым порядком точности по продольной координате и со вторым по поперечной. Численное решение системы осуществляется методом простой итерации. Продольная компонента скорости течения определяется из уравнения движения. Температура, плотность, поперечная компонента скорости и массовые концентрации определяются последовательно из решения уравнений энергии, состояния, неразрывности и диффузии. Массовые скорости образования компонентов смеси, или скорости изменения степеней диссоциации находятся из уравнений (11, 12, 13).

Для линеаризации системы на первой итерации используется решение с предыдущего шага по продольной координате. Для дальнейшего уточнения численного решения берутся результаты расчета с предыдущей итерации.

С целью обеспечения устойчивости численного решения, уравнения (11) необходимо преобразовать следующим образом

$\sum\limits_i {{{a}_{{1i}}}{{{\dot {m}}}_{i}}} = \frac{1}{{{{K}_{{p1}}}}}\frac{{d{{K}_{{p1}}}}}{{dT}}\rho \frac{{dT}}{{dt}} - \frac{\rho }{{2p}}\frac{{dp}}{{dt}},$

$\begin{gathered} \frac{1}{{{{K}_{{p1}}}}}\frac{{d{{K}_{{p1}}}}}{{dT}}\rho \frac{{dT}}{{dt}} - \frac{\rho }{{2p}}\frac{{dp}}{{dt}} = \frac{1}{{{{K}_{{p1}}}}}\frac{{d{{K}_{{p1}}}}}{{dT}}\frac{1}{{{{c}_{p}}}}\left( {\rho {{c}_{p}}\frac{{dT}}{{dt}}} \right) - \frac{\rho }{{2p}}\frac{{dp}}{{dt}} = \\ = \frac{1}{{{{K}_{{p1}}}}}\frac{{d{{K}_{{p1}}}}}{{dT}}\frac{1}{{{{c}_{p}}}}\left[ {\frac{1}{{\sqrt {{{g}_{{22}}}} }}u\frac{{\partial p}}{{\partial x}} + \mu {{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}}^{2}} + \frac{1}{{\sqrt g }}\frac{\partial }{{\partial y}}\left[ {\sqrt g \left( {\frac{{{{\mu }_{m}}}}{{{{{\Pr }}_{m}}}} + \frac{{{{\mu }_{t}}}}{{{{{\Pr }}_{t}}}}} \right){{c}_{p}}\frac{{\partial T}}{{\partial y}}} \right] - } \right. \\ \left. { - \,\,\sum\limits_i {{{H}_{i}}{{{\dot {m}}}_{i}}} + \sum\limits_i {\left( {\frac{{{{\mu }_{m}}}}{{S{{c}_{m}}}} + \frac{{{{\mu }_{t}}}}{{S{{c}_{t}}}}} \right)} {{c}_{p}}_{i}\frac{{\partial {{c}_{i}}}}{{\partial y}}\frac{{\partial T}}{{\partial y}}} \right] - \frac{\rho }{{2p}}\frac{{dp}}{{dt}}. \\ \end{gathered} $

Тогда первое уравнение может быть записано в виде

$\begin{gathered} \sum\limits_i {\left( {{{a}_{{1i}}} + \frac{1}{{{{K}_{{p1}}}}}\frac{{d{{K}_{{p1}}}}}{{dT}}\frac{1}{{{{c}_{p}}}}{{H}_{i}}} \right){{{\dot {m}}}_{i}} = } \\ = \frac{1}{{{{K}_{{p1}}}}}\frac{{d{{K}_{{p1}}}}}{{dT}}\frac{1}{{{{c}_{p}}}}\left[ {\frac{1}{{\sqrt {{{g}_{{22}}}} }}u\frac{{\partial p}}{{\partial x}} + \mu {{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}}^{2}} + \frac{1}{{\sqrt g }}\frac{\partial }{{\partial y}}\left[ {\sqrt g \left( {\frac{{{{\mu }_{m}}}}{{{{{\Pr }}_{m}}}} + \frac{{{{\mu }_{t}}}}{{{{{\Pr }}_{t}}}}} \right){{c}_{p}}\frac{{\partial T}}{{\partial y}}} \right] + } \right. \\ \left. { + \,\,\sum\limits_i {\left( {\frac{{{{\mu }_{m}}}}{{S{{c}_{m}}}} + \frac{{{{\mu }_{t}}}}{{S{{c}_{t}}}}} \right)} {{c}_{{{{p}_{i}}}}}\frac{{\partial {{c}_{i}}}}{{\partial y}}\frac{{\partial T}}{{\partial y}}} \right] - \frac{\rho }{{2p}}\frac{{dp}}{{dt}}, \\ \end{gathered} $

или

$\sum\limits_i {{{{\tilde {a}}}_{{1i}}}{{{\dot {m}}}_{i}}} = {{\tilde {b}}_{1}}.$

Аналогично преобразуются второе, третье и четвертое уравнения (11, 12, 13).

В областях химически замороженного течения величины всех массовых скоростей ${{\dot {m}}_{i}}$ полагаются равными нулю и расчет пограничного слоя выполняется по общему алгоритму. В качестве критерия для определения областей химически замороженного течения используется величина статической температуры продуктов сгорания топлива, которая в случае топливной пары кислород-водород принимается равной ${{T}_{{{\text{зам}}}}} \leqslant 1600{\kern 1pt} - {\kern 1pt} 1800\,\,{\text{K}}.$

Для численного расчета уравнения обезразмериваются в соответствие со следующей системой масштабов переменных

$\begin{gathered} {{u}_{s}} = {{u}_{{{\text{кр}}}}},\,\,\,\,{{\rho }_{s}} = {{\rho }_{{{\text{кр}}}}},\,\,\,\,{{p}_{s}} = {{\rho }_{s}}u_{s}^{2},\,\,\,\,{{c}_{{ps}}} = {{c}_{{{\text{кр}}}}},\,\,\,\,{{T}_{s}} = {{u_{s}^{2}} \mathord{\left/ {\vphantom {{u_{s}^{2}} {{{c}_{{ps}}}}}} \right. \kern-0em} {{{c}_{{ps}}}}},\,\,\,\,{{R}_{{ga{{s}_{S}}}}} = {{c}_{{ps}}}, \\ {{x}_{s}} = L,\,\,\,\,{{R}_{{nozzl{{e}_{S}}}}} = {{x}_{s}},\,\,\,\,{{\mu }_{s}} = {{\mu }_{{mol\;{\text{кр}}}}},\,\,\,\,\operatorname{Re} = {{{{\rho }_{s}}{{u}_{s}}{{x}_{s}}} \mathord{\left/ {\vphantom {{{{\rho }_{s}}{{u}_{s}}{{x}_{s}}} {{{\mu }_{s}}}}} \right. \kern-0em} {{{\mu }_{s}}}},\,\,\,\,{{v}_{s}} = {{{{u}_{s}}} \mathord{\left/ {\vphantom {{{{u}_{s}}} {\sqrt {\operatorname{Re} } }}} \right. \kern-0em} {\sqrt {\operatorname{Re} } }},\,\,\,\,{{y}_{s}} = {{{{x}_{s}}} \mathord{\left/ {\vphantom {{{{x}_{s}}} {\sqrt {\operatorname{Re} } }}} \right. \kern-0em} {\sqrt {\operatorname{Re} } }}, \\ \Gamma _{{{{{23}}_{S}}}}^{2} = {1 \mathord{\left/ {\vphantom {1 {{{y}_{s}}}}} \right. \kern-0em} {{{y}_{s}}}},\,\,\,\,{{g}_{{{{{11}}_{S}}}}} = R_{{nozzl{{e}_{S}}}}^{2},\,\,\,\,{{g}_{{{{{22}}_{S}}}}} = 1,\,\,\,\,{{g}_{s}} = R_{{nozzl{{e}_{S}}}}^{2},\,\,\,\,{{{\dot {m}}}_{{{{i}_{S}}}}} = {{{{\rho }_{s}}{{u}_{s}}} \mathord{\left/ {\vphantom {{{{\rho }_{s}}{{u}_{s}}} {{{x}_{s}}}}} \right. \kern-0em} {{{x}_{s}}}},\,\,\,\,{{h}_{{{{i}_{S}}}}} = {{H}_{{{{i}_{S}}}}} = u_{s}^{2}. \\ \end{gathered} $

В принятой системе масштабов переменных размерный и безразмерный вид уравнений совпадают.

Все вычисления выполняются с удвоенной точностью. Выбор величин шагов дискретной сетки и другие особенности численного решения системы уравнений турбулентного пограничного слоя рассмотрены в работе [7]. Для решения задач сопряженного теплообмена в работах [7, 8] предложены консервативные конечно-разностные схемы аппроксимации слагаемого с дивергенцией теплового потока, которые обеспечивают выполнение условия сохранения теплового потока на поверхностях разрыва теплофизических характеристик среды в точках границы газ-стенка.

РЕЗУЛЬТАТЫ ПАРАМЕТРИЧЕСКИХ РАСЧЕТОВ И ТЕСТИРОВАНИЕ ПОЛУЧЕННОГО ЧИСЛЕННОГО РЕШЕНИЯ

В качестве апробации предложенной термохимической модели неизоэнтропического сдвигового течения был выполнен расчет пограничного слоя на стенке камеры сгорания и сопла кислородно-водородного ракетного двигателя.

Верификация полученного численного решения осуществлялась посредством сравнения величин расчетных параметров течения на внешней границе пограничного слоя с величинами указанных параметров, вычисленными по пакету программ [1] для равновесного изоэнтропического расширения в сопле. Данный метод тестирования основан на том, что внешняя граница пограничного слоя мало подвержена действию вязких сил и диффузионному переносу, вследствие чего величины параметров течения в указанной области должны быть близки к величинам параметров изоэнтропического расширения.

Верификационный расчет был выполнен для сопла с адиабатической стенкой, при значении полной энтальпии компонентов топлива на входе в камеру сгорания равной нулю Н_кам = 0 и α_кам = 1.

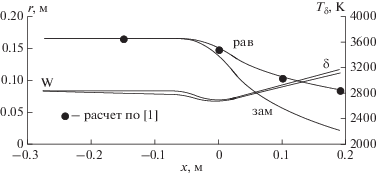
На графике (рис. 1) представлены продольные распределения статической температуры на внешней границе пограничного слоя для равновесного и полностью замороженного течения. Точками изображены результаты расчета равновесного изоэнтропического расширения, выполненные по программе [1]. Из сравнения полученных результатов непосредственно следует, что найденные значения статической температуры на внешней границе равновесного пограничного слоя с хорошей точностью совпадают с параметрами изоэнтропического расширения.

Рис. 1.

Продольные распределения статической температуры на внешней границе пограничного слоя для равновесного и полностью замороженного течения.

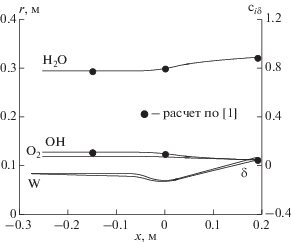
Продольные распределения величин массовых концентраций продуктов сгорания на внешней границе пограничного слоя даны на рис. 2. Точками изображены результаты расчета равновесного изоэнтропического расширения по программе [1]. Как и в предыдущем случае наблюдается хорошее совпадение величин сравниваемых параметров.

Рис. 2.

Продольные распределения массовых концентраций на внешней границе равновесного пограничного слоя.

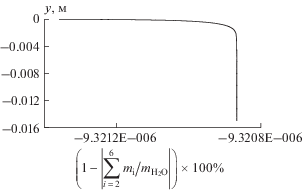
Верификация определения массовых скоростей образования продуктов сгорания топлива проводилась на основе проверки выполнения равенства $\sum\nolimits_i {{{{\dot {m}}}_{i}}} = 0$ в точках произвольно выбранного поперечного сечения пограничного слоя. На графике (рис. 3) приведено распределение относительной погрешности выполнения данного равенства в выходном сечении сопла. Величина погрешности составляет миллионные доли процента.

Рис. 3.

Распределение относительной погрешности определения массовых скоростей образования компонент продуктов сгорания топлива в выходном сечении сопла.

В качестве параметрического исследования был выполнен расчет течения в сопле с охлаждаемой стенкой постоянной температуры T_w = 800 K, при неизменных условиях на входе в камеру сгорания Н_кам = 0 и α_кам = 1.

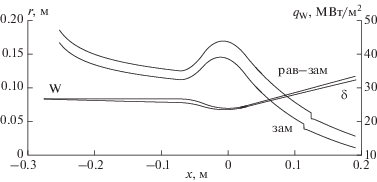
Продольные распределения теплового потока в стенку сопла для равновесного течения с замораживанием и полностью замороженного пограничного слоя даны на рис. 4.

Рис. 4.

Продольные распределения теплового потока в стенку сопла для равновесного течения с замораживанием и полностью замороженного пограничного слоя.

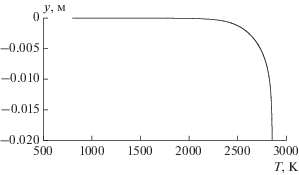
На графике (рис. 5) представлен профиль статической температуры в выходном сечении сопла для равновесного течения с замораживанием. Из графика следует, что в окрестности охлаждаемой стенки сопла существует тонкий подслой газа ${{\delta }_{{{\text{зам}}}}} \approx 20\,\,{\text{мкм}}$ с низкой температурой $T \leqslant 1800\,\,{\text{K}}.$ Скорости химических реакций в данном температурном диапазоне незначительны и течение в указанном подслое считается химически замороженным – массовые скорости образования продуктов сгорания топлива полагаются равными нулю ${{\dot {m}}_{i}} \equiv 0.$ Замораживание пристенного слоя приводит к уменьшению теплового потока в стенку сопла, вследствие чего максимальные величины теплового потока при равновесном течении с замораживанием и полностью замороженном пограничном слое (рис. 4) имеют небольшое различие (~10–15%).

Рис. 5.

Профиль статической температуры в выходном сечении сопла для равновесного течения с замораживанием.

Вторая серия параметрических расчетов была выполнена для сопла с охлаждаемой стенкой постоянной температуры T_w = 800 K и завесой охлаждения α_зав = 0.25, при неизменных условиях на входе в камеру сгорания Н_кам = 0 и α_кам = 1.

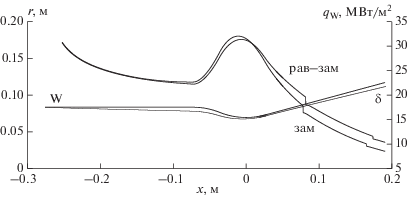
Продольные распределения теплового потока в стенку сопла для равновесного течения с замораживанием и полностью замороженного пограничного слоя даны на рис. 6.

Рис. 6.

Продольные распределения теплового потока в стенку сопла для равновесного течения с замораживанием и полностью замороженного пограничного слоя при наличии газовой завесы.

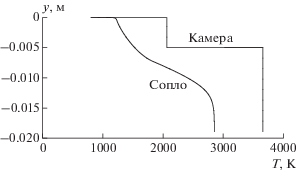
Профили статической температуры на входе в камеру сгорания и в выходном сечении сопла для равновесного течения с замораживанием приведены на рис. 7. Наличие охлаждающей завесы приводит к увеличению толщины пристенного слоя газа с низкой температурой $T \leqslant 1800\,\,{\text{K}}$ более чем на два порядка ${{\delta }_{{{\text{зам}}}}} \approx 7\,\,{\text{мм}}.$ Вследствие чего максимальные величины теплового потока в стенку сопла для химически равновесного течения с замораживанием и полностью замороженного пограничного слоя (рис. 6) практически не отличаются.

Рис. 7.

Профили статической температуры на входе в камеру сгорания и в выходном сечении сопла для равновесного течения с замораживанием при наличии газовой завесы.

Представленные результаты исследований позволяют сделать вывод о том, что расчет процессов течения и теплообмена в камерах сгорания и соплах ракетных двигателей в условиях наличия регенеративного и завесного охлаждения, которые характерны для всех типов жидкостных ракетных двигателей, можно проводить по модели полностью замороженного пограничного слоя.

Использование модели химически равновесного течения с замораживанием является необходимым только в случае обтекания неохлаждаемой поверхности камеры сгорания и сопла двигателя, который соответствует тепловому режиму работы твердотопливных ракетных двигателей.

ЗАКЛЮЧЕНИЕ

Сформулирован подход к решению проблемы термохимического моделирования неизоэнтропических сдвиговых течений в камерах сгорания и соплах ракетных двигателей. Для расчета химического равновесия продуктов сгорания топлива создана методика определения массовых скоростей образования компонентов смеси в неизоэнтропическом течении. В рамках сформулированного подхода, в качестве примера, проведен расчет пограничного слоя на стенке камеры сгорания и сопла кислородно-водородного ракетного двигателя. Выполнены параметрические исследования процессов течения и теплообмена. Полученные результаты позволяют сделать вывод о том, что расчет процессов течения и теплообмена в камерах сгорания и соплах жидкостных ракетных двигателей, при наличии регенеративного и завесного охлаждения, можно проводить по модели полностью замороженного пограничного слоя. Использование модели химически равновесного течения с замораживанием является необходимым только в случае обтекания неохлаждаемой поверхности камеры сгорания и сопла двигателя, который соответствует тепловому режиму работы твердотопливных ракетных двигателей.

Результаты тестирования подтверждают высокую точность полученного численного решения и позволяют рекомендовать предложенный подход для термохимического моделирования неизоэнтропических процессов в рабочих объемах и проточных трактах энергодвигательных установок.

Список литературы

Трусов Б.Г. Моделирование химических и фазовых равновесий при высоких температурах (Астра-4/рс). М.: Изд. МВТУ им. Э. Баумана, 1991.
Мельников Д.А., Пирумов У.Г., Сергиенко А.А., Семичастнов В.М. и др. Руководство для конструкторов по проектированию сверхзвуковых осесимметричных круглых сопел реактивных двигателей. М.: Изд. ОНТИ, 1964.
Кацкова О.Н. Расчет равновесных течений газа в сверхзвуковых соплах. М.: Изд. ВЦ АН СССР, 1964.
Лебединский Е.В., Калмыков Г.П., Мосолов С.В. и др., под ред. Академика РАН Коротеева А.С. Рабочие процессы в жидкостном ракетном двигателе и их моделирование. М.: Машиностроение, 2008.
Гурвич Л.В., Вейц И.В., Медведев В.А. и др. Термодинамические свойства индивидуальных веществ. Справочное издание в 4-х томах. М.: Наука, 1978.
Седов Л.И. Механика сплошной среды, том 1. Москва. “Наука”. Главная редакция физико-математической литературы, 1983.
Борисов Д.М., Шураев Ю.А., Миронов В.В. О некоторых особенностях численного моделирования систем регенеративного охлаждения энергодвигательных установок. // Изв. РАН. Энергетика. 2015. № 4. С. 152–157.
Борисов Д.М., Шураев Ю.А., Миронов В.В. Об определении теплового состояния профилированных сопловых насадков радиационного охлаждения. // Изв. РАН. Энергетика. 2018. № 5. С. 59–66.
Шевелев Ю.Д. Пространственные задачи вычислительной аэрогидродинамики. Москва. “Наука”, 1986.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал