Известия РАН. Энергетика, 2020, № 2, стр. 59-74
Алгоритмические аспекты расчета вероятностных показателей дефицита мощности в задаче балансовой надежности ОЭС
1 НИЦ “Надежность и ресурс больших систем и машин” УрО РАН
Екатеринбург, Россия
2 Уральский федеральный университет, УралЭНИН
Екатеринбург, Россия
* E-mail: vpo1704@mail.ru
Поступила в редакцию 16.12.2019
После доработки 13.01.2020
Принята к публикации 14.01.2020
Аннотация
Ключевой процедурой при определении показателей балансовой надежности объединенных электроэнергетических систем (ОЭС) является оптимальное распределение дефицита мощности (ДМ) между входящими в состав ОЭС электроэнергетическими системами (ЭЭС). В зависимости от постановки задачи возможны отличающиеся критерии оптимизации, которым соответствует совокупность целевых функций, систем ограничений и управляющих переменных. Показано, что при использовании методов статистического моделирования наиболее приемлемыми являются критерии минимума эксплуатационных затрат и пропорционального распределения ДМ между ЭЭС, а наиболее значимым ограничением является пропускная способность межсистемных связей. Рассмотрена специфика выбора управляющих переменных в зависимости от применяемых в оптимизационных процедурах методов нелинейного программирования. Показано, что в большинстве сочетаний целевых функций и управляющих переменных математическая постановка задачи может быть сведена к квадратичному программированию.
ВВЕДЕНИЕ
Расчеты показателей балансовой надежности (ПБН) объединенных электроэнергетических систем выполняются, как правило, в задачах перспективного развития и планирования режимов ОЭС с целью оценки рисков от ограничения поставки электроприемникам необходимого объема электроэнергии. К числу ПБН, в первую очередь, относятся вероятность и математическое ожидание (МО) дефицита мощности в отдельных районах ОЭС. Дополнительно могут быть определены такие индикативные вероятностные показатели как частота, МО и дисперсия длительности дефицитного состояния, коэффициенты обеспеченности потребителей электроэнергии, вероятности и МО перегрузки связей и сечений, МО коэффициента использования генерирующей мощности и др. [1–4]. При этом принимается во внимание стохастический характер мощности нагрузки, располагаемой генерации и топологии электрической сети. Основным математическим методом при оценке ПБН в настоящее время является метод статистических испытаний (Монте-Карло), как наиболее точный и адаптивный к учету множества реальных режимных ограничений [1–7]. Однако даже для отдельных концентрированных ЭЭС при расчете ПБН с приемлемой точностью число статистических реализаций должно превышать сотни тысяч [8], что приводит к недопустимо большой длительности расчетов и необходимости совершенствования вычислительных процедур [9, 10].
При анализе случайных событий, связанных с появлением дефицита мощности (ДМ) в ЭЭС, в каждой статистической реализации состава генерации, нагрузки и межсистемных связей (МСС) решается задача минимизации затрат на компенсацию издержек потребителей от ограничения электропотребления. Данная задача известна как задача оптимального распределения дефицита мощности (ОРДМ) в энергосистеме [4]. Развитие теории БН ЭЭС, по существу, связано с совершенствованием математических методов решения данной задачи с учетом значимых режимных ограничений. По результатам серийных расчетов определяются математические ожидания (МО) и среднеквадратические отклонения (СКО) величин, определяющих ПБН (недоотпуска электроэнергии потребителям и др.).
Наибольшее распространение при решении задачи ОРДМ получила линейная модель, где целевая функция (ЦФ) пропорциональна величине дефицита мощности, потери мощности учитываются приближенно через неизменный коэффициент потерь, а распределение мощности по межсистемным связям (МСС) соответствует модели транспортных потоков [4]. Известно, что решение такой задачи в общем виде может быть неоднозначным и, как правило, не удовлетворяет требованию пропорциональности распределения ДМ между потенциально дефицитными узлами. Дополнительная оптимизация с квадратичной ЦФ и дополнительным ограничением, отражающим результаты оптимизации первого этапа, позволяет решить проблему упомянутой многозначности [11]. Квадратичная ЦФ обеспечивает единственность решения в том числе и по критерию пропорциональности распределения ДМ [8–12].
К нелинейному виду приводит ОРДМ по критерию минимума ущербов (компенсационных затрат) при ограничении электропотребления, которые нелинейно зависят как от глубины, так и длительности ограничения нагрузки [13, 14]. Отсюда представление ЦФ в виде линейной формы с последующим применением линейного программирования (ЛП) не всегда обеспечивает приемлемое для практики решение задачи ОРДМ. Более точное решение обеспечивается применением математического аппарата нелинейного программирования вообще и квадратичного программирования (представление ЦФ в виде квадратичной формы при линейных ограничениях) в частности [8]. Нелинейное программирование позволяет учесть не только нелинейный характер ЦФ, но и нелинейность ограничений, в том числе более точно учесть потери мощности в электрической сети [8–12]. Отсюда нелинейное программирование должно быть превалирующим математическим аппаратом при решении задачи ОРДМ. Однако это не исключает использования ЛП, например, при линейной аппроксимации целевой функции и линейных ограничений.
Величина потерь мощности в межсистемных связях (МСС) сопоставима с ограничением электропотребления в ОЭС из-за дефицита мощности при вероятностном характере нагрузки, располагаемой генерации и состояния элементов МСС. Отсюда приближенный учет потерь мощности или их полный неучет приводит к существенным погрешностям при определении ПБН ОЭС. В то же время, уточненный расчет потерь мощности требует более точного знания электрических параметров, что, как правило, игнорируется при расчетах ПБН. Специфика задачи БН заключается в том, что в силу большой неопределенности нагрузки и состава генерирующей мощности невозможно определить достаточно точно параметры электрических режимов для удаленного момента времени (5–10 лет при перспективных расчетах). Отсюда в БН принимаются такие ограничения, как неучет закона Ома и 2-го закона Кирхгофа. В результате, сопротивления связей при расчете показателей БН в настоящее время не учитываются, а потери мощности, как это было упомянуто выше, учитываются приближенно через коэффициент потерь. В то же время МСС имеют более определенный характер, нежели концентрированная система – это одна или несколько конкретных существующих или проектируемых линий электропередачи, сопротивления которых известны. Это позволяет при расчете ПБН уточнить как потери мощности, так и распределение потоков мощности в электрической сети ОЭС согласно законам Ома и Кирхгофа.
Известно достаточно большое число ПБН, на определение которых направлена оценка БН ОЭС [1–7, 15]. Во многом их выбор определяется спецификой решаемой задачи (перспективного развития ОЭС; планирования ремонтов основного оборудования, распределения резервов мощности и др.). Среди упомянутых показателей необходимо выделить наиболее применяемые как ОЭС в целом, так и для отдельных территориальных зон: МО недоотпуска электрической энергии (мощности); МО затрат, связанных с ограничением нагрузки (компенсационные издержки); вероятность бездефицитной работы ЭЭС; коэффициент относительной обеспеченности потребителей электроэнергии; вероятность перегрузки электрической сети;
Среди зарубежных ПБН наибольшее распространение получили [16]: EUE (Expected Unserved Energy) – МО недоотпуска электрической энергии; LOLE (Loss of Load Expectation) – МО ограничения мощности нагрузки; LOEE (Loss of Energy Expectation) – МО ограничения электропотребления; LOLP (Loss of Load Probability) – вероятность ограничения мощности нагрузки; LOLH (Loss of Load Hour) – МО числа часов дефицитного состояния системы; LOLEV (Loss Of Load Events) – математическое ожидание числа случаев возникновения ограничения нагрузки. Сопоставление упомянутых показателей БН достаточно полно показано в [16].
В последнее время в связи с увеличением доли распределенной генерации и внедрением новых технологий производства электроэнергии, в основе которых заложено использование возобновляемых источников энергии, происходят существенные изменения, вызванные вытеснением энергоблоков, в частности, на угле. Возникает задача оценки их экономической эффективности, целесообразности их перевода в холодный резерв, демонтажа или консервации. Данная задача требует соответствующего информационного обеспечения, в том числе ПБН ЭЭС, отражающих динамику в структуре генерации. Такими показателями могут быть, например, коэффициент использования мощности, МО убытков от недоиспользования генерирующей мощности и др.
В представленной работе показана специфика применения и сопоставительная оценка расчетных процедур при решении задачи ОРДМ, в том числе направленных на решение задачи определения ПБН ЭЭС.
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ОРДМ
С целью получения ПБН в условиях вероятностно определенных узловых нагрузок, располагаемых генераций (случайные отключения энергоблоков) и топологии электрической сети (отключения межсистемных связей (МСС)) требуется выполнить оптимальное распределение возможного вероятностного глобального или локального (по ЭЭС) дефицита мощности в ОЭС с межсистемными связями ограниченной пропускной способности.
Критерии оптимизации. В качестве основных критериев оптимизации при решении задачи ОРДМ, в зависимости от выбора предпочтительных ПБН, как правило, рассматриваются:
• минимум недоотпуска электрической энергии (мощности);
• минимум затрат, связанных с производством электроэнергии и ограничением электропотребления;
• пропорциональное распределение дефицита мощности между отдельными ЭЭС, входящими в состав объединения.
Кроме указанных в практике находят применение похожие критерии: максимум коэффициента обеспеченности потребителей электроэнергии, минимум потерь мощности в межсистемных связях, минимум загрузки электрической сети; минимум СКО узловых инъекций или коэффициентов избыточности от заданных, например, полученных для некоторого идеального режима, и др. [4].
В задачах перспективного развития ЭЭС критерий минимума затрат на производство электроэнергии и ограничение электропотребления является основным при экономическом сопоставлении вариантов развития – он позволяет сопоставить капиталовложения в создание резервов мощности и энергии с рисками от недопоставки электроэнергии потребителям. В то же время он обладает и существенным недостатком – большой неопределенностью параметров характеристик затрат [4]. Это резко ограничивает область применения отмеченного критерия, вплоть до отказа от его применения при отсутствии необходимых данных. Альтернативой являются критерии, не использующие денежное выражение показателей надежности, например, те, что перечислены выше. Их использование в задачах перспективного развития ЭЭС может осуществляться через коэффициенты предпочтительности или в качестве критериальных ограничений. При таком подходе затраты можно трактовать в более широком смысле, например, как квадратичные функции предпочтительности.
Управляющие переменные: Отражающая критерий оптимальности целевая функция, как правило, адаптирует критерий к управляющим переменным (УП), среди которых наибольшее применение в задаче ОРДМ получили (в используемых нами обозначениях):
• текущая мощность нагрузки $0 \leqslant {{L}_{i}} \leqslant {{\bar {L}}_{i}},\,\,i = 1, \ldots ,n,$ где $n$ – число узлов в электрической сети; ${{\bar {L}}_{i}}$ – спрос мощности в узле $i$ (аналогом текущей нагрузке ${{L}_{i}}$ может служить величина ее ограничения, ${{z}_{i}} = {\text{\;}}\Delta {{L}_{i}} = {{\bar {L}}_{i}} - {{L}_{i}}{\text{\;}}$);
• текущая мощность генерации, $0 \leqslant {{G}_{i}} \leqslant {{\bar {G}}_{i}},\,\,i = 1, \ldots ,n,$ где ${{\bar {G}}_{i}}$ – располагаемая (установленная, за вычетом мощности планово- или аварийно отключенных энергоблоков) мощность; (аналогом может служить величина ограничения генерирующей мощности, $\Delta {{G}_{i}} = {\text{\;}}{{\bar {G}}_{i}} - {{G}_{i}}{\text{\;}}$);
• мощность, передаваемая в узел из электрической сети (сетевая инъекция), $ - {{\bar {G}}_{i}} \leqslant {{u}_{i}} \leqslant $ $ \leqslant {{\bar {L}}_{i}},\,\,~i = 1, \ldots ,n;$
• поток мощности по МСС, ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{l}} \leqslant {{x}_{l}} \leqslant {{\bar {x}}_{l}},\,\,l = 1, \ldots ,m,$ где $m$ – число МСС. Здесь переменная ${{x}_{l}},$ часто представляемая в виде ${{x}_{{ij}}},$ определяет мощность со стороны начального узла $i.$ Мощность в МСС со стороны конечного узла ${{x}_{{ji}}}$ отличается от ${{x}_{{ij}}}$ на величину потерь мощности ${{\pi }_{{ij}}}$ в рассматриваемой связи, ${{x}_{{ji}}} = {{\pi }_{{ij}}} - {{x}_{{ij}}}.$
Следует отметить специфику использования векторов потоков мощности $x~$ ($m~\,\,{\text{переменных}}$) и сетевых инъекций u ($n$ переменных). В электрических цепях определяемые законами Ома и Кирхгофа потоки мощности по связям $\left\{ {{{x}_{l}}} \right\}$ однозначно определяются вектором инъекций ${\mathbf{u}} = \left\{ {{{u}_{i}}} \right\}.$11 В то же время при $m \geqslant n$ и неучете законов Ома и Кирхгофа (часто при расчетах ПБН учитывается только первый закон Кирхгофа) одному и тому же вектору u соответствует бесконечно большое число комбинаций $\left\{ {{{x}_{l}}} \right\},$ в том числе таких, при которых происходит циркуляция потоков мощности по замкнутому контуру, что неприемлемо для неявно принятой в расчетах ПБН модели постоянного тока. Данное замечание было бы несущественным, если бы управление потоками мощности осуществлялось локально, без участия генерирующей подсистемы. Но реально изменение потоков в линиях электропередачи осуществляется изменением мощности в узлах генерации и функциональная связь ${\mathbf{x}}\left( {\mathbf{u}} \right)$ является более значимой, нежели ${\mathbf{u}}\left( {\mathbf{x}} \right)$ (через первую матрицу инциденций).
Отсюда при варьировании переменных x необходимо, чтобы вектор x удовлетворял требованию однозначного соответствия с вектором узловых инъекций, а при управлении инъекциями u для однозначного соответствия необходимо вводить дополнительные критерии, например, определять x через матрицу С потокораспределения, ${\mathbf{x}} = C{\mathbf{u}}.$ Как следствие, для решения задачи ОРДМ становится неприемлемым алгоритм Форда-Фалкерсона [17], где максимальный поток определяется варьированием потоков по связям без учета функциональной допустимости вектора управляющих переменных.
Ограничения. Согласно первому закона Кирхгофа для каждого узла ЭЭС должен соблюдаться баланс мощностей
Баланс мощностей для всей электрической сети определяется условием
Потоки мощности по МСС пропорциональны инъекциям (допущение, частично учитывающее второй закон Кирхгофа)
(3)
${{{\mathbf{P}}}_{{br}}} = - C{\mathbf{u}},\,\,\,\,{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P} }}}_{{br}}} \leqslant {{{\mathbf{P}}}_{{br}}} \leqslant {{{\mathbf{\bar {P}}}}_{{br}}},\,\,\,\,\dim \left( {{{{\mathbf{P}}}_{{br}}}} \right) = m;\,\,\,\,\dim \left( C \right) = \left( {m,n - 1} \right);$Выражение (3) может быть представлено в виде
Ограничения на генерацию и ограничения электропотребления
(5)
$0 \leqslant {{G}_{i}} \leqslant {{\bar {G}}_{i}};\,\,\,\,0 \leqslant {{z}_{i}} \leqslant {{\bar {L}}_{i}}$Дополнительные ограничения. Воздействие варьируемых переменных – генерации $\left\{ {{{G}_{i}}} \right\}$ и нагрузки$~\left\{ {{{L}_{i}}} \right\}$ (или ограничения электропотребления $\left\{ {{{z}_{i}}} \right\}$) в какой либо отдельной концентрированной ЭЭС на суммарный баланс мощности в ОЭС осуществляется через сетевые инъекции $~\left\{ {{{u}_{i}} = {{L}_{i}} - {{G}_{i}}} \right\}.$ В то же время при фиксированной инъекции $~{{u}_{i}}$ существует бесконечное множество $\left\{ {{{L}_{i}},{{G}_{i}}} \right\},$ удовлетворяющее упомянутому соотношению узлового баланса мощности. Отсюда необходим критерий взаимно-однозначного соответствия. Таким критерием может быть минимум суммарных компенсационных затрат от ограничения генерации и нагрузки. Другим вариантом является распределение $\left\{ {{{G}_{i}},~{{L}_{i}}} \right\}$ с условием – ограничение электропотребления осуществляется только при максимальной генерации, $\left\{ {\Delta {{L}_{i}} > 0|{{G}_{i}} = {{G}_{{i,{\text{max}}}}}~} \right\}.$ Последнее условие математически может быть записано в виде ограничения:
(7)
$\left( {{{{\bar {L}}}_{i}} - {{L}_{i}}} \right)\left( {{{{\bar {G}}}_{i}} - {{G}_{i}}} \right) = 0.$Данное ограничение алгоритмически легко реализуется при выборе инъекций $\left\{ {{{u}_{i}}} \right\}$ в качестве вектора управляющих переменных и достаточно не просто, если управляющими переменными являются $\left\{ {{{L}_{i}},{{G}_{i}}} \right\}$ (ограничения (7) нелинейны). В то же время при выборе в качестве ЦФ функции, зависящей от $\left\{ {{{L}_{i}},{{G}_{i}}} \right\}$ даже при выборе $\left\{ {{{u}_{i}}} \right\}$ в качестве УП в числе функциональных ограничений необходимо ввести условие (7). Ввод этого ограничения приводит к необходимости использования обобщенных процедур нелинейного программирования, что значительно снижает вычислительную эффективность задачи ОРДМ, которая, в свою очередь, является многократно исполняемым блоком в методе статистических испытаний.
Условие (7) является решением частного случая критерия минимума компенсационных затрат при заданной величине узловой инъекции, когда затраты на компенсацию ограничения электропотребления существенно превышают затраты на ограничение генерирующей мощности. Решение задачи оптимального распределения небаланса мощности узла между генерацией и ограничением нагрузки, которое можно рассматривать как дополнительную генерацию, не представляет каких-либо проблем и известно как распределение по критерию равенства относительных приростов затрат на производство электроэнергии [19]. Это позволяет определить функциональную зависимость компенсационных затрат от ограничения генерации и нагрузки ${\text{З}}\left( {\Delta G,\Delta L} \right)$ как функцию узловой инъекции, и включить данную зависимость в состав целевой функции.
МИНИМУМ СУММАРНЫХ ЗАТРАТ
Целевая функция. Как было отмечено выше, одним из основных критериев в задаче ОРДМ является “минимум суммарных (по всем узлам ЭЭС) затрат, связанных с ограничением нагрузки, и затрат на производство электроэнергии”. Затраты на генерацию, где превалирует топливная составляющая, обычно представляется параболической характеристикой [19]:
(8)
${{{\text{З}}}_{{{{G}_{i}}}}} = {{{\text{З}}}_{{i,0}}} + {{a}_{{G,i}}}{{G}_{i}} + {{b}_{{G,i}}}G_{i}^{2}.$Компенсационные затраты ${{{\text{У}}}_{i}}\left( {{{z}_{i}}} \right)$ за ограничение электропотребления ${{z}_{i}}$ зависят от глубины ограничения ${{z}_{{i*}}} = {{{{z}_{i}}} \mathord{\left/ {\vphantom {{{{z}_{i}}} {{{{\bar {L}}}_{i}}}}} \right. \kern-0em} {{{{\bar {L}}}_{i}}}},$ где ${{\bar {L}}_{i}}$ – спрос электропотребления. Обычно удельный ущерб от ограничения электропотребления представляется кусочно-линейной функцией с относительно большой долей первого участка [13, 14, 10]. Поэтому при определении показателей балансовой надежности ЭЭС уместно ограничиться первой линейной характеристикой удельного ущерба, ${{у}_{i}}\left( {{{z}_{{*i}}}} \right) = {{a}_{{L,i}}} + {{b}_{{L,i}}}{{z}_{{*i}}}.$ Отсюда компенсационные затраты также могут быть представлены квадратичными функциями
(9)
${{{\text{У}}}_{i}}\left( {{{z}_{i}}} \right) = {{{\text{у}}}_{i}}{{z}_{i}} = {{a}_{{L,i}}}{{z}_{i}} + {{b}_{{L,i}}}z_{i}^{2}.$В результате ЦФ (без учета постоянной составляющей):
(10)
$F = \sum\limits_{i = 1}^n {{{{\text{У}}}_{i}}\left( {{{z}_{i}}} \right)} + \sum\limits_{i = 1}^n {{{{\text{З}}}_{{{{G}_{i}}}}}\left( {{{G}_{i}}} \right)} = \sum\limits_{i = 1}^n {\left( {{{a}_{{L,i}}}{{z}_{i}} + {{b}_{{L,i}}}z_{i}^{2} + {{a}_{{G,i}}}{{G}_{i}} + {{b}_{{G,i}}}G_{i}^{2}} \right)} \Rightarrow \min ,$(11)
$\begin{gathered} F = \min \left( {{{{\mathbf{y}}}^{t}}H{\mathbf{y}} + {{{\mathbf{f}}}^{t}}{\mathbf{y}}} \right), \\ {{{\mathbf{P}}}_{{br}}} = - C{\mathbf{u}} = \left[ {\begin{array}{*{20}{c}} {C,}&C \end{array}} \right]\left[ {\begin{array}{*{20}{c}} z \\ {\mathbf{G}} \end{array}} \right] - C{\mathbf{\bar {L}}};\, \\ \end{gathered} $Генерация $\left\{ {{{G}_{i}}} \right\}~$и ограничение $\left\{ {{{z}_{i}}} \right\}$ мощности нагрузки потребителей определяют сетевую инъекцию мощности узла $\left\{ {{{u}_{i}} = {{L}_{i}} - {{G}_{i}} = \left( {{{{\bar {L}}}_{i}} - {{z}_{i}}} \right) - {{G}_{i}}} \right\},$ а, следовательно, и перетоки мощности по МСС,
Ограничение (2) преобразуется к виду:
Потери мощности в МСС являются квадратичной функцией потока мощности
(12)
${{\pi }_{\Sigma }} = \sum\limits_{l = 1}^m {\frac{{{{R}_{l}}}}{{{{V}^{2}}}}x_{l}^{2}} = {{{\mathbf{u}}}^{t}}A{\mathbf{u}},$При ориентировании на квадратичное программирование необходимо, чтобы все ограничения были представлены в линейной форме. Отсюда потери мощности (12), являющиеся квадратичной формой варьируемых переменных, желательно вывести из системы ограничений или представить их в виде линейного функционала управляющих переменных. Следует заметить, что потери мощности имеют относительно большую погрешность из-за существенной неопределенности электрических параметров МСС, которые могут быть эквивалентами, полученными в результате электрических преобразований электрической сети. Отсюда можно принять допущение о равенстве потерь мощности потерям некоторого идеального режима, например, режима без учета сетевых ограничений, ${{\pi }_{0}} = {\mathbf{u}}_{0}^{t}A{{{\mathbf{u}}}_{0}}$, где $A$ – матрица квадратичной формы.
Более точный расчет потерь наблюдается при линейной аппроксимации (12) в точке, соответствующей идеальному режиму:
Данное выражение можно представить как функцию вектора ${\mathbf{y}} = {{\left( {{\mathbf{z}},{\mathbf{G}}} \right)}^{t}}.$
Согласно (2), с учетом (13)
(14)
$\left( {{{{\mathbf{e}}}^{t}} + 2{\mathbf{u}}_{0}^{t}{{A}^{t}}} \right){\mathbf{u}} = {{\pi }_{0}}.$Отсюда
Уравнение баланса мощности в узлах преобразуется к виду
Следует отметить, что учет потерь в приведенном уравнении баланса мощности приводит к оптимизации распределения потоков мощности по МСС, в том числе и по критерию минимума потерь мощности. Таким образом, модель двойного блока переменных $\left( {{\mathbf{G,z}}} \right)$ позволяет привести задачу ОРДМ к виду, приемлемому для применения квадратичного программирования по расширенному критерию.
Как правило, при расчетах ПБН во главу угла ставится задача минимизации недоотпуска электроэнергии потребителям при произвольном распределении генерации между ее источниками. При такой постановке исключается составляющая (10), соответствующая затратам на генерацию и ЦФ принимает вид:
Такое представлении соответствует математической модели (10) при нулевых параметрах $\left\{ {{{a}_{{G,i}}},{{b}_{{G,i}}}} \right\}$ характеристики затрат на генерацию. Рассматриваемую специфику задачи можно учесть с помощью соотношения (7). Однако это приводит к появлению нелинейности в системе ограничений, а, следовательно, к необходимости перехода к обобщенному нелинейному программированию.
СЕТЕВЫЕ ИНЪЕКЦИИ В КАЧЕСТВЕ УПРАВЛЯЮЩИХ ПЕРЕМЕННЫХ
Другим, чаще используемым в электроэнергетических расчетах вариантом управляющих переменных является вектор сетевых инъекций узлов, $\left\{ {{{u}_{i}}} \right\}.$ При этом реализующая критерий минимума суммарных эксплуатационных затрат, при ограничениях (2), (3), (5), целевая функция (10) должна быть представлена как функция управляющих переменных $u{\kern 1pt} :$
(15)
$F = \mathop {\min }\limits_{\mathbf{u}} \sum\limits_{i = 1}^n {\left( {{{{\text{З}}}_{{z,i}}}\left( {{{z}_{i}}\left( u \right)} \right) + {{{\text{З}}}_{{G,i}}}\left( {{{G}_{i}}\left( u \right)} \right)} \right)} .$Локальная оптимизация затрат. Для получения функциональных зависимостей ${\text{З}}\left( {{{z}_{i}}\left( {{{u}_{i}}} \right)} \right),~{\text{З}}\left( {{{G}_{i}}\left( {{{u}_{i}}} \right)} \right)$ требуется оптимальное распределение инъекций $\left\{ {{{u}_{i}}} \right\}~$ между переменными $\left\{ {{{G}_{i}},{{z}_{i}}} \right\}.$ Следует заметить, что согласно уравнению (1) узлового баланса мощности переменные $\left\{ {{{G}_{i}},{{z}_{i}}} \right\}$ функционально зависимы только от инъекции ${{u}_{i}},$ ${{G}_{i}} = {{G}_{i}}\left( {{{u}_{i}}} \right),$ ${{z}_{i}} = {{z}_{i}}\left( {{{u}_{i}}} \right).$ Отсюда может быть реализована поузловая оптимизация по критерию (15).
Распределение суммарного спроса мощности $\left( {{{{\bar {L}}}_{i}} - {{u}_{i}}} \right)~$ узла $i$ между генерацией ${{G}_{i}}$ и ограничением электропотребления ${{z}_{i}}$, которое рассматривается как дополнительная генерация, определяется по критерию минимума затрат на суммарную генерацию. Отсюда при заданном экспорте ${{u}_{i}}$ переменные ${{G}_{i}},{{z}_{i}}$ определяются однозначно решением задачи наивыгоднейшего распределения нагрузки $\left( {{{{\bar {L}}}_{i}} - {{u}_{i}}} \right)$ между источнками (${{G}_{i}},{{z}_{i}}.$) Известно [19], что ее решением является условие равенства относительных приростов затрат (индекс номера узла опущен, чтобы не загромождать математические выражения, которые идентичны для всех узлов $i = 1, \ldots ,n~$)
(16)
$\left( {{{\varepsilon }_{G}}(G) = \frac{{d{{{\text{З}}}_{G}}(G)}}{{dG}}} \right) = \left( {{{\varepsilon }_{z}}(z) = \frac{{d{{{\text{З}}}_{z}}(z)}}{{dz}}} \right) = \lambda .$При квадратичной форме обеих составляющих суммарных затрат в виде (8), (9) условие равенства относительных приростов (16) представляется в виде соотношения ${{a}_{g}} + {{b}_{g}}G = {{a}_{z}} + {{b}_{z}}z = \lambda ,$ из которого определяются
(17)
$G = {{\left( {\lambda - {{a}_{g}}} \right)} \mathord{\left/ {\vphantom {{\left( {\lambda - {{a}_{g}}} \right)} {{{b}_{g}}}}} \right. \kern-0em} {{{b}_{g}}}};\,\,\,\,z = {{\left( {\lambda - {{a}_{z}}} \right)} \mathord{\left/ {\vphantom {{\left( {\lambda - {{a}_{z}}} \right)} {{{b}_{z}}}}} \right. \kern-0em} {{{b}_{z}}}}.$Неопределенный множитель Лагранжа $\lambda $ определяется из уравнения баланса мощности (1):
Подставляя полученное выражение для $\lambda $ в (17), получаем соотношения
(18)
${\mathbf{G}} = {{{\mathbf{v}}}_{g}} - \left[ {{{\beta }_{{g,i}}}} \right]{\mathbf{u}};\,\,\,\,z = {{{\mathbf{v}}}_{z}} - \left[ {{{\beta }_{{z,i}}}} \right]{\mathbf{u}}{\text{,}}$(19)
$\begin{gathered} {{{\mathbf{v}}}_{g}} = \left[ {\frac{1}{{{{b}_{{g,i}}} + {{b}_{{z,i}}}}}} \right]\left( {\left[ {{{b}_{{z,i}}}} \right]{\mathbf{\bar {L}}} + {{{\mathbf{a}}}_{z}} - {{{\mathbf{a}}}_{g}}} \right);\,\,\,\,{{\beta }_{g}} = \left[ {\frac{1}{{{{b}_{{g,i}}} + {{b}_{{z,i}}}}}} \right]{{{\mathbf{b}}}_{z}}; \hfill \\ {{{\mathbf{v}}}_{z}} = \left[ {\frac{1}{{{{b}_{{g,i}}} + {{b}_{{z,i}}}}}} \right]\left( {\left[ {{{b}_{{g,i}}}} \right]{\mathbf{\bar {L}}} + {{{\mathbf{a}}}_{g}} - {{{\mathbf{a}}}_{z}}} \right);\,\,\,\,{{\beta }_{z}} = \left[ {\frac{1}{{{{b}_{{g,i}}} + {{b}_{{z,i}}}}}} \right]{{{\mathbf{b}}}_{g}}. \hfill \\ \end{gathered} $ЦФ (15) после подстановки (18) в (15) и неучете постоянной составляющей принимает вид квадратичной формы
(20)
$F = \min \left( {\frac{1}{2}{{{\mathbf{u}}}^{t}}H{\mathbf{u}} - {{{\mathbf{f}}}^{t}}{\mathbf{u}}} \right),$(21)
$H = \left[ {{{b}_{{g,i}}}\beta _{{g,i}}^{2} + {{b}_{{z,i}}}\beta _{{z,i}}^{2}} \right];\,\,\,\,{\mathbf{f}} = \left[ {{{\beta }_{{g,i}}}} \right]\left( {{{{\mathbf{a}}}_{g}} + \left[ {{{b}_{{g,i}}}} \right]{{{\mathbf{v}}}_{g}}} \right) + \left[ {{{\beta }_{{z,i}}}} \right]\left( {{{{\mathbf{a}}}_{z}} - \left[ {{{b}_{{z,i}}}} \right]{{{\mathbf{v}}}_{z}}} \right).$Таким образом, величины ${{G}_{i}},{{z}_{i}}$ однозначно и линейно определяются через инъекции ${{u}_{i}}$, а подстановка (19) в (18) не меняет квадратичных характер ЦФ (15). Однако наличие простых ограничений $0 \leqslant {{G}_{i}} \leqslant {{\bar {G}}_{i}},{\text{\;}}0 \leqslant {{z}_{i}} \leqslant {{\bar {L}}_{i}}$ нарушает вид квадратичной формы (20). Область управляющих переменных $\left( { - {{{\bar {G}}}_{i}} \leqslant {{u}_{i}} \leqslant {{{\bar {L}}}_{i}}} \right),$ в зависимости от ${{G}_{i}},~{{z}_{i}}$, делится на три области: $\left( {{{u}_{i}}|{{G}_{i}} \geqslant 0,~{{z}_{i}} = 0} \right);~\left( {{{u}_{i}}|{{G}_{i}} > 0,~{{z}_{i}} > 0} \right);~\left( {{{u}_{i}}|{{G}_{i}} = {{{\bar {G}}}_{i}},~{{z}_{i}} \geqslant 0} \right).$ Это предполагает алгоритмическое разделение ЦФ, а, следовательно, и переход к обобщенному нелинейному программированию. Другим известным подходом является введение новых непересекающихся переменных (в зависимости от принадлежности области), но в этом случае задача ОРДМ сводится к рассмотренному выше, достаточно эффективному варианту двух типов переменных $\left( {{{G}_{i}},~{{z}_{i}}} \right).$
Двузонная ЦФ. В частном случае, при нулевых характеристиках относительных приростов генерации (неучет характеристик эксплуатационных затрат генераторов), ${{{\mathbf{a}}}_{g}} = {{{\mathbf{b}}}_{g}} = 0$ вектор ${{{\mathbf{\beta }}}_{z}} = 0.$ При этом, согласно (21) матрица квадратичной формы, Н = 0. Это приводит к вырожденности структуры квадратичного программирования (20), где затраты на генерацию равны нулю. В результате теряет смысл распределение нагрузки между источниками генерации. Ограничение нагрузки происходит только тогда, когда генераторы загружены до предельной мощности. Данное условие может быть исходным ограничением (7) при постановке задачи ОРДМ. Учет этого условия в виде ограничения приводит к необходимости применения обобщенного нелинейного программирования.
Поскольку в рассматриваемой постановке либо ${{z}_{i}}\left( {{{u}_{i}}} \right) = 0,$ либо ${{G}_{i}}\left( {{{u}_{i}}} \right) = $ ${{\bar {G}}_{i}},$ то в зависимости от ${{u}_{i}}$ ЦФ и система ограничений нелинейного программирования алгоритмически разбивается на две зоны сетевых инъекций: $ - {{\bar {G}}_{i}} \leqslant {{u}_{i}} \leqslant {{u}_{{i0}}},$ где ${{G}_{i}} = {{\bar {G}}_{i}},$ и ${{u}_{{i0}}} \leqslant {{u}_{i}} \leqslant {{\bar {L}}_{i}}$, где ${{z}_{i}}\left( {{{u}_{i}}} \right) = 0.$ Здесь ${{u}_{0}} = {{\bar {L}}_{i}} - {{\bar {G}}_{i}}.$ В первой зоне ЦФ $F = {\text{min}}\sum {{{{\text{З}}}_{{z,i}}}} \left( {{{u}_{{i0}}} - {{u}_{i}}} \right),$ а во второй $F = {\text{min}}\sum {{{{\text{З}}}_{{G,i}}}\left( {{{{\bar {L}}}_{i}} - {{u}_{i}}} \right)} .$ Здесь, как и в случае трех зон, проявляется проблема позонного учета индивидуальности ЦФ. Введение двух дополнительных, зонально определенных, непересекающихся переменных не улучшает и не упрощает вариант двух переменных $\left( {{{G}_{i}},~{{z}_{i}}} \right).$
ПРОПОРЦИОНАЛЬНОСТЬ ВЫНУЖДЕННЫХ ОГРАНИЧЕНИЙ НАГРУЗКИ И ГЕНЕРАЦИИ
Наиболее часто используемым в задаче ОРДМ критерием оптимальности является распределение дефицита мощности пропорционально нагрузкам узлов [1, 4]. Этот критерий соответствует принципу справедливости и технологической реализуемости – при дефиците мощности происходит снижение частоты, которое автоматически приводит к снижению электропотребления согласно регулирующему эффекту нагрузки.
При неучете сетевых ограничений данный критерий реализуется достаточно просто:
Принцип пропорциональности может быть распространен на систему генерации при избытке генерирующей мощности (ограничение генерации осуществляется системой регулирования энергоблока в ответ на изменение частоты):
Учет системных ограничений (5)–(7) нарушает свойство пропорциональности. Возникают локальные дефициты или избытки мощности, вызванные невозможностью их перераспределения между остальными узлами ОЭС из-за ограниченной ПС МСС. Это вызывает изменение узловых инъекций на величину $\Delta {{u}_{i}} = u_{i}^{{{\text{new}}}} - {{u}_{{i0}}},~$ где ${{u}_{{i0}}}$ – инъекция, соответствующая системному балансу мощности, ${{u}_{{i0}}} = {{\mu }_{{\Sigma }}}{{\bar {L}}_{i}} - {{\bar {G}}_{i}}$ при отсутствии системных ограничений. При этом $\Delta {{u}_{i}}$ компенсируется за счет изменения генерации ($\delta {{G}_{i}} = - \Delta {{u}_{i}},$) или нагрузки $\left( {\delta {{L}_{i}} = \Delta {{u}_{i}}} \right).$ Критерию равенства относительных изменений нагрузки соответствует ЦФ:
Согласно приведенной ЦФ в качестве управляющих переменных принимаются или $\left\{ {\Delta {{L}_{i}}} \right\},$ при ${{\mu }_{{\Sigma }}} < 1,$ или $\left\{ {\Delta {{G}_{i}}} \right\},{\text{при}}\,\,{{\mu }_{{\Sigma }}} > 1.$
При линейной аппроксимации (13) потерь мощности в ОЭС ограничения по балансу мощностей ОЭС имеют вид:
(22)
$\begin{gathered} {{{\mathbf{v}}}^{t}}\Delta {\mathbf{L}} = {{{\mathbf{v}}}^{t}}({\mathbf{\bar {L}}} - {\mathbf{\bar {G}}}) - {{\pi }_{{\Sigma 0}}},\,\,\,\,{{\mu }_{\Sigma }} < 1; \hfill \\ {{{\mathbf{v}}}^{t}}\Delta {\mathbf{G}} = {{\pi }_{{\Sigma 0}}} - {{{\mathbf{v}}}^{t}}({\mathbf{\bar {L}}} - {\mathbf{\bar {G}}}),\,\,\,\,{{\mu }_{\Sigma }} \geqslant 1, \hfill \\ \end{gathered} $Ограничение по ПС МСС согласно (3) трансформируется к виду:
Сетевые инъекции. Инъекции и переменные $\left\{ {\Delta L,~\Delta G} \right\}~$ связаны соотношениями:
Отсюда, с таким же успехом в качестве критерия оптимизации можно принять минимум суммы квадратов отклонений инъекций от идеальных, полученных без учета системных ограничений, а в качестве управляющих переменных – сетевые инъекции. При этом ЦФ:
Нормирующие множители $\left\{ {{{L}_{i}}} \right\}$ введены с целью обеспечения пропорциональности сетевых инъекций нагрузке узлов.
Ограничения по балансу мощностей ОЭС имеют вид (14). Согласно (3), (4) ограничения по ПС МСС: ${{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P} }}}_{{br}}} \leqslant - C{\mathbf{u}} \leqslant {{{\mathbf{\bar {P}}}}_{{br}}}.$ Простые ограничения определяются условием (6).
Минимум отклонений коэффициентов избыточности. Критерий минимума суммы квадратов отклонений от единого для всех узлов идеального коэффициента, полученного без учета сетевых ограничений, в максимальной степени обеспечивает поставленную задачу пропорциональности распределения дефицитов и избытков генерирующей мощности ОЭС. Соответствующая данному критерию ЦФ может быть представлена (например, относительно $\mu $) в виде:
или, исключая постоянную составляющую,Аналогичный вид имеет ЦФ для $\eta .$ Однако переменные $\left\{ {{{\mu }_{i}}} \right\}~$или $\left\{ {{{\eta }_{i}}} \right\}$ участвуют в системных ограничениях лишь опосредованно, через сетевые инъекции $\left\{ {{{u}_{i}}} \right\}.$ Отсюда качестве управляющих переменных целесообразно принять инъекции $\left\{ {{{u}_{i}}} \right\}.$ При этом квадратичность ЦФ не нарушается. Не нарушается и линейность простых и функциональных ограничений.
При выборе $\left\{ {{{u}_{i}}} \right\}$ в качестве управляющих переменных ЦФ (23) имеет вид
Специфической особенностью рассматриваемого подхода является учет узлов, где находится только либо генерация, либо нагрузка. Если в узле отсутствует нагрузка (электростанции), то определяемый соотношением ${{\mu }_{i}} = {{\left( {{{{\bar {G}}}_{i}} + {{u}_{i}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\bar {G}}}_{i}} + {{u}_{i}}} \right)} {{{{\bar {L}}}_{i}}}}} \right. \kern-0em} {{{{\bar {L}}}_{i}}}}$ локальный коэффициент избыточности здесь равен бесконечности. В чисто нагрузочном узле $\left( {{{G}_{i}} = 0} \right)$ какое-либо регулирование генерации невозможно. Отсюда инъекции узлов упомянутого типа могут быть исключены из числа варьируемых переменных. Они определяются либо нагрузкой, либо генерацией.
Минимум суммы квадратов отклонений инъекций. Согласно определению $\left\{ {{{\mu }_{i}}} \right\}$ пропорциональны инъекциям узлов. Отсюда критерий минимального отклонения $\left\{ {{{\mu }_{i}}} \right\}$ от своих идеальных (без учета сетевых ограничений) значений эквивалентен критерию минимального отклонения сетевых инъекций $\left\{ {{{u}_{{i~}}}} \right\}~$от своих идеальных значений $\left\{ {{{u}_{{i0~}}}} \right\}.$ Отсюда в качестве целевой функции может быть принята сумма взвешенных квадратов отклонений ($\Delta {{u}_{i}} = {{u}_{i}} - {{u}_{{i0}}}$) инъекций):
Отбрасывая постоянную составляющую, ЦФ (20) можно записать в виде:
Расчет потерь выполняется путем аппроксимации (12) в точке, соответствующей идеальному режиму:
Подстановка данного выражения в (2) не меняет линейную форму ограничения:
В рассматриваемой постановке варьируемыми переменными являются сетевые инъекции $\left\{ {{{u}_{i}}} \right\}.$ При известной матрице сетевых коэффициентов (4) потоки мощности по связям пропорциональны управляющим переменным, ${\mathbf{x}} = C{\mathbf{u}}.$ При этом ограничение (3) по ПС связей не имеет специфических особенностей.
Генерация и ограничение нагрузки узла определяются вне оптимизационной процедуры согласно выражениям (18), (19). Ограничения на генерацию и снижение электропотребления (5) реализуются в виде простых ограничений на варьируемые переменные (экспорт не превышает располагаемую генерацию, а импорт – величину нагрузки):
Использование в качестве управляющих иных переменных, например, $\left( {{\mathbf{G}},z} \right)$ возможно, но не имеет каких-либо преимуществ, поскольку ЦФ зависит непосредственно от инъекций, а число переменных $\left( {{\mathbf{G}},z} \right)$ возрастает вдвое.
ПРОВЕРОЧНЫЕ РАСЧЕТЫ
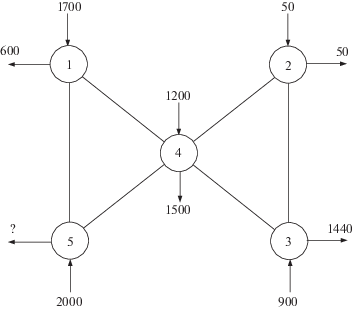
Апробирование рассмотренных методов выполнялось на тестовой схеме, представленной на рис. 1, где кроме топологии представлены МО нагрузки и генерации. СКО принято равными 10% от МО. МСС, пронумерованные в порядке {1-5; 1-4; 4-5; 2-4; 2-3; 3-4} МСС обладают сопротивлениями соответственно R = {10; 5; 5; 3; 1; 2}; Х = {100; 50; 50; 33; 10; 10}. Сопротивления необходимы для расчета потерь мощности и матрицы потокораспределения. Предельная ПС всех связей была принята равной 500 МВт. Расчеты выполнены методом статистических испытаний (Монте-Карло) с применением оптимизационной процедуры квадратичного программирования, основанной на методе внутренней точки, в среде MATHLAB, на ЭВМ с процессором Intel(R) Core(TM) i3-2100 CPU @ 3.10GHz 3.10GHz. Принятое число испытаний – 10 000. Расчеты показали, что при меньшем числе испытаний диапазон результирующих данных превышает 5%, что подтверждает [8].
В качестве основных критериев оптимизации рассматривались минимум суммарных затрат на производство и ограничение электроэнергии и пропорциональность ограничения электропотребления. При этом анализировались и сопоставлялись (табл. 1) описанные выше целевые функции: 1 – минимум среднеквадратичных отклонений сетевых инъекций от идеальных инъекций (при отсутствии сетевых ограничений); 2 – минимум среднеквадратичных отклонений от идеала коэффициентов загрузки; 3 – минимум затрат на производство электроэнергии и ограничение электропотребления. В качестве управляющих переменных рассматривались: А – сетевые инъекции; Б – текущие генерации и нагрузки; В – перетоки мощности по МСС.
Наиболее эффективным по длительности расчетов (28.8 с.) оказался подход, когда в качестве управляющих переменных принимались сетевые инъекции (тип А), а в качестве ЦФ принимались суммарные затраты (тип 3). Выбор в качестве управляющих векторов $\left\{ {{\mathbf{z}},{\mathbf{G}}} \right\}$ устойчиво эффективен при всех упомянутых комбинациях ЦФ, но наиболее эффективен для критерия “минимум затрат” (тип 3). Однако при необходимости управления балансом мощности одновременным изменением нагрузки и генерации суммарное ограничение мощности нагрузки увеличивается более, чем в 2 раза (согласно характеристикам относительных приростов затрат). Обнуление параметров характеристики затрат на генерацию приводит к исключению нагрузки из процесса регулирования и ограничение электропотребления происходит только тогда, когда мощность генерации выходит на свой максимальный предел. При таком искусственном приеме МО дефицита мощности становится тем, что приведен в табл. 1 при длительности расчетов 31.4 с. Выбор в качестве управляющих переменных перетоков мощности по МСС не эффективен из-за трехкратного увеличения длительности расчетов, что вызвано требованиями учета ограничений по величине сетевых инъекций и неоднозначностью функциональной связи “перетоки мощности-инъекции”.
Таблица 1.
Сравнение сочетаний ЦФ + управляющие переменные
| Сочетание: ЦФ + переменные | МО ограничения мощности в узлах | Т, сек | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| А + 1 | 0.21 | 0.09 | 2.05 | 2.61 | 4.48 | 99.1 |
| А + 2 | 0.27 | 0.04 | 2.26 | 13.40 | 4.43 | 99.3 |
| А + 3 | 0.20 | 0.09 | 2.05 | 2.77 | 4.78 | 28.8 |
| Б + 1 | 0.28 | 0.07 | 1.27 | 2.23 | 5.11 | 37.9 |
| Б + 2 | 0.27 | 0.07 | 1.16 | 2.08 | 5.07 | 32.4 |
| Б + 3 | 0.27 | 0.07 | 1.22 | 2.18 | 5.28 | 31.4 |
| В + 1 | 0.19 | 0.02 | 0.46 | 1.09 | 5.32 | 115 |
| В + 2 | 0.21 | 0.03 | 0.50 | 1.20 | 5.58 | 104 |
| В + 3 | 0.17 | 0.02 | 0.40 | 1.00 | 4.60 | 103.2 |
Таблица 2.
Результаты расчета тестовой схемы
| Узел | МО дефицита | Вер-ть дефицита | G, МВт | G, % | ЛКИ | Экспорт, МВт | МСС | Вер-ть перегрузки | МО загрузки |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.210 | 0.0123 | 1420 | 0.84 | 1.45 | 840 | b1-5 | 0.0035 | 393 |
| 2 | 0.090 | 0.0480 | 42 | 0.84 | 1.13 | –6 | b1-4 | 0.0923 | 447 |
| 3 | 2.015 | 0.0480 | 1223 | 0.85 | 1.21 | 354 | b4-5 | 0.0248 | 339 |
| 4 | 2.670 | 0.0503 | 996 | 0.83 | 1.11 | –456 | b2-4 | 0 | 66 |
| 5 | 4.590 | 0.0519 | 1230 | 0.82 | 1.11 | –708 | b2-3 | 0 | –72 |
| Всего | 9.576 | 1.20 | 24.0 | b3-4 | 0.0026 | 281 |
Усредненные (в результате нескольких повторов расчетной процедуры с априори отличающимися в методе статистического моделирования результатами ) результирующие поузловые данные представлены в табл. 2. Наименьшая вероятность ограничения мощности нагрузки (столбец “вер-ь ОМН”) наблюдается в избыточном узле 1. Все остальные узлы в силу специфики критерия пропорциональности имеют примерно одинаковую вероятность дефицита (с некоторым небольшим превышением в дефицитном узле 5). Все генераторы имеют примерно одинаковую относительную загрузку (столбец G%). Наиболее загруженной оказалась МСС 1–4 (447 МВт) с наибольшей вероятностью перегрузки (9.2%). Средние потери мощности в ОЭС составляют 24 МВт (столбец “экспорт”, “Всего”), что больше МО суммарного ограничения мощности нагрузки (9.576 МВт, столбец “МО дефицита”, “Всего”). Неучет потерь увеличивает суммарное ограничение нагрузки примерно на 30%.
ВЫВОДЫ
1. Предложенные комбинации целевых функций и управляющих переменных позволяют свести математическую модель нелинейного программирования при решении задачи оптимального распределения дефицита мощности в ОЭС к виду, приемлемому при использовании более эффективного квадратичного программирования.
2. Для адекватного отражения электрических свойств ОЭС, в том числе соответствия потоков мощности по МСС узловым инъекциям, необходим учет электрических параметров межсистемных связей. Математическая модель с матрицей потокораспределения обеспечивает выполнение неучитываемого ранее при расчетах ПБН ЭЭС закона Ома.
3. Неучет потерь мощности в электрической сети приводит к существенной погрешности результирующих показателей надежности. Их учет в виде квадратичной функции потоков мощности по МСС приводит к необходимости применения обобщенных процедур нелинейного программирования. Линейная аппроксимация потерь мощности позволяет использовать более эффективные процедуры квадратичного программирования.
4. Требования ограничения электропотребления только после использования всех генерирующих ресурсов учитывается введением дополнительного ограничения несовместимости областей определения управляющих переменных.
5. Наиболее универсальной и эффективной математической моделью ОРДМ по критерию минимальных затрат является квадратичная целевая функция затрат при выборе векторов $\left\{ {\Delta {\mathbf{L}},{\mathbf{G}}} \right\}$ в качестве управляющих переменных.
Список литературы
Дубицкий М.А., Руденко Ю.Н., Чельцов М.Б. Выбор и использование резервов генерирующей мощности в электроэнергетических системах. – М.: Энергоиздат, 1988. 272 с.
Endrenyi J. Reliability Modeling in Electric Power Systems. New York: John Wiley & Sons, 1979. 338 p.
Billinton R., Allan R.N. Reliability evaluation of power systems. New York: Plenum Press, 1996. 534 p.
Надежность систем энергетики и их оборудования. Спр. 4 т. / Под общей ред. Руденко Ю.Н. Т. 2. Надежность электроэнергетических систем. Справочник / Под ред. Розанова М.Н. – М.: Энергоатомиздат, 2000. 568 с.
Чукреев Ю.Я. Модели обеспечения надежности электроэнергетических систем. Сыктывкар: Изд-во Коми НЦ УрО РАН, 1995.
Чукреев Ю.Я., Чукреев М.Ю. Модели оценки показателей балансовой надежности при управлении развитием электроэнергетических систем. Сыктывкар: Коми научный центр УрО РАН, 2014. 207 с.
Ковалев Г.Ф., Лебедева Л.М. Надежность систем электроэнерегтики. Новосибирск: Сибирская издательская фирма “Наука” Академиздатцентра “Наука,” 2015.
Обоскалов В.П., Валиев Р.Т. Риск превышения пропускной способности межсистемных связей в задаче балансовой надежности ЭЭС / Изв. РАН. Энергетика 2018, № 5, с. 3–14
Mid-term Adequacy Forecast 2016 edition [Электронный ресурс] – Режим доступа: https://www.entsoe.eu/Documents/SDC%20documents/MAF/ENSTOE_MAF_2016.pdf
2016 Probabilistic Assessment [Электронный ресурс]: офиц. сайт. – Режим доступа: https://www.nerc.com/comm/PC/PAWG%20DL/2016%20Probabilistic%20Assessment.pdf
Зоркальцев В.И., Пержабинский С.М. Модели оценки дефицита мощности электроэнергетической системы // Сибирский журнал индустриальной математики 2012, № 1 (49).
Зоркальцев В.И., Ковалев Г.Ф., Лебедева Л.М., Пержабинский С.М. Минимизация дефицита мощности в ЭЭС с учетом потерь мощности в линиях электропередачи // Электричество. 2010, №9, С. 56–60.
Электротехнический справочник: в 4 т. Т. 3. Производство, передача и распределение электрической энергии. Под. Общ. Ред. Герасимова В.Г. – М.: Изд. МЭИ, 2004, 964 с.
Непомнящий В.А. Учет надежности при проектировании энергосистем. – М.: Энергия. 1978, 200 с.
Руденко Ю.Н., Ушаков И.А. Надежность систем энергетики. – М.: Наука, 1986. 252 с.
Чукреев Ю.Я. Сравнение отечественных и зарубежных вероятностных показателей балансовой надежности электроэнергетических систем. / Изв. РАН. Энергетика. 2012. № 6, С. 27–37.
Форд Л., Фалкерсон Д. Потоки в сетях. – М.: Мир. 1966.
Горнштейн В.М. Наивыгоднейшее распределение нагрузок между параллельно работающими электростанциями. М.: Госэнергоиздат, 1949.
Справочник по проектировнию электрических сетей / Под ред. Файбисовича Д.Л. // Москва: ЭНАС, 2012. 376 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика