Известия РАН. Энергетика, 2020, № 3, стр. 69-80
Применение суперпозиции независимых полумарковских процессов и скрытых марковских моделей к моделированию систем энергетики
Ю. Е. Обжерин 1, *, С. М. Сидоров 1, **, М. М. Никитин 1, ***
1 Федеральное государственное автономное образовательное учреждение высшего образования
“Севастопольский государственный университет”
Севастополь, Россия
* E-mail: objsev@mail.ru
** E-mail: xaevec@mail.ru
*** E-mail: m.nikitin.1979@gmail.com
Поступила в редакцию 26.02.2020
После доработки 22.05.2020
Принята к публикации 28.05.2020
Аннотация
Одними из основных задач теории и практики систем энергетики являются задачи создания информационных систем управления системами энергетики и переход к интеллектуальному управлению и инжинирингу. Решение этих задач возможно на основе построения математических моделей, касающихся различных аспектов структуры и функционирования этих систем. В работе рассматриваются возможности применения суперпозиции независимых полумарковских процессов, построенной в работах В.С. Королюка, А.Ф. Турбина, для моделирования систем энергетики и нахождения их характеристик. На примере суперпозиции двух независимых альтернирующих процессов восстановления рассмотрена возможность использования теории скрытых марковских моделей для уточнения модели, анализа динамики, и прогнозирования состояний систем энергетики на основе данных, полученных при функционировании системы.
ВВЕДЕНИЕ
Одними из задач теории и практики энергетики являются:
1. создание цифровых сетей, цифровых подстанций;
2. разработка информационных систем управления системами энергетики и переход к интеллектуальному управлению и инжинирингу.
Решение этих задач возможно на основе построения математических моделей, касающихся различных аспектов структуры и функционирования систем энергетики, и разработки на их основе алгоритмов и информационных систем поддержки принятия решений при проектировании и эксплуатации систем энергетики, а также прогнозирования их состояний.
Для моделирования систем различного назначения, в том числе систем энергетики, широко используются полумарковские процессы [1–8]. Исследования по этому направлению проводятся активно, в последние годы опубликовано несколько монографий по этой тематике [4, 6–8].
Полумарковские процессы могут быть эффективно использованы для построения моделей, касающихся различных аспектов структуры и функционирования систем энергетики: надежности, эффективности, контроля, диагностики и технического обслуживания [9–12].
В процессе функционирования системы, для которой построена полумарковская модель, необходимо определить, насколько хорошо построенная модель согласуется с результатами функционирования системы, провести анализ динамики и найти прогноз для состояний и характеристик системы. Одним из подходов к решению этих задач является использование теории скрытых марковских [13–16] и скрытых полумарковских [17–20] моделей.
Важной частью полумарковского процесса является вложенная цепь Маркова (ВЦМ), которая отвечает за переходы между состояниями системы. Фазовое пространство ВЦМ совпадает с фазовым пространством состояний полумарковского процесса. При функционировании систем, для которых построена полумарковская модель, не всегда удается при изменении ее состояний полностью получить информацию, содержащуюся в кодировке состояний, а есть только возможность получить некоторый сигнал (информацию), связанный с состояниями ВЦМ. Например, в фазовом пространстве состояний для каждого элемента системы указано находится он в рабочем состоянии или на восстановлении, а при функционировании системы можно получить сигнал только о числе работоспособных элементов системы. В некоторых случаях можно получить сигнал, только в каком блоке элементов системы произошло изменение состояния, без указания элемента, в котором произошло изменение состояния. В таких случаях состояния ВЦМ и полумарковского процесса можно считать скрытыми (ненаблюдаемыми). Возникают задачи уточнения параметров полумарковской модели, нахождения оценок характеристик системы и прогнозирования ее состояний на основе полученного вектора сигналов. Как отмечено ранее, для решения этих задач можно использовать аппарат теории скрытых марковских и полумарковских моделей.
В данной работе рассматриваются возможности применения суперпозиции независимых полумарковских процессов, построенной в работах В.С. Королюка, А.Ф. Турбина и их учеников [1, 5], для моделирования систем энергетики и нахождения их характеристик.
В работах [1, 2] построена суперпозиция независимых альтернирующих процессов восстановления, которая является частным случаем суперпозиции независимых полумарковских процессов. В данной работе на примере суперпозиции двух независимых альтернирующих процессов восстановления (дублированной системы) рассматривается возможность использования теории скрытых марковских моделей для анализа динамики, оценки характеристик и прогнозирования состояний систем энергетики на основе данных, полученных при функционировании системы.
Вначале, используя алгоритм стационарного фазового укрупнения [1, 2], строится укрупненная полумарковская модель этой системы. Далее для укрупненной полумарковской модели рассматривается скрытая марковская модель, построенная на основе сигналов о числе работоспособных элементов системы. Для укрупненной модели, используя построенную скрытую марковскую модель, решаются задачи уточнения модели, анализа динамики системы и прогнозирования ее состояний на основе полученного вектора сигналов.
1. ОПИСАНИЕ СУПЕРПОЗИЦИИ НЕЗАВИСИМЫХ ПОЛУМАРКОВСКИХ ПРОЦЕССОВ
Рассмотрим полумарковскую модель суперпозиции независимых полумарковских процессов, следуя работам [1, 5].
Система состоит из N независимых элементов (подсистем), функционирование каждого из которых описывается полумарковским процессом ${{\xi }^{{(i)}}}(t)$ с произвольным фазовым пространством ${{Z}^{{(i)}}},$ $i = \overline {1,N} .$
Для каждого ${{Z}^{{(i)}}}$ имеет место разбиение ${{Z}^{{(i)}}} = Z_{1}^{{(i)}} \cup Z_{0}^{{(i)}},$ $Z_{1}^{{(i)}} \cap Z_{0}^{{(i)}} \ne \emptyset ,$ $i = \overline {1,N} ,$ где $Z_{1}^{{(i)}}$ интерпретируется как множество работоспособных состояний i-го элемента (подсистемы), $Z_{0}^{{(i)}}$ – множество отказовых состояний i-го элемента (подсистемы).
Пусть
Векторный процесс $\varsigma (t)$ характеризует состояния системы в момент времени t по состояниям работоспособности или неработоспособности ее элементов (подсистем). Множество возможных значений процесса $\varsigma (t)$ есть множество двоичных векторов $\bar {d} = \left( {{{d}_{1}},{{d}_{2}},..., {{d}_{N}}} \right)$ от (00…0) до (11…1), обозначим его $D = \left\{ {\bar {d}} \right\}.$
Рассмотрим понятие отказа системы: на множестве значений двоичных векторов D задается функция $g(\bar {d})$ такая что:
Обозначим множество значений вектора $\bar {d},$ при которых система работоспособна, ${{D}_{1}},$ а множество значений, при которых система неработоспособна, ${{D}_{0}},$ т.е. ${{D}_{1}} = \left\{ {\bar {d}:g(\bar {d}) = 1} \right\},$ ${{D}_{0}} = \left\{ {\bar {d}:g(\bar {d}) = 0} \right\},$ по предположению, $D = {{D}_{1}} \cup {{D}_{0}},$ ${{D}_{1}} \cap {{D}_{0}} \ne \emptyset .$
В [1, 5] построена суперпозиция независимых ПМП ${{\xi }^{{(i)}}}(t),$ $i = \overline {1,N} $ и показано, что средняя стационарная наработка на отказ ${{T}_{1}},$ среднее стационарное время восстановления T0 и стационарный коэффициент готовности ${{K}_{{\text{Г}}}}$ суперпозиции могут быть определены по следующим формулам:
(1)
${{T}_{1}} = \sum\limits_{\bar {d} \in {{D}_{1}}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}{{{\left\{ {\sum\limits_{\bar {d} \in D_{1}^{'}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}} \sum\limits_{j \in G(\bar {d})} {\frac{1}{{T_{1}^{{(j)}}}}} } } \right\}}}^{{ - 1}}}} } = \sum\limits_{\bar {d} \in {{D}_{1}}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}{{{\left\{ {\sum\limits_{\bar {d} \in D_{0}^{'}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}} \sum\limits_{j \in I(\bar {d})} {\frac{1}{{T_{0}^{{(j)}}}}} } } \right\}}}^{{ - 1}}}} } ,$(2)
${{T}_{0}} = \sum\limits_{\bar {d} \in {{D}_{0}}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}{{{\left\{ {\sum\limits_{\bar {d} \in D_{1}^{'}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}} \sum\limits_{j \in G(\bar {d})} {\frac{1}{{T_{1}^{{(j)}}}}} } } \right\}}}^{{ - 1}}}} } = \sum\limits_{\bar {d} \in {{D}_{0}}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}{{{\left\{ {\sum\limits_{\bar {d} \in D_{0}^{'}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}} \sum\limits_{j \in I(\bar {d})} {\frac{1}{{T_{0}^{{(j)}}}}} } } \right\}}}^{{ - 1}}}} } ,$(3)
${{K}_{\Gamma }} = \sum\limits_{\bar {d} \in {{D}_{1}}} {\prod\limits_{i = 1}^N {T_{{{{d}_{i}}}}^{{(i)}}{{{\left\{ {\prod\limits_{i = 1}^N {\left( {T_{1}^{{(i)}} + T_{0}^{{(i)}}} \right)} } \right\}}}^{{ - 1}}}} } ,$${{D}_{0}}$ – множество векторов $\bar {d} \in {{D}_{0}}$ таких, что изменение значения некоторой одной компоненты с нуля на единицу переводит вектор $\bar {d}$ в множество ${{D}_{1}}$ ($D_{0}^{'}$ – множество пограничных отказовых состояний системы);
$G(\bar {d})$ – множество номеров компонент вектора $\bar {d} \in D_{1}^{'},$ изменение значения каждой из которых с единицы на ноль переводит вектор $\bar {d}$ во множество ${{D}_{0}}$;
$I(\bar {d})$ – множество номеров компонент вектора $\bar {d} \in D_{0}^{'},$ изменение значения каждой из которых с нуля на единицу переводит вектор $\bar {d}$ во множество $D_{1}^{'}$.
В [5] показано, что формулы (1)–(3) могут быть использованы для непосредственного вычисления показателей надежности различных типовых структур, а также, используя эти формулы и алгоритм поэтапного структурного укрупнения [5], можно находить характеристики надежности систем с большим числом элементов (подсистем).
При использовании формул (1)–(3) можно учитывать наличие ненагруженного резерва, проведение контроля, техническое обслуживание, наличие резерва времени и т.д. Для этого нужно найти соответствующие выражения для T1, T0 элементов (подсистем), например, в [5, 6, 11, 12] и использовать их в формулах (1)–(3). В работе [5] приведены приближенные формулы для T1, T0, KГ, справедливые при условии быстрого восстановления элементов системы. Используя построенную в [5] полумарковскую модель суперпозиции и найденное там стационарное распределение вложенной цепи Маркова, можно найти и другие характеристики системы, в том числе определяющие эффективность функционирования системы.
2. ПРИМЕР МОДЕЛИРОВАНИЯ СИСТЕМЫ ЭЛЕКТРОЭНЕРГЕТИКИ
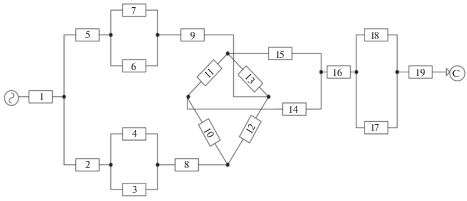
В качестве иллюстративного примера применения формул (1)–(3) для моделирования систем электроэнергетики найдем характеристики надежности электроэнергетической системы, структурная схема которой представлена на рис. 1, а показатели надежности ее элементов содержатся в табл. 1.
Таблица 1.
Показатели надежности элементов электроэнергетической системы
| № | Элементы системы | T+, г. | T– , г. | KΓ |
|---|---|---|---|---|
| 1 | Выходная шина электростанции | 3.0 | 0.04 | 0.9868 |
| 2 | Входная шина подстанции A | 1.5 | 0.031 | 0.9797 |
| 3 | Трансформатор 1 подстанции А | 1.7 | 0.027 | 0.9843 |
| 4 | Трансформатор 2 подстанции A | 0.9 | 0.033 | 0.9646 |
| 5 | Входная шина подстанции B | 2.1 | 0.02 | 0.9906 |
| 6 | Трансформатор 1 подстанции B | 1.1 | 0.018 | 0.9839 |
| 7 | Трансформатор 2 подстанции B | 1.5 | 0.01 | 0.9934 |
| 8 | Выходная шина подстанции A | 1.4 | 0.014 | 0.9901 |
| 9 | Выходная шина подстанции B | 1.3 | 0.017 | 0.9871 |
| 10 | Выключатель | 0.5 | 0.037 | 0.9311 |
| 11 | Выключатель | 0.36 | 0.016 | 0.9574 |
| 12 | Выключатель | 0.6 | 0.025 | 0.9600 |
| 13 | Выключатель | 0.8 | 0.015 | 0.9816 |
| 14 | Линия электропередачи | 1.2 | 0.0014 | 0.9988 |
| 15 | Линия электропередачи | 2.1 | 0.0015 | 0.9993 |
| 16 | Входная шина подстанции С | 0.5 | 0.028 | 0.9470 |
| 17 | Трансформатор 1 подстанции С | 1.0 | 0.021 | 0.9794 |
| 18 | Трансформатор 2 подстанции С | 1.1 | 0.024 | 0.9786 |
| 19 | Выходная шина подстанции С | 2.0 | 0.009 | 0.9955 |
Нахождение характеристик рассматриваемой системы с использованием формул (1)–(3) осуществляется по следующей схеме:
1. Параллельные элементы 3, 4, а также 6, 7 укрупняются до одного элемента.
2. Последовательные элементы 2, 8 и результат укрупнения 3 и 4, а также 5, 9 и результат укрупнения 6 и 7 укрупняются до одного элемента.
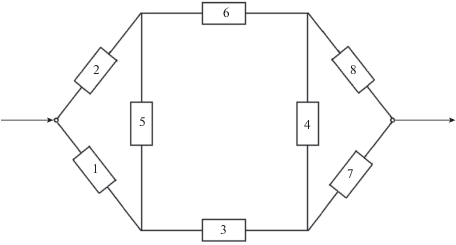
В результате получим укрупненную подсистему, структурная схема которой представлена на рис. 2.
На рисунке 2 элемент 1 соответствует результату укрупнения элементов 2, 3, 4, 8 исходной схемы, элемент 2 – результату укрупнения элементов 5, 6, 7, 9 исходной схемы. Элементы 3–8 соответствуют элементам 10–15 исходной схемы. Характеристики надежности полученной укрупненной подсистемы представлены в табл. 2.
Таблица 2.
Показатели надежности элементов укрупненной подсистемы
| Элементы подсистемы | T+, г. | T– , г. | KΓ |
|---|---|---|---|
| 1 | 0.7051 | 0.02217 | 0.9695 |
| 2 | 0.7924 | 0.01809 | 0.9777 |
| 3 | 0.5000 | 0.03700 | 0.9311 |
| 4 | 0.3600 | 0.01600 | 0.9574 |
| 5 | 0.6000 | 0.02500 | 0.9600 |
| 6 | 0.8000 | 0.01500 | 0.9816 |
| 7 | 1.2000 | 0.001400 | 0.9988 |
| 8 | 2.1000 | 0.001500 | 0.9993 |
3. В результате применения к подсистеме формул (1)–(3), (множество D1 содержит 84 вектора, D0 – 172 вектора), получим характеристики надежности подсистемы T+ = = 4.978 г., T– = 0.01013 г., Kг = 0.9980.
4. Подсистема из параллельных элементов 17–18 укрупняется до одного элемента, для нее получаем T+ = 25.4911 г., T– = 0.01120 г., KГ = 0.9996.
5. Представив исходную систему в виде последовательного соединения двух рассчитанных ранее подсистем между собой и с элементами 1, 16 и 19 исходной системы, укрупним их до одного элемента с характеристиками надежности
T+ = 0.3254 г., T– = 0.02523 г., KГ = 0.9280.
Таким образом, для рассматриваемой системы
T+ = 0.3254 г., T– = 0.02523 г., KГ = 0.9280.
Такой же результат для KГ рассматриваемой системы получается методом структурных функций [11].
3. ПОСТРОЕНИЕ УКРУПНЕННОЙ ПОЛУМАРКОВСКОЙ МОДЕЛИ
Опишем, следуя [1, 2], суперпозицию двух альтернирующих процессов восстановления. Рассматривается система S, состоящая из двух элементов K1 и K2. Каждый из элементов системы может находиться в двух состояниях: рабочем или на восстановлении. Времена безотказной работы элементов K1, K2 – случайные величины (СВ) ${{\alpha }_{i}}$ с функциями распределения (ФР) ${{F}_{i}}(t),$ а времена восстановления элементов – СВ ${{\beta }_{i}}$ с ФР ${{G}_{i}}(t),$ $i = 1,2.$ СВ ${{\alpha }_{i}},$ ${{\beta }_{i}},$ предполагаются независимыми в совокупности, имеющими конечные математические ожидания. Функционирование каждого элемента описывается альтернирующим процессом восстановления [1, 2], а функционирование всей системы S описывается суперпозицией двух независимых альтернирующих процессов восстановления. Предполагается, что элементы K1, K2 соединены параллельно.
В работах [1, 2] для построения полумарковской модели системы $S$ используется полумарковский процесс $\xi (t)$ с дискретно-непрерывным фазовым пространством состояний вида:
где $i = 1,2$ – номер элемента, в котором произошло изменение состояния. Координата ${{d}_{k}}$ вектора $\bar {d}$ описывает физическое состояние элемента с номером k:В [1] показано, что стационарное распределение ВЦМ суперпозиции имеет следующий вид:
(5)
$\begin{gathered} \rho (111x) = \rho (101x) = {{\rho }_{0}}{{{\bar {F}}}_{2}}(x),\,\,\,\,\rho (110x) = \rho (100x) = {{\rho }_{0}}{{{\bar {G}}}_{2}}(x), \\ \rho (211x) = \rho (210x) = {{\rho }_{0}}{{{\bar {F}}}_{1}}(x),\,\,\,\,\rho (201x) = \rho (200x) = {{\rho }_{0}}{{{\bar {G}}}_{1}}(x), \\ {{{\bar {F}}}_{i}}(x) = 1 - {{F}_{i}}(x),\,\,\,\,{{{\bar {G}}}_{i}}(x) = 1 - {{G}_{i}}(x), \\ \end{gathered} $Средняя стационарная наработка на отказ ${{Т}_{ + }},$ среднее стационарное время восстановления ${{Т}_{ - }}$ и стационарный коэффициент готовности ${{K}_{{\text{Г}}}}$ системы S (параллельное соединение элементов) равны [1]:
(6)
$\begin{gathered} {{Т}_{ + }} = \frac{{М{{\alpha }_{1}}М{{\alpha }_{2}} + М{{\alpha }_{1}}М{{\beta }_{2}} + М{{\beta }_{1}}М{{\alpha }_{2}}}}{{М{{\beta }_{1}} + М{{\beta }_{2}}}},\,\,\,\,{{Т}_{ - }} = \frac{{М{{\beta }_{1}}М{{\beta }_{2}}}}{{М{{\beta }_{1}} + М{{\beta }_{2}}}}, \\ {{К}_{{\text{Г}}}} = \frac{{{{Т}_{ + }}}}{{{{Т}_{ + }} + {{Т}_{ - }}}} = \frac{{М{{\alpha }_{1}}М{{\alpha }_{2}} + М{{\alpha }_{1}}М{{\beta }_{2}} + М{{\beta }_{1}}М{{\alpha }_{2}}}}{{М{{\alpha }_{1}}М{{\alpha }_{2}} + М{{\alpha }_{1}}М{{\beta }_{2}} + М{{\beta }_{1}}М{{\alpha }_{2}} + М{{\beta }_{1}}М{{\beta }_{2}}}}. \\ \end{gathered} $С целью упрощения модели системы S, построим укрупненную полумарковскую модель системы, используя алгоритм стационарного фазового укрупнения, предложенный в [1, 2]. Фазовое пространство состояний E исходной модели разобьем на N = 4 класса:
Опишем физический смысл, введенных классов состояний: ${{Е}_{{11}}}$ – оба элемента работоспособны; ${{Е}_{{10}}}$ – первый элемент работоспособен, второй восстанавливается; ${{Е}_{{01}}}$ – первый элемент восстанавливается, второй работоспособен; ${{Е}_{0}}$ – оба элемента восстанавливаются.
Определим вероятности перехода ВЦМ ${{\hat {p}}_{{kr}}}$ и средние времена пребывания в состояниях ${{\hat {m}}_{k}}$ укрупненной модели, которые согласно [1, 2] находятся по формулам:
(7)
${{\hat {p}}_{{kr}}} = \int\limits_{{{Е}_{к}}} {{{\rho (de)P(e,{{E}_{r}})} \mathord{\left/ {\vphantom {{\rho (de)P(e,{{E}_{r}})} {\rho ({{Е}_{к}})}}} \right. \kern-0em} {\rho ({{Е}_{к}})}}} ,\,\,\,\,k,r = \overline {1,N} ,$(8)
${{\hat {m}}_{k}} = М{{\hat {\theta }}_{k}} = \int\limits_{{{Е}_{к}}} {{{\rho (de)m(e)} \mathord{\left/ {\vphantom {{\rho (de)m(e)} {\rho ({{Е}_{к}})}}} \right. \kern-0em} {\rho ({{Е}_{к}})}}} ,\,\,\,\, k = \overline {1,N} ,$Используя формулу (7) и полумарковскую модель системы S, приведенную в [1, 2], найдем вероятности перехода ВЦМ укрупненной модели, которые будут использованы при построении скрытой марковской модели:
(9)
$\begin{gathered} P_{{11}}^{{10}} = \frac{{M{{\alpha }_{1}}}}{{M{{\alpha }_{1}} + M{{\alpha }_{2}}}},\,\,\,\,P_{{11}}^{{01}} = \frac{{M{{\alpha }_{2}}}}{{M{{\alpha }_{1}} + M{{\alpha }_{2}}}},\,\,\,\,P_{{10}}^{{11}} = \frac{{M{{\alpha }_{1}}}}{{M{{\alpha }_{1}} + M{{\beta }_{2}}}}, \\ P_{{10}}^{{00}} = \frac{{M{{\beta }_{2}}}}{{M{{\alpha }_{1}} + M{{\beta }_{2}}}},\,\,\,\,P_{{01}}^{{11}} = \frac{{M{{\alpha }_{2}}}}{{M{{\alpha }_{2}} + M{{\beta }_{1}}}},\,\,\,\,P_{{01}}^{{00}} = \frac{{M{{\beta }_{1}}}}{{M{{\alpha }_{2}} + M{{\beta }_{1}}}}, \\ P_{{00}}^{{10}} = \frac{{M{{\beta }_{2}}}}{{M{{\beta }_{1}} + M{{\beta }_{2}}}},\,\,\,\,P_{{00}}^{{01}} = \frac{{M{{\beta }_{1}}}}{{M{{\beta }_{1}} + M{{\beta }_{2}}}}. \\ \end{gathered} $Используя формулу (8), определим средние времена пребывания в состояниях укрупненной модели:
(10)
$\begin{gathered} {{m}_{{11}}} = \frac{{M{{\alpha }_{1}}M{{\alpha }_{2}}}}{{M{{\alpha }_{1}} + M{{\alpha }_{2}}}},\,\,\,\,{{m}_{{10}}} = \frac{{M{{\alpha }_{1}}M{{\beta }_{2}}}}{{M{{\alpha }_{1}} + M{{\beta }_{2}}}},\,\,\,\,{{m}_{{01}}} = \frac{{M{{\alpha }_{2}}M{{\beta }_{1}}}}{{M{{\alpha }_{2}} + M{{\beta }_{1}}}}, \\ {{m}_{{00}}} = \frac{{M{{\beta }_{1}}M{{\beta }_{2}}}}{{M{{\beta }_{1}} + M{{\beta }_{2}}}}. \\ \end{gathered} $Отметим, что укрупненная модель также является полумарковской, а формулы (9)–(10) инвариантны относительно законов распределения СВ ${{\alpha }_{1}},$ ${{\alpha }_{2}},$ ${{\beta }_{1}},$ ${{\beta }_{2}}.$
4. СКРЫТАЯ МАРКОВСКАЯ МОДЕЛЬ УКРУПНЕННОЙ ПОЛУМАРКОВСКОЙ МОДЕЛИ
Пусть $\{ {{X}_{n}},\,\, n = 1,2,...\} $ – ВЦМ укрупненной модели, вероятности переходов которой определяются формулами (9). В начальный момент времени укрупненная модель находится в состоянии 11.
Предположим, что при функционировании системы S состояния ВЦМ укрупненной модели не наблюдаются (скрытые состояния), а наблюдается только число работоспособных элементов системы S в момент перехода системы в новое состояние. Следовательно, множество сигналов имеет вид:
J = {0, 1, 2}.
Рассмотрим связь между состояниями ВЦМ укрупненной модели и сигналами, т.е. определим функцию связи $R(s{\text{|}}x)$ [15, 16]:
(11)
$R(s{\text{|}}x) = P({{S}_{n}} = s{\text{|}}{{X}_{n}} = x),\,\,\,\,x \in \hat {E},\,\,\,\,s \in J,\,\,\,\,\sum\limits_{s \in J} {R(s{\text{|}}x) = 1} ,$Функция $R(s{\text{|}}x)$ связи состояний ВЦМ укрупненной модели с сигналами представлена в табл. 3.
Таблица 3.
Функция связи $R(s{\text{|}}x)$ состояний ВЦМ укрупненной модели с сигналами
| Состояние, x | Сигнал, s | ||
|---|---|---|---|
| s = 0 | s = 1 | s = 2 | |
| 11 | 0 | 0 | 1 |
| 01 | 0 | 1 | 0 |
| 10 | 0 | 1 | 0 |
| 00 | 1 | 0 | 0 |
Таким образом, построенная скрытая марковская модель зависит от четырех параметров Mα1, Mα2, Mβ1, Mβ2, при этом Mβ1 и Mβ2 считаются постоянными (определенными на основе нормативных документов).
5. АНАЛИЗ ДИНАМИКИ УКРУПНЕННОЙ ПОЛУМАРКОВСКОЙ МОДЕЛИ
Следуя [15, 16], перейдем к анализу укрупненной полумарковской модели на основе построенной скрытой марковской модели.
Пусть ${{\bar {S}}^{n}} = ({{S}_{1}},{{S}_{2}},...,{{S}_{n}})$ – случайный вектор первых n сигналов. Для заданного вектора сигналов ${{\bar {s}}_{n}} = ({{s}_{1}},{{s}_{2}},...,{{s}_{n}})$ пусть ${{\bar {s}}_{k}} = ({{s}_{1}},{{s}_{2}},...,{{s}_{k}}),$ $k \leqslant n.$ Требуется оценить характеристики ВЦМ укрупненной (скрытой) модели на основе вектора сигналов ${{\bar {s}}_{n}}.$ Предполагается, что в начальный момент времени модель находится в состоянии 11.
Введем функции ${{F}_{k}}(i)$ [15, 16]:
которые называются прямыми переменными. Для этих функций справедлива следующая рекуррентная формула [15, 16]:(13)
${{F}_{k}}(i) = R({{s}_{k}}{\text{|}}i)\sum\limits_j {{{F}_{{k - 1}}}(j)P_{j}^{i}} ,\,\,\,\,{{F}_{1}}(i) = R({{s}_{1}}{\text{|}}i){{p}_{i}},$Рассмотрим также функции ${{B}_{k}}(i)$ [15, 16], которые называются обратными переменными:
Перейдем к анализу динамики укрупненной полумарковской модели на основе построенной скрытой марковской модели.
Рассмотрим систему S, у которой перед началом ее функционирования принято, что Mα1 = 10 ч, Mβ1 = 0.3 ч, Mα2 = 15 ч, Mβ2 = 0.2 ч (Mβ1, Mβ2 считаются постоянными).
Предположим, что в результате функционирования системы S получен следующий вектор сигналов:
Вначале, используя алгоритм Баума–Велша [16], определим параметры скрытой марковской модели, которые наиболее согласуются с полученным вектором сигналов. В результате применения этого алгоритма получаем, что с полученным вектором сигналов наиболее согласуются следующие значения параметров: Mα1 = 3.001 ч, Mα2 = 4.501 ч.
Рассмотрим другие задачи по оценке характеристик скрытой марковской модели с учетом уточненных параметров.
1. Определим вероятности состояний скрытой модели в момент испускания 30-го сигнала. Воспользуемся формулой [15, 16]:
(14)
$P\left( {{{X}_{n}} = i{\text{|}}{{{\bar {S}}}^{n}} = {{{\bar {s}}}_{n}}} \right) = \frac{{{{F}_{n}}(i)}}{{\sum\limits_j {{{F}_{n}}(j)} }}.$В результате получаем, что на 30-ом шаге укрупненная модель с вероятностью 0.400 находилась в состоянии 10 и с вероятностью 0.600 в состоянии 01. Для состояний 11, 00 эта вероятность равна нулю.
2. Найдем вероятности, с которыми скрытая модель осуществит переход в состояния на следующем 31-ом шаге. Для этого используем формулу [15, 16]:
(15)
$P({{X}_{{n + 1}}} = j{\text{|}}{{\bar {s}}_{n}}) = \sum\limits_i {P({{X}_{n}} = i{\text{|}}{{{\bar {s}}}_{n}})P_{i}^{j}} .$Получаем следующие вероятности перехода скрытой модели на 31-ом шаге: в состояние 11 с вероятностью 0.938; в состояние 00 – 0.062; для состояний 10, 01 эта вероятность равна нулю.
3. Определим вероятности появления сигналов на следующем 31-ом шаге, применим формулу [15]:
(16)
$P({{S}_{{n + 1}}} = {{s}_{{n + 1}}}{\text{|}}{{\bar {s}}_{n}}) = \sum\limits_i {P({{X}_{{n + 1}}} = i{\text{|}}{{{\bar {s}}}_{n}})R\left( {{{s}_{{n + 1}}}{\text{|}}i} \right)} ,$Получаем, что вероятность появления сигнала 2 на 31-м шаге равна 0.938; сигнала 1 – 0; сигнала 0 – 0.062.
4. Найдем вероятность появления (испускания) полученного вектора сигналов ${{\bar {s}}_{{30}}}.$
Для этого можно использовать формулы [15, 16]:
(17)
$P\left( {{{{\bar {S}}}^{n}} = {{{\bar {s}}}_{n}}} \right) = \sum\limits_i {{{F}_{n}}(i)} = \sum\limits_i {R({{s}_{1}}{\text{|}}i){{B}_{1}}(i)} {{p}_{i}},$Вероятность появления полученного вектора сигналов ${{\bar {s}}_{{30}}}$ при уточненных параметрах системы S равна 0.027.
5. Прогнозирование состояний скрытой модели по заданному вектору сигналов.
На основании заданного вектора сигналов ${{\bar {s}}_{{30}}}$ необходимо найти наиболее вероятные состояния скрытой модели на переходах. Для решения этой задачи используется формула [15, 16]:
(19)
$P\left( {{{X}_{k}} = i{\text{|}}{{{\bar {S}}}^{k}} = {{{\bar {s}}}_{k}}} \right) = \frac{{{{F}_{k}}(i){{B}_{k}}(i)}}{{\sum\limits_j {{{F}_{k}}(j){{B}_{k}}(j)} }}.$В таблице 4 указаны наиболее вероятные состояния скрытой модели на указанных в ней переходах и вероятности этих состояний.
Таблица 4.
Наиболее вероятные состояния скрытой модели на переходах
| Номер перехода | 1 | 7 | 11 | 17 | 22 | 26 | 29 |
|---|---|---|---|---|---|---|---|
| Наиболее вероятное состояние | 11 | 11 | 11 | 00 | 01 | 01 | 11 |
| Вероятность состояния | 1.000 | 1.000 | 1.000 | 1.000 | 0.600 | 0.600 | 1.000 |
Для нахождения наиболее вероятной цепочки состояний использовался алгоритм Витерби [15, 16]. Использование этого алгоритма показывает, что наиболее вероятной является следующая цепочка состояний: (11, 01, 11, 01, 11, 01, 11, 01, 11, 01, 11, 01, 11, 01, 11, 01, 00, 01, 11, 01, 11, 01, 11, 01, 11, 01, 11, 01, 11, 01).
Стационарные характеристики системы S при уточненных значениях параметров Mα1 = 3.001 ч, Mα2 = 4.501 ч, Mβ1 = 0.3 ч, Mβ2 = 0.2 ч, найденные по формулам (6), равны:
ЗАКЛЮЧЕНИЕ
В работе рассматриваются возможности применения суперпозиции независимых полумарковских процессов для моделирования многокомпонентных систем энергетики. Показано, что этот подход позволяет избавиться от ряда ограничений, в частности, от предположения об экспоненциальном законе распределения. Он дает возможность учесть в модели системы контроль, техническое обслуживание, временное резервирование и т.д. В отличие от некоторых других методов нахождения характеристик надежности и эффективности систем энергетики, он позволяет находить не только вероятностные, но и временные характеристики системы. Для решения проблемы размерности моделей можно использовать алгоритмы фазового укрупнения полумарковских систем, разработанные В.С. Королюком, А.Ф. Турбиным, А.В. Свищуком.
На примере стационарно фазово укрупненной суперпозиции двух альтернирующих процессов восстановления рассмотрена возможность применения теории скрытых марковских моделей для уточнения модели, анализа динамики и прогнозирования состояний моделируемой системы на основе полученного вектора сигналов.
В дальнейшем предполагается использование рассмотренного в работе подхода к анализу функционирования многокомпонентных систем энергетики.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (№ 18-01-00392а).
Список литературы
Королюк В.С., Турбин А.Ф. Процессы марковского восстановления в задачах надежности систем. Киев: Наук. думка, 1982. 236 с.
Королюк В.С. Стохастические модели систем. Киев: Наук. думка, 1989. 208 с.
Korolyuk V.S., Korolyuk V.V. Stochastic Models of Systems. Springer Science + Business Media, Dordrecht, 1999. 185 p.
Korolyuk V.S., Limnios N. Stochastic Systems in Merging Phase Space. World Scientific, Imperial Coledge Press, 2005. 348 p.
Корлат А.Н., Кузнецов В.Н., Новиков М.М., Турбин А.Ф. Полумарковские модели восстанавливаемых систем и систем массового обслуживания. Кишинев: Штиинца, 1991. 276 с.
Obzherin Y.E., Boyko E.G. Semi-Markov Models: Control of Restorable Systems with Latent Failures. London: Elsevier Academic Press, 2015. 212 p.
Grabski F. Semi-Markov Processes: Applications in System Reliability and Maintenance. Elsevier Science, 2014. 270 p.
Janssen J., Manca R. Applied Semi-Markov Processes. Springer Science + Business Media, 2006. 316 p.
Руденко Ю.Н., Ушаков И.А. Надежность систем энергетики. 2-е изд., перераб. и доп. Новосибирск: Наука. Сиб. отд-ние, 1989. 328 с.
Надежность систем энергетики и их оборудования: в 4 т. / [Г.Н. Антонов и др.], под общ. ред. Руденко Ю.Н. М.: Энергоатомиздат, 1994.
Beichelt F., Tittmann P. Reliability and Maintenance – Networks and Systems. Mathematical Models. Chapman & Hall, CRC Press, Boca Raton, London, New York, 2012. 326 p.
Каштанов В.А., Медведев А.И. Теория надежности сложных систем, 2-е изд. М.: Физматлит, 2010, 608 с.
Cappe´ O., Moulines E., Ryde’n T. Inference in Hidden Markov Models. Springer Science + Business Media, N.Y., 2005. 653 p.
Elliott R., Aggoun L., Moore J. Hidden Markov Models, Estimation and Control. Springer-Verlag New York, New York, USA, 1995. 382 p.
Ross S.M. Introduction to Probability Models, 9th ed. Elsevier Academic Press, USA, 2006. 800 p.
Kobayashi H., Mark B., & Turin W. Probability, Random Processes, and Statistical Analysis: Applications to Communications, Signal Processing, Queueing Theory and Mathematical Finance. Cambridge University Press, Cambridge, 2011. 812 p.
Elliott R., Limnios N., Swishchuk A. Filtering hidden semi-Markov chains, Stat. Probab. Lett. 2013. V. 83. P. 2007–2014.
Barbu V.S., Limnios N. Semi-Markov Chains and Hidden Semi-Markov Models Toward Applications: Their Use in Reliability and DNA Analysis. Springer, New York, 2008. 226 p.
Yu S.-Z. Hidden Semi-Markov Models: Theory, Algorithms and Applications. Elsevier Science, 2015. P. 208.
Obzherin Y.E., Sidorov S.M., Nikitin M.M. Hidden Markov Model of Information System with Component-Wise Storage Devices. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 11965 LNCS. 2019. P. 354–364.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика