Известия РАН. Энергетика, 2020, № 5, стр. 66-80
Крупномасштабные колебания в ЭРД холловского типа
В. И. Ильгисонис 1, В. П. Лахин 2, 3, Н. А. Марусов 2, 3, Е. А. Сорокина 2, 3, *
1 Государственная корпорация по атомной энергии “Росатом”
Москва, Россия
2 НИЦ “Курчатовский институт”
Москва, Россия
3 Российский университет дружбы народов
Москва, Россия
* E-mail: sorokina.ekaterina@gmail.com
Поступила в редакцию 12.06.2020
После доработки 27.07.2020
Принята к публикации 30.07.2020
Аннотация
Представлена трактовка формирования в плазменных потоках долгоживущих макроскопических структур, систематически наблюдаемых как в природных явлениях, так и в лабораторных плазмодинамических системах, к числу которых относятся и электрические ракетные двигатели (ЭРД) холловского типа. Показано, что причиной крупномасштабных осцилляций разряда в ЭРД в виде так называемых спиц (spokes – в англоязычной литературе) может служить неустойчивость малых возмущений электростатического потенциала плазмы, вызванная протеканием холловского тока. Обсуждаются механизмы генерации и результирующая пространственная структура крупномасштабных колебаний плазмы в ЭРД.
ВВЕДЕНИЕ
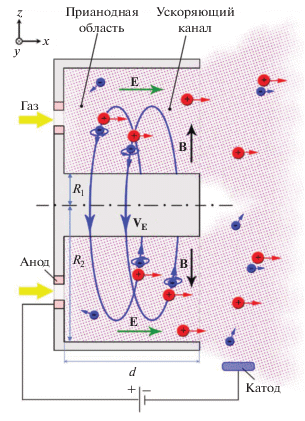
Электрические ракетные двигатели (ЭРД) холловского типа сегодня являются освоенной технологией создания электрической ракетной тяги в космосе [1–5]. Принцип их действия, как уже ясно из названия, основан на эффекте Холла, ответственном за поддержание постоянного “надтеплового” электрического поля в системе отсчета плазмы, помещенной во внешнее магнитное поле. Электрическое поле ${\mathbf{E}}$ в разрядной камере ЭРД создается между кольцевым анодом-газораспределителем, расположенным в глубине канала двигателя, и катодом-эмиттером, помещенным за выходом из канала – рис. 1. В основном объеме камеры присутствует магнитное поле ${\mathbf{B}}$, преимущественно радиальное. Электроны, эмитированные с катода, свободно движутся вдоль силовых линий магнитного поля, выравнивая электрический потенциал. Благодаря этому, круговые поверхности, образуемые магнитными силовыми линиями, являются эквипотенциалями – с точностью до поправок, связанных с конечным давлением электронов. При этом распределение электрического поля в канале практически не зависит от расположения катода. Величина магнитного поля подбирается таким образом, что размер ларморовского радиуса ионов ${{\rho }_{i}}$ значительно превышает длину ускоряющего канала $d,$ ${{\rho }_{i}} \gg d,$ в то время как для электронов выполняется обратное условие ${{\rho }_{e}} \ll d.$ В этом случае ионы, практически не отклоняясь магнитным полем, свободно ускоряются электрическим полем вдоль канала, что и приводит к возникновению тяги. Электроны же дрейфуют в азимутальном направлении со скоростью ${{{\mathbf{V}}}_{{\text{E}}}} = {{c\left[ {{\mathbf{E}} \times {\mathbf{B}}} \right]} \mathord{\left/ {\vphantom {{c\left[ {{\mathbf{E}} \times {\mathbf{B}}} \right]} {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}$ и, сталкиваясь с атомами рабочего газа (обычно ксенона), обеспечивают его эффективную ионизацию вплоть до 90%. “Замагниченные” электроны, “привязанные” к круговым магнитным поверхностям, компенсируют электрический заряд потока ионов, что позволяет избежать ограничений, связанных с образованием объемного заряда, и преодолеть тем самым известный предел по плотности тока в плазменном диоде, определяемый классическим законом Чайлда-Ленгмюра. В холловских разрядах удается получить стационарные потоки ускоренных частиц с плотностью тока $ \sim ~0.1~ - ~1$ А/см2 и энергией вплоть до нескольких кэВ при значениях КПД 0.6 и выше [6].
Идея холловских ЭРД, разрабатывавшаяся в 1960-х годах коллективами под руководством А.В. Жаринова (в варианте двигателя с анодным слоем – ДАС) и А.И. Морозова (в варианте стационарного плазменного двигателя – СПД), была воплощена в начале 1970-х годов в работоспособную конструкцию, положившую начало серийно выпускающимся двигателям семейства СПД. Более 200 двигателей было запущено в космос, при этом не было зарегистрировано ни одного отказа. Двигатели типа ДАС, отличавшиеся от СПД главным образом размером ускоряющего промежутка (в конструкциях ДАС ускорение происходит в относительно узком слое $ \sim {\kern 1pt} {{\rho }_{e}},$ тогда как в СПД А.И. Морозова создается распределенное электрическое поле на длине канала, значительно превышающей величину ларморовского радиуса электронов), также продемонстрировавшие свою работоспособность, серийного воплощения не получили.
С 1990-х годов конструкция СПД стала воспроизводиться за рубежом. Любопытно, что исходная схема А.И. Морозова не претерпела за это время каких-либо принципиальных изменений – см. монографии и обзоры [7–10]. Более того, попытки существенно изменить (как повысить, так и уменьшить) значения параметров СПД (прежде всего, мощность и тягу) путем оптимизации пространственной структуры электрического и магнитного полей при сохранении удельных и ресурсных параметров двигателя до сих пор не привели к заметным успехам, что стимулировало рост интереса к физической природе протекающих в них процессов. Начиная с 2000-х годов, результаты как теоретических, так и экспериментальных исследований физических процессов в холловских двигателях стали предметом массовых научных публикаций и обсуждений на представительных международных конференциях. В качестве современных модификаций ЭРД холловского типа стоит отметить гибридные ускорители, сочетающие принципиальные особенности работы как СПД, так и ДАС [2, 11], цилиндрические холловские двигатели (CHT – Cylindrical Hall Thruster) Принстонской плазменной лаборатории [12] с уменьшенным отношением площади поверхности к объему канала как удачную попытку масштабирования СПД в область меньших размеров и мощностей, модификации с центральным расположением катода [13] и ускорители с магнитным экранированием полюсов [14], обеспечивающим значительное снижение эрозии стенок ускоряющего канала.
Одним из направлений таких исследований в физике холловских разрядов сегодня является формирование крупномасштабных пространственных структур в плазменных потоках. В частности, в плазме холловских двигателей наблюдаются так называемые “спицы” или “споуки” (spokes – в англоязычной литературе) [15–18] – азимутальные волны повышенной концентрации плазмы с азимутальным волновым числом $m = 1~ - ~5,$ отчетливо видимые при скоростной видеосъемке с торца работающего двигателя. Спицы-споуки вращаются в направлении электрического дрейфа со скоростью много меньшей, чем скорость этого дрейфа. Частота $\omega ~$ колебаний составляет десятки килогерц, т.е. находится в интервале ${{\omega }_{{Bi}}} < \omega < {{\omega }_{{lh}}},$ где ${{\omega }_{{lh}}} = \sqrt {{{\omega }_{{Be}}}{{\omega }_{{Bi}}}} $ – нижнегибридная частота, а ${{\omega }_{{B\left( {e,i} \right)}}}$ – электронная и ионная циклотронные частоты соответственно. Аналогичные явления известны также в классических разрядах Пеннинга [19] и ионных магнетронах [20–22]. Считается, что азимутальное электрическое поле, ассоциируемое с вращением спиц, приводит к аномальному переносу электронов вдоль оси ускоряющего канала, критическим образом влияющего на рабочие характеристики разряда. Примечательно, что появление таких структур может быть связано как с переходом в улучшенные режимы работы системы [17], так и с деградацией разряда, что характерно, в частности, для миниатюрных цилиндрических плазменных двигателей [23]. Эксперименты с использованием сегментированных анодов в двигателе H6 с центральным расположением катода [24] и в CHT [25] показали, что в плазменных ускорителях спицы локализованы вблизи анода и способны переносить до половины разрядного тока. Именно с выявлением природы физических процессов, ответственных за формирование вращающихся структур в плазме холловских двигателей, в последнее время связывают возможности дальнейшего развития таких систем, крайне актуальных для современной космонавтики в области как больших (∼100 кВт), так и малых мощностей (∼100 Вт).
Общепризнанного механизма формирования крупномасштабных структур в плазме ЭРД не существует. Осесимметричные ($m = 0$) низкочастотные колебания тока разряда (breathing mode) связывают с аксиальной неустойчивостью фронта ионизации плазмы [26–28]. С концепцией критической скорости ионизации (CIV – Critical Ionization Velocity), предложенной Альфвеном [29], многие авторы, следуя классической работе [30], связывают и явление образования спиц. Однако CIV-механизм образования спиц оказался непредсказательным и не получил дальнейшего подтверждения [31]. Кроме того, расчетные характеристики колебаний, полученные на основе этих явлений, плохо согласуются с данными экспериментов.
К настоящему времени известен достаточно широкий спектр неустойчивостей холловской плазмы, существенных для организации плазменного потока, среди которых мы выделим градиентно-дрейфовую неустойчивость (ГДН). Градиентно-дрейфовая неустойчивость колебаний в нижнегибридном диапазоне частот, развивающаяся в пространственно неоднородной плазме при наличии источника свободной энергии в виде поперечного к внешнему магнитному полю тока [32], присуща системе типа СПД [10, 33], и именно из соображений ее подавления профиль магнитного поля в устройстве выбирают нарастающим от анода к выходу из ускоряющего канала. По своему физическому механизму ГДН вполне аналогична неустойчивости Рэлея-Тейлора, наиболее известным проявлением которой в физике плазмы служит желобковая неустойчивость. При градиентно-дрейфовой неустойчивости возмущение концентрации электронов в неоднородной плазме и соответствующее возмущение электрического поля нарастают во времени, привнося дополнительный (дрейфовый) вклад в электрический ток поперек магнитного поля. Понятно, что этот процесс носит нелокальный характер, так что в плазме могут формироваться макроскопические структурные образования (например, неоднородности плотности) или, наоборот, могут разрушаться имеющиеся. Эта неустойчивость активно исследуется в физике ионосферы и, в частности, является общепринятым механизмом измельчения нерегулярных структур в F-слое (см., например, [34]).
На возможную связь между неустойчивостью длинноволновой части спектра градиентно-дрейфовых волн c явлением формирования спиц было указано в [35, 36]. Существенным недостатком модели, использованной в [35], было приближение безынерционных электронов (${{m}_{e}} \to 0$). В этом приближении при выполнении локального критерия неустойчивости дестабилизируется весь спектр колебаний, причем инкремент неустойчивости неограниченно возрастает с уменьшением длины волны возмущений [37]. Это означает, что младшие азимутальные моды не являются самыми неустойчивыми в спектре, что не позволяет объяснить в рамках используемой модели возбуждение длинноволновых колебаний в плазме.
В настоящей обзорной работе мы представляем наши последние результаты по исследованию ГДН в условиях, характерных для плазмы в ЭРД холловского типа. Оказывается, что электронная инерция в холловской плазме с сильным поперечным током может стабилизировать коротковолновые возмущения, в результате чего в системе доминируют крупномасштабные колебания. Однако и в этом случае частота наиболее неустойчивых мод по порядку величины соответствует нижнегибридному диапазону, что заведомо превышает частоту вращающихся спиц. Это обстоятельство препятствовало до сих пор установлению причинно-следственной связи ГДН с наблюдаемыми крупномасштабными модами. Нами показано, что совместная раскачка собственных мод ГДН приводит к образованию волновых пакетов с существенно меньшей частотой огибающей, соответствующей диапазону частот наблюдаемых структур. Полученные результаты сопоставлены с результатами экспериментов.
Работа построена следующем образом. В разделе 2 описана базовая геометрия ЭРД холловского типа и приведены типичные профили распределения стационарных параметров плазмы и поля вдоль оси системы. В разделе 3 представлено общее дисперсионное соотношение для нижнегибридных волн, распространяющихся в ускоряющем канале поперек внешнего магнитного поля, и описаны результаты анализа их устойчивости. В разделе 4 исследована структура и характеристики глобальных мод ГДН. Проведено сравнение с экспериментом. Основные выводы статьи представлены в Заключении.
ПАРАМЕТРЫ И ГЕОМЕТРИЯ РАЗРЯДА В ЭРД ХОЛЛОВСКОГО ТИПА
В современных ЭРД холловского типа величина магнитного поля в зависимости от конструкции варьируется в пределах $B = 0.1~ - ~1$ кГс. В качестве рабочего вещества используются инертные газы, обычно ксенон или криптон, обладающие достаточно низкой энергией ионизации. Ионизованные атомы в типичных режимах работы ЭРД обладают сравнительно низкой температурой ${{T}_{i}} \sim 1$ эВ, тогда как температура электронов ${{T}_{e}}$ достигает $20~ - ~30$ эВ вблизи выхода из ускоряющего канала. Концентрация заряженных частиц в ускоряющем канале составляет порядка $ \sim {\kern 1pt} {{10}^{{12}}}$ см–3. При таких параметрах плазму в ЭРД в ряде практически важных случаев можно рассматривать как бесстолкновительную [6].
Для описания ключевых закономерностей волновых процессов в плазме ЭРД используем упрощенную геометрию скрещенных полей. Отметим, что в настоящее время имеются попытки рассмотрения неустойчивостей и с учетом изменения конфигурации полей и параметров плазмы на различных стадиях разряда, в том числе в рамках кинетического подхода [38], тогда как для целей настоящей работы это было бы превышением точности. Наши расчеты проведены для заданных электрического и магнитного полей; при этом возможное обратное влияние возникновения спицы на исходные профили физических величин не учитывается.
Введем декартову систему координат $\left\{ {x,~y,~z} \right\}$ с осью $z,$ направленной по радиусу – вдоль основной компоненты магнитного поля, ${\mathbf{B}} = B{{{\mathbf{e}}}_{z}}$ (рис. 1). Координату $x$ выберем вдоль оси системы и, следовательно, вдоль направления внешнего электрического поля ${\mathbf{E}} = - \nabla \Phi \left( x \right) = E\left( x \right){{{\mathbf{e}}}_{x}}$ (${\Phi }$ – электростатический потенциал плазмы). Вдоль оси $x$ будет направлена и скорость ионов ${{{\mathbf{v}}}_{i}} = {{{v}}_{i}}\left( x \right){{{\mathbf{e}}}_{x}};$ в этом же направлении ориентированы градиенты магнитного поля $B\left( x \right)$, концентрации ионов (плотности) квазинейтральной плазмы $n\left( x \right)$ и температуры электронов ${{T}_{e}}\left( x \right)$ (ионы считаем холодными). Направление вдоль оси $y$ играет роль азимутального и соответствует направлению электрического дрейфа электронов ${{{\mathbf{V}}}_{{\text{E}}}} = {{c\left[ {{\mathbf{E}} \times {\mathbf{B}}} \right]} \mathord{\left/ {\vphantom {{c\left[ {{\mathbf{E}} \times {\mathbf{B}}} \right]} {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}},$ где $c$ – скорость света; используется система единиц СГС.
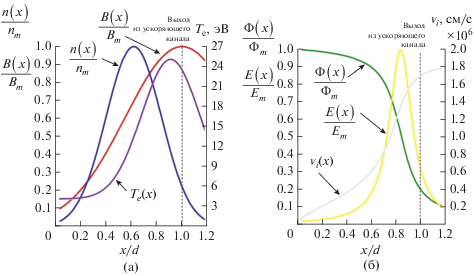
Разряды в современных ЭРД характеризуются схожими распределениями основных физических величин $B\left( x \right),$ $n\left( x \right),$ ${\Phi }\left( x \right),$ ${{T}_{e}}\left( x \right)$ вдоль оси $x$ [26, 39, 40]. В классической конфигурации холловского двигателя, например, СПД с протяженной зоной ускорения (длина $d$ которой значительно превышает величину ларморовского радиуса электронов, $d \gg {{\rho }_{e}}$) магнитное поле $B\left( x \right)$ растет от анода ($x = 0$) к катоду и достигает максимального значения ${{B}_{m}}$ на выходе из ускоряющего канала ($x = d$). Профили плотности и температуры плазмы, $n\left( x \right)$ и ${{T}_{e}}\left( x \right),$ имеют схожую с профилем магнитного поля форму, однако их максимумы смещены к центру ускоряющего канала. Отметим, что в области, где функция распределения электронов отлична от максвелловской, температура выступает как мера средней кинетической энергии электронов. Типичный вид профилей $B\left( x \right),$ $n\left( x \right)$ и ${{T}_{e}}\left( x \right)$ в двигателе семейства СПД представлен на рис. 2(a) [41]. Основное падение электрического потенциала ${\Phi }\left( x \right)$ происходит у выхода из ускоряющего канала, где электрическое поле $E\left( x \right) = {{ - d{\Phi }\left( x \right)} \mathord{\left/ {\vphantom {{ - d{\Phi }\left( x \right)} {dx}}} \right. \kern-0em} {dx}}$ достигает своего максимального значения ${{E}_{m}}$ – рис. 2(б). Все дальнейшие результаты приведены для следующих значений параметров системы, характерных для классической модели двигателя СПД-100: ${{B}_{m}}~ = ~180$ Гс, ${{n}_{m}} = 0.5 \times {{10}^{{12}}}$ см–3, ${{{\Phi }}_{m}} = 270$ В, ${{E}_{m}}~ = 100$ В/см, $d = 2.5$ см, ${{R}_{1}} = 3$ см и ${{R}_{2}} = 5~$ см – внутренний и внешний радиусы ускоряющего канала (полурадиус канала $R = {{\left( {{{R}_{1}} + {{R}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{R}_{1}} + {{R}_{2}}} \right)} 2}} \right. \kern-0em} 2} = 4$ см), рабочий газ – Xe. При выбранных параметрах величина ионной скорости достигает значения ∼106 см/c на выходе из ускоряющего канала двигателя.
Рис. 2.
Профили (а) магнитного поля ${{B\left( x \right)} \mathord{\left/ {\vphantom {{B\left( x \right)} {{{B}_{m}}}}} \right. \kern-0em} {{{B}_{m}}}},$ концентрации плазмы ${{n\left( x \right)} \mathord{\left/ {\vphantom {{n\left( x \right)} {{{n}_{m}}}}} \right. \kern-0em} {{{n}_{m}}}}$ и температуры электронов ${{T}_{e}}\left( x \right);$ (б) электрического потенциала ${{{\Phi }\left( x \right)} \mathord{\left/ {\vphantom {{{\Phi }\left( x \right)} {{{{\Phi }}_{m}}}}} \right. \kern-0em} {{{{\Phi }}_{m}}}},$ электрического поля ${{E\left( x \right)} \mathord{\left/ {\vphantom {{E\left( x \right)} {{{E}_{m}}}}} \right. \kern-0em} {{{E}_{m}}}}$ и скорости ионов ${{{v}}_{i}}\left( x \right)$ как функции координаты вдоль оси системы $x{\text{/}}d.$ Здесь индексом m обозначены максимальные значения соответствующих величин.
ЛОКАЛЬНЫЕ ХАРАКТЕРИСТИКИ НЕУСТОЙЧИВЫХ АЗИМУТАЛЬНЫХ ВОЛН В КАНАЛЕ ЭРД
Для анализа устойчивости поперечных электростатических волн нижнегибридного диапазона частот ${{\omega }_{{Bi}}} < \omega < {{\omega }_{{Be}}}$ в плазме холловского ЭРД воспользуемся ранее полученным нами локальным дисперсионным уравнением [42]:
(1)
$1 + \frac{{\omega _{{pe}}^{2}}}{{\omega _{{Be}}^{2}}}\frac{1}{{1 + k_{ \bot }^{2}\rho _{e}^{2}}} - \frac{{\omega _{{pi}}^{2}}}{{{{{\left( {\omega - {{k}_{x}}{{{v}}_{i}}} \right)}}^{2}}}} - \frac{{\omega _{{pe}}^{2}}}{{{{\omega }_{{Be}}}\left( {\omega - {{k}_{y}}{{V}_{E}} - {{k}_{y}}{{{\bar {V}}}_{D}}} \right)}}\frac{{{{k}_{y}}\left( {{{\kappa }_{n}} - 2{{{\bar {\kappa }}}_{B}}} \right)}}{{k_{ \bot }^{2}\left( {1 + k_{ \bot }^{2}\rho _{e}^{2}} \right)}} = 0.$Дисперсионное соотношение (1) применимо как для интересующих нас длинноволновых колебаний, так и для коротковолновых возмущений с частотой порядка нижнегибридной частоты, $\omega \simeq {{\omega }_{{lh}}},$ что позволяет использовать его для анализа спектра неустойчивых колебаний во всем объеме плазмы ЭРД, характеризуемой существенным изменением значений равновесных параметров вдоль оси системы. При этом рассеяние электронов на атомах нейтрального газа, существенное в зоне ионизации рабочего вещества внутри канала ускорителя, не оказывает заметного влияния на характер развития неустойчивости крупномасштабных колебаний. Несложно показать (см., например, [44]), что для азимутальных волн с ${{k}_{y}} \gg {{k}_{x}}$ столкновения важны при ${{k}_{y}} \gtrsim {{\left( {{{\kappa }_{n}} - 2{{\kappa }_{B}}} \right){{\omega }_{{Be}}}} \mathord{\left/ {\vphantom {{\left( {{{\kappa }_{n}} - 2{{\kappa }_{B}}} \right){{\omega }_{{Be}}}} {{{\nu }_{{en}}}}}} \right. \kern-0em} {{{\nu }_{{en}}}}},$ где ${{\nu }_{{en}}}$ – частота столкновений электронов с нейтралами, т.е. для очень коротковолновых возмущений ввиду ${{\omega }_{{Be}}} \gg {{\nu }_{{en}}}.$
Представим численное решение уравнения (1) для профилей параметров плазмы, изображенных на рис. 2, отслеживая изменение характеристик неустойчивых мод вдоль оси ускоряющего канала. При выполнении достаточного условия возникновения неустойчивости в фиксированной точке пространства одновременно возбуждается множество неустойчивых мод. Для нас основной интерес представляют самые неустойчивые (с наибольшими инкрементами) моды из этого множества, поскольку именно их развитие определяет наблюдаемую картину явления. Далее в (1) будем полагать ${{k}_{y}} \gg {{k}_{x}},$ ограничиваясь рассмотрением преимущественно азимутальных возмущений плазмы.
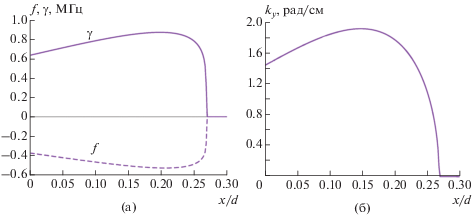
Область неустойчивости и характеристики (частоты, $f = {{{\text{Re}}\left( \omega \right)} \mathord{\left/ {\vphantom {{{\text{Re}}\left( \omega \right)} {2\pi }}} \right. \kern-0em} {2\pi }},$ инкременты, $\gamma = {{~{\text{Im}}\left( \omega \right)} \mathord{\left/ {\vphantom {{~{\text{Im}}\left( \omega \right)} {2\pi }}} \right. \kern-0em} {2\pi }},$ и волновые числа, ${{k}_{y}}$) наиболее неустойчивых возмущений внутри канала показаны на рис. 3 и 4 соответственно. Видно, что ГДН азимутальных волн развивается лишь в прианодной части двигателя при $0 < x{\text{/}}d \lesssim 0.27.$ Неустойчивость характеризуется большими длинами волн, при этом частоты и инкременты неустойчивых колебаний имеют порядок нижнегибридной частоты, ${{\omega }_{{lh}}}.$ Наиболее неустойчивая мода в канале локализована в сечении $x \simeq 0.2d;$ ее инкремент $\gamma \simeq 830$ кГц, частота $f \simeq - 520$ кГц, волновое число ${{k}_{y}} \simeq 1.~8$ рад/см. Отрицательный знак частоты означает, что волна распространяется в направлении ${\mathbf{E}} \times {\mathbf{B}}$-дрейфа электронов.
Рис. 3.
Область неустойчивости (x < 0.27d) азимутальных мод в ускоряющем канале СПД. Наклонная линия демонстрирует зависимость функции ${{d~{\text{ln}}\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} \mathord{\left/ {\vphantom {{d~{\text{ln}}\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} {dx}}} \right. \kern-0em} {dx}}$ от $x{\text{/}}d.$
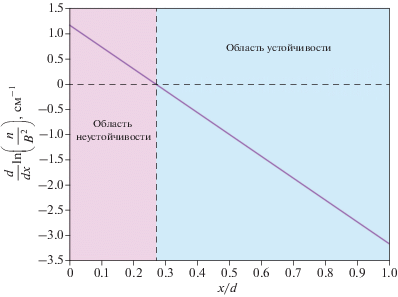
Рис. 4.
Зависимость характеристик неустойчивости от $x{\text{/}}d$ в прианодной части двигателя: (а) частота $f$ и инкремент $\gamma ;$ (б) волновое число ${{k}_{y}}.$
Необходимое условие неустойчивости крупномасштабных ($k_{ \bot }^{2}~\rho _{e}^{2} \ll 1$) азимутальных градиентно-дрейфовых мод с законом дисперсии (1) имеет вид [42]:
(2)
$\frac{{\left( {{{V}_{E}} + {{V}_{D}}} \right)\left( {{{\kappa }_{n}} - 2{{\kappa }_{B}}} \right)}}{{{{\omega }_{{Bi}}}}} < 0.$В однородном магнитном поле (${{\kappa }_{B}} = 0$) условие (2) сводится к известному критерию неустойчивости Саймона и Хо [45, 46]: ${\mathbf{E}}\cdot\nabla n > 0.$ В общем случае градиентно-дрейфовая неустойчивость возбуждается комбинацией потоков, связанных с электрическим ${\mathbf{E}} \times {\mathbf{B}}$ и магнитным дрейфами электронов, совместно с неоднородностью плотности плазмы и магнитного поля в поперечном направлении, выступающей триггером неустойчивости.
Для рассматриваемых профилей параметров плазмы и магнитного поля в ЭРД дрейфовая скорость электронов, ${{V}_{E}} + {{V}_{D}},$ является знакоопределенной всюду внутри канала (${{V}_{E}} + {{V}_{D}} < 0$). Необходимое условие неустойчивости (2) в этом случае имеет простейший вид ${{\kappa }_{n}} - 2{{\kappa }_{B}} > 0$ или (в физических переменных) ${{d~{\text{ln}}\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} \mathord{\left/ {\vphantom {{d~{\text{ln}}\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} {dx}}} \right. \kern-0em} {dx}} > 0.$ Тем самым область неустойчивости определяется исключительно характером изменения магнитного поля и плотности плазмы вдоль канала (рис. 3). Функция ${{d~{\text{ln}}\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} \mathord{\left/ {\vphantom {{d~{\text{ln}}\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} {dx}}} \right. \kern-0em} {dx}}$ убывает с ростом $x$ и обращается в нуль в точке $x{\text{/}}d \simeq 0.27,$ которая, как следует и из численного решения уравнения (1), ограничивает неустойчивую область вблизи анода.
Типичные условия работы холловских плазменных двигателей характеризуются высокой скоростью вращения электронов ($\left| {{{V}_{E}} + {{V}_{D}}} \right|$ вплоть до ${{10}^{8}}$ см/с). В пределе сильной накачки неустойчивости ($\left| {{{V}_{E}} + {{V}_{D}}} \right| \gg R{{\omega }_{{lh}}}$) характеристики наиболее опасных мод в канале ЭРД приближенно описываются следующими выражениями [43]:
(3)
$\begin{gathered} {{k}_{y}} = \frac{{{{\omega }_{{lh}}}}}{{\sqrt {{{\omega }_{{Bi}}}} }}~\sqrt { - \frac{{\left( {{{\kappa }_{n}} - 2{{\kappa }_{B}}} \right)}}{{\left( {{{V}_{E}} + {{V}_{D}}} \right)}}} ,\,\,\,\,f = \frac{{{{\omega }_{{lh}}}}}{{4\pi }}{{\left( { - \frac{{\left( {{{V}_{E}} + {{V}_{D}}} \right)\left( {{{\kappa }_{n}} - 2{{\kappa }_{B}}} \right)}}{{{{\omega }_{{Bi}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}{\text{sign}}\left( {{{k}_{y}}\left( {{{V}_{E}} + {{V}_{D}}} \right)} \right), \\ \gamma = \frac{{\sqrt 3 {{\omega }_{{lh}}}}}{{4\pi }}{{\left( { - \frac{{\left( {{{V}_{E}} + {{V}_{D}}} \right)\left( {{{\kappa }_{n}} - 2{{\kappa }_{B}}} \right)}}{{{{\omega }_{{Bi}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}~}}}. \\ \end{gathered} $Как следует из (3), зависимость частоты от знака ${{k}_{y}}\left( {{{V}_{E}} + {{V}_{D}}} \right)$ гарантирует распространение волны вдоль равновесного тока электронов.
Отметим, что учет “двумерности” возмущений (${{k}_{x}} \ne 0$) приводит к дестабилизации как основной части ускоряющего канала, так и области разлета плазменной струи под действием конечной скорости ионного потока [41]. Внутри канала и вблизи его выхода раскачиваются строго аксиальные колебания, а далеко за срезом доминируют косые волны. Неустойчивость таких колебаний является существенно коротковолновой. При этом ввиду малости ионной скорости учет ${{k}_{x}}$ не оказывает сколь-нибудь заметного влияния на характер длинноволновой неустойчивости вблизи анода.
СТРУКТУРА ГЛОБАЛЬНЫХ МОД
Для крупномасштабных мод, длина волны которых сопоставима с размером системы и с характерными размерами неоднородностей плазмы и магнитного поля, обычное представление в виде разложения по плоским волнами $ \sim ~{\text{exp}}\left( { - i{{k}_{x}}x} \right)$ становится неприменимым. При этом вид собственных функций должен быть определен из решения соответствующей задачи на собственные значения при заданных граничных условиях для потенциала возмущений вида
(4)
$\phi \left( {x,y,t} \right) = \sum {{{\phi }_{k}}} \left( x \right){\text{exp}}\left( { - i\omega t + i{{k}_{y}}y} \right).$Как обсуждалось ранее, эффекты конечной ионной скорости и электронной температуры не оказывают существенного влияния на устойчивость азимутальных колебаний внутри канала СПД, что позволяет далее при анализе устойчивости крупномасштабных мод ограничиться рассмотрением холодной плазмы и пренебрегать движением ионов. В данном приближении уравнение на собственные частоты глобальных градиентно-дрейфовых мод имеет вид [47]:
(5)
$\frac{{{{d}^{2}}{{\phi }_{k}}}}{{d{{x}^{2}}}} + {{\kappa }_{n}}\frac{{d{{\phi }_{k}}}}{{dx}} - k_{y}^{2}{{\phi }_{k}} - \frac{{{{\omega }^{2}}}}{{{{\omega }^{2}} - \omega _{{lh}}^{2}}}\left[ {2{{\kappa }_{B}}\frac{{d{{\phi }_{k}}}}{{dx}} - \frac{{{{k}_{y}}{\Lambda }\left( x \right)}}{{\omega - {{k}_{y}}{{V}_{E}}}}{{\phi }_{k}}} \right] = 0,$Уравнение (5) описывает аксиальную структуру глобальных электростатических градиентно-дрейфовых мод, вращающихся в направлении стационарного дрейфа электронов в скрещенных полях в неоднородной частично замагниченной плазме, и учитывает эффекты электронной инерции и неоднородности магнитного поля, а также шир равновесной скорости азимутального вращения электронов. Учет инерции электронов принципиален, поскольку именно она приводит к стабилизации коротковолновых колебаний плазмы [37].
Уравнения, схожие по виду с (5), хорошо известны в теории плазменных и гидродинамических неустойчивостей [32, 48, 49]. Например, в случае ${{\kappa }_{n}} = {{\kappa }_{B}} = 0$ и $\omega \gg {{\omega }_{{lh}}}$ уравнение (5) в точности принимает вид классического уравнения Рэлея [49], описывающего структуру собственных колебаний плоскопараллельных течений несжимаемой жидкости. Плазменный аналог (5) описывает случай желобковых колебаний газа заряженных частиц [48]. Применительно к проблеме устойчивости глобальных мод в ускорителях холловского типа схожие уравнения исследовались в [50]. Другим примером высокочастотной неустойчивости ($\omega \gg {{\omega }_{{lh}}}$), описываемой уравнением (5), является диокотронная неустойчивость пространственно-неоднородного электронного облака.
Для профилей стационарных параметров плазмы, показанных на рис. 2, уравнение (5) решается численно с нулевыми граничными условиями для возмущений потенциала плазмы на электродах $\phi \left( {x = 0} \right)$ = $\phi \left( {x = d} \right) = 0$ [47]. Выбранные граничные условия соответствуют фиксированным значениям потенциала на аноде и виртуальном катоде, т.е. магнитной поверхности, проходящей через катод-нейтрализатор на открытом конце системы. Для определенности будем считать, что виртуальный катод локализован на выходе из ускоряющего канала. Таким образом, рассматриваются возмущения, локализованные внутри ускоряющего канала двигателя. Спектр неустойчивых колебаний (зависимость $\gamma \left( f \right)$), полученный для данной геометрии, представляет собой набор из пяти длинноволновых неустойчивых мод с азимутальными волновыми числами $m \equiv {{k}_{y}}R = 1 - 5$ в нижнегибридном диапазоне частот $f = - \left( {0.26 - 0.67} \right)$ МГц и $\gamma = 0.26 - 0.38$ МГц – рис. 5(а).
Рис. 5.
Спектр собственных частот неустойчивых мод с азимутальными волновыми числами $m = {{k}_{y}}R$ (а); аксиальная структура собственных функций (б).
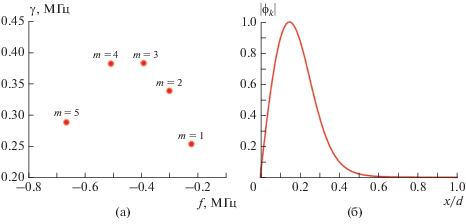
Все моды спектра обладают одинаковой аксиальной структурой собственных функций, представленной на рис. 5(б) в относительных единицах (по отношению к максимальному значению, которое в линейной теории не определено). Как видно, неустойчивые моды локализованы преимущественно в прианодной области ускоряющего канала, что согласуется с результатами локального анализа устойчивости.
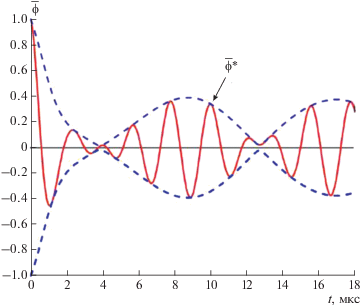
Спектр неустойчивости имеет характерный “параболический” вид с двумя преобладающими гармониками $m = 3$ и $m = 4$ с частотами $ \sim {\kern 1pt} 0.5$ МГц. В результате, на линейной стадии развития ГДН высокочастотный сигнал оказывается модулирован низкочастотной огибающей биений с частотой ${{f}_{b}} = {{\left( {{{f}_{3}} - {{f}_{4}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{3}} - {{f}_{4}}} \right)} 2}} \right. \kern-0em} 2} \sim 50$ кГц. Это проиллюстрировано на рис. 6, на котором показана временная эволюция нормированного потенциала возмущений $\bar {\phi } = \phi ~{\text{exp}}\left( { - {{\gamma }_{3}}t} \right)$ в фиксированной точке пространства. Видно, что возмущения равной начальной амплитуды релаксируют к биениям, образованными модами $m = 3$ и $m = 4,$ с огибающими $\bar {\phi }* \sim {\text{cos}}\left( {2\pi {{f}_{b}}t} \right).$ Частота формируемого волнового пакета соответствует наблюдаемому диапазону частот крупномасштабных осцилляций в ЭРД.
Рис. 6.
Зависимость функции $\bar {\phi } = \phi ~{\text{exp}}\left( { - {{\gamma }_{3}}t} \right)$ от времени $t$ в фиксированной точке пространства. Амплитуда функции в начальный момент времени нормирована на единицу. Пунктиром показана огибающая волнового пакета, $\bar {\phi }{\text{*}}.$
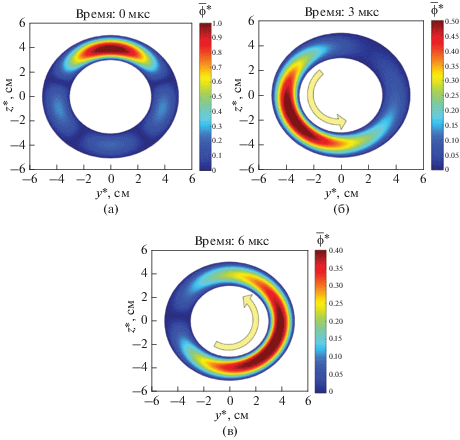
Особый интерес представляет динамика огибающей в аксиальном сечении $x = {\text{const,}}$ т.е. на срезе двигателя: именно в этой плоскости в экспериментах удается визуально наблюдать крупномасштабные структуры при помощи высокоскоростной видеофиксации – см., например, [17, 18, 25, 31]. Пространственно-временная эволюция волнового пакета в сечении $x = {\text{const}}$ представлена на рис. 7 в виде линий уровня огибающей функции $\bar {\phi }{\text{*}}$ [47]. Для иллюстрации выбрана параболическая зависимости возмущения потенциала от радиуса $z$ с нулями на внешнем ${{R}_{2}}$ и внутреннем ${{R}_{1}}$ радиусах ускоряющего канала. В начальный момент времени $t = 0$ волновой пакет представляет из себя локализованную структуру $m = 1$ с прослеживающимся вкладом от более высоких гармоник – рис. 7(а). Релаксируя к биениям на двух гармониках, наблюдаемая структура растягивается и смещается в направлении ${\mathbf{E}} \times {\mathbf{B}}$-дрейфа электронов – рис. 7(б, в). Групповая скорость огибающей $ \simeq {\kern 1pt} 5.5 \times {{10}^{5}}$ см/с, что составляет $ \sim {\kern 1pt} 0.02~{{V}_{E}}$ (${{V}_{E}}$ рассчитана в точке $x = 0.~15d,$ соответствующей максимальному значению амплитуды моды вдоль оси ускоряющего канала – рис. 5(б)). Повышенную светимость наблюдаемой в экспериментах спицы мы связываем с локальным повышением концентрации электронов из-за вышеописанных колебаний.
Рис. 7.
Линии уровня огибающей $\bar {\phi }{\text{*}}$ в сечении $x = {\text{const}}$ для различных моментов времени $t{\text{:}}$ (a) $0.0,$ (б) $3.0$ мкс, (в) $6.0$ мкс. На рисунке в плоскости $x = {\text{const}}$ введена декартова система координат $\left\{ {y*,~z{\text{*}}} \right\}.$
Рассматриваемая картина биений формируется лишь в случае, когда спектр собственных колебаний обладает хотя бы двумя модами с близкими по величине инкрементами. Данное обстоятельство объясняет возможность существования холловских разрядов и в отсутствии медленно вращающихся споуков. Частота огибающей волнового пакета и его групповая скорость напрямую зависят от “удаленности” мод (т.е. от разности частот колебаний с примерно равными $\gamma $). Форма спектра (на плоскости $f - \gamma $), в свою очередь, оказывается весьма чувствительной к изменению геометрических размеров СПД. Соответствующие расчеты [47] показывают, что увеличение радиуса ускоряющего канала приводит к сближению частот неустойчивых мод с близкими $\gamma ,$ что сопровождается уменьшением частоты биений ${{f}_{b}} \sim {1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0em} R}.$ Тенденция уменьшения частоты споуков с ростом радиуса ускоряющего канала явно наблюдается в экспериментах [31].
ЗАКЛЮЧЕНИЕ
Проведенное рассмотрение демонстрирует физическую возможность возникновения наблюдаемых в холловских разрядах крупномасштабных низкочастотных осцилляций в виде вращающихся спиц (споуков) в результате развития глобальных мод градиентно-дрейфовой неустойчивости.
Показано, что в прианодной части ЭРД холловского типа возбуждаются длинноволновые азимутальные колебания с ${{k}_{y}} \sim 1$ рад/см и частотами в типичном нижнегибридном диапазоне $f \sim - 0.~5$ МГц, распространяющиеся в ${\mathbf{E}} \times {\mathbf{B}}$-направлении. Механизм их неустойчивости связан с классической азимутальной градиентно-дрейфовой неустойчивостью [51], возникающей из-за неоднородности плотности плазмы и магнитного поля в соответствии с критерием ${{d~\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} \mathord{\left/ {\vphantom {{d~\left( {{n \mathord{\left/ {\vphantom {n {{{B}^{2}}}}} \right. \kern-0em} {{{B}^{2}}}}} \right)} {dx}}} \right. \kern-0em} {dx}} > 0.$ Характеристики неустойчивости в прианодной области хорошо описываются аналитическими выражениями (3).
Расчет устойчивости глобальных градиентно-дрейфовых волн в холловском плазменном двигателе показывает, что собственные неустойчивые колебания характеризуются крупномасштабной азимутальной $m = 1 - 5$ и аксиальной (рис. 5(б)) структурой собственных функций и локализованы в прианодной области ускоряющего канала. Важную роль в формировании спектра глобальных ГД-мод играет инерция электронов, стабилизирующая коротковолновые возмущения, а пространственная локализация мод объясняется выполнением локального критерия неустойчивости лишь в прианодной части устройства.
Показано, что для характерного “параболического” спектра (рис. 5(a)) глобальные моды на линейной стадии развития неустойчивости образуют волновые пакеты $m = 1$ с характерной частотой огибающей $ \sim {\kern 1pt} 50$ кГц и групповой скоростью $ \sim {\kern 1pt} 0.02~{{V}_{E}},$ при этом их частота ${{ \sim {\kern 1pt} 1} \mathord{\left/ {\vphantom {{ \sim {\kern 1pt} 1} R}} \right. \kern-0em} R}.$ Соответствие между основными характеристиками волновых пакетов и параметрами крупномасштабных азимутальных структур, наблюдаемых в холловских двигателях, как-то: прианодная локализация, десятикилогерцовая частота, низкие $m,$ медленное вращение в направлении ${\mathbf{E}} \times {\mathbf{B}}$-дрейфа, обратная пропорциональность частоты радиусу ускоряющего канала – позволяет сделать вывод о том, что именно градиентно-дрейфовая неустойчивость может служить наиболее вероятным механизмом возникновения квазикогерентных структур в виде спиц в ЭРД. Физические основания для данного механизма достаточно универсальны, тогда как наблюдаемые проявления (азимутальное волновое число, частота) могут быть специфичны для условий (в том числе геометрических) конкретного разряда и разрешения диагностического оборудования.
Работа частично поддержана грантом Российского фонда фундаментальных научных исследований #18–29–21041.
Список литературы
Koroteev A.S., Gorshkov O.A., Akimov V.N., Sinitsin A.A., Murashko V.M., Arkhipov B.A., Vinogradov V.N. // Acta Astronautica. 2004. V. 54. P. 25.
Горшков O.A., Муравлев B.A., Шагайда A.A. // Холловские и ионные плазменные двигатели для космических аппаратов / Под ред. академика РАН Коротеева А.С. М.: Изд-во “Машиностроение”, 2008. 280 с.
Ковальчук М.В., Ильгисонис В.И., Кулыгин В.М. // Природа. 2017. # 12. С. 33.
Ким В.П. // Физика плазмы. 2017. Т. 43. С. 406.
Levchenko I., Xu S., Mazouffre S., Lev D., Pedrini D., Goebel D., Garrigues L., Taccogna F., Bazaka K. // Phys. Plasmas. 2020. V. 27. Art. # 020601.
Плазменные ускорители / Под ред. Арцимовича Л.А., Гришина С.Д., Гродзовского Г.Л., Лескова Л.В., Морозова А.И., Дороднова А.М., Падалки В.Г., Пергамента М.И. М.: Изд-во “Машиностроение”, 1973. 312 с.
Морозов А.И. Введение в плазмодинамику. М.: Физматлит, 2006. 576 с.
Морозов А.И. Физические основы космических электрореактивных двигателей. Т. 1. Элементы динамики потоков в ЭРД. М.: Атомиздат, 1978. 328 с.
Морозов А.И., Лебедев С.В. // Вопросы теории плазмы, вып. 8 / Под ред. академика Леонтовича М.А. М.: Госатомиздат, 1974. С. 247.
Morozov A.I., Savelyev V.V. // in Reviews of Plasma Physics, vol. 21 / Ed. by Kadomtsev B.B. and Shafranov V.D. N.Y.: Consultants Bureau, 2000. P. 203.
Szabo J., Tedrake R., Metivier E., Paintal S., Taillefer Z. // in 53rd AIAA/SAE/ASEE Joint Propulsion Conference, AIAA 2017-4728, 2017.
Raitses Y., Fisch N.J. // Phys. Plasmas. 2001. V. 8. P. 2579.
Sekerak M.J., Longmier B.W., Gallimore A.D., Brown D.L., Hofer R.R., Polk J.E. // in 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, AIAA 2013-4116, 2013.
Grimauda L., Mazouffre S. // J. Appl. Phys. 2017. V. 122. Art. # 033305.
Есипчук Ю.В., Морозов А.И., Тилинин Г.Н., Трофимов А.В. // ЖТФ. 1973. Т. 43. С. 1466.
Chesta E., Lam C.M., Meezan N.B., Schmidt D.P., Cappelli M.A. // IEEE Trans. on Plasma Sci. 2001. V. 29. P. 582.
Sekerak M.J., Longmier B.W., Gallimore A.D., Brown D.L., Hofer R.R., Polk J.E. // IEEE Trans. on Plasma Sci. 2015. V. 43. P. 72.
Désangles V., Shcherbanev S., Charoy T., Clement N., Deltel C., Richard P., Vincent S., Chabert P., Bourdon A. // Atmosphere. 2020. V. 11. P. 518.
Thomassen K.I. // Phys. Fluids. 1966. V. 9. P. 1836.
Anders A., Ni. P., Rauch A. // J. Appl. Phys. 2012. V. 111. Art. # 053304.
Brenning N., Lundin D., Minea T., Costin C., Vitelaru C. // J. Phys. D: Appl. Phys. 2013. V. 46. Art. # 084005.
Hecimovic A., von Keudell A. // J. Phys. D: Appl. Phys. 2018. V. 51. Art. # 453001.
Parker J.B., Raitses Y., Fisch N.J. // Appl. Phys. Lett. 2010. V. 97. Art. # 091501.
McDonald M.S., Bellant C.K., Pierre B.A.St., Gallimore A.D. // in 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, AIAA 2011-5810, 2011.
Ellison C.L., Raitses Y., Fisch N.J. // Phys. Plasmas. 2012. V. 19. Art. # 013503.
Boeuf J., Garrigues L. // J. Appl. Phys. 1998. V. 84. P. 3541.
Barral S., Ahedo E. // Phys. Rev. E. 2009. V. 79. Art. # 046401.
Ромаданов И.В., Смоляков А.И., Сорокина Е.А., Андреев В.В., Марусов Н.А. // Физика плазмы. 2020. Т. 46. С. 318.
Alfvèn H. On the origin of the solar system. Oxford: Clarendon Press, 1954. 205 p.
Janes G.S., Lowder R.S. // Phys. Fluids. 1966. V. 9. P. 1115.
McDonald M.S., Gallimore A.D. // in 32nd Int. Electric Propulsion Conference, IEPC-2011-242, 2011.
Михайловский А.Б. Теория плазменных неустойчивостей. Т. 2. Неустойчивости неоднородной плазмы. М.: Атомиздат, 1971. 312 c.
Boeuf J.P. // Front. Phys. 2014. V. 2. P. 74.
Hargreaves J.K. The Solar-Terrestrial Environment. Cambridge University Press, 1992. 436 p.
Frias W., Smolyakov A.I., Kaganovich I.D., Raitses Y. // Phys. Plasmas. 2012. V. 19. Art. # 072112.
Frias W., Smolyakov A.I., Kaganovich I.D., Raitses Y. // Phys. Plasmas. 2013. V. 20. Art. # 052108.
Гордеев А.В., Гречиха А.В. // Физика плазмы. 1992. Т. 18. С. 3.
Chernyshev T., Son E., Gorshkov O. // J. Phys. D. 2019. V. 52. Art. # 444002.
Hofer R., Mikellides I., Katz I., Goebel D. // in 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, AIAA 2007-5267, 2007.
Kronhaus I., Kapulkin A., Balabanov V., Rubanovich M., Guelman M., Natan B. // J. Phys. D: Appl. Phys. 2012. V. 45. Art. # 175203.
Marusov N.A., Sorokina E.A., Lakhin V.P., Ilgisonis V.I., Smolyakov A.I. // Plasma Sources Sci. & Tech. 2019. V. 28. Art. # 015002.
Lakhin V.P., Ilgisonis V.I., Smolyakov A.I., Sorokina E.A., Marusov N.A. // Phys. Plasmas. 2018. V. 25. Art. # 012106.
Lakhin V.P., Ilgisonis V.I., Smolyakov A.I., Sorokina E.A., Marusov N.A. // Phys. Plasmas. 2018. V. 25. Art. # 012107.
Escobar D., Ahedo E. // in 34th Int. Electric Propulsion Conference, IEPC-2015-371, 2015.
Simon A. // Phys. Fluids. 1963. V. 6. P. 382.
Hoh F.C. // Phys. Fluids. 1963. V. 6. P. 1184.
Сорокина Е.А., Марусов Н.А., Лахин В.П., Ильгисонис В.И. // Физика плазмы. 2019. Т. 45. С. 3.
Тимофеев А.В. Резонансные явления в колебаниях плазмы. М.: Физматлит, 2000. 224 с.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 736 c.
Litvak A.A., Fisch N.J. // Phys. Plasmas. 2004. V. 11. P. 1379.
Есипчук Ю.В., Тилинин Г.Н. // ЖТФ. 1976. Т. 46. С. 718.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика