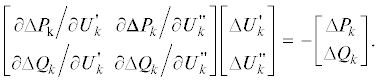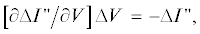Известия РАН. Энергетика, 2021, № 1, стр. 109-121

ВВЕДЕНИЕ

Расчеты установившихся режимов (УР) используются практически во всех областях современной теории режимов электрических систем (ЭС) и диспетчерского управления, будь то статическая или динамическая устойчивость, переходные процессы, оценивание состояния, оптимизация режимов или рынок электроэнергии, т.е. везде, где требуется учет и анализ режимных параметров ЭС. К настоящему времени развитие теории и практики привели к тому, что в основе всех вычислительно эффективных алгоритмов расчета УР, в том числе реализованных в промышленных (коммерческих) программах, используется метод Ньютона [1]–[2]. Метод Ньютона является относительно надежным даже при расчете “тяжелых” режимов ЭС, обладает квадратичной скоростью сходимости вблизи решения и обеспечивает расчет УР обычно за 3–6 итераций. Однако существенным его недостатком является требование достаточно хорошего начального приближения переменных для обеспечения сходимости итерационного процесса к решению. Практика расчетов и управления режимами ЭС показала, что вариации напряжения узлов ЭС относительно номинальных значений как правило не превышают нескольких процентов, а углы по линиям в обычных режимах довольно малы [3]. В случае отсутствия более точной оценки в качестве начального приближения напряжений узлов задаются номинальные значения, а фазовые углы узлов принимаются равными величине фазового угла базисного узла – так называемый “гладкий” (“плоский”) старт. Гладкий старт не всегда дает возможность получить решение, поэтому для оценки начального приближения были предложены так называемые “стартовые” алгоритмы [3]–[4]. В зависимости от ЭС “стартовые” алгоритмы не всегда помогают рассчитать УР, наоборот иногда инициируют расходимость итерационного процесса метода Ньютона, поэтому предпринимаются попытки разработки более надежных, но и более сложных и трудоемких методов расчета УР. Этому способствует тот факт, что быстродействие и объем требуемой памяти в большинстве ситуаций перестают быть критическими факторами, поскольку нивелируются современными возможностями компьютерной техники [5]. Определяющим показателем выступает надежность метода.

Целью статьи является исследование и разработка стартовых алгоритмов, повышающих надежность расчета УР методом Ньютона. В работе в качестве вычислительной модели метода Ньютона используется наиболее распространенная форма записи уравнений УР – в полярных координатах напряжения, которая позволяет эффективно учитывать особенности моделирования генераторных узлов. В секции II рассматриваются существующие алгоритмы оценки начального приближения переменных. В секции III представлены результаты вычислительных экспериментов по их применению в расчетах УР методом Ньютона. Анализ результатов и исследование условий сходимости метода Ньютона, приведенные в секции IV, позволили предложить и разработать в секции V стартовые алгоритмы, существенно повышающие надежность расчета УР методом Ньютона. Заключение представлено в секции VI. Для упрощения записи математических соотношений при представлении используется система относительных единиц.

СТАРТОВЫЕ АЛГОРИТМЫ

Важность оценки начального приближения переменных при расчете УР методом Ньютона была отмечена уже в работе [6], в которой впервые был представлен алгоритм расчета режима, а именно, решения уравнений УР (УУР) в форме баланса мощностей в полярной системе координат

где P, Q, V, δ – соответственно векторы активной и реактивной мощности, модуля и фазового угла напряжения в узлах, методом Ньютона с развитой технологией решения разреженной системы линеаризованных уравнений методом исключения Гаусса. Для оценки начального приближения переменных с ц-елью повышения надежности алгоритма выполнялась одна итерация метода “последовательных смещений” (method of successive displacements) [7, 8]. Метод последовательных смещений для расчета УР является разновидностью нелинейного метода Зейделя и использует уравнение узловых напряжений (УУН) ${{I}_{k}} = \sum\nolimits_m {{{Y}_{{km}}}{{U}_{m}}} $, где I_k, U_k, – комплекс тока и напряжения в узле k; Y_km – элемент матрицы узловых проводимостей, следующим образом. Очевидно в точке решения УУР величина тока для PQ-узлов должна отвечать выражению ${{P}_{k}} + j{{Q}_{k}} = {{U}_{k}}I_{k}^{*}.$ В итерационной схеме [8] корректировка напряжения выполняется последовательно по узлам, используя ранее полученные значения комплекса напряжения смежных узлов и соотношение причем при нахождении поправки членами второго порядка пренебрегают. Фактически это соответствует решению системы линеаризованных уравнений потокораспределения в прямоугольных координатах

Аналогичный подход реализуется для PV-узлов, только вместо линеаризованного уравнения баланса реактивной мощности в (4) используется линеаризованное уравнение невязки квадрата модуля напряжения .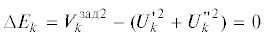

Согласно [1] начальное приближение переменных можно также оценить 1–2 итерациями метода Зейделя [9], в котором комплексы напряжения на итерации вычисляются последовательно по узлам, используя УУН в следующем виде:

где i – номер итерации или в альтернативной форме [2]

PV-узлы являются балансирующими по реактивной мощности, поэтому для них небаланс реактивной мощности обнуляют, т.е. принимают ${\Delta }Q_{k}^{i}$ = 0, а затем, используя (6), находят

Сравнение (6) с (3) показывает, что метод Зейделя (5)–(6) отличается от (4) только слагаемым $\Delta {{U}_{k}}I_{k}^{*}$ в (3). Скорость сходимости метода Зейделя существенно зависит от порядка нумерации узлов, наиболее эффективно нумеровать узлы, начиная от балансирующего. Выражения, аналогичные (5)–(7), реализуются также в методе Якоби (простой итерации), только в правой части (5) используются напряжения узлов, найденные на предыдущей итерации.

В [3] предложено для оценки начального приближения углов использовать так называемую модель постоянного тока

где H – матрица, получаемая при предположениях малости фазовых углов и единичных модулей напряжения в о.е. во всех узлах, пренебрежении шунтовыми элементами и активными сопротивлениями ветвей, отсутствия неноминальных коэффициентов трансформации, а оценку модулей напряжения находить решением системы линеаризованных уравнений баланса реактивных токов сформированной с учетом оценки углов (8). При этом утверждается, что (9) дает лучшее начальное приближение, чем система линеаризованных уравнений баланса реактивных мощностей

Дальнейшим развитием такого подхода явилась разработка разделенного, а впоследствии быстрого разделенного метода расчета потокораспределения (fast decoupled load flow, FDLF), который, согласно [10], “…в отличие от метода Ньютона не терпит неудачу ни на какой решаемой задаче”, и даже “…одна итерация в большинстве случаев дает адекватную оценку…” параметров режима. Это приводит к идее использования итерации быстрого разделенного метода для оценки начального приближения в методе Ньютона. С точки зрения современной терминологии, в [10] предложена так называемая XB модификация, в которой матрица для определения фазовых углов формируется только из индуктивных сопротивлений элементов сети, а другая матрица соответствует мнимой части подматрицы узловых проводимостей PQ-узлов. Исследования [11]–[12] показали, что в случае наличия ветвей с заметным отношением активного сопротивления к реактивному (r/x) более надежной является BX модификация. YY модификация быстрого разделенного метода, в котором матрицы формируются из полных проводимостей элементов сети, предложена в [13], где отмечается достаточно высокая надежность сходимости итерационной процедуры.

В [4] предложен стартовый алгоритм, в котором для ослабления влияния изменения фазовых углов на модули напряжения и наоборот используются модифицированные системы нелинейных уравнений:

причем ${{\Phi }_{k}}$ подбирается таким образом, чтобы минимизировать норму матрицы чувствительности $\left\| {{{\partial \delta } \mathord{\left/ {\vphantom {{\partial \delta } {\partial {\text{V}}}}} \right. \kern-0em} {\partial {\text{V}}}}} \right\|$, элементы которой определяются выражением ${{\partial {{\delta }_{k}}} \mathord{\left/ {\vphantom {{\partial {{\delta }_{k}}} {\partial {{V}_{m}}}}} \right. \kern-0em} {\partial {{V}_{m}}}} = - \frac{{{{\partial {{f}_{{\delta k}}}} \mathord{\left/ {\vphantom {{\partial {{f}_{{\delta k}}}} {\partial {{V}_{m}}}}} \right. \kern-0em} {\partial {{V}_{m}}}}}}{{{{\partial {{f}_{{\delta k}}}} \mathord{\left/ {\vphantom {{\partial {{f}_{{\delta k}}}} {\partial {{\delta }_{k}}}}} \right. \kern-0em} {\partial {{\delta }_{k}}}}}}$. Аналогичные требования минимизации нормы матрицы чувствительности $\left\| {{{\partial {\text{V}}} \mathord{\left/ {\vphantom {{\partial {\text{V}}} {\partial \delta }}} \right. \kern-0em} {\partial \delta }}} \right\|$ предъявляются для ${{\Theta }_{k}}$ при использовании (12). Разработчикам удалось получить аналитическое решение ${{\Phi }_{k}} = {\text{arctg}}({{{{G}_{{kk}}}} \mathord{\left/ {\vphantom {{{{G}_{{kk}}}} {{{B}_{{kk}}}}}} \right. \kern-0em} {{{B}_{{kk}}}}})$, ${{\Theta }_{k}} = - {\text{arctg(}}{{{{G}_{{kk}}}} \mathord{\left/ {\vphantom {{{{G}_{{kk}}}} {{{B}_{{kk}}}}}} \right. \kern-0em} {{{B}_{{kk}}}}})$ только для гладкого старта при отсутствии шунтов и несущественной неоднородности сети.

ТЕСТИРОВАНИЕ СТАРТОВЫХ АЛГОРИТМОВ

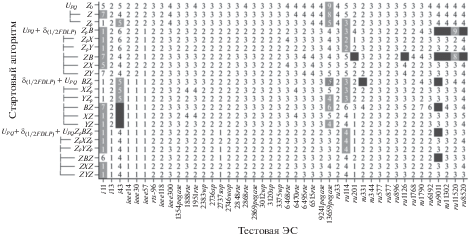
Результаты вычислительных экспериментов по расчету УР ЭС методом Ньютона с использованием описанных стартовых алгоритмов, реализованных на С++ в научно-исследовательском программном комплексе [18], представлены на рис. 1, где ячейка белого цвета отвечает успешному, а темного – неуспешному расчету режима. В качестве вычислительной модели для метода Ньютона использовались УУР в форме баланса мощностей в полярной системе координат. Ограничения по реактивной мощности генераторов не учитывались, поскольку, если расчет режима расходится без учета ограничений, он тем более не сходится при их учете. Ячейки рис. 1 содержат количество итераций, требуемых методом Ньютона для расчета УР с максимальным небалансом мощности в узлах не более 0.1 МВт/МВар с начальных приближений, полученных стартовыми алгоритмами. Светлая цифра на затемненном фоне указывает, что решением получен статически неустойчивый УР (“второе, низкое” решение), наклонный шрифт показывает, что в точке полученного решения в ряде узлов углы оказались больше 360°.

Тестирование проводилась на 44 ЭС. Число в их обозначении на рис. 1 показывает количество узлов в ЭС, за исключением 73-узловой rts-96. Префикс “i” в обозначении (i11 … i44) указывает на так называемые “плохо обусловленные” системы [14], довольно часто используемые зарубежными исследователями для демонстрации надежности предлагаемых методов. Схемы с префиксом “ieee” (ieee14… ieee300), а также rts-96 – это стандартные IEEE тестовые ЭС [15]. Схемы без префикса (1354pegase … 13659pegase) – это ЭС из библиотеки свободно распространяемого программного комплекса Matpower 6.0b1 в редакции 01.06.2016 [16]. Схемы с префиксом “ru” (ru33 … ru18520) – это схемы ЭС, ОЭС и ЕЭС России. Схема ru33 [17] в 70–80-х годах прошлого века использовалась ЦДУ ЕЭС СССР в качестве тестовой. Гистограмма вверху рис. 1 показывает коэффициенты запаса статической устойчивости УР в % для каждой ЭС, рассчитанные методом нелинейного программирования поиска предельного режима ЭС [18]–[19] в заданном направлении утяжеления – увеличения нагрузки и генерации во всех узлах прямо пропорционально исходным значениям мощностей узлов.

На рисунке 1 в условных обозначениях протестированных стартовых алгоритмов цифра перед “ит” указывает на количество выполненных итераций, а число в круглых скобках – на используемые расчетные формулы. Двухсимвольное обозначение в алгоритмах FDLF соответствует используемой модификации быстрого разделенного метода (одна полная итерация), в то время как трехсимвольное обозначение отражает тип полуитерации.

Анализ представленных результатов тестирования показывает, что стартовые алгоритмы могут как улучшить надежность и сходимость метода Ньютона, так и привести к обратному эффекту. Ни один стартовый алгоритм не обеспечил расчет УР методом Ньютона всех представленных ЭС. Для зарубежных тестовых ЭС наиболее подходящими показали себя BX и BY модификации быстрого разделенного метода, а также выполнение одной или двух итераций метода последовательных смещений (Ward) или метода Зейделя, хотя в работе [3] утверждается, что использование одной итерации метода Зейделя при расчете хорошо обусловленных систем улучшает сходимость метода Ньютона незначительно, а в сложных случаях немедленно инициирует его расходимость. Для российских ЭС наиболее подходящим оказалось применение одной, двух или трех итераций метода последовательных смещений или метода Зейделя. Интересно отметить, что результаты применения метода последовательных смещений и метода Зейделя почти полностью идентичны как для зарубежных, так и для российских ЭС. При этом, если для одной ЭС требуется только одна итерация, а при двух или трех итерациях метод Ньютона расходится, расчет другой ЭС требует именно две итерации, следующей – только три итерации, и т.д. Практика расчетов УР ЭС показывает [1], что в большинстве случаев метод Зейделя не сходится при наличии в сети отрицательных сопротивлений. В программном комплексе RastrWin [20] оценка начального приближения методом Зейделя реализуется с временной заменой отрицательных сопротивлений малыми положительными величинами (≈10^–3 о.е.), представлением нагрузки шунтом и использованием нумерации узлов от балансирующего. Из опыта эксплуатации RastrWin выявлено два основных класса ЭС. В первом из них достаточны 2–4 такие итерации метода Зейделя, при этом дальнейшее увеличение числа итераций приводит к ухудшению сходимости или расходимости метода Ньютона. Для второго класса ЭС все наоборот – прекрасная сходимость метода Ньютона обеспечивается после 14–16 итераций метода Зейделя, а уменьшение числа итераций Зейделя приводит к потере сходимости метода Ньютона.

Таким образом, к настоящему времени не существует стартового алгоритма, гарантирующего расчет УР методом Ньютона. Конечно, для конкретной ЭС можно подобрать адекватный стартовый алгоритм, или “подкорректировать” схему замещения. В крайнем случае опытный расчетчик всегда может рассчитать режим, временно назначая несколько балансирующих узлов, переводя некоторые PQ в PV-узлы, представляя нагрузки шунтами и т.д. [3], поэтому неудивительно, что постоянно появляются публикации, предлагающие более “надежные”, по мнению разработчиков, методы, чем метод Ньютона.

АНАЛИЗ УСЛОВИЙ СХОДИМОСТИ МЕТОДА НЬЮТОНА

Из анализа существующей литературы, затрагивающей применение стартовых алгоритмов, складывается впечатление, что предложенные стартовые алгоритмы являются результатами расчетной практики разработчиков, дополненные простыми и поэтому кажущимися верными предположениями. Но что означает хорошее начальное приближение переменных? Очевидно, когда метод Ньютона сходится к желаемому решению, т.е. когда начальное приближение находится в области сходимости метода Ньютона к этому решению.

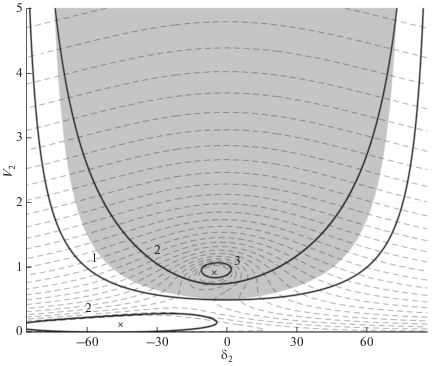
В качестве примера на рис. 2 представлена область сходимости метода Ньютона к решению двухузловой ЭС [21] с параметрами в о.е.: V₁ = 1, P₂ + jQ₂ = 0.9 + j0.6, Z₁₂ = = 0.01 + j0.1. Область сходимости получена многократными расчетами режима со всевозможных начальных значений переменных; крестиками отмечены два возможных решения для исходных данных. Кривая 1 идентифицирует точки вырожденности матрицы Якоби УУР, штриховые линии визуализируют линии равного уровня функции суммы квадратов небалансов мощности узла 2, в то время как линии 2 ограничивают области, в которых гессиан этой функции положительно определен. Как видно, метод Ньютона сходится к статически устойчивому режиму из любой точки, лежащей в области, где функция суммы квадратов небалансов мощности является выпуклой или слабо невыпуклой в ближайшей ее окрестности. Применение различных обобщений метода Ньютона [22, 23], корректирующих величину шага и при необходимости направление, позволяет расширить область его сходимости вплоть до линии 1 вырожденности матрицы Якоби.

В случае “реальных” ЭС геометрия области сходимости намного сложнее, а ее визуализация невозможна, но имеется ряд теорем о методе Ньютона. Согласно теореме Л.В. Канторовича [24] последовательность приближения процесса Ньютона сходится к решению системы нелинейных уравнений $\Delta F{\text{(}}X{\text{)}} = {\text{0}}$, если в точке начального приближения X₀ выполняются условия ${{h}_{0}} = {{B}_{0}}{{\eta }_{0}}K \leqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, $\left\| {{{{\left[ {{{\partial \Delta F({{X}_{0}})} \mathord{\left/ {\vphantom {{\partial \Delta F({{X}_{0}})} {\partial X}}} \right. \kern-0em} {\partial X}}} \right]}}^{{ - 1}}}} \right\| \leqslant {{B}_{0}}$, $\left\| {{{{\left[ {{{\partial \Delta F({{X}_{0}})} \mathord{\left/ {\vphantom {{\partial \Delta F({{X}_{0}})} {\partial X}}} \right. \kern-0em} {\partial X}}} \right]}}^{{ - 1}}}\Delta F({{X}_{0}})} \right\| \leqslant {{\eta }_{0}}$ и $\left\| {{{{{\partial }^{2}}\Delta F(X)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}\Delta F(X)} {\partial {{X}^{2}}}}} \right. \kern-0em} {\partial {{X}^{2}}}}} \right\| \leqslant K$ для любого X в окрестности $\left\| {X - {{X}_{{\text{0}}}}} \right\| \leqslant \frac{{1 - \sqrt {1 - 2{{h}_{0}}} }}{{{{h}_{0}}}}{{\eta }_{0}}$. Однако эта оценка, как и оценки области сходимости, устанавливаемые в теоремах других авторов, например, [25]–[27], рассчитаны на худший случай, т.е. отражают насколько далеко распространяется область квадратичной сходимости в направлении, в котором система УУР “более всего нелинейна” [27]. С другой стороны, в тех направлениях, в которых УУР “менее нелинейны”, область сходимости метода Ньютона простирается намного дальше [27]. Это один из случаев “платы” за использование интервалов и норм в математическом анализе. В качестве иллюстрации сказанного на рис. 2 показана область сходимости метода Ньютона, рассчитанная по условиям теоремы Л.В. Канторовича (кривая 3). Кроме этого, как отмечено в [27], использование подобных условий для проверки начального приближения переменных весьма проблематично. На практике оценка адекватных констант, например h₀, всегда требует больше труда, чем просто расчет режима методом Ньютона с целью установления факта его сходимости.

Более глубокий анализ результатов тестирования, представленных на рис. 1, показал, что во всех случаях метод Ньютона не смог рассчитать УР только тогда, когда число положительных и отрицательных ведущих элементов треугольного разложения матрицы Якоби в точке начального приближения в точности не соответствовало их числу в точке решения. Согласно теории матриц произведение ведущих элементов треугольного разложения отвечает величине ее определителя, который в свою очередь равен произведению собственных значений матрицы. Согласно теории линейной алгебры собственные значения непрерывно зависят от элементов матрицы. Используя закон инерции Сильверста [28], можно показать, что число положительных и отрицательных собственных значений симметричной матрицы равно соответственно количеству положительных и отрицательных ведущих элементов ее треугольного разложения. Для несимметричных матриц можно предположить, что несовпадение числа положительных и отрицательных ведущих элементов треугольных разложений матриц Якоби в точке начального приближения и в точке решения свидетельствует о несовпадении такого числа вещественных собственных значений соответствующих матриц. Возникает проблема задания начального приближения переменных, чтобы обеспечить такое соответствие, а полученное решение отвечало статически устойчивому УР ЭС.

ПРЕДЛАГАЕМЫЕ СТАРТОВЫЕ АЛГОРИТМЫ

Из-за сложности математических моделей в теории и практике расчета и анализа статической устойчивости ЭС обычно используют подход, предложенный П.С. Ждановым, т.е. полагают, что исходный режим статически устойчивый, затем утяжеляют его до тех пор, пока критерий статической устойчивости не изменит свой знак [29]–[30]. Матрица Якоби УУР является составной частью матрицы уравнений малых колебаний, и при определенных условиях определители этих матриц могут одновременно изменять свой знак, т.е. знак Якобиана УУР может дать информацию о статической устойчивости исследуемого режима [31]–[32]. Очевидно, режим холостого хода (ХХ) ЭС является статически устойчивым УР и, учитывая вышеизложенное, вызывает интерес использовать его как начальное приближение переменных для расчета УР.

Для PV-узлов модули напряжения, поддерживаемые системой АРВ, известны. С другой стороны, углы по линиям в режиме ХХ очень малы, поскольку вызваны только потерями ХХ. Принимая фазовые углы в PV узлах как в балансирующем узле (Vδ), т.е. ${{U}_{{PV + V\delta }}} = {{V}_{{PV + V\delta }}} + j0$, и используя УУН

с I = 0 для PQ-узлов, их комплексы напряжений ХХ можно оценить решением системы линейных уравнений (СЛУ) где $\left[ {{{Y}_{{PQ,PQ}}}} \right]$ – квадратная подматрица PQ узлов матрицы узловых проводимостей.

Результаты применения параметров режима ХХ (14) в качестве начального приближения переменных (Z₀-оценка) представлены на рис. 3, из которого видно, что метод Ньютона смог, наконец, рассчитать УР всех представленных ЭС.

Если УУН для PQ узлов представить в виде

их решение можно рассматривать как сумму двух слагаемых – напряжения ХХ (14) и изменения, вызванного токами нагрузки. В этом случае действие PV узлов аналогично балансирующему узлу, и нагрузка распределится между всеми этими узлами в зависимости от близости расположения. В свою очередь, если к правой части (15) прибавить и вычесть левую часть, то решение не изменится, но может быть представлено в виде [2] где $\Delta U_{{PQ}}^{i}$ находится решением СЛУ $\Delta I_{{PQ}}^{i}$ – вектор небалансов токов в PQ-узлах. При отсутствии в ЭС PV узлов такая запись соответствует методу Z-матрицы. С учетом сказанного вызывает интерес использовать решение (15) или (16)–(17) в качестве начального приближения переменных (Z-оценка). Результаты, представленные на рис. 3, показывают, что и в этом случае метод Ньютона также смог рассчитать режимы всех ЭС.

Довольно часто при проведении расчетов динамической устойчивости с использованием системы нелинейных уравнений (15) нагрузку представляют “шунтами”, аргументируя тем, что при новых значениях углов в генераторных узлах углы в нагрузочных узлах неизвестны. В этом случае получаемое решение соответствует СЛУ

где D – диагональная матрица проводимостей с элементами ${{D}_{{kk}}} = {{{{P}_{k}}} \mathord{\left/ {\vphantom {{{{P}_{k}}} {V_{k}^{2}}}} \right. \kern-0em} {V_{k}^{2}}} - {{j{{Q}_{k}}} \mathord{\left/ {\vphantom {{j{{Q}_{k}}} {V_{k}^{2}}}} \right. \kern-0em} {V_{k}^{2}}}$, $k \in PQ$. Если к правой части (18) прибавить и отнять ее левую часть, то можно показать, что ее решение также можно представить как (16), но $\Delta U_{{PQ}}^{i}$ отвечает СЛУ

Результаты использования решения (18) в качестве начального приближения переменных (Z_p-оценка) для расчета УР методом Ньютона также представлены на рис. 3.

Таким образом использование в качестве начального приближения параметров режима ХХ (14), так же как (15) или (18), позволили методу Ньютона рассчитать УР всех ЭС. Однако для некоторых ЭС полученное решение соответствовало статически неустойчивому режиму. Рассмотрим такие случаи подробно.

Согласно рис. 3 такие режимы получились для ЭС с очень малыми коэффициентами запаса статической устойчивости (см. рис. 1). 11-узловая i11 ЭС вообще имеет отрицательную величину коэффициента запаса. Точнее говоря эта ЭС при заданных исходных данных не имеет решения – УР считается с погрешностью 0.1 МВт/МВар и расходится при задании погрешности 0.01 МВт/МВар. В [22] это объясняется неточностью заданной исходной информации – всего 3 значащие десятичные цифры. Параметры полученного статически неустойчивого режима i11 ЭС практически не отличаются от параметров статически устойчивого режима, и только смена знака Якобиана позволила идентифицировать такой режим.

Другие i43 и ru114 ЭС имеют хотя положительный, но очень малый коэффициент запаса, и параметры статически неустойчивых режимов очень близки к параметрам соответствующих устойчивых УР.

Отдельный случай – 13659pegase ЭС из библиотеки Matpower [16]. В этой ЭС балансирующим узлом является генераторный узел небольшой мощности, слабо связанный с остальной ЭС. Хотя заданные суммарная нагрузка и генерация ЭС примерно соответствуют друг другу, но из-за особенностей представленной схемы замещения (много ветвей с отрицательным активным сопротивлением) на первой итерации возникает большой суммарный небаланс мощности, который приводит к существенному изменению угла по линии, отходящей от балансирующего узла. При использовании гладкого старта этот угол проворачивается несколько периодов и хорошо, что при таких больших углах попадает в область сходимости к статически устойчивому решению. На рисунке 1 это указано наклонным светлым шрифтом на сером фоне. В случае использования (14)–(19) на первой итерации метода Ньютона изменение этого угла также большое, но итерационный процесс перескакивает в область сходимости к статически неустойчивому решению. Поэтому вызывает интерес использование дополнительного механизма для оценки начального приближения углов.

На рисунке 3 представлены результаты применения двухшаговых стартовых алгоритмов “U_PQ + δ_(1/2FDLF)”, когда после решения СЛУ (15) или (18) выполняется полуитерация для углов быстрого разделенного метода соответствующей модификации. Как видно, это позволило получить решением статически устойчивый УР 13659pegase ЭС, причем с обычными углами. Более надежными оказались X и Y модификации быстрого разделенного метода.

В быстром разделенном методе на итерации сначала определяются изменения углов, а затем модулей напряжения. В то же время при проведении расчетов двухшаговыми стартовыми алгоритмами используется обратный порядок. Для сравнения на рис. 3 представлены также результаты тестирования при реализации в этих алгоритмах последовательности, аналогично разделенному методу “δ_(1/2FDLF)+ U_PQ”, которые показывают, что такая реализация дает менее надежные результаты.

Наконец на рис. 3 приведены результаты применения трехшаговых стартовых алгоритмов “U_PQ + δ_(1/2FDLF)+ U_PQ”, реализующих следующую последовательность: 1) решение СЛУ (18) или (15); 2) полуитерация для углов быстрого разделенного метода соответствующей модификации; 3) решение СЛУ (18) или (15).

В настоящее время расчеты УР используется в различных системах реального времени, например, в системе мониторинга запасов устойчивости, в которой для определения максимально допустимых перетоков по контролируемым сечениям осуществляется множество расчетов утяжеленных УР для различных аварийных ситуаций и с моделированием действий противоаварийной автоматики [33]. Такие расчеты осуществляются в реальном времени в автоматическом режиме и должны обладать максимальной надежностью, и в тоже время к ним предъявляются очень высокие требования по быстродействию и объему оперативной памяти. Все такие расчеты выполняются с известного, как правило, достаточно хорошего начального приближения, поэтому использование “плоского” старта для стартового алгоритма существенно снижает быстродействие. Но несмотря на наличие хорошего начального приближения, метод Ньютона может привести к расходимости итерационного процесса из-за ошибки в задании начального угла напряжения при отключении (или включении) узла или ветви ЭС. Ошибка в задании угла напряжения даже в одном узле может привести к расходимости метода Ньютона на первой итерации, несмотря на отсутствие небалансов в остальных узлах ЭС. Стартовый алгоритм в такой ситуации должен использовать преимущества хорошего начального приближения и в то же время устранять грубые ошибки в отдельных узлах. Этому в наибольшей степени соответствует предложенный трехшаговый стартовый алгоритм оценки начального приближения переменных.

ЗАКЛЮЧЕНИЕ

Рассмотрены существующие стартовые алгоритмы оценки начального приближения переменных расчета УР методом Ньютона. Представленные результаты тестирования на зарубежных и российских ЭС подтвердили, что существующие стартовые алгоритмы обеспечивают расчет УР методом Ньютона не для всех ЭС. Исследование условий сходимости метода Ньютона и анализ результатов вычислительных экспериментов позволили сформулировать главное требование к оценке начального приближения переменных для решения УУР методом Ньютона – начальное приближение должно отвечать параметрам статически устойчивого режима ЭС. В этом случае метод Ньютона является очень надежным методом расчета УР ЭС, в том числе тяжелых режимов, причем небалансы мощности в узлах при таком начальном приближении могут быть довольно большими. Оказалось неожиданным, что плоский старт для ряда ЭС не отвечает параметрам статически устойчивых режимов, что не позволяет методом Ньютона с этого начального приближения рассчитать даже “легкие” УР этих ЭС, включая режим “холостого хода”. Адекватность применения стартовых алгоритмов состоит именно в обеспечении “статически устойчивого” начального приближения переменных, а существующие стартовые алгоритмы этого не гарантируют. В работе предложено в качестве стартовых алгоритмов оценки начального приближения переменных использовать решение системы линейных уравнений узловых напряжений без нагрузки или с нагрузкой, модулируемой токами или шунтовыми проводимостями. Вычислительные эксперименты показали, что предложенные стартовые алгоритмы оценки начального приближения переменных обеспечили расчет УР методом Ньютона всех тестируемых ЭС, также как уменьшили число итераций.